Abstract
The purpose of this article is to achieve new soliton solutions of the Gilson–Pickering equation (GPE) with the assistance of Sardar’s subequation method (SSM) and Jacobi elliptic function method (JEFM). The applications of the GPE is wider because we study some valuable and vital equations such as Fornberg–Whitham equation (FWE), Rosenau–Hyman equation (RHE) and Fuchssteiner–Fokas–Camassa–Holm equation (FFCHE) obtained by particular choices of parameters involved in the GPE. Many techniques are available to convert PDEs into ODEs for extracting wave solutions. Most of these techniques are a case of symmetry reduction, known as nonclassical symmetry. In our work, this approach is used to convert a PDE to an ODE and obtain the exact solutions of the NLPDE. The solutions obtained are unique, remarkable, and significant for readers. Mathematica 11 software is used to derive the solutions of the presented model. Moreover, the diagrams of the acquired solutions for distinct values of parameters were demonstrated in two and three dimensions along with contour plots.
1. Introduction
In recent decades, mathematicians and physicists have shown their interest in the field of nonlinear evolution equations (NLEEs) due to their wide applications in every field of science [,,,,]. NLEEs have symmetries in different ways. Vinogradov presented four different ideas to study symmetries in nonlinear PDEs []. Researchers are referred to these papers to understand symmetry, its different definitions and applications on PDEs, etc. [,,,,,]. NLEEs have uncountable applications in daily life, which is the main reason for mathematicians, engineers, and physicists to study NLEEs. The significance of NLEEs has been increasing in diverse science fields such as optics, plasma physics, mechanical and electromagnetic waves, wave theory, mechanics, fluid dynamics, nonlinear optics, fibers, optical fibers, etc. Many important NLEEs describing the above stated fields are not easy to solve. Therefore, we need different and new techniques to solve such kinds of NLEEs. For this aspect, researchers have developed different, unique, and powerful techniques to solve NLEEs, which include the modified simple equation technique [,,], the variational iteration method [,], the variational method [], the first integral method [], the perturbation method [], method of integrability [], the nonperturbative technique [], the modified F-expansion method [,,], the exp-function method [,], the sine–cosine method [,,], the Riccatti–Bernoulli sub-ODE method [,], the Jacobi elliptic function method [,], the generalized Kudryashov method [,], the functional variable method [,], the modified Khater method [,], the new extended direct algebraic method [,], the Lie symmetry technique [,], the -expansion method [], the tanh–coth method [,], the new auxiliary equation method [,], the -expansion method [], the technique of [], the addendum to Kudryashov’s method [], and many others [,,,,,].
Here, the third-order nonlinear GPE [,] is solved, and we find possible exact solutions with the help of Sardar’s subequation method (SSM) [,,,], the Jacobi elliptic function method (JEFM) [,], and the generalized derivative technique []. The GPE can be written as
The parameters , k, , and are arbitrary constants. When we choose particular values for the parameters, such as , , and , then Equation (1) becomes an FWE [,]
For substituting the values , , and in Equation (1), then the RHE [] is obtained.
For choosing the values , and in Equation (1), then the GPE converts into an FFCHE [,]
This paper is presented in the following manner: A brief discussion about the SSM is presented in Section 2. Section 3 and Section 4 illustrate the solutions of the GPE using the SSM and JEFM, respectively. The fifth section is devoted to the result and discussion. The last section consists of a conclusion.
2. Sardar’s Subequation Method (SSM)
In this section, we discuss briefly the SSM in the following steps:
Step 1: Suppose the NLEE
Utilizing the following wave transformation
Equation (4) changes in the following nonlinear ODE
Step 2: Consider a solution of Equation (6) as
, ( 0, 1, …,s) are constants, and is the solution of the following equation:
where a and are unknown parameters. Equation (8) provides solutions of the form:
Case I: If and then
where , .
Case II: If and then
where , .
Case III: If and then
where , .
Case IV: If a > 0 and then
where ,
The process starts by extracting s with the support of the balancing rule. When s is collected, the predicted solution in Equation (7) is substituted into Equation (6). To obtain a nonzero solution (), every coefficient of the same power of are equated to zero. Then, the resulting system of the algebraic equations is solved to obtain the values of unknown parameters, especially and V.
3. Implementation of the Method
Substituting Equation (5) into Equation (1) and after simplification, we obtain
Integrating with respect to once implies
where C is the integration constant.
For finding the value s, we use balancing principle on Equation (10), and get .
From Equation (7), we have
where , , and are arbitrary constants.
Substituting Equation (11) and Equation (8) in Equation (10), we get all the terms having the same power of . Setting these polynomials equal to zero, we obtain
From Equations (10)–(12), we evaluate the following solutions:
Case I: If and then
Case II: If and then
Case III: If and , then
Case IV: If a > 0 and , then
4. Implementation of Jacobi Elliptic Function Method Depending on
To find out the solutions of Equation (10), the JEFM is utilized [,]. As a consequence, we are capable of acquiring the solutions of Equation (1).
Suppose the solution of Equation (10) has the form
where F satisfies the following ODE
where r, q, and p are parameters. Equation (28) has different solutions depending upon the values of r, q, and p.
, , , and are Jacobi elliptic functions (JEFs). When , then the JEFs are changed to the following hyperbolic functions:
After applying the balancing principle, we obtain the solution of Equation (7) as
where , , and are arbitrary constants.
Substituting Equation (30) and Equation (28) into Equation (10), we obtain the system of equations in the powers of . By taking each coefficient of equal to zero, the following system of equations is obtained
Solving system (31) for the involved constants, we get
Hence, the solution in Equation (30) becomes
The solutions for Equation (28) are given in Table 1.

Table 1.
All the solutions of .

Table 2.
All the solutions of when .
F can be collected from the last column of Table 2.
Case I: For , , and , we have
Case II: For , , and , we have
Case III: For , , and , we have
5. Results and Discussion
A graphical representation plays a fundamental role in the article because graphs show the physical activities of solutions. Here, we explore the behavior and physical interpretation of the solutions of the Gilson–Pickering equation that we have obtained with the assistance of the SSM and JEFM. It is noted that the results provided in [] have only the form of a periodic singular soliton, bright soliton, and shock waves. In the present method, we give the solutions in form of dark, singular, bright, periodic singular, dark–bright-combined and dark–singular-combined solitons. Using the SSM, the solutions and provide the bright and dark solitons, respectively. , , , , , , and illustrate the singular solitons while , , and represent periodic singular solitons. Dark–bright-combined, dark–singular-combined solitons are elaborated by and , respectively. The solutions , , and obtained by the JEFM provide dark, singular, and bright solitons, respectively. We depict 2D, 3D, and contour plots of some of the obtained solutions with the appropriate values of constants obtained by the SSM and JEFM. We can say that graphs are nonlinear data structures that illustrate the properties and behavior which actually demonstrate the solutions.
The graphs in Figure 1 and Figure 2 show a singular soliton and a dark–bright soliton, respectively, obtained by the SSM. Moreover, some solutions acquired from the JEFM are plotted in Figure 3, Figure 4 and Figure 5, representing the dark, singular, and bright solutions. Maple 18 software was used to draw these graphs.
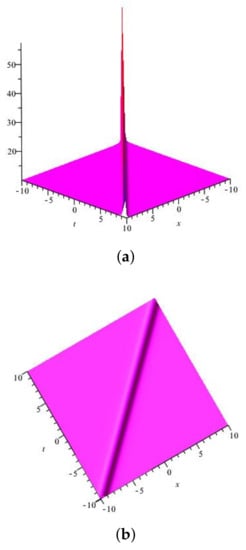
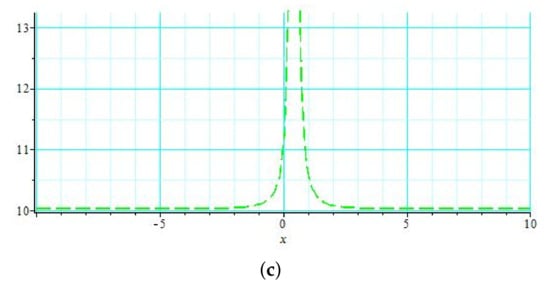
Figure 1.
(a) Three-dimensional graph for and ; (b) contour graph for and ; (c) 2D graph for and .
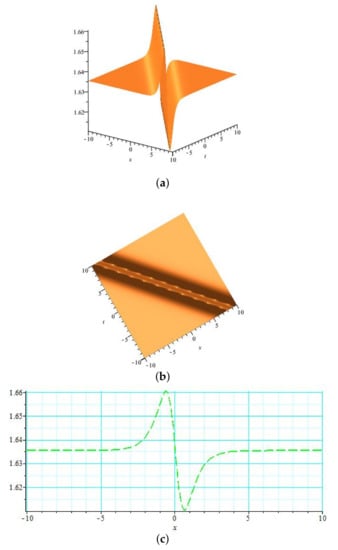
Figure 2.
(a) Three-dimensional graph and ; (b) contour graph for and ; (c) 2D graph for and .
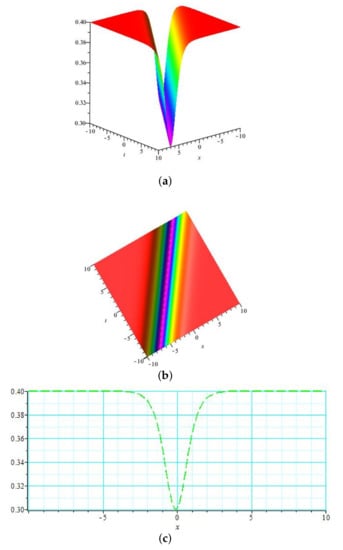
Figure 3.
(a) Three-dimensional graph and ; (b) contour graph for and ; (c) 2D graph for and .
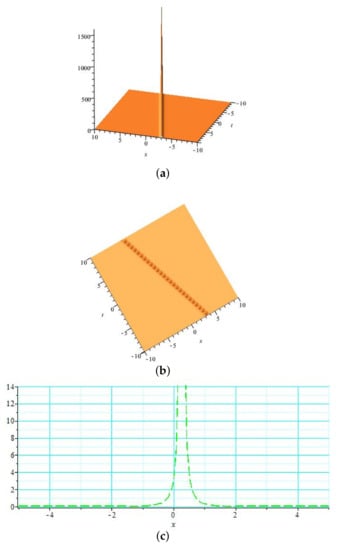
Figure 4.
(a) Three-dimensional graph and ; (b) contour graph for and ; (c) 2D graph for and .
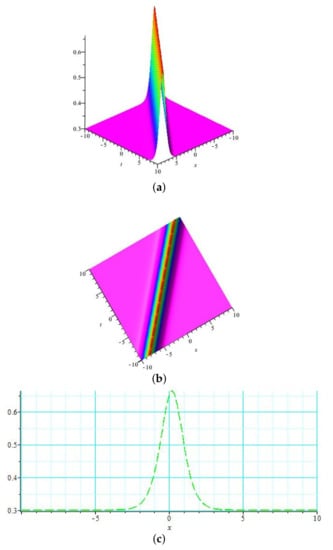
Figure 5.
(a) Three-dimensional graph and ; (b) contour graph for and ; (c) 2D graph for and .
In Figure 1, the graph of is drawn for the values: , , , , , , , and , which demonstrates the shape of a singular soliton where (a) and (b) represent the 3D and contour graphs for , while (c) shows the 2D graph for with . The graph of presented in Figure 2 illustrates the combined dark–bright soliton for the values: , , , , , , , and , where (a) and (b) demonstrate the 3D and contour graphs for , while (c) depicts the 2D graph for with . Figure 3 represents the graph of for the values: , , , , , , and . It illustrates the shape of a dark soliton where (a) and (b) are the 3D and contour graphs for , while (c) is the 2D graph for with . The graph of solution provides the singular soliton for the values: , , , , , , and ; it is illustrated in Figure 4, where (a) and (b) represent the 3D and contour graphs for , respectively, while (c) depicts the 2D graph for with . The graph of for , , , , , , and is drawn in Figure 5, which elaborates the bright soliton, where (a) and (b) represent the 3D and contour graphs for , while (c) demonstrates the 2D graph for with .
6. Conclusions
In this paper, the SSM and JEFM were used effectively to investigate the behavior of the GPE, which has applications in different fields of applied sciences. The affluent families of solutions were explored in single and combined forms. These families of solutions in the single form were singular soliton, singular periodic soliton, dark soliton, and bright soliton, while in combined form, the combined bright–dark soliton and combined dark–singular solitons were obtained. Moreover, some rational solutions also occurred through derivation. The solutions obtained from the proposed methods were distinct, unique, fruitful, and had a specific physical structure. Graphical illustrations of some solutions were also presented in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. Mathematica 11 and Maple 18 were used to derive the solutions of the presented model and for plotting graphs, respectively. Finally, we can say that the Sardar’s subequation method and the Jacobi elliptic function method are helpful and powerful techniques for solving NLEEs.
Author Contributions
Conceptualization, Methodology and Supervision, H.U.R.; Formal analysis, A.U.A. and M.U.H.; Funding acquisition and Validation, E.M.T.-E.; Investigation, M.U.H.; Project administration and Visualization, A.U.A.; Resources and Software, S.A.A.; Writing—original draft, M.U.H.; Writing—review and editing, S.A.A. and H.U.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by grant code: 22UQU4330955DSR04. The author (H.U.R) would also like to thank the University of Okara for the grant no. UO/R/2021/6774.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdelrahman, M.A.; Kunik, M. The ultra-relativistic Euler equations. Math. Methods Appl. Sci. 2015, 38, 1247–1264. [Google Scholar] [CrossRef]
- Abdelrahman, M.A. Global solutions for the ultra-relativistic Euler equations. Nonlinear Anal. 2017, 155, 140–162. [Google Scholar] [CrossRef]
- Abdelrahman, M.A. On the shallow water equations. Zeitschrift fur Naturforschung A 2017, 72, 873–879. [Google Scholar] [CrossRef]
- Younis, M.; Ali, S.; Mahmood, S.A. Solitons for compound KdV Burgers equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. 2015, 81, 1191–1196. [Google Scholar] [CrossRef]
- Bhrawy, A.H. An efficient Jacobi pseudo spectral approximation for nonlinear complex generalized Zakharov system. Appl. Math. Comput. 2014, 247, 30–46. [Google Scholar]
- Vinogradov, A.M. What are symmetries of nonlinear PDEs and what are they themselves? arXiv 2013, arXiv:1308.5861. [Google Scholar]
- Aliyu, A.I.; Inc, M.; Yusuf, A.; Baleanu, D. Symmetry analysis, explicit solutions, and conservation laws of a sixth-order nonlinear ramani equation. Symmetry 2018, 10, 341. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science & Business Media: Berlin, Germany, 2018; Volume 107. [Google Scholar]
- Lou, S.Y.; Hu, X.; Chen, Y. Nonlocal symmetries related to Bcklund transformation and their applications. J. Phys. A Math. Theor. 2012, 45, 155209. [Google Scholar] [CrossRef]
- Buhe, E.; Bluman, G.W. Symmetry reductions, exact solutions, and conservation laws of the generalized Zakharov equations. J. Math. Phys. 2012, 56, 101501. [Google Scholar] [CrossRef]
- Gao, B. Symmetry analysis and explicit power series solutions of the Boussinesq Whitham Broer Kaup equation. Waves Random Complex Media 2017, 27, 700–710. [Google Scholar] [CrossRef]
- Feng, L.L.; Tian, S.F.; Zhang, T.T.; Zhou, J. Lie symmetries, conservation laws and analytical solutions for two-component integrable equations. Chin. J. Phys. 2017, 55, 996–1010. [Google Scholar] [CrossRef]
- Kayum, M.; Akbar, M.A.; Osman, M.S. Competent closed form soliton solutions to the nonlinear transmission and the low-pass electrical transmission lines. Eur. Phys. J. Plus 2020, 135, 1–20. [Google Scholar] [CrossRef]
- Kayum, M.A.; Ara, S.; Barman, H.K.; Akbar, M.A. Soliton solutions to voltage analysis in nonlinear electrical transmission lines and electric signals in telegraph lines. Results Phys. 2020, 18, 103269. [Google Scholar] [CrossRef]
- Kayum, M.A.; Seadawy, A.R.; Akbar, A.M.; Sugati, T.G. Stable solutions to the nonlinear RLC transmission line equation and the Sinh Poisson equation arising in mathematical physics. Open Phys. 2020, 18, 710–725. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Kaur, L. Optical solitons and Peregrine solitons for nonlinear Schrodinger equation by variational iteration method. Optik 2019, 179, 804–809. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonus, H.M.; Prakasha, D.G.; Kumar, P. A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos Solitons Fractals 2020, 138, 109929. [Google Scholar] [CrossRef]
- Seadawy, A.R. Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus 2015, 130, 1–10. [Google Scholar] [CrossRef]
- Kudryashov, N.A. First integrals and solutions of the traveling wave reduction for the Triki Biswas equation. Optik 2019, 185, 275–281. [Google Scholar] [CrossRef]
- He, J.H. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Feng, Y.Y. On integrability of the time fractional nonlinear heat conduction equation. J. Geom. Phys. 2019, 144, 190–198. [Google Scholar] [CrossRef]
- Momani, S. Non-perturbative analytical solutions of the space-and time-fractional Burgers equations. Chaos Solitons Fractals 2006, 28, 930–937. [Google Scholar] [CrossRef]
- Xue-Qin, Z.; Hong-Yan, Z. An improved F-expansion method and its application to coupled Drinfel’dr Sokolov Wilson equation. Commun. Theor. Phys. 2008, 50, 309. [Google Scholar] [CrossRef]
- Abdou, M.A. The extended F-expansion method and its application for a class of nonlinear evolution equations. Chaos Solitons Fractals 2007, 31, 95–104. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Akinyemi, L.; Elagan, S.K.; El-Shorbagy, M.A.; Alfalqi, S.H.; Alzaidi, J.F.; Alshehri, N.A. Bright dark soliton waves dynamics in pseudo spherical surfaces through the nonlinear kaup-Kupershmidt equation. Symmetry 2021, 13, 13060963. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. Traveling wave solutions of the (2+ 1)-dimensional Zoomeron equation and the Burgers equations via the MSE method and the Exp-function method. Ain Shams Eng. J. 2014, 5, 247–256. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-F(ϕ)) expansion method for finding travelling wave solutions of Vakhnenko Parkes equation. Int. J. Dyn. Syst. Differ. 2014, 5, 72–83. [Google Scholar]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The sine cosine method for obtaining solutions with compact and noncompact structures. Appl. Math. Comput. 2004, 159, 559–576. [Google Scholar] [CrossRef]
- Raza, N.; Aslam, M.R.; Rezazadeh, H. Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerr law media. Opt. Quantum Electron. 2019, 51, 1–12. [Google Scholar] [CrossRef]
- Albosaily, S.; Mohammed, W.W.; Aiyashi, M.A.; Abdelrahman, M.A. Exact solutions of the (2+ 1)-dimensional stochastic chiral nonlinear Schrodinger equation. Symmetry 2020, 12, 1874. [Google Scholar] [CrossRef]
- Abdelijabbar, A.; Roshid, H.-O.; Abdurayhim, A. Bright, Dark, and Rogue Wave soliton solutions of the quadratic nonlinear Klein-Gordon equation. Symmetry 2022, 14, 1223. [Google Scholar] [CrossRef]
- Raza, N.A. Bright, dark and dark-singular soliton solutions of nonlinear Schrodinger’s equation with spatio-temporal dispersion. J. Mod. Opt. 2018, 65, 1975–1982. [Google Scholar] [CrossRef]
- Qian, L.; Attia, R.A.; Qiu, Y.; Lu, D.; Khater, M.M. The shock peakon wave solutions of the general Degasperis-Procesi equation. Int. J. Mod. Physics B 2019, 33, 1950351. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. New exact solutions of the conformable space-time Sharma Tasso Olver equation using two reliable methods. Symmetry 2020, 12, 644. [Google Scholar] [CrossRef]
- Çenesiz, Y.; Tasbozan, O.; Kurt, A. Functional variable method for conformable fractional modified KdV-ZK equation and Maccari system. Tbil. Math. J. 2017, 10, 117–125. [Google Scholar] [CrossRef]
- Eslami, M.; Rezazadeh, H.; Rezazadeh, M.; Mosavi, S.S. Exact solutions to the space time fractional Schrodinger Hirota equation and the space time modified KDV Zakharov Kuznetsov equation. Opt. Quantum Electron. 2017, 49, 1–15. [Google Scholar] [CrossRef]
- Khater, M.; Park, C.; Lu, D.; Attia, R.A. Analytical, semi-analytical, and numerical solutions for the Cahn Allen equation. Adv. Differ. Equ. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Lu, D. Computational and numerical simulations for the nonlinear fractional Kolmogorov Petrovskii Piskunov (FKPP) equation. Phys. Scripta 2020, 95, 055213. [Google Scholar] [CrossRef]
- Tozar, A.; Kurt, A.; Tasbozan, O. New wave solutions of time fractional integrable dispersive wave equation arising in ocean engineering models. Kuwait J. Sci. 2020, 47, 22–33. [Google Scholar]
- Rezazadeh, H.; Mirhosseini-Alizamini, S.M.; Eslami, M.; Rezazadeh, M.; Mirzazadeh, M.; Abbagari, S. New optical solitons of nonlinear conformable fractional Schrodinger-Hirota equation. Optik 2018, 172, 545–553. [Google Scholar] [CrossRef]
- Rehman, H.U.; Ullah, N.; Imran, M.A.; Akgul, A. Optical solitons of two non-linear models in birefringent fibres using extended direct algebraic method. Int. J. Appl. Comput. Math. 2021, 7, 1–26. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K.; Baleanu, D.; Osman, M.S.; Wazwaz, A.-M. Lie symmetries, closed-form solutions, and various dynamical profiles of solitons for the variable coefficient (2+1)-Dimensional KP equations. Symmetry 2022, 14, 597. [Google Scholar] [CrossRef]
- Bruzon, M.S.; Garrido, T.M.; de la Rose, R. Symmetry analysis, Exact Solutions and conservation laws of a Benjamin-Bona-Mahony-Burgers equation in 2+1-Dimensions. Symmetry 2021, 13, 2083. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A.; Mohyud-Din, S.T. A novel (G’/G)-expansion method and its application to the Boussinesq equation. Chin. Phys. B 2013, 23, 020203. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh coth method for solitons and kink solutions for nonlinear parabolic equations. Appl. Math. Comput. 2007, 188, 1467–1475. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh coth method for new compactons and solitons solutions for the K (n, n) and the K (n+ 1, n+ 1) equations. Appl. Math. Comput. 2007, 188, 1930–1940. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X. A note on the auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2006, 348, 222–227. [Google Scholar] [CrossRef]
- Khater, M.M.; Seadawy, A.R.; Lu, D. Dispersive optical soliton solutions for higher order nonlinear Sasa-Satsuma equation in mono mode fibers via new auxiliary equation method. Superlattices Microstruct. 2018, 113, 346–358. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.S.; Akbar, M.A.; Seadawy, A.R. New applications of the two variable (G’/G, 1/G)-expansion method for closed form traveling wave solutions of integro-differential equations. J. Ocean. Eng. Sci. 2019, 4, 132–143. [Google Scholar] [CrossRef]
- Durur, H.; Ilhan, E.; Bulut, H. Novel complex wave solutions of the (2+ 1)-dimensional hyperbolic nonlinear Schrodinger equation. Fractal Fract. 2020, 4, 41. [Google Scholar] [CrossRef]
- Alotaibi, H. Travelling wave solutions to the nonlinear evoluation equation using expension and addendum to kudryashove’s method. Symmetry 2021, 13, 2126. [Google Scholar] [CrossRef]
- Ramzan, M.; Chu, Y.M.; ur Rehman, H.; Saleem, M.S.; Park, C. Soliton solutions for anti-cubic nonlinearity using three analytical approches. J. Appl. Anal. Comput. 2021, 11, 2177–2192. [Google Scholar]
- Awan, A.U.; Tahir, M.; Rehman, H.U. Singular and bright-singular combo optical solitons in birefringent fibers to the Biswas-Arshed equation. Optik 2020, 210, 164489. [Google Scholar] [CrossRef]
- Tahir, M.; Awan, A.U.; Rehman, H.U. Dark and singular optical solitons to the Biswas-Arshed model with Kerr and power law nonlinearity. Optik 2019, 185, 777–783. [Google Scholar] [CrossRef]
- Awan, A.U.; Tahir, M.; Rehman, H.U. On traveling wave solutions: The WuZhang system describing dispersive long waves. Mod. Phys. Lett. B 2019, 33, 1950059. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Abro, K.A.; El Din, E.M.T.; Jafar, S.; Galal, A.M. A non-linear study of optical solitons for Kaup-Newell equation without four-wave mixing. J. King-Saud Univ.-Sci. 2022, 34, 102056. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Habib, A.; Gamaoun, F.; El Din, E.M.T.; Galal, A.M. Solitary wave solutions for a strain wave equation in a microstructured solid. Results Phys. 2022, 39, 105755. [Google Scholar] [CrossRef]
- Gilson, C.; Pickering, A. Factorization and painlev analysics of a class of nonlinear third-order partial differential equations. J. Phys. A Math. Gen. 1995, 28, 2871. [Google Scholar] [CrossRef]
- Hadi, R.; Adil, J.; Eric, T.; Mir, S.H.; Sumaira, S.; Hijab, A.; Shao-wen, Y. New wave surfaces and bifurcation of nonlinear periodic waves for Gilson-Pickering equation. Results Phys. 2021, 24, 104192. [Google Scholar]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+ 1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Abazari, R.; Khater, M.M.; Baleanu, D. New optical solitons of conformable resonant nonlinear Schrodingers equation. Open Phys. 2020, 18, 761–769. [Google Scholar] [CrossRef]
- Rehman, H.U.; Seadawy, A.R.; Younis, M.; Yasin, S.; Raza, S.T.; Althobaiti, S. Monochromatic optical beam propagation of paraxial dynamical model in Kerr media. Results Phys. 2021, 31, 105015. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Allahyani, S.A.; Tag-ElDin, E.M.; Binyamin, M.A.; Yasin, S. Exact solution of paraxial wave dynamical model with Kerr Media by using ϕ6 model expansion technique. Results Phys. 2022, 42, 105975. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W. The analytical solutions of the stochastic fractional RKL equation via Jacobi elliptic function method. Adv. Math. Phys. 2022, 2022, 1534067. [Google Scholar] [CrossRef]
- Ali, M.N.; Husnine, S.M.; Saha, A.; Bhowmik, S.K.; Dhawan, S.; Ak, T. Exact solutions, conservation laws, bifurcation of nonlinear and supernonlinear traveling waves for Sharma Tasso Olver equation. Nonlinear Dyn. 2018, 94, 1791–1801. [Google Scholar] [CrossRef]
- Hyder, A.-A.; Barakat, M.A.; Soliman, A.H.; Almoneef, A.A.; Cesarano, C. New analytical solutions for coupled Stochastic korteweg-de Vries equation via Generalized Derivatives. Symmetry 2022, 14, 1770. [Google Scholar] [CrossRef]
- Ebadi, G.; Kara, A.H.; Petkovic, M.D.; Biswas, A. Soliton solutions and conservation laws of the Gilson Pickering equation. Waves Random Complex Media 2011, 21, 378–385. [Google Scholar] [CrossRef]
- Aslan, I. Exact and explicit solutions to nonlinear evolution equations using the division theorem. Appl. Math. Comput. 2011, 217, 8134–8139. [Google Scholar] [CrossRef]
- Zhang, Z.; Xia, F.L.; Li, X.P. Bifurcation analysis and the travelling wave solutions of the Klein Gordon Zakharov equations. Pramana 2013, 80, 41–59. [Google Scholar] [CrossRef]
- Aksoy, E.; Kaplan, M.; Bekir, A. Exponential rational function method for space time fractional differential equations. Waves Random Complex Media 2016, 26, 142–151. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).