Method of an Asymptotic Analysis of the Nonlinear Monotonic Stability of the Oscillation at the Problem of Damping of the Angle of Attack of a Symmetric Spacecraft

Abstract

One of the current directions in the development of the modern theory of oscillations is the elaboration of effective methods for analyzing the stability of solutions of dynamical systems. The aim of the work is to develop a new asymptotic method for studying the nonlinear monotonic stability of the amplitude of plane oscillations in a dynamic system of equations with one fast phase. The method is based on the use of the method of variation of an arbitrary constant, the averaging method, and the classical method of mathematical research of the function of one independent variable. It is assumed that the resulting approximate analytical function is defined and twice continuously differentiable on the entire considered interval of change of the independent variable. It describes the nonlinear and monotonic evolution of the oscillation amplitude on the entire considered interval of change of the independent variable. In the paper, this method is applied to the problem of nonlinear monotonic aerodynamic damping of the amplitude of oscillations of the angle of attack during the descent of a symmetric spacecraft in the atmosphere of Mars. The method presented in this paper made it possible to find all characteristic cases of nonlinear monotonic stability and instability of the oscillation amplitude of the angle of attack. In addition, one should speak of a symmetrical quantity of different cases of stability and instability, located on different sides of the zero value of the first average derivative of the angle of attack.

1. Introduction

In modern engineering, symmetrical designs and other types of dampers and absorbers are widespread. In particular, the article [1] considered the amplitude–frequency dependence of a nonlinear symmetrical panel absorber fixed on a flexible wall. In this study, a weighted residual elliptic integral method was applied to solve this problem, which includes the nonlinear multimode governing equations of two flexible panels, in combination with a cavity. The aim of the work [2] was to study the non-linear dynamics of a supporting symmetrical structure of pipeline supports, covered with a damping element using elastic-porous metal rubber. In this work, a dynamic model of a symmetrical pipeline system based on an impulse response matrix was created to reliably describe its non-linear behavior, for example, during energy dissipation.

Another well-known work [3] proposed a numerical method for predicting damping in gears with ring dampers. The nonlinear damping when friction is taken into account is expressed as equivalent mechanical damping as a function of vibration stress. In the work [4], the periodically distributed masses are supported on the plate by coupling springs and dampers. The study [5] was devoted to obtaining approximate solutions of the controlled mass-damper-spring model by the harmonic balance method. The stability of the solutions was tested using the Floquet theory.

The study [6] proposed a negative-speed cubic feedback controller to suppress non-trivial subharmonic resonance oscillations of the 1:3 order of the mass-damper-spring system. Based on the averaging method, the equation of motion of the system was approximately solved and its stability was checked. In the paper [7], the primary structure and the damper were proposed for consideration as an analytical and an experimental substructure, respectively. The general approach is to model the analytical substructure using the finite element method. In addition, the effects on the frame structure of a fluid damper, a particle damper, and a particle-tuned mass damper were virtually explored. In [8], a new model of double friction between a shaft and a dry friction damper with several stages of helicopter tail rotors was proposed. The dynamics of multiple vibration suppression, as well as static and dynamic misalignment, were studied to illustrate the accuracy of the results obtained using the model.

The paper [9] proposed an adaptive landing system for a reusable launch vehicle with semi-active control units. The landing system under consideration can adjust the damping forces of the shock absorbers of the struts by means of semi-actively adjustable currents according to practical landing conditions.

The article [10] demonstrated an innovative approach to planning the trajectories of mechanical systems using time-reversal symmetry. Two case studies were also presented: a mass-spring-damper pendulum and an inverted pendulum on a bogie. The proposed solution makes it possible to compensate for the influence of relationships that violate temporal symmetry using a special proposed measure.

The paper [11] analyzed the entropy of the mechanical system mass-spring-damper in accordance with the definition of a consonant fractional operator. The authors determined the optimal values of the parameters of the mechanical system to obtain the highest response efficiency.

The work [12] proposed an equivalent method for numerically predicting the damping of an annular damper under axial vibration in the aircraft gas turbine engines. Using the method, the significant influence of the design parameters of the annular damper on the frictional damping in gears under axial vibration was studied.

In the process of modeling and studying the laws of functioning of dampers and absorbers, various methods are used to analyze the stability of solutions of the differential equations. It is known that the modern theory of differential equations contains the concepts of strong and weak stability of solutions. The introduction of these concepts makes it possible to effectively classify various types of stability of solutions. Moreover, when solving some types of equations in mathematical physics, the concepts of strong and weak resonances are used, particularly in the works [13,14,15].

In a general case, one can speak separately about the external and internal stability of resonances in dynamical systems modeling the perturbed motion of rigid bodies. The internal stability of resonances is considered, for example, in works [16,17]. In these studies, the stability of oscillations of mechanical coupled oscillators was analyzed in a small neighborhood of the resonances. The external stability characterizes the ability of resonances to be attractors that attract the trajectories of the system from non-resonant regions to an asymptotically small resonance region. It should be noted that a significant number of works have been devoted to the analysis of the evolution of slow variables and the study of the external stability of various dynamical systems with fast and slow variables in the non-resonant case. In particular, the article [18] studied the condition of the external stability of the resonance during the descent of a spacecraft with a small asymmetry at small angles of attack in the Martian atmosphere.

Note, that in [19] the problem of stabilization with a fixed time was considered for a class of the indefinite nonlinear systems of the second order. At the same time, a new approach has been developed that can be used to obtain a feedback controller, together with the corresponding Lyapunov function. In this case, it is possible to make the closed dynamical system stable at a fixed point in time.

The aim of this work is to develop a new asymptotic method for analyzing the nonlinear monotonic stability of the amplitude of plane oscillations in a dynamic system of original differential equations containing one fast and several slow variables. Dynamical systems are often used in practice to simulate the motion of solid bodies with geometric symmetry.

The method formulated in the paper is based on the analysis of the signs of the first and second derivatives of the desired approximate analytical function. In this case, it is assumed that the resulting approximate analytical function is defined and twice continuously differentiable over the entire considered interval of variation of the independent variable. In addition, this approximate analytical function describes the nonlinear and monotonic evolution of the oscillation amplitude over the entire interval of the independent variable. In this work, the concepts of weak or strong stability are replaced by more traditional concepts from a mathematical point of view, namely, when the decreasing curve considered in the analysis of nonlinear monotonic stability is convex upwards or downwards.

As a result of applying the method under consideration, it is required to obtain all characteristic cases of nonlinear monotonic stability of oscillations as well as all characteristic cases of nonlinear monotonic instability of oscillations of the amplitude of oscillations. It should be noted that, for definiteness, it is assumed that the investigated approximate analytical function has no more than one inflection point over the entire interval of the independent variable.

In this paper, the formulated method is used to study stability in the problem of nonlinear monotonic aerodynamic damping of the amplitude of plane oscillations of the angle of attack during an uncontrolled descent of a symmetrical spacecraft of the segmental-conical shape in the atmosphere of Mars. As an example, Figure 1 shows the Schiaparelli, a spacecraft designed to descend into the atmosphere of Mars [20].

2. Nonlinear Monotone Stability Analysis Method

The task of the planar motion of the symmetrical spacecraft relative to the center of mass in the Martian atmosphere is considered. In this case, the initial angular speed is equatorial (${\mathsf{\omega }}_x(0)=0$) and it is directed normally to the plane of the angle of attack. In addition, the spacecraft speed vector does not change its direction noticeably during the interval under consideration. The equation of in-plane motion of the spacecraft relative to the center of mass [21] after a number of simplifications has the form:

$$\frac{{\mathrm{d}}^2\mathsf{\alpha }}{\mathrm{d}{\mathrm{t}}^2}+\mathsf{\epsilon }\left[\frac{{\mathrm{c}}_{\mathrm{y}\mathrm{v}}^{\mathsf{\alpha }}\mathrm{q}\mathrm{S}}{\mathrm{m}\mathrm{V}}\right]\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathrm{t}}-\frac{{\mathrm{m}}_{\mathrm{z}}\mathrm{q}\mathrm{S}\mathrm{L}}{\mathrm{I}}=0.$$

(1)

Here $\mathsf{\alpha }$ is the angle of attack, $\mathsf{\epsilon }$ is the designation of a small dimensionless parameter, m is the mass of the spacecraft, V is the velocity of the center of mass of the spacecraft, L is the length of the spacecraft, S is the largest area of the transverse section of the spacecraft, I is the moments of the inertia of the spacecraft relative to the principal axes Y and Z ($\mathrm{I}={\mathrm{I}}_{\mathrm{y}}={\mathrm{I}}_{\mathrm{z}}$), q is the dynamic pressure ($\mathrm{q}=\frac{\mathsf{\rho }{\mathrm{V}}^2}{2}$), $\mathsf{\rho }$ is the atmosphere density, ${\mathrm{c}}_{\mathrm{y}\mathrm{v}}^{\mathsf{\alpha }},{\mathrm{m}}_{\mathrm{z}}$ are the known values of aerodynamic coefficients.

In Equation (1), we neglect the change in the value ${\mathrm{c}}_{\mathrm{y}\mathrm{v}}^{\mathsf{\alpha }}$ at the intervals of the change in the independent variable t. In addition, decomposition is applicable. In addition, we will further apply the first approximate expression ${\mathrm{m}}_{\mathrm{z}}\approx {\mathrm{m}}_{\mathrm{z}}^{\mathsf{\alpha }}\mathsf{\alpha }$. It should be noted that taking into account the second and subsequent approximations in this expression will lead to a significant complication of the problem being solved and is not considered in this paper. As a result, we obtain from Equation (1) a linear differential equation of the second order in the homogenous form with variable coefficients, as follows:

$$\frac{{\mathrm{d}}^2\mathsf{\alpha }}{\mathrm{d}{\mathrm{t}}^2}+\mathsf{\epsilon }{\mathrm{f}}_1\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathrm{t}}+{\mathsf{\omega }}^2\mathsf{\alpha }=0.$$

(2)

Here ${\mathsf{\omega }}^2=\left|-\frac{{\mathrm{m}}_{\mathrm{z}}^{\mathsf{\alpha }}\mathrm{q}\mathrm{S}\mathrm{L}}{\mathrm{I}}\right|$, ${\mathrm{f}}_1=\frac{{\mathrm{c}}_{\mathrm{y}\mathrm{v}}^{\mathsf{\alpha }}\mathrm{q}\mathrm{S}}{\mathrm{m}\mathrm{v}}$. Traditionally, the initial values of the angle of attack $\mathsf{\alpha }(0)$ and the derivative of the attack $\mathrm{d}\mathsf{\alpha }(0)/\mathrm{d}\mathrm{t}$ are set at the point of entry of the spacecraft into the atmosphere.

Given the change in the variable ${\mathsf{\omega }}_{\mathsf{\alpha }}=\mathrm{d}\mathsf{\alpha }/\mathrm{d}\mathrm{t}$, we will write Equation (2) in the form of an equation system

$$\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathrm{t}}={\mathsf{\omega }}_{\mathsf{\alpha }},$$

(3)

$$\frac{\mathrm{d}{\mathsf{\omega }}_{\mathsf{\alpha }}}{\mathrm{d}\mathrm{t}}=-\mathsf{\epsilon }{\mathrm{f}}_1\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathrm{t}}-{\mathsf{\omega }}^2\mathsf{\alpha }.$$

(4)

Note that the system of Equations (3) and (4) is completely equivalent to Equation (2). If the aerodynamic damping in Equation (2) is absent (from the point of view of oscillation theory, this can be formally denoted as $\mathsf{\epsilon }$ = 0), and then we get an equation

$$\frac{{\mathrm{d}}^2\mathsf{\alpha }}{\mathrm{d}{\mathrm{t}}^2}+{\mathsf{\omega }}^2\mathsf{\alpha }=0.$$

(5)

Equation (5) has a private solution

$$\mathsf{\alpha }=\mathrm{A}\cos \mathsf{\phi }.$$

(6)

Here A is the constant amplitude of oscillations, $\mathsf{\phi }$ is the phase of oscillations, $\mathsf{\phi }={\mathsf{\phi }}_0+\mathsf{\omega }\mathrm{t}$, $\mathsf{\omega }$ is the constant frequency of oscillations (in case without damping), ${\mathsf{\phi }}_0$ is the constant initial phase of oscillations.

By performing differentiation $\mathsf{\alpha }$ by the variable t taking into account (6), we obtain

$${\mathsf{\omega }}_{\mathsf{\alpha }}=\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathrm{t}}=-\mathrm{A}\mathsf{\omega }\sin \mathsf{\phi }.$$

(7)

To find a solution to the perturbed Equation (2), we apply the method of variation of an arbitrary constant. According to this method, we will replace variables $\mathsf{\alpha }$, ${\mathsf{\omega }}_{\mathsf{\alpha }}$ with variables A, $\mathsf{\phi }$ in the perturbed system (3) and (4). Note that the solution of Equation (2) describes oscillatory motions, since the influence of perturbations is small. As a result, we obtain the differential equations for new variables A, $\mathsf{\phi }$.

Next, the substitution of expressions (6) and (7) should be performed in the system of Equations (3) and (4). Taking into account the variability of the values A and $\mathsf{\phi }$, we obtain

$$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}\cos \mathsf{\phi }-\mathrm{A}\frac{\mathrm{d}\mathsf{\phi }}{\mathrm{d}\mathrm{t}}\sin \mathsf{\phi }=-\mathrm{A}\mathsf{\omega }\sin \mathsf{\phi },$$

(8)

$$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}\sin \mathsf{\phi }+\mathrm{A}\frac{\mathrm{d}\mathsf{\phi }}{\mathrm{d}\mathrm{t}}\cos \mathsf{\phi }=\mathrm{A}\mathsf{\omega }\cos \mathsf{\phi }-\mathsf{\epsilon }\mathrm{A}{\mathrm{f}}_1\sin \mathsf{\phi }.$$

(9)

Further, from the solutions of the system (8) and (9) we find

$$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}=-\mathsf{\epsilon }\mathrm{A}{\mathrm{f}}_{`}{}_1{\sin }^2\mathsf{\phi },$$

(10)

$$\frac{\mathrm{d}\mathsf{\phi }}{\mathrm{d}\mathrm{t}}=\mathsf{\omega }-\mathsf{\epsilon }{\mathrm{f}}_{`}{}_1\sin \mathsf{\phi }\cos \mathsf{\phi }.$$

(11)

The system of Equations (10) and (11) is equivalent to Equation (2). From the system of Equations (10) and (11) it follows that the amplitude $\mathrm{A}(\mathrm{t})$ is the slow variable, and the phase $\mathsf{\phi }(\mathrm{t})$ is the fast variable.

It should be noted that in the analysis of the stability of oscillations, the study of the behavior of the amplitude of oscillations $\mathrm{A}(\mathrm{t})$ is of the greatest interest. However, the direct use of Equation (10) to achieve this goal is difficult due to the dependence of the right side of this equation on the rapid variable $\mathsf{\phi }(\mathrm{t})$. To exclude from the right side of Equation (10) the fast variable $\mathsf{\phi }(\mathrm{t})$, we apply a well-known method of averaging equations systems with one fast variable [22,23]. We will apply this method outside the resonant region, which has the order $\mathsf{\omega }=o(\mathsf{\epsilon })$. In the first approximation of the method of averaging, we get $\langle \frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}\rangle =-\mathsf{\epsilon }\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\mathrm{A}{\mathrm{f}}_{`}{}_1{\sin }^2\mathsf{\phi }\mathrm{d}\mathsf{\phi }}=-\mathsf{\epsilon }\frac{\overline{\mathrm{A}}{\mathrm{f}}_{`}{}_1}{2}$. To simplify the subsequent expressions, we will not indicate the average value and its derivatives line on top, corresponding to the average values. Therefore, the average equation for the amplitude of oscillations has the form

$$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}=-\mathsf{\epsilon }\frac{{\mathrm{f}}_{`}{}_1}{2}\mathrm{A}.$$

(12)

Thus, we will analyze the behavior not of the amplitude itself, but its average value. According to the method of averaging, the amplitude and its averaged value differs by a small value that has order $\mathsf{\epsilon }$.

Equation (12) is a linear differential equation of the first order with a variable coefficient. The solution of this equation can be found using the method of separating variables. As a result, we get

$$\mathrm{A}={\mathrm{A}}_0\exp (-{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\frac{{\mathrm{f}}_{`}{}_1}{2}}\mathrm{d}\mathrm{t}).$$

(13)

Here ${\mathrm{A}}_0$ is the initial value of the amplitude $\mathrm{A}$ at the entry into the atmosphere (t = 0). Note that the initial conditions are the values of the spacecraft motion variables at the point of entry into the Martian atmosphere (when the spacecraft reaches an altitude of 110 km).

Further, it is assumed that the average amplitude is a monotonous and twice differentiated function determined on the entire unreasonable interval of values.

We find the first and second derivatives of the average amplitude of the angle of attack. Calculating the first and second derivatives of Expression (13), we obtain

$$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}=-\frac{{\mathrm{A}}_0{\mathrm{f}}_{`}{}_1}{2}\exp (-{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\frac{{\mathrm{f}}_{`}{}_1}{2}}\mathrm{d}\mathrm{t}),$$

(14)

$$\frac{{\mathrm{d}}^2\mathrm{A}}{\mathrm{d}{\mathrm{t}}^2}=\left[-\frac{{\mathrm{A}}_0}{2}\frac{\mathrm{d}{\mathrm{f}}_{`}{}_1}{\mathrm{d}\mathrm{t}}+\frac{{\mathrm{A}}_0}{4}{({\mathrm{f}}_{`}{}_1)}^2\right]\exp (-{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\frac{{\mathrm{f}}_{`}{}_1}{2}}\mathrm{d}\mathrm{t}),$$

(15)

Here, the right parts of Equations (14) and (15) are monotonic and continuous in the considered non-resonant region.

Let us analyze the nonlinear monotonic stability of the change in the average amplitude of the oscillations of the angle of attack.

Definition 1.

The nonlinear monotonic stability of the average amplitude of oscillations is a change in the amplitude of oscillations such that, according to Equations (14) and (15), the following conditions are simultaneously satisfied throughout the considered interval of variation of the independent variable: $\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}<0$; $\frac{{\mathrm{d}}^2\mathrm{A}}{\mathrm{d}{\mathrm{t}}^2}>0$ or $\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}<0$; $\frac{{\mathrm{d}}^2\mathrm{A}}{\mathrm{d}{\mathrm{t}}^2}<0$.

In the course of this analysis, we will apply expressions for the first (14) and second derivative (15). Since the initial amplitude is ${\mathrm{A}}_0>0$, then when the condition ${\mathrm{f}}_{`}{}_1>0$ is satisfied from Equation (14), we obtain that $\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}<0$. Therefore, the amplitude of the angle of attack decreases at ${\mathrm{f}}_{`}{}_1>0$. The sign of the second derivative (15) under the condition ${\mathrm{f}}_{`}{}_1>0$ is completely determined by the sign of the expression in square brackets ${\mathrm{f}}_{`}{}_2=-\frac{{\mathrm{A}}_0}{2}\frac{\mathrm{d}{\mathrm{f}}_{`}{}_1}{\mathrm{d}\mathrm{t}}+\frac{{\mathrm{A}}_0}{4}{({\mathrm{f}}_{`}{}_1)}^2$. The following theorem about the nonlinear monotonic stability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$ is true.

Theorem 1.

If the following conditions are satisfied: (1.1.) the initial amplitude is a positive${\mathrm{A}}_0>0$; (1.2.) the smooth function${\mathrm{f}}_{`}{}_1(\mathrm{t})$in the Equations (13)–(15) is positive over the entire interval values of independent variable (${\mathrm{f}}_{`}{}_1>0$); (1.3.) the smooth function$\mathrm{A}(\mathrm{t})$has at most one inflection point over the entire interval values of independent variable, then there are four different cases of nonlinear monotonic stability of average oscillation amplitude$\mathrm{A}(\mathrm{t})$over the entire interval values of independent variable.

Proof of Theorem 1.

Let us consider all characteristic cases of nonlinear monotonic stability.

Case 1. When ${\mathrm{A}}_0>0$, ${\mathrm{f}}_{`}{}_1>0$ and ${\mathrm{f}}_{`}{}_2>0$, we obtain the case of monotonic nonlinearity of stability of the oscillation amplitude, which leads to a monotonic decrease in the amplitude $\mathrm{A}(\mathrm{t})$ with unchangeable downward convexity.

Case 2. When ${\mathrm{A}}_0>0$,${\mathrm{f}}_{`}{}_1>0$ and ${\mathrm{f}}_{`}{}_2<0$, we obtain the case of monotonic nonlinearity of stability of the oscillation amplitude, which leads to a monotonic decrease in the amplitude $\mathrm{A}(\mathrm{t})$ with unchangeable upward convexity.

Cases 1 and 2 describe nonlinear monotonic stability of the oscillation amplitude $\mathrm{A}(\mathrm{t})$ in the absence of inflection points. It is obvious that there are no other cases of nonlinear monotonic stability $\mathrm{A}(\mathrm{t})$ on average without the implementation of inflection points.

Next, consider the cases of implementation of nonlinear monotonic stability $\mathrm{A}(\mathrm{t})$ on average with the formation of only one inflection point over the entire interval of change of the independent variable. Obviously, there are only two cases.

Case 3. In the initial interval, there is a monotonous decrease in the amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1>0$, ${\mathrm{A}}_0>0$) with unchangeable downward convexity (at ${\mathrm{f}}_{`}{}_2>0$). Further, one inflection point of the curve $\mathrm{A}(\mathrm{t})$ is formed (at ${\mathrm{f}}_{`}{}_2(\mathrm{t})=0$). Subsequently, the monotonous decrease in amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1>0$) occurs with unchangeable upward convexity (at ${\mathrm{f}}_{`}{}_2<0$).

Case 4. In the initial interval, there is a monotonous decrease in the amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1>0$, ${\mathrm{A}}_0>0$) with unchangeable upward convexity (at ${\mathrm{f}}_{`}{}_2<0$). Further, one inflection point of the curve $\mathrm{A}(\mathrm{t})$ is formed (${\mathrm{f}}_{`}{}_2(\mathrm{t})=0$). Subsequently, the monotonic decrease in amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1>0$) occurs with unchangeable downward convexity (at ${\mathrm{f}}_{`}{}_2>0$). Thus, when conditions 1.1–1.3 are satisfied, there are only four cases of nonlinear monotonic stability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$. Obviously, there are no other cases of monotonic nonlinear stability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$. The theorem is proved. □

Remark 1.

If there are several inflection points of the curve$\mathrm{A}(\mathrm{t})$, then the classification of stability cases should be extended. Moreover, using the considered method, it is not difficult to obtain all the extended classification cases of nonlinear monotonic stability of the average oscillation amplitude$\mathrm{A}(\mathrm{t})$.

Next, we analyze the nonlinear monotonic instability of the change in the amplitude of the average oscillations of the angle of attack.

Definition 2.

The nonlinear monotonic instability of the average amplitude of oscillations$\mathrm{A}(\mathrm{t})$is a change in the amplitude of oscillations such that, according to Equations (14) and (15), the following conditions are simultaneously satisfied throughout the considered interval of variation of the independent variable: $\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}>0$; $\frac{{\mathrm{d}}^2\mathrm{A}}{\mathrm{d}{\mathrm{t}}^2}>0$ or $\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}>0$; $\frac{{\mathrm{d}}^2\mathrm{A}}{\mathrm{d}{\mathrm{t}}^2}<0$.

The following theorem about of the nonlinear monotonic instability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$ is true.

Theorem 2.

If the following conditions are satisfied: (2.1.) the initial amplitude is a positive${\mathrm{A}}_0>0$; (2.2.) the smooth function${\mathrm{f}}_{`}{}_1(\mathrm{t})$in the Equations (13)–(15) is negative over the entire interval values of an independent variable (${\mathrm{f}}_{`}{}_1<0$); (2.3.) the smooth function $\mathrm{A}(\mathrm{t})$ has at most one inflection point over the entire interval values of independent variable, then there are four different cases of nonlinear monotonic instability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$ over the entire interval values of an independent variable.

Proof of Theorem 2.

Let us consider all characteristic cases of nonlinear monotonic instability.

Case 5. When ${\mathrm{A}}_0>0$, ${\mathrm{f}}_{`}{}_1<0$ and ${\mathrm{f}}_{`}{}_2>0$, we obtain the case of monotonic nonlinear instability of the amplitude $\mathrm{A}(\mathrm{t})$, leading to a monotonic increase in the given amplitude with unchangeable downward convexity.

Case 6. When ${\mathrm{A}}_0>0$, ${\mathrm{f}}_{`}{}_1<0$ and ${\mathrm{f}}_{`}{}_2<0$, we obtain the case of monotonic nonlinear instability of the amplitude $\mathrm{A}(\mathrm{t})$, leading to a monotonic increase in this amplitude with unchangeable upward convexity.

Cases 5 and 6 describe nonlinear monotonic instability $\mathrm{A}(\mathrm{t})$ in the absence of inflection points. It is obvious that there are no other cases of nonlinear monotonic instability $\mathrm{A}(\mathrm{t})$ on average without the implementation of inflection points.

Next, we write the cases of implementation of nonlinear monotonic instability $\mathrm{A}(\mathrm{t})$ on average with the formation of only one inflection point over the entire interval of change of the independent variable. Obviously, there are only two cases.

Case 7. In the initial interval, there is a monotonous increase in the amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1<0$, ${\mathrm{A}}_0>0$) with unchangeable downward convexity (at ${\mathrm{f}}_{`}{}_2>0$). Further, one inflection point of the curve $\mathrm{A}(\mathrm{t})$ (${\mathrm{f}}_{`}{}_2(\mathrm{t})=0$) is formed. Subsequently, a monotonous increase (at ${\mathrm{f}}_{`}{}_1<0$) in amplitude $\mathrm{A}(\mathrm{t})$ occurs with unchangeable upward convexity (at ${\mathrm{f}}_{`}{}_2<0$).

Case 8. In the initial interval, there is a monotonous increase in the amplitude $\mathrm{A}(\mathrm{t})$ (at ${\mathrm{f}}_{`}{}_1<0$, ${\mathrm{A}}_0>0$) with unchangeable upward convexity (at ${\mathrm{f}}_{`}{}_2<0$). Further, one inflection point of the curve $\mathrm{A}(\mathrm{t})$ (${\mathrm{f}}_{`}{}_2(\mathrm{t})=0$) is formed. Further, a monotonous increase (at ${\mathrm{f}}_{`}{}_1<0$) in amplitude $\mathrm{A}(\mathrm{t})$ occurs with unchangeable downward convexity (at ${\mathrm{f}}_{`}{}_2>0$).

Thus, if the conditions 2.1–2.3 are satisfied, there are only four cases of nonlinear monotonic instability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$. Obviously, there are no other cases of monotonic nonlinear instability of the average oscillation amplitude $\mathrm{A}(\mathrm{t})$. The theorem is proved. □

Remark 2.

If there are several inflection points of the curve$\mathrm{A}(\mathrm{t})$, then the classification of instability cases needs to be extended. Arguing in a similar way, one can obtain all the required cases of the extended classification with a nonlinear monotonic instability of the oscillation amplitude$\mathrm{A}(\mathrm{t})$.

Remark 3.

Therefore, the considered method allows finding all four cases of nonlinear monotonic stability of the average amplitude of the angle of attack. In addition, this method also makes it possible to find all four cases of nonlinear monotonic instability of the average amplitude of the angle of attack, that differ from the corresponding cases of stability by the sign of the first derivative. In this sense, one should talk about a symmetrical quantity (with respect to the zero magnitude of the first average derivative$\frac{\mathrm{d}\mathrm{A}}{\mathrm{d}\mathrm{t}}=0$) in different cases of stability and instability.

3. Numerical Results

Let us analyze the characteristic numerical results describing the nonlinear monotonic stability and instability of the oscillations of the angle of attack (on average) during the motion of a symmetrical spacecraft in the Martian atmosphere. In this case, we will apply the expressions (13)–(15), which describe the change in the amplitude of oscillations, and its average derivative of the first, as well as the second order.

Let the mass of the small descent spacecraft equal m = 40 kg, the length of the spacecraft is 0.7 m. Let us introduce the notation $\mathrm{c}={\mathrm{f}}_{`}{}_1/4\pi$. The initial speed of the spacecraft is V(0) = 3.54 kms⁻¹. The initial value of the average density of the Martian atmosphere is 10⁻⁷ kgm⁻³. The principal central moments of inertia of the spacecraft are $\mathrm{I}={\mathrm{I}}_{\mathrm{y}}={\mathrm{I}}_{\mathrm{z}}$ = 4.58 kgm². The values of the aerodynamic coefficients ${\mathrm{c}}_{\mathrm{y}\mathrm{v}}^{\mathsf{\alpha }},{\mathrm{m}}_{\mathrm{z}}$ are similar to the results contained in the work [24].

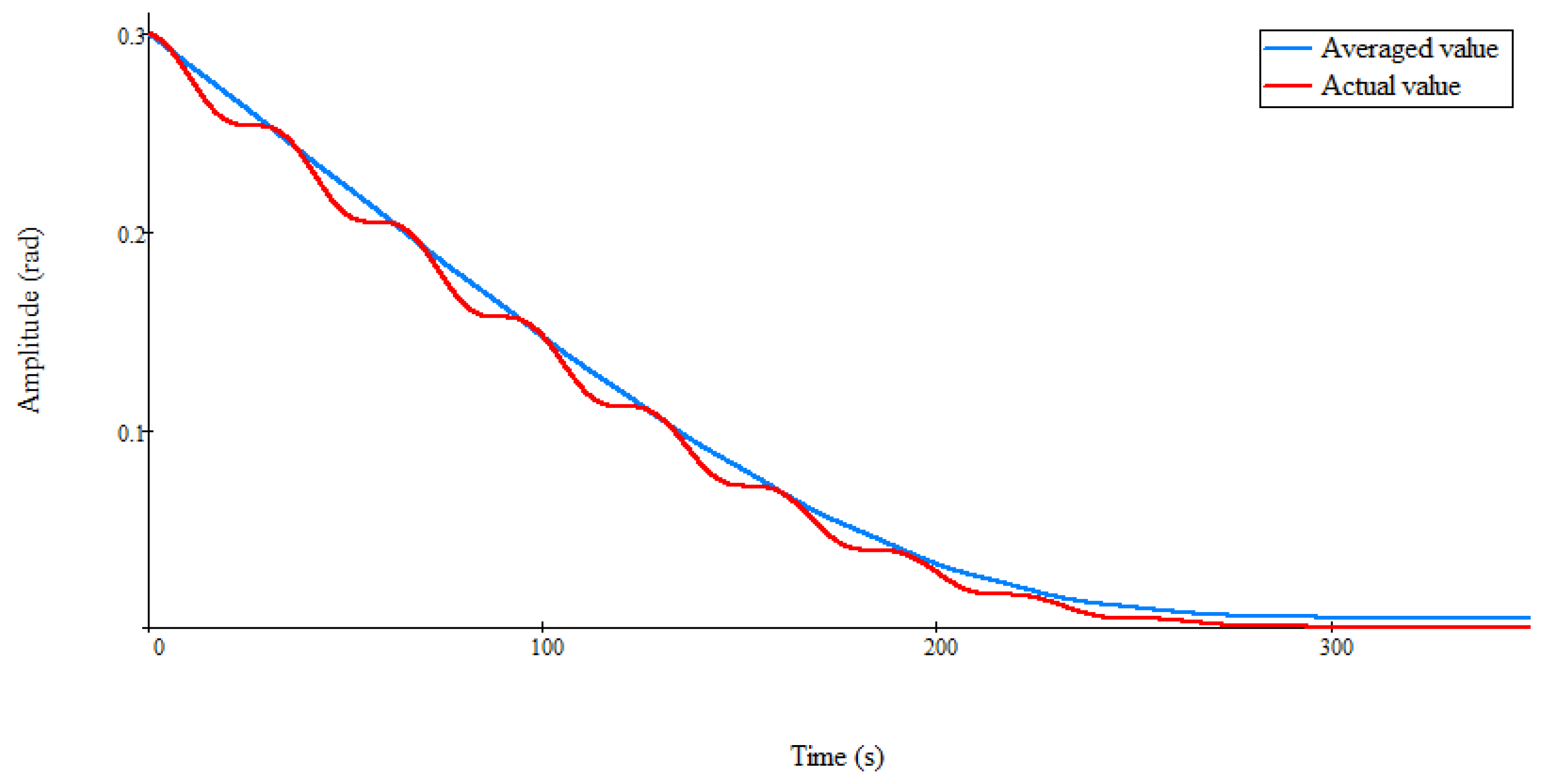
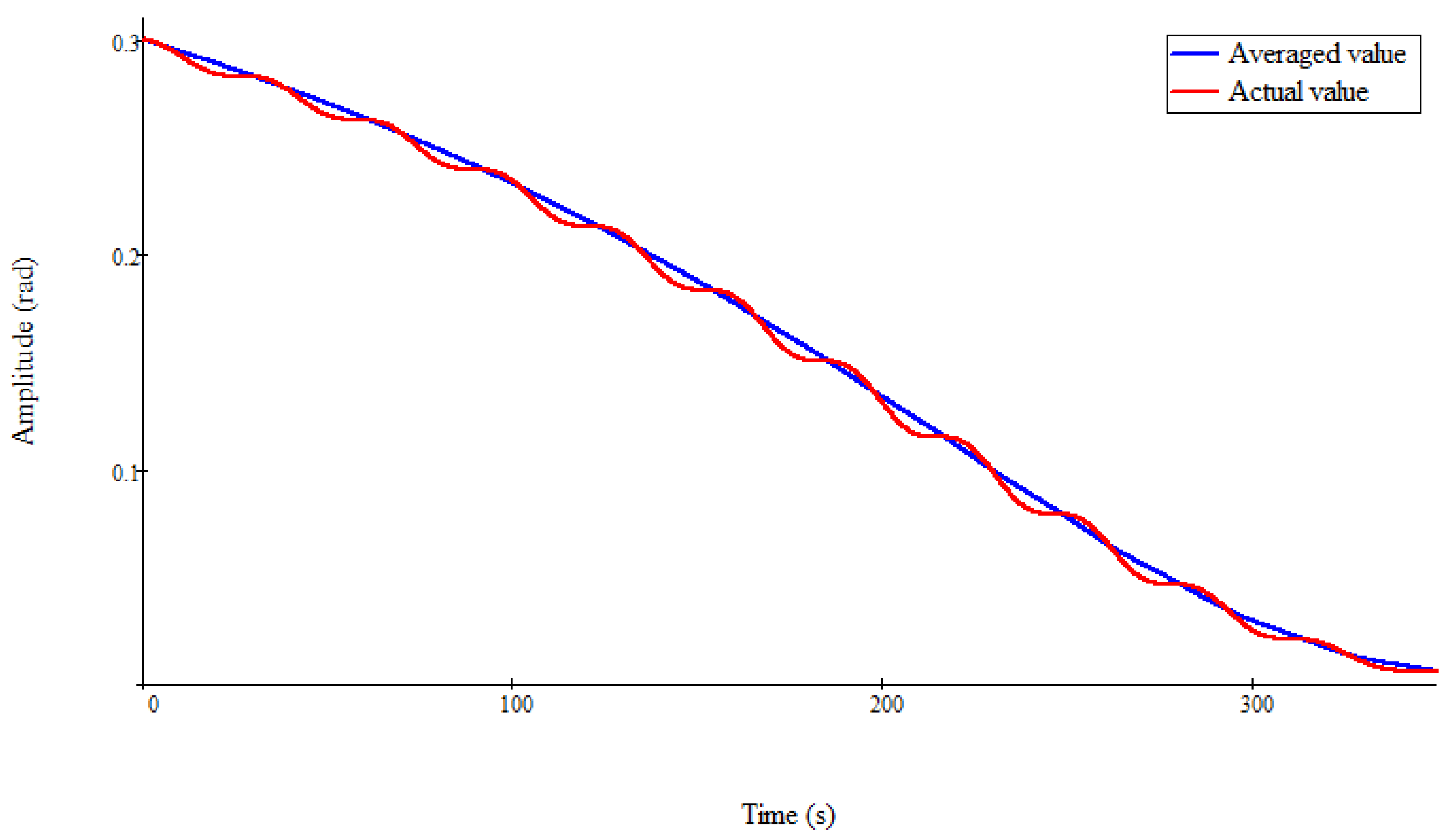
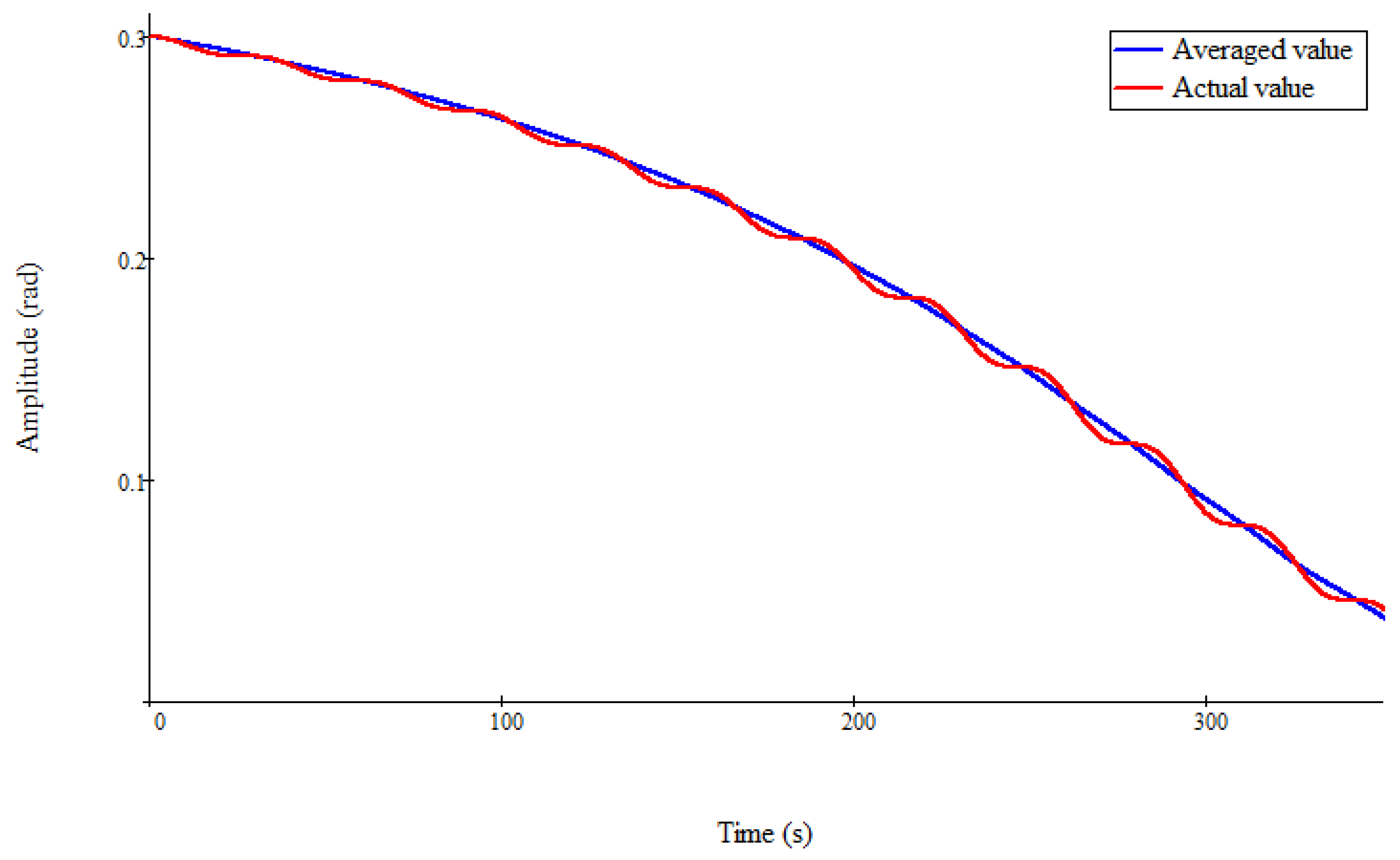
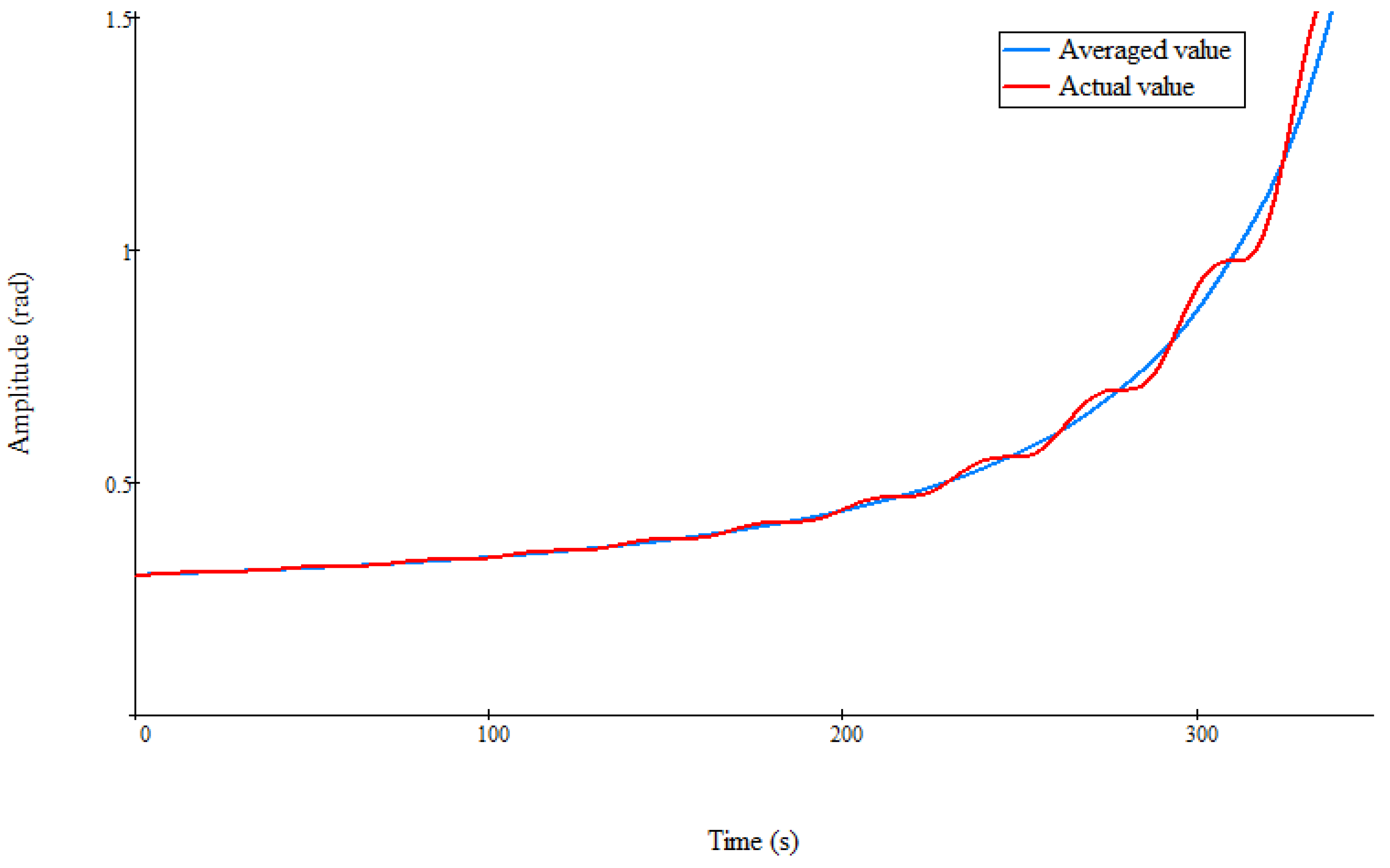
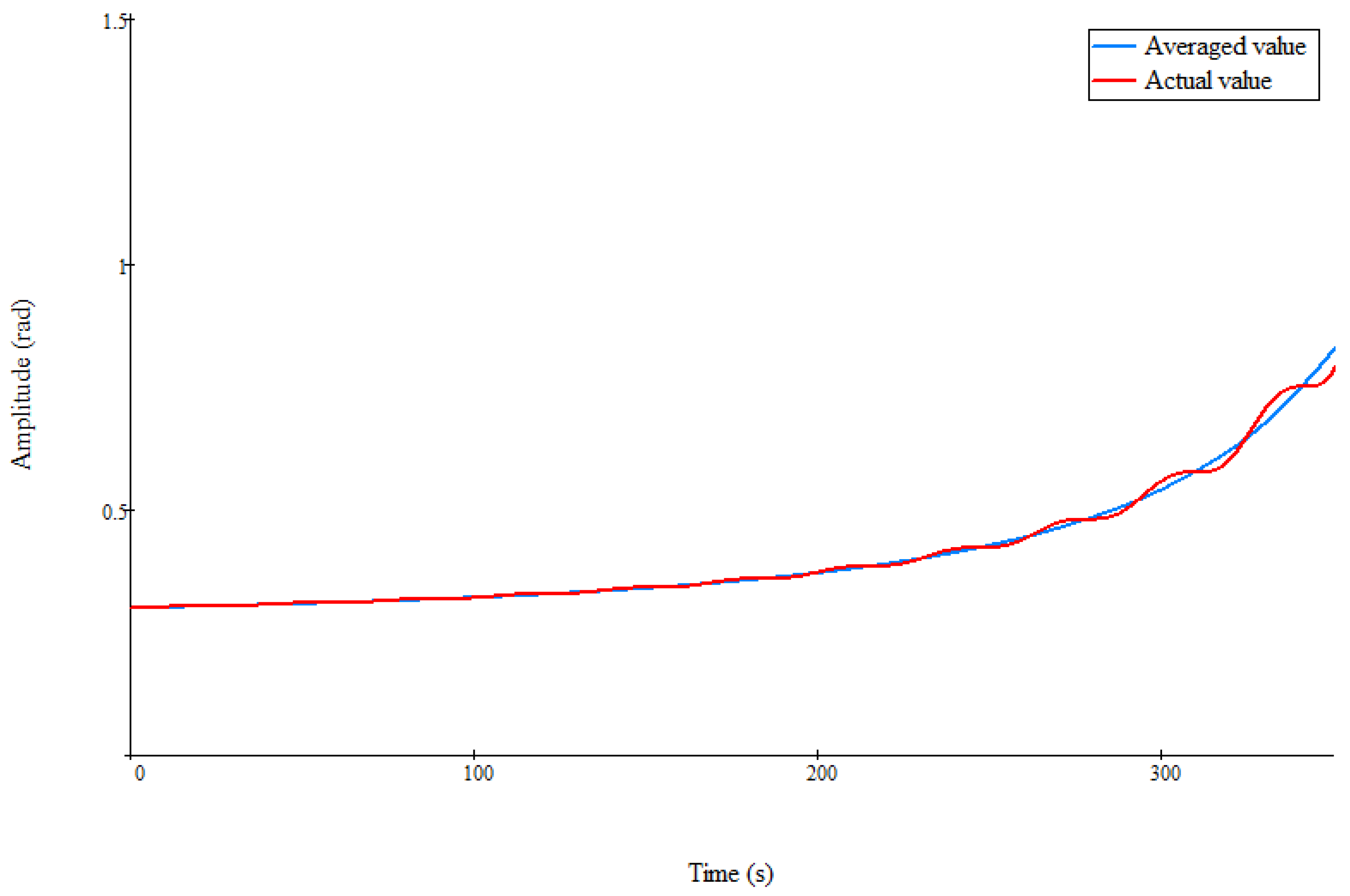
Figure 2, Figure 3 and Figure 4 show characteristic numerical results demonstrating the nonlinear monotonic stability of the average oscillation amplitude, obtained when the condition ${\mathrm{f}}_{`}{}_1>0$ is true. In these figures, the blue line shows the change in the value of the average value of the angle of attack, obtained from the numerical solution of Equation (12). In this case, Figure 2, Figure 3 and Figure 4 in the form of a solid red line show the change in the actual value of the amplitude of the angle of attack, obtained from the numerical solution of Equations (10) and (11).

These figures are obtained with different values of the maximum cross-sectional area s. All three cases presented in Figure 2, Figure 3 and Figure 4 demonstrate nonlinear monotonic stability at small values of the average amplitude of oscillations of the angle of attack and differ only in the convexity type. Therefore, these figures show the implementation of aerodynamic damping of the angle of attack during the descent of a symmetrical spacecraft in the Martian atmosphere. In particular, in Figure 2, the curve of the monotonic change in the amplitude of oscillations is convex downwards. This numerical result corresponds to Case 1. In Figure 3, the curve of monotonic decrease in the amplitude of oscillations changes the character of the convexity from upward to downward convexity.

In this case, an inflection point is formed on the curve $\mathrm{A}(\mathrm{t})$. This numerical result is similar to Case 4. In Figure 4, the curve of monotonic decrease in the oscillation amplitude is convex upwards, which corresponds to Case 2. Thus, an increase in the maximum cross-section of a small symmetrical spacecraft leads to an increase in aerodynamic damping. In this case, the nonlinear monotonic stability of the amplitude of the angle of attack is preserved. However, the nature of this resilience is changing.

Indeed, Figure 2, Figure 3 and Figure 4 show that for different values of the area s, different characteristic cases of stability are realized. In addition, with an increase in the area s, the damping of the angle of attack of a symmetrical spacecraft accelerates.

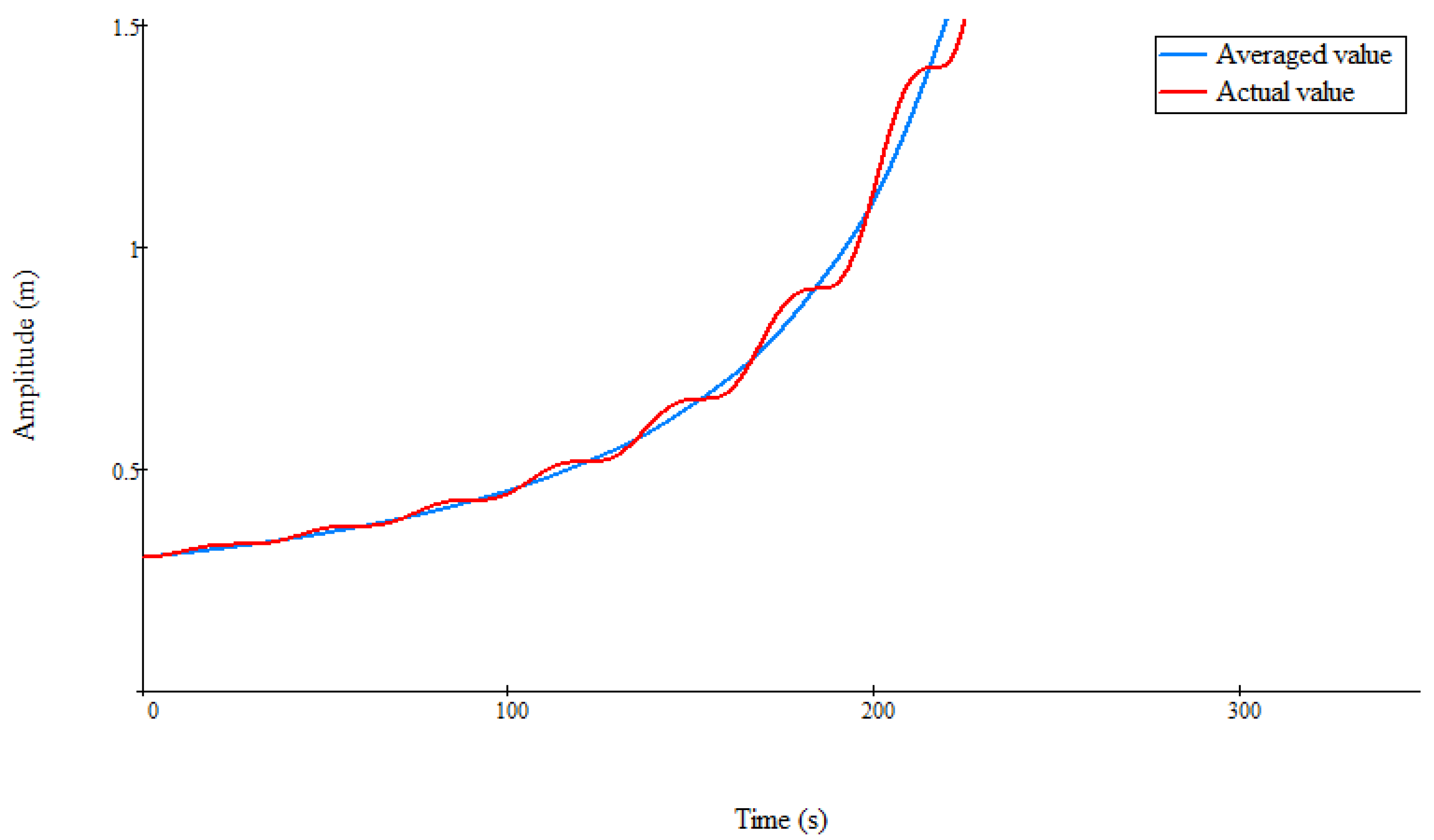
Figure 5, Figure 6 and Figure 7 show characteristic numerical results demonstrating the nonlinear monotonic instability of the average oscillation amplitude. At the same time, the mass and length of the spacecraft remained unchanged. In these figures, the solid blue line also shows the change in the average value of the angle of attack, obtained from the numerical solution of Equation (12). At the same time, in Figure 5, Figure 6 and Figure 7, in the form of a solid red line, the change in the actual value of the amplitude of the angle of attack, obtained from the numerical solution of Equations (10) and (11), is also shown. These figures are also obtained for different values of the maximum cross-sectional area s of a symmetrical spacecraft. Thus, these figures show the implementation of aerodynamic anti-damping of the angle of attack during the descent of the symmetrical spacecraft in the Martian atmosphere. The results of [25] were used to model the characteristics of the Martian atmosphere. At the same time, in Figure 5, Figure 6 and Figure 7, the curves of a monotonous increase in the amplitude of oscillations are convex downwards. These numerical results correspond to Case 5. However, from a technical point of view, Figure 5, Figure 6 and Figure 7 show different situations. As expected, the stability of the oscillation amplitude depends on the sign of the damping coefficient ${\mathrm{f}}_{`}{}_1$. Namely, in Figure 5, a monotonous increase in the amplitude of the oscillations of the angle of attack to a value of 1.5 radians occurs during a time shorter than the interval of uncontrolled movement of the spacecraft in the atmosphere. This interval of uncontrolled descent of the spacecraft can be 4 min. In this case, the symmetrical spacecraft will be deployed to the oncoming flow by the side unprotected from overheating, and overheating of the onboard equipment may occur. In addition, large values of the angle of attack can contribute to an accident associated with the entanglement of parachute lines that unfold after the end of the uncontrolled descent stage. Figure 6 considers the case when the amplitude of the angle of attack does not reach 1.5 radians during the entire four-minute time span of the uncontrolled descent of the spacecraft. Consequently, overheating of the onboard equipment does not occur. However, a monotonous increase in the oscillation amplitude leads to the departure of the angle of attack from the region of small values, not exceeding 0.3 radians. It is known that for this reason, an emergency situation with the brake parachute system can also be observed. Note that the considered model does not take into account the process of deploying the parachute braking system. The case of monotonic nonlinear instability, shown in Figure 7, is the most favorable from a practical point of view. In this case, of course, the comparison is only with cases reflecting nonlinear instability.

Indeed, in this case, the amplitude of the angle of attack changes insignificantly during the entire four-minute time interval of the uncontrolled descent of the spacecraft in the Martian atmosphere. For this reason, one should not expect both overheating of the internal equipment and an emergency situation in the operation of the parachute system.

In general, it also follows from Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 that the numerical results presented in them are reliable. Indeed, in these figures, small fluctuations of the actual values of the amplitude of the angle of attack relative to the average values of this amplitude are observed. Therefore, these numerical results are in full agreement with the described method for analyzing nonlinear monotonic stability.

It is known that in [26], the influence of various combinations of geometric parameters of a conical-shaped symmetrical spacecraft with spherical bluntness descending in the Earth’s atmosphere on its stability in terms of the angle of attack was considered. It should be noted that the numerical results obtained in this article do not contradict these known results but develop them from the point of view of both the analysis of nonlinear monotonic stability and the study of the nonlinear monotonic instability of the amplitude of the angle of attack of a symmetrical spacecraft descending in the Martian atmosphere.

4. Discussion

The paper considers a new method for the asymptotic analysis of the nonlinear monotonic stability of the amplitude of plane oscillations in one dynamical system. The presented method is based on the use of the method of variation of an arbitrary constant, the method of averaging, and the method of mathematical study of the function of one independent variable. In fact, this method is based on the analysis of the signs of the first and second derivatives of the desired approximate analytical function. At the same time, it was assumed that the resulting approximate analytical function, which describes the change in the amplitude of oscillations in the considered dynamic system, is defined and twice continuously differentiable over the entire interval of change in the independent variable. Moreover, the obtained approximate analytical function describes the nonlinear and monotonic evolution of the oscillation amplitude over the entire interval of the independent variable. In the traditional problem statement, the problem of studying the stability of a trivial solution to the original equation, in particular, requires obtaining an analytical solution to this differential equation that describes the change in the angle of attack. The application of this and other traditional approaches to the study of stability in this problem is difficult due to the variability and nonlinearity of the aerodynamic coefficients included in this equation. However, the use of the considered method makes it possible (without solving the initial equation) to reveal the characteristic features of the nonlinear evolution of the angle of attack amplitude, and to determine all cases of nonlinear monotonic stability (instability) of the angle of attack amplitude caused by small aerodynamic damping (anti-damping). Both, the four characteristic cases of nonlinear monotonic stability of oscillations and the four characteristic cases of nonlinear monotonic instability of oscillations of the oscillation amplitude, were found in the work. This number of characteristic cases is precisely determined under the assumption that the investigated approximate analytical function has no more than one inflection point over the entire range of the independent variable. It should be noted that the described method can be extended to the cases of realization of any finite number of inflection points. Naturally, in this case, the exact number of characteristic cases obtained by this method will be more than considered in the article. It should be noted that a symmetrical quantity of different cases of stability and instability was obtained, which are located on opposite sides of the zero value of the first average derivative of the angle of attack. Furthermore, this method can be used to analyze the nonlinear monotonic stability of the average oscillation amplitude in dynamic systems with one fast and several slow variables in the non-resonant case. In addition, it is of both scientific and practical interest to generalize the method described in this work for studying the monotonic nonlinear stability of average oscillations, as applied to dynamic systems with two or more fast variables. These results are beyond the scope of this article but may be considered in future publications. In this paper, the described method is directly applied to the problem of nonlinear monotonic aerodynamic damping of the amplitude of the oscillations of the angle of attack during the descent of a symmetrical spacecraft in the atmosphere, which has a segmental-conical shape. The obtained numerical results correspond to the characteristic cases described in the method. Moreover, these numerical results do not contradict the known results.