On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations
Abstract
1. Introduction
2. Copulas, Stochastic Differential Equations, and Measures of Association
2.1. Stochastic Differential Equation Structure
2.2. Trivariate Normal Copula
2.3. Semiparametric Maximum Pseudo-Likelihood Procedure for Copulas
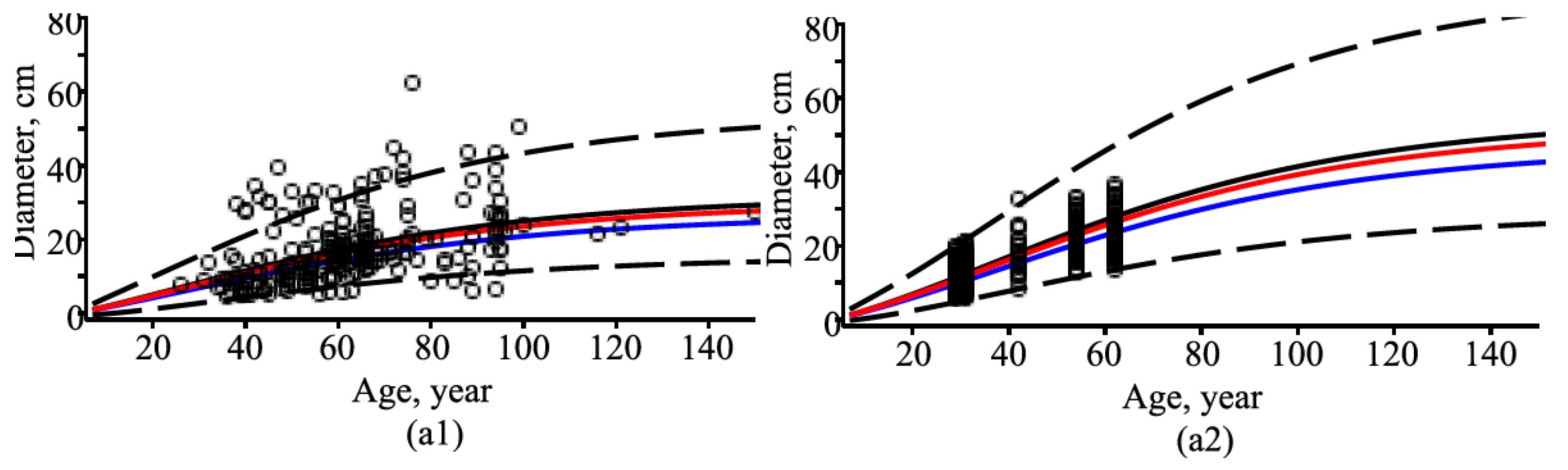
3. Results and Discussion
3.1. Parameter Estimates
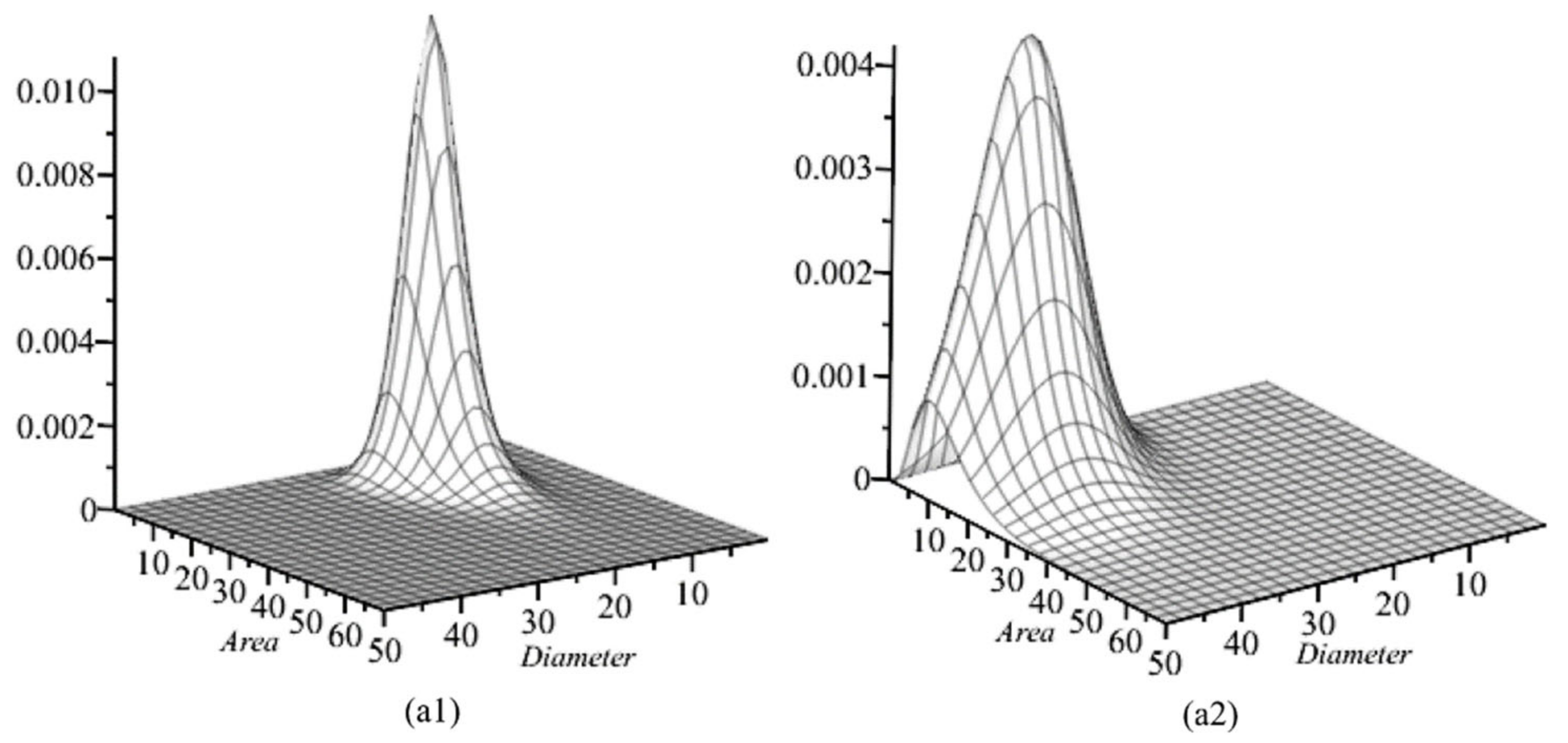
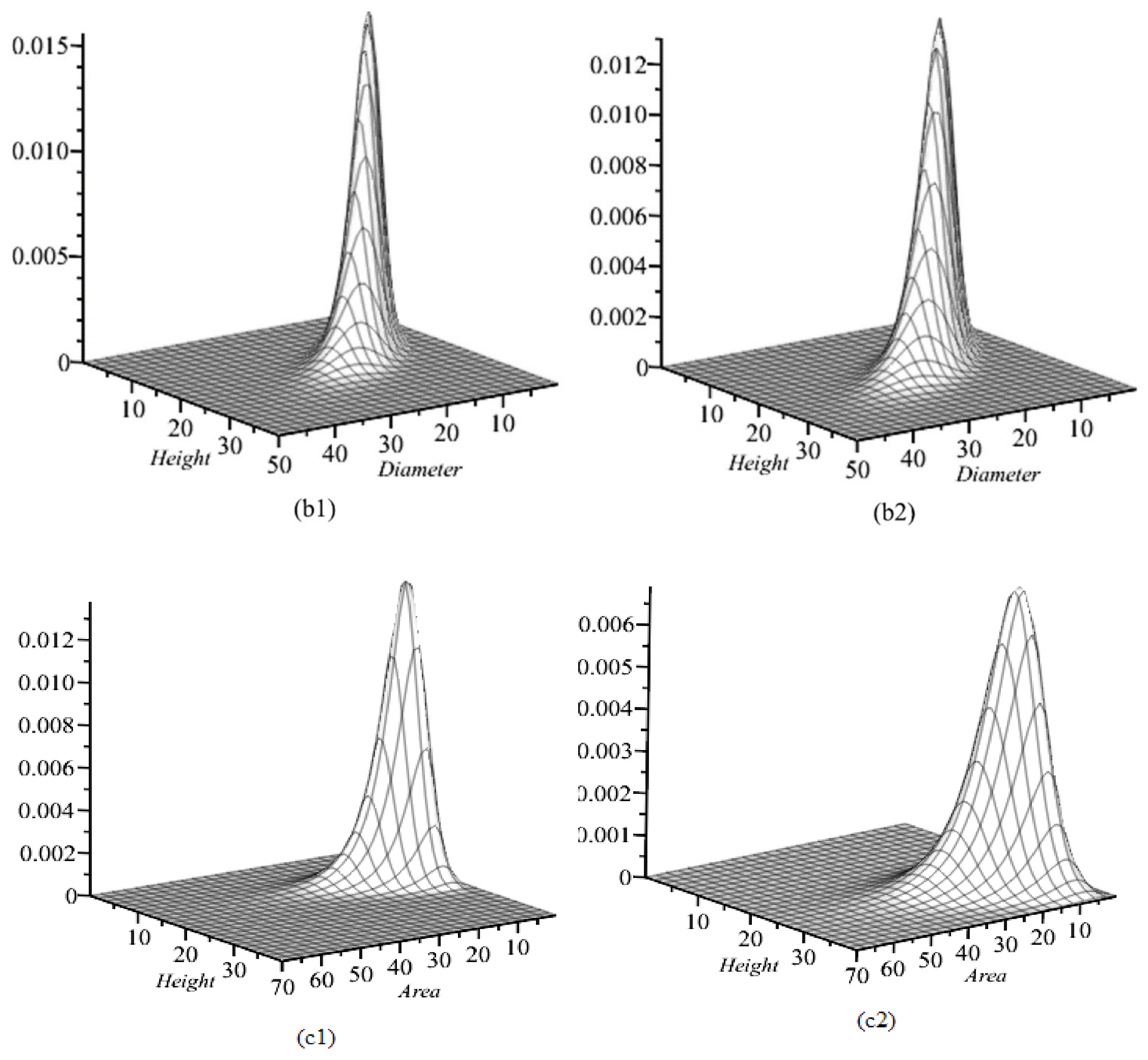
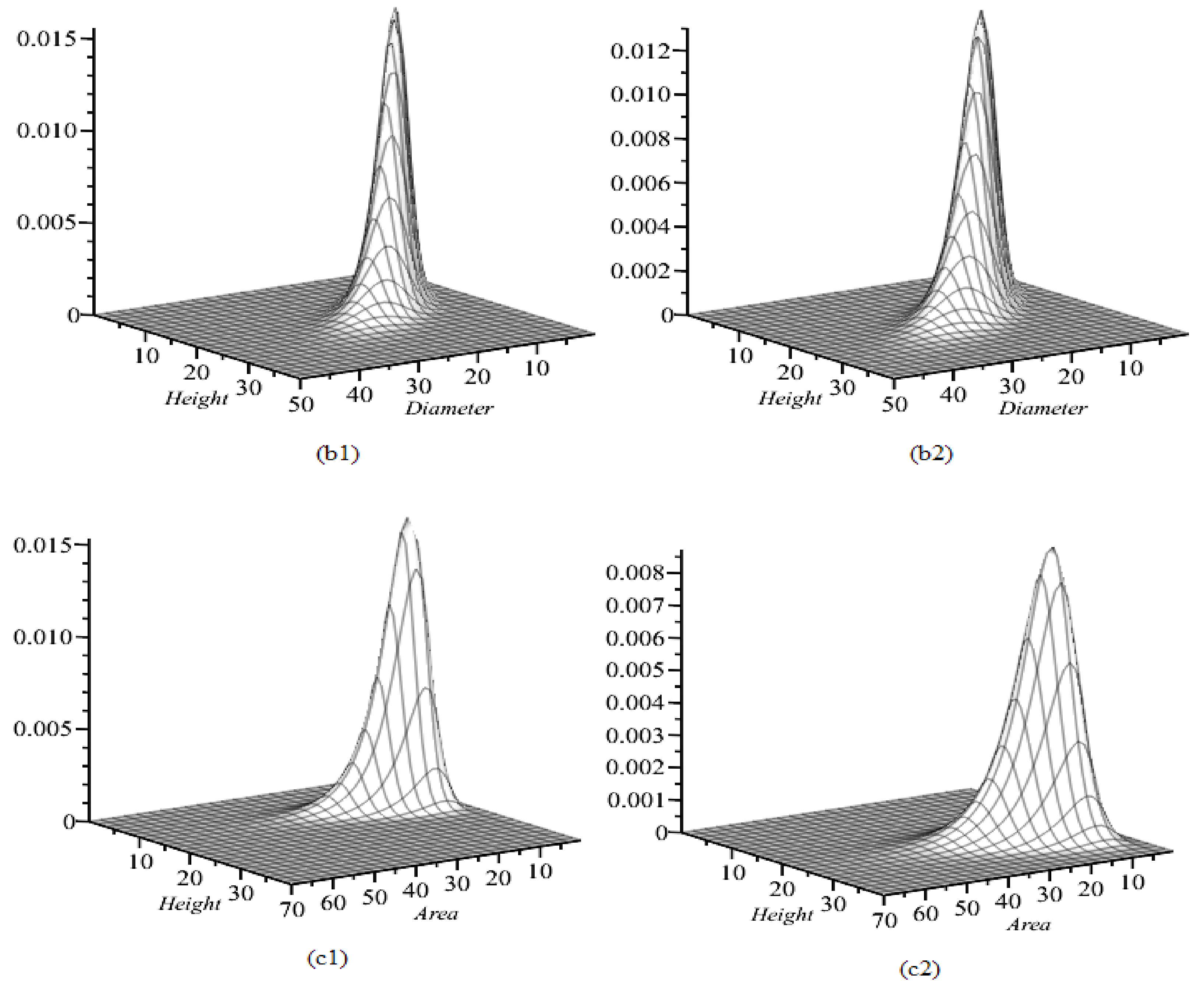
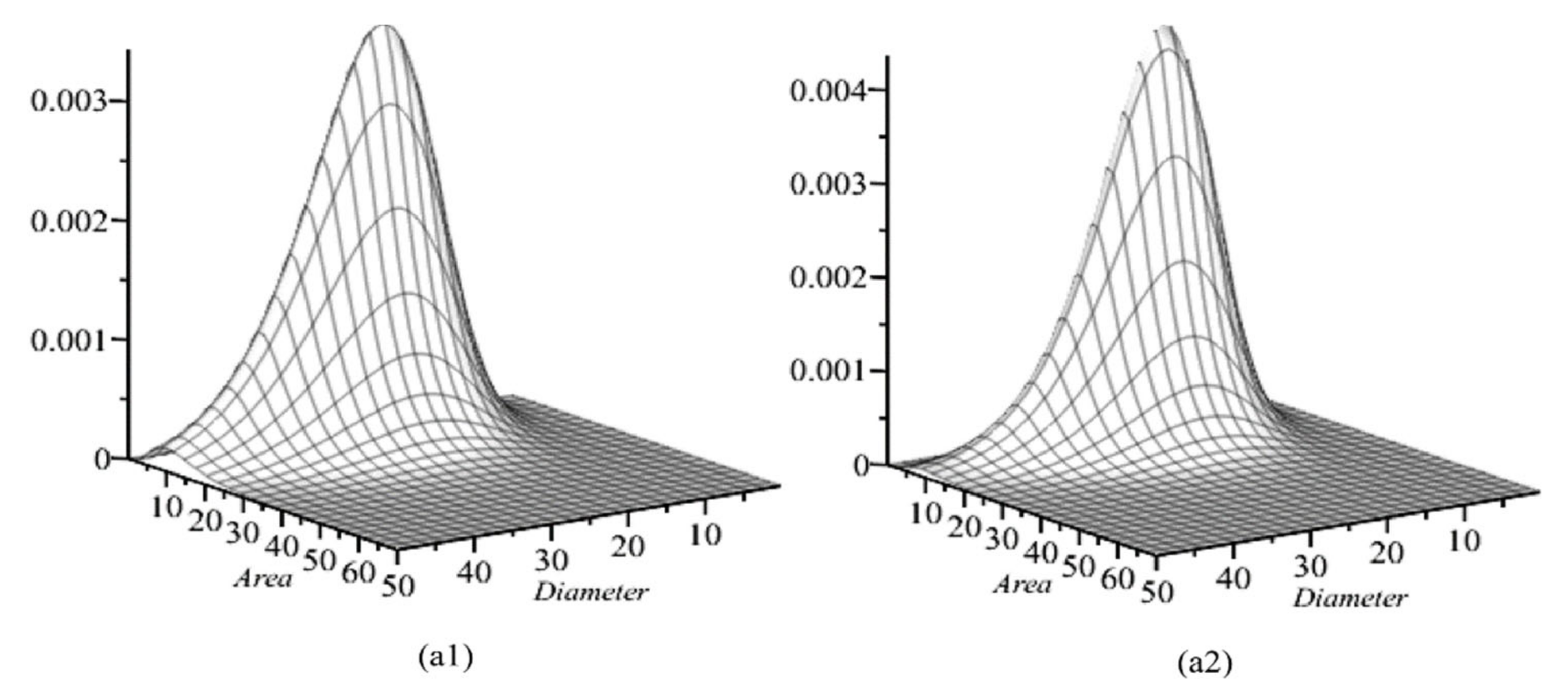
3.2. Visualization of Trivariate, Bivariate, and Univariate Conditional Copula Densities
3.3. Tree Diameter, Potentially Available Area, and Height Dynamic
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghosh, S.; Bhuyan, P.; Finkelstein, M. On a bivariate copula for modeling negative dependence: Application to New York air quality data. Stat. Methods Appl. 2022, 1–25. [Google Scholar] [CrossRef]
- Emura, T.; Michimae, H.; Matsui, S. Dynamic Risk Prediction via a Joint Frailty-Copula Model and IPD Meta-Analysis: Building Web Applications. Entropy 2022, 24, 589. [Google Scholar] [CrossRef]
- Dewick, P.R.; Liu, S. Copula Modelling to Analyse Financial Data. J. Risk Financ. Manag. 2022, 15, 104. [Google Scholar] [CrossRef]
- Kupka, I.; Kiseľák, J.; Ishimura, N.; Yoshizawa, Y.; Salazar, L.; Stehlík, M. Time evolutions of copulas and foreign exchange markets. Inf. Sci. 2018, 467, 163–178. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Gijbels, I.; Omelka, M.; Veraverbeke, N. Estimation of a copula when a covariate affects only marginal distributions. Scand. J. Stat. 2015, 42, 1109–1126. [Google Scholar] [CrossRef]
- Abegaz, F.; Gijbels, I.; Veraverbeke, N. Semiparametric estimation of conditional copulas. J. Multivar. Anal. 2012, 110, 43–73. [Google Scholar] [CrossRef]
- Rupšys, P. Stochastic Mixed-Effects Parameters Bertalanffy Process, with Applications to Tree Crown Width Modeling. Math. Probl. Eng. 2015, 2015, 375270. [Google Scholar] [CrossRef]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Baltic For. 2013, 19, 43–151. [Google Scholar]
- Rupšys, P. Understanding the Evolution of Tree Size Diversity within the Multivariate nonsymmetrical Diffusion Process and Information Measures. Mathematics 2019, 7, 761. [Google Scholar] [CrossRef]
- Narmontas, M.; Rupšys, P.; Petrauskas, E. Models for Tree Taper Form: The Gompertz and Vasicek Diffusion Processes Framework. Symmetry 2020, 12, 80. [Google Scholar] [CrossRef]
- Lima, L.d.S. Fractional Stochastic Differential Equation Approach for Spreading of Diseases. Entropy 2022, 24, 719. [Google Scholar] [CrossRef] [PubMed]
- Di Crescenzo, A.; Martinucci, B.; Mustaro, V. A Model Based on Fractional Brownian Motion for Temperature Fluctuation in the Campi Flegrei Caldera. Fractal Fract. 2022, 6, 421. [Google Scholar] [CrossRef]
- Wagner, V.; Radde, N.E. SiCaSMA: An Alternative Stochastic Description via Concatenation of Markov Processes for a Class of Catalytic Systems. Mathematics 2021, 9, 1074. [Google Scholar] [CrossRef]
- Rupšys, P. Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests 2019, 10, 506. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Analysis of Longitudinal Forest Data on Individual-Tree and Whole-Stand Attributes Using a Stochastic Differential Equation Model. Forests 2022, 13, 425. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, Q.V.; Qu, Y.; Zhang, J. Deriving tree growth models from stand models based on the self-thinning rule of Chinese fir plantations. IForest 2022, 15, 1–7. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Symmetric and Asymmetric Diffusions through Age-Varying Mixed-Species Stand Parameters. Symmetry 2021, 13, 1457. [Google Scholar] [CrossRef]
- Narmontas, M.; Rupšys, P.; Petrauskas, E. Construction of Reducible Stochastic Differential Equation Systems for Tree Height–Diameter Connections. Mathematics 2020, 8, 1363. [Google Scholar] [CrossRef]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; Mccarron, J. Maple Advanced Programming Guide; Maplesoft: Waterloo, Canada, 2007. [Google Scholar]
- Itô, K. Stochastic integral. Proc. Imp. Acad. 1944, 20, 519–524. [Google Scholar] [CrossRef]
- Cherny, A.S.; Engelbert, H. Singular Stochastic Differential Equations; No. 1858.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Rupšys, P.; Narmontas, M.; Petrauskas, E. A Multivariate Hybrid Stochastic Differential Equation Model for Whole-Stand Dynamics. Mathematics 2020, 8, 2230. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. 1959, 8, 229–231. [Google Scholar]
- Genest, C.; Ghoudi, K.; Rivest, L.P. A semiparametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika 1995, 82, 543–552. [Google Scholar] [CrossRef]
- Liebscher, E. Semiparametric estimation of the parameters of multivariate copulas. Kybernetika 2009, 45, 972–991. [Google Scholar]
- Gao, H.; Liu, Q.; Song, Y.; Jiang, M.; Yin, Y. Modeling Primary Branch Diameter and Length for Planted Pinus koraiensis by Incorporating Neighbor Competition in Northeast China. Forests 2022, 13, 912. [Google Scholar] [CrossRef]
- Tian, N.; Gan, J.; Pelkki, M. Stem profile of red oaks in a bottomland hardwood restoration plantation forest in the Arkansas Delta (USA). iForest 2022, 15, 179–186. [Google Scholar] [CrossRef]
- Ishihara, M.I.; Konno, Y.; Umeki, K.; Ohno, Y.; Kikuzawa, K. A new model for size-dependent tree growth in forests. PLoS ONE 2016, 11, e0152219. [Google Scholar] [CrossRef][Green Version]
- Rupšys, P.; Petrauskas, E. Evolution of Bivariate Tree Diameter and Height Distribution via Stand Age: Von Bertalanffy Bivariate Diffusion Process Approach. J. Forest Res. 2019, 24, 16–26. [Google Scholar] [CrossRef]
- Bai, Z.; Wei, H.; Xiao, Y.; Song, S.; Kucherenko, S. A Vine Copula-Based Global Sensitivity Analysis Method for Structures with Multidimensional Dependent Variables. Mathematics 2021, 9, 2489. [Google Scholar] [CrossRef]


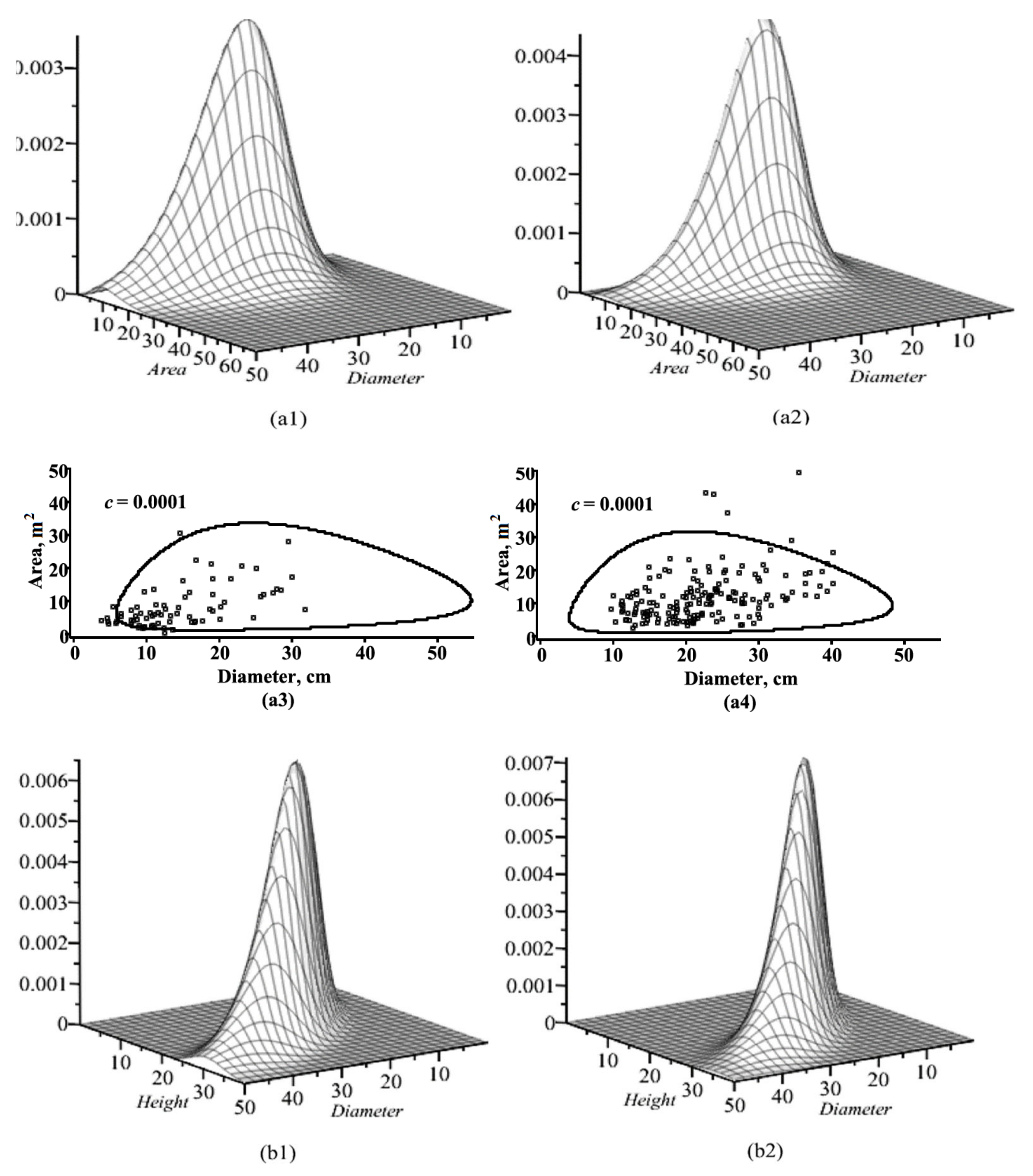
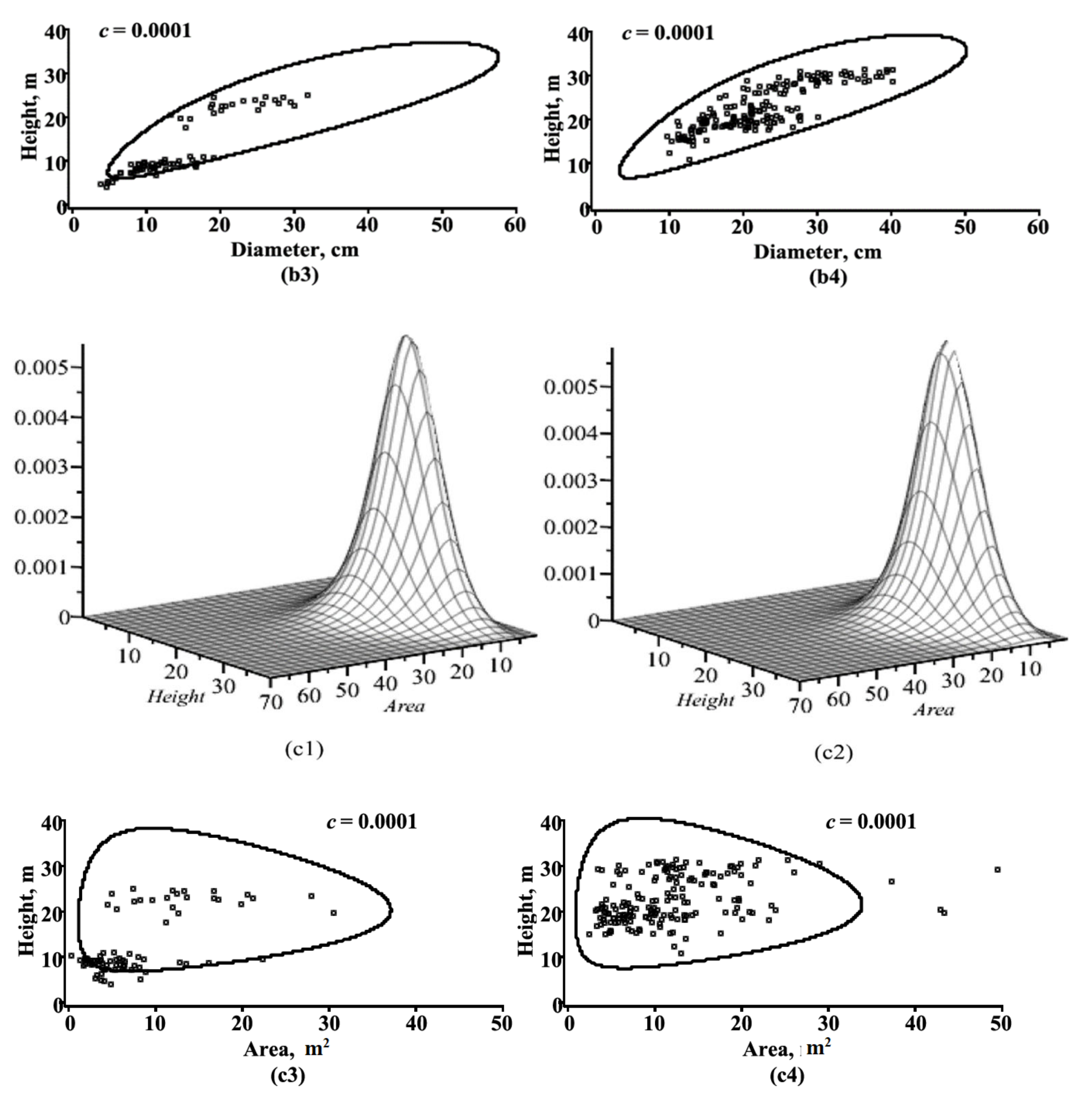
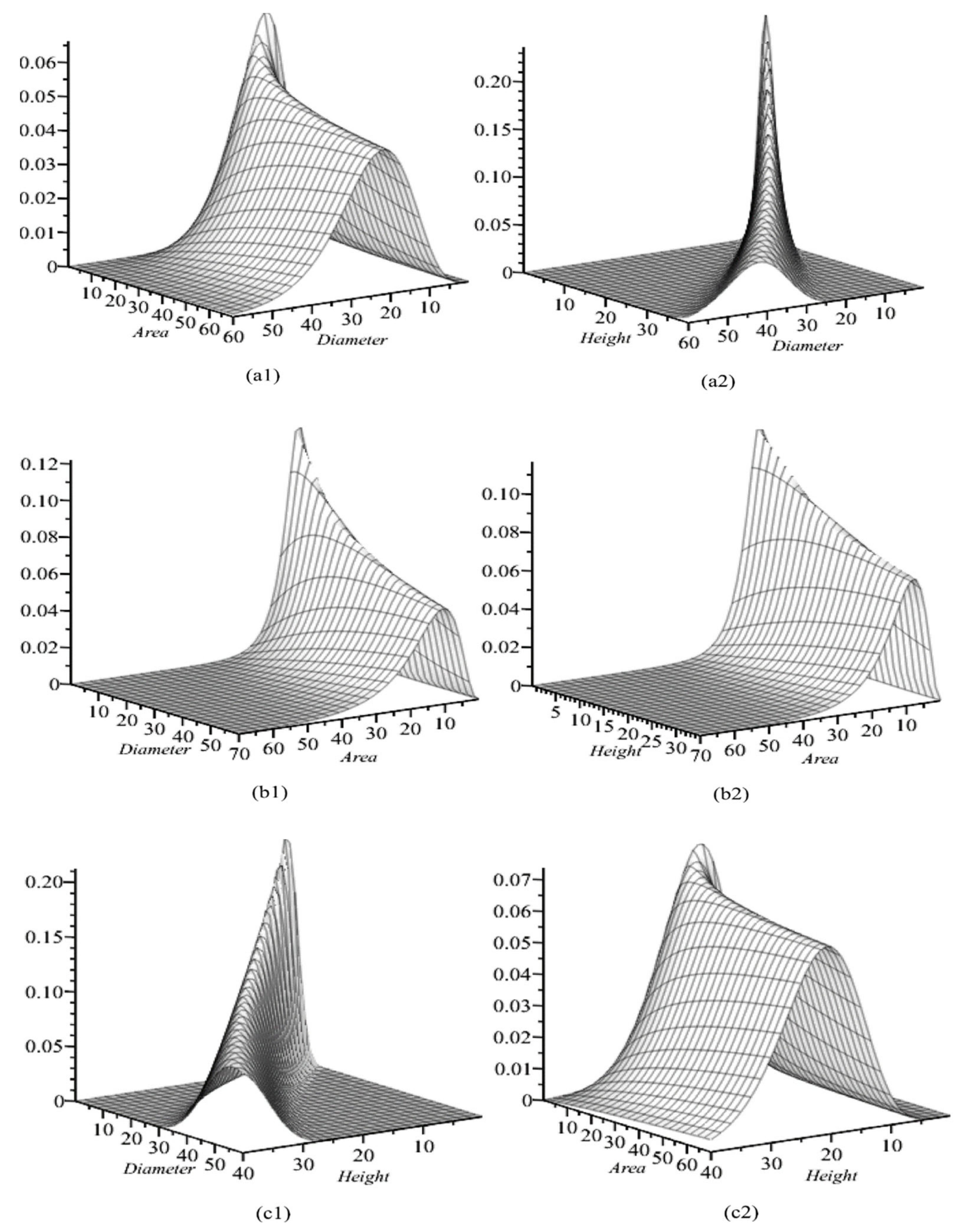
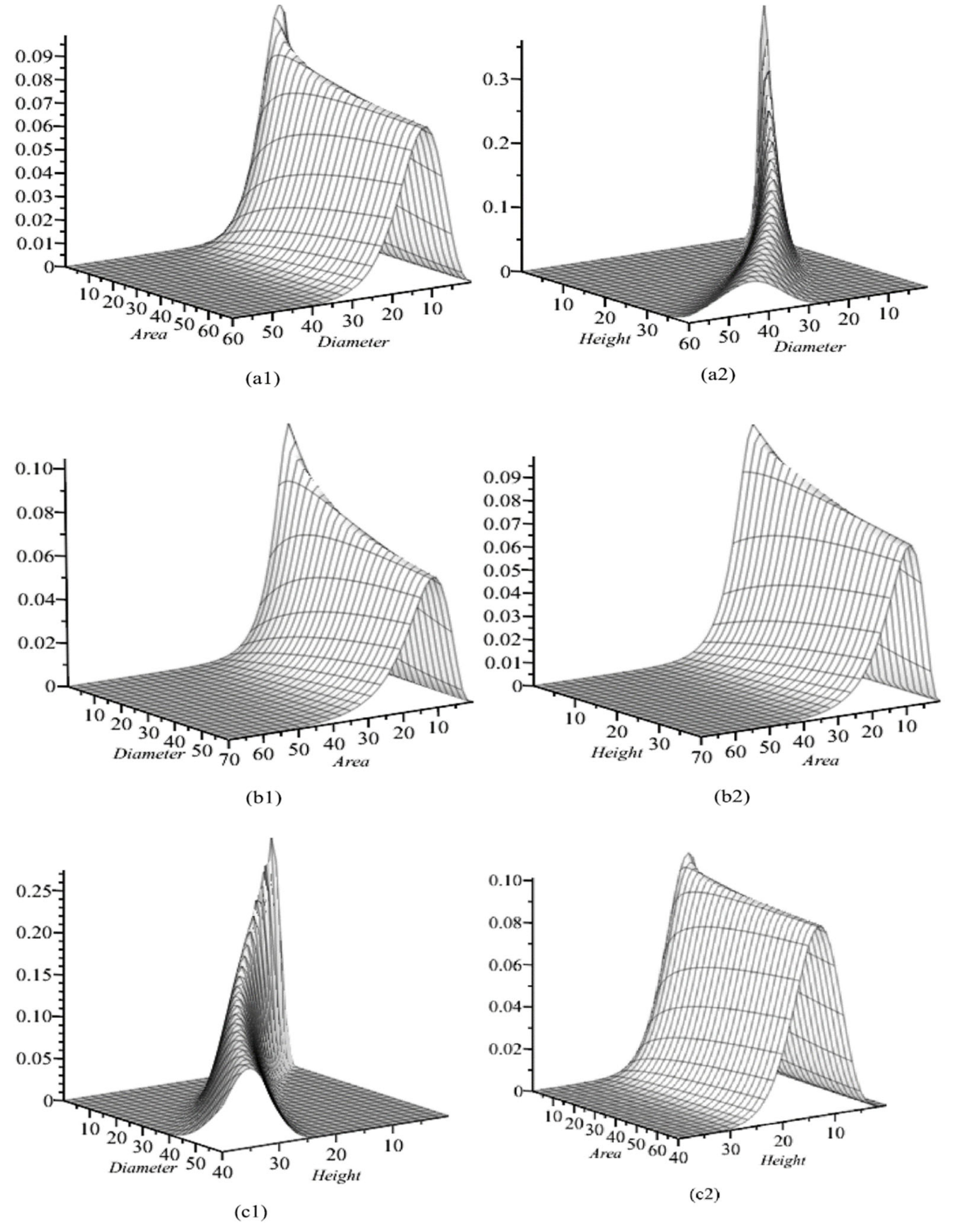

| Attribute | α | β | ɣ | σ | δ | σx |
|---|---|---|---|---|---|---|
| Fixed effect scenario models (1) | ||||||
| Diameter | 0.0860 (0.0014) | 0.0226 (0.0005) | −11.9338 (0.4604) | 0.0037 (0.0002) | - | - |
| Area | 0.0641 (0.0011) | 0.0186 (0.0004) | −1.3008 (0.0514) | 0.0139 (0.0003) | 1.7570 (0.0277) | - |
| Height | 0.0827 (0.0026) | 0.0214 (0.0001) | −14.1101 (1.6421) | 0.0017 (0.0003) | - | - |
| Mixed effect scenario models (1) | ||||||
| Diameter | 0.0850 (0.0006) | 0.0226 (0.0002) | −7.1108 (0.0953) | 0.0042 (0.0001) | - | 0.0069 (0.0010) |
| Area | 0.0617 (0.0006) | 0.0186 (0.0002) | −1.3260 (0.0358) | 0.0102 (0.0001) | 1.6151 (0.0237) | 0.0094 (0.0014) |
| Height | 0.0827 (0.0011) | 0.0213 (0.0003) | −13.3459 (0.3489) | 0.0013 (0.00005) | - | 0.0042 (0.0006) |
| ρ12 | ρ13 | ρ23 |
|---|---|---|
| Fixed effect scenario | ||
| 0.2390 (0.0103) | 0.8619 (0.0021) | 0.1720 (0.0100) |
| Mixed effect scenario | ||
| 0.1513 (0.0101) | 0.8528 (0.0022) | 0.0877 (0.0100) |
| Predictors (Equation) | Individual Tree Case | Whole-Stand Case | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B * (%) | AB (%) | RMSE (%) | R2 | T p-Value | B (%) | AB (%) | RMSE (%) | R2 | T p-Value | |
| Tree diameter | ||||||||||
| t: (5) | −0.1180 (−34.83) | 4.8240 (55.80) | 6.5364 (40.52) | 0.6348 | 0.0938 | −0.4769(−2.13) | 1.5016 (7.51) | 2.0481 (10.05) | 0.9102 | 0.0172 |
| t, A: (29) | 0.0909 (−33.57) | 4.7460 (55.12) | 6.4493 (39.98) | 0.6445 | 0.1906 | −0.3283 (−1.98) | 1.3798 (7.13) | 1.9083 (9.36) | 0.9238 | 0.0766 |
| t, H: (29) | −0.0920 (−8.45) | 2.4136 (22.08) | 3.4921 (21.65) | 0.8958 | 0.0145 | 0.1634 (0.94) | 0.8813 (4.67) | 1.3568 (6.66) | 0.9621 | 0.2134 |
| T, A, H: (30) | −0.1093 (−8.49) | 2.3725 (21.92) | 3.4242 (21.23) | 0.8998 | 0.0044 | 0.0387 (0.31) | 0.8684 (4.61) | 1.3495 (6.62) | 0.9630 | 0.7661 |
| Tree area | ||||||||||
| t: (5) | −0.1092 (−37.26) | 3.9093 (60.74) | 6.0131 (63.98) | 0.4390 | 0.0919 | −0.2376 (−2.24) | 1.0706 (9.16) | 1.5444 (12.37) | 0.9412 | 0.1127 |
| t, D: (29) | −0.0840 (−35.98) | 3.8417 (59.31) | 5.9327 (63.12) | 0.4541 | 0.1886 | −0.2128 (−2.48) | 0.9978 (8.86) | 1.3948 (11.17) | 0.9521 | 0.1157 |
| t, H: (29) | −0.0864 (−36.59) | 3.8832 (60.09) | 5.9846 (63.67) | 0.4445 | 0.1801 | −0.1691 (−2.06) | 0.9867 (8.74) | 1.4184 (11.36) | 0.9509 | 0.2178 |
| T, D, H: (30) | −0.0775 (−35.92) | 3.8191(59.12) | 5.9044 (62.82) | 0.4593 | 0.2229 | −0.2495 (−2.80) | 1.0414 (9.22) | 1.4316 (11.46) | 0.9491 | 0.0728 |
| Tree height | ||||||||||
| t: (5) | −0.0035 (−18.37) | 3.3658 (35.56) | 4.5945 (29.41) | 0.7487 | 0.9436 | −0.2657 (−1.44) | 0.9825 (5.41) | 1.2777 (6.61) | 0.9524 | 0.0329 |
| t, D: (29) | 0.0229 (−6.22) | 1.6828 (15.84) | 2.3341 (14.94) | 0.9351 | 0.3609 | −0.3530 (−2.20) | 0.6799 (3.90) | 0.9609 (4.46) | 0.9758 | 0.0001 |
| t, A: (29) | 0.0292 (−18.30) | 3.3495 (35.43) | 4.5647 (29.22) | 0.7518 | 0.5516 | −0.3061 (−1.76) | 0.9416 (5.28) | 1.2044 (6.23) | 0.9568 | 0.0095 |
| T, D, A: (30) | 0.0235 (−6.12) | 1.6721 (15.75) | 2.3232 (14.87) | 0.9357 | 0.3462 | −0.3062 (−1.95) | 0.6572 (3.77) | 0.8661 (14.03) | 0.9764 | 0.0004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rupšys, P.; Petrauskas, E. On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations. Symmetry 2022, 14, 2127. https://doi.org/10.3390/sym14102127
Rupšys P, Petrauskas E. On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations. Symmetry. 2022; 14(10):2127. https://doi.org/10.3390/sym14102127
Chicago/Turabian StyleRupšys, Petras, and Edmundas Petrauskas. 2022. "On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations" Symmetry 14, no. 10: 2127. https://doi.org/10.3390/sym14102127
APA StyleRupšys, P., & Petrauskas, E. (2022). On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations. Symmetry, 14(10), 2127. https://doi.org/10.3390/sym14102127






