Abstract
The multi-objective reliability-based design optimization (MORBDO) of an aircraft structure employing a non-probabilistic model, at present, still has a high level of analysis complexity while solving the possibility safety index (PSI) as they are a triple-loop nested problem. Many techniques have been proposed to expedite the process of solving their inner loop with a single objective function; however, research on applying multi-objective optimization to complete this task is required. This research paper aims to reduce the solution complexity in the MORBDO of an aircraft wing structure, which is a symmetrical part of the aircraft structure. The present framework is comprised of a two-step technique that begins with the multi-objective optimization (MODO) of the wing structure, followed by its reliability analysis. A non-probabilistic model is adopted for uncertainty consideration, contrary to frequently used probabilistic models. The reliability design problem has aircraft wing mass, flutter speed, and the possibility safety index as objective functions. According to the results, the proposed MORBDO technique is highly effective in reducing the complexity of aircraft wing structural design and can generate more conservative and feasible design solutions with various PSI values. Such a design can be achieved within a single run, which has not been done in previous studies. The results show that the highest reliability aircraft wing structure mass is 104.8504 kg at a flutter speed of 584.5670 m/s. Additionally, the developed framework explicitly states the relationship between MODO and MORBDO.
1. Introduction
Modern aircraft require significant weight reduction, which makes optimization an effective design tool. The major issue in engineering design, particularly in the structure of an aircraft, is the real-world uncertainty factors. As the whole aircraft structure involves numerous uncertainties, the deterministic design optimization approach cannot handle it [1]. The optimal design result obtained through these conventional deterministic techniques cannot be used in practice because of numerous uncertainties, deviating the actual performance of an aircraft far from the obtained one. To avoid this impracticality, reliability-based design optimization (RBDO) has been used to accomplish the quantification of uncertainties and their incorporation into a particular deterministic design process. In the past, many uncertainty quantification techniques have been proposed, which are expected to analyze the reliability or failure probability of a design problem [2,3,4,5]. Traditionally, probabilistic approaches are commonly used to quantify the failure probability rather than non-probabilistic techniques. The former group includes the first-order reliability method (FORM), the first-order and second moment (FOSM), and the second-order reliability method (SORM) [6]. Many adaptation forms are proposed to calculate the reliability index of the design space at the most probable point (MPP). The polynomial chaos expansion (PCE) technique has been successfully used to estimate the uncertainties in the Goland wing design. This approach composes a random process into the deterministic and orthogonal functions of space and time, respectively, before redistributing the variables. The reliability index of the aeroelastic phenomena is predicted with this technique [7]. Reducing the number of random variables improved the results, as seen in [8]. Also, the technique has been used to study the uncertainty quantification of a generic UAV wing [9]. However, the disadvantage of this type of technique is the need for more precise data. The more precise calculation leads to a computational burden almost as severe as using a Monte Carlo simulation (MCS). A variant of Latin hypercube sampling (LHS), which is the optimum Latin hypercube sampling (OLHS), was also employed to improve a more precise probability distributed function (PDF) [10].
To overcome the computational complexity of the first group, non-probabilistic techniques are developed to solve the RBDO without the precise PDF requirement. The examples in this group are a convex set [3], an interval method [4], and fuzzy set theory [5]. Because of the probability of failure calculation and optimization solving, typically, RBDO issues are considered double-looped nested problems. The task will be changed to a triple-looped nested problem due to the possibility safety index (PSI) calculation in the case of the non-probability approach. The PSI value has been proven to be related to failure probability, but it is more conservative when compared with the probability approach [5]. Likewise, it is called the possibility safety index-based design optimization (PSIBDO). The target-performance-based design approach (TPBDA) has been used to solve the triple-looped problem by transforming it into a double-loop nested framework [5]. Furthermore, the double-loop nested problem can be simplified to a single one using the interval perturbation method (IMP) [11].
Recently, the triple-loop nested problem has been solved by employing multi-objective MHs [1,12,13]. This technique transforms the original single-objective optimization problem into a new multi-objective optimization problem, whereas the additional objective function is an equivalent possibilistic safety index (EPSI). The complexity due to a double-loop nested problem can be reduced to a single one, which can be accomplished within one optimization run [12].
Future airplane components will be composed of composite materials rather than isotropic materials due to the advancement of aviation materials. These materials, including carbon fiber, pose high mechanical strength-to-weight, low volume-weight ratios [14,15], enhanced corrosion resistance, and thermal insulation properties relative to conventionally used materials.
The RBDO of aircraft aeroelasticity often requires high computational time due to aircraft structure complexity. Further, it becomes more challenging to solve with non-probabilistic techniques as the double-loop nested problem changes to a triple-loop nested issue. Presently, only a few techniques introduce the non-probabilistic reliability index into the aeroelastic optimization design of aircraft wings [6]. In a fairly recent study, the worst-case scenario was used to design an aeroelastic two-dimensional wing using MHs [1]. Another type of artificial intelligence (AI), i.e., deep neural networks (DNNs), has been used to predict the lift of the turbofan engine, which is expected to increase the reliability and safety of the engine system [16].
Instead of being a straightforward single-objective optimization, the practical RBDO of aircraft wing structures is a sophisticated multi-objective optimization problem [1]. Luo and Grandhi suggested a two-step approach that efficiently combined RBDO with a multi-objective evolutionary algorithm (MOEA) to solve challenging truss structures [17]. In the past, multi-objective optimization has been improved [18,19,20,21,22] in combination with the regression surrogate models for solving aerostructures [10], tolerance-aware problems [23,24,25], etc. Such studies use interesting techniques in the group of probability for uncertainty quantification. A regression surrogate has been proposed for reducing time consumption. In a group of non-probability techniques, the study applies reliability-index and target-performance-based methodology [12,26] to handle double-loop nested RBDO problems. Later, many researchers proposed different techniques to solve the RBDO of structures, including the safety factor concept-based decoupled method suggested by Shayanfar et al. [27], Safaeian et al. [28], and Ho-Huu et al. [29,30] suggested adaptive elitist differential evolution (aeDE) and integrated a double loop method and design amplification factor-based efficient single loop method [31]. The response surface has also been used to suppress the computational time of RBDO [32].
In general, to tackle RBDO, a two-step approach for optimization and reliability is needed. Thus, in this study, an RBDO of an aircraft wing structure is performed by a multi-objective evolutionary optimization, followed by its reliability analysis. This study couples a non-probabilistic approach to realize reliability with single-objective design optimization that can be split into multi-objective optimization. This study is an extension of a recent study that used fuzzy modeling to solve an RBDO of an airplane wing structure [33,34], which is a symmetrical part of the aircraft structure. The former studies expected to reduce mass by performing the PSIBDO approach in the form of single and multi-objective optimization, respectively. Both problems are performed continuously rather than separated into two steps as in the present work.
The rest of this paper is divided into four sections; Section 2 illustrates the two-step multi-objective reliability-based design using PSI and fuzzy set framework. Adopted numerical experiment settings are presented in Section 3, while the results are discussed in Section 4. Finally, the conclusions of this investigation and developed prospects are shown in Section 5.
2. A Two-Step Multi-Objective Reliability-Based Design Using Fuzzy Set Model
2.1. Possibility Safety Index
Firstly, the relationship between RBDO and multi-objective design optimization (MODO) has been proposed by the comparative study presented in [32]. The study reveals the relation and extension of a new approach based on the combination of MOEA and reliability analysis, which has some advantages over the traditional technique as it can find the reliable, optimum solution set in one optimization run. Next, the technique starts with formulating and solving a MODO problem, followed by a reliability analysis of a solution set. The suggested technique can reduce the time for finding a reliable solution set by starting to search from the deterministic solution set rather than from random points.
The deterministic design optimization of a real-world problem can be formulated as Equation (1), where the objective is to minimize certain goal functions with design constraints. The single-objective or multi-objective design optimization problem can be expressed as
where i = 1 for a single objective design, i > 1 for a multi-objective problem, x is a vector of design variables with a lower limit (xl) and the upper limit (xu), gj are inequality constraints, and N is the number of inequality constraint.
Min fi (x) i = 1, ..., M
Subject to gj(x) ≥ 0 j = 1,2, ..., N
xl ≤ x ≤ xu
The solution of (1) is called a deterministic solution. The uncertainty can disturb the optimum solution, rendering it unsuitable in real applications. In cases of a non-probability technique, random variables or uncertainties are modeled with a fuzzy (a) function. The RBDO and the fuzzy function can be performed with the possibility safety index (PSI) of constraints [9], as shown here:
where “sup” is the supremum.
From (1) and (2), the RBDO problem can be rearranged from the deterministic design optimization problem based on the PSI and a fuzzy set model, as shown as
where a = (a1, a2, …, al) is a vector of fuzzy variables, πfmax is an allowable possibility safety index, and πfj is the PSI of each constraint.
Min fi (x) i = 1, ..., M
Subject to πfj = Pos (gj(x,a) ≤ 0) ≤ πfmax j = 1,2, ..., N
xl ≤ x ≤ xu
The PSI value πfj can be found by solving a double-loop nested problem in (4) having μ(gj(x,a)) membership function as illustrated in Figure 1.
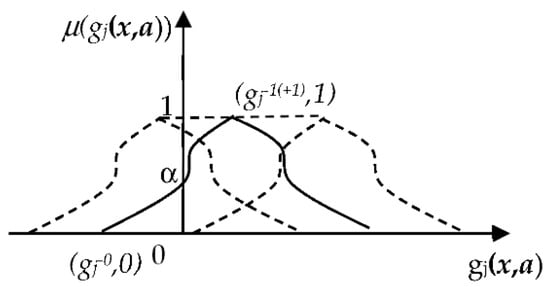
Figure 1.
Membership function μ(gj(x,a)).
The solution of this equation can be calculated if gj−0 and gj−1 are known. If gj−0 ≤ 0, we can obtain that Pos(gj(x,a) ≤ 0) = 0 or 1, and the solution procedure can be terminated. In cases where gj−0 ≤ 0 ≤ gj−1, the equation gj−α = 0 should be solved, and its solution α will be the value of πfj = Pos(gj(x,a) ≤ 0). The bi-section method is used to compute πfj, which uses the procedure detailed in [12,13]. The procedure can be expressed in the form of a flow diagram, as presented in Figure 2. When the bisection technique is used to solve the sub-problem (lower level) to find the possibility safety index, only the PSI calculation of the constraint should be solved N times at each step of modification of x in the upper level of (3). Calculating the PSI value results in a double-loop nested problem, which subsequently becomes a triple-loop nested issue when combined with the optimization of the objective function [11,12,13].
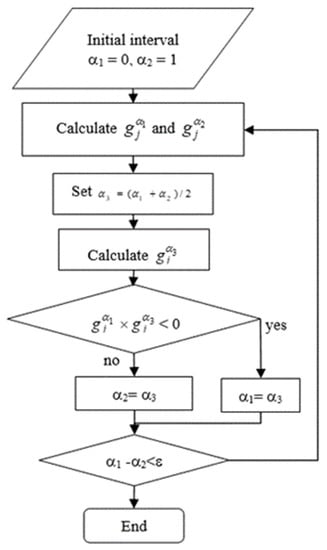
Figure 2.
Flow diagram of a bisection method for solving PSI.
The present idea is to reduce the complexity of the triple-loop nested problem so that the MORBDO can perform in one optimization run with a two-step approach.
2.2. Two-Step Approach
The elementary RBDO problem of Equation (3) is reorganized into a MORBDO problem based on the PSI and a fuzzy set model by incorporating the maximum PSI as one of the objective functions as follows:
where πfmax is the maximum PSI, and πfj is the PSI of each constraint.
Min {fi(x), πfmax} i = 1, ..., M
Subject to Pos(gj(x,a) ≤ 0) = πfjmax j = 1,2, ..., N
max(πfjmax) = πfmax j = 1,2, ..., N
xl ≤ x ≤ xu
From problems (1) and (5), it can relate MODO and reliability through a two-step concept as follows:
- To perform the multi-objective optimization run to find the solution set.
- To perform the multi-objective reliability-based analysis to find the solution set using the solution set from step 1.
On the other hand, the two-step framework leads to some advantages:
- The new technique solution is a solution set with various PSI values derived from a single optimization run, which saves time. A designer can use it for an aircraft wing structure design with a different PSI value or an equivalent of probability failure.
- It is simple to handle and apply to the real optimization problem, which is a MODO problem.
- The present technique is simple to combine with a high-performance MOEA.
2.3. ARPBIL-DE Optimizer
In this study, the two-step approach is solved with real code population-based incremental learning and differential evolution (RPBIL-DE), which is a hybrid method. The adaptation RPBIL-DE (aRPBIL-DE) has been used to study reliability-based design optimization of a steering linkage [13]. In general, the RPBIL creates a population according to the probability matrix . Either row (or column) of the matrix will establish a subpopulation, which is essential to create a population of the design variable’s solutions iteratively. The obtained population is modified by using DE reproduction, which is the DE/best/2/bin scheme.
Optimization problem (5) can be solved with MHs. Although MH approaches are capable of handling a triple-loop nested task, they add computational complexity. Since non-probabilistic techniques are powerful, can cut down on computing time, and have limited investigations, it is crucial to investigate their effectiveness in dealing with the design of aeroelastic wing structures.
3. Numerical Experiment
The aeroelastic design of a composite aircraft wing with fuzzy material property uncertainties and permitted transverse wing displacement serves as the design demonstration of this research. The Goland wing [35] is used as the model of an aircraft wing’s structure (Figure 3). In general, the geometry of the Goland wing is 1.216 m in chord length and 6.096 m in the semi-span wing. The aircraft wing has two major materials. The main structures are aluminum spars and ribs. The whole skin of the wing is made from three layers of laminated carbon fiber, and the general properties of the aluminum and carbon fiber are listed in Table 1.
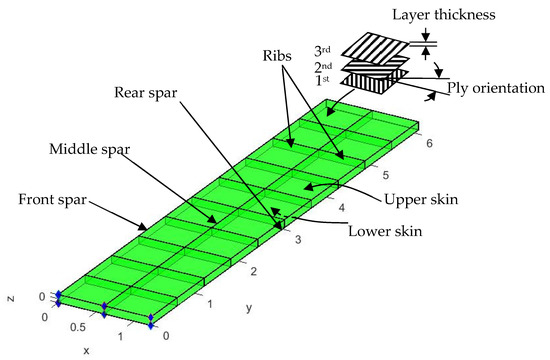
Figure 3.
Goland wing geometry model.

Table 1.
Aluminum and carbon fiber properties.
The optimization problem can be formulated as follows:
where vf is found from solving dynamics aeroelasticity, which is called flutter speed. The speed should be defined as higher than an allowable flutter speed, vf,al. The constraint defines handling the wing operating far from a critical speed. To control the flexibility of the aircraft wing, the maximum transverse displacement on the wing, umax, should be suppressed to lower than an allowable transverse displacement, ual. ηL and ηL,al are wing lift effectiveness and its allowable value, respectively. Aerodynamic conditions, structural constraints, and aeroelastic limits are set as ρair is 1.2 kg/m3, free stream air velocity is 40 m/s, ual is 0.1 m, ηL,al is 0.9, and vf,al is 180 m/s, respectively.
Min f(x) = {mass, −vf}
Subject to −vf,al + vf ≥ 0
−umax + ual ≥ 0
xl ≤ x ≤ xu
As mentioned in the previous section, the aircraft wing is made of aluminum spars and ribs, while the skin is made of three layers of laminated carbon fiber, as shown in Figure 3. The thicknesses of the aircraft wing structures and the ply orientations of the skin layers are set as design variables. The total number of design variables is 14, considered from 2 groups of the aircraft wing structure, i.e., the thickness of the rib, spar and skin, and composite ply orientations, which can be described as follows.
x1–3 = upper skin thickness(1st–3rd layer)
x4–6 = lower skin thickness(1st–3rd layer)
x7 = rib thicknes
x8 = spar thickness
x9–11 = lower skin ply orientations(1st–3rd layer)
x12–14 = upper skin ply orientations(1st–3rd layer)
Undoubtedly, to make our model realizable in practice, the design variables are assigned being discrete, where the bound constraints are set as follows:
xi ∈ {0.0005, 0.001, 0.0015, 0.002, 0.0025, 0.003, 0.0035, 0.004, 0.0045, 0.005}m for x1–8 and xi∈{0 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165} degree for x9–14.
Aircraft wing structural analyses are carried out based on finite element analysis using the quadrilateral Mindlin shell elements with a drilling degree of freedom for both static and dynamic analyses. An aerodynamic analysis is performed by using a vortex ring method [10]. The flutter analysis is then conducted using a quasi-steady aerodynamic technique, which produces findings comparable to those of commercial tools. The structural mass is selected as an objective function of a modern aircraft design due to energy saving. The dynamic aeroelastic is considered only the flutter speed, while the static aeroelastic is lift effectiveness. To handle aircraft structural performance in flight, flutter speed is selected as the objective and constraint function. The flexibility in the aerodynamics of the aircraft wing is depicted when the lift effectiveness is higher than the defined allowable value. This parameter has been used to specify the performance of the wing structure as a morphing structure [36]. The last constraints are the limitation of the design variable, which is defined depending on the safety requirements of the operating conditions.
The optimizer for solving the MRBDO problem is aPBIL-DE, which is efficient for solving multi-objective optimization problems [13,34].
4. Results and Discussions
Uncertainty is considered in this research for the material property and allowable transverse displacement on the wing, which are Young’s modulus and ual, respectively. In this study, the uncertainties are modeled with normal fuzzy membership functions: , E11 = and , where Em =70 GPa, E11m = 207.7 GPa, and are the core of functions, respectively. By using the two-step technique, Equation (6) can be arranged into Equation (5) using a triple-loop nested scheme to solve the problem. A PC with the following specifications, an AMD Ryzen 5 4600 H with Radeon Graphics 3.00 GHz, 8.00 GB, and 64-bit Window 10 OS, is used to accomplish the computational analysis. The initial value settings of the optimizer are a population size of 68 and an 800 iteration number in both steps for MODO and MORBDO, while the Pareto archive size considered is 20.
The obtained optimum Pareto solution set of MODO and MORBDO is presented in Figure 4a. Selected optimum solutions are shown in Figure 4b and Table 2. The deterministic Pareto solution set distributes on top of Figure 4a with a PSI = 1.0. The relation between the deterministic solution and the reliability-based solution set is closely related, as mentioned by [32]. Additionally, the relation can be observed from the top view in Figure 4a for two dimensions of mass and flutter axis, as shown in Figure 5. From the figure, we can conclude that the MORBDO solution is closely related to that obtained by using MODO. The two-step approach starts with the optimum solution set of MODO, which can make searching the MORBDO solution easier, as shown by observation of the distribution of MORBDO that has greater distribution than the MODO solution set.
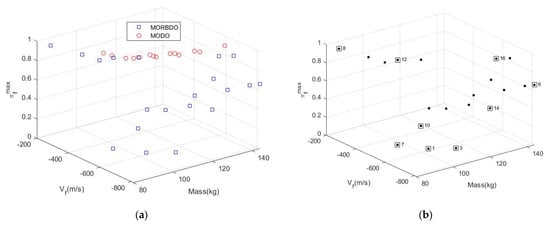
Figure 4.
(a) Pareto frontier; (b) Selected solution of the composite wing.

Table 2.
Selected optimum reliability-based design results of the aircraft wing design.
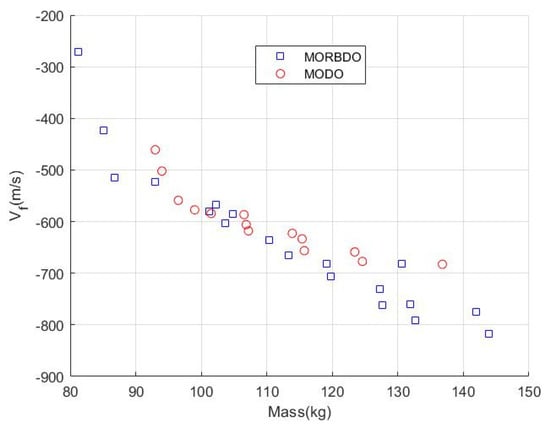
Figure 5.
Comparison of MODO and MORBDO solution set in 2-Dimension (Mass-Vf).
The validation of the proposed technique with the traditional MCS probabilistic approach is needed to confirm that the proposed technique can generate an equivalent reliability solution. The validation experiment starts by selecting design solutions from the Pareto front in Figure 4b, which are the solution numbers 7, 1, 14, and 6. The selected solutions are the non-dominated solution for the bi-objective problem. To make it possible to compare with the probability technique, MCS is used to generate the set of 10,000 sampling points of the random variables at those selected non-dominated solutions. Then function evaluations by means of finite element analysis and computational aeroelastic analysis of those 10,000 points of random variables are performed and used for computing the reliability value (R) for all selected solutions. Moreover, the convergence analysis examined in solution 1 is presented in Figure 6, which demonstrates that the reliability index R converges at 10,000 random numbers. The reliability values of the selected solutions are presented in Table 3. The results show that the increasing reliability values correspond to the decreasing PSI values in the sense that the higher R or the lower πfmax means the safer structure. The new approach can be used to generate more reliable solutions when compared with the MCS, which is supported by the previous research in [12,33,34]. Furthermore, the results demonstrate that the proposed technique, which was developed to describe epistemic uncertainties, is acceptably good. It, nevertheless, needs the experience of a good designer to define the criteria of uncertainty [11].
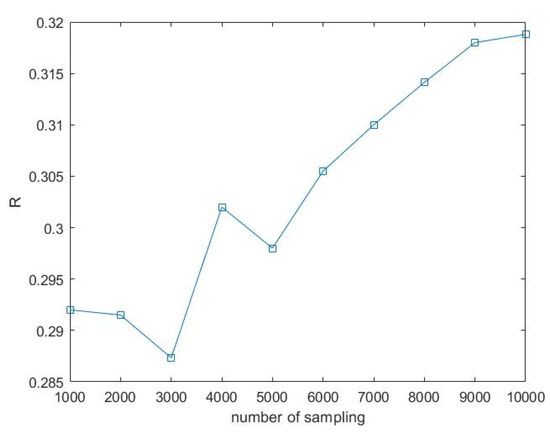
Figure 6.
Convergence plot (R-number of sampling) of solution 1 at a random variable.

Table 3.
Comparative reliability values and PSI values of selected optimum solutions of the aircraft wing design.
The deterministic solution is represented with πfmax = 1 in Table 2. The results of selected allowable PSIs of the composite aircraft wing are selected using the clustering technique [36], as illustrated in the remaining data in the same table. The results reveal that the group of the reliability design (πfmax < 1) gets higher mass aircraft structures when compared with the deterministic design (πfmax = 1). Overall, the permissible PSIs generally decrease as the mass of the aircraft structure increases; however, this is not always the case. It implies that less permissible PSIs have a safer structure, according to previous studies [5,11,12,33]. In fact, the aeroelastic results and structural constraints can be designed to meet the proposed constraints in (6). Some specific design factors from the Table 2 design findings are displayed in Table 4. The outcomes illustrate that the rib, spar, upper skin layer two, and three thicknesses realize a higher value in the case of the reliability design (πfmax < 1) when compared with the deterministic design. The remaining skin thicknesses approach their lower limits. The cross-ply orientations at 90° and 45° are received in a group of the reliability design, while the deterministic design gets 60°. The ply orientation of 90° is obtained as with [33], but the 45° ply orientation is obtained only in this study. The 90 and 45° cross-ply orientations feature medium bending and torsional strength and flexible and high torsional strength, respectively. The traditional cross-ply orientation only occurs in the case of reliability-based design, which makes it safer [33]. The highest reliability aircraft wing structure (πfmax = 0.0011) of the present study has a mass of 104.8504 kg, which is slightly higher than that in [33], but the flutter speed is significantly higher than the previous study. Selected aircraft wing structures are presented in Figure 7 with different πfmax that cause the different aircraft geometry in the sense that the lower πfmax is the safer structure. The proposed new technique was found capable of generating nearly all reliability-based optimum solutions of the composite aircraft wing design in one optimization run by starting from the optimum solution set of MODO issue, which has never been studied. The designer can use their experience to select a more conservative solution from the solution set by considering the allowable PSI value, mass, flutter speed, and design criteria as opposed to the previous study, which only considered objective function and design criteria. Nevertheless, the reliability and deterministic solutions cannot be related to the PSI values from an initial stage, but they can be randomly generated in a range from 0.001–1.

Table 4.
Selected optimum design variables from Table 2.
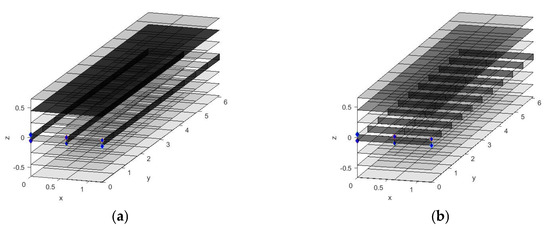
Figure 7.
Selected aircraft wing structure from Table 3 (a) πfmax = 0.0011; (b) Deterministic (πfmax = 1).
From the results, it can be shown that the proposed technique is an alternative for solving an RBDO problem due to its advantages and disadvantages compared to other state-of-the-art techniques, as shown in Table 5. The MCS technique is arguably the most straightforward. It is simple to use but considerably time-consuming because of the incredibly large number of random points and, consequently, the number of function evaluations needed for the reliability calculation of one design solution. It can be less accurate if the space-filling quality of the sampling points is poor. On the other hand, the traditional most probable point is based on the first-order approximation or linearization. This implies that it can be much less accurate if a limit state function is highly nonlinear. Moreover, the method requires an inner loop to search for a reliability index. It is also required to predefine the probability distributions for random variables. Meanwhile, the proposed method does not require probability distribution of the random variables, but it requires the proper intervals of the random variables. The technique needs a bi-section method for determining the PSI, which is still less time-consuming compared to searching for the most probable point. It is also possible to combine all design constraints into one constraint by taking only the maximum value when using the PSI. The present technique, however, has a disadvantage in that the PSI is not statistically meaningful like the reliability index because, as we know, the lower the PSI, the better.

Table 5.
Advantages and disadvantages of some uncertainty quantification techniques.
5. Conclusions
This research presents a new MORBDO, demonstrated with a Goland wing design using the two-step approach, which begins with multi-objective optimization (MODO) of the wing structure, followed by its reliability analysis. Since the deterministic optimum aircraft structure design may be impractical due to the presence of uncertainties, the uncertainties are accounted for in the design problem. A non-probabilistic approach has been examined to find the reliability-based design solution set for aeroelastic structures in the least number of computational runs. Being one of the posteriori-techniques, the suggested approach begins by locating all potential solutions before choosing one. Therefore, the present study uses a fuzzy technique to model the uncertainties and find all possible conservative solutions. Findings demonstrate that the proposed two-step MORBDO can generate all deterministic and conservative optimal aircraft structure designs in one optimization run to be selected later by a designer, which saves running time. The proposed technique is simple for use with a high-performance MOEA and applications to real-world MODO problems rather than a single objective optimization problem. The proposed technique can generate aircraft wing structures with various PSI values in one optimization run in the range of [0.001, 1.0]. From the results, the proposed MORBDO technique is highly effective in reducing the complexity of aircraft wing structural design. Additionally, the developed framework explicitly states the relationship between MODO and MORBDO. Furthermore, the results show the highest reliability aircraft wing structure mass of 104.8504 kg and a flutter speed of 584.5670 m/s. Nevertheless, the exact PSI values cannot be assigned at an initial stage, which will be improved in future studies.
Author Contributions
Conceptualization, S.S. and S.B.; methodology, S.S. and S.B.; Setup and design of the numerical experiments, S.S. and S.B.; performance of the numerical experiments; S.S.; data analysis, S.S., S.K. and S.B.; writing—original draft, S.S. and S.K.; writing—review and editing, S.S., S.K. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support provided by King Mongkut’s Institute of Technology Ladkrabang and the National Research Council Thailand (N42A650549).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful for the financial support provided by King Mongkut’s Institute of Technology Ladkrabang and the National Research Council Thailand.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Sleesongsom, S.; Yooyen, S.; Prapamonthon, P.; Bureerat, S. Reliability-based design optimization of classical wing aeroelasticity. IOP Conf. Ser. Mater. Sci. Eng. 2020, 886, 012015. [Google Scholar] [CrossRef]
- Elishakoff, I.; Colombi, P. Combination of probabilistic and convex models of uncertainty when scare knowledge is present on acoustic excitation parameters. Comput. Methods Appl. Mech. Eng. 1993, 104, 187–209. [Google Scholar] [CrossRef]
- Fang, J.; Smith, S.M.; Elishakoffk, I. Combination of anti-optimization and fuzzy-set-based analyses for structural optimization under uncertainty. Math. Probl. Eng. 1998, 4, 187–200. [Google Scholar] [CrossRef]
- Moller, B.; Graf, W.; Beer, M. Fuzzy structural analysis using α-level optimization. Comput. Mech. 2000, 26, 547–565. [Google Scholar] [CrossRef]
- Tang, Z.C.; Lu, Z.Z.; Hu, J.X. An efficient approach for design optimization of structures involving fuzzy variables. Fuzzy Set. Syst. 2014, 255, 52–73. [Google Scholar] [CrossRef]
- Wang, L.; Lui, G.; Qiu, Z. Review: Recent developments in the uncertainty-based aero-structural design optimization for aerospace vehicles. J. Harbin. Inst. Technol. 2018, 25, 1–15. [Google Scholar]
- Manan, A.; Cooper, J. Design of composite wings including uncertainties: A probabilistic approach. J. Aircr. 2009, 46, 601–607. [Google Scholar] [CrossRef]
- Scarth, C.; Cooper, J.E.; Weaver, P.M.; Silva, G.H.C. Uncertainty quantification of aeroelastic stability of composite plate wings using lamination parameters. Comput. Struct. 2014, 116, 84–93. [Google Scholar] [CrossRef]
- Cook, R.G.; Wales, C.; Gaitonde, A.; Jones, D.; Cooper, J.E.; Tartinville, B.; van der Ven, D. Uncertainty quantification of aeroelastic systems with structural or aerodynamic nonlinearities. In Proceedings of the Applied Aerodynamics Conference, Atlanta, Georgia, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Wansaseub, K.; Sleesongsom, S.; Panagant, N.; Pholdee, N.; Bureerat, S. Surrogate-assisted reliability optimisation of an aircraft wing with static and dynamic aeroelastic constraints. Int. J. Aeronaut. Space Sci. 2020, 21, 723–732. [Google Scholar] [CrossRef]
- Yin, H.; Yu, D.; Xia, R. Reliability-based topology optimization for structures using fuzzy set model. Comput. Methods Appl. Mech. Eng. 2018, 333, 197–217. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Multi-objective reliability-based topology optimization of structures using a fuzzy set model. J. Mech. Sci. Technol. 2020, 34, 3973–3980. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Multi-objective, reliability-based design optimization of a steering linkage. Appl. Sci. 2020, 10, 5748. [Google Scholar] [CrossRef]
- Scarth, C.; Cooper, J.E. Reliability-based aeroelastic design of composite plate wings using a stability margin. Struct. Multi. Discip. Optim. 2018, 57, 1695–1709. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Z.; Guo, S. Efficient method for aeroelastic tailoring of composite wing to minimize gust response. J. Aerosp. Eng. 2017, 1592527. [Google Scholar] [CrossRef]
- Muneer, A.; Taib, S.M.; Naseer, S.; Ali, R.F.; Aziz, I.A. Data-driven deep learning-based attention mechanism for remaining useful life prediction: Case study application to turbofan engine analysis. Electronics 2021, 10, 2453. [Google Scholar] [CrossRef]
- Luo, X.; Grandhi, R.V. Astros for reliability-based multidisciplinary structural analysis and optimization. Comput. Struct. 1997, 62, 737–745. [Google Scholar] [CrossRef]
- Amrit, A.; Leifsson, L.; Koziel, S. Fast multi-objective aerodynamic optimization using sequential domain patching and multifidelity models. J. Aircr. 2020, 57, 388–398. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Accelerated multiobjective design of miniaturized microwave components by means of nested kriging surrogates. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22124. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Rapid multi-objective optimization of antennas using nested kriging surrogates and single-fidelity EM simulation models. Eng. Comput. Int. J. Comput. Aided Eng. 2019, 37, 1491–1512. [Google Scholar] [CrossRef]
- Koziel, S.; PietrenkoDabrowska, A. Fast multi-objective optimization of antenna structures by means of data-driven surrogates and dimensionality reduction. IEEE Access 2020, 8, 183300–183311. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Constrained multi-objective optimization of compact microwave circuits by design triangulation and pareto front interpolation. Eur. J. Oper. Res. 2022, 299, 302–312. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A.; Ullah, U. Tolerance-aware optimization of microwave circuits by means of principal directions and domain-restricted metamodels. IEEE Trans. Microw. Theory Techn. 2022, 70, 4085–4093. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Tolerance optimization of antenna structures by means of response feature surrogates. IEEE Trans. Ant. Prop. 2022. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Tolerance-aware multi-objective optimization of antennas by means of feature-based regression surrogates. IEEE Trans. Ant. Prop. 2022, 70, 5636–5646. [Google Scholar] [CrossRef]
- Lee, J.O.; Yang, Y.S.; Ruy, W.S. A comparative study on reliability-index and target-performance based probabilistic structural design optimization. Comput. Struct. 2002, 80, 257–269. [Google Scholar] [CrossRef]
- Shayanfar, M.; Abbasnia, R.; Khodam, A. Development of a GA-based method for reliability-based optimization of structures with discrete and continuous design variables using Open Sees and Tcl. Finite. Elem. Anal. Des. 2014, 90, 61–73. [Google Scholar] [CrossRef]
- Safaeian Hamzehkolaei, N.; Miri, M.; Rashki, M. An enhanced simulation-based design method coupled with meta-heuristic search algorithm for accurate reliability-based design optimization. Eng. Comput. 2016, 32, 477–495. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Vo-Duy, T.; Nguyen-Thoi, T.; Ho-Nhat, L. Optimization of truss structures with reliability-based frequency constraints under uncertainties of loadings and material properties. In Proceedings of the 1st International Conference on Applied Mathematics in Engineering and Reliability, Ho Chi Minh City, Vietnam, 4–6 May 2016; CRC Press: Boca Raton, FL, USA; pp. 59–65. [Google Scholar]
- Ho-Huu, V.; Le-Duc, T.; Le-Anh, L.; Vo-Duy, T.; Nguyen-Thoi, T. A global single-loop deterministic approach for reliability-based design optimization of structures with continuous and discrete design variables. Eng. Optim. 2018, 50, 2071–2090. [Google Scholar] [CrossRef]
- Dizangian, B.; Ghasemi, M.R. An efficient method for reliable optimum design of trusses. Steel Compos. Struct. 2016, 21, 1069–1084. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Duong-Gia, D.; Vo-Duy, T.; Le-Duc, T.; Nguyen-Thoi, T. An efficient combination of multi-objective evolutionary optimization and reliability analysis for reliability-based design optimization of truss structures. Expert Syst. Appl. 2018, 102, 262–272. [Google Scholar] [CrossRef]
- Winyangkul, S.; Sleesongsom, S.; Bureerat, S. Reliability-based design of an aircraft wing using a fuzzy-based metaheuristic. Appl. Sci. 2021, 11, 6463. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Winyangkul, S.; Bureerat, S. Multiobjective reliability-based design of an aircraft wing using a fuzzy-based metaheuristic. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Volume 13: Safety Engineering, Risk, and Reliability Analysis, Research Posters, Virtual, 1–5 November 2021; V013T14A016. ASME: New York, NY, USA, 2021. [Google Scholar]
- Goland, M. The flutter of a uniform cantilever wing. J. Appl. Mech. 1945, 12, A197–A208. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S.; Tai, K. Aircraft morphing wing design by using partial topology optimization. Struct. Multidiscip. Optim. 2013, 48, 1109–1128. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).