Analytical Model with Independent Control of Load–Displacement Curve Branches for Brittle Material Strength Prediction Using Pre-Peak Test Loads
Abstract
1. Introduction
1.1. General Description of the Research Problem
1.2. Existing Models of the Class in Question and the Purpose of the Study
1.3. A Flow Chart of the Research Approach
- A brief review of the literature and justification of the problem, working hypothesis, and purpose of the study.
- A review of analytical models, the distinctive feature of which is that they describe the full load–strain curve for brittle materials using only one equation: methodological aspects.
- The development of a model with completely separate control of the left and right branches of the load–strain curve using the Heaviside function.
- The application of the model to the analysis of known data and comparison of simulation results with experimental data.
- The application of the developed model to predict the peak external load (bearing capacity) based on the results of pre-peak tests.
- The development of a prediction algorithm.
- An analysis of the limitations of the scope of the algorithm.
- An analysis of examples of applications of the developed model and methodology for forecasting peak values of external load for brittle materials.
- A discussion of the results and analysis of the possible development of the topic of the performed research to improve the understanding of the behavior of brittle materials during their loading, as well as concluding remarks.
2. Methodology
2.1. Preliminary Remarks
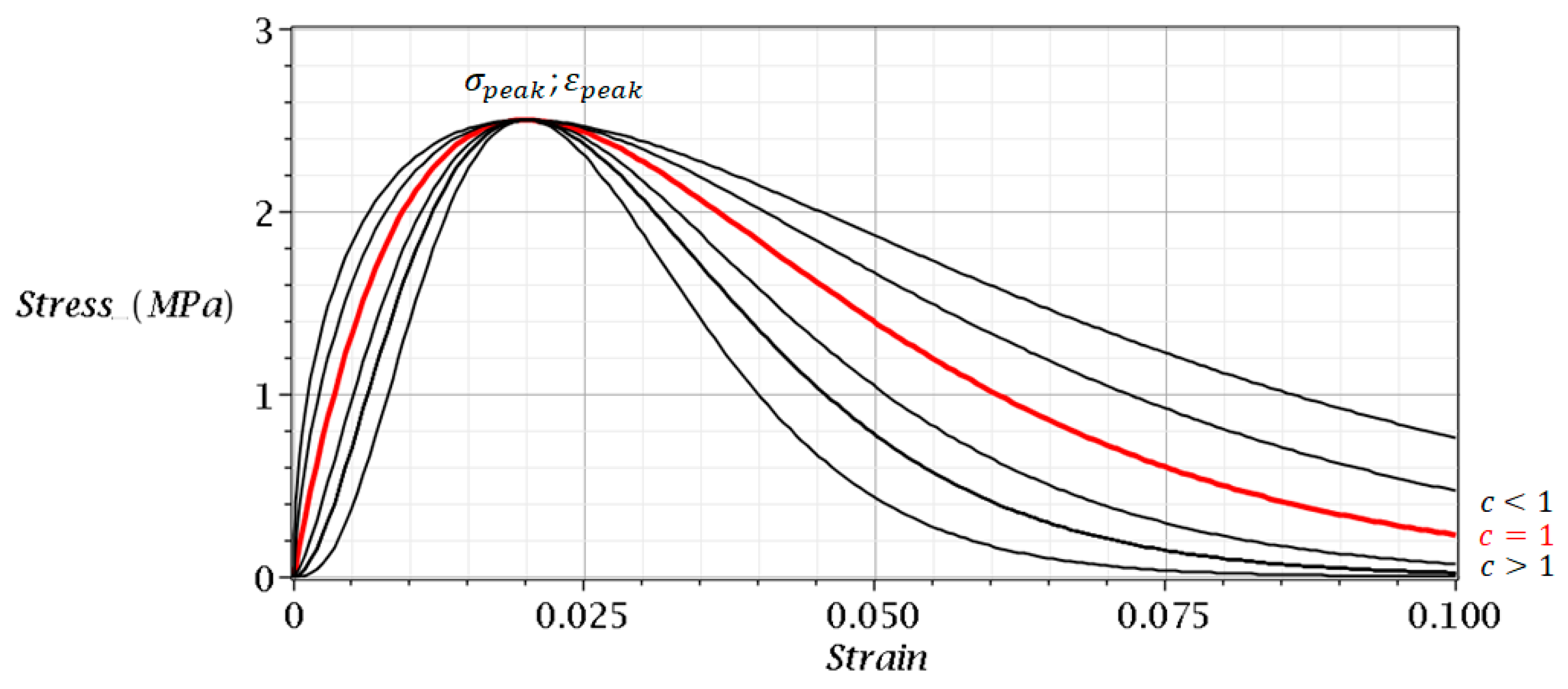
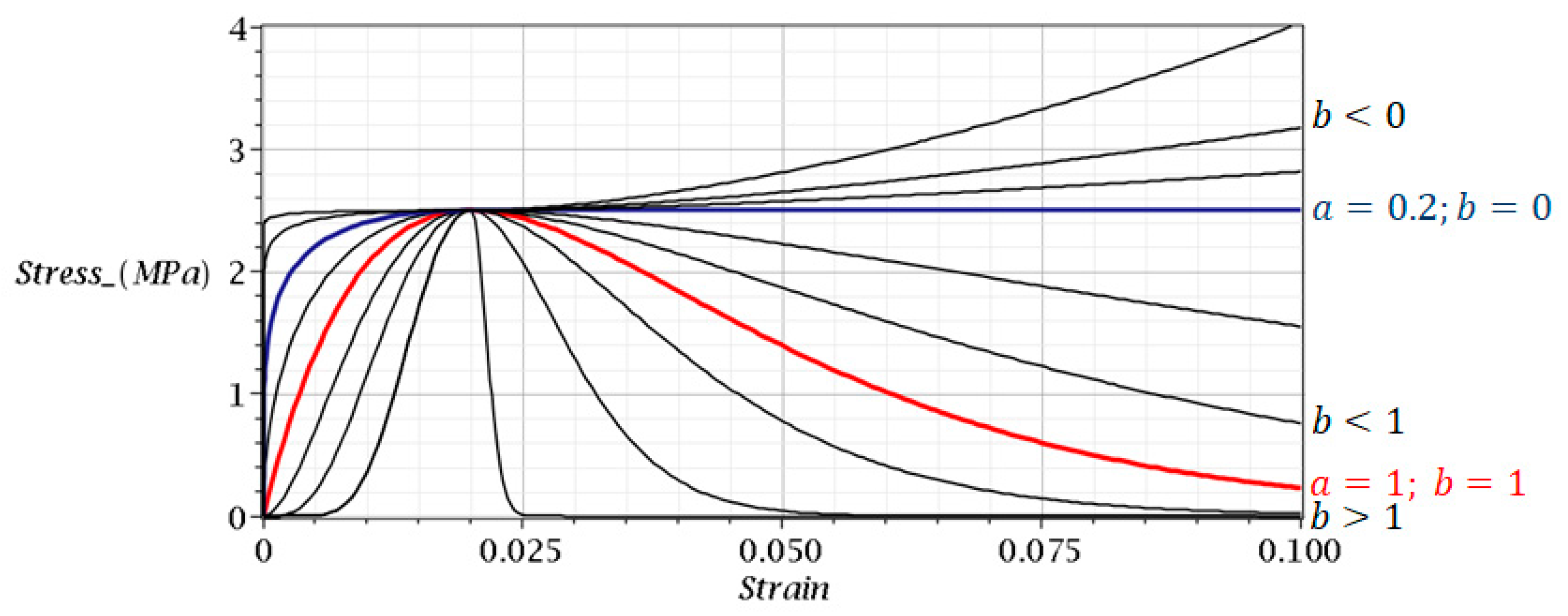
2.2. Model with Fully Separate Left and Right Branch Control
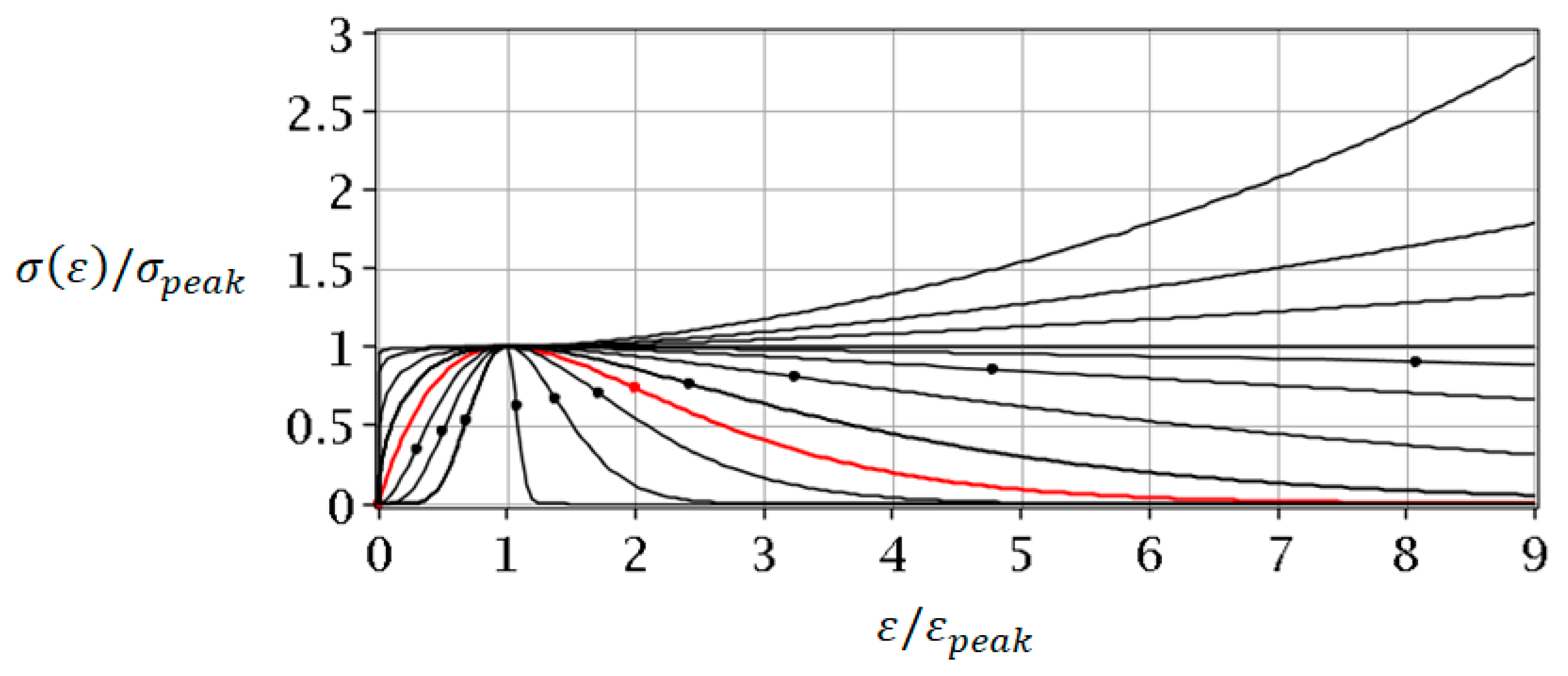
3. Results and Comments
3.1. Comparison with Experimental Data Known from the Literature
3.2. Predicting Values and
3.2.1. Prediction Methodology
3.2.2. Prediction Algorithm
- Initial data: and .
- Parameter (13) is calculated.
- (12) is calculated.
- (10) is calculated.
- If the dependence is linear, then, for example, (11) and theoretically, , which does not correspond to the physical meaning of task.
3.2.3. Limiting the Algorithm Scope
3.2.4. Example of the Algorithm Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, Z.; Ma, R.; Wang, D.; Chen, A. A review of lattice type model in fracture mechanics: Theory, applications, and perspectives. Eng. Fract. Mech. 2018, 190, 382–409. [Google Scholar] [CrossRef]
- de Borst, R. Fracture in quasi-brittle materials: A review of continuum damage-based approaches. Eng. Fract. Mech. 2002, 69, 95–112. [Google Scholar] [CrossRef]
- Pugno, N.M. Dynamic quantized fracture mechanics. Int. J. Fract. 2006, 140, 159–168. [Google Scholar] [CrossRef]
- Zheng, B.; Li, T.; Qi, H.; Gao, L.; Liu, X.; Yuan, L. Physics-informed machine learning model for computational fracture of quasi-brittle materials without labelled data. Int. J. Mech. Sci. 2022, 223, 107282. [Google Scholar] [CrossRef]
- Cervera, M.; Barbat, G.B.; Chiumenti, M.; Wu, J.Y. A Comparative Review of XFEM, Mixed FEM and Phase-Field Models for Quasi-brittle Cracking. Arch. Comput. Methods Eng. 2022, 29, 1009–1083. [Google Scholar] [CrossRef]
- Zhu, R.; Gao, H.; Zhan, Y.; Wu, Z.-X. Construction of Discrete Element Constitutive Relationship and Simulation of Fracture Performance of Quasi-Brittle Materials. Materials 2022, 15, 1964. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.X.; Zhu, L.; Xiong, F.; Liu, J.; Gao, W. A Particle-Based Cohesive Crack Model for Brittle Fracture Problems. Materials 2020, 13, 3573. [Google Scholar] [CrossRef]
- Ying, J.; Guo, J. Fracture Behaviour of Real Coarse Aggregate Distributed Concrete under Uniaxial Compressive Load Based on Cohesive Zone Model. Materials 2021, 14, 4314. [Google Scholar] [CrossRef]
- Hurley, R.C.; Hogan, J.D. Workshop on Mathematical Challenges in Brittle Material Failure. J. Dyn. Behav. Mater. 2020, 6, 14–23. [Google Scholar] [CrossRef]
- Sánchez, M.; Cicero, S.; Arrieta, S.; Martínez, V. Fracture Load Predictions in Additively Manufactured ABS U-Notched Specimens Using Average Strain Energy Density Criteria. Materials 2022, 15, 2372. [Google Scholar] [CrossRef] [PubMed]
- Kovalchenko, A.M. Studies of the ductile mode of cutting brittle materials (A review). J. Superhard Mater. 2013, 35, 259–276. [Google Scholar] [CrossRef]
- Oucif, C.; Mauludin, L.M. Continuum Damage-Healing and Super Healing Mechanics in Brittle Materials: A State-of-the-Art Review. Appl. Sci. 2018, 8, 2350. [Google Scholar] [CrossRef]
- Iskander, M.; Shrive, N. Fracture of brittle and quasi-brittle materials in compression: A review of the current state of knowledge and a different approach. Theor. Appl. Fract. Mech. 2018, 97, 250–257. [Google Scholar] [CrossRef]
- Xiao, P.; Zhao, G.; Liu, H. Failure Transition and Validity of Brazilian Disc Test under Different Loading Configurations: A Numerical Study. Mathematics 2022, 10, 2681. [Google Scholar] [CrossRef]
- Stojković, N.; Perić, D.; Stojić, D.; Marković, N. New stress-strain model for concrete at high temperatures. Teh. Vjesn. 2017, 24, 863–868. [Google Scholar]
- Baldwin, R.; North, M.A. Stress-strain curves of concrete at high temperature-A review. Fire Saf. Sci. 1969, 785, 1. Available online: http://www.iafss.org/publications/frn/785/-1/view/frn_785.pdf (accessed on 12 October 2021).
- Blagojević, M.; Pešić, D.; Mijalković, M.; Glišović, S. Jedinstvena funkcija za opisivanje naprezanja i deformacije betona u požaru. Građevinar 2011, 63, 19–24. Available online: https://hrcak.srce.hr/clanak/96329 (accessed on 14 July 2022).
- Kolesnikov, G. Damage Function of a Quasi-Brittle Material, Damage Rate, Acceleration and Jerk during Uniaxial Compression: Model and Application to Analysis of Trabecular Bone Tissue Destruction. Symmetry 2021, 13, 1759. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Yao, Z. Physical and mechanical performance of frozen rocks and soil in different regions. Adv. Civ. Eng. 2020, 2020, 8867414. [Google Scholar] [CrossRef]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect Measurement of Ground Reaction Forces and Moments by Means of Wearable Inertial Sensors: A Systematic Review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef]
- Hou, P.Y.; Cai, M.; Zhang, X.W.; Feng, X.T. Post-peak Stress–Strain Curves of Brittle Rocks Under Axial and Lateral-Strain-Controlled Loadings. Rock Mech. Rock Eng. 2021, 147, 855–884. [Google Scholar] [CrossRef]
- Cai, M.; Hou, P.Y.; Zhang, X.W.; Feng, X.T. Post-peak stress–strain curves of brittle hard rocks under axial-strain-controlled loading. Int. J. Rock Mech. Min. Sci. 2021, 147, 104921. [Google Scholar] [CrossRef]
- Astbury, B.; Leeuw, F.L. Unpacking black boxes: Mechanisms and theory building in evaluation. Am. J. Eval. 2010, 31, 363–381. [Google Scholar] [CrossRef]
- Salviato, M.; Chau, V.T.; Li, W.; Bažant, Z.P.; Cusatis, G. Direct Testing of Gradual Postpeak Softening of Fracture Specimens of Fiber Composites Stabilized by Enhanced Grip Stiffness and Mass. J. Appl. Mech. 2016, 83, 111003. [Google Scholar] [CrossRef]
- Zhuang, J.; Xu, R.; Pan, C.; Li, H. Dynamic stress–strain relationship of steel fiber-reinforced rubber self-compacting concrete. Constr. Build. Mater. 2022, 344, 128197. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, H.; Wang, X.; Liu, J.; Guo, L. Statistical Damage Constitutive Model for High-Strength Concrete Based on Dissipation Energy Density. Crystals 2021, 11, 800. [Google Scholar] [CrossRef]
- Yadollahi, M.M.; Benli, A. Stress-strain behavior of geopolymer under uniaxial compression. Comput. Concr. 2017, 20, 381–389. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Yan, F. Synthesis and mechanical properties of metakaolinite-based geopolymer. Colloids Surf. A Physicochem. Eng. Asp. 2005, 268, 1–6. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymer: Man-made rocks geosynthesis and the resulting development of very early high strength cement. J. Mat. Educ. 1994, 16, 91–139. [Google Scholar]
- Dal Poggetto, G.; D’Angelo, A.; Catauro, M.; Barbieri, L.; Leonelli, C. Recycling of Waste Corundum Abrasive Powder in MK-Based Geopolymers. Polymers 2022, 14, 2173. [Google Scholar] [CrossRef]
- Kolesnikov, G.; Gavrilov, T. Sandstone Modeling under Axial Compression and Axisymmetric Lateral Pressure. Symmetry 2022, 14, 796. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.; Wei, M.; Wang, L.; Cheng, B. Hysteretic Behavior of Geopolymer Concrete with Active Confinement Subjected to Monotonic and Cyclic Axial Compression: An Experimental Study. Materials 2020, 13, 3997. [Google Scholar] [CrossRef] [PubMed]
- Abdellah, M.Y.; Zuwawi, A.-R.; Azam, S.A.; Hassan, M.K. A Comparative Study to Evaluate the Essential Work of Fracture to Measure the Fracture Toughness of Quasi-Brittle Material. Materials 2022, 15, 4514. [Google Scholar] [CrossRef] [PubMed]
- Kolesnikov, G. Analysis of Concrete Failure on the Descending Branch of the Load-Displacement Curve. Crystals 2020, 10, 921. [Google Scholar] [CrossRef]
- Katarov, V.; Syunev, V.; Kolesnikov, G. Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation. Forests 2022, 13, 1538. [Google Scholar] [CrossRef]
- Li, Z. A Numerical Method for Applying Cohesive Stress on Fracture Process Zone in Concrete Using Nonlinear Spring Element. Materials 2022, 15, 1251. [Google Scholar] [CrossRef] [PubMed]
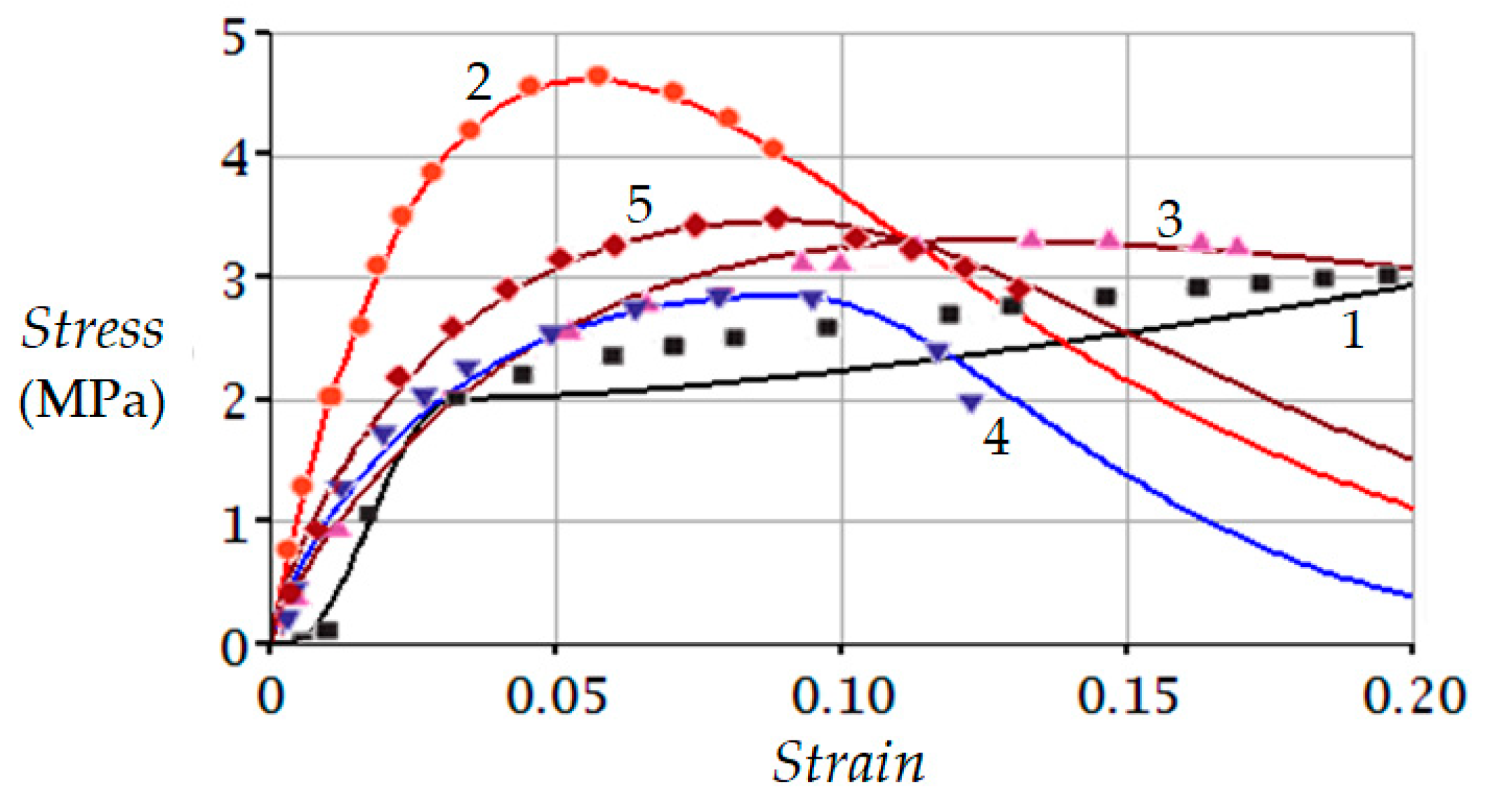
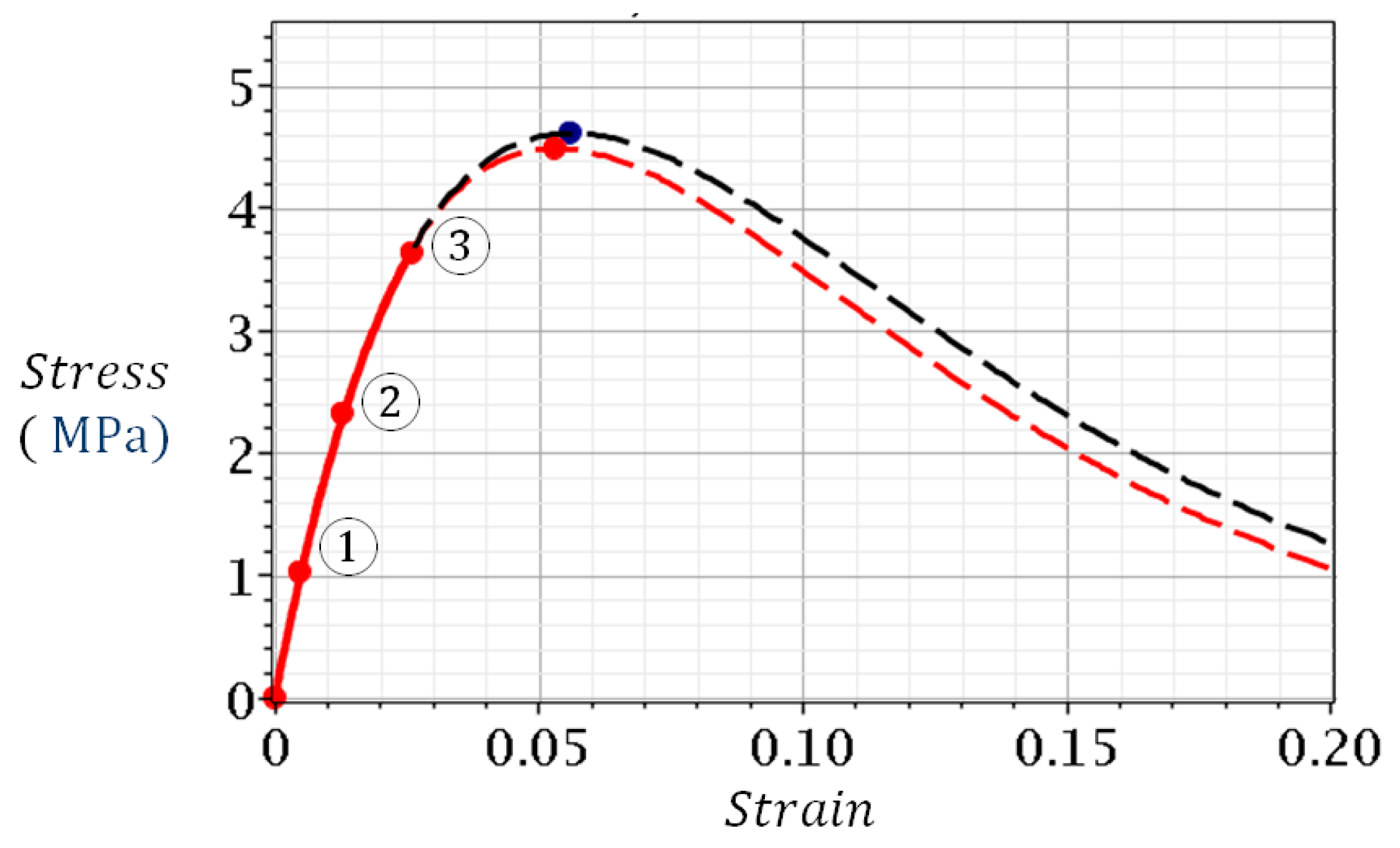

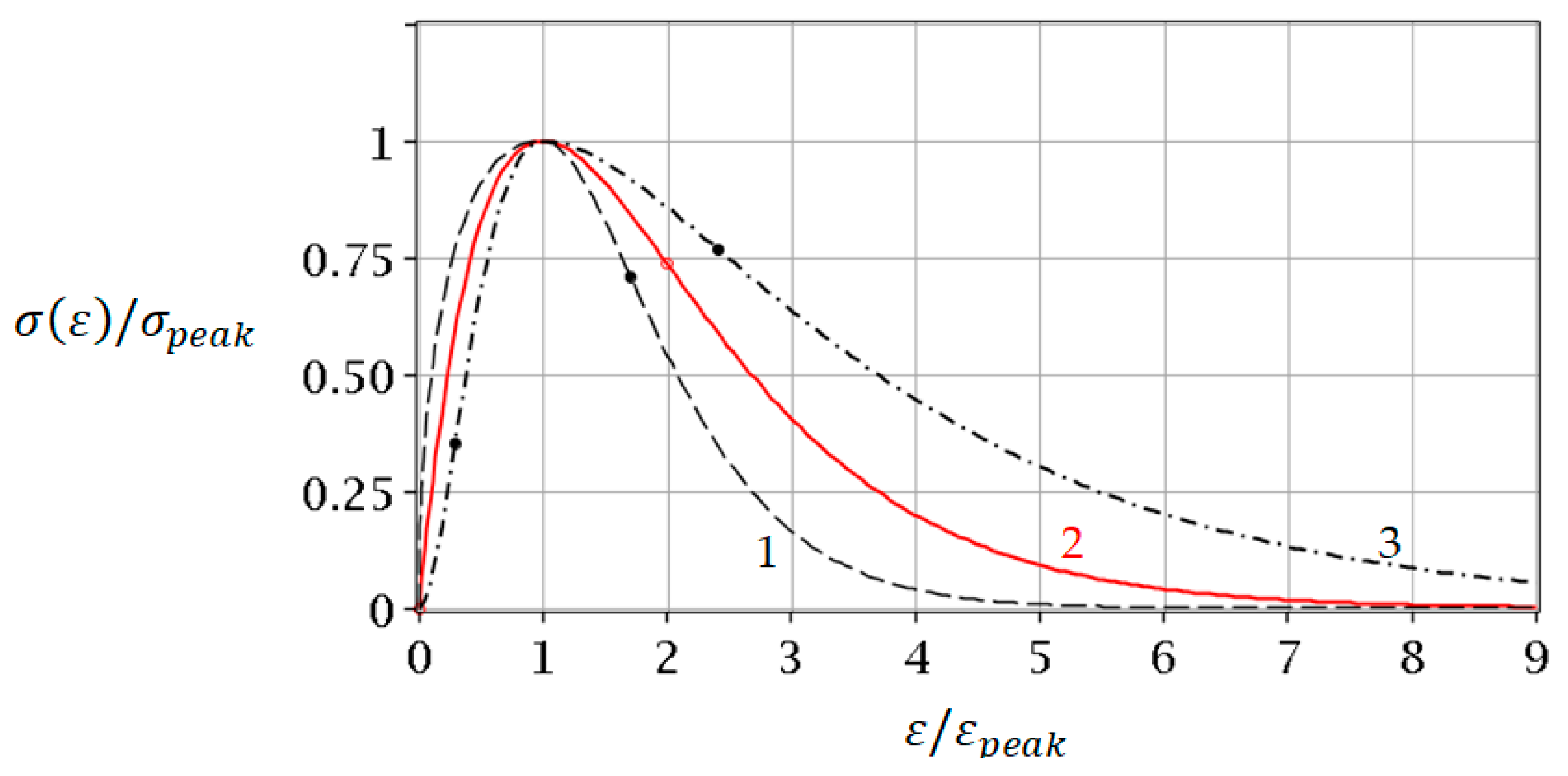
| Number | Soil | (MPa) | |||
|---|---|---|---|---|---|
| 1 | Mucky soil * | 2.00 * | 0.0335 * | 4.00 | −0.12 |
| 2 | Medium coarse sand * | 4.61 * | 0.0560 * | 1.00 | 1.10 |
| 3 | Clay * | 3.29 * | 0.1226 * | 0.85 | 0.50 |
| 4 | Calcareous clay * | 2.84 * | 0.0914 * | 0.80 | 5.00 |
| 5 | Sandy clay * | 3.45 * | 0.0905 * | 0.80 | 2.00 |
| 1.000 | 0.000 | 0.125 | 3.828 |
| 2.000 | 0.293 | 0.250 | 3.000 |
| 3.000 | 0.423 | 1.000 | 2.000 |
| 4.000 | 0.500 | 2.000 | 1.500 |
| 5.000 | 0.553 | 4.000 | 1.447 |
| Point Number | (MPa) | (MPa) | |||
|---|---|---|---|---|---|
| Initial data: | Calculation results: | ||||
| 1 | 0.004855 | 1.0278 | |||
| 2 | 0.012923 | 2.3224 | 0.99 | 0.053 (105%) | 4.49 (97%) |
| 3 | 0.026087 | 3.6364 | |||
| The experiment 1: | 0.056 (100%) | 4.61 (100%) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolesnikov, G.; Zaitseva, M.; Petrov, A. Analytical Model with Independent Control of Load–Displacement Curve Branches for Brittle Material Strength Prediction Using Pre-Peak Test Loads. Symmetry 2022, 14, 2089. https://doi.org/10.3390/sym14102089
Kolesnikov G, Zaitseva M, Petrov A. Analytical Model with Independent Control of Load–Displacement Curve Branches for Brittle Material Strength Prediction Using Pre-Peak Test Loads. Symmetry. 2022; 14(10):2089. https://doi.org/10.3390/sym14102089
Chicago/Turabian StyleKolesnikov, Gennady, Maria Zaitseva, and Aleksey Petrov. 2022. "Analytical Model with Independent Control of Load–Displacement Curve Branches for Brittle Material Strength Prediction Using Pre-Peak Test Loads" Symmetry 14, no. 10: 2089. https://doi.org/10.3390/sym14102089
APA StyleKolesnikov, G., Zaitseva, M., & Petrov, A. (2022). Analytical Model with Independent Control of Load–Displacement Curve Branches for Brittle Material Strength Prediction Using Pre-Peak Test Loads. Symmetry, 14(10), 2089. https://doi.org/10.3390/sym14102089






