Numerical Simulation of Entropy Optimization in Radiative Hybrid Nanofluid Flow in a Variable Features Darcy–Forchheimer Curved Surface
Abstract
1. Introduction
- To investigate how hybrid nanofluid is more efficient than nanofluid and base fluid.
- To examine the thermal effects of hybrid nanomaterials with thermal radiation, EHS, and viscous dissipation.
- What are the effects of skin friction and Nusselt number in regard to relevant physical constraints?
- How does the addition of a Darcy–Forchheimer term with variable permeability and porosity features to the momentum equation impact the hybrid nanofluid flow?
- How does the inclusion of cobalt ferrite and gold nano particulates enhance the thermal efficiency of ethylene glycol?
2. Mathematical Modeling
3. Entropy Analysis
4. Numerical Solution
5. Discussion or Outcomes



6. Conclusions
- Heat transfer efficiency is escalated by the combination of ethylene glycol and water.
- The inclusion of Au and CoFe2O4 nanoparticles in the base fluid positively affect heat transmission.
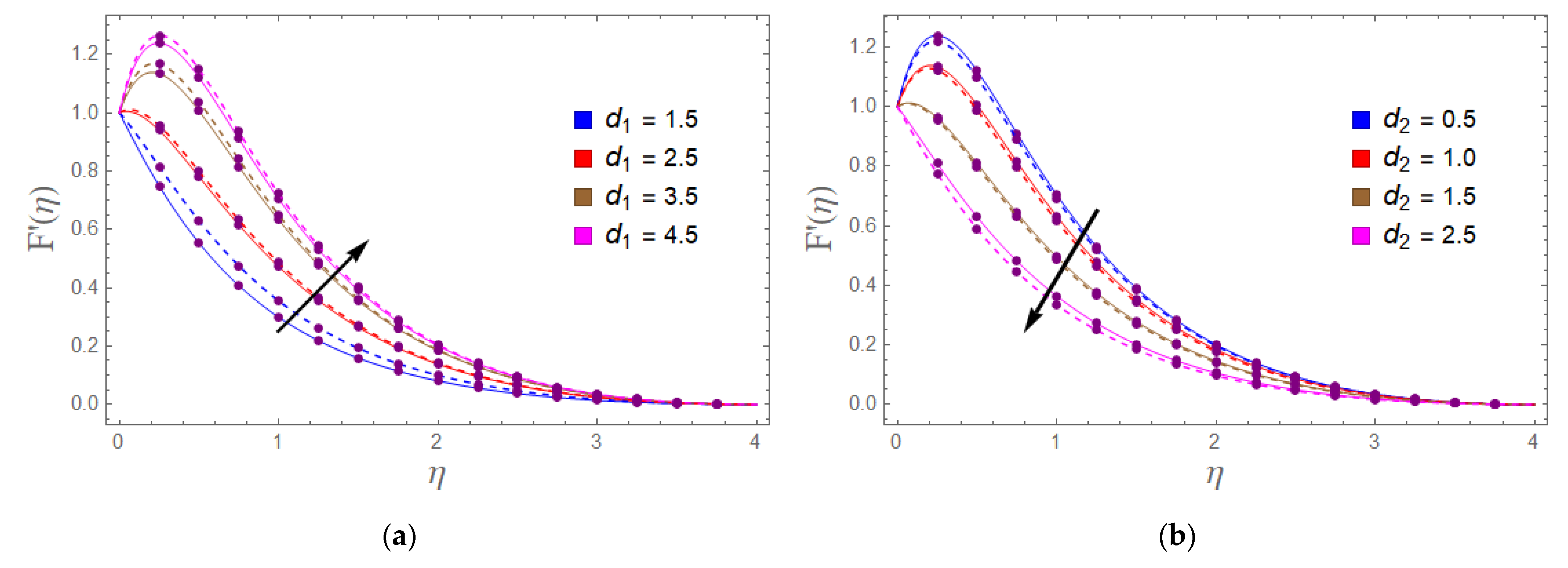
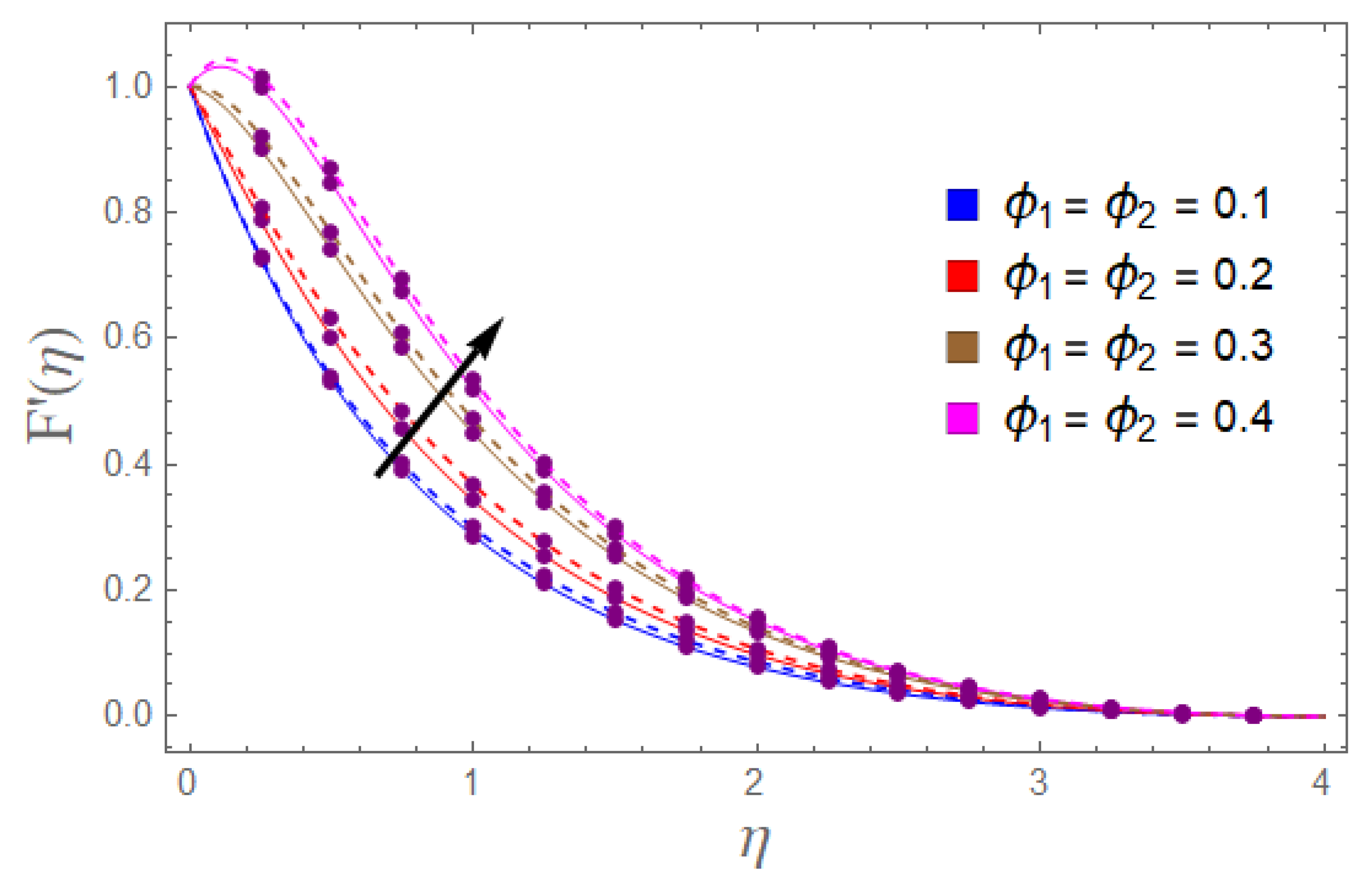
- Velocity distribution is enhanced with the higher values of variable permeability , while it diminishes with the variable porosity factor and inertia coefficient.
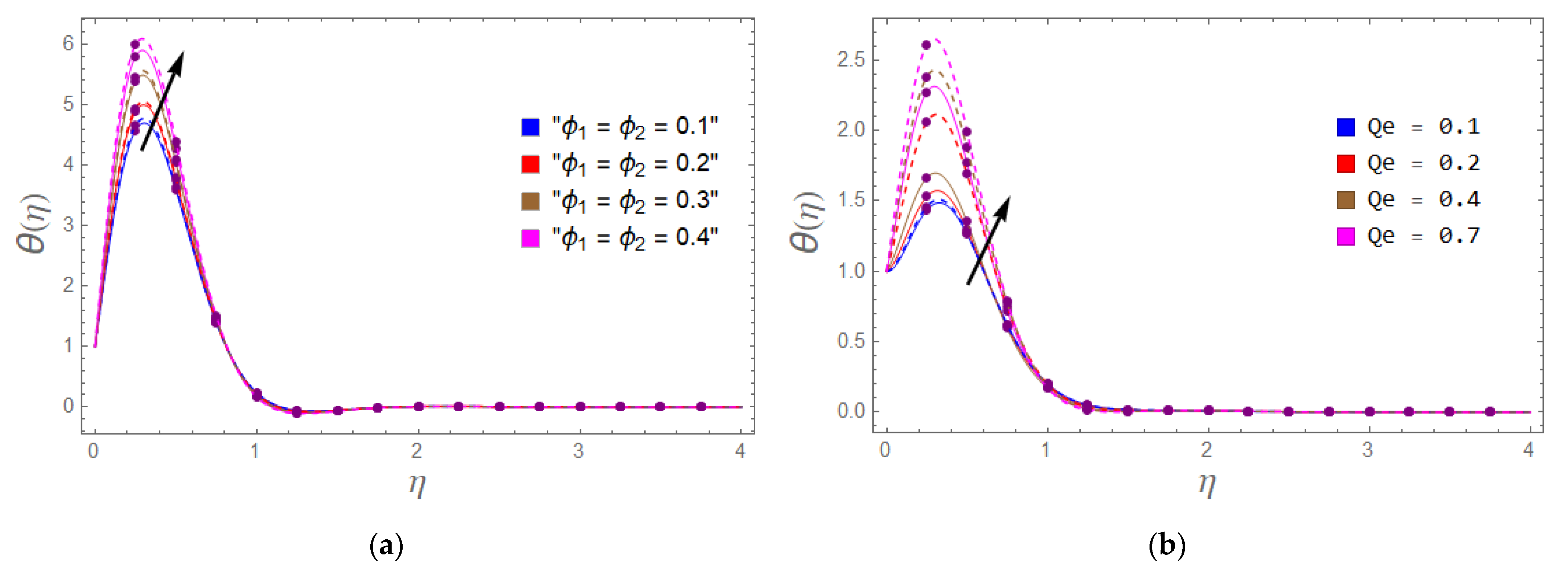
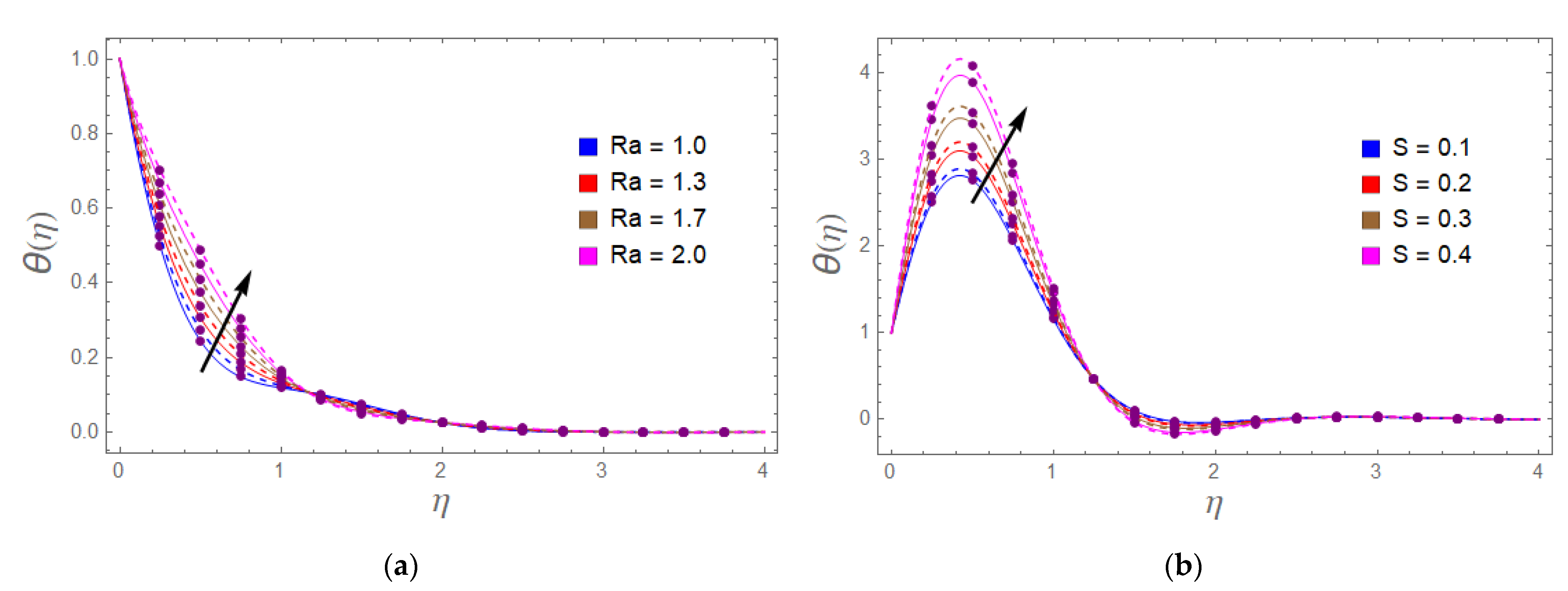
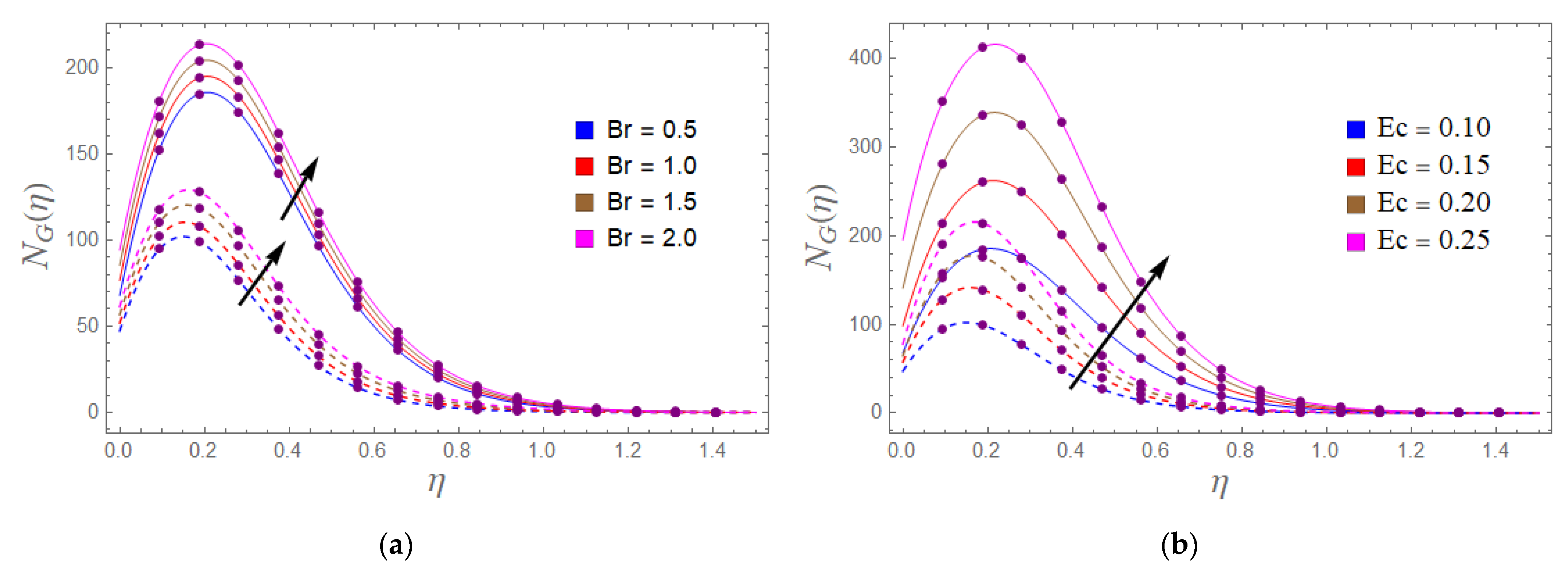
- Temperature augmented with the enhancing trend of exponential heat source and the Brinkman number.
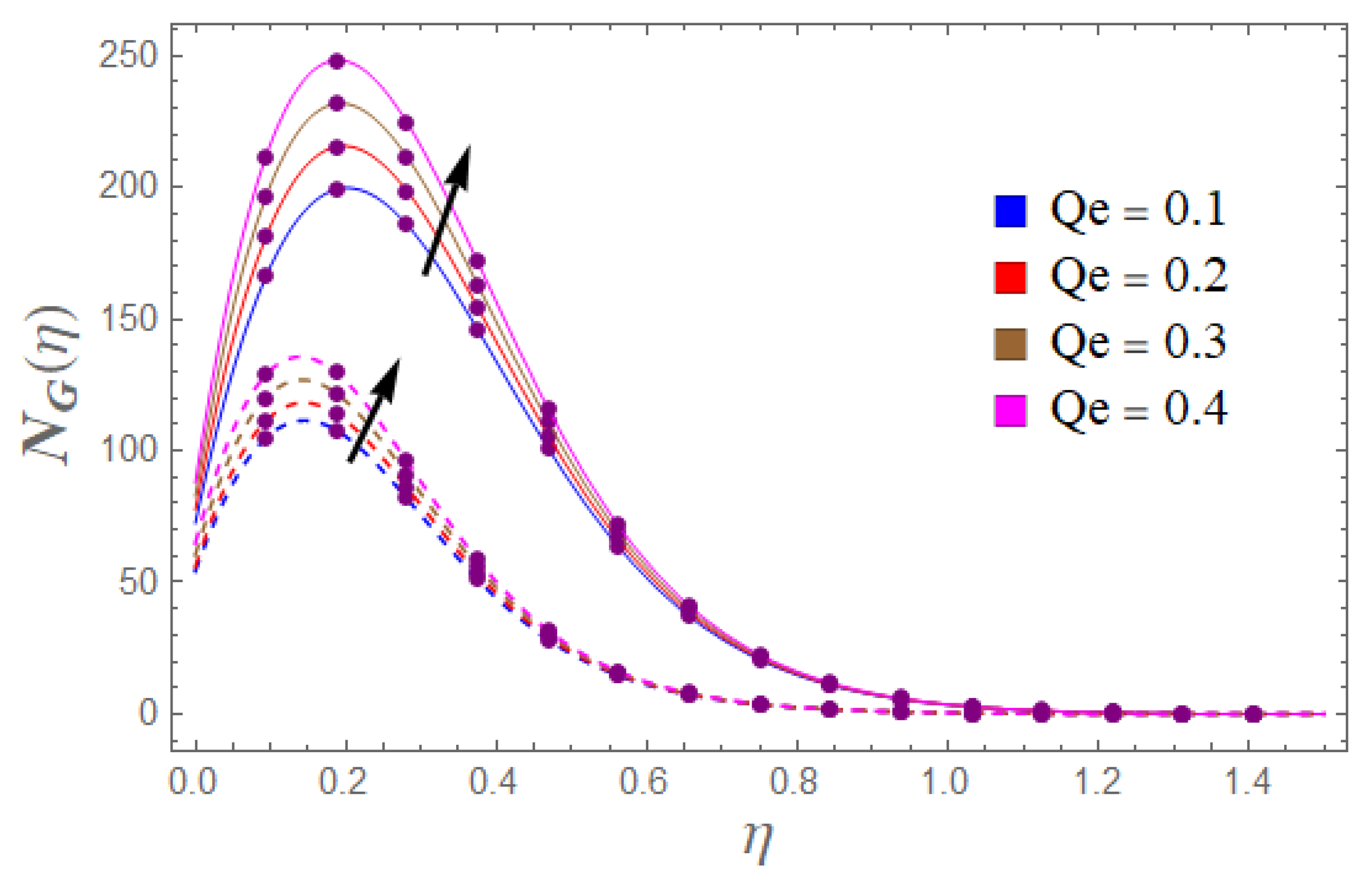
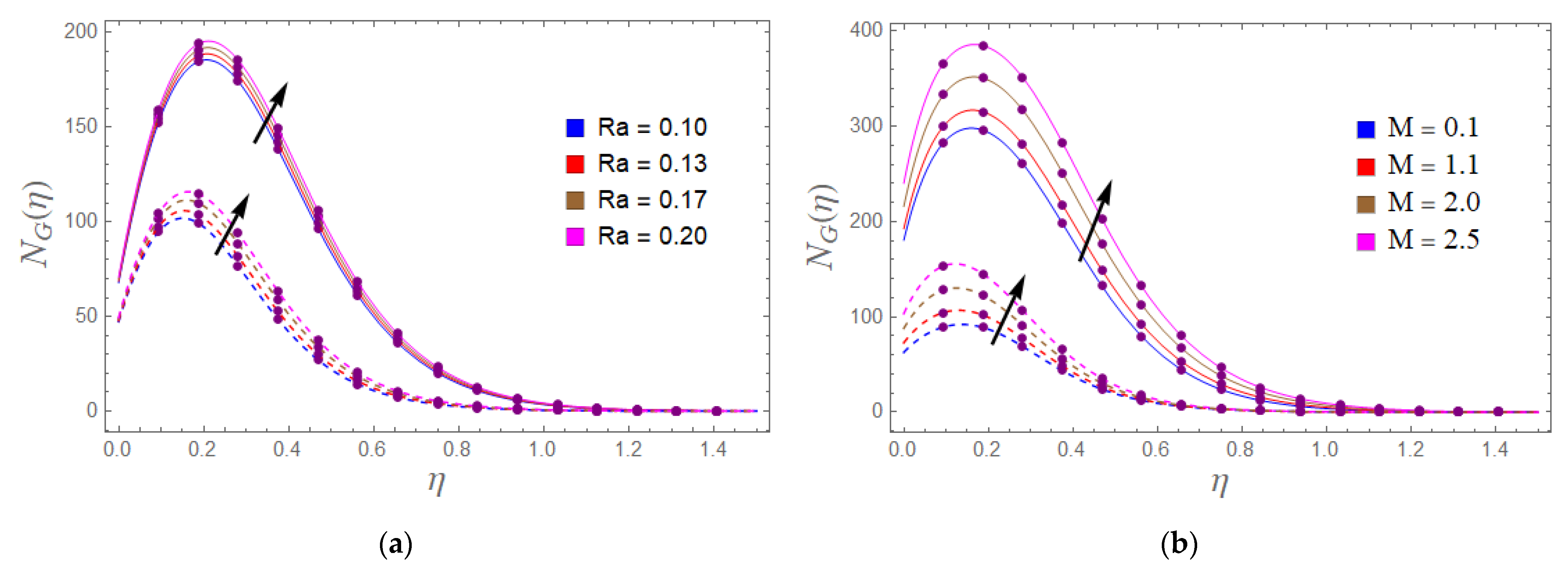
- Entropy generation improves with the increment of the radiation and magnetic effect.
- Skin friction shows a decay behavior against the higher value of
- The Nusselt number improves for high values of while diminishing for and
- Overall hybrid nanofluid has dominant behavior as compared to nanofluid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Dimensionless velocity | P | Pressure [Kgm−1s−2] | |
| Stream function | Velocity components | ||
| Similarity variable | Curvature parameter | ||
| Density [] | Magnetic field strength | ||
| Dynamic viscosity [] | Dimensionless temperature | ||
| Permeability parameter | Specific heat capacity [] | ||
| Ambient temperature [] | Dimensionless magnetic field | ||
| Brinkman number | b < 0 | Shrinking sheet | |
| T | Temperature of fluid [] | Radiation variable | |
| Temperature-dependent heat source | Pr | Prandtl number | |
| Kinematic viscosity [] | Heat flux | ||
| Stefan-Boltzmann constant | Dimensionless heat source parameter | ||
| Variable porosity | Length dimension, | ||
| Variable permeability of porous medium | Wall temperature [] | ||
| Exponential heat source | Variable permeability | ||
| Surface porosity, | Drag coefficient | ||
| Thermal conductivity [] | Static sheet | ||
| Surface permeability | Inertia coefficient | ||
| Stretching velocity | Stretching sheet | ||
| Eckert number | Shear stress | ||
| Temperature ratio parameter | Reynold number | ||
| Porousty of the porrous medium | |||
| Subscripts | |||
| Bf | Base fluid | hnf | Hybrid nanofluid |
| Nf | Nanofluid | f | Fluid |
References
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Deutsch Ing. 1901, 45, 1782–1788. [Google Scholar]
- Ullah, I.; Ullah, R.; Alqarni, M.S.; Xia, W.F.; Muhammad, T. Combined heat source and zero mass flux features on magnetized nanofluid flow by radial disk with the applications of Coriolis force and activation energy. Int. Commun. Heat Mass Transf. 2021, 126, 105416. [Google Scholar] [CrossRef]
- Alotaibi, H.; Eid, M.R. Thermal analysis of 3D electromagnetic radiative nanofluid flow with suction/blowing: Darcy–Forchheimer scheme. Micromachines 2021, 12, 1395. [Google Scholar] [CrossRef] [PubMed]
- Naveen Kumar, R.; Gowda, R.J.; Gireesha, B.J.; Prasannakumara, B.C. Non-Newtonian hybrid nanofluid flow over vertically upward/downward moving rotating disk in a Darcy–Forchheimer porous medium. Eur. Phys. J. Spec. Top. 2021, 230, 1227–1237. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Alsaedi, A.; Ahmad, B. Unsteady flow of nanofluid through porous medium with variable characteristics. Int. Commun. Heat Mass Transf. 2020, 119, 104904. [Google Scholar] [CrossRef]
- Gautam, A.K.; Verma, A.K.; Bhattacharyya, K.; Mukhopadhyay, S.; Chamkha, A.J. Impacts of activation energy and binary chemical reaction on MHD flow of Williamson nanofluid in Darcy–Forchheimer porous medium: A case of expanding sheet of variable thickness. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Mallikarjuna, H.B.; Nirmala, T.; Punith Gowda, R.J.; Manghat, R.; Varun Kumar, R.S. Two-dimensional Darcy–Forchheimer flow of a dusty hybrid nanofluid over a stretching sheet with viscous dissipation. Heat Transf. 2021, 50, 3934–3947. [Google Scholar] [CrossRef]
- Saeed, A.; Kumam, P.; Gul, T.; Alghamdi, W.; Kumam, W.; Khan, A. Darcy–Forchheimer couple stress hybrid nanofluids flow with variable fluid properties. Sci. Rep. 2021, 11, 19612. [Google Scholar] [CrossRef] [PubMed]
- Punith Gowda, R.J.; Naveen Kumar, R.; Prasannakumara, B.C. Two-phase Darcy-Forchheimer flow of dusty hybrid nanofluid with viscous dissipation over a cylinder. Int. J. Appl. Comput. Math. 2021, 7, 95. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Hussain, S.; Zaydan, M.; Wakif, A.; Chamkha, A.J.; Bhutta, M.S. Significance of Rosseland’s Radiative Process on Reactive Maxwell Nanofluid Flows over an Isothermally Heated Stretching Sheet in the Presence of Darcy–Forchheimer and Lorentz Forces: Towards a New Perspective on Buongiorno’s Model. Micromachines 2022, 13, 368. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. An optimal analysis for Darcy-Forchheimer 3D flow of Carreau nanofluid with convectively heated surface. Results Phys. 2018, 9, 598–608. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Ullah, I.; Hayat, T.; Alsaadi, F.E. Entropy generation in nonlinear mixed convective flow of nanofluid in porous space influenced by Arrhenius activation energy and thermal radiation. J. Therm. Anal. Calorim. 2020, 140, 799–809. [Google Scholar] [CrossRef]
- Hayat, T.; Ullah, I.; Alsaedi, A.; Momani, S. Entropy optimization in nonlinear mixed convective flow of nanomaterials through porous space. J. Non-Equilib. Thermodyn. 2021, 46, 191–203. [Google Scholar] [CrossRef]
- Ullah, I. Activation energy with exothermic/endothermic reaction and Coriolis force effects on magnetized nanomaterials flow through Darcy–Forchheimer porous space with variable features. Waves Random Complex Media 2022, 1–14. [Google Scholar] [CrossRef]
- Ma, T.; Guo, Z.; Lin, M.; Wang, Q. Recent trends on nanofluid heat transfer machine learning research applied to renewable energy. Renew. Sustain. Energy Rev. 2021, 138, 110494. [Google Scholar] [CrossRef]
- Soltani, O.; Akbari, M. Effects of temperature and particles concentration on the dynamic viscosity of MgO-MWCNT/ethylene glycol hybrid nanofluid: Experimental study. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 84, 564–570. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Muhammad, T.; Manzoor, U. Importance of shape factor in Sisko nanofluid flow considering gold nanoparticles. Alex. Eng. J. 2022, 61, 3665–3672. [Google Scholar] [CrossRef]
- Li, B.; Hong, W.; Li, H.; Lan, J.; Zi, J. Optimized energy distribution management in the nanofluid-assisted photovoltaic/thermal system via exergy efficiency analysis. Energy 2022, 242, 123018. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Bakar, S.A.; Animasaun, I.L.; Yook, S.J. Insights into the dynamics of blood conveying gold nanoparticles on a curved surface when suction, thermal radiation, and Lorentz force are significant: The case of non-Newtonian Williamson fluid. Math. Comput. Simul. 2022, 193, 250–268. [Google Scholar] [CrossRef]
- Mbambo, M.C.; Madito, M.J.; Khamliche, T.; Mtshali, C.B.; Khumalo, Z.M.; Madiba, I.G.; Maaza, M. Thermal conductivity enhancement in gold decorated graphene nanosheets in ethylene glycol based nanofluid. Sci. Rep. 2020, 10, 14730. [Google Scholar] [CrossRef]
- Mishra, A.; Upreti, H. A comparative study of Ag-MgO/water and Fe3O4-CoFe2O4/EG-water hybrid nanofluid flow over a curved surface with chemical reaction using Buongiorno model. Partial. Differ. Equ. Appl. Math. 2022, 5, 100322. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Wahid, N.S.; Arifin, N.M.; Pop, I. Insight into three-dimensional flow of three different dynamics of nanofluids subject to thermal radiation: The case of water–cobalt ferrite, water–manganese–zinc ferrite, and water–magnetite. Heat Transf. 2022, 51, 4434–4450. [Google Scholar] [CrossRef]
- Ullah, I.; Hayat, T.; Aziz, A.; Alsaedi, A. Significance of Entropy Generation and the Coriolis Force on the Three-Dimensional Non-Darcy Flow of Ethylene-Glycol Conveying Carbon Nanotubes (SWCNTs and MWCNTs). J. Non-Equilib. Thermodyn. 2022, 47, 61–75. [Google Scholar] [CrossRef]
- Ullah, I.; Hayat, T.; Alsaedi, A.; Asghar, S. Dissipative flow of hybrid nanoliquid (H2O-aluminum alloy nanoparticles) with thermal radiation. Phys. Scr. 2019, 94, 125708. [Google Scholar] [CrossRef]
- Ullah, Z.; Ullah, I.; Zaman, G.; Sun, T.C. A numerical approach to interpret melting and activation energy phenomenon on the magnetized transient flow of Prandtl–Eyring fluid with the application of Cattaneo–Christov theory. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation and dissipative heat transfer analysis of mixed convective hydromagnetic flow of a Casson nanofluid with thermal radiation and Hall current. Sci. Rep. 2021, 11, 3926. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Al-Nimr, M.A.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Ullah, I.; Hayat, T.; Alsaedi, A. Optimization of entropy production in flow of hybrid nanomaterials through Darcy–Forchheimer porous space. J. Therm. Anal. Calorim. 2022, 147, 5855–5864. [Google Scholar] [CrossRef]
- Fares, R.; Mebarek-Oudina, F.; Aissa, A.; Bilal, S.M.; Öztop, H.F. Optimal entropy generation in Darcy-Forchheimer magnetized flow in a square enclosure filled with silver-based water nanoliquid. J. Therm. Anal. Calorim. 2022, 147, 1571–1581. [Google Scholar] [CrossRef]
- Aziz, A.; Aziz, A.; Ullah, I.; Subhani, M. Numerical simulation for 3D rotating flow of nanofluid with entropy generation. Int. J. Model. Simul. 2022, 1–22. [Google Scholar] [CrossRef]
- Alsallami, S.A.; Zahir, H.; Muhammad, T.; Hayat, A.U.; Khan, M.R.; Ali, A. Numerical simulation of Marangoni Maxwell nanofluid flow with Arrhenius activation energy and entropy anatomization over a rotating disk. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Ullah, I.; Hayat, T.; Alsaedi, A.; Fardoun, H.M. Numerical treatment of melting heat transfer and entropy generation in stagnation point flow of hybrid nanomaterials (SWCNT-MWCNT/engine oil). Mod. Phys. Lett. B 2021, 35, 2150102. [Google Scholar] [CrossRef]
- Revathi, G.; Sajja, V.S.; Babu, M.J.; Raju, C.S.K.; Shehzad, S.A.; Bapanayya, C. Entropy optimization in hybrid radiative nanofluid (CH3OH + SiO2 + Al2O3) flow by a curved stretching sheet with cross-diffusion effects. Appl. Nanosci. 2021, 1–15. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Haider, F.; Hayat, T. Entropy Generation Analysis of Hybrid Nanomaterial through Porous Space with Variable Characteristics. Entropy 2021, 23, 89. [Google Scholar] [CrossRef]
- Ullah, I.; Alajlani, Y.; Pasha, A.A.; Adil, M.; Weera, W. Theoretical investigation of hybrid nanomaterials transient flow through variable feature of Darcy–Forchheimer space with exponential heat source and slip condition. Sci. Rep. 2022, 12, 15085. [Google Scholar] [CrossRef]
- Sanni, K.M.; Asghar, S.; Jalil, M.; Okechi, N.F. Flow of viscous fluid along a nonlinearly stretching curved surface. Results Phys. 2017, 7, 1–4. [Google Scholar] [CrossRef]
- Sajid, M.; Ali, N.; Javed, T.; Abbas, Z. Stretching a curved surface in a viscous fluid. Chin. Phys. Lett. 2010, 27, 024703. [Google Scholar] [CrossRef]
- Abbas, Z.; Naveed, M.; Sajid, M. Heat transfer analysis for stretching flow over a curved surface with magnetic field. J. Eng. Thermophys. 2013, 22, 337–345. [Google Scholar] [CrossRef]
- Siryk, S.V. Analysis of lumped approximations in the finite-element method for convection–diffusion problems. Cybern. Syst. Anal. 2013, 49, 774–784. [Google Scholar] [CrossRef]
- Siryk, S.V. Accuracy and stability of the Petrov–Galerkin method for solving the stationary convection-diffusion equation. Cybern. Syst. Anal. 2014, 50, 278–287. [Google Scholar] [CrossRef]
- John, V.; Knobloch, P.; Novo, J. Finite elements for scalar convection-dominated equations and incompressible flow problems: A never-ending story? Comput. Vis. Sci. 2018, 19, 47–63. [Google Scholar] [CrossRef]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; p. 24. [Google Scholar]
- Stynes, M.; Stynes, D. Convection-Diffusion Problems; American Mathematical Society: Providence, RI, USA, 2018; Volume 196. [Google Scholar]
- AbdulRidha, M.W.; Kashkool, H.A. Space-Time Petrov-Discontinuous Galerkin Finite Element Method for Solving Linear Convection-Diffusion Problems. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2322, p. 012007. [Google Scholar]


| Water + EG | 0.425 | 0.00509 | 1056 | 3288 |
| CoFe2O4 | 3.7 | 4907 | 700 | |
| Au | 318 | 19,300 | 129 |
| Properties | |
|---|---|
| Viscosity | |
| Density | |
| Thermal Capacity | |
| Thermal Conductivity | |
| Electrical Conductivity |
| Parameters | ||||||
|---|---|---|---|---|---|---|
| Nanofluid | Hybrid Nanofluid | |||||
| 0.10 | 1.0 | 4.0 | 0.5 | 1.0 | 0.875321 | 0.875431 |
| 0.15 | 0.884051 | 0.884174 | ||||
| 1.20 | 0.980286 | 0.980395 | ||||
| 0.10 | 0.5 | 4.0 | 0.5 | 1.0 | 0.982732 | 0.982844 |
| 1.0 | 1.156850 | 1.156923 | ||||
| 1.5 | 1.174401 | 1.174532 | ||||
| 0.10 | 1.0 | 5.7 | 0.5 | 1.0 | 1.307815 | 1.307922 |
| 6.5 | 1.182130 | 1.182363 | ||||
| 7.2 | 1.158347 | 1.158469 | ||||
| 0.10 | 1.0 | 4.0 | 0.2 | 1.0 | 0.871631 | 0.871753 |
| 0.4 | 0.889332 | 0.889425 | ||||
| 0.6 | 0.903041 | 0.903172 | ||||
| 0.10 | 1.0 | 4.0 | 0.5 | 0.8 | 1.220220 | 1.221230 |
| 1.6 | 1.31930 | 1.31941 | ||||
| 2.4 | 1.38311 | 1.38329 | ||||
| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Nanofluid | Hybrid Nanofluid | ||||||
| 0.2 | 0.5 | 5.0 | 0.3 | 0.4 | 1.0 | 1.36168407 | 1.36168519 |
| 0.3 | 1.24639352 | 1.24639463 | |||||
| 0.4 | 1.10356053 | 1.10356145 | |||||
| 0.2 | 0.4 | 5.0 | 0.3 | 0.4 | 1.0 | 0.86776427 | 0.86776535 |
| 0.5 | 0.65271754 | 0.65271869 | |||||
| 0.6 | 0.47516205 | 0.47516319 | |||||
| 0.2 | 0.5 | 3.0 | 0.3 | 0.4 | 1.0 | 0.42130812 | 0.42130926 |
| 6.0 | 0.49321677 | 0.49321789 | |||||
| 9.0 | 0.50219742 | 0.50219873 | |||||
| 0.2 | 0.5 | 5.0 | 1.0 | 0.4 | 1.0 | 0.74307507 | 0.74307619 |
| 2.0 | 0.69315325 | 0.69315406 | |||||
| 3.0 | 0.61025614 | 0.61025827 | |||||
| 0.3 | 0.2 | 1.20398502 | 1.20398613 | ||||
| 0.6 | 1.52109772 | 1.52109891 | |||||
| 1.0 | 1.63874243 | 1.63874352 | |||||
| 0.2 | 0.5 | 5.0 | 1.0 | 0.4 | 0.1 | 0.53866970 | 0.53867081 |
| 0.3 | 0.40721617 | 0.40721708 | |||||
| 0.5 | 0.21309744 | 0.21309865 | |||||
| Sanni et al. [37] | Sajid et al. [38] | Zaheer et al. [39] | Present | |
|---|---|---|---|---|
| 5 | 1.1576 | 0.7576 | 1.1576 | 1.1584 |
| 10 | 1.0734 | 0.8735 | 1.0735 | 1.0738 |
| 20 | 1.0355 | 0.9356 | 1.0356 | 1.0339 |
| 30 | 1.0235 | 0.9569 | 1.0235 | 1.0240 |
| 40 | 1.0176 | 0.9676 | 1.0176 | 1.0171 |
| 50 | 1.0140 | 0.9741 | 1.0141 | 1.0147 |
| 100 | 1.0070 | 0.9870 | 1.0070 | 1.0083 |
| 200 | 1.0036 | 0.9936 | 1.0036 | 1.0042 |
| 1000 | 1.0008 | 0.9988 | 1.0008 | 1.0005 |
| 1 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayat, A.U.; Ullah, I.; Khan, H.; Weera, W.; Galal, A.M. Numerical Simulation of Entropy Optimization in Radiative Hybrid Nanofluid Flow in a Variable Features Darcy–Forchheimer Curved Surface. Symmetry 2022, 14, 2057. https://doi.org/10.3390/sym14102057
Hayat AU, Ullah I, Khan H, Weera W, Galal AM. Numerical Simulation of Entropy Optimization in Radiative Hybrid Nanofluid Flow in a Variable Features Darcy–Forchheimer Curved Surface. Symmetry. 2022; 14(10):2057. https://doi.org/10.3390/sym14102057
Chicago/Turabian StyleHayat, Asif Ullah, Ikram Ullah, Hassan Khan, Wajaree Weera, and Ahmed M. Galal. 2022. "Numerical Simulation of Entropy Optimization in Radiative Hybrid Nanofluid Flow in a Variable Features Darcy–Forchheimer Curved Surface" Symmetry 14, no. 10: 2057. https://doi.org/10.3390/sym14102057
APA StyleHayat, A. U., Ullah, I., Khan, H., Weera, W., & Galal, A. M. (2022). Numerical Simulation of Entropy Optimization in Radiative Hybrid Nanofluid Flow in a Variable Features Darcy–Forchheimer Curved Surface. Symmetry, 14(10), 2057. https://doi.org/10.3390/sym14102057







