An Intelligent Genetic Scheme for Multi-Objective Collaboration Services Scheduling
Abstract
1. Introduction
- The initial population generation strategy has changed. The proposed IGS reduces the generation time of the initial population by generating all the population randomly to generate a part of the population randomly, and then generating the remaining population in the way of approximately randomly generated chromosomes.
- In order to ensure the diversity of the population, the selection method was changed from one based on symmetric exchange to one based on asymmetric exchange.
- Some individuals with lower physical fitness are retained. Individuals may have low adaptability due to one or two inferior genes. However, these genes may have better gene fragments.
- Adaptive mutation rate is used. In this way, the mutation rate of newly generated individuals is dynamically determined according to the fitness of their parents.
2. Related Work
3. Our Proposed Intelligent Genetic Scheme
3.1. Problem Formulation
3.1.1. Representation of Application Deployment
3.1.2. Chromosome Coding
- Each available resource needs to be chromosomally encoded.If N is defined as the number of available resources, the number of gene positions c for each available resource on the chromosome is determined as follows:In the traditional expression, the above chromosomes require N bits to represent each available resource. By contrast, using Equation (4) can compress the length of the chromosome based on the traditional expression, reduce the memory consumption required by the experiment, and improve the speed of the evolution.
- Chromosomal encoding for each application array X.After encoding the available resources, the chromosomes are encoded according to the assignment of each element in X. If M is defined as the number of web services in the application, the length L of the chromosome is as follows:For example, if the number of available resources is , then the number of gene bits per available resource on the chromosome is determined according to Equation (4), , and the coding for the available resources is shown in Table 1.Table 1. An example of available resources coding.
Available resources 1 2 3 4 5 6 Coding 000 001 010 011 100 101 If the number of web services in the application is defined as , then the overall chromosome length is 27, and the chromosome coding is as follows: 0001010000110100.In the process of application deployment, users need to comprehensively evaluate the composite scheme based on the three aspects of cost, time and service quality. Therefore, this section includes three parts of the application deployment model: the cost model, time model and service quality model. - Cost modelThe total cost of application execution is the sum of the cost of executing each web service. In turn, the cost of executing each web service on all available resources can be represented as a matrix , where represents the cost of executing a web service j on the available resource i. If the cost of executing web service is defined as j on the available resource i in the synergistic service array X, the final total cost of application execution can be obtained as follows:When an application array X is generated and the above operation is performed, the total cost of executing the application can be obtained. According to the obtained from each synergy service array X, the minimum cost and the optimal application-deploying scheme corresponding to the minimum cost can be determined.
- Time modelThe start execution time of the first web service in the application is defined as 0. According to the application array X and the partial order relationship between web services, along with the length of time required by the available resources to execute different web services , the completion time of the last web service can be obtained. Matrix T stores the time cost of each web service executed by each available resource; this is an matrix, where is the time cost of web service j being executed by available resource i; moreover, the M column of the matrix corresponds to M web services, and these M web services have a temporal topology sequence. Therefore, the total time (defined as ) required to execute the entire application can be obtained as follows:
- Service usability modelGiven the widespread differences in computing power, memory, network bandwidth, and many other aspects of available resources, the QoS for each available resource is different when the same web service is being performed. The QoS of the available resources when performing web services is expressed as matrix A, where represents the QoS of the available resources i when executing web services j. The QoS corresponding to the synergetic service array X can thus be expressed as follows:
- Target of modelThe aim of deploying these applications is a) to reduce the cost as much as possible and b) to reduce the execution time of the application with the goal of ensuring service usability. Therefore, the objective function can be established as follows:The , and in Equation (9) is the normalized value of , and which are calculated using Equation (10). Equation (9) needs to satisfy Equations (2) and (3). Thus, the term constraint described below refers to Equations (2) and (3). The parameters a and b of in Equation (9) are formulated according to the emphasis placed by the user on each factor.
3.2. Intelligent Genetic Scheme
3.2.1. Generation of Initial Populations
| Algorithm 1 IGS algorithm |
Input: initial population number |
Output: individual fitness |
|
| Algorithm 2 Initialize the population algorithm |
Input: initial population number , percentage of initial inner point M, number of randomly generated individuals |
Output: initial population |
|
3.2.2. Selection Based on Crossing between Populations
3.2.3. Adaptive Mutation Rate
| Algorithm 3 Inter-population cross-method individual selection algorithm |
Inter-population cross-method individual selection algorithm |
Input: initial and its size |
Output: child generation |
|
| Algorithm 4 Preserving low fitness individual algorithms |
Input: initial population and its size , retained low fitness individual ratio |
Output: selected population |
|
4. Simulation Experiments and Results Analysis
4.1. Experimental Setup Instructions
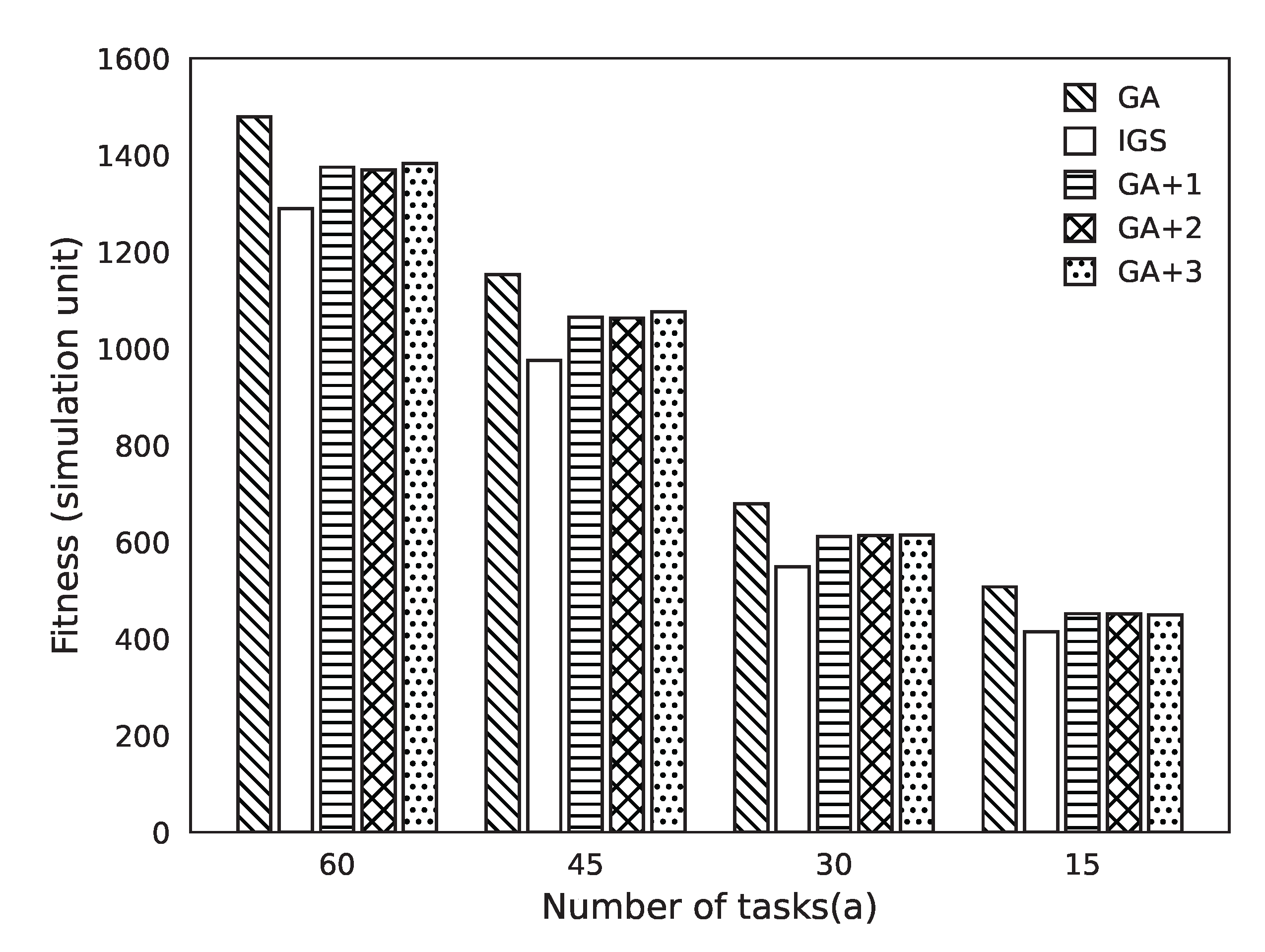
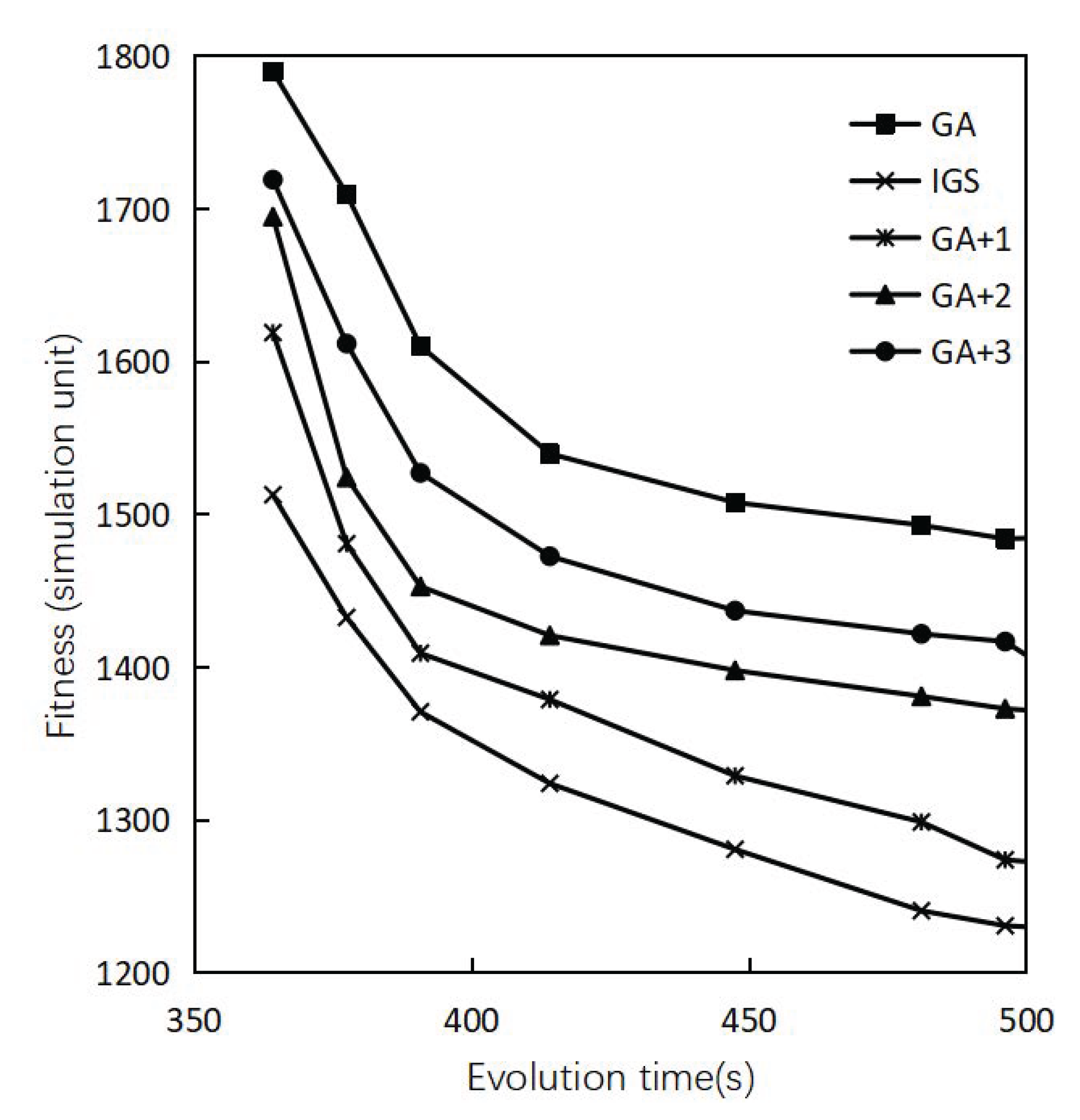
- GA: Genetic algorithm, implemented using the classical genetic algorithm; genetic operator adopts crossover and mutation evolution [14].
- IGS: The improved intelligent genetic scheme proposed in this paper.
- GA+1: Based on the genetic algorithm GA, the algorithm is optimized for the initial population in Section 3.2.1 [20].
- GA+2: Based on the genetic algorithm GA, the algorithm is optimized for the crossover between populations in Section 3.2.2 [21].
- GA+3: Based on the genetic algorithm GA, the algorithm optimizes the adaptive mutation rate in Section 3.2.3 [22].
- CGA: The genetic algorithm that uses the adaptive mutation rate in [24].
This is an example of a quote.
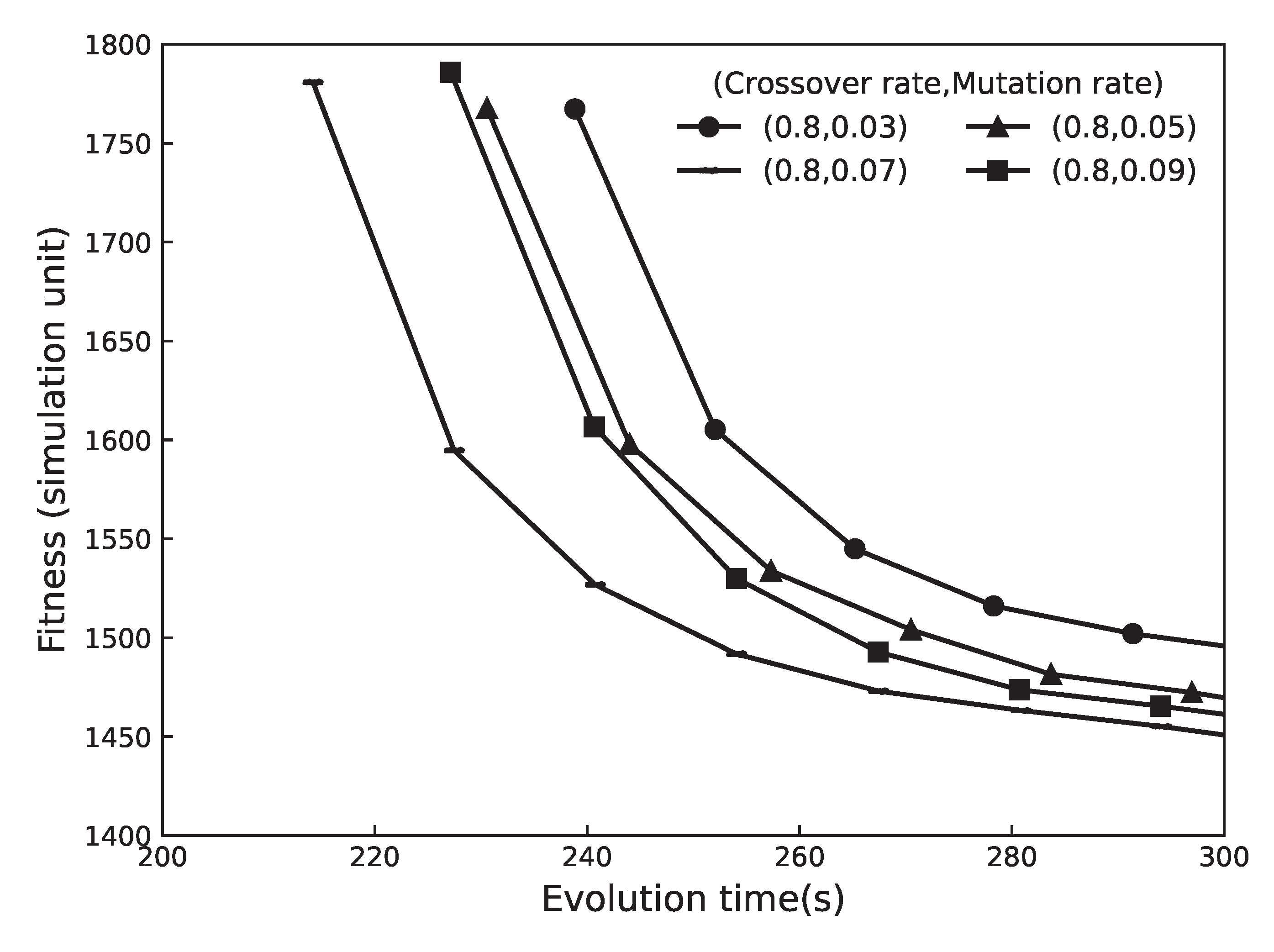
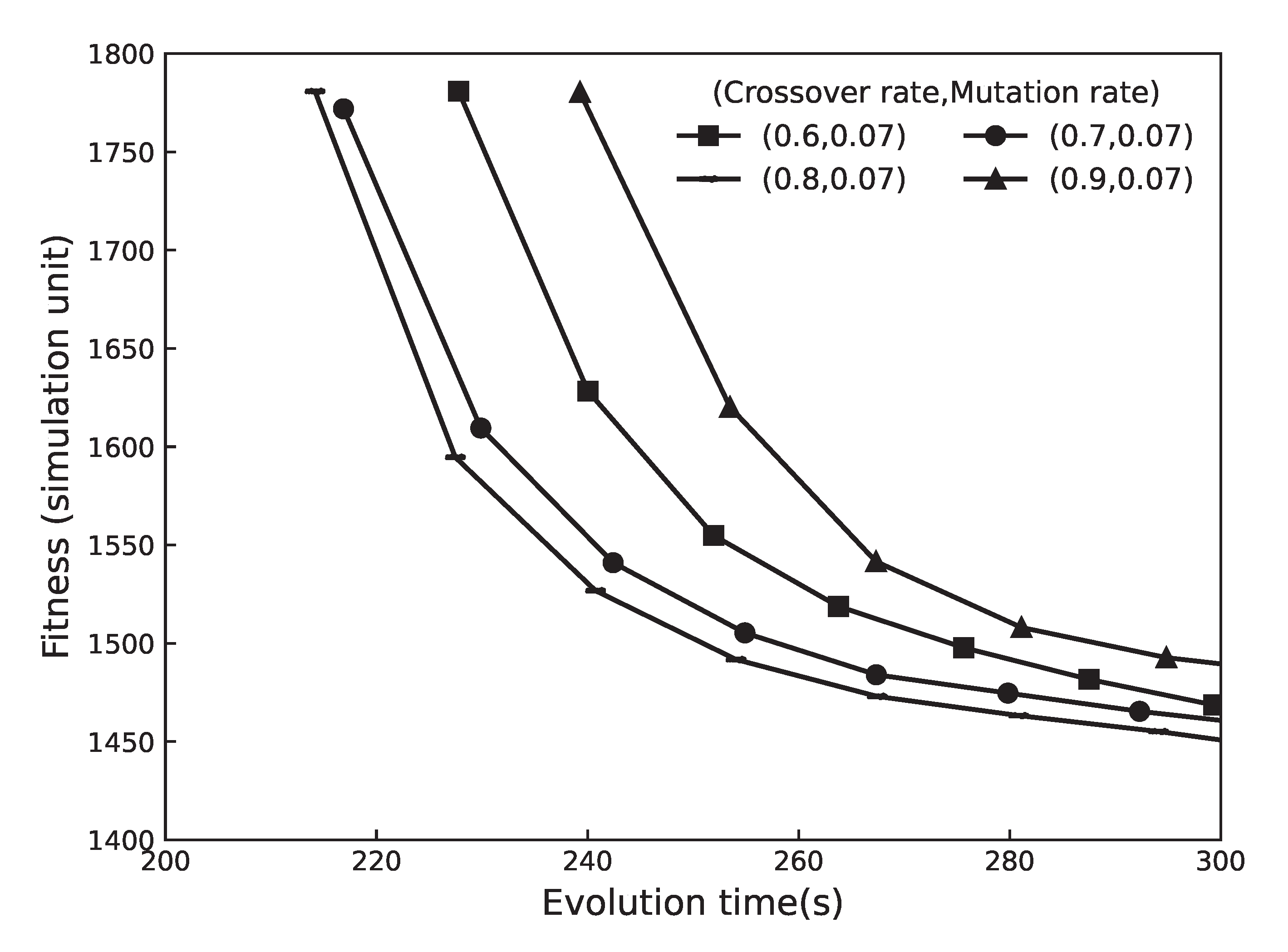
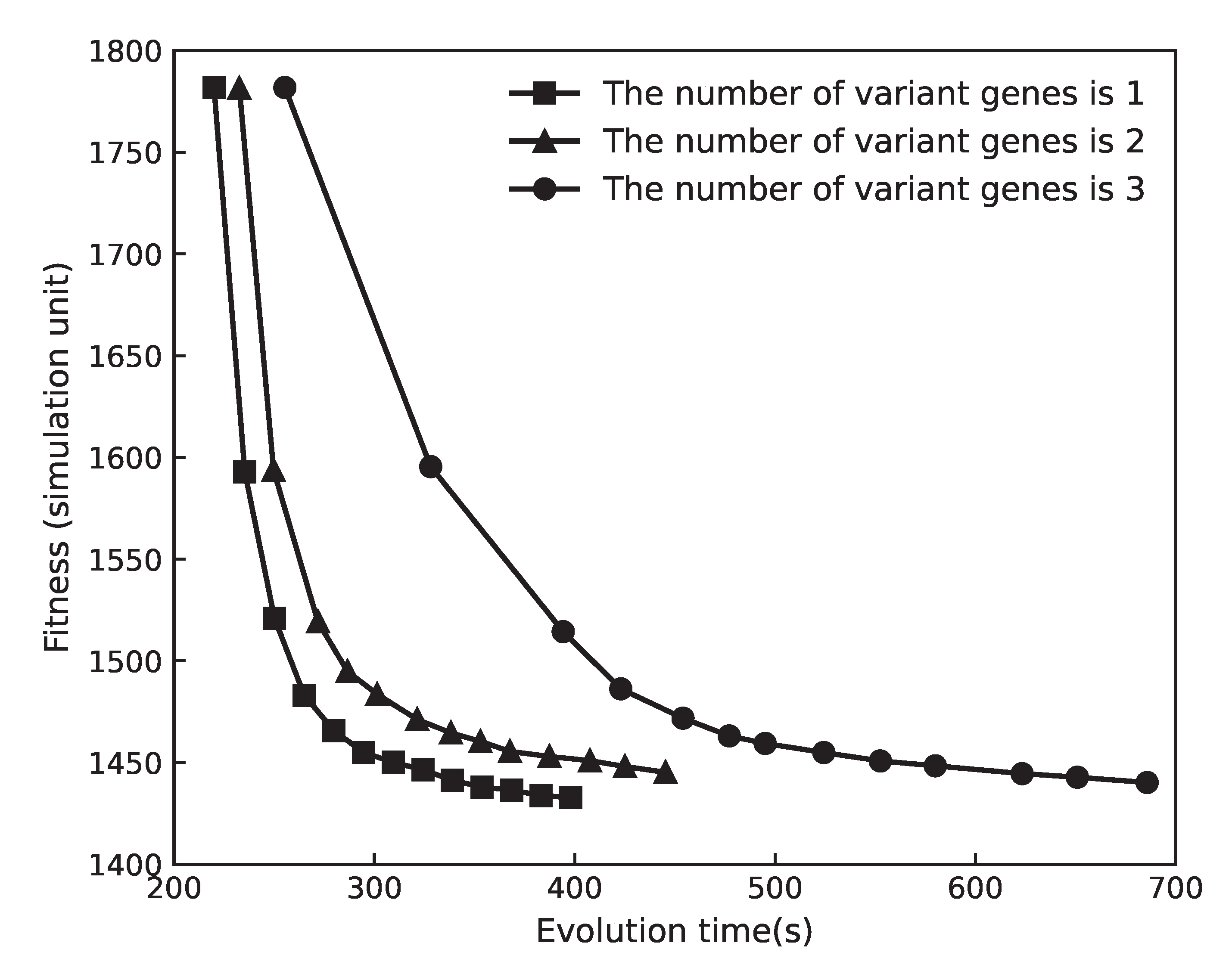
4.2. Experimental Parameter Determination
4.3. Performance Analysis: Comparison with Existing Main Schemes
5. Discussion and Limitations
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, Z.; Miao, W.; Li, S.; Liao, X.; Zhang, M.; Zhang, R.; Teng, C. Adaptive Task Scheduling in Cloud-Edge System for Edge Intelligence Application. In Proceedings of the 2021 IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), New York City, NY, USA, 30 September–3 October 2021; pp. 1682–1689. [Google Scholar] [CrossRef]
- Wan, L.; Wei, L.; Xiong, N.; Yuan, J.; Xiong, J. Pareto optimization for the two-agent scheduling problems with linear non-increasing deterioration based on internet of things. Future Gener. Comput. Syst. 2017, 76, 293–300. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Yang, Y.; Xu, Y.; Zhang, Y. Collaborative Production Task Decomposition and Allocation among Multiple Manufacturing Enterprises in a Big Data Environment. Symmetry 2021, 13, 2268. [Google Scholar] [CrossRef]
- Cheng, Y.; Bi, L.; Tao, F.; Ji, P. Hypernetwork-based manufacturing service scheduling for distributed and collaborative manufacturing operations towards smart manufacturing. J. Intell. Manuf. 2020, 31, 1707–1720. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, L.; Lu, Z.; Du, X.; Wu, J.; Hung, P.C. An Adaptive Mechanism for Dynamically Collaborative Computing Power and Task Scheduling in Edge Environment. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Shi, L.; Fu, X.; Li, J. Mobility prediction-based service scheduling optimization algorithm in cloudlets. In Proceedings of the 3rd International Conference on Cloud Computing and Security, Nanjing, China, 16–18 June 2017; pp. 619–630. [Google Scholar] [CrossRef]
- Yin, J.; Lo, W.; Deng, S.; Li, Y.; Wu, Z.; Xiong, N. Colbar: A collaborative location-based regularization framework for QoS prediction. Inf. Sci. 2014, 265, 68–84. [Google Scholar] [CrossRef]
- Yuan, D.; Yang, Y.; Liu, X.; Chen, J. A data placement strategy in scientific cloud workflows. Future Gener. Comput. Syst. 2010, 26, 1200–1214. [Google Scholar] [CrossRef]
- Cheng, H.; Su, Z.; Xiong, N.; Xiao, Y. Energy-efficient node scheduling algorithms for wireless sensor networks using Markov random field model. Inf. Sci. 2016, 329, 461–477. [Google Scholar] [CrossRef]
- Benayoun, R.; De Montgolfier, J.; Tergny, J.; Laritchev, O. Linear programming with multiple objective functions: Step method (stem). Math. Program. 1971, 1, 366–375. [Google Scholar] [CrossRef]
- Meng, F.C.; Chu, D.H.; Li, K.Q.; Zhou, X.Q. Solving SaaS components optimization placement problem with hybrid genetic and simulated annealing algorithm. J. Softw. 2016, 27, 916–932. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Xiang, T.; Guo, X.; Jia, Z.H.; He, Q. Quality prediction for services based on SOM neural network. J. Softw. 2018, 29, 3388–3399. [Google Scholar] [CrossRef]
- Hu, W.; Yen, G.G.; Zhang, X. Multiobjective particle swarm optimization based on pareto entropy. J. Softw. 2014, 25, 1025–1050. [Google Scholar] [CrossRef]
- Keshanchi, B.; Souri, A.; Navimipour, N.J. An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: Formal verification, simulation, and statistical testing. J. Syst. Softw. 2017, 124, 1–21. [Google Scholar] [CrossRef]
- Jiang, Y.; Tong, G.; Yin, H.; Xiong, N. A pedestrian detection method based on genetic algorithm for optimize XGBoost training parameters. IEEE Access 2019, 7, 118310–118321. [Google Scholar] [CrossRef]
- Yu, X.; Xiong, N.; Zhang, W. Research on mining rules from multi-criterion group decision making based on genetic algorithms. In Proceedings of the 13th IEEE International Conference on Computational Science and Engineering, Hong Kong, China, 11–13 December 2010; pp. 302–307. [Google Scholar] [CrossRef]
- De Oliveira, L.L.; Freitas, A.A.; Tinós, R. Multi-objective genetic algorithms in the study of the genetic code’s adaptability. Inf. Sci. 2018, 425, 48–61. [Google Scholar] [CrossRef]
- Bello-Orgaz, G.; Salcedo-Sanz, S.; Camacho, D. A multi-objective genetic algorithm for overlapping community detection based on edge encoding. Inf. Sci. 2018, 462, 290–314. [Google Scholar] [CrossRef]
- Toroslu, I.; Arslanoglu, Y. Genetic algorithm for the personnel assignment problem with multiple objectives. Inf. Sci. 2007, 177, 787–803. [Google Scholar] [CrossRef]
- Goren, H.; Tunali, S.; Jans, R. A review of applications of genetic algorithms in lot sizing. J. Intell. Manuf. 2008, 21, 575–590. [Google Scholar] [CrossRef]
- Hyun, C.; Kim, Y.; Kim, Y. A genetic algorithm for multiple objective sequencing problems in mixed model assembly lines computers. Comput. Oper. Res. 1998, 25, 675–690. [Google Scholar] [CrossRef]
- Qu, H.; Xing, K.; Alexander, T. An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots. Neurocomputing 2013, 120, 509–517. [Google Scholar] [CrossRef]
- Górski, T.; Oźniak, A.P.W. Optimization of Business Process Execution in Services Architecture: A Systematic Literature Review. IEEE Access 2021, 9, 111833–111852. [Google Scholar] [CrossRef]
- Fang, W.; Yin, X.; An, Y.; Xiong, N.; Guo, Q.; Li, J. Optimal scheduling for data transmission between mobile devices and cloud. Inf. Sci. 2015, 301, 169–180. [Google Scholar] [CrossRef]
- Lin, B.; Guo, W.; Chen, G.; Xiong, N.; Li, R. Cost-driven scheduling for deadline-constrained workflow on multi-clouds. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium Workshop, Hyderabad, India, 25–29 May 2015; pp. 1191–1198. [Google Scholar] [CrossRef]
- Wan, J.; Yang, L.T.; Li, Y.; Xu, X.; Xiong, N. An adaptive management mechanism for resource scheduling in multiple virtual machine system. In Proceedings of the 8th International Conference on Autonomic and Trusted Computing, Banff, AB, Canada, 2–4 September 2011; pp. 60–74. [Google Scholar] [CrossRef]
- Xu, J.; Liu, A.; Xiong, N.; Wang, T.; Zuo, Z. Integrated collaborative filtering recommendation in social cyber-physical systems. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717749745. [Google Scholar] [CrossRef]
- Solnon, C. Ants can solve constraint satisfaction problems. IEEE Trans. Evol. Comput. 2002, 6, 347–357. [Google Scholar] [CrossRef]
- Stutzle, T.; Hoos, H. MAX-MIN ant system and local search for the traveling salesman problem. In Proceedings of the IEEE International Conference on Evolutionary Computation, (ICEC ‘97), Indianapolis, IN, USA, 13–16 April 1997; pp. 309–314. [Google Scholar] [CrossRef]
- Xia, Y.M.; Cheng, B.; Chen, J.L.; Meng, X.W.; Liu, D. Optimizing services composition based on improved ant colony algorithm. Chin. J. Comput. 2012, 35, 270–281. [Google Scholar] [CrossRef]
- Coello, C.; Pulido, G.; Lechuga, M. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Yang, J.-Q.; Chen, C.-H.; Li, J.-Y.; Liu, D.; Li, T.; Zhan, Z.-H. Compressed-Encoding Particle Swarm Optimization with Fuzzy Learning for Large-Scale Feature Selection. Symmetry 2022, 14, 1142. [Google Scholar] [CrossRef]
- Guo, W.; Xiong, N.; Chao, H.C.; Hussain, S.; Chen, G. Design and analysis of self-adapted task scheduling strategies in wireless sensor networks. Sensors 2011, 11, 6533–6554. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Zhang, J. Cooperative differential evolution with multiple populations for multiobjective optimization. IEEE Trans. Cybern. 2015, 46, 2848–2861. [Google Scholar] [CrossRef] [PubMed]
- Antonio, L.; Coello, C. Use of cooperative coevolution for solving large scale multiobjective optimization problems. In Proceedings of the IEEE Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2758–2765. [Google Scholar] [CrossRef]
- Kuo, T.; Hwang, S. Using disruptive selection to maintain diversity in genetic algorithms. Appl. Intell. 1997, 7, 257–267. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Du, H.; Feldman, M.W. A genetic algorithm with local search strategy for improved detection of community structure. Complexity 2010, 15, 53–60. [Google Scholar] [CrossRef]
- Pereira, A.; Andrade, B. On the genetic algorithm with adaptive mutation rate and selected statistical applications. Comput. Stat. 2014, 30, 131–150. [Google Scholar] [CrossRef]
- Zhang, D.; Li, P.; Wulamu, A. An Improved Multi-Label Learning Method with ELM-RBF and a Synergistic Adaptive Genetic Algorithm. Algorithms 2022, 15, 185. [Google Scholar] [CrossRef]
- Ide, J.; Köbis, E.; Kuroiwa, D.; Schöbel, A.; Tammer, C. The relationship between multi-objective robustness concepts and set-valued optimization. Fixed Point Theory Appl. 2014, 83, 1–20. [Google Scholar] [CrossRef]
- Donca, I.-C.; Stan, O.P.; Misaros, M.; Gota, D.; Miclea, L. Method for Continuous Integration and Deployment Using a Pipeline Generator for Agile Software Projects. Sensors 2022, 22, 4637. [Google Scholar] [CrossRef]
| Fitness | Number of tasks(a) | 60 | 45 | 30 | 15 |
|---|---|---|---|---|---|
| name | |||||
| IGS | 251.43 | 20.62 | 6.61 | 1.21 | |
| GA | 439.10 | 54.98 | 23.81 | 5.61 | |
| GA+1 | 273.98 | 31.43 | 10.48 | 1.68 | |
| GA+2 | 420.26 | 47.21 | 24.49 | 4.58 | |
| GA+3 | 430.08 | 42.20 | 23.74 | 4.15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Kong, L.; Lu, X.; Cui, L. An Intelligent Genetic Scheme for Multi-Objective Collaboration Services Scheduling. Symmetry 2022, 14, 2037. https://doi.org/10.3390/sym14102037
Guo W, Kong L, Lu X, Cui L. An Intelligent Genetic Scheme for Multi-Objective Collaboration Services Scheduling. Symmetry. 2022; 14(10):2037. https://doi.org/10.3390/sym14102037
Chicago/Turabian StyleGuo, Wei, Lanju Kong, Xudong Lu, and Lizhen Cui. 2022. "An Intelligent Genetic Scheme for Multi-Objective Collaboration Services Scheduling" Symmetry 14, no. 10: 2037. https://doi.org/10.3390/sym14102037
APA StyleGuo, W., Kong, L., Lu, X., & Cui, L. (2022). An Intelligent Genetic Scheme for Multi-Objective Collaboration Services Scheduling. Symmetry, 14(10), 2037. https://doi.org/10.3390/sym14102037






