Abstract
In this paper, we construct variants of Bawazir’s iterative methods for solving nonlinear equations having simple roots. The proposed methods are two-step and three-step methods, with and without memory. The Newton method, weight function and divided differences are used to develop the optimal fourth- and eighth-order without-memory methods while the methods with memory are derivative-free and use two accelerating parameters to increase the order of convergence without any additional function evaluations. The methods without memory satisfy the Kung–Traub conjecture. The convergence properties of the proposed methods are thoroughly investigated using the main theorems that demonstrate the convergence order. We demonstrate the convergence speed of the introduced methods as compared with existing methods by applying the methods to various nonlinear functions and engineering problems. Numerical comparisons specify that the proposed methods are efficient and give tough competition to some well known existing methods.
1. Introduction
Finding the roots of nonlinear equations is one of the most challenging problems in applied mathematics, engineering and scientific computing. Analytical methods are generally ineffective for finding the roots of a nonlinear equation. Consequently, iterative methods are employed to obtain the approximate roots of nonlinear equations. Many iterative methods for solving nonlinear equations have been developed and studied. Among these, Newton’s method is one of the most widely used [1], which is defined as follows:
Other well-known iterative approaches for solving nonlinear equations include the Chebyshev [2], Halley [2] and Ostrowski [3], methods. Most of the authors try to improve the order of convergence. As the order of convergence rises, so does the quantity of functional evaluations. As a result, iterative methods’ efficiency index falls. The efficiency index [2,3] of an iterative method determines the method’s efficiency, which is defined by the formula below:
where is the order of convergence and is the number of functional evaluations per step. Kung–Traub conjectured [2] that the order of convergence of an iterative method without memory is at most . The optimal method is one in which the order of convergence is . In 2022, Panday S. et al., created optimal methods [4]. In 2015, Kumar M. et al., developed a fifth-order derivative-free method [5]. Choubey N. et al., introduced the derivative-free eighth-order method [6] in 2015. Tao Y. et al., developed optimal methods [7]. Neta B. also developed a derivative-free method [8]. Singh M. Kumar et al., developed the eighth-order optimal method in 2021 [9]. In 2021, Said Solaiman O. et al. [10] developed an optimal eighth-order method. Chanu W.H. et al. [11] created a nonoptimal tenth-order method in 2022. This paper presents optimal fourth- and optimal eighth-order methods for solving simple roots of nonlinear equations, with efficiency indice of and , respectively. The efficiency indice of with-memory methods of orders 5.7 and 11 are and respectively. The remaining part of the manuscript is structured as follows. In Section 2, we describe the development of methods without memory using divided difference and weight function techniques. The order of convergence of without memory with derivative is analysed in Section 2. The development of derivative free with-memory methods along with convergence analysis are in Section 3. We present numerical tests to compare the proposed methods with other known optimal methods in Section 4. In Section 5, the proposed without memory methods are discussed in the complex plane using the basins of attraction. Finally, Section 6 covers the conclusions of the study.
2. Development of the Methods and Convergence Analysis
In 2021, Bawazir H. M. developed the following nonoptimal seventh-order method [12]
where
We take the first and second steps of method (3) and replace by the divided difference ; weighted by a function , we obtain the following fourth-order optimal method.
where and is the weight function, which is a sufficiently differentiable function at the point 0 with
Theorem 1.
Proof of Theorem 1.
Let be the simple root of and let be the error of iteration. Using Taylor expansion, we obtain
where
Using Equations (6) and (7) in the first step of (4), we obtain the following
Expanding about , we obtain
Using the expansion of and , we obtain
Moreover,
Using (6), (7), (9) and (11), we obtain
Using (9), (11) and (12) in (4), we obtain
To achieve the fourth order of convergence, we put , and and obtain the following error equation
From Equation (14), we conclude that the method (4) is of the fourth order of convergence. □
The new eighth-order optimal method is obtained by adding the following equation as the third step to the method (4).
where is the second step of method (4). To obtain the optimal method, is approximated by and weighted by a function , and the method is given by
where , and and are the weight functions with and
Theorem 2.
Let be a real-valued, sufficiently differentiable function. Let be a simple root of f and be sufficiently close to μ; then, the iterative scheme defined in (16) is of the eighth order of convergence if and satisfy the following conditions , and , , , , , , , , and . Equation (16) satisfies the following error equation
Proof of Theorem 2.
Considering all the assumptions made in Theorem 1, from Equation (14) we have
Expanding about , we obtain
Further,
Using (19) and (20) in the third step of method (16), we obtain
To eliminate , , we put , , , , , , , , . Then, we obtain
From Equation (22), we conclude that (16) is of the eighth order of convergence. □
3. Derivative-Free and with-Memory Methods
In this section, we present derivative-free parametric and with memory iterative methods. Another Bawazir’s iterative method is written as [12]
where This method uses five function evaluation to achieve the twelfth order of convergence. We modify the method given in (23) by adding two parameters and as follows:
where and is the weight function with , [13] and
Theorem 3.
Let be a real-valued, sufficiently differentiable function. Let be a simple root of f and be sufficiently close to μ; then, the iterative scheme defined in (24) is of the fourth order of convergence if satisfies the following conditions , and . The iterative scheme (24) satisfies the following error equation
Proof of Theorem 3
Let be the simple root of and let be the error of iteration. Using Taylor expansion, we obtain
where Using (26) in , we obtain
By Taylor series expansion, we obtain
Using (26) and (28) in the first step of (24), we obtain
Using Taylor series expansion, we obtain
Using (26) and (30), we obtain
Using (26), (28), (30) and (31) in second step of (24), we obtain
. etc. Putting , and , Equation (32) becomes
From Equation (33), we can conclude that the method (24) has fourth order of convergence, which completes the proof of Theorem 3. □
The eighth-order method is given as follows:
where & are the weight functions with , and , [13].
Theorem 4.
Let be a real-valued, sufficiently differentiable function. Let be a simple root of f and be sufficiently close to μ; then, the iterative scheme defined in (34) is of eighth order of convergence ifandsatisfy the following conditions , , , , , and . The iterative scheme (34) satisfies the following error equation
Proof of Theorem 4.
Considering all the assumptions made in Theorem 3, we have from (33),
where ’s are constants formed by , and .
Development of with Memory Methods
We are going to develop with-memory methods from (24) and (34) using the two parameters. From Equations (25) and (35), we clearly see that the order of convergence of the method (34) is sixth and evelenth if and . With the choice and , the error Equation (25) becomes
and the error Equation (35) becomes
In order to obtain with-memory method, we choose and , as the iteration proceeds by the formulas and . In method (24), we use the following approximation
where and are Newton’s interpolating polynomial of third and fourth degrees, respectively. We obtain the following with memory iterative method:
For method (34), we use the following approximation
where and are Newton’s interpolating polynomial of fourth and fifth degree, respectively. We obtain the following with-memory iterative method:
Remark 2.
Accelerating methods obtained by recursively calculated free parameter may also be called self-accelerating methods. The initial value and should be chosen before starting the iterative process [14].
We are going to analyse the convergence behaviours of the with-memory methods. If the sequence converges to the root of f with the order p, we write , where . To prove the order of convergence of methods (44) and (47), we use the following lemma, introduced in [15].
Lemma 1.
Ifand, , the estimates
and
hold.
Let us consider the following theorems.
Theorem 5.
If an initial guess is sufficiently close to the simple root μ of , f is real sufficiently differentiable function; then, the R-order of convergence of the method (44) is at least 5.7075.
Proof.
Let be a sequence of approximations generated by the with-memory iterative method defined in (44). If the sequence converges to the root of f with order q, we obtain the following:
Let us assume that the iterative sequences and have the orders and , respectively. Then, Equation (48) gives the following:
By Theorem 3, we can write
Using Lemma 1, we obtain the following:
Comparing the power of of Equations (50)–(55), (51)–(56) and (49)–(57), we obtain the following system of equations
By solving this system of equations, we obtain , and . Thus, the proof is complete. □
Lemma 2.
If and , , the estimates
and
hold.
Theorem 6.
If an initial guess is sufficiently close to the simple root μ of , f is real sufficiently differentiable function; then, the R-order of convergence of the method (47) is at least 11.
Proof.
Let be a sequence of approximations generated by the with-memory iterative method defined in (44). If the sequence converges to the root of f with order q, we obtain the following equation:
Let us assume that the iterative sequences , and have the order , and , respectively. Then, Equation (61) gives the following:
By Theorem 4, we can write
Using Lemma 1, we obtain the following:
Comparing the power of of Equations (63)–(70), (64)–(71), (65)–(72) and (62)–(73), we obtain the following system of equations:
By solving this system of equations, we obtain , , and . Thus, the proof is complete. □
4. Numerical Results
In this section, we consider the peculiar attitude of the introduced iterative methods (4) and (16) over the existing methods having the same order of convergence. To demonstrate the behaviours of the newly defined methods, we apply the methods to several numerical examples. For comparison, we consider the following methods:
Fourth-order method (M4th(a)) introduced by Chun et al. [16]:
Fourth-order method (M4th(b)) introduced by Singh et al. [17]:
In the year 2019, Francisco et al., developed the following method (M4th(c)) [18]:
Ekta et al., introduced the following method (M4th(d)) [19] in 2020:
where
Eighth-order method (M8th(a)) developed by Petkovic et al. [20] is given as follows:
where with . Cordero A. et al., developed the following eighth-order method (M8th(b)) [21]:
where with and .
Another eighth-order method (M8th(c)) developed by A. Cordero et al. [21] is written as follows:
where and with , and . Abbas H. M. et al., developed the following eighth-order method (M8th(d)) [22]:
where ,
The following nonlinear equations are taken as test functions, and their corresponding initial guesses are also given:
Example 1:
,
Example 2:
,
Example 3:
Example 4:
,
Example 5:
,
Example 6:
,
In Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we provide the errors of two consecutive iterations after the fourth iteration; modulus value of approximate root after fourth iteration, i.e., with 17-significance digits; and the residual error, i.e., after fourth iteration. We provide the computational order of convergence [23], which is formulated by
We also provide the CPU running time for each method. The elapsed CPU times are computed by selecting as the stopping condition. Note that CPU running time is not unique and depends entirely on the computer’s specification; however, here, we present an average of three performances to ensure the robustness of the methods. The results are carried out with Mathematica software on a 2.30 GHz Intel(R) Core(TM) i3-8145U CPU with 4 GB of RAM running Windows 10.

Table 1.
Convergence behaviour on .

Table 2.
Convergence behaviour on .

Table 3.
Convergence behaviour on .

Table 4.
Convergence behaviour on .

Table 5.
Convergence behaviour on .

Table 6.
Convergence behaviour on .
Remark 3.
From the results in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we observe that the newly presented methods are highly competitive, with the errors obtained in the different results being highly accurate as compared with the other existing methods and better than them in all cases.
Applications on Real-World Problem
Here, we take some real-world problems from other papers:
Problem 1.
Projectile Motion Problem: This problem expresses motion of the projectile, it is represented by the following nonlinear equation (see more details in [7])
where h is height of the tower from which the projectile is launched, v is initial velocity of the projectile, g is acceleration due to gravity and is the impact function. In particular, we choose , , , and .
Table 7 shows that the convergence behaviour of newly introduced methods performs better than that of the other existing methods.

Table 7.
Convergence behaviour on projectile motion problem.
Problem 2.
Height of a moving object: An object falling vertically through the air is subjected to viscous resistance as well as the force of gravity (see [24] Ch2, p-66). Let us assume that the object with mass m is dropped from a height and that the height of the object after t seconds is represented by the following equation:
where k represents coefficient of air resistance in lb-s/ft and g is the acceleration due to gravity. To solve Equation (89), we choose , and lb-s/ft. We have to find the time taken for the object to reach the ground. We rewrite Equation (89) in the following nonlinear form
Table 8 shows that the convergence behaviour of newly introduced methods performs better than that of the other existing methods.

Table 8.
Convergence behaviour on height of a moving object problem.
Problem 3.
Fractional Conversion: Fractional conversion of nitrogen hydrogen feed to ammonia at 500 temperature and 250 atm. pressure is given by the following nonlinear equation (see [25,26]):
Equation (91) can be reduced to a polynomial of degree four
Table 9 shows that the convergence behaviour of the newly introduced methods performs better than that of the other existing methods.

Table 9.
Convergence behaviour on fractional conversion problem.
Problem 4.
Open channel flow: Open channel flow is a problem to find the depth of water in a rectangular channel for a given quantity of water; the problem is represented by the following nonlinear equation (see [25,27]):
where F represents water flow, which is formulated as . s is the slope of the channel, a is the area the channel, r is the hydraulic radius of the channel, n is Manning’s roughness coefficient and b is the width of the channel. Taking the different values of the parameters as b = 4.572 m, s = 0.017 and n = 0.0015, we obtain the following equation
Table 10 shows that convergence behaviour of newly introduced method performs better than that of the other existing methods.

Table 10.
Convergence behaviour on open channel flow problem.
5. Basins of Attraction
In this section, we discuss the dynamical behaviours of the without-memory iterative methods in the complex plane. This gives useful information about the stability and reliability of the iterative methods. Here, we compare the stability of the introduced methods with other methods. For the comparison, we apply the iterative methods to the complex polynomial of orders four and three, and . We take a square of grid points and lay on a colour to each point , according to the roots corresponding to which the method starting from z converges. The roots of the polynomial are represented by the white dots. We spot the point z—where the methods diverge from a root with the tolerance and a maximum iteration 100—as black, and these black points are considered as divergent points. In the basins of attraction of each iterative method, a brighter colour region indicates that the iterative method converges to the root in the minimum number of iterations and a darker region indicates that the method needs more iterations to converge towards the root.
The basins of attraction of fourth-order iterative methods on polynomials and are given in Figure 1. Figure 2 and Figure 3 are the basins of attraction of eighth-order iterative methods on polynomials and , respectively. From the figures, we can observe that the newly presented methods produce competitive basins and perform better than the other methods in some cases.


Figure 1.
Basins of attraction for fourth-order methods for and .
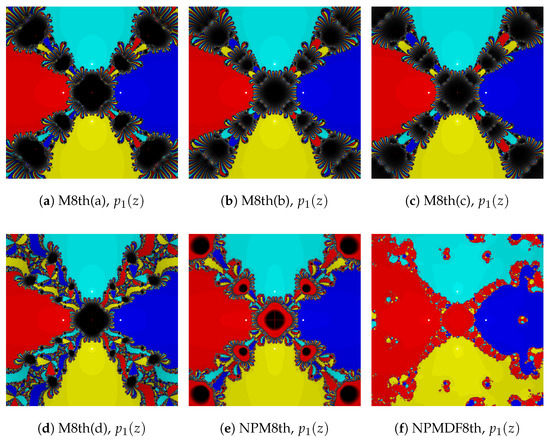
Figure 2.
Basins of attraction for eighth-order methods for .
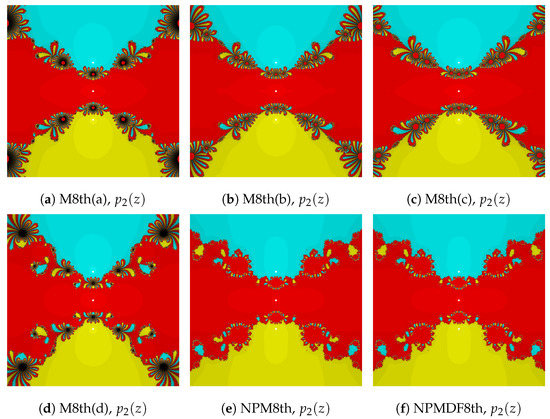
Figure 3.
Basins of attraction for eighth-order methods for .
6. Conclusions
We have introduced the fourth and eighth-order without-memory iterative methods and with-memory methods of orders 5.7 and 11. The weight function and divided difference techniques are used to develop the without-memory methods. The derivative-free with-memory iterative methods are developed using two accelerating parameters, which are computed using Newton interpolating polynomials, thereby increasing the order of convergence from 4 to for two-step and from 8 to 11 for three-step methods without any additional function evaluation. The presented methods are compared with other existing methods using some examples of nonlinear equations. The results given in the tables clarify the competitive nature of the presented methods in comparison with the existing methods and will be valuable in finding an adequate estimate of the exact solution of nonlinear equations. The current work can be extended to find solutions of multivariate nonlinear equations.
Author Contributions
Conceptualization, W.H.C., G.T. and S.P.; methodology, W.H.C. and S.P.; software, W.H.C. and G.T.; validation, W.H.C., G.T. and S.P.; formal analysis, S.P.; investigation, W.H.C., S.P. and G.T.; resources, W.H.C.; data curation, W.H.C. and G.T.; writing—original draft preparation, W.H.C.; writing—review and editing, W.H.C., G.T. and S.P.; visualization, G.T.; supervision, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jamaludin, N.A.A.; Nik Long, N.M.A.; Salimi, M.; Sharifi, S. Review of Some Iterative Methods for Solving Nonlinear Equations with Multiple Zeros. Afrika Matematika 2019, 30, 355–369. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Space; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Panday, S.; Sharma, A.; Thangkhenpau, G. Optimal fourth and eighth-order iterative methods for non-linear equations. J. Appl. Math. Comput. 2022, 1–19. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, A.K.; Srivastava, A. A New Fifth Order Derivative Free Newton-Type Method for Solving Nonlinear Equations. Appl. Math. Inf. Sci. 2015, 9, 1507–1513. [Google Scholar]
- Choubey, N.; Jaiswal, J.P. A Derivative-Free Method of Eighth-Order For Finding Simple Root of Nonlinear Equations. Commun. Numer. Anal. 2015, 2, 90–103. [Google Scholar] [CrossRef]
- Tao, Y.; Madhu, K. Optimal fourth, eighth and sixteenth Order Methods by using Divided Difference Techniques and Their Basins of Attractions and Its Applications. Mathematics 2019, 7, 322. [Google Scholar] [CrossRef]
- Neta, B. A Derivative-Free Method to Solve Nonlinear Equations. Mathematics 2021, 9, 583. [Google Scholar] [CrossRef]
- Singh, M.K.; Singh, A.K. The Optimal Order Newton’s Like Methods with Dynamics. Mathematics 2021, 9, 527. [Google Scholar] [CrossRef]
- Solaiman, O.S.; Hashim, I. Optimal Eighth-Order Solver for Nonlinear Equations with Applications in Chemical Engineering. Intell. Autom. Soft Comput. 2021, 13, 87–93. [Google Scholar] [CrossRef]
- Chanu, W.H.; Panday, S. Excellent Higher Order Iterative Scheme for Solving Non-linear Equations. IAENG Int. J. Appl. Math. 2022, 52, 1–7. [Google Scholar]
- Bawazir, H.M. Seventh and Twelfth-Order Iterative Methods for Roots of Nonlinear Equations. Hadhramout Univ. J. Nat. Appl. Sci. 2021, 18, 2. [Google Scholar]
- Torkashvand, V.; Kazemi, M.; Moccari, M. Sturcture A Family of Three-Step With-Memory Methods for Solving nonlinear Equations and Their Dynamics. Math. Anal. Convex Optim. 2021, 2, 119–137. [Google Scholar]
- Lotfi, T.; Soleymani, F.; Noori, Z.; Kılıçman, A.; Khaksar Haghani, F. Efficient Iterative Methods with and without Memory Possessing High Efficiency Indices. Discret. Dyn. Nat. Soc. 2014, 2014, 912796. [Google Scholar] [CrossRef]
- Dzunic, J. On Efficient Two-Parameter Methods for Solving Nonlinear Equations. Numer. Algorithms 2012, 63, 549–569. [Google Scholar] [CrossRef]
- Chun, C.; Lee, M.Y.; Neta, B.; Dzunic, J. On optimal fourth-order iterative methods free from second derivative and their dynamics. Appl. Math. Comput. 2012, 218, 6427–6438. [Google Scholar] [CrossRef]
- Singh, A.; Jaiswal, J.P. Several new third-order and fourth-order iterative methods for solving nonlinear equations. Int. J. Eng. Math. 2014, 2014, 828409. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. Wide stability in a new family of optimal fourth-orderiterative methods. Comput. Math. Methods 2019, 1, e1023. [Google Scholar] [CrossRef]
- Sharma, E.; Panday, S.; Dwivedi, M. New Optimal Fourth Order Iterative Method for Solving Nonlinear Equations. Int. J. Emerg. Technol. 2020, 11, 755–758. [Google Scholar]
- Petkovic, M.S.; Neta, B.; Petkovic, L.D.; Dzunic, J. Multipoint Methods for Solving Nonlinear Equations; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Cordero, A.; Lotfi, T.; Mahdiani, K.; Torregrosa, J.R. Two Optimal General Classes of Iterative Methods with Eighth-order. Acta. Appl. Math. 2014, 134, 64–74. [Google Scholar] [CrossRef]
- Abbas, H.M.; Al-Subaihi, I.A. A New Family of Optimal Eighth-Order Iterative Method for Solving Nonlinear Equations. Appl. Math. Comput. 2022, 8, 10–17. [Google Scholar]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Richard, L.B.; Douglas, J.F. Numerical Analysis, 9th ed.; India Brooks/Cole Cengage Larning: Boston, MA, USA, 2019. [Google Scholar]
- Rehman, M.A.; Naseem, A.; Abdeljawad, T. Some Novel Sixth-Order Schemes for Computing Zeros of Nonlinear Scalar Equations and Their apllications in Engineering. J. Funct. Spaces 2021, 2021, 5566379. [Google Scholar]
- Balaji, G.V.; Seader, J.D. Application of interval Newton’s method to chemical engineering problems. Reliab. Comput. 1995, 1, 215–223. [Google Scholar] [CrossRef]
- Manning, R. On the flow of water in open channels and pipes. Trans. Inst. Civ. Eng. Irel. 1891, 20, 161–207. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).