An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting
Abstract
1. Introduction and Motivation
2. Related Work
3. Unsupervised MultiDBN-T
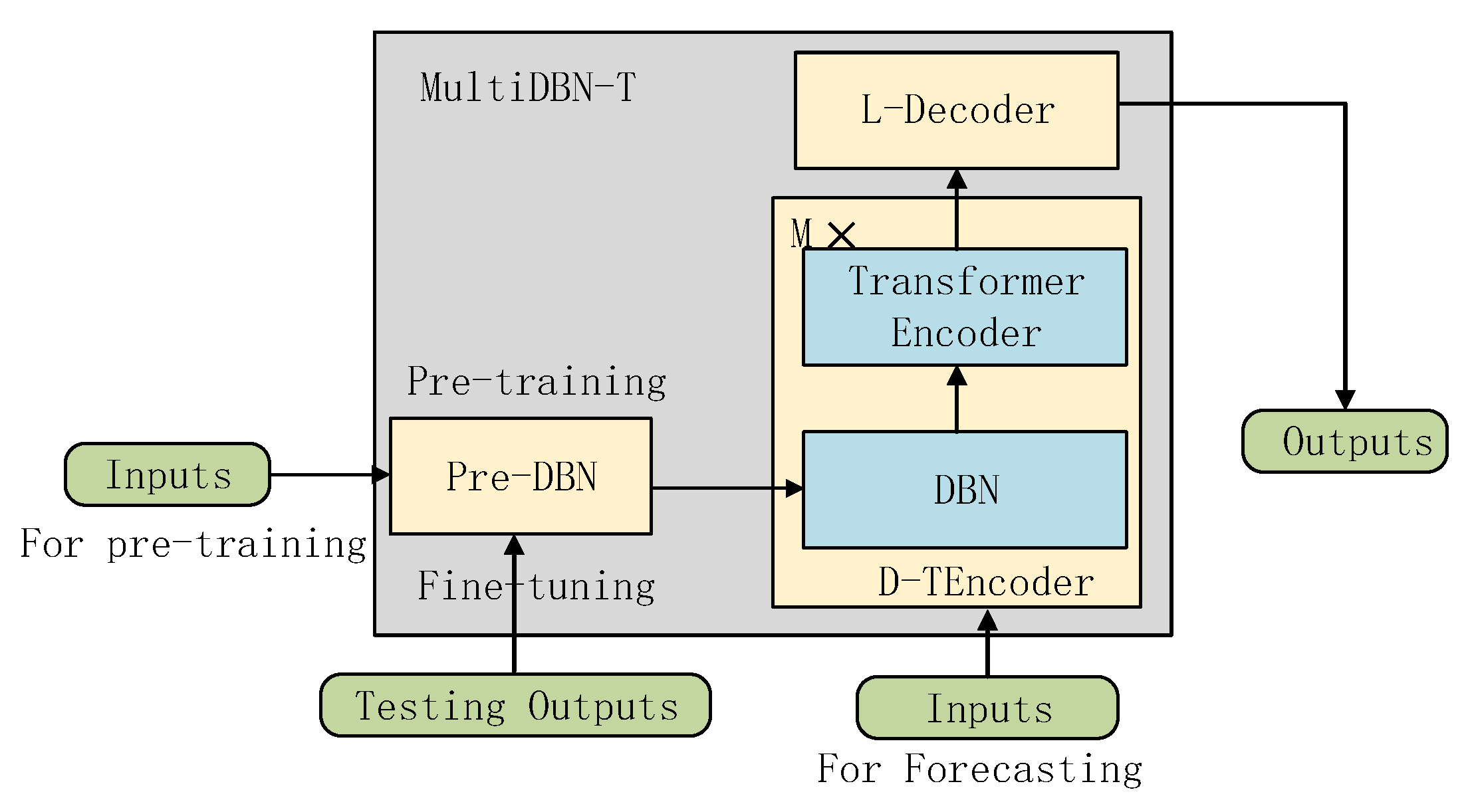
3.1. MultiDBN-T Architecture
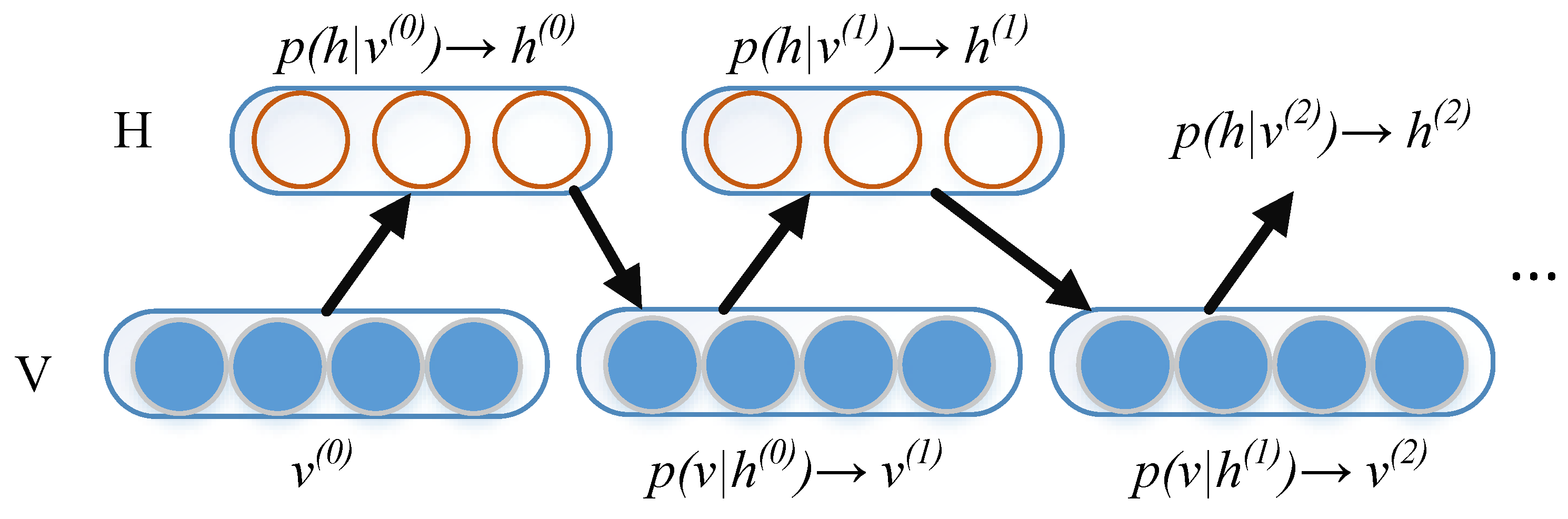
3.2. Pre-DBN
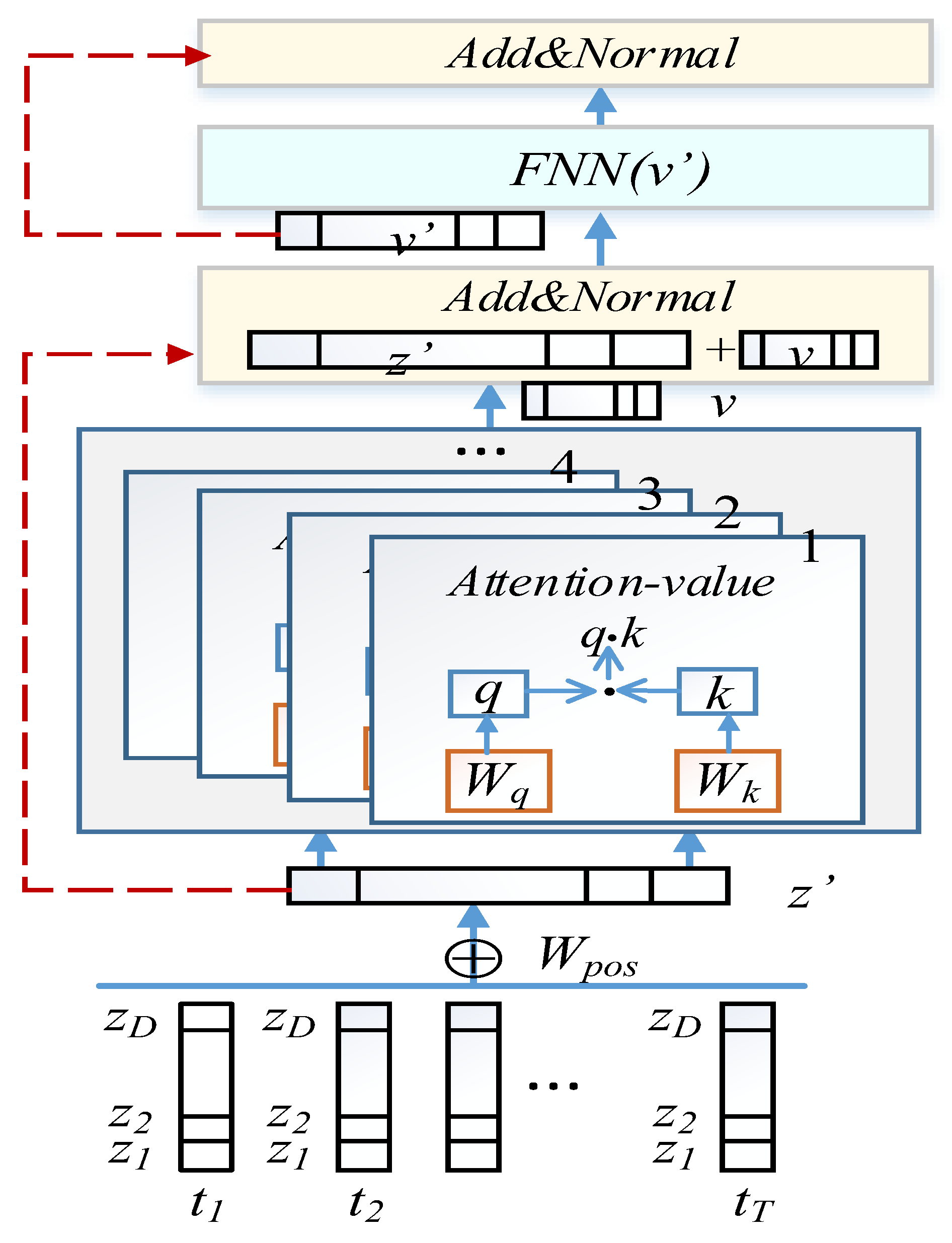
3.3. D-TEncoder
3.4. L-Decoder
3.5. Training Algorithm and Optimal Configuration
| Algorithm 1: MultiDBN-T algorithm based on pre-DBN and D-TEncoder feature learning |
| Input: |
| Output: |
| 1. 2.For i = 1 to 3 Do 3. ;//Use to solve GG−RBM according to//Equations (1)−(7) 4. //According to Equations (8) and (9), use the//fine-tuning mode of DBN to obtain the initial weights of the network parameters of//the corresponding layer of MultiDBN-T 5. For e = 1 to epoch Do 6. ;//Complete the parameter learning of //MultiDBN-T according to Equations (10)–(14) 7. Return |
4. Data Description and Data Formatting
4.1. Data Description
4.2. Description of Observable Variables
4.3. Data Format Conversion
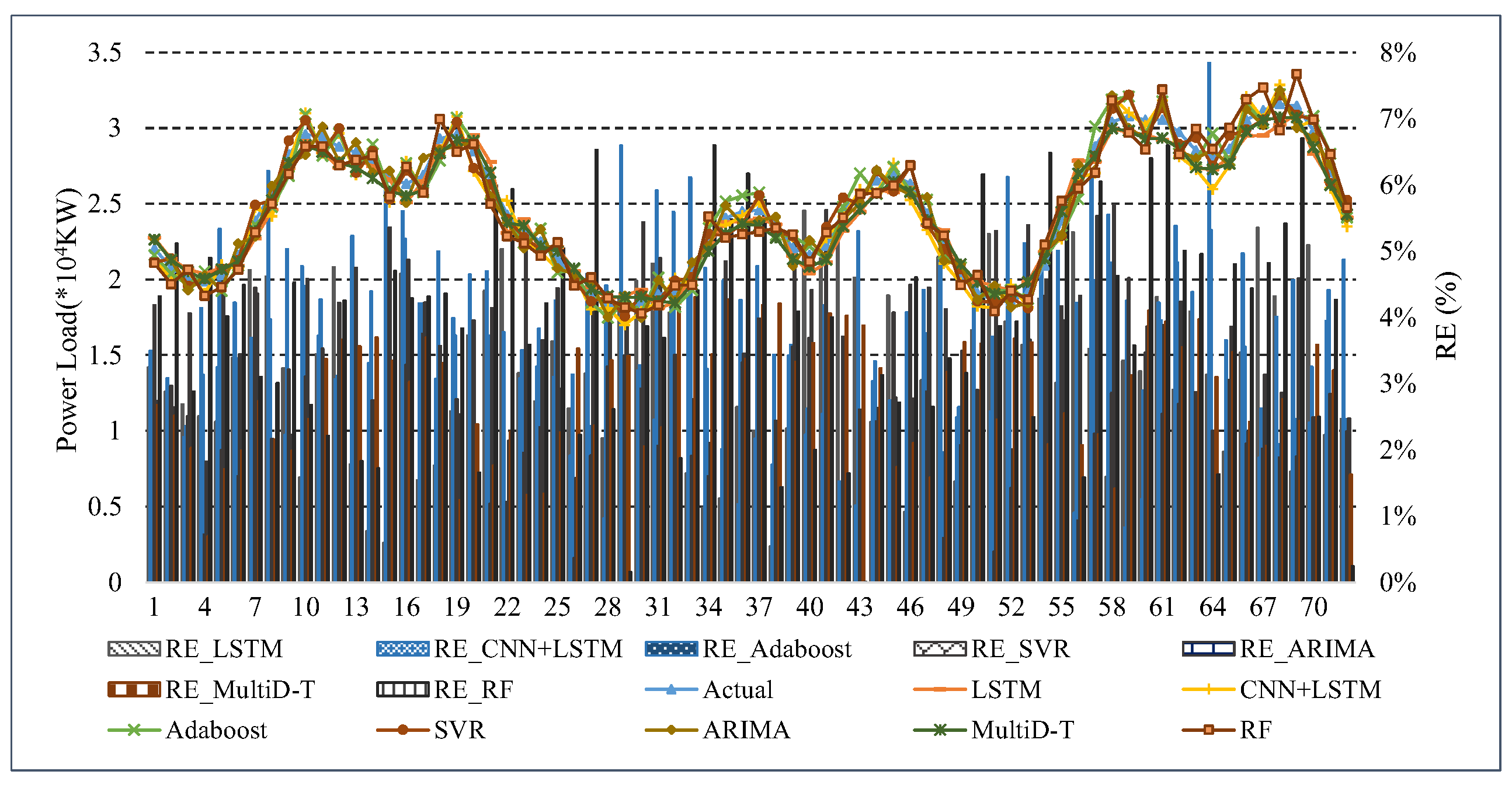
5. Experiment and Result Analysis
5.1. Evaluation Metric
5.2. Experimental Setup
5.3. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Shahid, F.; Zameer, A.; Muneeb, M. A novel genetic LSTM model for wind power forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Phan, Q.T.; Wu, Y.K.; Phan, Q.D. A hybrid wind power forecasting model with XGBoost, data preprocessing considering different NWPs. Appl. Sci. 2021, 11, 1100. [Google Scholar] [CrossRef]
- Lai, X.; Huang, Y.; Han, X.; Gu, H.; Zheng, Y. A novel method for state of energy estimation of lithium-ion batteries using particle filter and extended Kalman filter. J. Energy Storage 2021, 43, 103269. [Google Scholar] [CrossRef]
- Ti, Z.; Deng, X.W.; Zhang, M. Artificial Neural Networks based wake model for power prediction of wind farm. Renew. Energy 2021, 172, 618–631. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Jamaludin, S.Z.M.; Mansor, M.A.; Wahab, H.A.; Ghadzi, S.M.S. Supervised Learning Perspective in Logic Mining. Mathematics 2022, 10, 915. [Google Scholar] [CrossRef]
- Mohd Jamaludin, S.Z.; Mohd Kasihmuddin, M.S.; Md Ismail, A.I.; Mansor, M.A.; Md Basir, M.F. Energy based logic mining analysis with hopfield neural network for recruitment evaluation. Entropy 2020, 23, 40. [Google Scholar] [CrossRef]
- Jamaludin, S.Z.M.; Romli, N.A.; Kasihmuddin, M.S.M.; Baharum, A.; Mansor, M.A.; Marsani, M.F. Novel Logic Mining Incorporating Log Linear Approach. J. King Saud Univ.-Comput. Inf. Sci. 2022; in press. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Luo, H.; Zhou, P.; Shu, L.; Mou, J.; Zheng, H.; Jiang, C.; Wang, Y. Energy performance curves prediction of centrifugal pumps based on constrained PSO-SVR model. Energies 2022, 15, 3309. [Google Scholar] [CrossRef]
- Liu, M.D.; Ding, L.; Bai, Y.L. Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction. Energy Convers. Manag. 2021, 233, 113917. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Duan, J.; Liu, J.; Zeng, F. Daily natural gas load forecasting based on a hybrid deep learning model. Energies 2019, 12, 218. [Google Scholar] [CrossRef]
- Lu, H.; Azimi, M.; Iseley, T. Short-term load forecasting of urban gas using a hybrid model based on improved fruit fly optimization algorithm and support vector machine. Energy Rep. 2019, 5, 666–677. [Google Scholar] [CrossRef]
- Wenlong, H.; Yahui, W. Load forecast of gas region based on ARIMA algorithm. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 1960–1965. [Google Scholar]
- Musbah, H.; El-Hawary, M. SARIMA model forecasting of short-term electrical load data augmented by fast fourier transform seasonality detection. In Proceedings of the IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Yildiz, B.; Bilbao, J.; Sproul, A. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Tayaba, U.B.; Zia, A.; Yanga, F.; Lu, J.; Kashif, M. Short-term load forecasting for microgrid energy management system using hybrid HHO-FNN model with best-basis stationary wavelet packet transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- Panapakidis, I.; Katsivelakis, M.; Bargiotas, D. A Metaheuristics-Based Inputs Selection and Training Set Formation Method for Load Forecasting. Symmetry 2022, 14, 1733. [Google Scholar] [CrossRef]
- Ahmed, W.; Ansari, H.; Khan, B.; Ullah, Z.; Ali, S.M.; Mehmood, C.A.A. Machine learning based energy management model for smart grid and renewable energy districts. IEEE Access 2020, 8, 185059–185078. [Google Scholar] [CrossRef]
- Shabbir, N.; Kutt, L.; Jawad, M.; Iqbal, M.N.; Ghahfarokhi, P.S. Forecasting of energy consumption and production using recurrent neural networks. Adv. Electr. Electron. Eng. 2020, 18, 190–197. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nizami, A.; Khazen, M.; Nik-Bakht, M. Medium-term regional electricity load forecasting through machine learning and deep learning. Designs 2021, 5, 27. [Google Scholar] [CrossRef]
- Fan, G.-F.; Guo, Y.-H.; Zheng, J.-M.; Hong, W.-C. Application of the weighted K-nearest neighbor algorithm for short-term load forecasting. Energies 2019, 12, 916. [Google Scholar] [CrossRef]
- Madrid, E.A.; Antonio, N. Short-term electricity load forecasting with machine learning. Information 2021, 12, 50. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Wang, X.; Gao, X.; Wang, Z.; Ma, C.; Song, Z. A Combined Model Based on EOBL-CSSA-LSSVM for Power Load Forecasting. Symmetry 2021, 13, 1579. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting. arXiv 2022, preprint. arXiv:2201.12740. [Google Scholar]
- Xuan, W.; Shouxiang, W.; Qianyu, Z.; Shaomin, W.; Liwei, F. A multi-energy load prediction model based on deep multi-task learning and ensemble approach for regional integrated energy systems. Int. J. Electr. Power Energy Syst. 2021, 126, 106583. [Google Scholar] [CrossRef]
- Zhou, B.; Meng, Y.; Huang, W.; Wang, H.; Deng, L.; Huang, S.; Wei, J. Multi-energy net load forecasting for integrated local energy systems with heterogeneous prosumers. Int. J. Electr. Power Energy Syst. 2021, 126, 106542. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Ding, Z.; Zheng, T.; Hu, J.; Zhang, K. A Transformer-Based Method of Multi-Energy Load Forecasting in Integrated Energy System. IEEE Trans. Smart Grid 2022, 13, 2703–2714. [Google Scholar] [CrossRef]
- Phyo, P.P.; Byun, Y.C. Hybrid Ensemble Deep Learning-Based Approach for Time Series Energy Prediction. Symmetry 2021, 13, 1942. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Schölkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward causal representation learning. Proc. IEEE 2021, 109, 612–634. [Google Scholar] [CrossRef]
- Hinton, G.E. A practical guide to training restricted Boltzmann machines. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 599–619. [Google Scholar]
- Zhang, Z.; Zhao, J. A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 2017, 107, 395–407. [Google Scholar] [CrossRef]





| Symbol | Description and Meaning |
|---|---|
| MultiDBN-T network parameter set; e is the training parameter epoch | |
| MultiDBN-T output layer network parameters | |
| Network parameters obtained by the i-th layer GG-RBM, | |
| Position encoding information in D-TEncoder | |
| Multi-head self-attention parameters in D-TEncoder, | |
| Parameters in in D-TEncoder, |
| Term | Description and Number of Observable Variables |
|---|---|
| Time | 2 columns: time and holiday labels |
| Electricity production | 14 columns: various power production capacities |
| Electrical load | 1 column: actual consumption of electric energy per hour |
| Electricity price | 1 column: average price of electricity for a company |
| Weather | 9 columns: data of various weather indicators |
| City label | 5 columns: city names |
| Module/Parameter | Description and Number of Observable Variables |
|---|---|
| Pre-DBN | GG-RBM1 (63 × 72, 32 × 72), GG-RBM2 (32 × 72, 16 × 72) GG-RBM3 (16 × 72, 8 × 72), Linear (63 × 72) |
| D-TEncoder | Feedforward (256), Multi-Head (8), Output-Dimension (256) Blocks (3), Dropout (0.1) |
| L-Decoder | Linear (1 × 24) |
| Learning rate | 0.01 |
| Batch size | 128 |
| Algorithm | MAE (KW) | RMSLE | ||
|---|---|---|---|---|
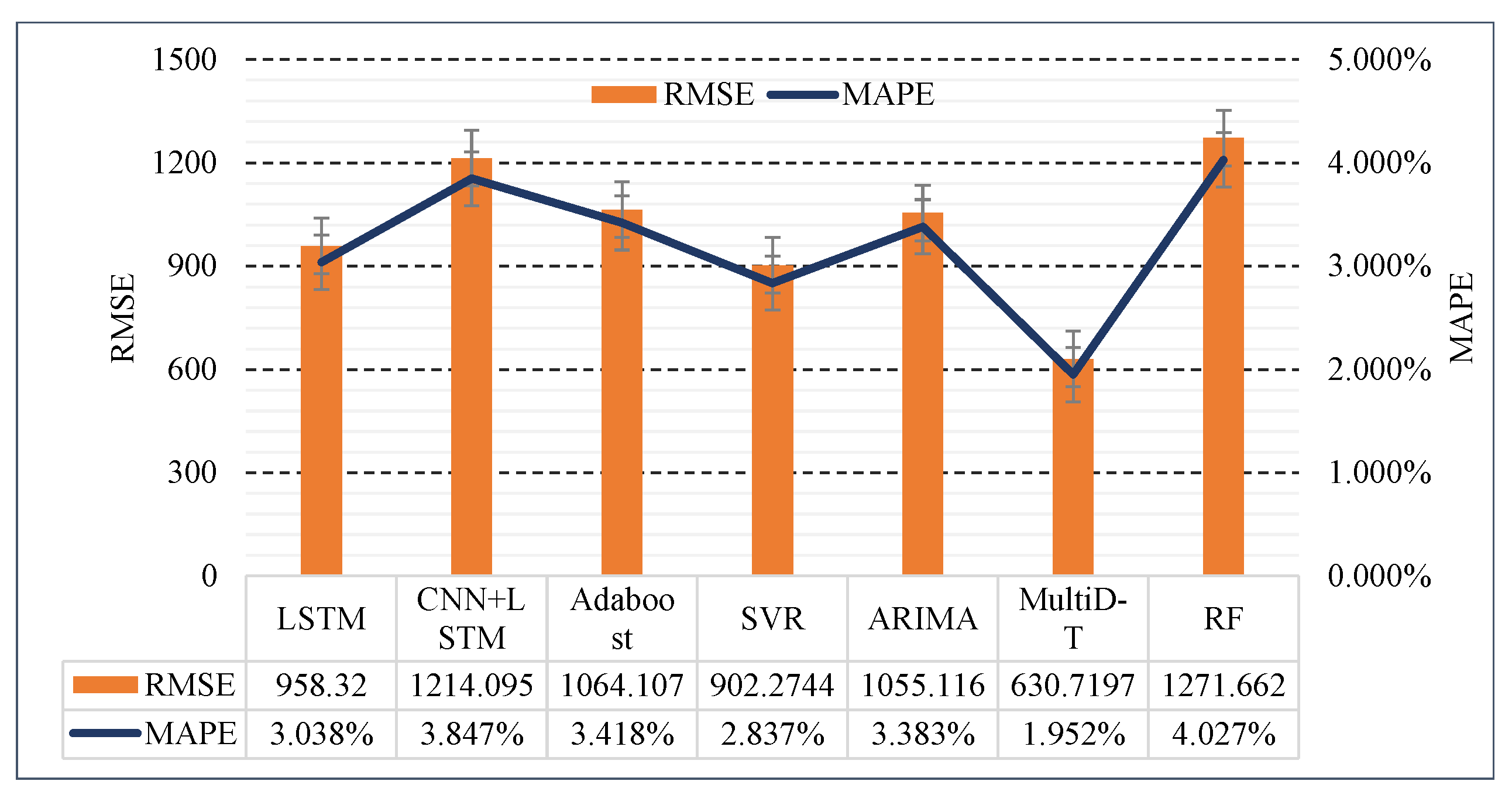
| LSTM | 3.038% | 958.320 | 878.1204 | 0.032806 |
| CNN+LSTM | 3.847% | 1214.095 | 1113.74 | 0.041546 |
| Adaboost | 3.418% | 1064.107 | 987.7954 | 0.036448 |
| SVR | 2.837% | 902.274 | 820.3937 | 0.030889 |
| ARIMA | 3.383% | 1055.116 | 978.5581 | 0.036015 |
| RF | 4.027% | 1271.662 | 1165.123 | 0.043685 |
| MultiDBN-T | 1.952% | 630.720 | 566.3686 | 0.021454 |
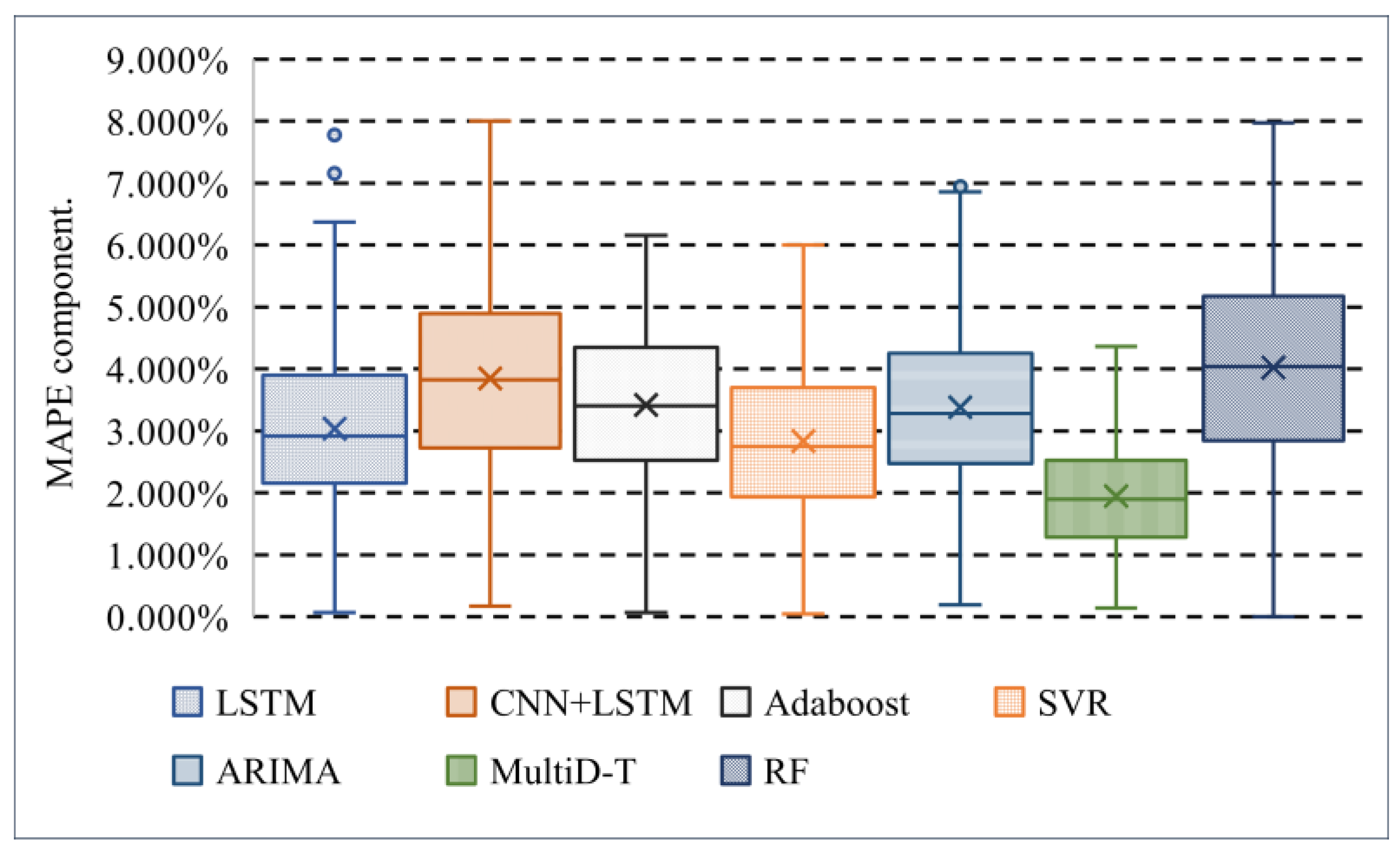
| Metrics | LSTM | CNN + LSTM | Adaboost | SVR | ARIMA | RF | MultiDBN-T |
|---|---|---|---|---|---|---|---|
| Max | 5.369% | 8.005% | 6.157% | 5.999% | 6.861% | 7.970% | 4.361% |
| Q1 | 3.899% | 4.894% | 4.346% | 3.701% | 4.249% | 5.177% | 2.524% |
| Median | 3.038% | 3.847% | 3.418% | 2.837% | 3.383% | 4.027% | 1.952% |
| Q2 | 2.918% | 3.825% | 3.401% | 2.745% | 3.275% | 4.038% | 1.898% |
| Q3 | 2.157% | 2.724% | 2.523% | 1.931% | 2.477% | 2.846% | 1.288% |
| Min | 0.067% | 0.172% | 0.065% | 0.047% | 0.192% | 0.0% | 0.138% |
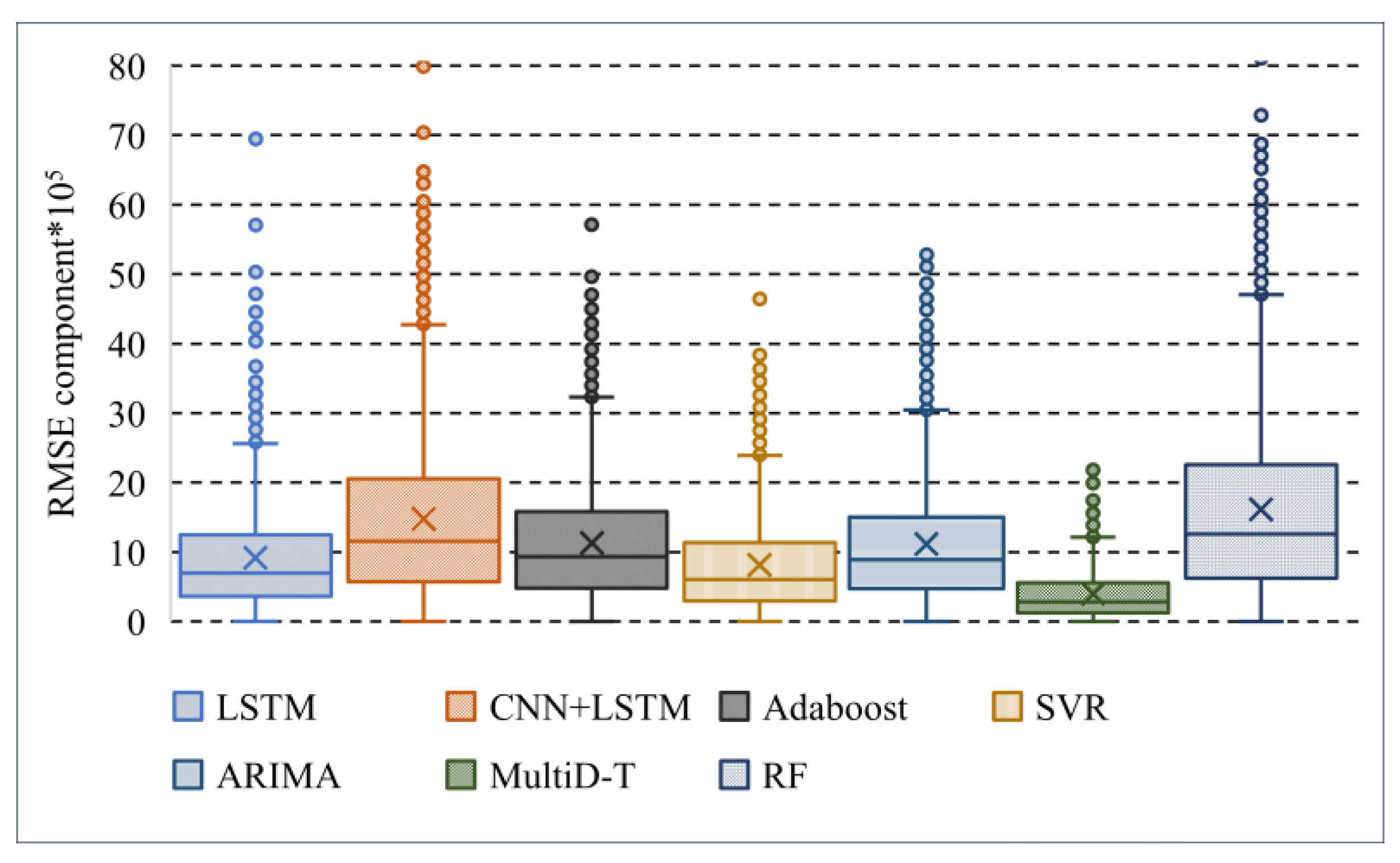
| Metrics | LSTM | CNN + LSTM | Adaboost | SVR | ARIMA | RF | MultiDBN-T |
|---|---|---|---|---|---|---|---|
| Max | 2562.184 | 4274.847 | 3226.730 | 2387.311 | 3042.323 | 4706.446 | 1212.348 |
| Q1 | 1248.420 | 2052.355 | 1581.224 | 1133.856 | 1501.843 | 2255.543 | 560.560 |
| Median | 918.115 | 1476.606 | 1132.002 | 813.867 | 1112.953 | 1616.663 | 397.694 |
| Q2 | 693.523 | 1154.171 | 931.083 | 602.291 | 884.029 | 1258.970 | 284.569 |
| Q3 | 360.841 | 570.103 | 482.006 | 296.404 | 474.368 | 621.096 | 125.185 |
| Min | 0.247 | 1.214 | 0.525 | 0.240 | 1.055 | 0.000004 | 0.630719 |
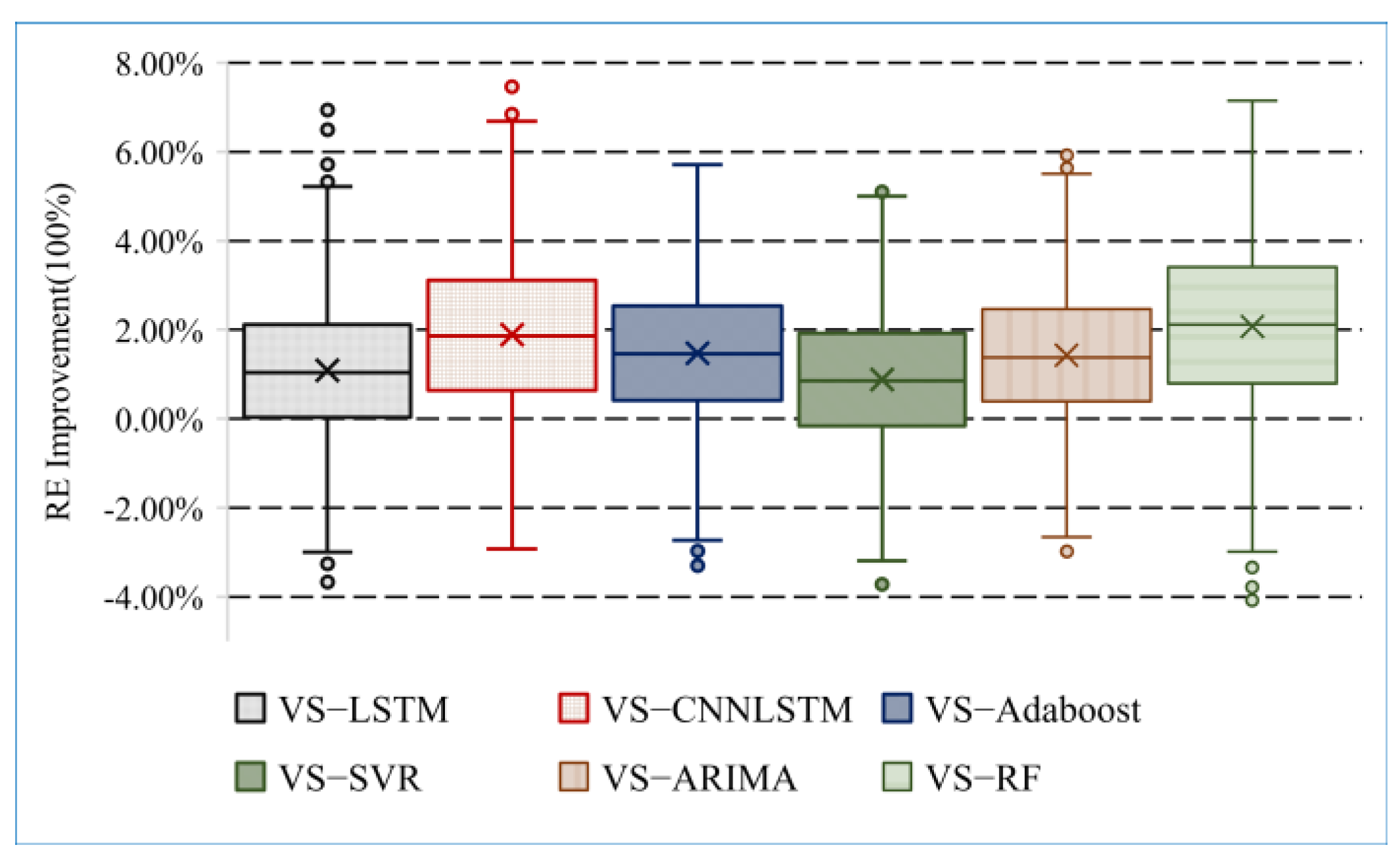
| Metrics | VS-LSTM | VS-CNN + LSTM | VS-Adaboost | VS-SVR | VS-ARIMA | VS-RF |
|---|---|---|---|---|---|---|
| Max | 5.22% | 6.69% | 5.72% | 5.00% | 5.50% | 7.15% |
| Q1 | 2.12% | 3.11% | 2.54% | 1.93% | 2.46% | 3.41% |
| Median | 1.09% | 1.90% | 1.47% | 0.89% | 1.43% | 2.08% |
| Q2 | 1.04% | 1.86% | 1.46% | 0.85% | 1.38% | 2.12% |
| Q3 | 0.03% | 0.63% | 0.41% | −0.16% | 0.39% | 0.79% |
| Min | −3.00% | −2.93% | −2.73% | −3.19% | −2.66% | −2.99% |
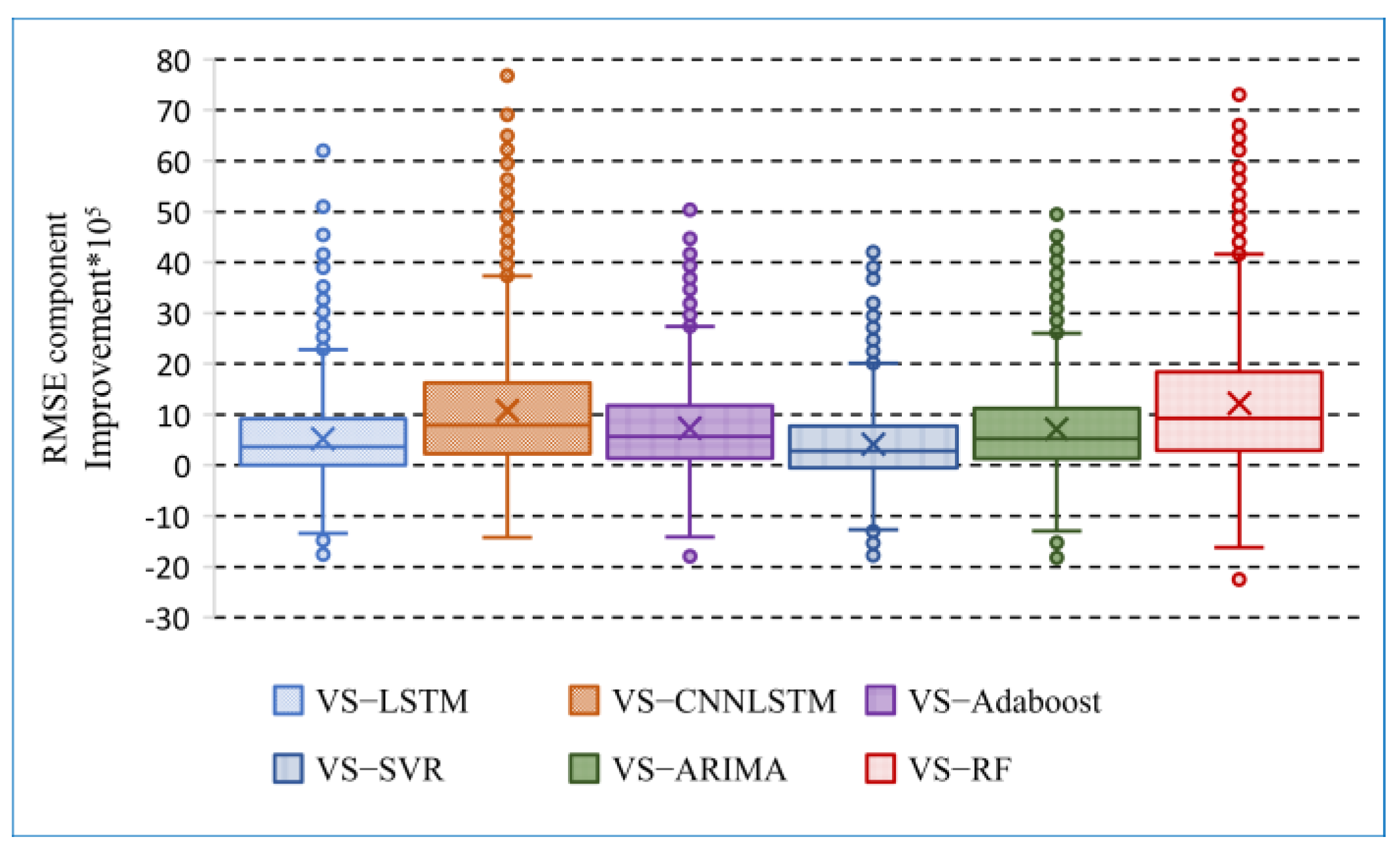
| Metrics | VS-LSTM | VS-CNN + LSTM | VS-Adaboost | VS-SVR | VS-ARIMA | VS-RF |
|---|---|---|---|---|---|---|
| Max | 2281.035 | 3730.698 | 2739.107 | 2012.757 | 2599.928 | 4161.327 |
| Q1 | 918.079 | 1628.529 | 1178.128 | 778.153 | 1120.156 | 1842.060 |
| Median | 520.569 | 1076.218 | 734.517 | 416.291 | 715.463 | 1219.317 |
| Q2 | 362.080 | 788.596 | 567.339 | 279.695 | 524.671 | 923.383 |
| Q3 | 6.568 | 226.248 | 136.731 | −47.682 | 126.794 | 290.765 |
| Min | −1338.101 | −1422.029 | −1412.882 | −1265.45 | −1297.318 | −1618.46 |
| Period | LSTM | CNN + LSTM | Adaboost | SVR | ARIMA | RF | MultiDBN-T |
|---|---|---|---|---|---|---|---|
| 2018-08-08 to 2018-08-10 | 3.026% | 3.897% | 3.430% | 2.907% | 3.472% | 3.803% | 1.993% |
| 2018-12-24 to 2018-12-26 | 3.231% | 3.696% | 3.517% | 2.900% | 3.293% | 3.903% | 2.882% |
| Algorithm | MAE Imp | RMSLE Imp | ||
|---|---|---|---|---|
| LSTM | 35.76% | 34.18% | 35.50% | 34.60% |
| CNN+LSTM | 49.27% | 48.05% | 49.15% | 48.36% |
| Adaboost | 42.91% | 40.73% | 42.66% | 41.14% |
| SVR | 31.21% | 30.10% | 30.96% | 30.55% |
| ARIMA | 42.30% | 40.22% | 42.12% | 40.43% |
| RF | 51.54% | 50.40% | 51.39% | 50.89% |
| Average Improvement | 42.16% | 40.61% | 41.96% | 40.99% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, W.; Zhu, J.; Zhao, J.; Cai, W.; Li, K. An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting. Symmetry 2022, 14, 1999. https://doi.org/10.3390/sym14101999
Bai W, Zhu J, Zhao J, Cai W, Li K. An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting. Symmetry. 2022; 14(10):1999. https://doi.org/10.3390/sym14101999
Chicago/Turabian StyleBai, Weihua, Jiaxian Zhu, Jialing Zhao, Wenwei Cai, and Keqin Li. 2022. "An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting" Symmetry 14, no. 10: 1999. https://doi.org/10.3390/sym14101999
APA StyleBai, W., Zhu, J., Zhao, J., Cai, W., & Li, K. (2022). An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting. Symmetry, 14(10), 1999. https://doi.org/10.3390/sym14101999







