Abstract
The crisis that affected Brazil as a result of the coronavirus disease 2019 (COVID-19) pandemic impacted several businesses. However, the distribution of products sold by e-commerce is one business that had increased its demand on a large scale. The Southeastern Region of Brazil has a wide territorial extension, a high number of inhabitants, and difficulties with transport logistics. Thus, this work presents a solution for choosing a location for the installation of an e-commerce warehouse, considering three possible locations, in two different Brazilian states: Rio de Janeiro and Sao Paulo. Our main objective is to identify policies that allow a balance in the trade-off between risks and service levels. Specifically, we seek to decrease logistics costs and ensure improvements in services. The choice of a location for a warehouse is a decision problem that can be solved with multiple criteria decision-making (MCDM). Three methods of MCDM have been applied: Fuzzy Decision Approach (FDA), Multi-Attribute Utility Theory (MAUT), and Multi-Attribute Value Theory (MAVT). The reasons for the application of the MAUT and MAVT methods originate from their easy understanding and use, while the concepts of FDA address the consideration of uncertainty. To maintain the simplicity of MCDM application, the FDA model is symmetric, even with symmetrical and asymmetrical fuzzy sets. Important criteria were the distance from capital cities, distance to ports, distance to airports, distance to highways, and the costs of land. Three different locations were considered for the installation of the warehouse. All three methods, FDA, MAUT, and MAVT, resulted in Location 1 as the best location for the installation of the warehouse for the distribution of e-commerce products. A discussion on conceptual qualitative divergences and the small quantitative divergence of results is also included in the conclusions.
1. Introduction
Coronavirus disease 2019 (COVID-19) was declared a global pandemic on 11 March 2020. In addition to the health crisis, COVID-19 has generated an economic crisis, with local and global supply chain interruptions resulting from customers’ quarantines, plant closures, travel restrictions, and other drops in several service activities [1]. Another impact was more commercial than economic, with customers purchasing more and more products directly delivered to their homes [2]. Therefore, the distribution of products sold by e-commerce is one business that had increased its demand on a large scale [3].
For markets with wide territorial extension, increasing demand is a challenge. In this situation, companies may decide to acquire assets such as equipment or raw materials, increasing their need for logistics resources. One option is to relocate assets among current facilities. Another option is to search for a new place, with current or new assets. Resource allocation (RA) is a major decision problem regarding supply chain management [4]. This paper presents a case of choosing a new place for a warehouse by an e-commerce company.
A supply chain manager may solve these problems by considering a single criterion—for instance, costs, customer satisfaction, or delivery time. With multiple criteria decision-making (MCDM), the supply chain manager may combine such criteria to achieve a compromised solution [4,5]. Our research question concerns how to apply an MCDM method to solve the decision problem of warehouse location for product distribution by e-commerce. There are several MCDM methods [6,7]. Therefore, the first aim of the research was to identify MCDM methods suitable for the solution of the decision problem of warehouse location. Then, Multi-Attribute Utility Theory (MAUT) [8] and Fuzzy Decision Approach (FDA) [9] were identified. Next, FDA, MAUT, and Multi-Attribute Value Theory (MAVT), a MAUT variation, were applied in the same case. The same sets of alternatives and criteria were considered in FDA, MAUT, and MAVT applications.
Therefore, this work presents two major contributions. One contribution is in the field of resource location [10]. This decision problem of supply chain management will be addressed with the application of MCDM methods in a Brazilian case of e-commerce. This work also contributes to the MCDM discipline, comparing the applications of three MCDM methods, for the solution of the same problem, with a symmetrical model [11].
This manuscript has five sections, including this Introduction. Section 2 presents the main concepts of MCDM methods FDA, MAUT, and MAVT. Section 3 presents the results of these applications. Section 4 presents a discussion and the delimitation of this work. Finally, Section 5 presents conclusions and themes for future research.
2. Methodology
2.1. Multiple Criteria Decision-Making
MCDM is divided into two branches: multi-attribute analysis and multi-objective optimization [7]. Multi-attribute analysis deals with a finite number of alternatives, e.g., only two alternatives. Multi-objective optimization deals with larger sets of alternatives, even infinite alternatives [12]. This paper focuses on multi-attribute analysis since a finite number of alternatives will be considered. This work does not deal with the optimization of an extensive set of locations for a warehouse. This is due to the nature of resource allocation problems. Usually, resource allocation deals with a limited set of alternatives—for example, cities, countries, or regions [4,10].
The decision matrix X is the main tool in multi-attribute analysis, as presented in Table 1. Components of decision matrix represent the performance of Alternative i according to Criterion j. There are several methods for multi-attribute analysis. The ways in which are identified and processed is what makes one method different from another. There are also conceptual differences, expressed by different terminologies, as presented in Section 2.2 and Section 2.3.

Table 1.
Decision matrix.
Although there is a wide variety of methods for multi-attribute analysis, the research on supply chain management basically focuses on the application of three methods: the Analytic Hierarchy Process (AHP), Data Envelopment Analysis (DEA), and Technique of Order Preference by Similarity to the Ideal Solution (TOPSIS) [13]. AHP and TOPSIS are methods for multi-attribute analysis, while DEA is for multi-objective optimization. Multi-method application is a trend in AHP, DEA, TOPSIS, or even in MCDM research [14].
This research seeks to contribute to the study of MCDM, applying unusual methods, such as FDA, MAUT, and MAVT. More than leaving the comfort zone, the aim is to assess whether methods proposed a few decades ago are still applicable to current problems. Moreover, FDA, MAUT, and MAVT have been selected because they are methods for multi-attribute analysis. Finally, MAUT and MAVT are easy to understand and apply, while FDA allows uncertainty to be considered. “Simplicity of execution”, “comprehensive structure”, and “logical–mathematical procedure” are desirable attributes for an MCDM method [6].
2.2. Multi-Attribute Utility and Value Theories
As AHP, MAUT is an MCDM method for multi-attribute analysis, i.e., for the evaluation of a small set of alternatives. In AHP, components of X are obtained with the eigenvector of comparison matrices. MAUT has the main advantage of not requiring pairwise comparisons [15]. Two consequences are as follows. First, the AHP’s upper limit of nine criteria or nine alternatives [16,17] does not apply to MAUT; second, MAUT application is simpler, not requiring AHP’s concepts as the Saaty Scale.
“Utility” is a concept from the Nineteenth Century’s Economics, representing the satisfaction grade obtained with the choice for an alternative [18]. In MAUT, the components of X are obtained with utility functions u [19]. The interval is the codomain of the utility function, with for the worst alternative, and for the best alternative. For the intermediate alternatives, the decision-maker needs to identify one among several possibilities for the utility functions. This work adopts only linear utility functions. Non-linear utility functions consider risk aversion or risk preference. In this work, risks and uncertainty will be considered with FDA.
For quantitative criteria, performance scores are available for all alternatives. However, these scores may be measured in different units, such as dollars or kilograms. For positive measures, i.e., the higher the better, as with profit or revenue, utility of Alternative i regarding Criterion j can be obtained with the linear function expressed by Equation (1).
For negative measures, i.e., the lower the better, such as costs or expenses, a different linear function is required, as in Equation (2).
For qualitative criteria, a five-point adapted Likert Scale is usually adopted [10]. Table 2 presents a slight variation, adding a sixth point for the performance level of Null.

Table 2.
Adapted Likert Scale.
Utility of Alternative i is obtained by associating its score from Table 2 as its and replacing it in Equation (1). For example, if the performances of three alternatives are assessed as Good, Very Good, and Excellent, respectively, they have Scores of 3, 4, and 5, according to Table 2. Their utilities will be , , and .
MAVT is a variation of MAUT with value functions v, instead of utility functions u [20]. For quantitative criteria, with positive measures, the value of alternative performance can be obtained with Equation (3).
For negative measures, i.e., the lower the better, such as costs or expenses, a different linear function is required, as in Equation (4).
The interval [0, 1] is the codomain for both functions u and v. However, in MAUT, for each attribute, there will be always at least one alternative with . In MAVT, zero values only result from null scores. Then, for Scores 3, 4, and 5, values will be , , and .
In both MAUT and MAVT, the utilities and values according to each criterion need to be aggregated, resulting in the joint utility U, for MAUT, and in the aggregate value V, for MAVT. This aggregation is usually done with the weighted sum [8]. For this, criteria weight w must be identified.
2.3. Fuzzy Decision Approach
FDA was proposed with trapezoidal fuzzy sets for a case of resource allocation: facility site selection [9]. A trapezoidal fuzzy set is usually represented as a vector: , with . The symmetry of a trapezoidal fuzzy set is observed when , as in Figure 1. In this case, the trapezoidal fuzzy set is symmetric with respect to .
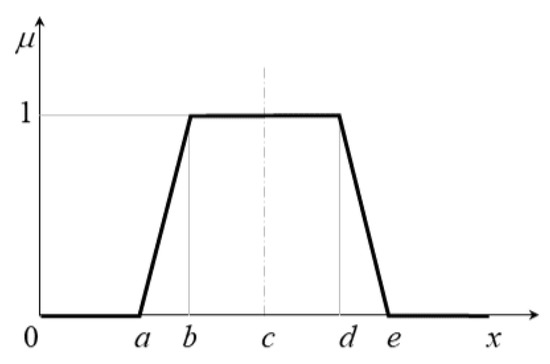
Figure 1.
Symmetric trapezoidal fuzzy set .
Equation (5) presents the membership function for the trapezoidal fuzzy set .
This paper adopts triangular fuzzy sets, a particular case of trapezoidal fuzzy sets, with . The vector representation of a triangular fuzzy set is simply . The symmetry condition is also simpler for triangular fuzzy sets as , as observed in Figure 2.
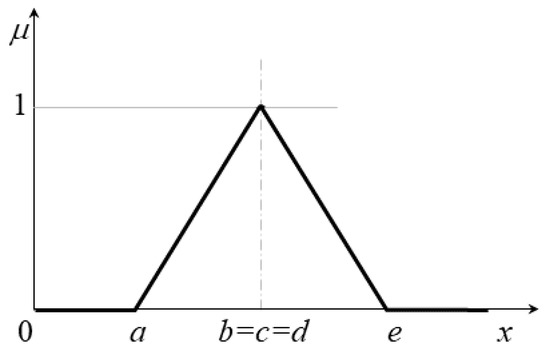
Figure 2.
Symmetric triangular fuzzy set .
Equation (6) presents the membership function for the triangular fuzzy set .
Simplicity is a concept related to symmetry [21]. The adoption of triangular fuzzy sets simplifies the decision model. Therefore, the choice of triangular fuzzy sets instead of trapezoidal fuzzy sets aligns better with the theory of symmetry.
In FDA, the performances of the alternatives regarding each criterion, and the weights of the criteria, are fuzzy sets, associated by the decision-maker with linguistics variables, as presented in Table 3 and Table 4.

Table 3.
Fuzzy sets on the weights of the criteria.

Table 4.
Fuzzy sets on the performance of the alternatives.
Three fuzzy sets in Table 3 are symmetric: , , and . Two fuzzy sets are asymmetric: and . However, the whole model is symmetric, since the asymmetric fuzzy sets and the sets of fuzzy sets have symmetry with respect to 5, in the range of 0–10.
All the fuzzy sets in Table 4 are symmetric. The set of fuzzy sets also has symmetry with respect to 5. There are two more fuzzy sets on the alternatives’ performance than on the criteria weights, resulting from the greater uncertainty related to the alternatives than the criteria. This is due to the alternatives being related to what suppliers may offer, and the criteria related to the company’s expectations.
As in MAUT and MAVT, the overall performances of alternatives must be obtained by weighting the decision matrix with the criteria weights. For every Alternative i, the “fuzzy suitability index” must be obtained, with Equation (7), where n is the number of criteria, is the vector of the alternatives’ performance, and is the vector of weights for the criteria.
To rank the alternatives, FDA adopts the defuzzification of the suitability index in the ranking value presented in Equation (8), for , where m is the number of alternatives.
3. Results
3.1. Case Study
Brazilian territory is divided into five main regions: central–west, north, northeast, south, and southeast (www.ibge.gov.br, accessed on 2 August 2022). The second-smallest region, the southeast, is the richest and the most populated. The southeast is composed of four states: Espirito Santo, Minas Gerais, Rio de Janeiro, and Sao Paulo. As in the whole country, highways are the main carrier of freight and passengers in the southeast region. This paper focuses on an e-commerce company that had an increased demand from COVID-19. The studied company mainly operates in the state capital cities of Rio de Janeiro and Sao Paulo. To improve the level of service to its customers, the company is considering installing a new warehouse. Three locations were considered, named here as Locations 1 to 3.
The company’s CEO and the logistics manager acted as decision-makers. Their opinions were collected and provided in the same meeting and aggregated by consensus. Decision-makers have defined five main criteria for deciding on a new warehouse:
- Distance to Sao Paulo state capital (DC), the main consumer market.
- Distance to Port of Santos (DP), the busiest container port in Latin America (LA).
- Distance to a cargo airport (DA) connected to Brazilian international airports.
- Distance to highways (DR), measured basically as the distance to Via Dutra, the federal highway that connects Rio de Janeiro City to Sao Paulo City.
- Land costs (LC), the market value of land, but including the built-up area such as the shed, railings, walls, and entrance.
Table 5 presents the data collected for Locations 1 to 3. The data for all criteria are in kilometers [km], except the data for LC, in Brazilian reais [BRL].

Table 5.
Performance of alternatives in five criteria.
The variation in DA is low. Thus, the decision-makers decided to delete this criterion in the MCDM model. The decision-makers defined the weights for criteria as 50% for DC, 20% for DP, 20% for DR, and 10% for LC.
3.2. MAUT and MAVT Applications
Table 6 presents the utilities for the performances of Locations 1 to 3. Table 6 also presents their joint utility.

Table 6.
Utilities of the performances of the alternatives.
Location 1 has its joint utility in bold because it is the highest joint utility. Locations 2 and 3’s joint utilities are crossed out because they are lower than 0.5. This means that the choice of Location 2 or 3 would be unsatisfactory. Therefore, the result of the MAUT application is that Location 1 must be chosen, and if it is not available, Locations 2 and 3 shall not be considered. In this case, the decision-makers will need to find another location for the warehouse, different to Locations 2 and 3.
Table 7 presents the values for the performances of Locations 1 to 3. Table 7 also presents their aggregate values.

Table 7.
Values of the performance of the alternatives.
Location 1 has its aggregate value in bold because it is the highest aggregate value. Location 2’s aggregate value is crossed out because it is lower than 0.5. This means that only the choice of Location 2 would be valueless. Therefore, the result of MAVT application is that Location 1 must be chosen, and if it is not available, Location 3 could be considered. The decision-makers will only need to find another location for the warehouse if Locations 1 and 3 become unavailable.
3.3. FDA Application
Based on the weights for criteria previously identified in the MAUT and MAVT applications, the association with Table 3 is “High” for DC, “Medium” for DP and for DR, and “Low” for LC.
Table 8 presents linguistic variables for the performances of Locations 1 to 3. These variables should be associated with their fuzzy sets in Table 4, then substituted in Equation (7), to find locations’ fuzzy suitability indices.

Table 8.
Linguistic variables of the performance of the alternatives.
Table 9 presents the fuzzy suitability indices of alternatives and their ranking values.

Table 9.
Fuzzy suitability indices and ranking values of alternatives.
Location 1 has its ranking value in bold because it is the highest-ranking value. Locations 2 and 3’s ranking values are uncrossed because there is no lower limit for FDA, as for MAUT and MAVT. Then, the only result of FDA application is that Location 1 must be chosen. If Location 1 became unavailable, it cannot be affirmed that Locations 2 or 3 could be considered. In this case, the decision-makers are not sure if they would need to find another location for the warehouse, different to Locations 2 or 3, if Location 1 became unavailable.
4. Discussion and Limitations
All three methods, MAUT, MAVT, and FDA, resulted in Location 1 as the best location for the installation of the warehouse for the distribution of e-commerce products. The application indicates Locations 2 and 3 as alternatives to be avoided. MAVT indicates Location 3 as an acceptable alternative if Location 1 became unavailable. FDA is not conclusive in this regard, not indicating and not discarding Locations 2 and 3 as alternative locations in the case of missing Location 1.
For this reason, the decision-makers preferred MAUT and MAVT over FDA. They were not unanimous in indicating a preference for MAUT or MAVT. All three methods were applied only with spreadsheets. No MCDM software was necessary.
It is important to note that the choice of Location 1 resulted from the highest weight for DC, which is the distance to the main consumer market, and the lowest weight for LC, the land costs. Table 10 and Table 11 present the results of FDA, MAUT, and MAVT in two different situations: equal weights for criteria, and the highest weight for LC with the lowest weight for DC.

Table 10.
Results from FDA, MAUT, and MAVT with equal weights for the criteria.

Table 11.
Results from FDA, MAUT, and MAVT with the highest weight for LC and the lowest weight for DC.
Decreasing the weight of DC implies increasing Location 3’s overall performance with all MCDM methods applied. With MAUT and MAVT, Location 3 surpasses Location 1 in a scenario of higher-weighted costs. With FDA, Location 1 and Location 2’s overall performance is the same in the three scenarios. This was due to the uncertainty expressed by the fuzzy sets. In this case, the decision-makers did not accept this result, as there was a minimal variation that was not considered by the FDA method.
Despite the case studied being of a company in Southeastern Brazilian e-commerce, the model may be applied for different cases, mutatis mutandis. After all, a better infrastructure transportation system, as in Europe, would affect all alternatives. On the other hand, a less structured system, as in Central Africa, would also affect the performance of all alternatives.
As the whole applications, including the variation of the weights, were performed only with spreadsheets, the decision-makers acknowledged having learned the steps to apply the MCDM methods to future decision problems, not only involving resource allocation. However, to manage the information in a broader context, they plan to develop an “enterprise architecture” [22,23,24].
5. Conclusions
This work presented applications of FDA, MAUT, and MAVT, three different MCDM methods, to solve a problem of resource allocation. Specifically, the problem was the choice of a warehouse location by a Brazilian e-commerce company. One method considered uncertainty with fuzzy sets; the other two methods did not consider this, with linear utility or linear value functions. All applications converged to the same solution for the decision problem: the choice of Location 1. However, applications diverged in allowing the choice of a second location, if the best location became unavailable. For this reason, the decision-makers preferred MAUT/MAVT’s results over FDA’s results.
Of course, a single case is not conclusive for the preference of one method over another. Therefore, the replication of the proposed model, in different situations and locations, is the first theme for future research.
Another theme for new research is the application of new MCDM methods, such as the Best–Worst Method (BWM), the Complex Proportional Assessment (COPRAS), or the Step-Wise Weight Assessment Ratio Analysis (SWARA) [25,26]. New approaches to fuzzy sets theory, such as Fuzzy Type-2 or Hesitant Fuzzy Sets [27], also may be considered in future research.
Author Contributions
Conceptualization, N.M.M.T., E.L., S.A.G. and V.M.P.; methodology, N.M.M.T., E.L., S.A.G. and V.M.P.; software, N.M.M.T., E.L., S.A.G. and V.M.P.; validation, N.M.M.T., E.L., S.A.G. and V.M.P.; formal analysis, N.M.M.T., V.A.P.S., E.L., S.A.G. and V.M.P.; resources, N.M.M.T., E.L., S.A.G. and V.M.P.; data curation, N.M.M.T., E.L., S.A.G. and V.M.P.; writing—original draft preparation, N.M.M.T., E.L., S.A.G. and V.M.P.; writing—review and editing, N.M.M.T. and V.A.P.S.; visualization, N.M.M.T., E.L., S.A.G. and V.M.P.; supervision, V.A.P.S.; project administration, N.M.M.T.; funding acquisition, V.A.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
São Paulo Research Foundation (FAPESP), Grant Nos. 2017/22963-6 and 2022/03734-4.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boone, L. Tackling the fallout from COVID-19. In Economics in the Time of COVID-19; Baldwin, R., Di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 37–44. [Google Scholar]
- Unnikrishnan, A.; Figliozzi, M. Exploratory analysis of factors affecting levels of home deliveries before, during, and post-COVID-19. Transp. Res. Interdiscip. Perspect. 2021, 10, 100402. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Guo, F.; Wang, Z. Coordination analysis of revenue sharing in e-commerce logistics service supply chain with cooperative distribution. SAGE Open 2019, 9, 2158244019870536. [Google Scholar] [CrossRef]
- Salomon, V.A.P.; Tramarico, C.L.; Marins, F.A.S. Analytic hierarchy process applied to supply chain management. In Applications and Theory of Analytic Hierarchy Process; De Felice, F., Petrillo, A., Saaty, T.L., Eds.; In Tech Open: London, UK, 2016; pp. 1–16. [Google Scholar] [CrossRef]
- Pelissari, R.; Oliveira, M.C.; Abackerli, A.J.; Ben-Amor, S.; Assumpção, M.R.P. Techniques to model uncertain input data of multi-criteria decision-making problems: A literature review. Int. Trans. Oper. Res. 2018, 28, 523–559. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ergu, D. When a is a decision-making method trustworthy? Criteria for evaluating multi-criteria decision-making methods. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1171–1187. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turkis, Z.; Kildiene, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis; Wiley: Chichester, UK, 2013. [Google Scholar] [CrossRef]
- Liang, G.; Wang, M. A fuzzy multi-criteria decision making method for facility site selection. Int. J. Prod. Res. 1991, 29, 2313–2330. [Google Scholar] [CrossRef]
- Martino Neto, J.; Salomon, V.A.P.; Ortiz-Barrios, M.A.; Petrillo, A. Compatibility and correlation of multi-attribute decision making: A case of industrial relocation. Ann. Oper. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Faizi, S.; Salabun, W.; Ullah, S.; Rashid, T.; Wieckowski, J. A new method to support decision-making in an uncertain environment based on normalized interval-valued triangular fuzzy numbers and COMET technique. Symmetry 2022, 12, 516. [Google Scholar] [CrossRef]
- Lombardi Netto, A.; Salomon, V.A.P.; Ortiz-Barrios, M.A.; Florek-Paszkowska, A.K.; Petrillo, A.; De Oliveira, O.J. Multiple criteria assessment of sustainability programs in the textile industry. Int. Trans. Oper. Res. 2021, 28, 1550–1572. [Google Scholar] [CrossRef]
- Khan, S.A.; Chaabane, A.; Dweiri, F.T. Multi-criteria decision-making methods application in supply chain management: A systematic literature review. In Multi-Criteria Methods and Techniques Applied to Supply Chain Management; Salomon, V.A.P., Ed.; In Tech Open: London, UK, 2018; pp. 3–31. [Google Scholar] [CrossRef]
- Lombardi Netto, A.; Salomon, V.A.P.; Ortiz-Barrios, M.A. Multi-criteria analysis of green bonds: A hybrid multi-method application. Sustainability 2021, 13, 10512. [Google Scholar] [CrossRef]
- Doczy, R.; Abdel Razig, Y. Green buildings case study analysis using AHP and MAUT in sustainability and costs. J. Archit. Eng. 2017, 23, 05017002. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ozdemir, M.S. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Salomon, V.A.P. Absolute measurement and ideal synthesis on AHP. Int. J. AHP 2016, 8, 538–545. [Google Scholar] [CrossRef]
- Torrance, G.; Feeny, D. Utilities and quality-adjusted life years. Int. J. Technol. Assess. 1989, 5, 559–575. [Google Scholar] [CrossRef] [PubMed]
- Askar, S. On dynamic investigations of Cournot Duopoly Game: When firms want to maximize their relative profits. Symmetry 2021, 13, 2235. [Google Scholar] [CrossRef]
- Davahli, M.R.; Karwowski, W.; Fiok, K.; Wan, T.; Parsaei, H.R. Controlling safety of artificial intelligence-based systems in healthcare. Symmetry 2021, 13, 102. [Google Scholar] [CrossRef]
- Mainzer, K. Symmetry and Complexity; World Scientific: Singapore, 2005. [Google Scholar] [CrossRef]
- Gorski, T. Towards enterprise architecture for capital group in energy sector. In Proceedings of the 2018 IEEE 22nd International Conference on Intelligent Engineering Systems (INES), Las Palmas de Gran Canaria, Spain, 21–23 June 2018; pp. 239–244. [Google Scholar] [CrossRef]
- Gonçalves, D.; Ferreira, L.; Campos, N. Enterprise architecture for high flexible and agile company in automotive industry. Procedia Comput. Sci. 2021, 181, 1077–1082. [Google Scholar] [CrossRef]
- Van Den Berg, M.; Slot, R.; Van Steenbergen, M.; Faasse, P.; Van Vliet, H. How enterprise architecture improves the quality of IT investment decisions. J. Syst. Softw. 2019, 152, 134–150. [Google Scholar] [CrossRef]
- Rezaei, R. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Alinezhad, A.; Khalili, J. New Methods and Applications in Multiple Attribute Decision Making (MADM); Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Ohta, R.; Salomon, V.A.P.; Silva, M.B. Classical, fuzzy, hesitant fuzzy and intuitionistic fuzzy analytic hierarchy processes applied to industrial maintenance management. J. Intel. Fuzzy Syst. 2020, 38, 601–608. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).