Symmetry Control of Comfortable Vehicle Suspension Based on H∞

Abstract

Suspension is an important part of intelligent and safe transportation; it is the balance point between the comfort and handling stability of a vehicle under intelligent traffic conditions. In this study, a control method of left-right symmetry of air suspension based on H∞ theory was proposed, which was verified under intelligent traffic conditions. First, the control stability caused by the active suspension control system running on uneven roads needs to be ensured. To address this issue, a 1/4 vehicle active suspension model was established, and the vertical acceleration of the vehicle body was applied as the main index of ride comfort. H∞ performance constraint output indicators of the controller contained the tire dynamic load, suspension dynamic stroke, and actuator control force limit. Based on the Lyapunov stability theory, an output feedback control law with H∞-guaranteed performance was proposed to constrain multiple targets. This way, the control problem was transformed into a solution to the Riccati equation. The simulation results showed that when dealing with general road disturbances, the proposed control strategy can reduce the vehicle body acceleration by about 20% and meet the requirements of an ultimate suspension dynamic deflection of 0.08 m and a dynamic tire load of 1500 N. Using this symmetrical control method can significantly improve the ride comfort and driving stability of a vehicle under intelligent traffic conditions.

1. Introduction

The travel smoothness of a vehicle is largely dependent on the performance of the suspension, and the development of new suspension control technologies is important for improving the smoothness of vehicles and the steady stability [1]. Active suspension can regulate the rigidity and damping of the suspension according to the different road conditions of driving to meet the higher requirements of the suspension performance in various driving states. The active suspension system is more degenerate in isolating road vibration [2]. Therefore, research into vehicle active control technology has become key, such as adaptive control [3,4,5]. Adaptive control methods are divided into self-tuning control and model reference adaptive control. The self-adaptive method can self-adjust parameters to produce a control effect as the environment changes, ensuring the stability and performance of the system. The problem of adaptive control is that the structural parameters of the system need to be identified on-line, which leads to a large amount of calculation and poor real-time performance. Model reference adaptive control involves the accuracy of road surface information acquisition. For sliding mode control [6,7,8,9,10,11], due to the characteristics of the sliding mode, the closed-loop system has strong robustness. The advantage of sliding mode control is that its sliding mode is fully adaptive to the disturbance and system perturbation imposed on the system. The active suspension system can overcome the nonlinear characteristics and time-varying characteristics of hydraulic actuators, and auxiliary compensation control can be introduced to improve the driving safety performance of the car, such as fuzzy control [12,13,14,15] and H∞ control [16,17,18,19,20,21]. The fuzzy control method imitates the intelligent learning function of the human brain, does not need to establish an accurate mathematical model, and establishes the corresponding rule base through artificial experience. It has gradually become the main method to solve the system’s nonlinear and uncertain factors. The fuzzy control method has a fast response speed, strong adaptability, and can achieve a better control effect. However, the stability of fuzzy control has only been tested through some simulation processes, and the theoretical standard for judging its stability has not yet taken shape. Fuzzy controller is only suitable for certain parameter indexes. This table of tire performance will make the control effect worse, the control effect has a great dependence on the nature of the road surface, and its effect can only be judged by actual measurement. During the vehicle operation, the active suspension system is easily disturbed by uncertain road disturbances, which changes internal parameters of the system and thus affects the ride comfort. Due to the influence of measurement error and noise, the feedback signal forms a deviation among models. As a result, how to ensure the stability of the active suspension controller is particularly crucial. The robust control theory can ensure the dynamic stability of each loop of the active suspension system and perfectly achieve preset performance indicators of the system. Recently, it has been identified that the robust H∞ theory can be used to control vehicle active suspension.

The output feedback of the time-varying input delay has progressed, and a new dynamic output feedback H∞ controller can make the active suspension system gradually stable, ensuring robust system performance [16]. In order to ensure compatibility with the vehicle ride comfort and manipulation stability, two adaptive H∞ controllers are designed; the wavelet generator and radial basis function support vector machine are used to verify the nonlinear vehicle suspension system [17]. Output feedback control is easily implemented compared to state feedback control, as some state variables are inextricable in practice. Therefore, research on dynamic output feedback is more practical. In [18], a static output feedback controller was derived for guaranteeing good suspension performance under possible sensor fault or suspension component breakdown. The researchers in [19] considered quadratic stabilizability and H∞ feedback control for stochastic discrete-time uncertain systems with state- and control-dependent noise. In [20], a robust fix-order dynamic output-feedback controller was designed for a nonlinear uncertain vehicle suspension system. The researchers in [21] considered issues related to optimizing static output feedback control, and some constraint conditions were added and verified in the semi-active suspension system.

The researchers in [22,23] investigated the active suspension controller of a two-degree-of-freedom vehicle model using H∞ state feedback control. However, it was difficult to observe variables such as wheel travel and road surface disturbance. Hence, the research on state feedback control only remains at the theoretical stage. However, H∞ output feedback research exhibits great application value. In [24,25], the weighting function was used to adjust the frequency domain characteristics of the system, and the H∞ output feedback controller was designed via linear matrix inequality programming constraint equations. The work in [26] studied the frequency-integer H∞ active suspension control. The output performance of the system can be adjusted by using the frequency weighting function via the H∞ method, enhancing the performance of the suspension system.

At present, great progress has been made in the design of vehicle active suspension controllers with individual control indicators of H∞ and H2. Due to the obvious advantages and disadvantages of H∞ and H2 control theory, hybrid H∞/H2 controllers for robust stability with resistance to external disturbances are under development. For example, in [27], a hybrid H2/H∞ controller based on linear matrix inequality was designed to enhance the dynamic characteristics of active suspension. Compared with active suspension with the H∞ controller, the parameter perturbation was not considered. The researchers in [28,29,30,31] applied H2 performance, H∞ performance, and regional pole assignment to design hybrid H2/H∞ controllers for active suspensions, while model parameter uncertainty was not considered. The method of solving linear matrix inequality is applied in most of the currently designed H2/H∞ controllers. In this study, the H∞ multi-objective optimal robust controller was designed by converting the multi-objective constraint control problem into a Riccati equation problem. The feasibility and effectiveness of the controller in practice were verified by simulation and experiments. However, the research theory in the above references has limited use because the calculation process of the controller is cumbersome, and a large amount of variable conversion is performed during the derivation process. Therefore, this study was designed based on the Riccati equation active suspension control system, which is prioritized to satisfy the actuator saturation and hard constraint restrictions, and a simplified efficient output feedback H∞ controller was proposed. Compared to the controller in previous references, new controllers can achieve better manipulation of the stability and ride comfort and meet suspension stroke restrictions and road holders. After simulation analysis, it is effective to verify the novel design method, and it can form complementarity with other vehicle controllers.

This paper has the following structure layout. In the second quarter, a math model of suspension is established. In the third quarter, the H∞-optimized output feedback controller is derived for the active suspension system. In the fourth quarter, a comparison is made with the previous H∞ controller.

Notation

In this paper, the superscript T indicates the row and column change position in the matrix. The symbol X > 0 (X ≥ 0) means that X is a symmetric matrix; X is also a positive definite matrix. Asterisk * indicates a transposition block in a symmetrical position of the matrix. A⁻¹ represents the inverse matrix of matrix A. x represents rows of matrices or column vectors. $\parallel ·\parallel$₂ indicates the L2 norm of vectors. $\parallel ·\parallel$_∞ indicates the H∞ norm of the transfer function. The formula of RMS can be expressed as $X_{RMS}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{X}_i^2}{N}}$.

2. System Model and Problem Formulation

The inherent vibration frequency of a car equipped with an air suspension is lower than that of a passive suspension. The change in load has little effect on the vibration frequency of the car body. The range of vibration frequencies of a car equipped with an air suspension is small. The air suspension improves vehicle comfort and is highly controllable in the structure. The car can adjust the height of the vehicle body and the stiffness of the suspension while driving, so that it can respond to different road conditions in time. The control system is the core component of the air suspension. The performance of the air suspension largely depends on the performance of the controller of the control system. The performance of the air suspension has great influence on the ride comfort and handling stability of the car. During normal driving, the air springs become softer and damper, resulting in a comfortable ride. When turning sharply or braking, it can be quickly converted into a hard air spring and strong damping to improve the stability of the body. Due to the outstanding characteristics of the air suspension, this study designed a H∞ output feedback controller to make the superiority of the air suspension better.

In this study, key suspension performances (such as ride comfort, suspension deflection, and grip) were considered as control design goals for the vehicle’s active suspension system. As the ride comfort can usually be quantified by the vehicle body acceleration in the vertical direction, it is reasonable to select the vehicle body acceleration as the first control output, that is, ${\ddot{z}}_s\left(t\right)$. When designing an output feedback controller, one of our main goals is to minimize the vertical acceleration ${\ddot{z}}_s\left(t\right)$. Therefore, we can apply the H∞ norm to measure performance, and its value actually produces an upper limit of the root-mean-square (RMS) gain. In addition, our other main goal is to minimize the H∞ norm of the transfer function from the disturbance $w\left(t\right)$ to the control output $z_1\left(t\right)={\ddot{z}}_s\left(t\right)$ to improve the vehicle’s riding comfort.

2.1. The Quarter Vehicle Model

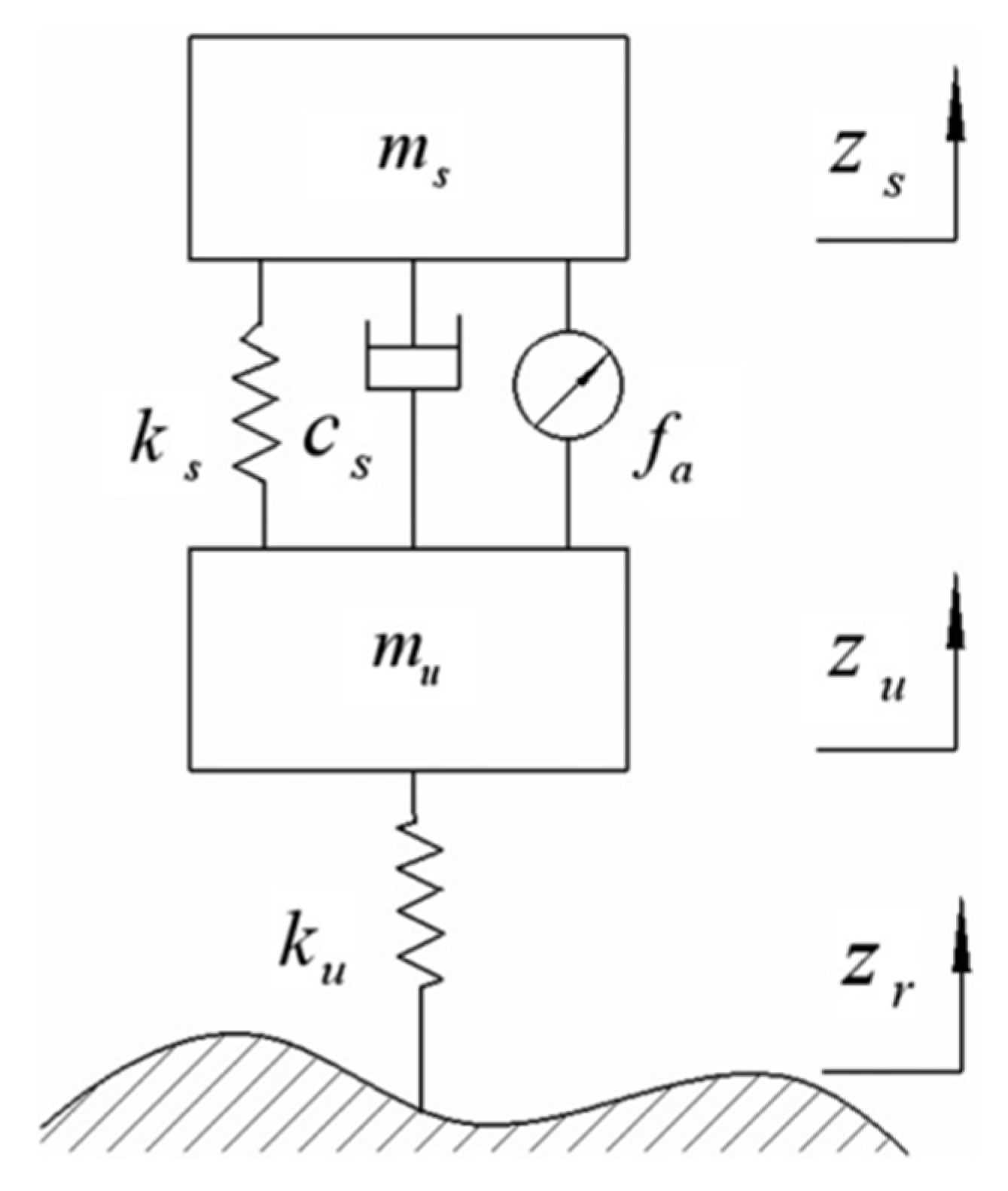
The quarter vehicle model (single-wheel model) is the basic model to design the active suspension controller, which can express well the basic characteristics of the suspension system. Figure 1 displays a two-degree-of-freedom quarter vehicle active suspension model. The dynamic equations are described as follows:

$${\ddot{z}}_s=-\frac{k_s}{m_s}\left(z_s-z_u\right)-\frac{c_s}{m_s}\left({\dot{z}}_s-{\dot{z}}_u\right)+\frac{1}{m_s}{f}_a$$

(1)

$${\ddot{z}}_u=\frac{k_s}{m_u}\left(z_s-z_u\right)+\frac{c_s}{m_u}\left({\dot{z}}_s-{\dot{z}}_u\right)-\frac{k_u}{m_u}\left(z_u-z_r\right)-\frac{1}{m_u}{f}_a$$

(2)

The model contains the following parameters: $m_s$ is the mass of the vehicle body; $m_u$ refers to the mass of the wheel; $k_s$ represents the spring stiffness of the suspension; $c_s$ is the damping force of the suspension; $k_u$ denotes the spring stiffness of the tire; $z_s$ is the vertical displacement of the body; $z_u$ is the vertical displacement of the wheel; $z_r$ refers to the irregular excitation from the road surface under nonstationary running; and $f_a$ is the active control force input at the suspension location.

2.2. Establishment of Nonstationary Road Disturbance Model

When the vehicle is driving at variable speed, the road disturbance in the space domain $z_r$(s) is regarded as a stationary process, while the road disturbance in the time domain $z_r$(t) is considered as a nonstationary process. According to the white noise method of simulation filtering based on stable random theory, the differential equation for road space unevenness can be expressed as follows:

$$z_r\left(s\right)+{\Omega }_c{z}_r\left(s\right)=2\pi n_0\sqrt{s_q\left(n_0\right)}W\left(s\right)$$

(3)

In this equation, ${\Omega }_c=2\pi n_c$ is the road spatial cut-off angular frequency; $n_c=0.01$ m⁻¹ refers to the road spatial cut-off frequency; $n_c=0.1$ m⁻¹ is the standard spatial frequency; $s_q\left(n_0\right)$ denotes the coefficient of road roughness; and $W\left(s\right)$ is the stationary white noise in the space domain.

According to the space–time relationship, it has

$$\frac{d}{ds}=\frac{1}{\dot{s}}\frac{d}{dt}$$

(4)

Substituting Equation (4) into Equation (3), the road excitation in the nonstationary running process can be obtained.

$${\dot{z}}_r\left(t\right)+\dot{s}2\pi n_c{z}_r\left(t\right)=2\pi n_0\sqrt{s_q\left(n_0\right)\dot{s}}W\left(t\right)$$

(5)

In the formula, $\dot{s}$ is given in $\dot{s}=v_0+at$; $v_0$ is the initial vehicle velocity; and $a$ is the acceleration.

Let $a_1=\dot{s}2\pi n_c$ and $b_1=2\pi n_0\sqrt{s_q\left(n_0\right)\dot{s}}$, and substitute them into Equation (5). Then, the road disturbance in the time domain is given by

$${\dot{z}}_r\left(t\right)=-a_1{z}_r\left(t\right)+b_{1}W\left(t\right)$$

(6)

2.3. Control Equation of Active Suspension System

The state variables of the system are set as:

$$x_1=z_s-z_u,x_2={\dot{z}}_s,x_3=z_u-z_r,x_4={\dot{z}}_u,x_5=z_r$$

After combining with the road nonstationary disturbances, Equation (3), the control equation of the quarter-vehicle active suspension can be given by:

$$\dot{x}\left(t\right)=Ax\left(t\right)+B_{w}w\left(t\right)+B_{u}u\left(t\right)$$

(7)

$$A=\left[\begin{array}{ccccc}0& 1& 0& -1& 0\\ -\frac{k_s}{m_s}& -\frac{c_s}{m_s}& 0& \frac{c_s}{m_s}& 0\\ 0& 0& 0& 1& a_1\\ \frac{k_s}{m_u}& \frac{c_s}{m_u}& -\frac{k_u}{m_u}& -\frac{c_s}{m_u}& 0\\ 0& 0& 0& 0& -a_1\end{array}\right]$$

$$B_w=\left[\begin{array}{ccccc}0& 0& -b_1& 0& b_1\end{array}\right]T$$

$$B_u=\left[\begin{array}{ccccc}0& \frac{1}{m_s}& 0& -\frac{1}{m_u}& 0\end{array}\right]T$$

$u\left(t\right)=f_a$ is the control force input.

In the suspension system design, vehicle comfort is the primary performance requirement. The vertical acceleration ${\ddot{z}}_s$ of the vehicle body is the main index to evaluate ride comfort. Ride comfort is the second performance requirement. That is to say, the static load of the wheel should be larger than the dynamic load of the wheel.

$$k_u\left(z_u-z_r\right)<\left(m_u+m_s\right)g$$

(8)

In the formula, $g$ is the acceleration due to gravity.

In addition, the stroke limitation of suspension movement is taken into account to make the suspension not affect the position limiter and the vehicle ride comfort.

$$\left|z_s-z_u\right|\le S_{max}$$

(9)

In the above inequality, $S_{max}$ is the maximum dynamic stroke of the suspension.

In the end, the saturation or limitation of control force output imposed on the suspensions should be considered, which can be defined as follows,

$$\left|f_a\right|\le F_{max}$$

(10)

Thus, we can suppose

$$z_1={\ddot{z}}_s, z_2=\left[\begin{array}{ccc}\frac{z_s-z_u}{S_{max}}& \frac{k_u\left(z_u-z_r\right)}{\left(m_u+m_s\right)g}& \frac{f_a}{F_{max}}\end{array}\right]T$$

(11)

$z_1$ is the control output that needs to be obtained, and $z_2$ is the limit constraint. The suspension system design aims to find a control law that can stabilize the closed-loop of the suspension system and minimize $z_1$ while satisfying all constraints (including the absolute value of $z_2$ output less than 1).

3. H∞ Optimal Output-Feedback Controller Design

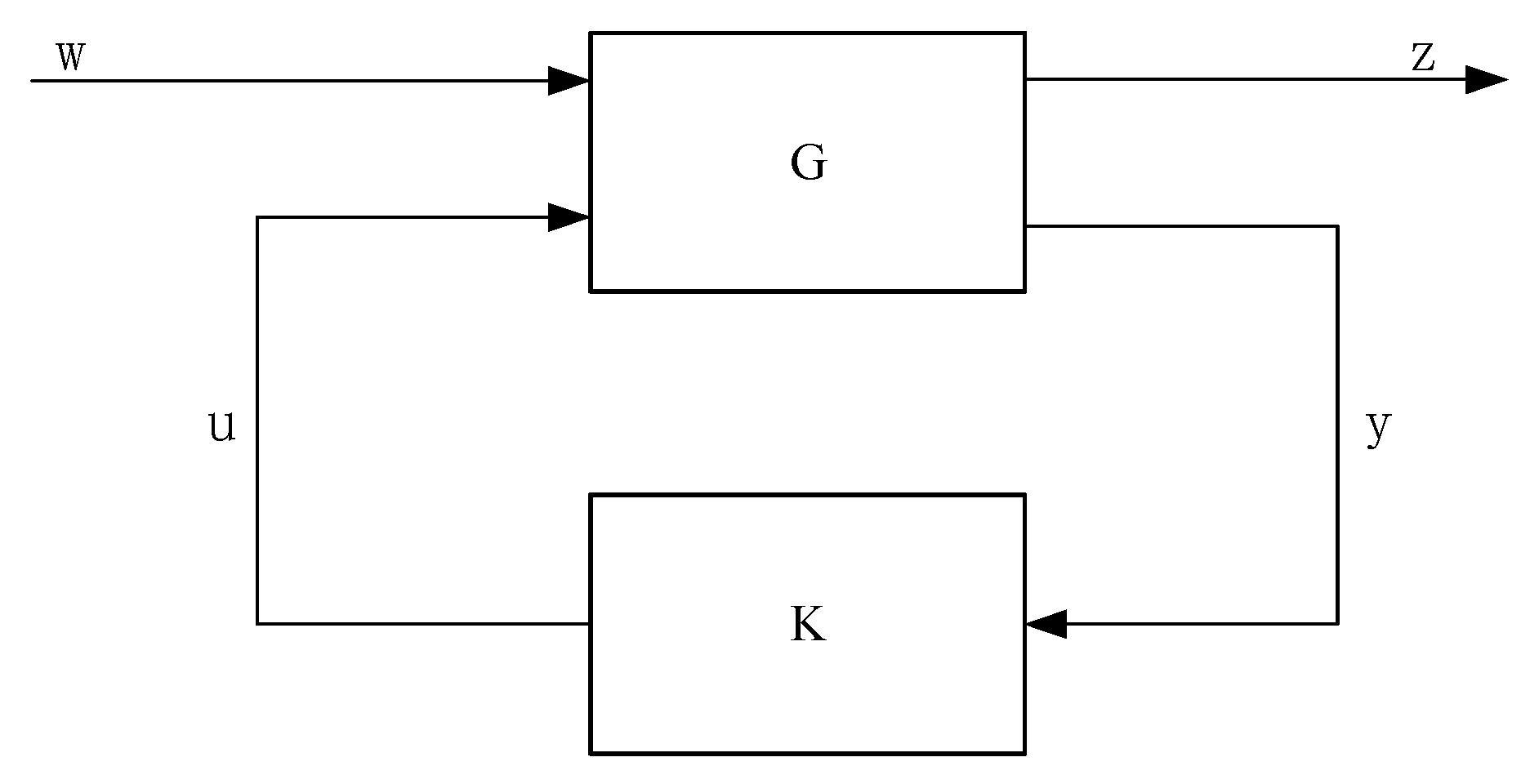
The dynamic feedback controller makes the closed-loop system shown in Figure 2 stable and $G_{zw}{\left(s\right)}_{\infty }<1$ a necessary and sufficient condition for the Riccati equation.

$$AY+Y{A}^T+Y\left(C_1^T{C}_1-C_2^T{C}_2\right)Y+B_1{B}_1^T=0$$

(12)

Having a semi-positive definite solution $Y\ge 0$ makes $A^T+\left(C_1^T{C}_1-C_2^T{C}_2\right)Y$ a stable matrix. If such $Y$ exists, the solution to the H∞ standard problem is:

$$K\left(s\right)=\left[\begin{array}{cc}A-B_2{C}_1-L{C}_2& -L\\ C_1& 0\end{array}\right]$$

(13)

In $K\left(s\right)$,

$$L=Y{C}_2^T$$

(14)

The suspension control system can be expressed by the following state equations:

$$\dot{x}\left(t\right)=Ax\left(t\right)+B_{w}w\left(t\right)+B_{u}u\left(t\right)$$

(15a)

$$z_1\left(t\right)=C_{1}x\left(t\right)+D_{1w}w\left(t\right)+D_{1u}u\left(t\right)$$

(15b)

$$z_2\left(t\right)=C_{2}x\left(t\right)+D_{2u}u\left(t\right)$$

(15c)

In this matrix, $z_1\left(t\right)$ is the controlled output and $z_2\left(t\right)$ is the constrained output,

$$\left|z_{2i}\left(t\right)\right|\le z_{2max},C_1=\left[\begin{array}{ccccc}-\frac{k_s}{m_s}& -\frac{c_s}{m_s}& 0& \frac{c_s}{m_s}& 0\end{array}\right],$$

$$D_{1w}=0, D_{1u}=\frac{1}{m_s},$$

$$C_2=\left[\begin{array}{ccccc}1/Smax& 0& 0& 0& 0\\ 0& 0& \frac{k_u}{\left(m_u+m_s\right)g}& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],$$

$$D_{2u}=\left[\begin{array}{ccccc}0& 0& 1/Fmax& 0& 0\end{array}\right]T$$

Designing the output feedback control law $u=K\left(s\right)Y$, the transfer function $G\left(z\right)$ of external disturbance $w$ to $z_1$ should satisfy the relationship $G\left(z\right)\le \gamma$ (a specified positive value), and the suspension system equation should satisfy all constraints (including that the absolute value of the output of $z_2$ is less than 1). The necessary and sufficient condition for a given γ > 0 and the system Equation (15) is the [32] RICCATI equation

$$A^T{X}_{\infty }+X_{\infty }A+X_{\infty }\left({\gamma }^{-2}{B}_1{B}_1^T-B_2{B}_2^T\right)X_{\infty }+C_1^T{C}_1=0$$

(16)

$$A{Y}_{\infty }+Y_{\infty }{A}^T+Y_{\infty }\left({\gamma }^{-2}{C}_1^T{C}_1-C_2^T{C}_2\right)Y_{\infty }+B_1{B}_1^T=0$$

(17)

The solution is $X_{\infty }\ge 0$, $Y_{\infty }\ge 0$

$$\overline{\sigma }\left(X_{\infty }{Y}_{\infty }\right)<{\gamma }^2$$

(18)

In the formula, $\overline{\sigma }$ represents the maximum eigenvalue of the matrix.

If the above conditions are true, the output feedback controller that stabilizes the closed-loop system and satisfies $G\left(z\right)\le \gamma$ can be described as:

$$K\left(s\right)=\left[\begin{array}{cc}{\widehat{A}}_{\infty }& -Z_{\infty }{L}_{\infty }\\ F_{\infty }& 0\end{array}\right]$$

(19)

In $K\left(s\right)$,

$${\widehat{A}}_{\infty }=A+{\gamma }^{-2}{B}_1{B}_1^T{X}_{\infty }+B_2{F}_{\infty }+Z_{\infty }{L}_{\infty }{C}_2,F_{\infty }=-B_2^T{X}_{\infty },L_{\infty }=-Y_{\infty }{C}_2^T,Z_{\infty }={\left(I-{\gamma }^2{X}_{\infty }{Y}_{\infty }\right)}^{-1}.$$

The problem of finding the output feedback controller $u=K\left(s\right)Y$ can be converted into that of obtaining the control signal $u\left(t\right)$. This problem can be considered from the perspective of the system signal relationship. For the purpose of control, the interference should be reduced to the minimum value or less than a given value [33]. Obviously, the interference mentioned here refers to the norm of operators of the closed-loop system from $w$ to $z$, namely, the $H_{\infty }$ norm of the closed-loop system. The state space of the controller $K\left(s\right)$ of Equation (19) can be described as:

$$\dot{\widehat{x}}=A\widehat{x}+B_1{\widehat{w}}_{worst}+B_{2}u-Z_{\infty }{L}_{\infty }\left(y-C_2\widehat{x}\right)$$

(20a)

$$u=-B_2^T{X}_{\infty }\widehat{x}$$

(20b)

$${\widehat{w}}_{worst}={\gamma }^{-2}{B}_1^T{X}_{\infty }\widehat{x}$$

(21a)

$$Z_{\infty }={\left(I-{\gamma }^2{X}_{\infty }{Y}_{\infty }\right)}^{-1}$$

(21b)

$$L_{\infty }=-Y_{\infty }{C}_2^T$$

(21c)

Figure 3 illustrates the system structure. As shown in Figure 3, the output feedback H∞ controller can be divided into two parts, in which the first part is a state estimator and the other one is a term for feedback control using state estimates.

4. Simulation Results

The following is a time-domain analysis diagram of the vehicle-road coupling excitation when the vehicle passes through the speed reduction zone, and then the spring mass output of the closed-loop system after the H∞ controller that introduces a first-order low-pass filtering weighting function for the graded road is added. 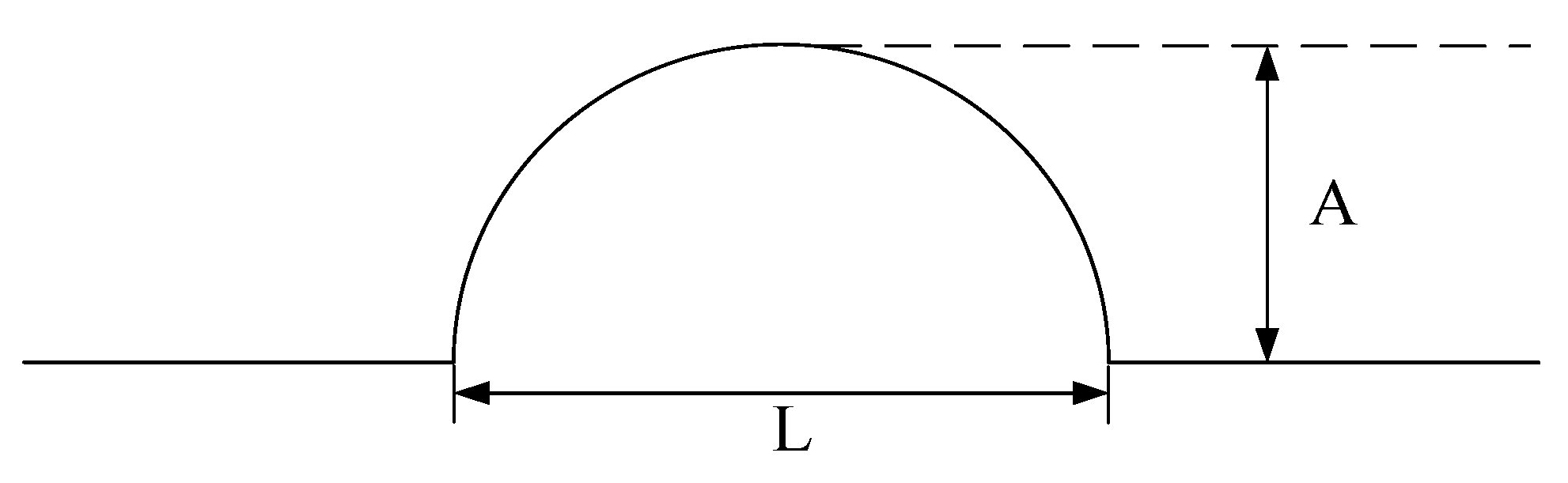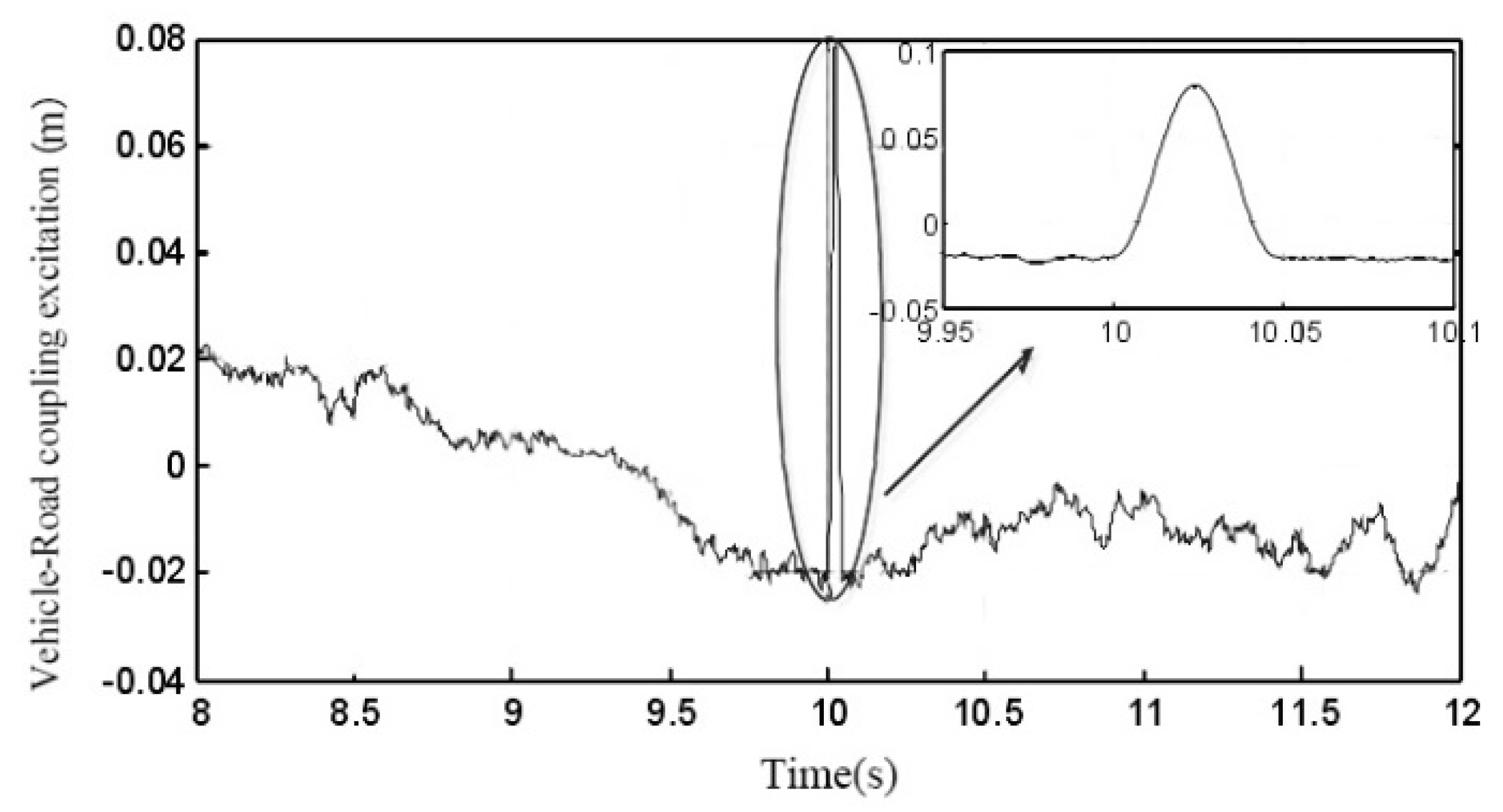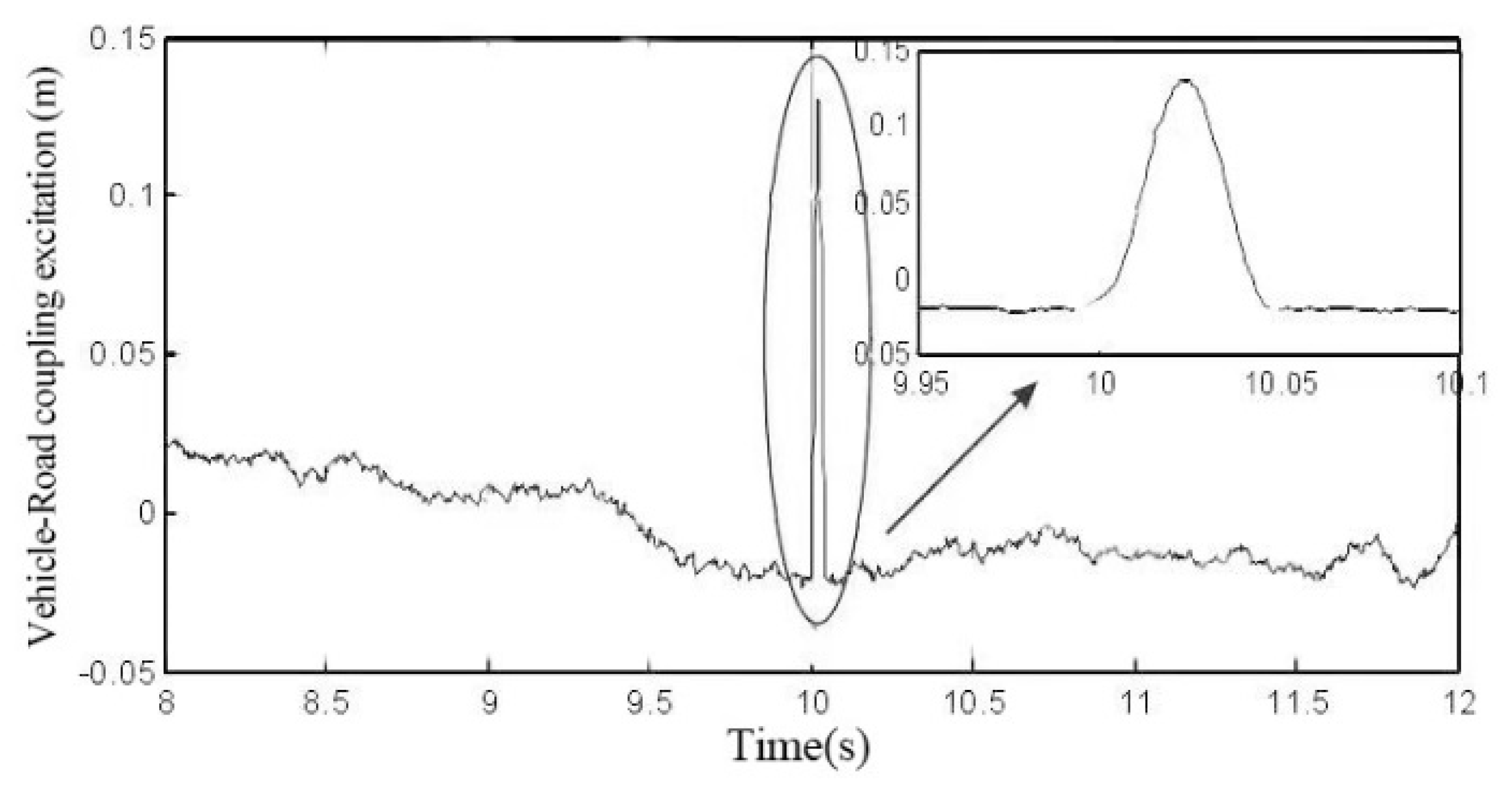Time–frequency analysis is performed to the acceleration, the effect of the controller on the road disturbance control considered in this paper is observed, and the importance of the H∞ controller is determined. The cross-sectional shape of common speed reduction belts in China can be approximated as a circular arc curve [34]. The following Figure 4 can be used to characterize the vehicle–road coupling excitation signal input when a vehicle passes through a speed reduction belt and other pits. Among them, A and L, respectively, represent the amplitude and length of the road bump or depression in units of m. The classification of road simulation conditions is shown in

Table 1. Classification of simulation conditions.

Simulation Condition	Vehicle Speed	Amplitude of the Road Bump	Length of the Road Bump
I	30 km/h	0.1 m	0.4 m
II	30 km/h	0.1 m	0.3 m
III	40 km/h	0.15 m	0.4 m

.

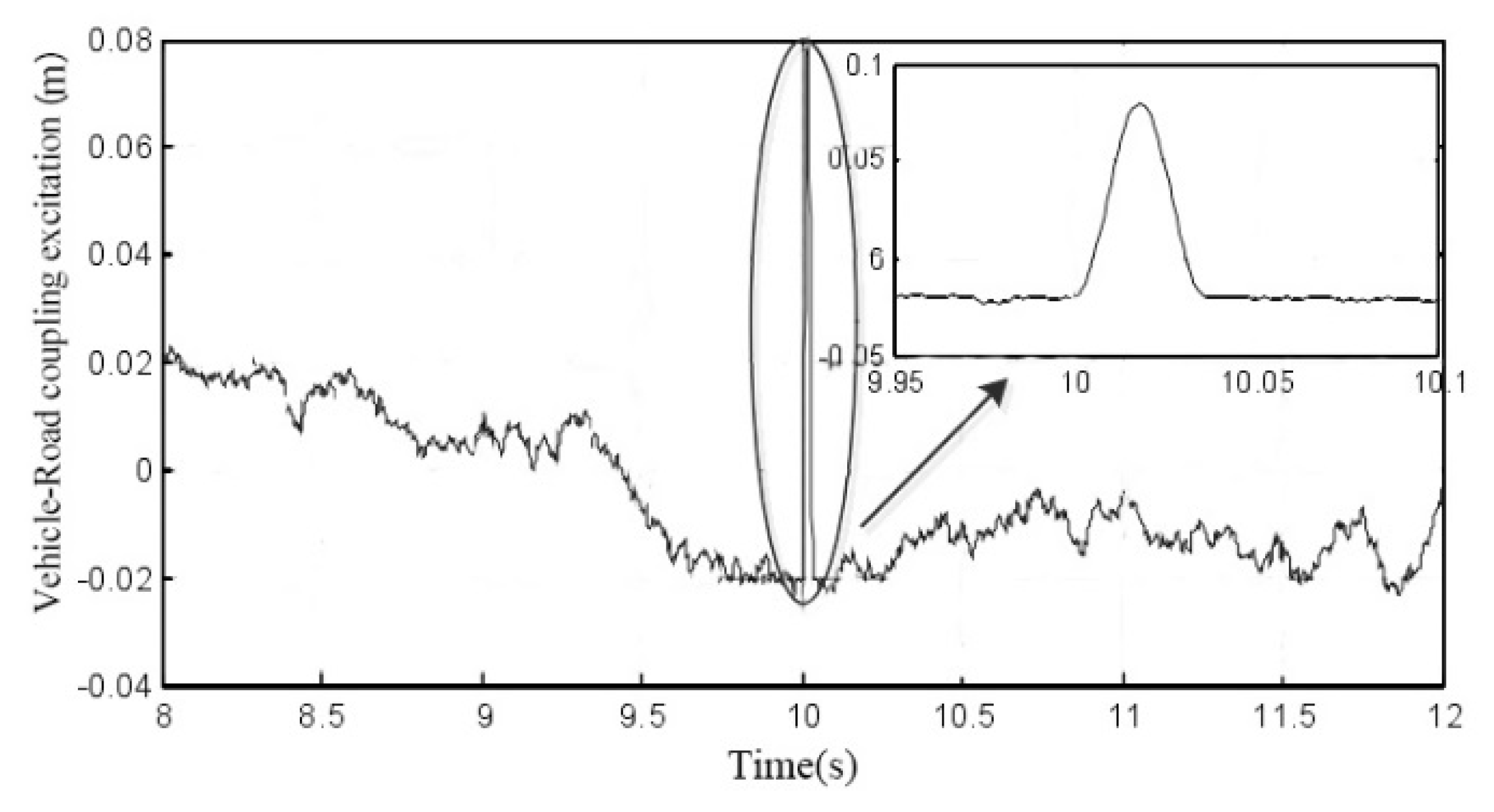
According to the road conditions I to III, the road coupling excitation curve simulated from the respective simulation is Figure 5, Figure 6 and Figure 7, it can be known that when a vehicle is driving on a Class B road through a speed bump and a pit road with different parameters, the greater the length L of the road convexity or depression, the smaller the main frequency at the road deceleration zone. At this time, the impact change is slowed down. It can also be found that the larger the amplitude of the height of the road bump or depression, the greater the amplitude change of the vehicle–road coupling excitation, resulting in a faster impact change [35]. On this occasion, the main frequency at the speed bump is not affected. However, this does not affect the speed at the deceleration zone. When the vehicle is traveling at the same speed on the Class B road at different speeds, the greater the speed of the road-coupled vehicle, and the greater the main frequency at the road speed reduction zone and the vehicle–road coupling excitation at the same fixed point in time. The larger the value is, the shorter the time it takes for a vehicle to pass through a single speed reduction zone. Therefore, when the vehicle passes through the road at a variable speed, the main frequency of the vehicle–road coupling excitation has little effect. The main frequency and amplitude of the vehicle–road coupling excitation signal are related to the length and height of the road bump or depression. At the same time, it changes with the speed of the vehicle when driving across the road. It has the characteristics of nonstationary excitation signals.

4.1. Random Pavement Response Analysis

By writing the matlab control algorithm, the output feedback gain of the controller can be calculated as $K\left(s\right)={10}^4\times \left[\begin{array}{ccccc}1.6783& 0.0823& -0.0015& -0.0981& 0.0160\end{array}\right]$.

This article uses Carsim, Matlab, and Simulink for joint simulation. First, carsim is used to set the suspension parameters, which are input into the controller module built by simulink to obtain the simulation result. The simulation is carried out under random road disturbance and compared with the H∞ output feedback controller (hereinafter referred to as the C2 controller) proposed in [24], which used a weighted function to adjust the frequency domain characteristics of the system. C1 represents the H∞ output feedback controller designed in this paper.

Table 2. Vehicle model parameters.

Parameters (Symbol)	Values (Unit)
$\mathrm{Suspension}\mathrm{mass}(m_s$)	300 kg
$\mathrm{Suspension}\mathrm{damping}(c_s$)	1000 N/m/s
$\mathrm{Suspension}\mathrm{nonspring}\mathrm{mass}(m_u$)	60 kg
$\mathrm{Tire}\mathrm{stiffness}(k_u$)	185,000 N/m
$\mathrm{Suspension}\mathrm{stiffness}(k_s$)	15,900 N/m
$\mathrm{maximum}\mathrm{force}\mathrm{of}\mathrm{actuator}(F_{\max }$)	1500 N
$\mathrm{maximum}\mathrm{stroke}\mathrm{of}\mathrm{suspension}(S_{\max }$)	0.08 m

displays the parameters of the defined suspension model. The vehicle moves at a speed of 30 m/s under the disturbance of the Class B road surface, and the comparison response curves of the vertical acceleration of the active control suspension and the C2 controller suspension in the vehicle body, dynamic deflection of the suspension, and dynamic travel of the tire are given. Figure 8, Figure 9 and Figure 10 show comparative analysis diagrams of corresponding simulated control effects. 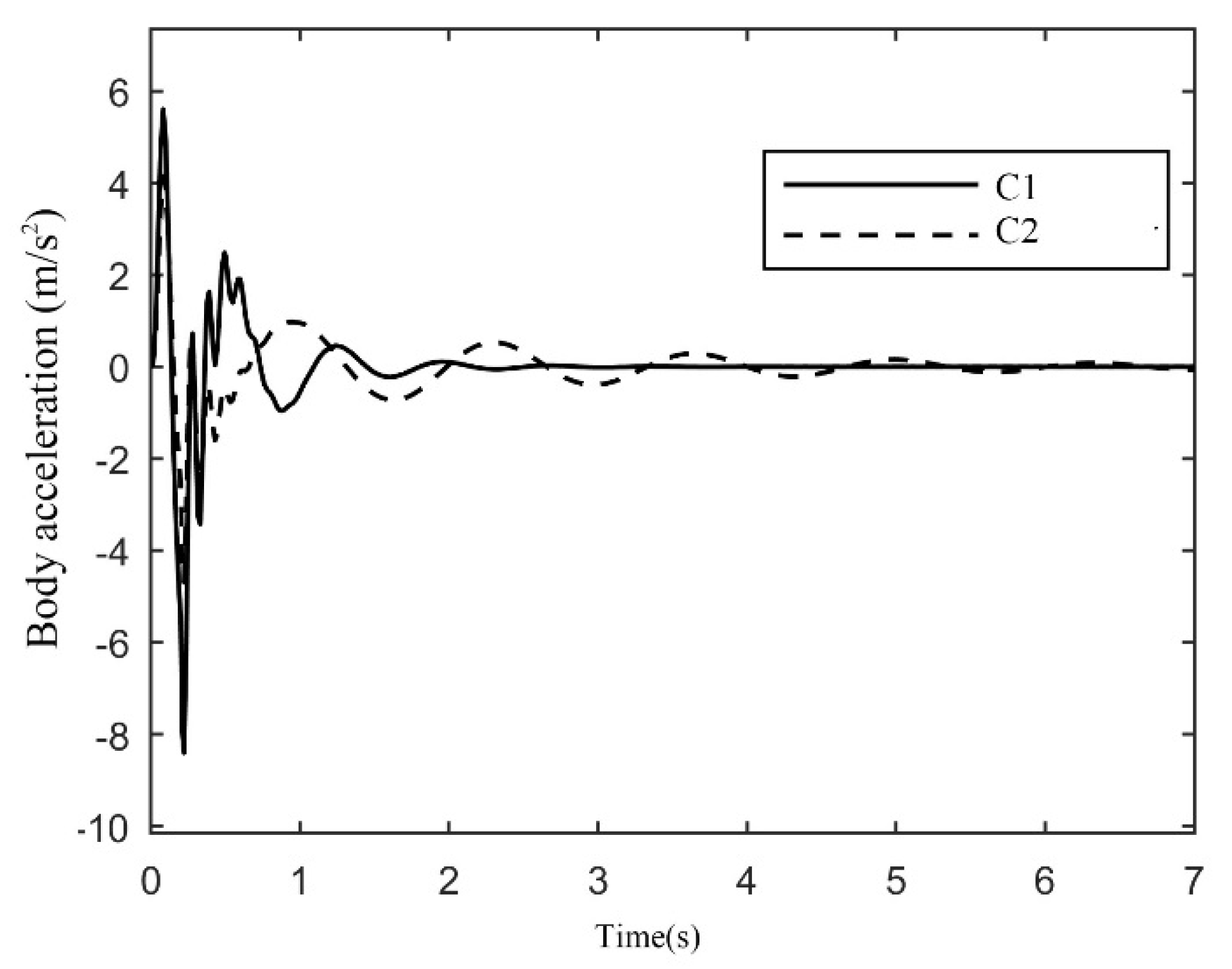As shown in Figure 8, under the interference of the Class B road, the acceleration of the vehicle body of the active suspension using C1 is smaller than that of the C2 controller suspension. In addition, the ride comfort is greatly improved compared to that of the passive suspension. 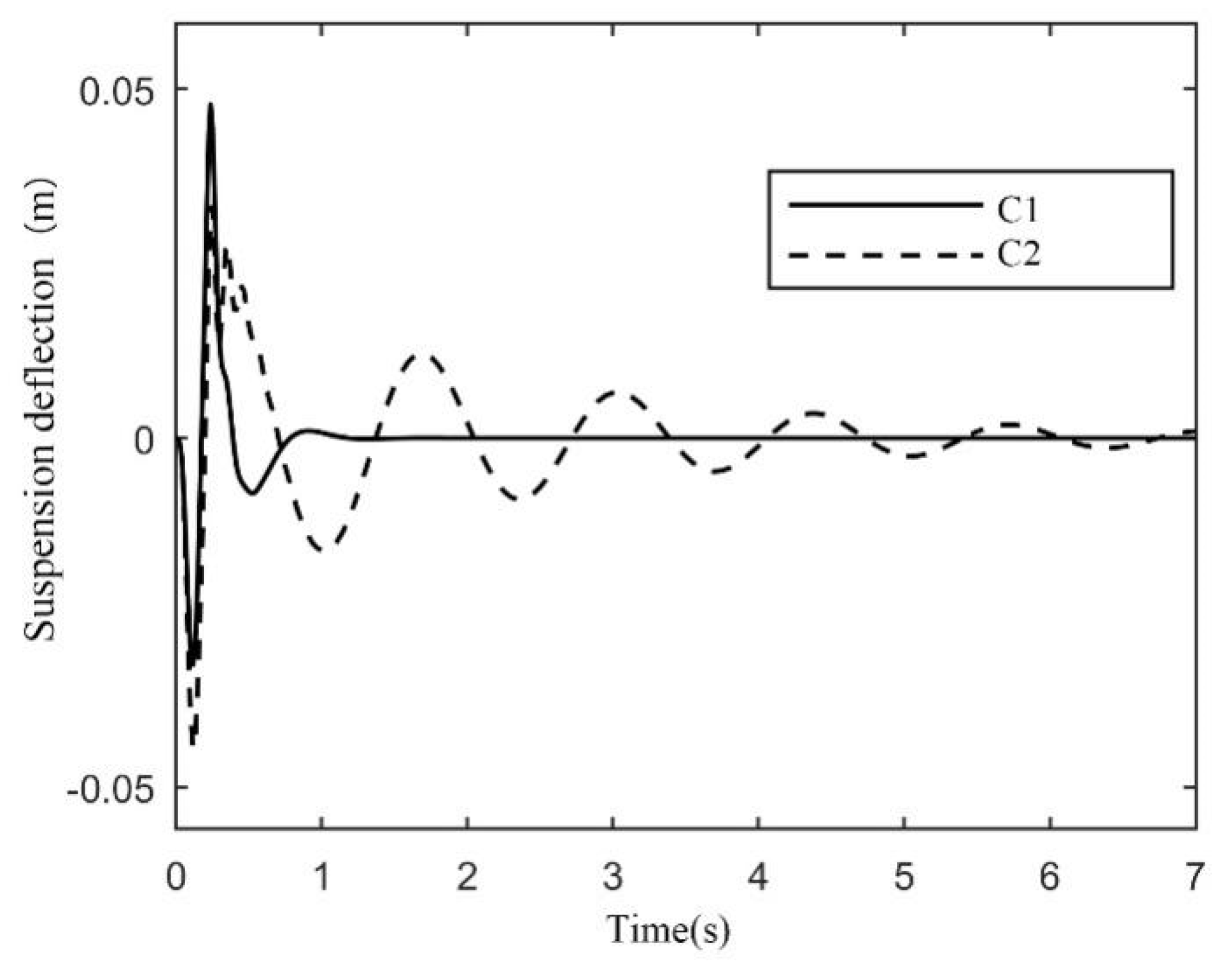Figure 9 illustrates that the active deflection of the active suspension using C1 is smaller than that of the C2 controller. Suspension deflection is equivalent to $\left(z_u-z_r\right)$. Moreover, it should be noticed that it meets the maximum height limit of the suspension (80 cm). 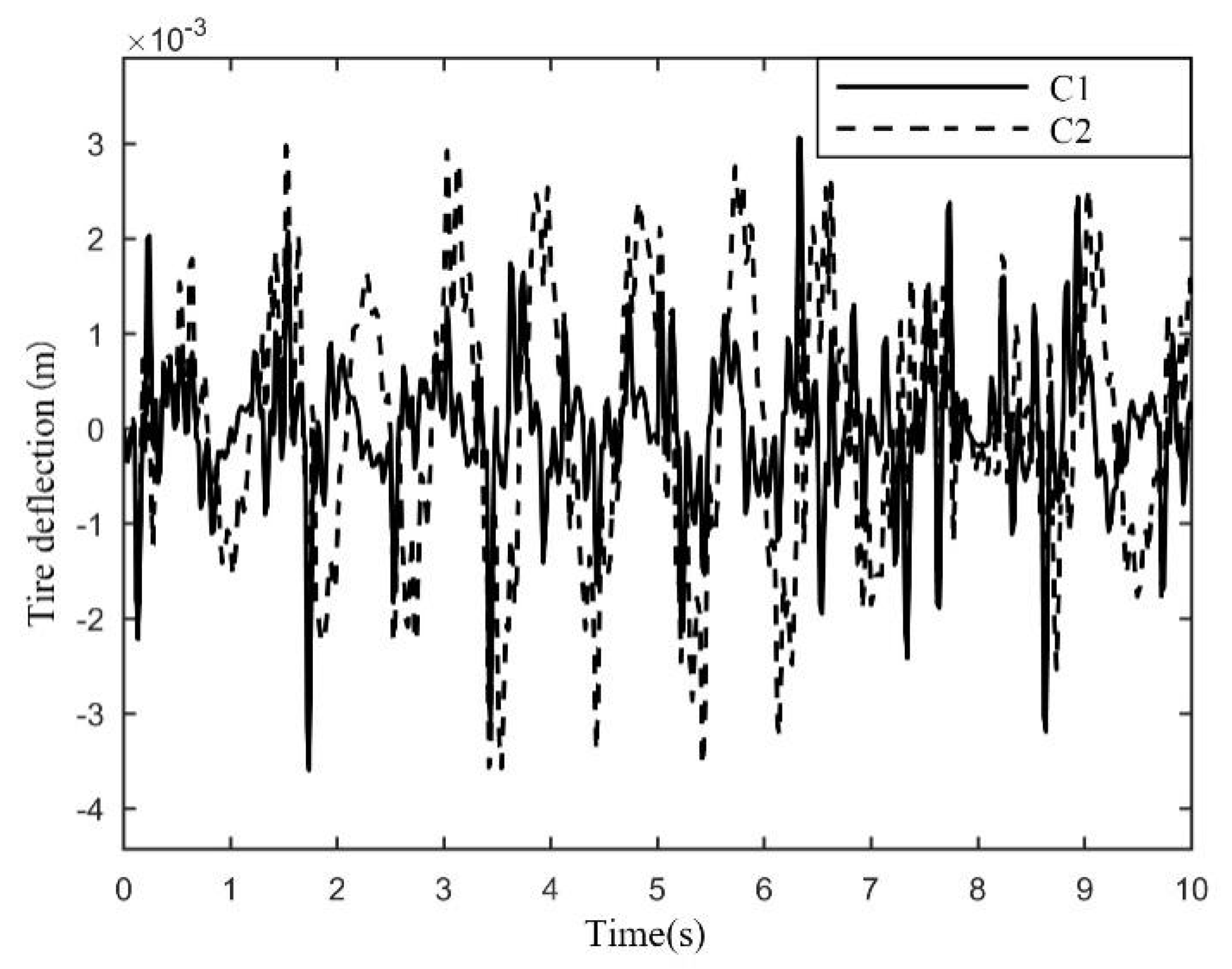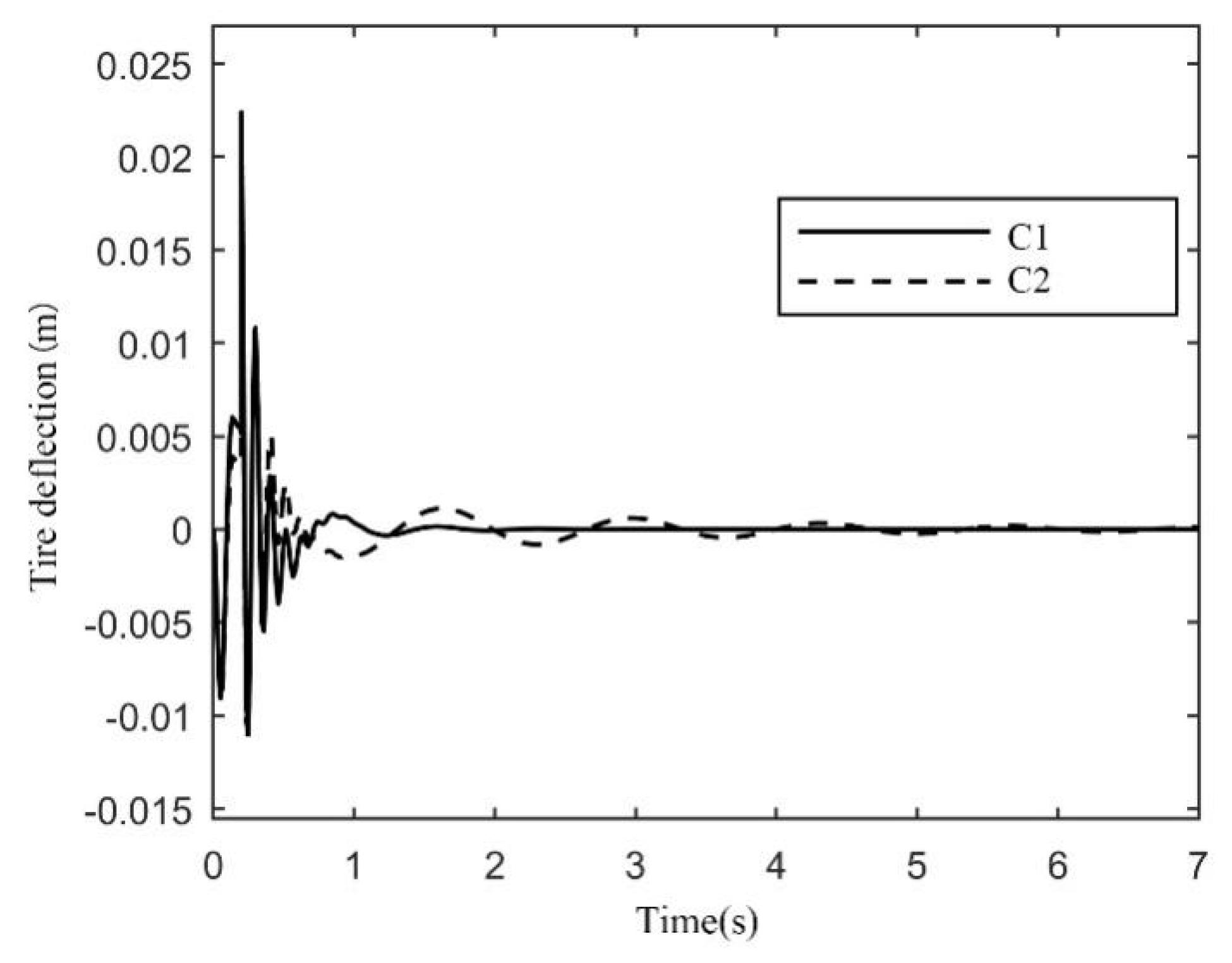In Figure 10, the tire dynamic stroke of the active suspension satisfies the constraint Formula (28), and it is smaller than that of the C2 controller. Tire deflection is equivalent to $\left(z_u-z_r\right)$. The obtained results indicate that the ride comfort of the vehicle using the controller is effectively enhanced in comparison with that of the vehicle using the C2 controller suspension.

The RMS comparison of the vehicle dynamic responses under Class B road excitation is shown in

Table 3. Comparison of dynamic response of vehicles equipped with C1 controller and C2 controller on Class B roads.

Term (RMS)	C2	C1
Body acceleration/(m/s2)	3.9	3.1
Degree of improvement	-	20.5%
Suspension deflection/(m)	0.19	0.15
Degree of improvement	-	22.7%
Tire deflection/(m)	0.11	0.08
Degree of improvement	-	27.2%

.

4.2. Response Analysis of Bump Road

To further investigate the controller’s effectiveness, a bumping road was selected for simulation. According to the international standard ISO2361, a short-time and high-intensity bump road was selected as the disturbance input. The expression is described as follows:

$$Z_r\left(t\right)=\{\begin{array}{c}\frac{A_m}{2}\left(1-cos\frac{2\pi u}{L}t,0\le t\le \frac{L}{u}\right)\\ 0,other\end{array}$$

(22)

In the formula, $A_m$ and $L$ represent the height and length of the bump input, respectively, in which $A_m$ = 50 mm and $L$= 8 m; the car ran at a constant speed of $u$= 30 m/s. Under the interference of the bump road, the C2 controller and C1 controller were compared. Figure 11, Figure 12 and Figure 13 display response analysis curves of the vertical acceleration of the vehicle body, dynamic deflection of the suspension, and dynamic stroke of tires in two control modes. As shown in Figure 11, the active suspension with the C1 controller has a higher acceleration response peak than that of the active suspension with the C2 control system. However, it can quickly reach a steady state, effectively improving ride comfort. In Figure 12, the dynamic deflection of the suspension controlled by the C1 controller is smaller than the value of the C2 control system. In addition, it can meet the requirements of the height constraint of the suspension limit, effectively reduce the influence of the suspension and the limit block, increase the suspension service life, reduce the suspension damage risk, and ensure the vehicle operation stability. Figure 13 shows that the tire dynamic stroke of the active suspension with the C1 controller fluctuates more than the C2 control suspension at the initial stage, while it becomes smaller than that of the C2 control system suspension in the middle and late stages. Moreover, the steady-state response time is remarkably reduced. During the process of bumping, the tire leaves the ground in a very short period of time, which hardly results in the unsafe phenomenon of “wheel jump” and, thus, improves the ride comfort of the vehicle [36]. In addition, these two constraints of suspension dynamic deflection and tire dynamic load have a small floating range, can reach a steady state quickly, and exhibit good dynamic characteristics.

The RMS comparison of the vehicle dynamic responses under bump road excitation is shown in

Table 4. RMS comparison of the dynamic response of vehicles equipped with C1 controller and C2 controller on bump.

Term (RMS)	C2	C1
Body acceleration/(m/s2)	5.8	4.5
Degree of improvement	-	22.4%
Suspension deflection/(m)	0.23	0.18
Degree of improvement	-	21.7%
Tire deflection/(m)	0.12	0.09
Degree of improvement	-	25.0%

.

4.3. Robustness Analysis

In order to analyze the robustness of the designed active suspension controller, the parameter uncertainty of the controller was set [37]. The relationship of quarter $m_s={\tilde{m}}_s\left(1+d_{ms}{\mathsf{\delta }}_{ms}\right)$ and $k_s={\tilde{k}}_s\left(1+d_{ks}{\mathsf{\delta }}_{ks}\right)$, where $d_{ms}$ is the spring mass disturbance coefficient and $d_{ks}$ is the spring stiffness disturbance coefficient. According to the parameter uncertainty disturbance range of suspension stiffness and vehicle mass, two models were set [38], namely: (1) Model 1 with $d_{ms}=-0.4$,$d_{ks}=-0.1$; (2) Model 2 with $d_{ms}=0.4$, $d_{ks}=0.1$. 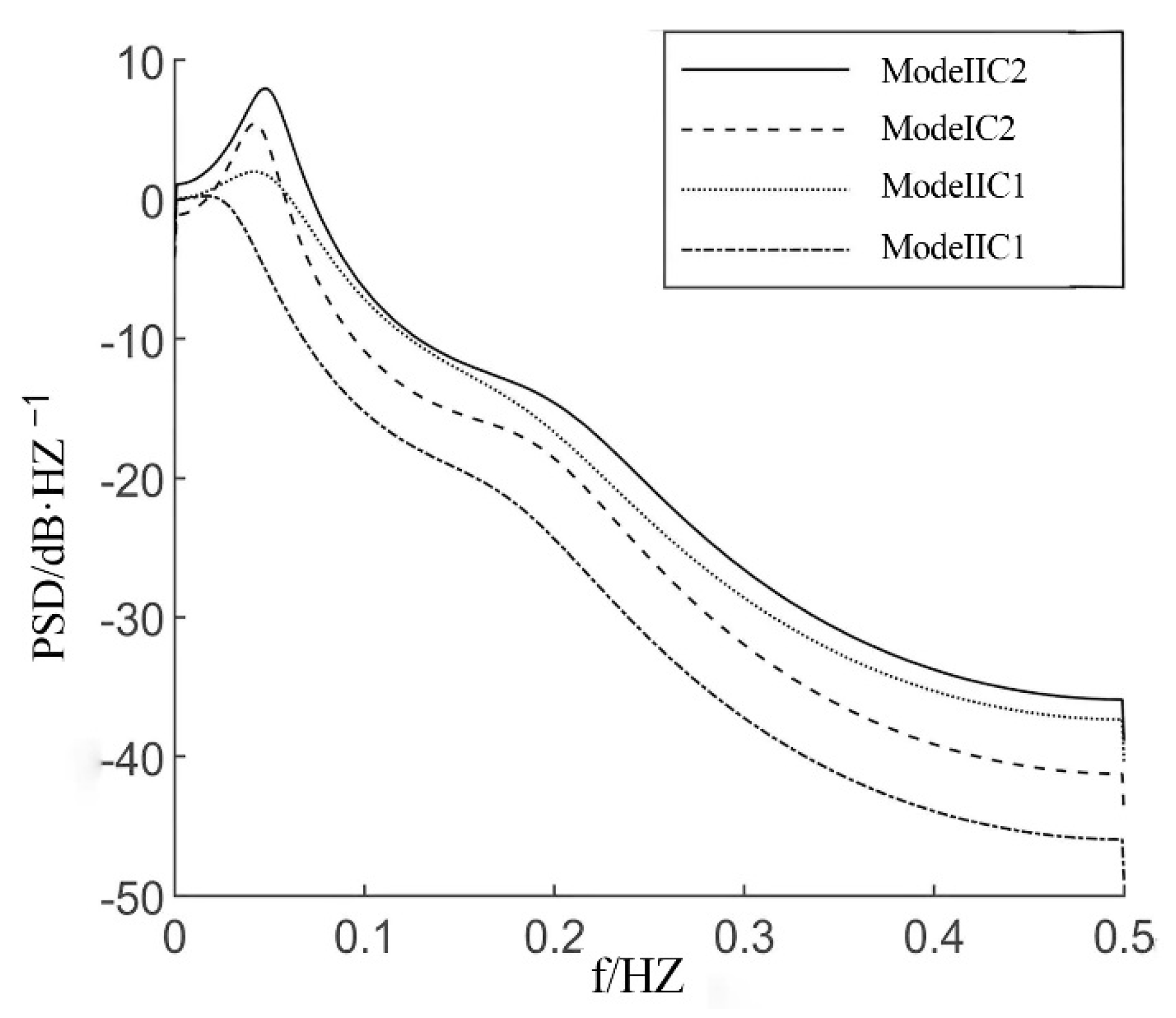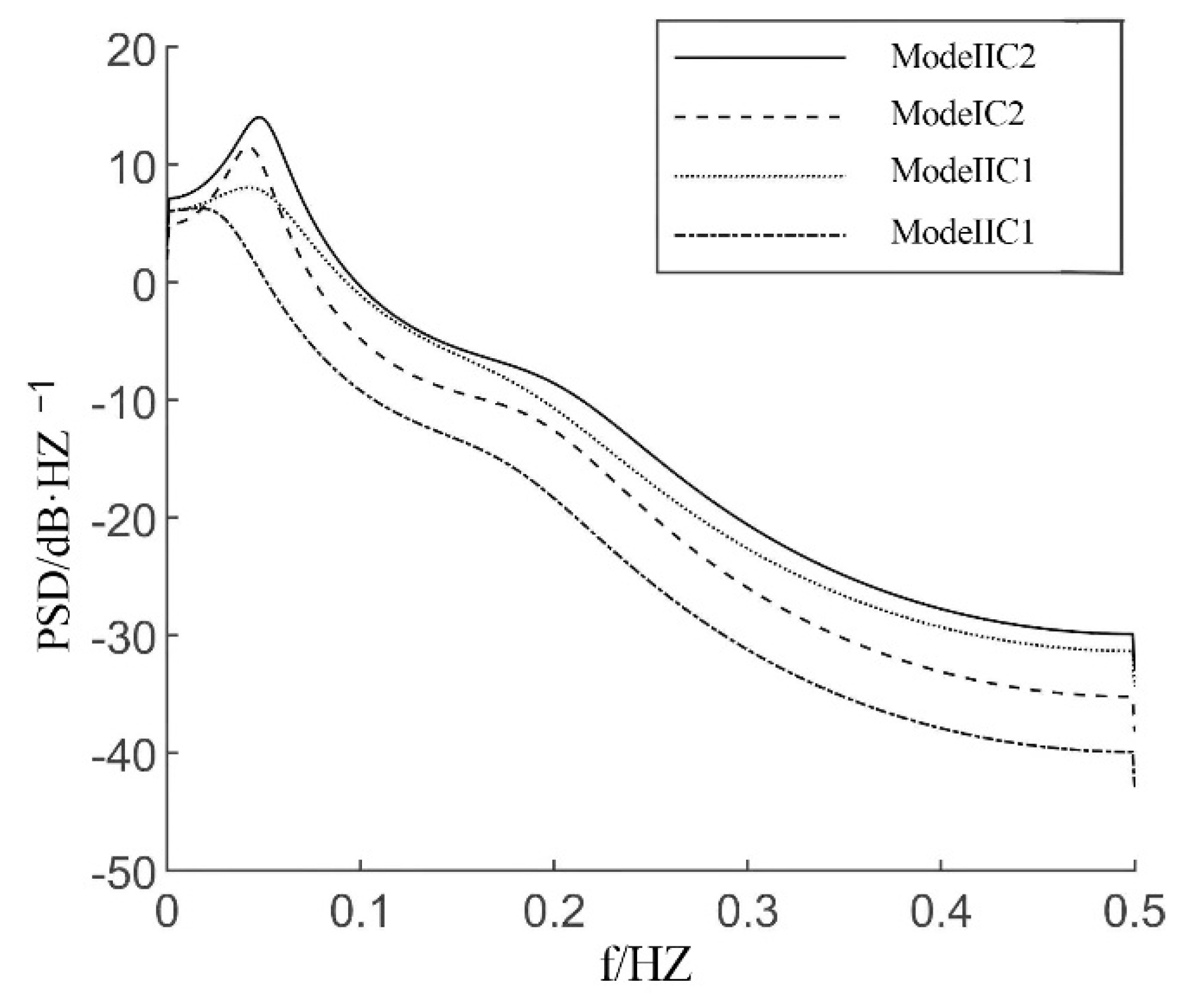Figure 14 shows the power spectral density of the acceleration of the vehicle body driving on Class C roads (for driving at the same acceleration (a = 3 ms⁻²) on Class C roads, $s_q\left(n_0\right)=256\times {10}^{-6}{\mathrm{m}}^3$), and Figure 15 shows the body acceleration power spectral density running under the conditions of Class B roads (for driving at the same acceleration (a = 3 ms⁻²) on Class B roads, $s_q\left(n_0\right)=64\times {10}^{-6}{\mathrm{m}}^3$). 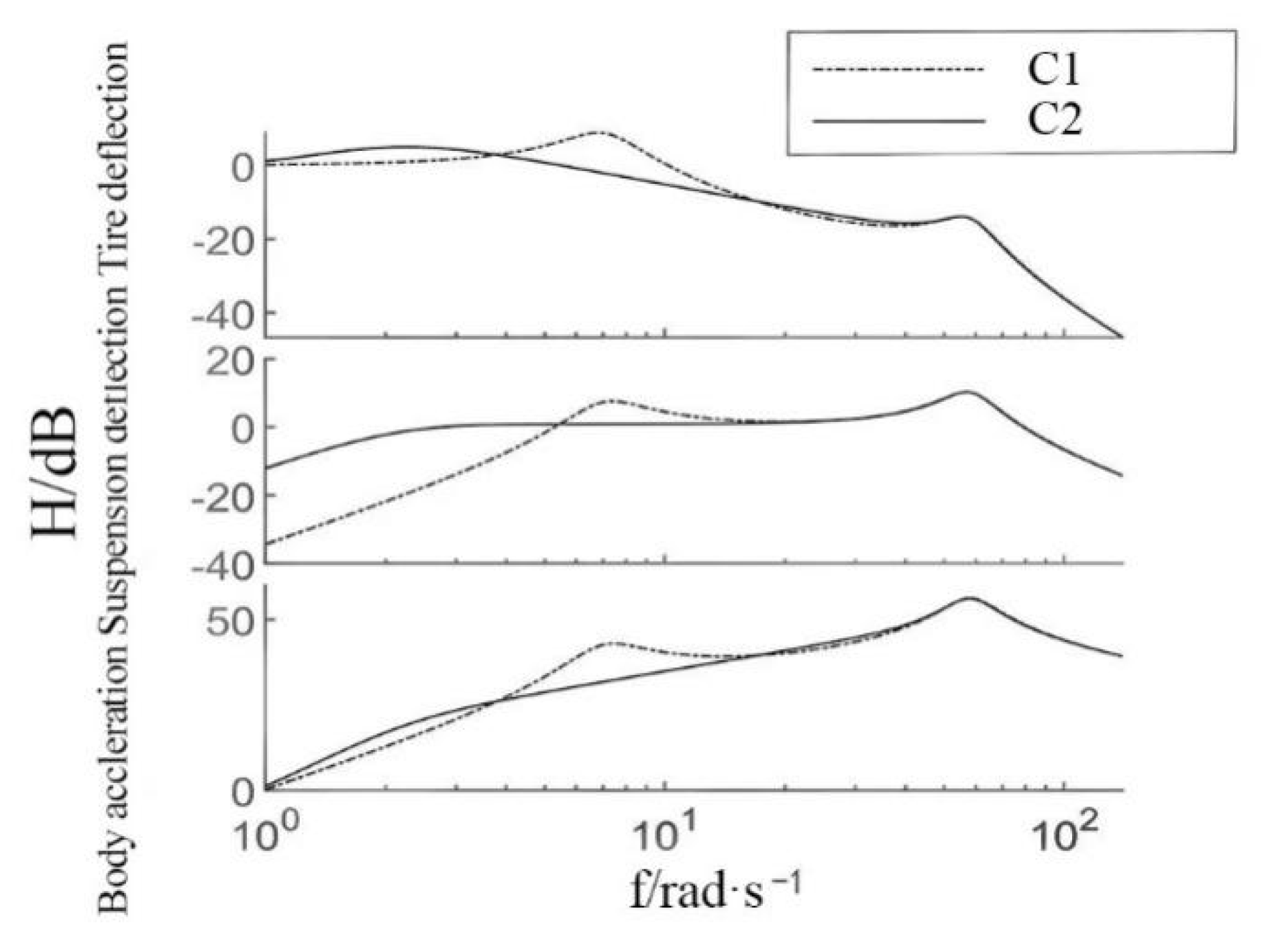In both cases, the robustness of the active suspension with the C1 controller is much better than that of the active suspension with the C2 control system. The peak value of the body acceleration of the active suspension with the C1 controller is 45% lower than that of the active suspension with the C2 control system.

Figure 16 shows the comparison results of the suspension dynamic deflection and the vehicle body vertical acceleration body diagram of the active suspension with the C1 controller and the active suspension with the C2 control system under road pulse input. The results showed that the active suspension with the C1 controller can significantly improve the amplitude–frequency characteristics of suspension deflection, especially in the low-frequency range of 0 to 16 Hz. In terms of body acceleration, in the low-frequency range, the body’s vertical acceleration significantly improves. The active suspension with the C2 control system reaches its first peak at around 8 Hz and is larger than that of the active suspension with the C1 controller. The body acceleration of the active suspension with the C1 controller is slowly increasing. At about 13 Hz, the second peak of the active suspension with the C1 controller and the active suspension with the C2 control system almost coincide. In the comparison, the suspension dynamic deflection of the active suspension with the C1 controller in the low-frequency range is lower than that of the active suspension with the C2 control system, and it has always been flat. At high frequencies, the dynamic deflection of the active suspension with the C2 control system tends to coincide. The research results showed that under the condition of parameter perturbation, the active suspension with the C1 controller has a much better ride comfort than the active suspension with the C2 control system, and the designed active suspension controller has good robustness.

5. Conclusions

In this study, a two-degree-of-freedom 1/4 suspension system parameter model was established, and an H∞ output feedback control strategy was proposed. Additionally, a solution to the control parameters of output feedback was expressed in the form of a Riccati equation. Under the multi-objective control framework, the optimal guaranteed output feedback control law that minimizes the body acceleration performance index was obtained to improve riding comfort. The simulation results demonstrated that this guaranteed output H∞ output feedback control has a lower peak vertical acceleration of the vehicle body, and two output indicators of the suspension dynamic deflection constraint and tire dynamic load constraint decline at different degrees, which improves vehicle-driving ride and meets the safety requirements of the suspension system. It was proven that this control strategy delivers an ideal control effect on active suspension and can be applied at a large scale.

There are also some shortcomings in the approach presented in this paper. The effects of input time-delay and the nonlinear factors were not considered. However, it is foreseeable that these factors will not affect the effectiveness of the controller design method proposed in this paper.