Abstract
Neutron stars host the strongest magnetic fields that we know of in the Universe. Their magnetic fields are the main means of generating their radiation, either magnetospheric or through the crust. Moreover, the evolution of the magnetic field has been intimately related to explosive events of magnetars, which host strong magnetic fields, and their persistent thermal emission. The evolution of the magnetic field in the crusts of neutron stars has been described within the framework of the Hall effect and Ohmic dissipation. Yet, this description is limited by the fact that the Maxwell stresses exerted on the crusts of strongly magnetised neutron stars may lead to failure and temperature variations. In the former case, a failed crust does not completely fulfil the necessary conditions for the Hall effect. In the latter, the variations of temperature are strongly related to the magnetic field evolution. Finally, sharp gradients of the star’s temperature may activate battery terms and alter the magnetic field structure, especially in weakly magnetised neutron stars. In this review, we discuss the recent progress made on these effects. We argue that these phenomena are likely to provide novel insight into our understanding of neutron stars and their observable properties.
1. Introduction
The magnetic field evolution has been a central topic in the study of the physics of neutron stars (NS). Even before their observational discovery [] it had been proposed that NSs host strong magnetic fields which lead to energy emission []. Shortly after the discovery of the first few tens of pulsars, it has been proposed that the distribution of their periods implies that the magnetic field evolves within time-scales of years []. Early studies of the conductivity of the crust of NS due to phonon scattering and impurities [] suggested decay times for the magnetic field to be at least of the order of years. These results were revised a few years later in more detailed calculations []. Despite the high thermal conductivity of the crust, their temperature is neither homogeneous nor isotropic, as heating is produced in regions where the electric currents are stronger and is primarily conducted along magnetic field lines. The impact of temperature gradients within the NS has been presented in [,], where it has been proposed that the magnetic field of NSs can be created due to Biermann battery effects []. The effect of Hall drift in addition to Ohmic decay was discussed in [], who proposed that the decay of the magnetic field is mediated by Hall drift. In the seminal work of [] three main effects have been proposed to operate in NSs affecting the evolution and eventual decay of the magnetic field: Ohmic decay, Hall drift and ambipolar diffusion. The Ohmic decay is due to the finite conductivity of the crust of the NS, which leads to dissipation of the magnetic field and conversation of energy into thermal power [,,]. Hall drift is related to the presence of free electrons in the crust which carry the electric current while the ion lattice remains rigid, thus, any Lorentz force remains in equilibrium due to crust elasticity. Finally, ambipolar diffusion is caused by the interaction of the charged particles with the abundant neutrons, leading to the dissipation of the currents.
This has motivated several studies aiming to understand the dynamics of magnetic field evolution. Moreover, the discovery of Anomalous X-ray Pulsars (AXPs) and Soft Gamma-ray Repeaters (SGRs) [,,,,,], comprising the magnetar population [,,,], has generated a large interest in the overall evolution of the magnetic field in NSs, as in such sources, it is not the rotational kinetic energy loss rate that dominates, but rather the magnetic field decay. The main aims of these studies are to provide a mechanism for the efficient conversion of magnetic field energy into heat and to study the possibility of instabilities that could lead to explosive events. This is because the magnetic field energy reservoir can provide sufficient heat, and power the luminosity of these objects [,,,]. Therefore, their persistent emission can be attributed to their magnetic field. Furthermore, these strong magnetic fields can trigger explosive events which are observed in the forms of bursts, outbursts and flares [,].
The interplay between the Hall effect and Ohmic decay has been explored in detail using analytical and numerical techniques [,,,,,,,,,,,,,,,,,,,,]. Apart from the isotropic conductivity of the lattice, pasta phases such as rods, slabs, tubes and bubbles, appearing at the base of the crust, where the nuclear forces and charge screening play an important role lead to enhancements of the resistivity and changes to its overall properties [,]. These models have successfully addressed observational properties of NSs and they have revealed, moreover, rich effects in terms of magnetohydrodynamical evolution, arising from the non-linear nature of the equations. These effects include instabilities and turbulent cascades and are of broader applications within the realm of magnetohydrodynamics [,,,,,,,,,,,,,,,].
The assumption of Hall and Ohmic evolution as formulated in [] is valid for NSs whose magnetic field is moderately strong. NSs with very strong magnetic fields are susceptible to crust failure, as deformations beyond the crust elastic limit lead to permanent deformation [,,,,,,,,]. Thus, the assumption of a rigid crust that can absorb the stresses induced by the magnetic field and maintain its equilibrium does not hold any more. The failure of the crust may be due to magnetic field strength and be associated to magnetar activity [,,,] or even due to binary interaction [,,]. Therefore, in the regime of strong magnetic fields, the crust of the NS can no longer be treated as a rigid background and the description due to the Hall effect should be complimented to account for these effects.
The evolution of the magnetic field in NSs with weaker fields, on the contrary, is not dominated by the Hall effect, as the associated timescale is much longer. In this regime other causes of magnetic field evolution may be critical such as Biermann Battery. Independently of the magnetic field strength, thermal anisotropies can lead to interplay between magnetic and thermal terms in the evolution and drive magnetic field evolution. The electric conductivity increases when NS cools down and phonons do not contribute to the resistivity anymore [,]. Moreover, deeper in the crust, the effects of ambipolar diffusion become critical where the electric currents interacts, yet as this effect is mostly relevant to the physics of the NS core, it will not be discussed in detail in this review.
The aim of this review is to present the conditions under which the Hall effect is no longer dominant in the crust of NSs, and also the evolution regimes dominating beyond the Hall effect. In particular, we will be focusing on the effects of plastic evolution, magnetothermal evolution and battery effects.
In Section 2 we present the basic theory of the Hall-Ohmic evolution and the region of applicability. In Section 3 we present the effect of Plastic evolution. In Section 4 we present the effects related to magneto-thermal evolution and, in particular, the thermal battery effects are addressed in Section 5. We conclude in Section 6.
2. Hall-Ohmic Evolution
The crust of a NS comprises an ion lattice and free electrons while neutrons become abundant at densities deeper than the neutron drip point marking the transition from the outer to the inner crust []. The electrons have the freedom to move within the crust and are the carriers of the electric current. On the contrary, ions stay at fixed locations, as long as the crust remains rigid. This allows a single fluid MHD-description, with a direct relation between the electric current and the electron fluid velocity. The rigidity of the ion lattice is sustained provided that the crust remains within its elastic limit in terms of the deformations that are due to the stresses acting upon the crust. Therefore, the momentum equation is identically satisfied and the evolution of the system is described through the following Hall-Ohmic induction equation:
where is the magnetic field, e is the electron charge, is the electron number density, is the electric conductivity and c is the speed of light. The first term on the right hand side is the Hall term, describing the advection of the magnetic field by the electron fluid, while the second one is the Ohmic dissipation term. While the Hall term is conservative, it facilitates and accelerates magnetic field decay, as it leads to the formation of small-scale structures, which dissipate faster due to Ohmic decay. The above equation is a non-linear partial differential equation which bears some resemblance to the vorticity equation from fluid dynamics. This has motivated several works studying the effects of electron-MHD turbulence [,,,]. A remarkable effect that differentiates the electron-MHD evolution from the typical fluid turbulence is the fact that while a turbulent spectrum develops, the temporal evolution freezes-out and the field maintains its structure, attaining a Hall-attractor state [].
The implications of Hall evolution in NSs crusts have been rather profound. First, it has been shown that the magnetic field evolves faster once its strength is higher. Thus, magnetars, not only have a larger reservoir of magnetic energy, but they convert it faster into heat. This effect can be directly related to the steep dependence of the X-ray bolometric power on the dipole magnetic field strength [,,]. Second, the magnetic field evolution is rapid in young NSs and results in explosive events. The evolution later saturates, leading to the dichotomy between magnetars and older NSs shining in X-rays [,,]. Third, the magnetic field evolution leaves its imprint on the timing evolution of NSs, either in the form of enhanced noise, or through their braking indices [,,,,,,]. Fourth, the evolution of the magnetic field leads to the spontaneous formations of spots, arcades and multipolar structures [,,,,] which have been related to magnetars and have been directly observed in several NSs, either directly or as spectral features [,,,,]. Fifth, apart from the obvious connection to strongly magnetised NSs, the Hall effect has been related to Central Compact Objects [,,,,,,], in the scenario of the re-emergence of the buried magnetic field. In this context, the magnetic field has been buried following the formation of the NS, and while it provides heat so that the star shines in X-rays, its dipole strength is relatively weak [,,,,]. Finally, the role of the Hall effect has been central in the study of the entire NS population. The magnetic field evolution has been a major ingredient of the grand unification of NSs [,,].
Therefore, the detailed study of the magnetic field evolution due to the Hall effect has been proven fruitful and successful. It has not only provided a rich range of effects from a theoretical perspective, but it has also led to direct applications to observable properties of NSs, not only in the range of the strongly magnetised ones but across the entire NS population.
3. Plastic Evolution
The plethora of explosive events accompanying strongly magnetised NSs is strong evidence of the rapid and drastic changes happening in NSs. The various scaling relations between the magnetic field strength and the intensity of the X-ray bolometric luminosity and the power emitted in outbursts [] is evident that these phenomena are driven by the magnetic field. The energy emitted in explosive events [,,] can be stored in the form of twisted field lines in the magnetosphere and released through explosive reconnection [,,,,,,,,,,,,,,,]. Alternatively, the energy can be stored within the crust directly in the form of magnetic field energy or elastic energy due to the deformation caused by the magnetic field [,,,,,,,]. An explosive event in the latter case can occur if the crust becomes deformed beyond its elastic limit. The details of the evolution of the magnetic field once the crust has failed depend strongly on the properties of the crust and the exact process following the crust failure. We can obtain a generic view of the evolution of a failed crust through the Navier-Stokes equation []:
where is the density, is the plastic flow velocity, P is the pressure, is the gravitational potential, is the viscosity and is the elastic stress tensor. In the above equation the gravitational potential gradient and the radial pressure gradient are by far the strongest terms, and considering a stably stratified crust, they would not lead to radial velocities once perturbed by the other terms. Possibly, a strong magnetic field and rapid rotation may lead to deformation from spherical symmetry. Moreover, the plastic flow velocity is anticipated to be slow, thus the quadratic term and the acceleration terms can be safely neglected. As the crust is incompressible, the continuity equation reduces to the following expression for the velocity:
The momentum equation can be further simplified if one considers the fact that the crust freezes in a stressed state determined by the initial magnetic field. As the magnetic field evolves, the amount of stress exerted onto the crust changes, and it could lead to deformations exceeding the elastic limit. In this case, the failed crust will adopt a plastic flow caused by the excess stress compared to the initial state which we set a reference state. An important aspect is that the diagonal terms of the stress tensor (volumetric), are related to compression of the crust, whereas the off-diagonal ones (deviatoric) are relevant to shearing terms. Thus, the relevant part of the Maxwell stress tensor that leads to crust failure is the following:
where is the i-th component of the magnetic field, and is the Kronecker delta. As the plastic flow is rather constrained, and the evolutionary time-scale is long compared to the dynamical time-scale, the momentum equation is satisfied for an appropriate velocity profile so that the viscous term equates the divergence of the difference between the current state and the reference state of the field []:
Consequently, the crust is no longer in a fully rigid state, for the Hall Equation (1) to hold. Nevertheless, a modification of the induction equation describes the magnetic field evolution:
where the plastic flow velocity is determined by Equation (5).
A further ingredient needed for the solution of the problem is the conditions under which the crust fails. The microphysics of the crust allows the determination of the critical value of , above which the crust is no longer in the elastic regime. This is implemented through the von Mises criterion:
where is the deviatoric part of the stress tensor, which for the Maxwell stresses takes the following form:
where is the reference magnetic field corresponding to the freezing state of the crust and is its current value.
The value can be determined by the microphysics of the crust, therefore, from Equation (8) one can find the regions where the crust fails. The failure is not necessarily concentrated only in the region determined by the von Mises criterion, but it can affect a larger fraction of the star [,]. Nevertheless, it is unlikely that a failure can affect the entire crust and it will be more likely a local phenomenon, with the probable exception of giant flares. Following that, the magnetic field evolution Equation (6) can be integrated and provide the value of the magnetic field throughout the evolution.
The value of as a function of the microphysical parameters is the following []:
where Z is the atomic number, the Coulomb parameter, the ion number density and the ion sphere radius. Using the above relation and the ratio of the Hall to the Ohmic timescales, it is possible to find the combinations of magnetic field strength and density, or equivalently radius, where the crust fails. Moreover, comparing the Hall and Ohmic timescales one can find the region in the parameter space where the field evolution is driven by the Hall effect and Ohmic decay. These results are summarized in Figure 1. It is evident that this effect is crucial near the surface of the star, as the value of drops drastically there, yet the strength of the magnetic is not substantially weaker [].
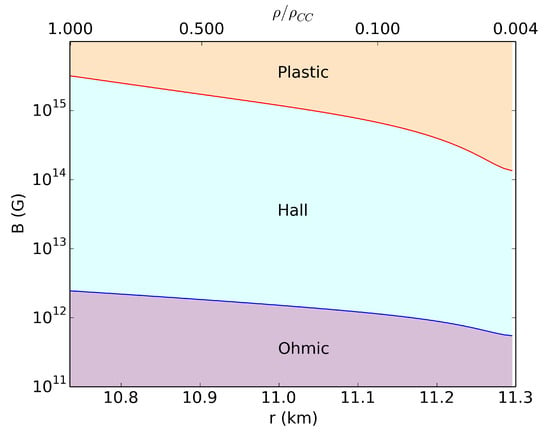
Figure 1.
Dominance of Plastic flow, Hall evolution and Ohmic decay as a function of the magnetic field strength and the radial distance from the centre. The left boundary starts at the crust-core interface and the right at the neutron drip point. Figure adapted from [].
Thus, these suffice for the solution of the magnetic field evolution equation. The results of these solutions have been presented recently describing the evolution of the magnetic field in stressed crusts flowing plastically [,,,,,]. An example is shown in Figure 2. The main conclusions are the following:
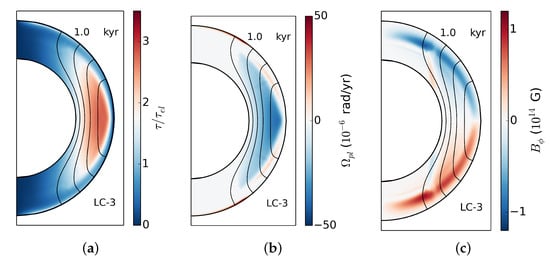
Figure 2.
Evolution with plastic flow of the magnetic field at age of 1 kyr. In these models a local failure is modelled. The black lines are the poloidal field lines. The crust has been expanded for for clarity, in reality it corresponds to of the stellar radius. In panel (a) the stresses that have been developed are shown, in panel (b) the plastic flow velocity and in panel (c) the toroidal field in the crust. Figure adapted from [].
- For strong magnentic fields, G, plastic flow occurs everywhere in the crust and large parts of the crust fail.
- For magnetic fields of strength G, plastic flow essentially shuts down.
- For magnetic fields between G, failure occurs sporadically in various crust regions.
- In general, plastic flow opposes the evolution generated by the Hall effect. Nevertheless, it does not completely annul the magnetic field evolution generated by the Hall effect, even under strong magnetic fields.
- The evolution is sensitive to the parameter of the plastic flow viscosity. A plastic viscosity of g cm s leads to velocities of 10–100 cm/yr.
- While plastic flow is a dissipative process, it does not expedite drastically the decay of the magnetic field as it opposes the creation of small-scale fields that would dissipate faster due to the Ohmic effect.
- The results are sensitive to the type of failure, whether it affects a small part of the crust (local failure) or a more extended one (global failure).
- Numerical simulations and analytical solutions have explored so far simple geometries: cartesian plane-parallel and axisymmetric ones. Thus, the full 3D evolution due to plastic flow may be complex than the results found so far.
4. Magneto-Thermal Evolution
Both electric current and thermal flux are transported by electrons in the NS crust. In a strong magnetic field, electrons can freely move along the magnetic field lines but their motion in the direction orthogonal to magnetic field lines is strongly suppressed. Thus, heat is easily transported only along the magnetic field lines. Therefore, two distant regions connected by field lines have the same temperature. On the contrary, two geometrically close regions separated by magnetic fields could have a large temperature difference.
The equation for heat transfer is written as follows
where T is the temperature, is the heat capacity, is the electron entropy and is the thermal conductivity tensor, which depends on the magnetic field strength and direction. The first term on the right-hand-side describes anisotropic heat transfer; the second term corresponds to heat released due to Ohmic losses in the NS crust and the last term is the thermopower one.
Even in the case of relatively simple magnetic field configuration such as the poloidal dipolar magnetic field, certain regions become thermally isolated from the NS core. In Figure 3 we show the temperature and magnetic field configuration inside the NS crust computed using the PARODY code [,,,,,,]. In Figure 4 we show the corresponding surface temperature distribution. We obtain these surface temperature distributions using the following simplified relation [] between the surface temperature and the temperature at the bottom of the envelope
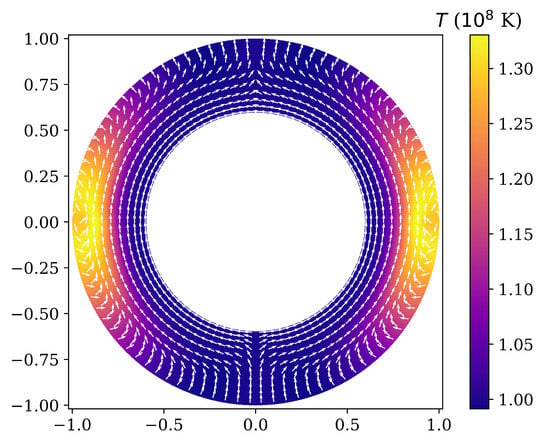
Figure 3.
Magneto-thermal structure in vertical slice of NS at age of 9 kyr. The initial magnetic field configuration consists of only a dipolar poloidal magnetic field. The orientation of the magnetic field is shown only in every 12th radial point and every 4th angular point. White arrows show the direction of magnetic field. The thickness of the NS crust is scaled up to show details of the magneto-thermal structure. The equatorial region is thermally isolated from the colder core.
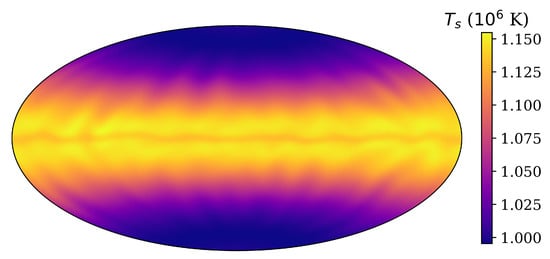
Figure 4.
Surface temperature distribution for NS at age 9 kyr. The initial magnetic field configuration consists of only dipolar poloidal magnetic field.
In this configuration the equatorial regions become thermally decoupled from the NS core. These regions could be heated due to the ohmic decay of the magnetic field creating a hot belt around the NSs. At the same time, these regions could also become colder than the polar regions due to the more efficient neutrino cooling and smaller heat capacity of the crust []. Therefore, the surface thermal distribution is strongly affected by magnetic field configuration in the NS crust. The surface temperature distribution is an important ingredient to model the quiescent emission of magnetars and eventually to probe their magnetic fields and emission properties; see for example a recent review [].
Moreover, the Hall evolution couples poloidal and toroidal magnetic fields. For example, in a case where the toroidal magnetic component is much stronger than the poloidal one, we observe the toroidal field instability [] that leads to a significant increase of small scale poloidal magnetic fields in the NS crust. Thus, this instability leaves footprints at surface temperature distribution. Namely, it leads to formation of long hot or cold filaments extending from the northern hemisphere to southern hemisphere; see example in Figure 5.
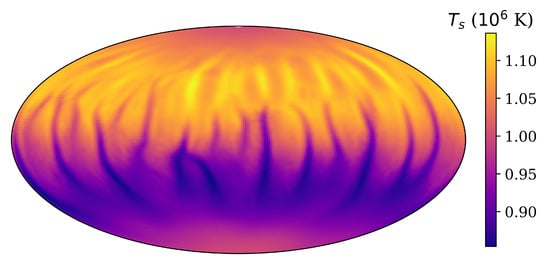
Figure 5.
Surface temperature distribution for a NS at age of 40 kyr. The initial magnetic field configuration consists of a dipolar poloidal magnetic field and a toroidal magnetic field which contains of the total magnetic energy.
It is quite uncertain at the moment what the exact initial conditions are for the internal magnetic fields of NSs. The initial magnetic fields could be large-scale (dipole or quadropole) or, instead, it could consists of a superposition of modes with length-scales comparable to the NS crust depth. Such configurations are predicted e.g., by models of stochastic dynamos []. On the other hand, it is thought that large scale magnetic fields are generated if the NS initially spins fast, with periods comparable to a few msec. In reality, initial periods of radio pulsars with strong fields G range from msec values to s [,].
In general, the large scale magnetic field creates the surface temperature distribution with hot and cold regions of relatively large size (typically comparable to half of the total surface). Typically, the surface thermal distributions produced in these cases have a high degree of axial symmetry. Only specific initial conditions, such as an addition of toroidal magnetic field inclined with respect to the poloidal component, could cause the appearance of relatively small hot regions []. Such a configuration could explain a large pulsed fraction (up to 50%) for thermal X-ray emission which is observed in some quiescent magnetars [].
In the case of stochastic dynamos, when the whole magnetic field consists mostly of small-scale fields, the surface temperature distribution becomes patchy with small hot and cold spots with typical size ∼1 km. At any orientation of the NS, a distant observer sees multiple hot and cold regions simultaneously. Therefore, their contribution averages out. This means that NSs with such a surface thermal distribution cannot produce a pulsed fraction above ≈10%. They could, however, contain significant internal magnetic energy. Thus, these NSs could emit more in thermal surface radiation than it is normally expected from NS of a similar age. Moreover, since the spin-down is caused by the dipolar component only, the field estimates based on measurements of the period and its derivative can be orders of magnitude lower than the actual maximum field value. Therefore such NSs with small-scale magnetic field provide a viable explanation for properties of central compact objects [,].
5. Battery Effects
As discussed in the previous section, the large conductivity in a NS crust makes so that its thermal structure and evolution tends to follow that of the magnetic field. This allows one to use the thermal structure of the crust as a direct and, to a certain extent, observable realisation of the Hall evolution. However, temperature itself affects the induction equation both through the thermal dependence of microphysical quantities (electric conductivity, electron relaxation time, etc.) and thermoelectric effects proper.
The latter appear in the presence of a temperature gradient, and are in general quite weak. The application of these mechanisms to compact object astrophysics dates back to Dolginov and Urpin [] (for white dwarfs) and Blandford et al. [] (who extended the analysis to NSs). Thermoelectric effects were studied with the Hall effect in great mathematical detail in a series of papers by Geppert and Wiebicke [,,,,,], which laid the foundations for many magnetothermal evolution models (e.g., [], see also Pons and Viganò [] for a review), but they ended up being quite overlooked in the last decades. However, the necessity of revisiting them more systematically has recently become apparent for at least two reasons: first, computational advancements [] showed that the thermal structure of a NS crust can be quite variegated; second, transient bursting phenomena are often linked to some sort of heat deposition in the crust other than the ohmic dissipation that locally enhance thermal gradients []. Although the exact mechanisms underlying these events are not fully understood, the strong temperature gradients they produce may be the source of the additional field. This is of particular interest in the context of highly magnetised environments, i.e., in the modelling of the transient activity of magnetars [].
The physics underlying thermoelectric effects is again encapsulated by the basic fact that electrons are the main carriers of both electric currents and thermal energy in a NS crust. Thus, a temperature gradient alters the charge balance, generating an electric field given by (e.g., [])
where the tensor G is the so called thermopower. In general, it is composed of an isotropic part (the Seebeck term)and of anisotropic one (the Ettingshausen-Nernst term); the simplest choice is to only consider the former, which for a completely degenerate Fermi gas gives ; this form has been used to write the last term in Equation (10). This electric field enters the induction Equation (1) as an additional term, so that it is able to generate a magnetic field; this process is known as the Biermann battery effect []. The Biermann battery is able to amplify to a great extent a small seed field, and as such is a popular mechanism to explain magnetic structure formation on cosmological scale (e.g., []) and in relativistic jets (e.g., []).
A realisation of an efficient battery effect in the crust of a NS can be expected in cases when strong temperature gradients are established by a mechanism not contained in the usual magnetothermal evolution equations. The energy source could still be the magnetic field itself, if it undergoes phenomena of reconnection, or come from external agents like accretion or backflowing magnetospheric currents. As a model of the latter case, Figure 6 shows the effect of heating a circular patch of radius ∼1 km in the outermost region of the crust with erg/s for a few years, until a quasi stationary state is reached. The initial state was that of a purely dipolar field, which had previously been evolved for ∼10 yr (see [] for more details). The additional temperature gradient builds up a sizeable magnetic field, which can be extrapolated to the low magnetosphere to give rise to small scale magnetic loops. Indeed, small scale magnetic loops have been invoked to explain the observed absorption features in some magnetars [], even though a comprehensive analysis of these phenomena in terms of battery effects has not been attempted as yet due to the numerical hindrances associated to it (see e.g., []).
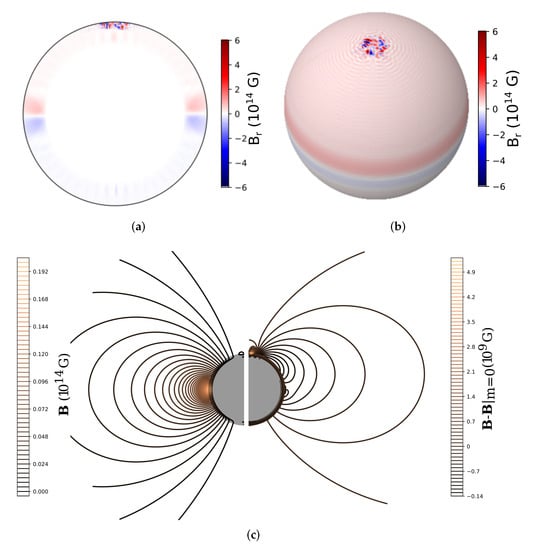
Figure 6.
Effect of the battery term after a episode of heat injection in a small patch of the crust. Panel (a): the radial component of the magnetic field shown in a cut along the prime meridian (crust width for visualisation); Panel (b): shown on a projection of the surface; Panel (c): magnetic field lines in the magnetosphere obtained by continuation of the boundary condition . The right half shows the lines of the asymmetric component on the prime meridian, obtained by subtracting the component which is dominated by the dipolar field. Figure adapted from [], Copyright AAS. Reproduced with permission.
6. Conclusions
When the crucial role of the magnetic field in the physics of NSs was assessed, it was modelled as a dipolar field, unchanged for the entire life of the star. It was soon realised that the role of Ohmic decay on astrophysically relevant timescales was crucial, establishing the idea that the field may indeed evolve. Models then turned to the Hall effect that, while not dissipating the field, is able to alter it and enhance Ohmic decay. The study of the impact of the Hall effect in the magnetic field evolution of NSs has been a successful endeavour. It has resolved many questions related to the nature of NSs, observable quantities, and it has also motivated studies in the areas of Applied Mathematics, fluid dynamics and computational physics. Yet, some of the physical assumptions postulated for the development of Hall-Ohmic equations may not hold in their entirety, especially in the most extreme cases, either in the NSs with the strongest magnetic fields, the hottest ones, or the ones with sharp temperature gradients.
In this review, we have focused on effects that are beyond the standard Hall evolution in the crust. Namely, we have studied the impact of the effects of a plastic flow once the magnetic field is substantially strong so that the crust fails, the magneto-thermal evolution, where the interplay of the heat released by the Ohmic decay and its transport mediated by the magnetic field are discussed and battery effects, arising from temperature gradients. We have shown that these phenomena widely enrich the evolutionary paths of the magnetic field and their observable appearance. We remark that, while great progress has been made so far, there are still areas for progress. Plastic flows have been studied only in axisymmetric and plane-parallel cartesian geometries, and a full 3D model is yet to be resolved. The magnetothermal evolution has been implemented in 3D studies, nevertheless, the huge parameter space of microphysical properties, such as variations of the thermal and electric conductivities, is still to be explored. Finally, battery effects have been studied in a small subset of cases and they clearly deserve a more detailed exploration of the many different mechanisms that can generate temperature gradients. We strongly believe that such studies will widen the horizons and pave the way for a clear comprehension of NSs, both in terms of their phenomenology and of their use as benchmarks for fundamental physics applications.
Author Contributions
Conceptualization, K.N.G., D.D.G. and A.I.; writing—original draft preparation, K.N.G., D.D.G. and A.I.; writing—review and editing, K.N.G., D.D.G. and A.I. All authors have read and agreed to the published version of the manuscript.
Funding
K.N.G. acknowledges funding from grant FK 81641 “Theoretical and Computational Astrophysics”, ELKE. A.I. acknowledges funding from STFC grant no. ST/S000275/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Numerical data related to this study are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Pacini, F. Energy Emission from a Neutron Star. Nature 1967, 216, 567–568. [Google Scholar] [CrossRef]
- Pacini, F. Magnetic Field Decay in a Neutron Star and the Distribution of Pulsar Periods. Nature 1969, 224, 160. [Google Scholar] [CrossRef]
- Ewart, G.M.; Guyer, R.A.; Greenstein, G. Electrical conductivity and magnetic field decay in neutron stars. Astrophys. J. 1975, 202, 238–247. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Urpin, V.A. Thermal and Electrical Conductivity in White Dwarfs and Neutron Stars. Sov. Astronom. 1980, 24, 303. [Google Scholar]
- Urpin, V.A.; Yakovlev, D.G. Thermogalvanomagnetic Effects in White Dwarfs and Neutron Stars. Sov. Astronom. 1980, 24, 425. [Google Scholar]
- Blandford, R.D.; Applegate, J.H.; Hernquist, L. Thermal origin of neutron star magnetic fields. Mon. Not. R. Astron. Soc. 1983, 204, 1025–1048. [Google Scholar] [CrossRef]
- Biermann, L. Über den Ursprung der Magnetfelder auf Sternen und im interstellaren Raum (miteinem Anhang von A. Schlüter). Zeitschrift Naturforschung Teil A 1950, 5, 65. [Google Scholar]
- Jones, P.B. Neutron star magnetic field decay—Hall drift and Ohmic diffusion. Mon. Not. R. Astron. Soc. 1988, 233, 875–885. [Google Scholar] [CrossRef]
- Goldreich, P.; Reisenegger, A. Magnetic Field Decay in Isolated Neutron Stars. Astrophys. J. 1992, 395, 250. [Google Scholar] [CrossRef]
- Haensel, P.; Urpin, V.A.; Yakovlev, D.G. Ohmic decay of internal magnetic fields in neutron stars. Astron. Astrophys. 1990, 229, 133–137. [Google Scholar]
- Miralles, J.A.; Urpin, V.; Konenkov, D. Joule Heating and the Thermal Evolution of Old Neutron Stars. Astrophys. J. 1998, 503, 368–373. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Yakovlev, D.G.; Potekhin, A.Y.; Shibazaki, N.; Shternin, P.S.; Gnedin, O.Y. Magnetars as cooling neutron stars with internal heating. Mon. Not. R. Astron. Soc. 2006, 371, 477–483. [Google Scholar] [CrossRef]
- Mazets, E.P.; Golentskii, S.V.; Ilinskii, V.N.; Aptekar, R.L.; Guryan, I.A. Observations of a flaring X-ray pulsar in Dorado. Nature 1979, 282, 587–589. [Google Scholar] [CrossRef]
- Fahlman, G.G.; Gregory, P.C. An X-ray pulsar in SNR G109.1-1.0. Nature 1981, 293, 202–204. [Google Scholar] [CrossRef]
- Laros, J.G.; Fenimore, E.E.; Klebesadel, R.W.; Atteia, J.L.; Boer, M.; Hurley, K.; Niel, M.; Vedrenne, G.; Kane, S.R.; Kouveliotou, C.; et al. A New Type of Repetitive Behavior in a High-Energy Transient. Astrophys. J. Lett. 1987, 320, L111. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Norris, J.P.; Cline, T.L.; Dennis, B.R.; Desai, U.D.; Orwig, L.E.; Fenimore, E.E.; Klebesadel, R.W.; Laros, J.G.; Atteia, J.L.; et al. SMM Hard X-Ray Observations of the Soft Gamma-Ray Repeater 1806-20. Astrophys. J. Lett. 1987, 322, L21. [Google Scholar] [CrossRef]
- Gavriil, F.P.; Kaspi, V.M.; Woods, P.M. Magnetar-like X-ray bursts from an anomalous X-ray pulsar. Nature 2002, 419, 142–144. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Gavriil, F.P.; Woods, P.M.; Jensen, J.B.; Roberts, M.S.E.; Chakrabarty, D. A Major Soft Gamma Repeater-like Outburst and Rotation Glitch in the No-longer-so-anomalous X-Ray Pulsar 1E 2259+586. Astrophys. J. Lett. 2003, 588, L93–L96. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Heyl, J.S.; Kulkarni, S.R. How Common Are Magnetars? The Consequences of Magnetic Field Decay. Astrophys. J. Lett. 1998, 506, L61–L64. [Google Scholar] [CrossRef]
- Kaspi, V.M. Grand unification of neutron stars. Proc. Natl. Acad. Sci. USA 2010, 107, 7147–7152. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Beloborodov, A.M. Magnetars. Annu. Rev. Astron. Astrophys. 2017, 55, 261–301. [Google Scholar] [CrossRef]
- Pérez-Azorín, J.F.; Miralles, J.A.; Pons, J.A. Thermal radiation from magnetic neutron star surfaces. Astron. Astrophys. 2005, 433, 275–283. [Google Scholar] [CrossRef][Green Version]
- Pons, J.A.; Link, B.; Miralles, J.A.; Geppert, U. Evidence for Heating of Neutron Stars by Magnetic-Field Decay. Phys. Rev. Lett. 2007, 98, 071101. [Google Scholar] [CrossRef] [PubMed]
- Urpin, V.; Konenkov, D. Joule heating in high magnetic field pulsars. Astron. Astrophys. 2008, 483, 223–230. [Google Scholar] [CrossRef][Green Version]
- Gusakov, M.E.; Kantor, E.M.; Ofengeim, D.D. Evolution of the magnetic field in neutron stars. Phys. Rev. D 2017, 96, 103012. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Esposito, P. Strongly Magnetized Pulsars: Explosive Events and Evolution. In Astrophysics and Space Science Library; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2018; Volume 457, p. 57. [Google Scholar] [CrossRef]
- Esposito, P.; Rea, N.; Israel, G.L. Magnetars: A Short Review and Some Sparse Considerations. In Astrophysics and Space Science Library; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, pp. 97–142. [Google Scholar] [CrossRef]
- Shalybkov, D.A.; Urpin, V.A. The Hall effect and the decay of magnetic fields. Astron. Astrophys. 1997, 321, 685–690. [Google Scholar]
- Hollerbach, R.; Rüdiger, G. The influence of Hall drift on the magnetic fields of neutron stars. Mon. Not. R. Astron. Soc. 2002, 337, 216–224. [Google Scholar] [CrossRef]
- Rheinhardt, M.; Geppert, U. Hall-Drift Induced Magnetic Field Instability in Neutron Stars. Phys. Rev. Lett. 2002, 88, 101103. [Google Scholar] [CrossRef]
- Cumming, A.; Arras, P.; Zweibel, E. Magnetic Field Evolution in Neutron Star Crusts Due to the Hall Effect and Ohmic Decay. Astrophys. J. 2004, 609, 999–1017. [Google Scholar] [CrossRef]
- Hollerbach, R.; Rüdiger, G. Hall drift in the stratified crusts of neutron stars. Mon. Not. R. Astron. Soc. 2004, 347, 1273–1278. [Google Scholar] [CrossRef]
- Reisenegger, A.; Benguria, R.; Prieto, J.P.; Araya, P.A.; Lai, D. Hall drift of axisymmetric magnetic fields in solid neutron-star matter. Astron. Astrophys. 2007, 472, 233–240. [Google Scholar] [CrossRef]
- Pons, J.A.; Geppert, U. Magnetic field dissipation in neutron star crusts: From magnetars to isolated neutron stars. Astron. Astrophys. 2007, 470, 303–315. [Google Scholar] [CrossRef]
- Viganò, D.; Pons, J.A.; Miralles, J.A. A new code for the Hall-driven magnetic evolution of neutron stars. Comput. Phys. Commun. 2012, 183, 2042–2053. [Google Scholar] [CrossRef][Green Version]
- Kojima, Y.; Kisaka, S. Magnetic field decay with Hall drift in neutron star crusts. Mon. Not. R. Astron. Soc. 2012, 421, 2722–2730. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Cumming, A.; Reisenegger, A.; Armaza, C.; Lyutikov, M.; Valdivia, J.A. Hall equilibria with toroidal and poloidal fields: Application to neutron stars. Mon. Not. R. Astron. Soc. 2013, 434, 2480–2490. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Cumming, A. Hall effect in neutron star crusts: Evolution, endpoint and dependence on initial conditions. Mon. Not. R. Astron. Soc. 2014, 438, 1618–1629. [Google Scholar] [CrossRef]
- Wood, T.S.; Hollerbach, R. Three Dimensional Simulation of the Magnetic Stress in a Neutron Star Crust. Phys. Rev. Lett. 2015, 114, 191101. [Google Scholar] [CrossRef] [PubMed]
- Gourgouliatos, K.N.; Wood, T.S.; Hollerbach, R. Magnetic field evolution in magnetar crusts through three-dimensional simulations. Proc. Natl. Acad. Sci. USA 2016, 113, 3944–3949. [Google Scholar] [CrossRef]
- Elfritz, J.G.; Pons, J.A.; Rea, N.; Glampedakis, K.; Viganò, D. Simulated magnetic field expulsion in neutron star cores. Mon. Not. R. Astron. Soc. 2016, 456, 4461–4474. [Google Scholar] [CrossRef][Green Version]
- Popov, S.B.; Igoshev, A.P.; Taverna, R.; Turolla, R. Looking for Hall attractor in astrophysical sources. J. Phys. Conf. Ser. 2017, 932, 012048. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Hollerbach, R.; Archibald, R.F. Modelling neutron star magnetic fields. Astron. Geophys. 2018, 59, 5.37–5.42. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Hollerbach, R. Magnetic Axis Drift and Magnetic Spot Formation in Neutron Stars with Toroidal Fields. Astrophys. J. 2018, 852, 21. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D. Magnetic, thermal and rotational evolution of isolated neutron stars. Living Rev. Comput. Astrophys. 2019, 5, 3. [Google Scholar] [CrossRef]
- Brandenburg, A. Hall Cascade with Fractional Magnetic Helicity in Neutron Star Crusts. Astrophys. J. 2020, 901, 18. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Hollerbach, R.; Igoshev, A.P. Powering central compact objects with a tangled crustal magnetic field. Mon. Not. R. Astron. Soc. 2020, 495, 1692–1699. [Google Scholar] [CrossRef]
- Viganò, D.; Garcia-Garcia, A.; Pons, J.A.; Dehman, C.; Graber, V. Magneto-thermal evolution of neutron stars with coupled Ohmic, Hall and ambipolar effects via accurate finite-volume simulations. Comput. Phys. Commun. 2021, 265, 108001. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D.; Rea, N. A highly resistive layer within the crust of X-ray pulsars limits their spin periods. Nat. Phys. 2013, 9, 431–434. [Google Scholar] [CrossRef]
- Xia, C.J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Zhang, Y.X. Nuclear pasta structures and symmetry energy. Phys. Rev. C 2021, 103, 055812. [Google Scholar] [CrossRef]
- Biskamp, D.; Schwarz, E.; Zeiler, A.; Celani, A.; Drake, J.F. Electron magnetohydrodynamic turbulence. Phys. Plasmas 1999, 6, 751–758. [Google Scholar] [CrossRef]
- Rheinhardt, M.; Konenkov, D.; Geppert, U. The occurrence of the Hall instability in crusts of isolated neutron stars. Astron. Astrophys. 2004, 420, 631–645. [Google Scholar] [CrossRef]
- Wareing, C.J.; Hollerbach, R. Forward and inverse cascades in decaying two-dimensional electron magnetohydrodynamic turbulence. Phys. Plasmas 2009, 16, 042307. [Google Scholar] [CrossRef]
- Wareing, C.J.; Hollerbach, R. Hall cascades versus instabilities in neutron star magnetic fields. Astron. Astrophys. 2009, 508, L39–L42. [Google Scholar] [CrossRef]
- Cho, J.; Lazarian, A. Simulations of Electron Magnetohydrodynamic Turbulence. Astrophys. J. 2009, 701, 236–252. [Google Scholar] [CrossRef]
- Pons, J.A.; Miralles, J.A.; Geppert, U. Magneto-thermal evolution of neutron stars. Astron. Astrophys. 2009, 496, 207–216. [Google Scholar] [CrossRef]
- Wareing, C.J.; Hollerbach, R. Cascades in decaying three-dimensional electron magnetohydrodynamic turbulence. J. Plasma Phys. 2010, 76, 117–128. [Google Scholar] [CrossRef]
- Pons, J.A.; Geppert, U. Confirmation of the occurrence of the Hall instability in the non-linear regime. Astron. Astrophys. 2010, 513, L12. [Google Scholar] [CrossRef]
- Marchant, P.; Reisenegger, A.; Valdivia, J.A.; Hoyos, J.H. Stability of Hall Equilibria in Neutron Star Crusts. Astrophys. J. 2014, 796, 94. [Google Scholar] [CrossRef]
- Wood, T.S.; Hollerbach, R.; Lyutikov, M. Density-shear instability in electron magneto-hydrodynamics. Phys. Plasmas 2014, 21, 052110. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Kondić, T.; Lyutikov, M.; Hollerbach, R. Magnetar activity via the density-shear instability in Hall-MHD. Mon. Not. R. Astron. Soc. 2015, 453, L93–L97. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Hollerbach, R. Resistive tearing instability in electron MHD: Application to neutron star crusts. Mon. Not. R. Astron. Soc. 2016, 463, 3381–3389. [Google Scholar] [CrossRef]
- Kitchatinov, L.L. Double Hall instability: A catalyzer of magnetic energy release. Astron. Lett. 2017, 43, 624–633. [Google Scholar] [CrossRef][Green Version]
- Gourgouliatos, K.N.; Pons, J.A. Nonaxisymmetric Hall instability: A key to understanding magnetars. Phys. Rev. Res. 2019, 1, 032049. [Google Scholar] [CrossRef]
- Kitchatinov, L. Stability of a force-free Hall equilibrium and release of magnetic energy. Astron. Nachrichten 2019, 340, 475–482. [Google Scholar] [CrossRef]
- Kitchatinov, L. Hall instability: Origin, properties and asymptotic theory for its tearing mode. J. Plasma Phys. 2021, 87, 905870404. [Google Scholar] [CrossRef]
- Ruderman, M. Neutron Star Crustal Plate Tectonics. III. Cracking, Glitches, and Gamma-Ray Bursts. Astrophys. J. 1991, 382, 587. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Kadau, K. Breaking Strain of Neutron Star Crust and Gravitational Waves. Phys. Rev. Lett. 2009, 102, 191102. [Google Scholar] [CrossRef]
- Chugunov, A.I.; Horowitz, C.J. Breaking stress of neutron star crust. Mon. Not. R. Astron. Soc. 2010, 407, L54–L58. [Google Scholar] [CrossRef]
- Baiko, D.A. Shear modulus of neutron star crust. Mon. Not. R. Astron. Soc. 2011, 416, 22–31. [Google Scholar] [CrossRef]
- Hoffman, K.; Heyl, J. Mechanical properties of non-accreting neutron star crusts. Mon. Not. R. Astron. Soc. 2012, 426, 2404–2412. [Google Scholar] [CrossRef][Green Version]
- Chugunov, A.I.; Horowitz, C.J. Durabiity of Neutron Star Crust. Contrib. Plasma Phys. 2012, 52, 122–125. [Google Scholar] [CrossRef]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Baiko, D.A.; Chugunov, A.I. Breaking properties of neutron star crust. Mon. Not. R. Astron. Soc. 2018, 480, 5511–5516. [Google Scholar] [CrossRef]
- Giliberti, E.; Cambiotti, G.; Antonelli, M.; Pizzochero, P.M. Modelling strains and stresses in continuously stratified rotating neutron stars. Mon. Not. R. Astron. Soc. 2020, 491, 1064–1078. [Google Scholar] [CrossRef]
- Pons, J.A.; Perna, R. Magnetars versus High Magnetic Field Pulsars: A Theoretical Interpretation of the Apparent Dichotomy. Astrophys. J. 2011, 741, 123. [Google Scholar] [CrossRef][Green Version]
- Perna, R.; Pons, J.A. A Unified Model of the Magnetar and Radio Pulsar Bursting Phenomenology. Astrophys. J. Lett. 2011, 727, L51. [Google Scholar] [CrossRef]
- Dehman, C.; Viganò, D.; Rea, N.; Pons, J.A.; Perna, R.; Garcia-Garcia, A. On the Rate of Crustal Failures in Young Magnetars. Astrophys. J. Lett. 2020, 902, L32. [Google Scholar] [CrossRef]
- De Grandis, D.; Turolla, R.; Wood, T.S.; Zane, S.; Taverna, R.; Gourgouliatos, K.N. Three-dimensional Modeling of the Magnetothermal Evolution of Neutron Stars: Method and Test Cases. Astrophys. J. 2020, 903, 40. [Google Scholar] [CrossRef]
- Tsang, D.; Read, J.S.; Hinderer, T.; Piro, A.L.; Bondarescu, R. Resonant Shattering of Neutron Star Crusts. Phys. Rev. Lett. 2012, 108, 011102. [Google Scholar] [CrossRef]
- Tsang, D. Shattering Flares during Close Encounters of Neutron Stars. Astrophys. J. 2013, 777, 103. [Google Scholar] [CrossRef]
- Neill, D.; Tsang, D.; van Eerten, H.; Ryan, G.; Newton, W.G. Resonant Shattering Flares in Black Hole-Neutron Star and Binary Neutron Star Mergers. arXiv 2021, arXiv:2111.03686. [Google Scholar]
- Igoshev, A.P.; Popov, S.B. Magnetic field decay in normal radio pulsars. Astron. Nachrichten 2015, 336, 831. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B. Modified pulsar current analysis: Probing magnetic field evolution. Mon. Not. R. Astron. Soc. 2014, 444, 1066–1076. [Google Scholar] [CrossRef][Green Version]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Cumming, A. Hall Attractor in Axially Symmetric Magnetic Fields in Neutron Star Crusts. Phys. Rev. Lett. 2014, 112, 171101. [Google Scholar] [CrossRef]
- Viganò, D.; Rea, N.; Pons, J.A.; Perna, R.; Aguilera, D.N.; Miralles, J.A. Unifying the observational diversity of isolated neutron stars via magneto-thermal evolution models. Mon. Not. R. Astron. Soc. 2013, 434, 123–141. [Google Scholar] [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill Magnetar Catalog. Astrophys. J. Supp. Ser. 2014, 212, 6. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D.; Geppert, U. Pulsar timing irregularities and the imprint of magnetic field evolution. Astron. Astrophys. 2012, 547, A9. [Google Scholar] [CrossRef][Green Version]
- Tsang, D.; Gourgouliatos, K.N. Timing Noise in Pulsars and Magnetars and the Magnetospheric Moment of Inertia. Astrophys. J. Lett. 2013, 773, L17. [Google Scholar] [CrossRef][Green Version]
- Gourgouliatos, K.N.; Cumming, A. Hall drift and the braking indices of young pulsars. Mon. Not. R. Astron. Soc. 2015, 446, 1121–1128. [Google Scholar] [CrossRef]
- Gao, Z.F.; Li, X.D.; Wang, N.; Yuan, J.P.; Wang, P.; Peng, Q.H.; Du, Y.J. Constraining the braking indices of magnetars. Mon. Not. R. Astron. Soc. 2016, 456, 55–65. [Google Scholar] [CrossRef]
- Gao, Z.F.; Wang, N.; Shan, H.; Li, X.D.; Wang, W. The Dipole Magnetic Field and Spin-down Evolutions of the High Braking Index Pulsar PSR J1640-4631. Astrophys. J. 2017, 849, 19. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, S.N. The Effective Magnetic Field Decay of Radio Pulsars: Insights from the Statistical Properties of Their Spin Frequency’s Second Derivatives. Astrophys. J. 2019, 880, 123. [Google Scholar] [CrossRef]
- Chang, Z.; Zhu, Q.H. Could acceleration of a pulsar affect braking index? Eur. Phys. J. C 2020, 80, 411. [Google Scholar] [CrossRef]
- Geppert, U.; Gil, J.; Melikidze, G. Radio pulsar activity and the crustal Hall drift. Mon. Not. R. Astron. Soc. 2013, 435, 3262–3271. [Google Scholar] [CrossRef][Green Version]
- Geppert, U.; Viganò, D. Creation of magnetic spots at the neutron star surface. Mon. Not. R. Astron. Soc. 2014, 444, 3198–3208. [Google Scholar] [CrossRef][Green Version]
- Borghese, A.; Rea, N.; Coti Zelati, F.; Tiengo, A.; Turolla, R. Discovery of a Strongly Phase-variable Spectral Feature in the Isolated Neutron Star RX J0720.4-3125. Astrophys. J. Lett. 2015, 807, L20. [Google Scholar] [CrossRef]
- Bignami, G.F.; Caraveo, P.A.; De Luca, A.; Mereghetti, S. The magnetic field of an isolated neutron star from X-ray cyclotron absorption lines. Nature 2003, 423, 725–727. [Google Scholar] [CrossRef] [PubMed]
- Güver, T.; Göǧüş, E.; Özel, F. A magnetar strength surface magnetic field for the slowly spinning down SGR 0418+5729. Mon. Not. R. Astron. Soc. 2011, 418, 2773–2778. [Google Scholar] [CrossRef]
- Tiengo, A.; Esposito, P.; Mereghetti, S.; Turolla, R.; Nobili, L.; Gastaldello, F.; Götz, D.; Israel, G.L.; Rea, N.; Stella, L.; et al. A variable absorption feature in the X-ray spectrum of a magnetar. Nature 2013, 500, 312–314. [Google Scholar] [CrossRef]
- Pizzocaro, D.; Tiengo, A.; Mereghetti, S.; Turolla, R.; Esposito, P.; Stella, L.; Zane, S.; Rea, N.; Coti Zelati, F.; Israel, G. Detailed X-ray spectroscopy of the magnetar 1E 2259+586. Astron. Astrophys. 2019, 626, A39. [Google Scholar] [CrossRef]
- Arumugasamy, P.; Mitra, D. Evaluating the evidence of multipolar surface magnetic field in PSR J0108-1431. Mon. Not. R. Astron. Soc. 2019, 489, 4589–4605. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Halpern, J.P.; Seward, F.D. Discovery of a 105 ms X-ray Pulsar in Kesteven 79: On the Nature of Compact Central Objects in Supernova Remnants. Astrophys. J. 2005, 627, 390–396. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Halpern, J.P. Precise Timing of the X-ray Pulsar 1E 1207.4-5209: A Steady Neutron Star Weakly Magnetized at Birth. Astrophys. J. Lett. 2007, 664, L35–L38. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Halpern, J.P. Discovery of a 112 ms X-Ray Pulsar in Puppis A: Further Evidence of Neutron Stars Weakly Magnetized at Birth. Astrophys. J. Lett. 2009, 695, L35–L39. [Google Scholar] [CrossRef]
- Halpern, J.P.; Gotthelf, E.V. Spin-Down Measurement of PSR J1852+0040 in Kesteven 79: Central Compact Objects as Anti-Magnetars. Astrophys. J. 2010, 709, 436–446. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Halpern, J.P.; Alford, J. The Spin-down of PSR J0821-4300 and PSR J1210-5226: Confirmation of Central Compact Objects as Anti-magnetars. Astrophys. J. 2013, 765, 58. [Google Scholar] [CrossRef]
- Bogdanov, S.; Ng, C.Y.; Kaspi, V.M. Constraining the Evolutionary Fate of Central Compact Objects: “Old” Radio Pulsars in Supernova Remnants. Astrophys. J. Lett. 2014, 792, L36. [Google Scholar] [CrossRef]
- De Luca, A. Central compact objects in supernova remnants. J. Phys. Conf. Ser. 2017, 932, 012006. [Google Scholar] [CrossRef]
- Viganò, D.; Pons, J.A. Central compact objects and the hidden magnetic field scenario. Mon. Not. R. Astron. Soc. 2012, 425, 2487–2492. [Google Scholar] [CrossRef]
- Ho, W.C.G. Evolution of a buried magnetic field in the central compact object neutron stars. Mon. Not. R. Astron. Soc. 2011, 414, 2567–2575. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Elfritz, J.G.; Popov, S.B. Post-fall-back evolution of multipolar magnetic fields and radio pulsar activation. Mon. Not. R. Astron. Soc. 2016, 462, 3689–3702. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Gourgouliatos, K.N.; Hollerbach, R.; Wood, T.S. 3D Magnetothermal Simulations of Tangled Crustal Magnetic Field in Central Compact Objects. Astrophys. J. 2021, 909, 101. [Google Scholar] [CrossRef]
- Gullón, M.; Miralles, J.A.; Viganò, D.; Pons, J.A. Population synthesis of isolated neutron stars with magneto-rotational evolution. Mon. Not. R. Astron. Soc. 2014, 443, 1891–1899. [Google Scholar] [CrossRef]
- Gullón, M.; Pons, J.A.; Miralles, J.A.; Viganò, D.; Rea, N.; Perna, R. Population synthesis of isolated neutron stars with magneto-rotational evolution—II. From radio-pulsars to magnetars. Mon. Not. R. Astron. Soc. 2015, 454, 615–625. [Google Scholar] [CrossRef]
- Coti Zelati, F.; Rea, N.; Pons, J.A.; Campana, S.; Esposito, P. Systematic study of magnetar outbursts. Mon. Not. R. Astron. Soc. 2018, 474, 961–1017. [Google Scholar] [CrossRef]
- Hurley, K.; Cline, T.; Mazets, E.; Barthelmy, S.; Butterworth, P.; Marshall, F.; Palmer, D.; Aptekar, R.; Golenetskii, S.; Il’Inskii, V.; et al. A giant periodic flare from the soft γ-ray repeater SGR1900+14. Nature 1999, 397, 41–43. [Google Scholar] [CrossRef]
- Hurley, K.; Boggs, S.E.; Smith, D.M.; Duncan, R.C.; Lin, R.; Zoglauer, A.; Krucker, S.; Hurford, G.; Hudson, H.; Wigger, C.; et al. An exceptionally bright flare from SGR 1806-20 and the origins of short-duration γ-ray bursts. Nature 2005, 434, 1098–1103. [Google Scholar] [CrossRef]
- Palmer, D.M.; Barthelmy, S.; Gehrels, N.; Kippen, R.M.; Cayton, T.; Kouveliotou, C.; Eichler, D.; Wijers, R.A.M.J.; Woods, P.M.; Granot, J.; et al. A giant γ-ray flare from the magnetar SGR 1806–20. Nature 2005, 434, 1107–1109. [Google Scholar] [CrossRef]
- Low, B.C. Blowup of Force-free Magnetic Fields in the Infinite Region of Space. Astrophys. J. 1986, 307, 205. [Google Scholar] [CrossRef]
- Aly, J.J. How Much Energy Can Be Stored in a Three-dimensional Force-free Magnetic Field? Astrophys. J. Lett. 1991, 375, L61. [Google Scholar] [CrossRef]
- Cowley, S.C.; Artun, M. Explosive instabilities and detonation in magnetohydrodynamics. Phys. Rep. 1997, 283, 185–211. [Google Scholar] [CrossRef]
- Lyutikov, M. Explosive reconnection in magnetars. Mon. Not. R. Astron. Soc. 2003, 346, 540–554. [Google Scholar] [CrossRef]
- Lyutikov, M. Magnetar giant flares and afterglows as relativistic magnetized explosions. Mon. Not. R. Astron. Soc. 2006, 367, 1594–1602. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Thompson, C. Corona of Magnetars. Astrophys. J. 2007, 657, 967–993. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Barkov, M.; Lyutikov, M. Tearing instability in relativistic magnetically dominated plasmas. Mon. Not. R. Astron. Soc. 2007, 374, 415–426. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N. Self-similar magnetic arcades. Mon. Not. R. Astron. Soc. 2008, 385, 875–882. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Lynden-Bell, D. Fields from a relativistic magnetic explosion. Mon. Not. R. Astron. Soc. 2008, 391, 268–282. [Google Scholar] [CrossRef][Green Version]
- Beloborodov, A.M. Untwisting Magnetospheres of Neutron Stars. Astrophys. J. 2009, 703, 1044–1060. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Vlahakis, N. Relativistic expansion of a magnetized fluid. Geophys. Astrophys. Fluid Dyn. 2010, 104, 431–450. [Google Scholar] [CrossRef][Green Version]
- Parfrey, K.; Beloborodov, A.M.; Hui, L. Introducing PHAEDRA: A new spectral code for simulations of relativistic magnetospheres. Mon. Not. R. Astron. Soc. 2012, 423, 1416–1436. [Google Scholar] [CrossRef]
- Parfrey, K.; Beloborodov, A.M.; Hui, L. Dynamics of Strongly Twisted Relativistic Magnetospheres. Astrophys. J. 2013, 774, 92. [Google Scholar] [CrossRef]
- Huang, L.; Yu, C. Magnetar Giant Flares in Multipolar Magnetic Fields. I. Fully and Partially Open Eruptions of Flux Ropes. Astrophys. J. 2014, 784, 168. [Google Scholar] [CrossRef]
- Akgün, T.; Cerdá-Durán, P.; Miralles, J.A.; Pons, J.A. The force-free twisted magnetosphere of a neutron star - II. Degeneracies of the Grad-Shafranov equation. Mon. Not. R. Astron. Soc. 2018, 474, 625–635. [Google Scholar] [CrossRef]
- Mahlmann, J.F.; Akgün, T.; Pons, J.A.; Aloy, M.A.; Cerdá-Durán, P. Instability of twisted magnetar magnetospheres. Mon. Not. R. Astron. Soc. 2019, 490, 4858–4876. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The soft gamma repeaters as very strongly magnetized neutron stars—I. Radiative mechanism for outbursts. Mon. Not. R. Astron. Soc. 1995, 275, 255–300. [Google Scholar] [CrossRef]
- Levin, Y.; Lyutikov, M. On the dynamics of mechanical failures in magnetized neutron star crusts. Mon. Not. R. Astron. Soc. 2012, 427, 1574–1579. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Levin, Y. Thermoplastic Waves in Magnetars. Astrophys. J. Lett. 2014, 794, L24. [Google Scholar] [CrossRef]
- Lander, S.K.; Andersson, N.; Antonopoulou, D.; Watts, A.L. Magnetically driven crustquakes in neutron stars. Mon. Not. R. Astron. Soc. 2015, 449, 2047–2058. [Google Scholar] [CrossRef]
- Li, X.; Levin, Y.; Beloborodov, A.M. Magnetar Outbursts from Avalanches of Hall Waves and Crustal Failures. Astrophys. J. 2016, 833, 189. [Google Scholar] [CrossRef]
- Suvorov, A.G.; Kokkotas, K.D. Young magnetars with fracturing crusts as fast radio burst repeaters. Mon. Not. R. Astron. Soc. 2019, 488, 5887–5897. [Google Scholar] [CrossRef]
- Kojima, Y.; Kisaka, S.; Fujisawa, K. Magneto-elastic equilibrium of a neutron star crust. Mon. Not. R. Astron. Soc. 2021, 506, 3936–3945. [Google Scholar] [CrossRef]
- Lander, S.K. Magnetar Field Evolution and Crustal Plasticity. Astrophys. J. Lett. 2016, 824, L21. [Google Scholar] [CrossRef]
- Lander, S.K.; Gourgouliatos, K.N. Magnetic-field evolution in a plastically failing neutron-star crust. Mon. Not. R. Astron. Soc. 2019, 486, 4130–4143. [Google Scholar] [CrossRef]
- Thompson, C.; Yang, H.; Ortiz, N. Global Crustal Dynamics of Magnetars in Relation to Their Bright X-ray Outbursts. Astrophys. J. 2017, 841, 54. [Google Scholar] [CrossRef]
- Kojima, Y.; Suzuki, K. Magnetic-field evolution with large-scale velocity circulation in a neutron-star crust. Mon. Not. R. Astron. Soc. 2020, 494, 3790–3798. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Lander, S.K. Axisymmetric magneto-plastic evolution of neutron-star crusts. Mon. Not. R. Astron. Soc. 2021, 506, 3578–3587. [Google Scholar] [CrossRef]
- Kojima, Y.; Kisaka, S.; Fujisawa, K. Evolution of magnetic deformation in neutron star crust. Mon. Not. R. Astron. Soc. 2021, 502, 2097–2104. [Google Scholar] [CrossRef]
- Dormy, E.; Cardin, P.; Jault, D. MHD flow in a slightly differentially rotating spherical shell, with conducting inner core, in a dipolar magnetic field. Earth Planet. Sci. Lett. 1998, 160, 15–30. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Hollerbach, R.; Wood, T.; Gourgouliatos, K.N. Strong toroidal magnetic fields required by quiescent X-ray emission of magnetars. Nat. Astron. 2021, 5, 145–149. [Google Scholar] [CrossRef]
- De Grandis, D.; Taverna, R.; Turolla, R.; Gnarini, A.; Popov, S.B.; Zane, S.; Wood, T.S. X-Ray Emission from Isolated Neutron Stars Revisited: 3D Magnetothermal Simulations. Astrophys. J. 2021, 914, 118. [Google Scholar] [CrossRef]
- Gudmundsson, E.H.; Pethick, C.J.; Epstein, R.I. Structure of neutron star envelopes. Astrophys. J. 1983, 272, 286–300. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B.; Hollerbach, R. Evolution of Neutron Star Magnetic Fields. Universe 2021, 7, 351. [Google Scholar] [CrossRef]
- Thompson, C.; Murray, N. Transport of Magnetic Fields in Convective, Accreting Supernova Cores. Astrophys. J. 2001, 560, 339–357. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B. Neutron star’s initial spin period distribution. Mon. Not. R. Astron. Soc. 2013, 432, 967–972. [Google Scholar] [CrossRef]
- Popov, S.B.; Turolla, R. Initial spin periods of neutron stars in supernova remnants. Astrophys. Space Sci. 2012, 341, 457–464. [Google Scholar] [CrossRef][Green Version]
- Dolginov, A.Z.; Urpin, V.A. The Spontaneous Development of a Magnetic Field in a Degenerate White Dwarf Core. Sov. Astronom. 1980, 24, 177–182. [Google Scholar]
- Geppert, U.; Wiebicke, H.J. Amplification of neutron star magnetic fields by thermoelectric effects. I—General formalism. Astron. Astrophys. Suppl. 1991, 87, 217–228. [Google Scholar]
- Wiebicke, H.J.; Geppert, U. Amplification of neutron star magnetic fields by thermoelectric effects. II—Linear approximation. Astron. Astrophys. 1991, 245, 331–340. [Google Scholar]
- Wiebicke, H.J.; Geppert, U. Amplification of neutron star magnetic fields by thermoelectric effects. III—Growth limits in nonlinear calculations. Astron. Astrophys. 1992, 262, 125–130. [Google Scholar]
- Wiebicke, H.J.; Geppert, U. Amplification of neutron star magnetic fields by thermoelectric effects. IV. Averaged small-scale modes and selection rules for large-scale modes. Astron. Astrophys. 1995, 294, 303–312. [Google Scholar]
- Geppert, U.; Wiebicke, H.J. Amplification of neutron star magnetic fields by thermoelectric effects. V. Induction of large-scale toroidal fields. Astron. Astrophys. 1995, 300, 429. [Google Scholar]
- Wiebicke, H.J.; Geppert, U. Amplification of neutron star magnetic fields by thermoelectric effects. VI. Analytical approach. Astron. Astrophys. 1996, 309, 203–212. [Google Scholar]
- Pons, J.A.; Rea, N. Modeling Magnetar outbursts: Flux enhancement and the connection with short bursts and glitches. Astrophys. J. 2012, 750, L6. [Google Scholar] [CrossRef]
- Turolla, R.; Zane, S.; Watts, A.L. Magnetars: The physics behind observations. A review. Rep. Prog. Phys. 2015, 78, 116901. [Google Scholar] [CrossRef] [PubMed]
- Ziman, J. Principles of the Theory of Solids; Cambridge University Press: Cambridge, UK, 1972. [Google Scholar]
- Gnedin, N.Y.; Ferrara, A.; Zweibel, E.G. Generation of the Primordial Magnetic Fields during Cosmological Reionization. Astrophys. J. 2000, 539, 505–516. [Google Scholar] [CrossRef]
- Prior, C.; Gourgouliatos, K.N. Observational signatures of magnetic field structure in relativistic AGN jets. Astron. Astrophys. 2019, 622, A122. [Google Scholar] [CrossRef]
- Graziani, C.; Tzeferacos, P.; Lee, D.; Lamb, D.Q.; Weide, K.; Fatenejad, M.; Miller, J. The Biermann Catastrophe in Numerical Magnetohydrodynamics. Astrophys. J. 2015, 802, 43. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).