The Double Phospho/Dephosphorylation Cycle as a Benchmark to Validate an Effective Taylor Series Method to Integrate Ordinary Differential Equations
Abstract
:1. Introduction
2. Exact Quadratization and Approximate Integration of Differential Equations
2.1. Exact Quadratization of -ODEs into Driver-Type Differential Equations
2.2. Approximate Taylor Series Integration Method
3. The Double Phosphosphorylation–Dephosphorylation Cycle
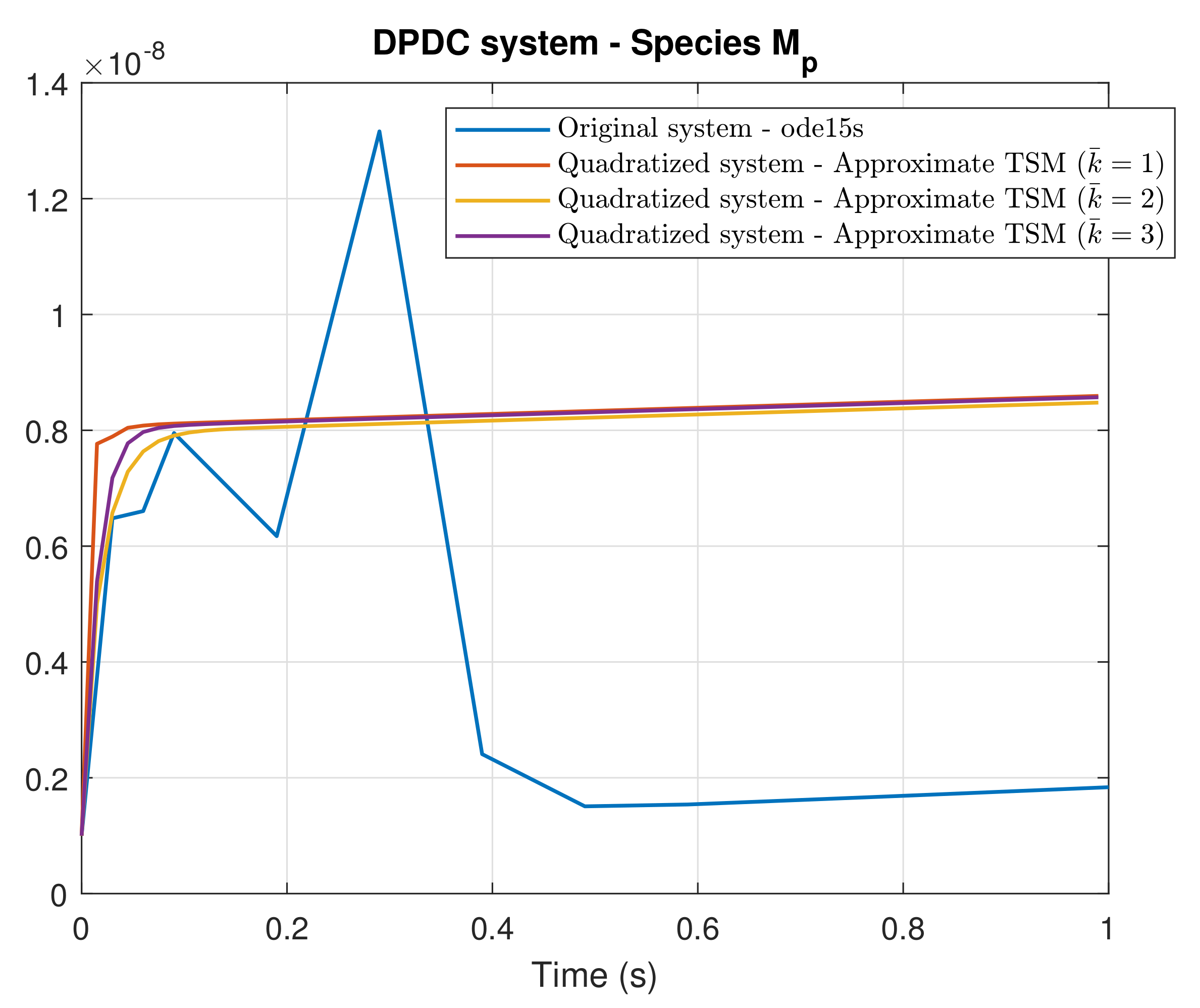
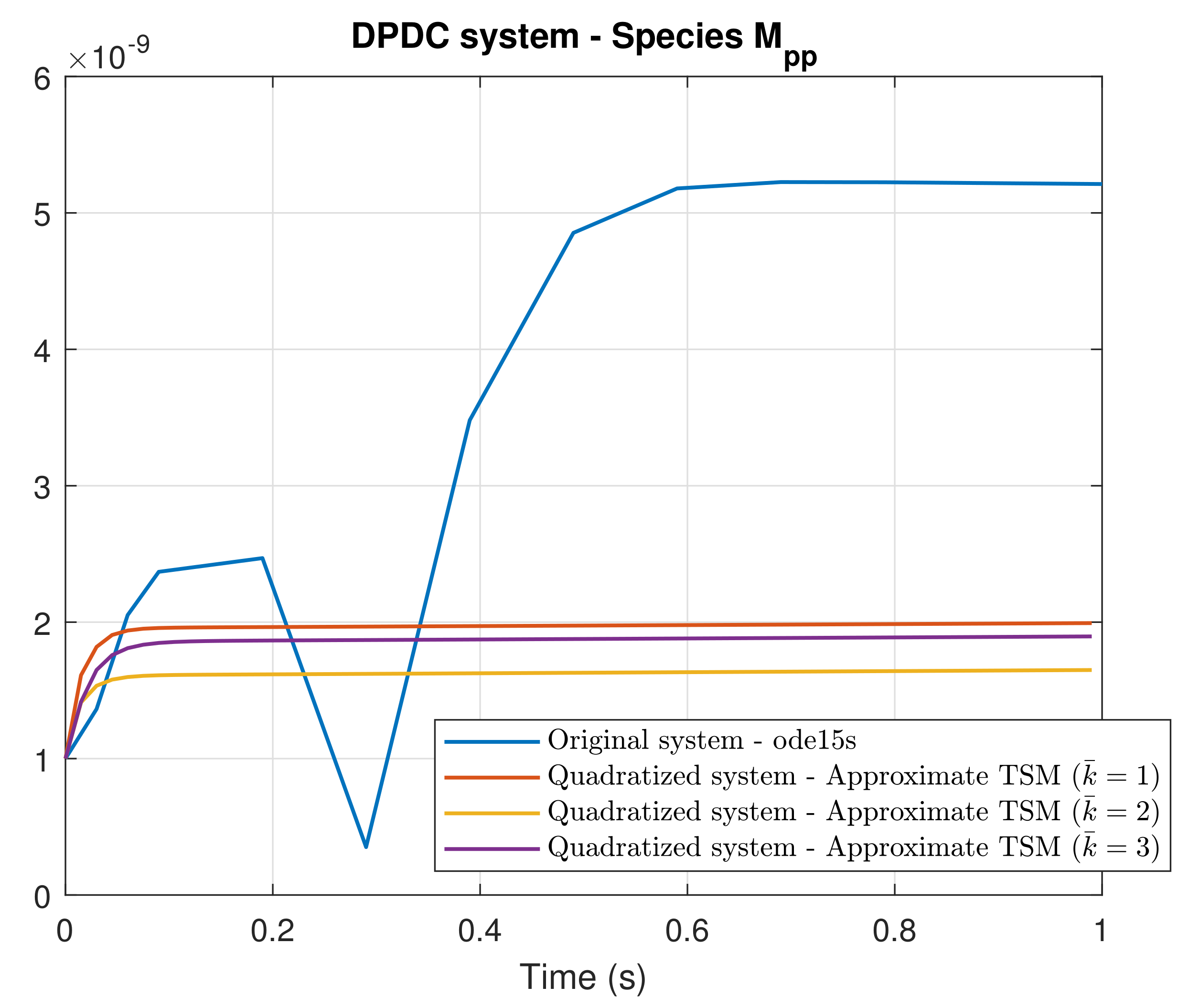
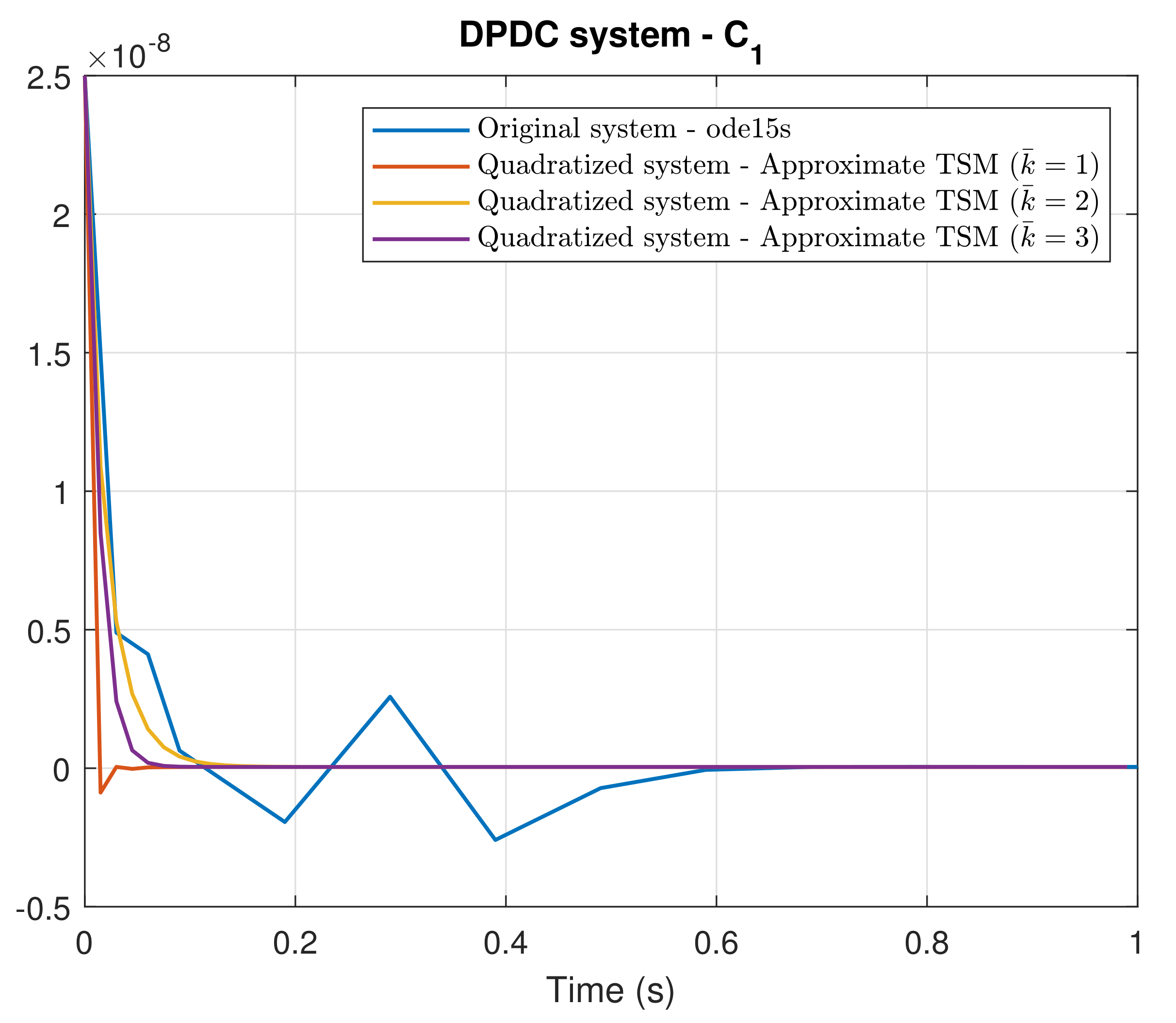
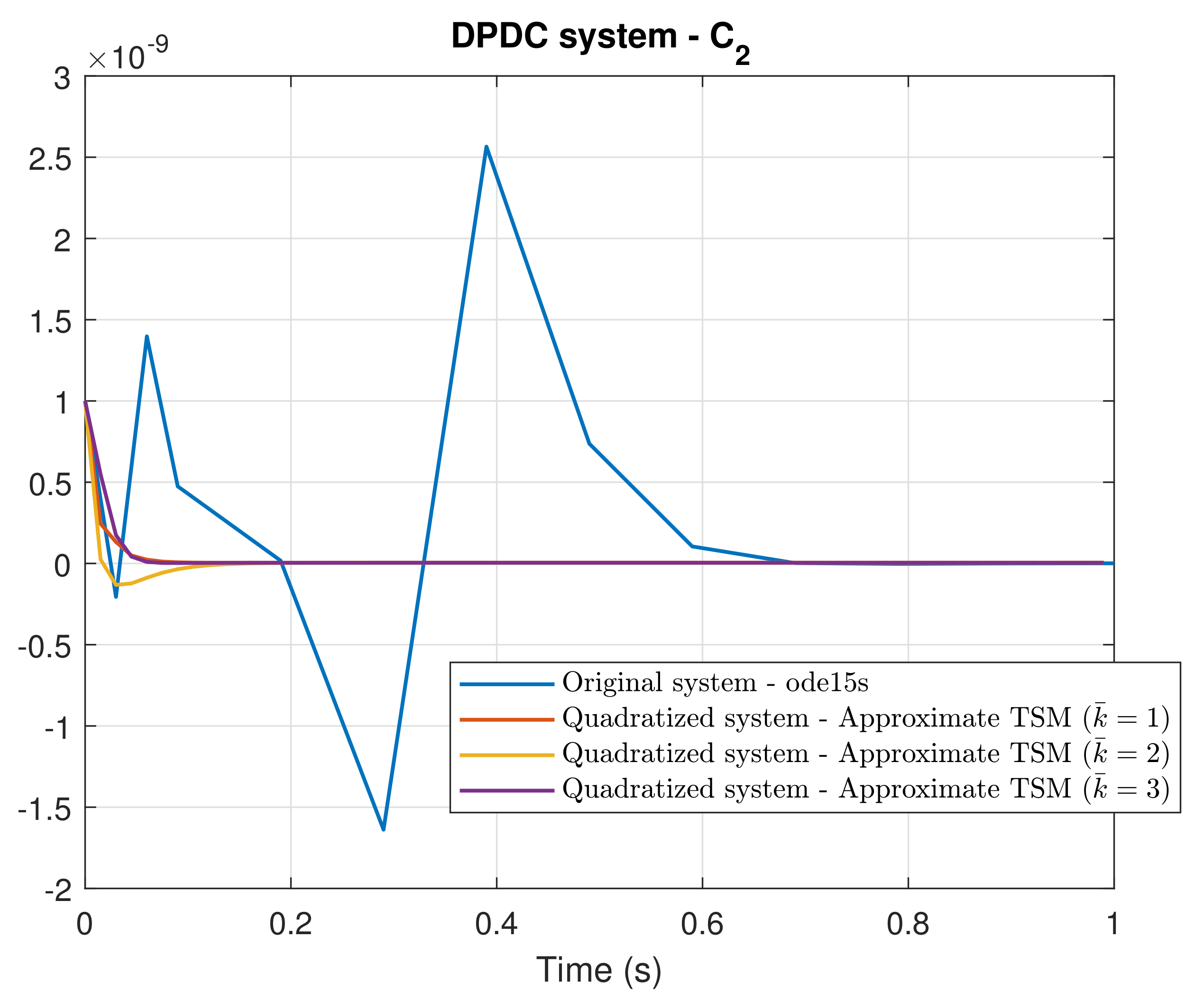
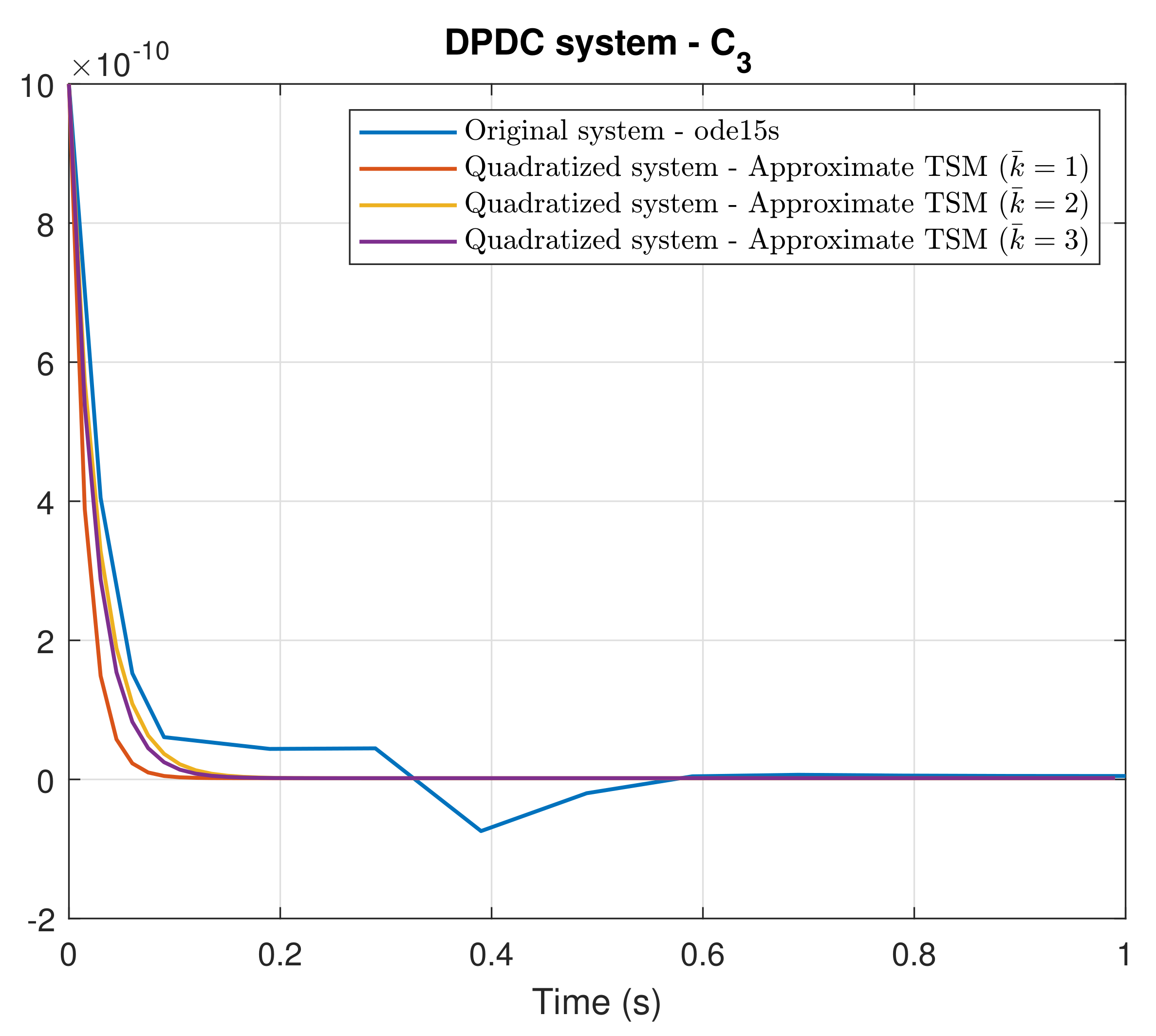
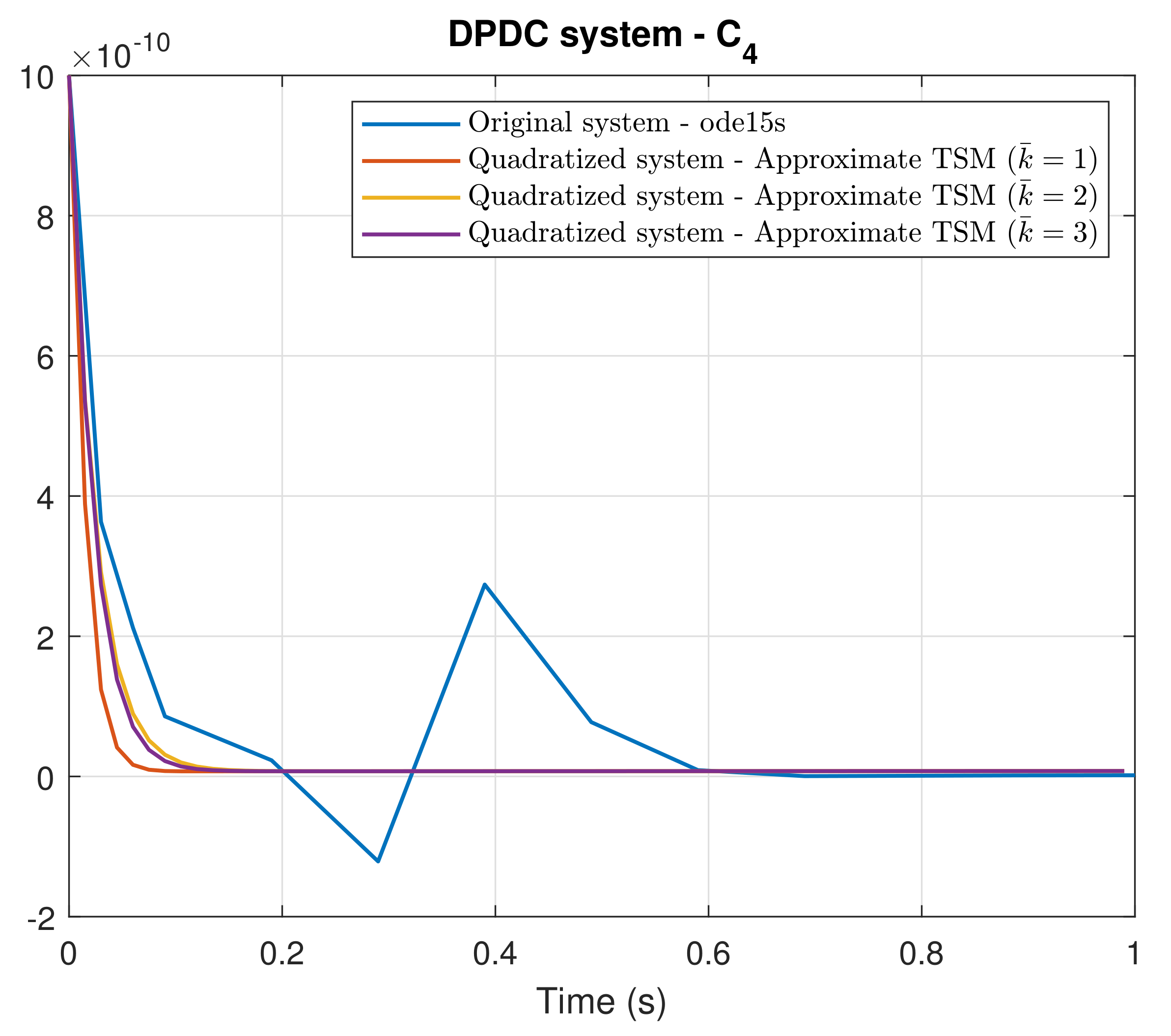
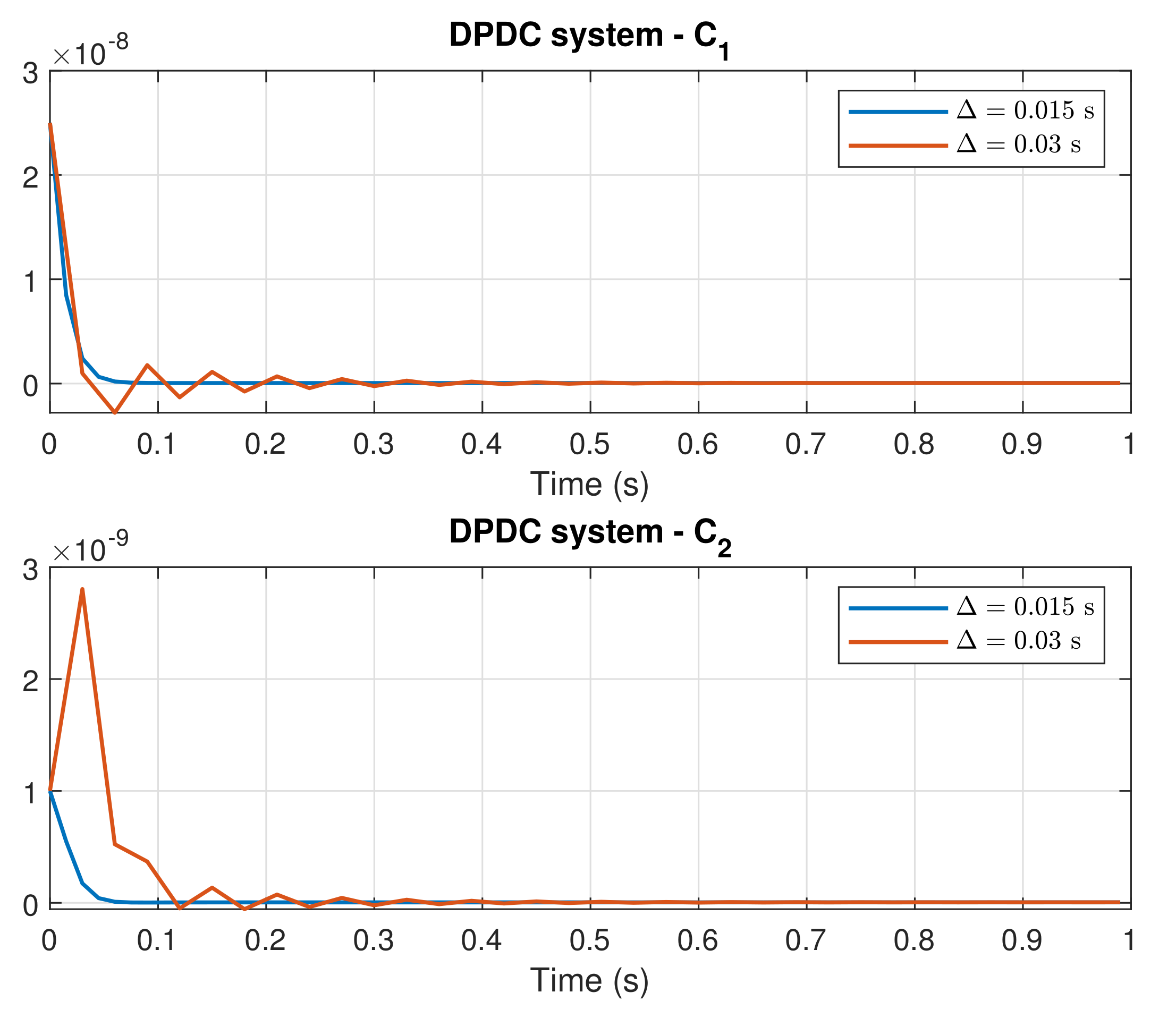
4. Simulation Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cooper, G. The Cell, a Molecular Approach; Sinauer Associates: Sunderland, MA, USA, 2000. [Google Scholar]
- Chang, R. Physical Chemistry for the Chemical and Biological Sciences; University Science Books: New York, NY, USA, 2000. [Google Scholar]
- Nash, P.; Tang, X.; Orlicky, S.; Chen, Q.; Gertler, F.B.; Mendenhall, M.D.; Sicheri, F.; Pawson, T.; Tyers, M. Multisite phosphorylation of a CDK inhibitor sets a threshold for the onset of DNA replication. Nature 2001, 414, 514–521. [Google Scholar] [CrossRef]
- Palumbo, P.; Vanoni, M.; Cusimano, V.; Busti, S.; Marano, F.; Manes, C.; Alberghina, L. Whi5 phosphorylation embedded in the G1/S network dynamically controls critical cell size and cell fate. Nat. Commun. 2016, 7, 11372. [Google Scholar] [CrossRef] [Green Version]
- Ionescu, A.E.; Mentel, M.; Munteanu, C.V.A.; Sima, L.E.; Martin, E.C.; Necula-Petrareanu, G.; Szedlacsek, S.E. Analysis of EYA3 Phosphorylation by Src Kinase Identifies Residues Involved in Cell Proliferation. Int. J. Mol. Sci. 2019, 20, 6307. [Google Scholar] [CrossRef] [Green Version]
- Salazar, C.; Höfer, T. Multisite protein phosphorylation—From molecular mechanisms to kinetic models. FEBS J. 2009, 276, 3177–3198. [Google Scholar] [CrossRef]
- Salazar, C.; Brümmer, A.; Alberghina, L.; Höfer, T. Timing control in regulatory networks by multisite protein modifications. Trends Cell Biol. 2010, 20, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Ortega, F.; Garcés, J.L.; Mas, F.; Kholodenko, B.N.; Cascante, M. Bistability from double phosphorylation in signal transduction. FEBS J. 2006, 273, 3915–3926. [Google Scholar] [CrossRef]
- Bersani, A.M.; Borri, A.; Carravetta, F.; Mavelli, G.; Palumbo, P. On a stochastic approach to model the double phosphorylation/dephosphorylation cycle. Math. Mech. Complex Syst. 2020, 8, 261–285. [Google Scholar] [CrossRef]
- Ramesh, V.; Krishnan, J. Symmetry breaking meets multisite modification. Elife 2021, 10, e65358. [Google Scholar] [CrossRef] [PubMed]
- Bersani, A.M.; Bersani, E.; Dell’Acqua, G.; Pedersen, M.G. New trends and perspectives in nonlinear intracellular dynamics: One century from Michaelis–Menten paper. Contin. Mech. Termodyn. 2015, 27, 659–684. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. One hundred years of Michaelis-Menten kinetics. Perspect. Sci. 2015, 4, 3–9. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M. Kinetics of invertase action. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Segel, L. On the validity of the steady state assumption of enzyme kinetics. Bull. Math. Biol. 1988, 50, 579–593. [Google Scholar] [CrossRef]
- Barrio, R.; Martínez, M.A.; Pérez, L.; Pueyo, E. Bifurcations and Slow-Fast Analysis in a Cardiac Cell Model for Investigation of Early Afterdepolarizations. Mathematics 2020, 8, 880. [Google Scholar] [CrossRef]
- Mohd Ijam, H.; Ibrahim, Z.B. Diagonally Implicit Block Backward Differentiation Formula with Optimal Stability Properties for Stiff Ordinary Differential Equations. Symmetry 2019, 11, 1342. [Google Scholar] [CrossRef] [Green Version]
- Borri, A.; Carravetta, F.; Palumbo, P. Time series expansion to find solutions of nonlinear systems: An application to enzymatic reactions. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 749–754. [Google Scholar]
- Bersani, A.M.; Dell’Acqua, G.; Tomassetti, G. On stationary states in the double phosphorylation-dephosphorylation cycle. In Proceedings of the AIP Conference Proceedings, College Park, MD, USA, 28–31 July 2011; American Institute of Physics: College Park, MD, USA, 2011; Volume 1389. [Google Scholar]
- Barton, D.; Willers, I.M.; Zahar, R.V.M. Taylor Series Methods for Ordinary Differential Equations—An Evaluation. In Mathematical Software; Rice, J.R., Ed.; Academic Press: New York, NY, USA, 1972; pp. 369–389. [Google Scholar]
- Corliss, F.; Chang, Y.F. Solving ordinary differential equations using Taylor Series. ACM Trans. Math. Softw. 1994, 8, 209–233. [Google Scholar] [CrossRef]
- Corliss, G.F.; Kirlinger, G. On implicit Taylor series method for stiff ODEs. In Proceedings of the SCAN 91: International Symposium on Computer Arithmetic and Scientific Computing, Oldenburg, Germany, 1–4 October 1991. [Google Scholar]
- Barton, D. On Taylor series and stiff equations. ACM Trans. Math. Softw. 1980, 6, 280–294. [Google Scholar] [CrossRef]
- Barrio, R. Sensitivity analysis of ODEs/DAEs using the Taylor series method. SIAM J. Sci. Comput. 2006, 6, 1929–1947. [Google Scholar] [CrossRef]
- Carravetta, F. Global Exact Quadratization of Continuous-Time Nonlinear Control Systems. SIAM J. Control Optim. 2015, 53, 235–261. [Google Scholar] [CrossRef]
- Carravetta, F. On the Solution Calculation of Nonlinear Ordinary Differential Equations via Exact Quadratization. J. Differ. Equ. 2020, 269, 11328–11365. [Google Scholar] [CrossRef]
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Jäntschi, L.; Bálint, D.; Bolboacă, S.D. Multiple Linear Regressions by Maximizing the Likelihood under Assumption of Generalized Gauss-Laplace Distribution of the Error. Comput. Math. Methods Med. 2016, 2016, 8578156. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borri, A.; Carravetta, F.; Palumbo, P. The Double Phospho/Dephosphorylation Cycle as a Benchmark to Validate an Effective Taylor Series Method to Integrate Ordinary Differential Equations. Symmetry 2021, 13, 1684. https://doi.org/10.3390/sym13091684
Borri A, Carravetta F, Palumbo P. The Double Phospho/Dephosphorylation Cycle as a Benchmark to Validate an Effective Taylor Series Method to Integrate Ordinary Differential Equations. Symmetry. 2021; 13(9):1684. https://doi.org/10.3390/sym13091684
Chicago/Turabian StyleBorri, Alessandro, Francesco Carravetta, and Pasquale Palumbo. 2021. "The Double Phospho/Dephosphorylation Cycle as a Benchmark to Validate an Effective Taylor Series Method to Integrate Ordinary Differential Equations" Symmetry 13, no. 9: 1684. https://doi.org/10.3390/sym13091684
APA StyleBorri, A., Carravetta, F., & Palumbo, P. (2021). The Double Phospho/Dephosphorylation Cycle as a Benchmark to Validate an Effective Taylor Series Method to Integrate Ordinary Differential Equations. Symmetry, 13(9), 1684. https://doi.org/10.3390/sym13091684






