Abstract
This study aims to provide a way to increase the energy dissipation of flow in the inclined drop with environmental and economic considerations. Eighty-one experiments were performed on three types of simple inclined drop and inclined drop equipped with hole and without hole fishway elements with a 200~600 L/min flow rate. In this study, the effect of using fishway elements on hydraulic parameters regarding flow pattern, energy dissipation, relative downstream depth, relative aeration length, relative length of the hydraulic jump, and downstream Froude number of an inclined drop was investigated through physical modeling following the symmetry law. The results showed that in all experimental models, with increasing the relative critical depth parameter, the energy dissipation values increase, and the downstream Froude number decreases. The parameters of relative downstream depth, relative length of a hydraulic jump, and relative aeration length also increase with increasing relative critical depth. On average, 88% of the flow energy dissipation increases with the design of the fishway elements on the structure compared to the simple drop. Model M7 (with holes fish elements) shows the highest energy dissipation, and Model M2 (without holes fish elements) has the highest flow aeration length and relative downstream water depth.
1. Introduction
Freshwater ecosystems, especially rivers, are under increasing pressures due to the construction of hydraulic structures such as dams and weirs, which cause longitudinal fragmentation, impair upstream and downstream migration patterns, especially among fish populations, and transform free-flowing rivers lentic habitats [1,2,3,4].
In addition to the impacts induced by hydraulic structure, climate change is already inducing extra pressure to the fluvial ecosystems by threatening the aquatic biodiversity, especially in arid and semi-arid regions [5,6]. On the other side, different hydraulic structures built on the fluvial ecosystem serve multiple purposes, e.g., energy generation, irrigation, water supply, and recreation. While the impacts of large dams are well known and reported in the literature, the impacts of small dams and/or weirs remain still debatable; nevertheless, some recent studies report that the cumulative impacts of such structures might be even more significant than estimated [2,7,8,9]. Usually, the small weirs or spillways are commonly associated with small hydropower plants, typically those of Run-of-River (RoR) type. Allowing fish to emigrate through these structures is vital to maintain the biodiversity of the fluvial ecosystem; nevertheless, the success of fish migration depends on the design of the spillway and whether the release of residual water and environmental flows over the spillway occurs during the migration period, and if fishes are energetically able to go through the river. As the number of small hydropower plants is increasing, it is crucial to improve the hydraulic performance of spillways and weirs to support fish and other freshwater aquatic animals’ migration [2]. In this regard, one of the critical issues in Iran is the scarcity of fish-friendly hydraulic structures. In recent years, the extinction of fish due to the collision of these living organisms with concrete blocks in stilling basins and extinction has increased due to incorrect design [10]. In general, the effects of a low-head diversion dam equipped with a spillway on the survival and injury of fish passing downstream are poorly investigated and understood [9,11]. Fishways are hydraulic structures that allow fish to be transported upstream of a water supply system by constructing engineering structures and river obstruction [12]. Fishways are defined by Boiten [13] as hydraulic structures which can facilitate upstream and downstream migration of certain fish species in rivers where natural and human-made obstructions prevent a free migration. These structures are constructed when required for environmental or economic considerations. Ideally, these structures should be designed in such a way that they allow the fish to quickly enter and exit for spawning without any pressure and injury. Also, a well-designed fishway allows the fish species to access their spawning ground with an acceptable delay. Some of the most common fishways are vertical slots, pool-weir, Denil, and Culvert fishways [12]. However, some fish species tend to move over the spillway during residual flow releases, where they can get injured or killed if the spillway structure is not adequately designed. Each fishway type’s flow and turbulence patterns provide suitable swimming conditions for specific fish species but do not for others [14,15].
The first research on fishway structures dates back to Rajaratnam et al. [16] and Rajaratnam et al. [17]. Wu et al. [18] investigated the flow structure in a path with vertical fishway elements at a scale of 1:2.67 for three ranges of a slope, 5, 10, and 20%, considering several discharges scenarios. The results showed two flow patterns in the pools; in pattern 1, the mainstream moves from one gap to another, and in pattern 2, the flow to the channel wall and creating a rotational zone moves to the bottom of the channel pool. Puertas et al. [19] examined the flow structure in fishway paths for Rajaratnam, Katopodis, and Solanki [16], with two slopes of 5.7 and 10%. They acknowledged the linear relationship that Rajaratnam, Katopodis, and Solanki [16] provided for flow and relative depth. Liu et al. [20] conducted an experimental study of flow turbulence in a fishway with slit amplitudes of 5.06 and 10.52%, respectively.
Rodríguez, Agudo, Mosquera, and González [14] evaluated vertical gap fishing road designs regarding fish swimming capability. Results showed that the value of energy dissipation rate per unit pool volume should not exceed 200 W/m3 for the large anadromous salmon species and 150 W/m3 for smaller species, including trout. Wu, Rajaratnam, and Katopodis [18] numerically investigated the mean turbulence depth and symmetry boundary condition to simulate flow in vertical fishway paths. The results showed that the importance of the turbulence model in numerical simulation could be considered a valuable tool for practical design purposes. Yagci [21] examined the hydraulic aspects of pool-weir fishways as the ecologically friendly water structure. Results showed that turbulence intensity is also effective and must be specified. Flow velocity and depth affect the fish’s swimming capability. Flow patterns and turbulence in fishways provide suitable swimming conditions for some specific fish species.
For water transfer in erodible waterways and when the height difference is more than 1.5 m, the inclined drop is recommended [22]. The structure of this type of drop is rectangular and with a fixed width. In addition to transferring water from a higher level to a lower level, it also dissipates the extra kinematic energy of the flow. Among the commonly used drops, the inclined drop has the lowest energy dissipation [23,24]. The background of researches in the field of rectangular inclined drop shows that due to the low dissipation of this structure, limited and few studies have been done in the field of energy dissipation of this type of inclined drop.
The first studies on inclined drop were conducted by Wagner [25], Peterka [26], and Bos et al. [27]. Sholichin and Akib [28] estimated the hydraulic jump length using a drop number (D) downstream of vertical and inclined drop. These researchers aimed to investigate the efficiency and application of drop numbers in vertical and inclined drop structures. The results showed that the vertical length of the drop and the hydraulic jump length could be predicted based on the drop for the vertical drop. While for inclined drop structures based on the drop number. Daneshgar et al. [29] investigated energy dissipation and relative downstream depth in gabion and simple inclined drop experimentally. By conducting 120 different experiments for two types of drops with three angles and two heights, the researchers showed that in both models, increasing the relative critical depth reduced the relative energy dissipation and increased the relative depth of the downstream. They also concluded that gabions on the sloping surface increase the energy dissipation efficiency and the relative depth of the downstream by 56.1% and 50.1%, respectively, compared to the simple inclined drop.
Daneshfaraz et al. [30] compared the hydraulic parameters of solid and gabion inclined drops. The results showed that with gabion type, the relative energy loss and downstream relative depth increase by 82% and 50%, respectively. Daneshfaraz, Majedi Asl, and Bagherzadeh [29] conducted an experimental study of energy dissipation and relative depth of the inclined gabion drops. The results showed that gabions increased energy dissipation and relative depth downstream compared to simple drops. Daneshfaraz et al. [31] first investigated the vertical hydraulic parameters of the vertical drop with double horizontal screens experimentally and then by support vector machine model. The experimental and numerical work results showed that the parameters of the relative distance between screens and the porosity of horizontal screens are adequate for the relative length of the inclined drop.
Examining the studies done in the past, it was ensured that the fishway structures had not been done on the inclined drop so far. All the studies done about this structure have been done on the spillways. On the other hand, the effect of fishway elements on energy dissipation has been investigated for the first time in this research. Therefore, in this study, an attempt is made to design an inclined drop with environmental considerations, which at the same time can have the maximum energy dissipation to protect downstream structures and water aeration, in addition to helping water self-purification a structure suitable for fish passage. Turbulence and the formation of mixing water and air are effective ways to increase energy dissipation downstream of the drop. Since the flow regimes upstream of the inclined drop are often subcritical, it becomes critical at the edge of the drop. It becomes supercritical as the flow continues downstream. The destructive kinetic energy resulting from the supercritical flow causes the erosion of the wall and the channel bed. To lose this energy, roughness on the sloping surface and additional structures are usually used. In addition to high operating costs, the use of these methods is created only for energy dissipation, so in the present study, with a new approach to achieve high energy dissipation with economic and environmental considerations, fishway’s elements have been used. In addition to low operating costs and high energy dissipation, these elements can also be used in fish ponds. Because in addition to creating a path for fishes to pass, it increases the supply of oxygen to the water and prevents fish loss due to high water energy. The rest of the paper is organized as follows: Section 2 presents all procedures related to the experimental work conducted in laboratory conditions; Section 3 shows the main results and the relevance of the main findings from the experimental work. The present study aims to comprehensively investigate the effect of holes and non-holes fishway elements on the performance of an inclined drop in the plain of symmetry principle. Finally, the main conclusions drawn from this study are presented in Section 4.
2. Materials and Methods
2.1. Experimentally Equipment
The entire experimental work was conducted in laboratory conditions. The experimental flume types of equipment are presented along with the specifications of the research model in Table 1.

Table 1.
Specifications of laboratory flume and installed types of equipment.
In the present study, the depths of the flow at specific points (i.e., in five points of the channel width were taken), and the average of these five depths was considered the final depth. This technique has been used in previous studies, such as Daneshfaraz, Bagherzadeh, Esmaeeli, Norouzi, and Abraham [31] and Ghaderi et al. [32]. The flow rate used in the present study was considered from 200~600 L per minute. The experimental model includes a simple inclined drop as a control model, an inclined drop equipped with hole and non-hole fishways. A vertical sluice gate downstream of the laboratory flume has also stabilized the hydraulic jump [33]. A general schematic presentation of the flume is provided together with the prototype models in Figure 1.
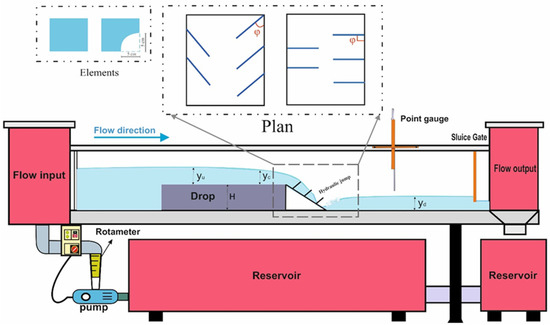

Figure 1.
General schematic and actual image of laboratory flume and prototype models tested in this study.
2.2. Dimensional Analysis
Considering the geometric and hydraulic properties of the present research models, the effective parameters for the inclined drop together with the fishway elements are presented in Equation (1).
where: q is the discharge unit width, H is the height of the drop, θ is slope angle with the horizon, yu is upstream flow depth, yc is critical depth, yd is downstream flow depth, μ is dynamic viscosity, ρ is density, g is gravity acceleration, φ is the angle of position of fishway elements, a and b are the length and height of the opening of the elements, respectively, x is the distance of the elements from each other, Lair is aeration length, Lj is the length of a hydraulic jump, Eu and Ed are upstream and downstream specific energy, respectively.
Using the Pi–Buckingham method, dimensional analysis was performed. By considering parameters ρ, g, and H as iterative parameters, Equation (2) was obtained.
By simplifying and dividing some dimensionless parameters, Equation (3) was obtained as follows.
As the Reynolds number range of the present study is between 38,986 to 582,857. The current is turbulent in all models, so the Reynolds number’s dimensional parameter can be ignored [17,34,35]. Parameters x/H and θ were also eliminated due to their constant values. As the upstream flow regime of the models is subcritical and its range is 0.5~0.8, the effect of the upstream Froude number parameter can be ignored [26]. Therefore, dimensionless dependent parameters are presented for the model of non-hole elements according to Equation (4), and dimensionless dependent parameters are presented for the model of hole elements according to Equation (5).
2.3. Specific Energy Equations and Evaluation Criteria
Equations (6)–(8) are used to calculate the upstream and downstream energy of the inclined drop and the relative energy dissipation, respectively.
Based on the experiments, equations for estimating the hydraulic parameters of this study are presented. For this purpose, the dependent parameter was considered as a function of independent parameters. To obtain the equations, 80% of the experimental data were randomly selected and used as input. Using the GRG Nonlinear algorithm in Excel, the coefficients were obtained by trial and error. The remaining 20% of the data was used to validate the obtained equations. Also, statistical indices of correlation coefficient (R2), root mean square error (RMSE), relative error (Erelative error), and Kling–Gupta statistic (KGE) were used to evaluate the quality of equations.
In the above equations, MExp is laboratory data, MCal is calculated data from extractive equations, N is the number of data, and are the sum of laboratory and computational data, and are the average of laboratory and computational data, respectively. It should be noted that the best solution is when the RMSE coefficient is zero, and the R2 coefficient is one [36]. The quality range of the KGE coefficient is as follows.
Table 2 presents the prototype models tested in this study, abbreviated with the symbols M1 to M7 for convenience and ease of expression.

Table 2.
The models examined in this study.
2.4. Study’s Limitations
In this study, due to some bureaucratic issues, we could not test the performance of fish movements through the proposed elements. The ability of these elements to facilitate the fish movements was based solely on the assessment of specific hydraulic variables that are key in facilitating the fish movements [37]. Based on previous studies on similar topics [38,39], we assumed that the proposed fish elements would be particularly effective for European eels (Anguilla anguilla). One of the limitations of the proposed fishway elements investigated in this study is related to the hole geometry functionality. Over time and with the accumulation of debris in the holes of these elements, the holes may be blocked, and the function of these cavities to enable fish movement will be impaired. Therefore, these elements should be checked regularly, and if it is blocked, it should be removed. In addition, future studies of special interest could involve testing different fish elements geometry under various hydraulic conditions, while considering different fish species as well.
3. Results and Discussion
3.1. Experimentally Observations
This study consists solely of the hydraulic performance assessment of the prototype models; we did not test fishes’ performance due to the small size of the models. Therefore, the conclusion on the ability of these fishway elements to support downstream fish passage is also based on the fish requirements concerning specific hydraulic parameters such as flow depth, velocity, and regime type [14,15,17]. According to the laboratory findings, it was observed that the flow passes through the M1 model with the least energy dissipation and transmits the high-energy flow downstream of the inclined drop (Figure 2a). In this study, by adding fishway elements, it was observed that these elements act as an obstacle against the flow and by colliding the flow with these elements, which along with impact, change of direction, and collision of flow lines with each other on the drop structure it causes energy loss. Figure 2 shows the flow through an inclined drop equipped with fishway elements with the same hydraulic conditions. During the experiments, it was observed that in the inclined drop equipped with fishway elements non-hole at an angle of 90 degrees, the flow in all discharges overflows from the elements and moves downstream. When the flow falls from these elements, it enables aeration of the water flow, which creates turbulence that increases energy loss, causing oxygen delivery to the water. If there is fish in the oxygen system, the fish needs are provided and, at the same time to helps fish move in a controlled way downstream of the obstacle [10,40]. In an inclined drop equipped with hole fishway elements at all angles, part of the flow is created from the hole due to the presence of the cavity. The other part passes through the elements in a spiral. However, due to the presence of this hole, the flow does not overflow from the fishway elements, unlike the model’s non-hole (Figure 2e–g), because a considerable amount of flow is transmitted downstream through the holes created.


Figure 2.
Flow on an inclined drop equipped with fishway elements: (a) Smooth drop (Model M1); (b) Model M2; (c) Model M3 (d) Model M4; (e) Model M5; (f) Model M6; (g) Model M7.
Therefore, according to the above results, if the purpose of using fishway elements is energy dissipation, non-hole elements are more suitable due to increased energy dissipation; however, if the purpose of designing these elements is also environmental issues, hole elements are recommended because of the presence of a hole, the movement of fish and aquatic animals through these pores is much easier and more minor damage is done to aquatic animals [41,42,43].
3.2. Energy Dissipation
The values of the relative energy dissipation changes for the tested models are presented in Figure 3. It is observed that the relative critical depth is inversely related to the relative energy dissipation of the flow; in other words, the relative energy dissipation decreases with increasing relative critical depth.
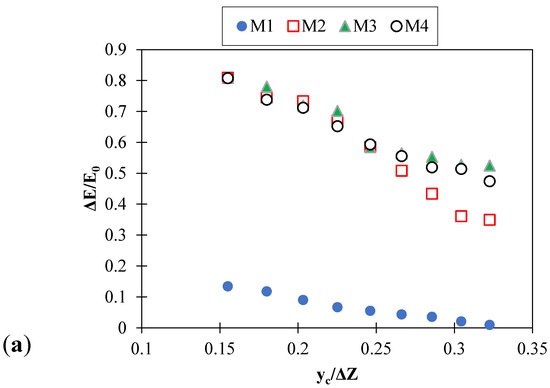
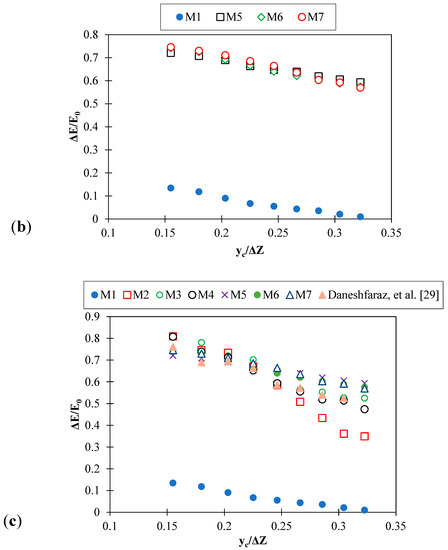
Figure 3.
Relative energy dissipation changes versus relative critical depth: (a) fishway elements without holes; (b) fishway elements with holes; (c) compare models with each other.
A simple inclined drop has the lowest energy dissipation, and the M7 model has the highest energy dissipation. For low-flow discharges, among the models with non-hole fishway elements, the M3 model has better performance. For the hole elements, the M7 model has the highest energy dissipation. Examining the angles of the elements, it is concluded that an angle of 60 degrees is a good option for non-hole elements in terms of energy dissipation. In contrast, for hole elements, an angle of 45 degrees has the best performance in terms of energy dissipation. The energy dissipation values for hole fishway elements are slightly different from those non-hole types, which can be attributed to the fact that no flow overflows from the elements even at high flow rates.
In general, the inclusion of fishway elements increases the flow energy dissipation by an average of 88% compared to a simple inclined drop, which is a significant reduction. Increasing the flow rate increases the safety of the downstream structures, reduces the flow’s destructive energy, scouring the bed and channel walls, and provides better conditions for fish passing through the structure [20,26]. The energy dissipation results of the present study were also compared with the results of the Daneshfaraz, Majedi Asl, and Bagherzadeh [29] study, which investigated the energy dissipation of inclined gabion drop. According to Figure 3c, the use of fishway hole elements increases the energy dissipation rate by 40.31% compared to the inclined gabion.
3.3. Relative Downstream Depth
Figure 4 shows the changes in the relative downstream depth versus the relative critical depth for all models in the present study.
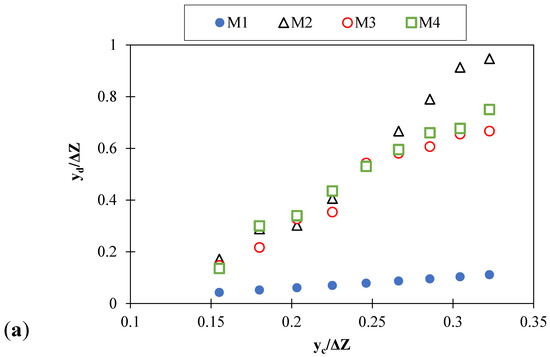
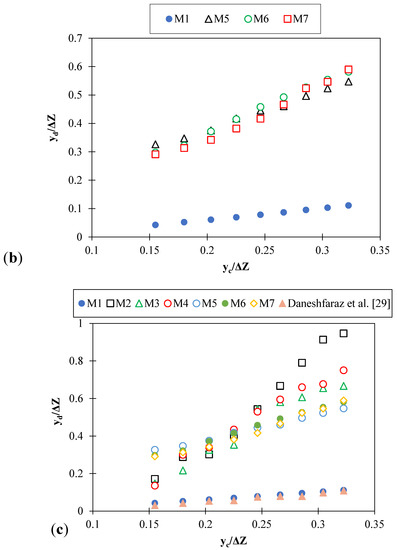
Figure 4.
Relative downstream depth changes versus relative critical depth: (a) fishway elements without holes; (b) fishway elements with holes; (c) compare models with each other.
As the relative critical depth increases for all models, the trend of downstream relative depth increases. It can be seen that the use of fishway elements has significantly increased the downstream depth [44]. Increasing the relative downstream depth for a simple inclined drop equipped with hole fishway elements is a gentle slope. In contrast, for inclined drop models with a non-hole element, this trend is more sloping. Of the seven models studied, it is clear that M2 has the highest relative downstream depth overall. This is more understandable at the end flow rates where the flow velocity increases. The elements of model M2 achieve a greater relative downstream depth by being positioned 90 degrees to the flow. The main advantage of increasing the downstream water depth is a significant reduction in the Froude number, which will cause a little turbulence in the flow.
On the other hand, due to the increase in water depth downstream in terms of the design of the stilling basins, the height of the sidewalls of the stilling basins should be increased. The results of the relative downstream depth were compared with the results of Daneshfaraz, Majedi Asl, and Bagherzadeh [29], which investigated the energy dissipation of inclined gabion drop. As shown in Figure 4c, the use of fishway elements increases the relative downstream depth by 85.66% compared to the inclined gabion.
3.4. Relative Aeration Length
By examining the data obtained from the experimental results presented in Figure 5, for all the present study models, by increasing the relative critical depth parameter, the relative aeration length is also increased. For all relative critical depths, model M2 has the maximum flow aeration length.

Figure 5.
Relative aeration length changes versus relative critical depth.
Changing the angle of the element also changes the amount of air entering the water. For a constant relative critical depth, the relative aeration length values are also increased by increasing the element angle. The more vertical the elements are in front of the stream, the more strongly the flow strikes the elements and causes good aeration. Aeration causes, in addition to the entry of oxygen into the water, which causes the water to purify itself, it also reduces the speed of the inlet flow downstream. This reduction in flow velocity effectively protects existing structures and prevents scouring and channel flooring issues.
3.5. Relative Length of Hydraulic Jump and Downstream Froude Number
Figure 6 shows the relative length changes of hydraulic jump versus the relative critical depth. The trend of changes in the relative length of the hydraulic jump is upward the relative critical depth. For elementary discharges, the rate of change is almost the same for all models. The M1 model has the lowest relative length of the hydraulic jump. By increasing the flow rate, the M2 model had a good performance in increasing the relative length of the hydraulic jump. Increasing this length causes more energy to be wasted from the flow and a hydraulic jump to occur inside the stilling basins.
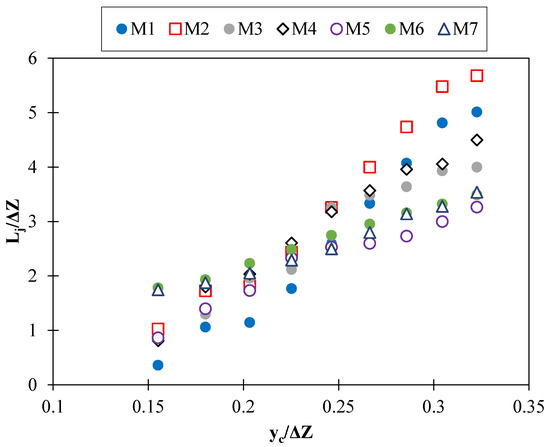
Figure 6.
Relative jump length changes versus relative critical depth.
To form a hydraulic jump inside the stilling basins, the depth of the bottom needs to be considered, and measures such as increasing or decreasing the level of the channel bed. are required; however, with the use of fishways, hydraulic jumps occur inside the stilling basins, and the downstream flow becomes subcritical. Figure 7 shows the variation of the downstream Froude number of the inclined drop equipped with fishway elements against the relative critical depth.
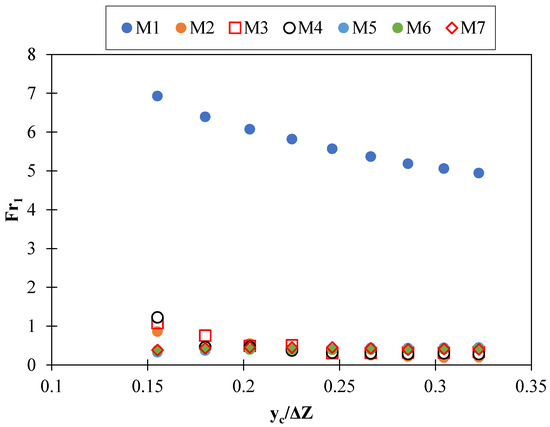
Figure 7.
Downstream Froude number changes versus relative critical depth.
Carefully inferred from this figure, the downstream Froude number of the inclined drop equipped with fishways is significantly reduced, so that these elements reduce the Froude number by 93% compared to a simple inclined drop. Models M6 and M7 reduce the downstream Froude number by a minimal difference compared to other models. Changing the angle and using a hole in fishway structures do not significantly reduce the Froude number. A significant decrease in the Froude number of flow regimes is desirable. The reducing Froude number has several benefits: design and implementation of stilling basin with smaller dimensions, reducing scour the seabed, increased confidence in the sustainability of existing structures downstream, and suitable habitat conditions for the aquatic animals. Designers and consultants should carefully consider this issue in the economical and eco-friendly design of stilling basins.
3.6. Experimental Equations
Experimental equations were presented to investigate the effect of independent parameters and estimate the relative energy dissipation and the relative downstream depth values. The equations are obtained using the solver command in an excel sheet. Nearly 80% of the data were selected for training to extract these equations, and 20% were selected for testing. Equations (13) and (14) used for calculating the parameters above for non-hole and hole are presented below.
The values of its constant parameters and the evaluation criteria are listed in Table 3. After extracting the experimental equations to estimate the relative downstream depth and the relative energy dissipation, the values obtained from the experimental data are compared with the values obtained from Equations (13) and (14). The results are shown in Figure 8.

Table 3.
Value of constant parameters of Equations (13) and (14).
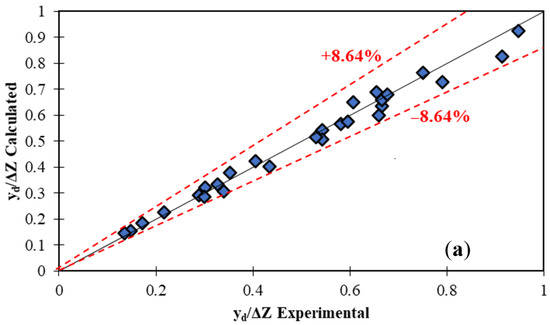
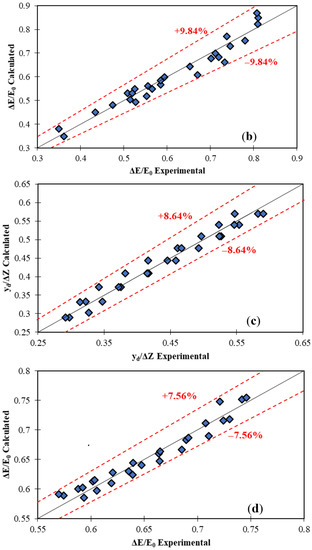
Figure 8.
Compare experimental data with calculated data from Equations (13) and (14): (a) relative downstream depth for Equation (13); (b) relative energy dissipation for Equation (13); (c) relative downstream depth for Equation (14); (d) relative energy dissipation for Equation (14).
Figure 8 shows a comparison of experimentally with calculated data from Equations (13) and (14) for relative downstream depth and relative energy dissipation. Based on Figure 8a,b, Equation (13) can estimate relative downstream depth values and relative energy dissipation with a maximum relative error of ±8.64% and ±9.84% for the M2, M3, and M4 models, respectively. According to Figure 8c,d, Equation (14) can estimate relative downstream depth values and relative energy dissipation with maximum relative error ±8.64% and ±7.56% for the M5, M6, and M7 models, respectively. The values of the evaluation parameters, which include the RMSE, R2, and KGE criteria, are detailed in Table 3.
4. Conclusions
In this study, the effect of fishway elements on the parameters of relative downstream depth, energy dissipation, aeration length, length of a hydraulic jump, and downstream Froude number in the inclined drop structure was experimentally investigated. To achieve the objectives of this study, 81 experiments were performed for three types of simple inclined drop, equipped with hole and non-hole fishway elements and a flow rate of 200 to 600 L per minute. The results showed that:
- By increasing the relative critical depth parameter, the relative energy dissipation decreases. The simple inclined drop has the lowest energy dissipation, and the M7 model has the highest energy dissipation. Adding fishway elements to a simple inclined drop increases the flow energy dissipation by an average of 88%, which is a significant value.
- Model M2 has the maximum length of flow aeration. By reducing the angle of the element, the amount of air entering the water also decreases. Increasing the amount of aeration and energy dissipation of the flow reduces the outlet flow downstream. It prevents scouring and foaming problems of the channel. In addition to the positive economic impact, increasing aeration is of particular importance on aquatic animals.
- For all models, the relative depth of the downstream is directly related to the relative critical depth. The use of fishway elements has significantly increased the downstream depth. The M2 model has the highest relative depth of the downstream overall.
- The use of fishway elements on the inclined drop structure causes more energy to be lost from the flow and a hydraulic jump to occur inside the stilling basins. On the other hand, these elements significantly reduce the Froude number for all relative critical depths, which is an essential point in the design of inclined drops.
- The advantages of using fishway elements in comparison with other dissipating structures, in addition to environmental considerations, are also economic considerations. Some dissipators, such as screens and stilling basins, are expensive costs to build. However, in addition to environmental considerations, fishway structures have a meager construction cost. They have also helped a lot in energy dissipation.
As the hydraulic structure construction is still expanding due to the rising demand for water supply and renewable energy, developing and testing innovative fishway designs is imperative to improve these facilities. In this regard, particularly in Mediterranean regions and other arid and/or semi-arid regions, discharge-efficient passage systems are needed. Therefore, future studies should consider testing eco-friendly and sustainable fishways design considering also testing the passage performance of specific native fish species in those new fishways designs.
Author Contributions
Conceptualization, R.D., E.A., M.B., A.G., A.K., A.N. and A.M.R.; methodology, E.A., A.G., A.K., experimental set-up, A.N. and E.A.; validation, E.A., M.B., A.G. and A.K.; formal analysis, E.A., A.G. and A.K.; investigation, R.D., E.A., M.B., A.G., A.K., A.N. and A.M.R.; resources, E.A. and A.G.; data curation, E.A. and A.G.; writing—original draft preparation, R.D., E.A., M.B., A.G., A.K. and A.N.; writing—review and editing, R.D., E.A., M.B., A.G., A.K. and A.M.R.; visualization, E.A. and A.G.; supervision, R.D.; project administration, R.D. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the articles.
Acknowledgments
A.K. and A.M.R. acknowledge the support of the Portuguese Foundation for Science and Technology (FCT) through the project PTDC/CTA-OHR/30561/2017 (WinTherface).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jager, H.I.; Chandler, J.A.; Lepla, K.B.; Van Winkle, W. A Theoretical Study of River Fragmentation by Dams and its Effects on White Sturgeon Populations. Environ. Biol. Fishes 2001, 60, 347–361. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological impacts of run-of-river hydropower plants—Current status and future prospects on the brink of energy transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
- Andersson, E.; Nilsson, C.; Johansson, M. Effects of river fragmentation on plant dispersal and riparian flora. Regul. Rivers Res. Manag. Int. J. Devoted River Res. Manag. 2000, 16, 83–89. [Google Scholar] [CrossRef]
- van Puijenbroek, P.J.; Buijse, A.D.; Kraak, M.H.; Verdonschot, P.F. Species and river specific effects of river fragmentation on European anadromous fish species. River Res. Appl. 2019, 35, 68–77. [Google Scholar] [CrossRef]
- Heino, J.; Virkkala, R.; Toivonen, H. Climate change and freshwater biodiversity: Detected patterns, future trends and adaptations in northern regions. Biol. Rev. 2009, 84, 39–54. [Google Scholar] [CrossRef]
- Moss, B.; Hering, D.; Green, A.J.; Aidoud, A.; Becares, E.; Beklioglu, M.; Bennion, H.; Boix, D.; Brucet, S.; Carvalho, L.; et al. Climate Change and the Future of Freshwater Biodiversity in Europe: A Primer for Policy-Makers. Freshw. Rev. 2009, 2, 103–130. [Google Scholar] [CrossRef]
- Belletti, B.; Garcia de Leaniz, C.; Jones, J.; Bizzi, S.; Börger, L.; Segura, G.; Castelletti, A.; van de Bund, W.; Aarestrup, K.; Barry, J.; et al. More than one million barriers fragment Europe’s rivers. Nature 2020, 588, 436–441. [Google Scholar] [CrossRef]
- Lucas, M.C.; Bubb, D.H.; Jang, M.H.; Ha, K.; Masters, J.E. Availability of and access to critical habitats in regulated rivers: Effects of low-head barriers on threatened lampreys. Freshw. Biol. 2009, 54, 621–634. [Google Scholar] [CrossRef]
- Branco, P.; Amaral, S.D.; Ferreira, M.T.; Santos, J.M. Do small barriers affect the movement of freshwater fish by increasing residency? Sci. Total. Environ. 2017, 581, 486–494. [Google Scholar] [CrossRef] [PubMed]
- Bestgen, K.R.; Mefford, B.; Compton, R.I. Mortality and injury rates for small fish passing over three diversion dam spillway models. Ecol. Eng. 2018, 123, 141–150. [Google Scholar] [CrossRef]
- Rytwinski, T.; Algera, D.A.; Taylor, J.J.; Smokorowski, K.E.; Bennett, J.R.; Harrison, P.M.; Cooke, S. What are the consequences of fish entrainment and impingement associated with hydroelectric dams on fish productivity? A systematic review protocol. Environ. Evid. 2017, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Clay, C.H. Design of Fishways and Other Fish Facilities; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Boiten, W. Flow measurement structures. Flow Meas. Instrum. 2002, 13, 203–207. [Google Scholar] [CrossRef]
- Rodríguez, T.T.; Agudo, J.P.; Mosquera, L.P.; González, E.P. Evaluating vertical-slot fishway designs in terms of fish swimming capabilities. Ecol. Eng. 2006, 27, 37–48. [Google Scholar] [CrossRef]
- Romão, F.; Branco, P.; Quaresma, A.L.; Amaral, S.D.; Pinheiro, A.N. Effectiveness of a multi-slot vertical slot fishway versus a standard vertical slot fishway for potamodromous cyprinids. Hydrobiologia 2018, 816, 153–163. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Katopodis, C.; Solanki, S. New designs for vertical slot fishways. Can. J. Civil. Eng. 1992, 19, 402–414. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Van der Vinne, G.; Katopodis, C. Hydraulics of vertical slot fishways. J. Hydraul. Eng. 1986, 112, 909–927. [Google Scholar] [CrossRef]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of flow in vertical slot fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Puertas, J.; Pena, L.; Teijeiro, T. Experimental approach to the hydraulics of vertical slot fishways. J. Hydraul. Eng. 2004, 130, 10–23. [Google Scholar] [CrossRef]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Mean flow and turbulence structure in vertical slot fishways. J. Hydraul. Eng. 2006, 132, 765–777. [Google Scholar] [CrossRef]
- Yagci, O. Hydraulic aspects of pool-weir fishways as ecologically friendly water structure. Ecol. Eng. 2010, 36, 36–46. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Aminvash, E.; Ghaderi, A.; Kuriqi, A.; Abraham, J. Three-Dimensional Investigation of Hydraulic Properties of Vertical Drop in the Presence of Step and Grid Dissipators. Symmetry 2021, 13, 895. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Aminvash, E.; Ghaderi, A.; Abraham, J.; Bagherzadeh, M. SVM Performance for Predicting the Effect of Horizontal Screen Diameters on the Hydraulic Parameters of a Vertical Drop. Appl. Sci. 2021, 11, 4238. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A.; Di Francesco, S.; Khajei, N. Experimental study of the effect of horizontal screen diameter on hydraulic parameters of vertical drop. Water Supply 2021. [Google Scholar] [CrossRef]
- Wagner, W. Hydraulic model studies of the check intake structure-potholes east canal. Bur. Reclam. Hydraul. Lab. Rep. Hyd. 1956, 411, 7. [Google Scholar]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1964.
- Bos, M.G.; Replogle, J.A.; Clemmens, A.J. Flow Measuring Flumes for Open Channel Systems; John Wiley & Sons Inc.: New York, NY, USA, 1984; Volume 19, 321p, ISBN Z-0471-80637-4. [Google Scholar]
- Sholichin, M.; Akib, S. Development of drop number performance for estimate hydraulic jump on vertical and sloped drop structure. Int. J. Phys. Sci. 2010, 5, 1678–1687. [Google Scholar]
- Daneshfaraz, R.; Majedi Asl, M.; Bagherzadeh, M. Experimental Investigation of the Energy Dissipation and the Downstream Relative Depth of Pool in the Sloped Gabion Drop and the Sloped simple Drop. Amirkabir J. Civil. Eng. 2021, 53, 4-4. [Google Scholar]
- Daneshfaraz, R.; Bagherzadeh, M.; Ghaderi, A.; Di Francesco, S.; Majedi Asl, M. Experimental investigation of gabion inclined drops as a sustainable solution for hydraulic energy loss. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Bagherzadeh, M.; Esmaeeli, R.; Norouzi, R.; Abraham, J. Study of the performance of support vector machine for predicting vertical drop hydraulic parameters in the presence of dual horizontal screens. Water Supply 2020, 21, 217–231. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Torabi, M.; Abraham, J.; Azamathulla, H.M. Experimental investigation on effective scouring parameters downstream from stepped spillways. Water Supply 2020, 20, 1988–1998. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A.; Akhtari, A.; Di Francesco, S. On the Effect of Block Roughness in Ogee Spillways with Flip Buckets. Fluids 2020, 5, 182. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Aminvash, E.; Esmaeli, R.; Sadeghfam, S.; Abraham, J.; Vol, E. Experimental and numerical investigation for energy dissipation of supercritical flow in sudden contractions. J. Groundw. Sci. 2020, 8, 396–406. [Google Scholar]
- Ghaderi, A.; Abbasi, S. Experimental and Numerical Study of the Effects of Geometric Appendance Elements on Energy Dissipation over Stepped Spillway. Water 2021, 13, 957. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Shokri, M.; Abraham, J. Estimation of Actual Evapotranspiration Using the Remote Sensing Method and SEBAL Algorithm: A Case Study in Ein Khosh Plain, Iran. Hydrology 2020, 7, 36. [Google Scholar] [CrossRef]
- Silva, A.T.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N.; Katopodis, C. Effects of water velocity and turbulence on the behaviour of Iberian barbel (Luciobarbus bocagei, Steindachner 1864) in an experimental pool-type fishway. River Res. Appl. 2011, 27, 360–373. [Google Scholar] [CrossRef]
- Silva, A.; Katopodis, C.; Tachie, M.; Santos, J.; Ferreira, M. Downstream swimming behaviour of catadromous and potamodromous fish over spillways. River Res. Appl. 2016, 32, 935–945. [Google Scholar] [CrossRef]
- Urban, A.; Gulliver, J.S.; Johnson, D. Modeling total dissolved gas concentration downstream of spillways. J. Hydraul. Eng. 2008, 134, 550–561. [Google Scholar] [CrossRef]
- Hou, H.; Deng, Z.D.; Martinez, J.J.; Fu, T.; Duncan, J.P.; Johnson, G.E.; Lu, J.; Skalski, J.R.; Townsend, R.L.; Tan, L. A Hydropower Biological Evaluation Toolset (HBET) for Characterizing Hydraulic Conditions and Impacts of Hydro-Structures on Fish. Energies 2018, 11, 990. [Google Scholar] [CrossRef] [Green Version]
- Algera, D.A.; Rytwinski, T.; Taylor, J.J.; Bennett, J.R.; Smokorowski, K.E.; Harrison, P.M.; Clarke, K.D.; Enders, E.C.; Power, M.; Bevelhimer, M.S.; et al. What are the relative risks of mortality and injury for fish during downstream passage at hydroelectric dams in temperate regions? A systematic review. Environ. Evid. 2020, 9, 3. [Google Scholar] [CrossRef]
- Goodman, D.H.; Reid, S.B. Climbing above the competition: Innovative approaches and recommendations for improving Pacific Lamprey passage at fishways. Ecol. Eng. 2017, 107, 224–232. [Google Scholar] [CrossRef]
- Côrtes, M.O.; Peressin, A.; Godinho, A.L. Less effort but equal result: Introducing the daily run-size estimation method for quantifying fish passage in fishways. PLoS ONE 2021, 16, e0252183. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Majedi Asl, M.; Bazyar, A.; Abraham, J.; Norouzi, R. The laboratory study of energy dissipation in inclined drops equipped with a screen. J. Appl. Water Eng. Res. 2020, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).