On Symmetrical Methods for Charged Particle Dynamics
Abstract
:1. Introduction
2. Energy-Conserving Methods
3. Numerical Experiments
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Brugnano, L.; Montijano, J.I.; Rández, L. High-order energy-conserving Line Integral Methods for charged particle dynamics. J. Comput. Math. 2019, 396, 209–227. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Zhang, S.X.; Xiao, J.Y.; Liu, J.; Sun, Y.J.; Tang, W.M. Why is Boris algorithm so good? Phys. Plasmas 2013, 20, 084503. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Wang, B. Efficient energy-preserving methods for charged-particle dynamics. Appl. Math. Comput. 2019, 361, 703–714. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Iavernaro, F.; Zhang, R. Arbitrarily high-order energy-preserving methods for simulating the gyrocenter dynamics of charged particles. J. Comput. Appl. Math. 2020, 380, 112994. [Google Scholar] [CrossRef]
- Cao, W.; Li, D.; Zhang, Z. Optimal Superconvergence of Energy Conserving Local Discontinuous Galerkin Methods for Wave Equations. Commu. Comput. Phys. 2017, 21, 211–236. [Google Scholar] [CrossRef]
- Sanz-Serna, J.M. Runge-Kutta schemes for Hamilton systems. BIT Numer. Math. 1988, 28, 877–883. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cooper, G.J. Stability of Runge–Kutta Methods for Trajectory Problems. IMA J. Numer. Anal. 1987, 7, 1–13. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Line Integral Solution of Hamiltonian. PDEs Math. 2019, 7, 275. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Xu, J.; Yang, J. The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 2018, 353, 407–416. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J.; Yang, J. A New Class of Efficient and Robust Energy Stable Schemes for Gradient Flows. SIAM Rev. 2019, 61, 474–506. [Google Scholar] [CrossRef] [Green Version]
- Akrivis, G.; Li, B.; Li, D. Energy–Decaying Extrapolated RK–SAV Methods for the Allen–Cahn and Cahn–Hilliard Equations. SIAM J. Sci. Comput. 2019, 41, A3703–A3727. [Google Scholar] [CrossRef]
- Li, D.; Sun, W. Linearly implicit and high-order energy-conserving schemes for nonlinear wave equations. J. Sci. Comput. 2020, 83, 65. [Google Scholar] [CrossRef]
- Li, X.; Wen, J.; Li, D. Mass- and energy-conserving difference schemes for nonlinear fractional Schrödinger equations. Appl. Math. Lett. 2021, 111, 106686. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, X.; Song, S. Novel high–order energy–preserving diagonally implicit Runge–Kutta schemes for nonlinear Hamiltonian ODEs. Appl. Math. Lett. 2020, 102, 106091. [Google Scholar] [CrossRef]
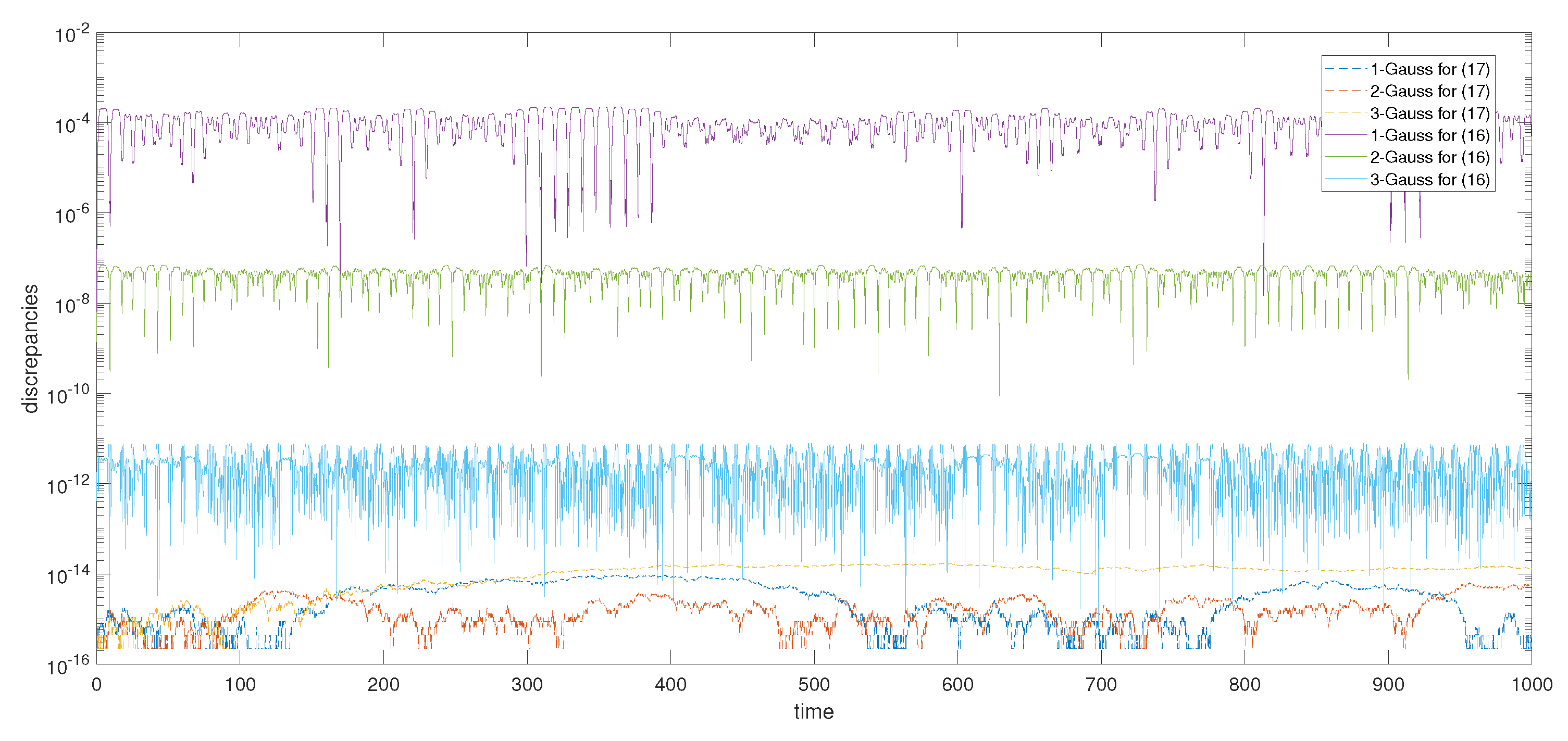
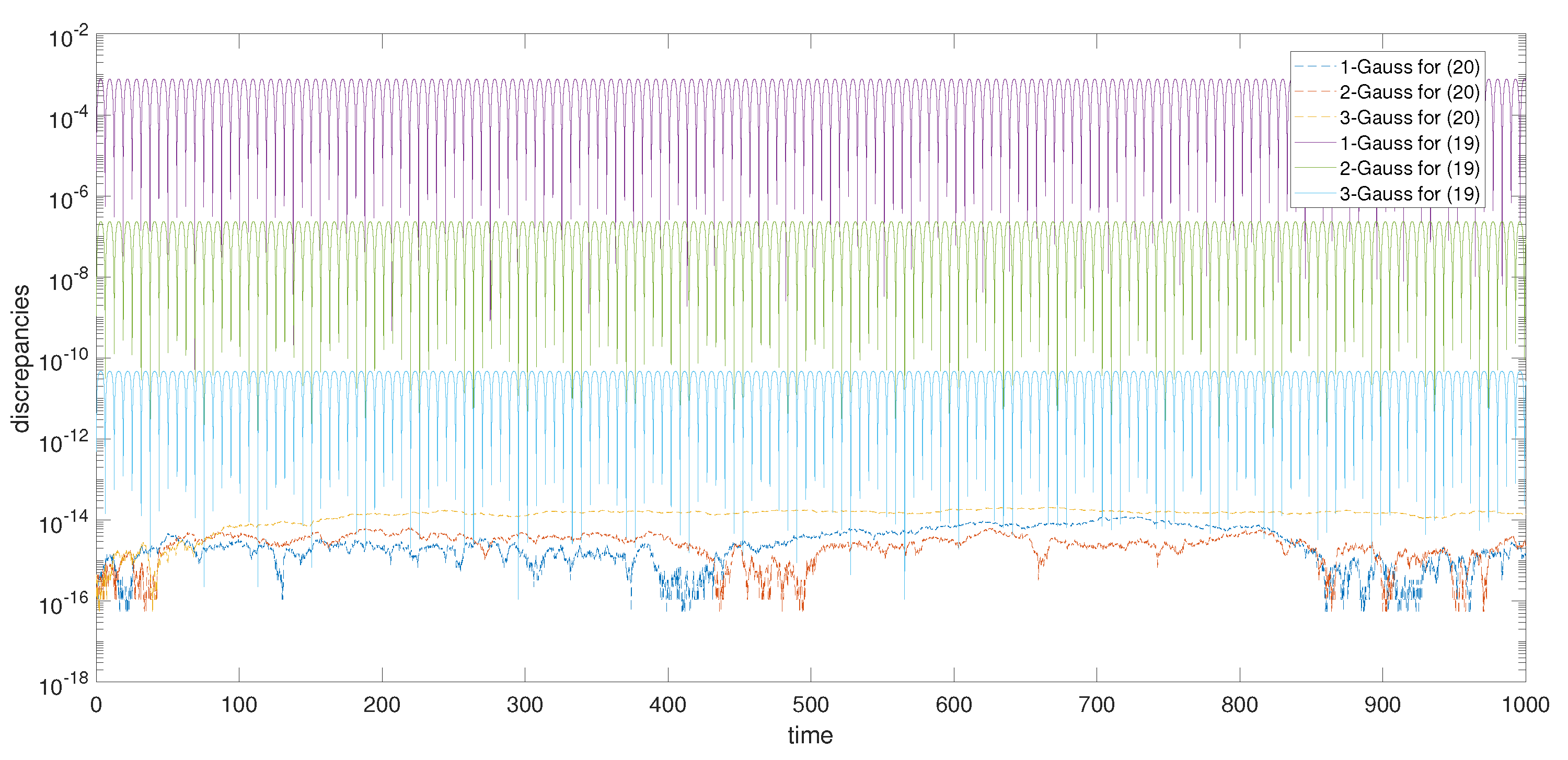
| Method | h | p | q | r | |||
|---|---|---|---|---|---|---|---|
| e | Order | e | Order | e | Order | ||
| 1/10 | 7.06E−2 | - | 2.45E−2 | - | 7.49E−3 | - | |
| 1-Gauss | 1/20 | 1.18E−2 | 1.98 | 6.27E−3 | 1.97 | 1.89E−3 | 1.99 |
| 1/40 | 4.50E−3 | 1.98 | 1.58E−3 | 1.98 | 4.74E−4 | 1.99 | |
| 1/80 | 1.13E−3 | 1.99 | 3.95E−3 | 1.99 | 1.19E−4 | 1.99 | |
| 1/10 | 4.75E−4 | - | 1.26E−4 | - | 4.82E−5 | - | |
| 2-Gauss | 1/20 | 3.00E−5 | 3.99 | 8.09E−6 | 3.97 | 3.69E−6 | 3.71 |
| 1/40 | 1.88E−6 | 3.99 | 5.08E−7 | 3.98 | 2.30E−7 | 3.85 | |
| 1/80 | 1.18E−7 | 3.99 | 3.18E−8 | 3.99 | 1.45E−8 | 3.90 | |
| 1/10 | 3.10E−6 | - | 6.79E−7 | - | 4.41E−7 | - | |
| 3-Gauss | 1/20 | 5.22E−8 | 5.90 | 1.09E−8 | 5.96 | 9.96E−9 | 5.47 |
| 1/40 | 8.19E−10 | 5.94 | 1.73E−10 | 5.97 | 1.51E−10 | 5.76 | |
| 1/80 | 1.28E−11 | 5.96 | 2.71E−12 | 5.98 | 2.34E−12 | 5.84 | |
| Method | h | p | q | r | |||
|---|---|---|---|---|---|---|---|
| e | Order | e | Order | e | Order | ||
| 1/10 | 1.14E−4 | - | 1.27E−4 | - | 3.39E−5 | - | |
| 1-Gauss | 1/20 | 2.86E−5 | 2.00 | 3.18E−5 | 2.00 | 8.49E−6 | 2.00 |
| 1/40 | 7.14E−6 | 2.00 | 7.95E−6 | 2.00 | 2.12E−6 | 2.00 | |
| 1/80 | 1.79E−6 | 2.00 | 1.99E−6 | 2.00 | 5.31E−7 | 2.00 | |
| 1/10 | 3.45E−8 | - | 3.69E−8 | - | 1.03E−8 | - | |
| 2-Gauss | 1/20 | 2.16E−9 | 4.00 | 2.31E−9 | 4.00 | 6.46E−10 | 4.00 |
| 1/40 | 1.35E−10 | 4.00 | 1.44E−10 | 4.00 | 4.04E−11 | 4.00 | |
| 1/80 | 8.43E−12 | 4.00 | 9.02E−12 | 4.00 | 2.52E−12 | 4.00 | |
| 1/4 | 1.03E−9 | - | 1.12E−9 | - | 3.23E−10 | - | |
| 3-Gauss | 1/8 | 1.61E−11 | 6.00 | 1.75E−11 | 6.00 | 5.05E−12 | 6.00 |
| 1/16 | 2.54E−13 | 5.99 | 2.67E−13 | 6.02 | 7.90E−14 | 6.00 | |
| 1/32 | 5.55E−15 | 5.83 | 4.22E−15 | 6.01 | 1.94E−15 | 5.78 | |
| Method | h | p | q | r | |||
|---|---|---|---|---|---|---|---|
| e | Order | e | Order | e | Order | ||
| 1/10 | 1.41E−2 | - | 6.74E−3 | - | 9.77E−3 | - | |
| 1-Gauss | 1/20 | 3.55E−3 | 2.00 | 1.68E−3 | 2.00 | 2.43E−3 | 2.01 |
| 1/40 | 8.89E−4 | 2.00 | 4.21E−4 | 2.00 | 6.07E−4 | 2.00 | |
| 1/80 | 2.22E−4 | 2.00 | 1.05E−4 | 2.00 | 1.52E−4 | 2.00 | |
| 1/10 | 4.38E−6 | - | 2.03E−6 | - | 1.60E−6 | - | |
| 2-Gauss | 1/20 | 2.80E−7 | 3.97 | 1.27E−7 | 4.00 | 1.02E−7 | 3.98 |
| 1/40 | 1.76E−8 | 3.98 | 7.95E−9 | 4.00 | 6.43E−9 | 3.98 | |
| 1/80 | 1.10E−9 | 3.99 | 4.97E−10 | 4.00 | 4.02E−10 | 3.99 | |
| 1/4 | 2.03E−6 | - | 1.39E−6 | - | 8.64E−7 | - | |
| 3-Gauss | 1/8 | 2.73E−8 | 6.21 | 1.62E−8 | 6.42 | 1.20E−8 | 6.17 |
| 1/16 | 4.16E−10 | 6.13 | 2.48E−10 | 6.23 | 1.76E−10 | 6.13 | |
| 1/32 | 6.48E−12 | 6.09 | 3.83E−12 | 6.16 | 2.73E−12 | 6.09 | |
| Method | h | p | q | r | |||
|---|---|---|---|---|---|---|---|
| e | Order | e | Order | e | Order | ||
| 1/4 | 2.43E−3 | - | 5.03E−3 | - | 2.07E−4 | - | |
| 1-Gauss | 1/8 | 6.14E−4 | 1.99 | 1.28E−3 | 1.98 | 5.31E−5 | 1.96 |
| 1/16 | 1.54E−4 | 2.00 | 3.20E−4 | 2.00 | 1.34E−5 | 1.99 | |
| 1/32 | 3.85E−5 | 2.00 | 8.01E−5 | 2.00 | 3.35E−6 | 2.00 | |
| 1/4 | 6.64E−6 | - | 7.73E−6 | - | 1.11E−6 | - | |
| 2-Gauss | 1/8 | 4.15E−7 | 4.00 | 4.87E−7 | 3.99 | 6.90E−8 | 4.00 |
| 1/16 | 2.59E−8 | 4.00 | 3.05E−8 | 4.00 | 4.31E−9 | 4.00 | |
| 1/32 | 1.62E−9 | 4.00 | 1.91E−9 | 4.00 | 2.69E−10 | 4.00 | |
| 1/4 | 2.71E−9 | - | 1.25E−8 | - | 3.80E−10 | - | |
| 3-Gauss | 1/8 | 4.40E−11 | 5.95 | 1.96E−10 | 6.00 | 5.56E−12 | 6.09 |
| 1/12 | 3.88E−12 | 5.99 | 1.73E−11 | 6.00 | 4.86E−13 | 6.01 | |
| 1/16 | 6.90E−13 | 6.01 | 3.07E−12 | 6.00 | 8.93E−14 | 5.89 | |
| Method | h | p | q | r | |||
|---|---|---|---|---|---|---|---|
| e | Order | e | Order | e | Order | ||
| 1/4 | 3.28E−2 | - | 1.36E−2 | - | 8.82E−3 | - | |
| 1-Gauss | 1/8 | 7.86E−3 | 2.06 | 3.27E−3 | 2.05 | 2.04E−3 | 2.11 |
| 1/16 | 1.95E−3 | 2.01 | 8.11E−4 | 2.01 | 5.01E−4 | 2.03 | |
| 1/32 | 4.85E−4 | 2.00 | 2.02E−4 | 2.00 | 1.25E−4 | 2.01 | |
| 1/4 | 8.43E−5 | - | 4.76E−5 | - | 2.24E−5 | - | |
| 2-Gauss | 1/8 | 5.30E−6 | 3.99 | 2.99E−6 | 3.99 | 1.41E−6 | 3.99 |
| 1/16 | 3.32E−7 | 4.00 | 1.87E−7 | 4.00 | 8.84E−8 | 4.00 | |
| 1/32 | 2.08E−8 | 4.00 | 1.17E−8 | 4.00 | 5.53E−9 | 4.00 | |
| 1/4 | 1.14E−7 | - | 8.42E−8 | - | 4.12E−8 | - | |
| 3-Gauss | 1/8 | 1.80E−9 | 5.99 | 1.32E−9 | 6.00 | 6.48E−10 | 5.99 |
| 1/16 | 2.81E−11 | 6.00 | 2.07E−11 | 6.00 | 1.01E−11 | 6.00 | |
| 1/32 | 4.42E−13 | 5.99 | 3.26E−13 | 5.98 | 1.54E−13 | 6.04 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Li, D. On Symmetrical Methods for Charged Particle Dynamics. Symmetry 2021, 13, 1626. https://doi.org/10.3390/sym13091626
Tang R, Li D. On Symmetrical Methods for Charged Particle Dynamics. Symmetry. 2021; 13(9):1626. https://doi.org/10.3390/sym13091626
Chicago/Turabian StyleTang, Renxuan, and Dongfang Li. 2021. "On Symmetrical Methods for Charged Particle Dynamics" Symmetry 13, no. 9: 1626. https://doi.org/10.3390/sym13091626
APA StyleTang, R., & Li, D. (2021). On Symmetrical Methods for Charged Particle Dynamics. Symmetry, 13(9), 1626. https://doi.org/10.3390/sym13091626







