Identifying Influential Nodes in Complex Networks Based on Node Itself and Neighbor Layer Information
Abstract
:1. Introduction
2. Materials and Methods
2.1. Node Influence Based on Node and Neighbor Layer Information
| Algorithm 1. The NINLp Method |
| Input: the network G = (V, E) |
| Output: node influence of NINLp centrality |
| 1: for i = 1 to |V| |
| 2: for j = 1 to |V| |
| 3: calculate the shortest path length between node i and node j |
| 4: end for |
| 5: end for |
| 6: calculate average path length L |
| 7: for i = 1 to |V| |
| 8: calculate the Degree centrality of node i |
| 9: end for |
| 10: for i = 1 to |V| |
| 11: find the neighbor nodes with a radius of ceil(L) from the node i |
| 12: calculate NINL0 of node i according to Equation (1) |
| 13: end for |
| 14: for i = 1 to |V| |
| 15: find the nearest neighbor nodes of node i |
| 16: end for |
| 17: set the value of p |
| 18: Recursively calculate NINLp centrality according to Equation (2) |
| 19: return NINLp centrality |
2.2. Benchmark Methods
2.2.1. Degree Centrality
2.2.2. Betweenness Centrality
2.2.3. Closeness Centrality
2.2.4. Density Centrality
2.2.5. Gravity Model
2.2.6. Clustered Local-Degree (CLD) Method
2.2.7. GLI Method
3. Experimental Data and Evaluation Criteria
3.1. Datasets
3.2. Spreading Model and Evaluation Criteria
3.2.1. SIR Model
3.2.2. CCDF Method
3.2.3. Kendall Correlation Coefficient
3.2.4. Jaccard Similarity Coefficient
4. Experiment and Analysis
4.1. Discrimination Experiment
4.2. Accuracy Experiment
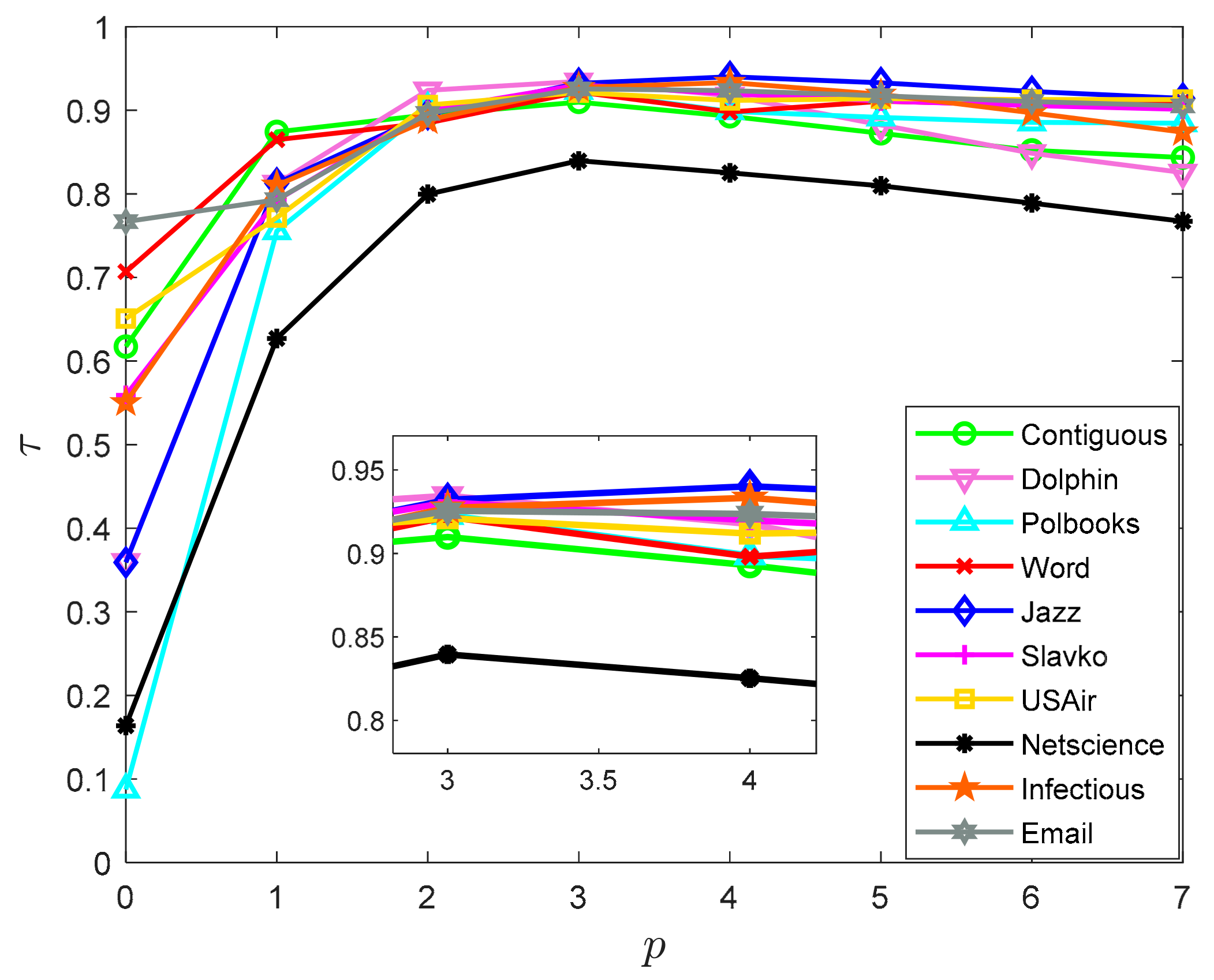
4.2.1. Selection of p-Value
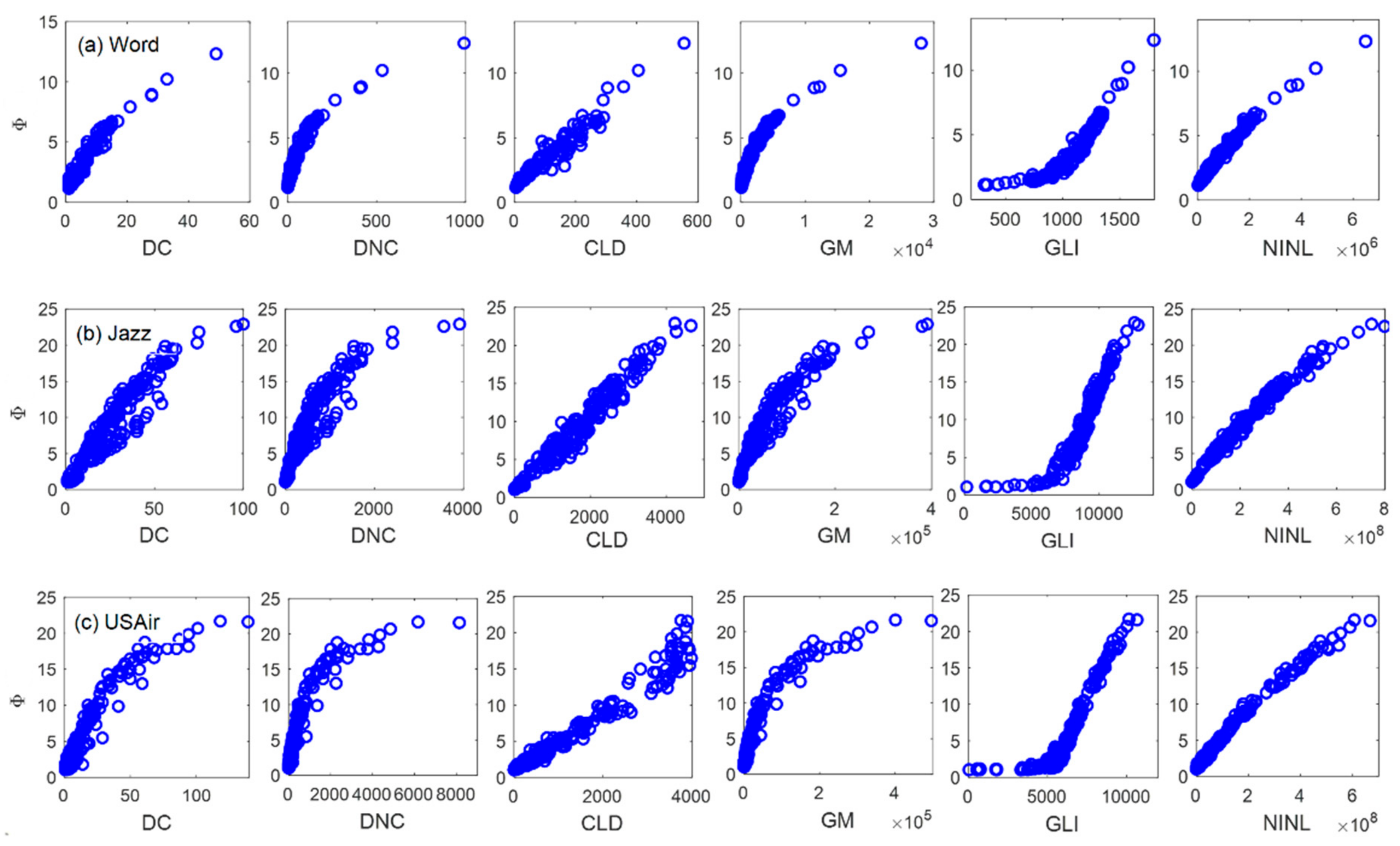
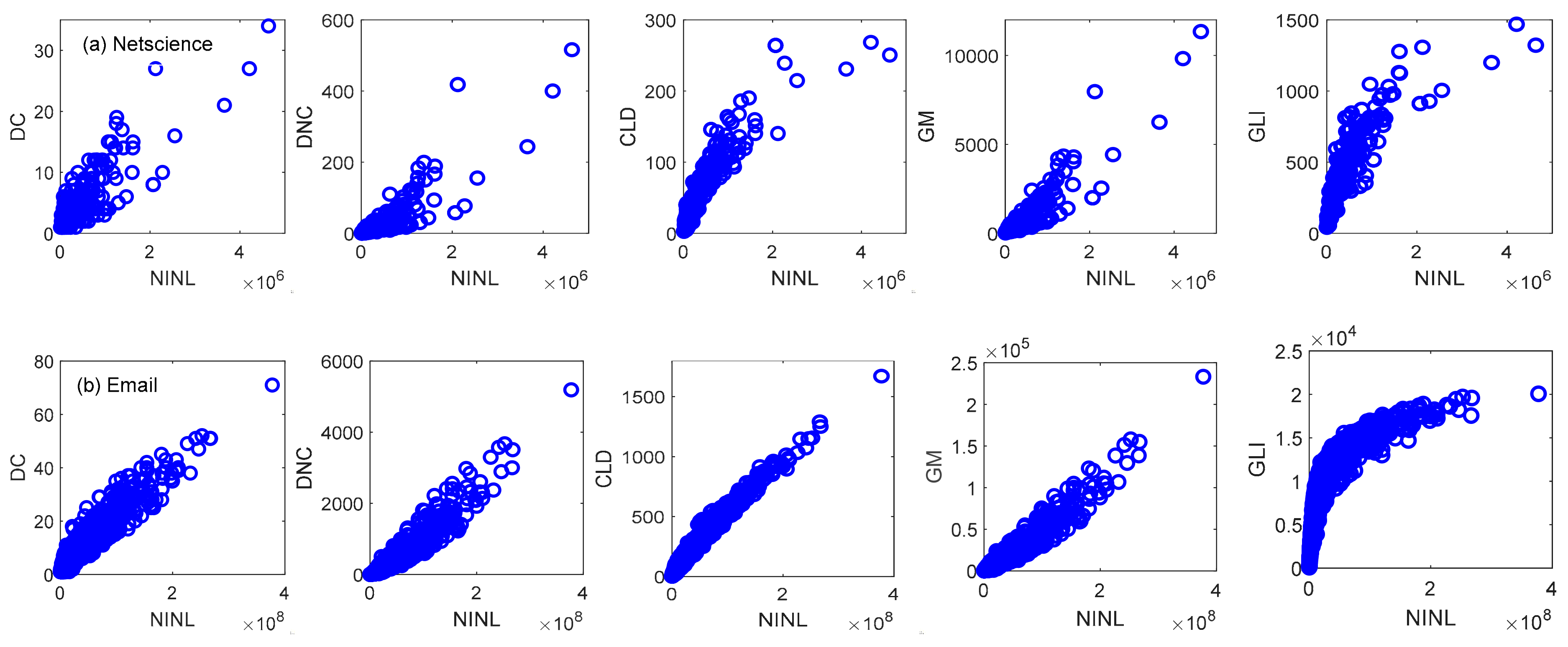
4.2.2. Influence Consistency Experiment
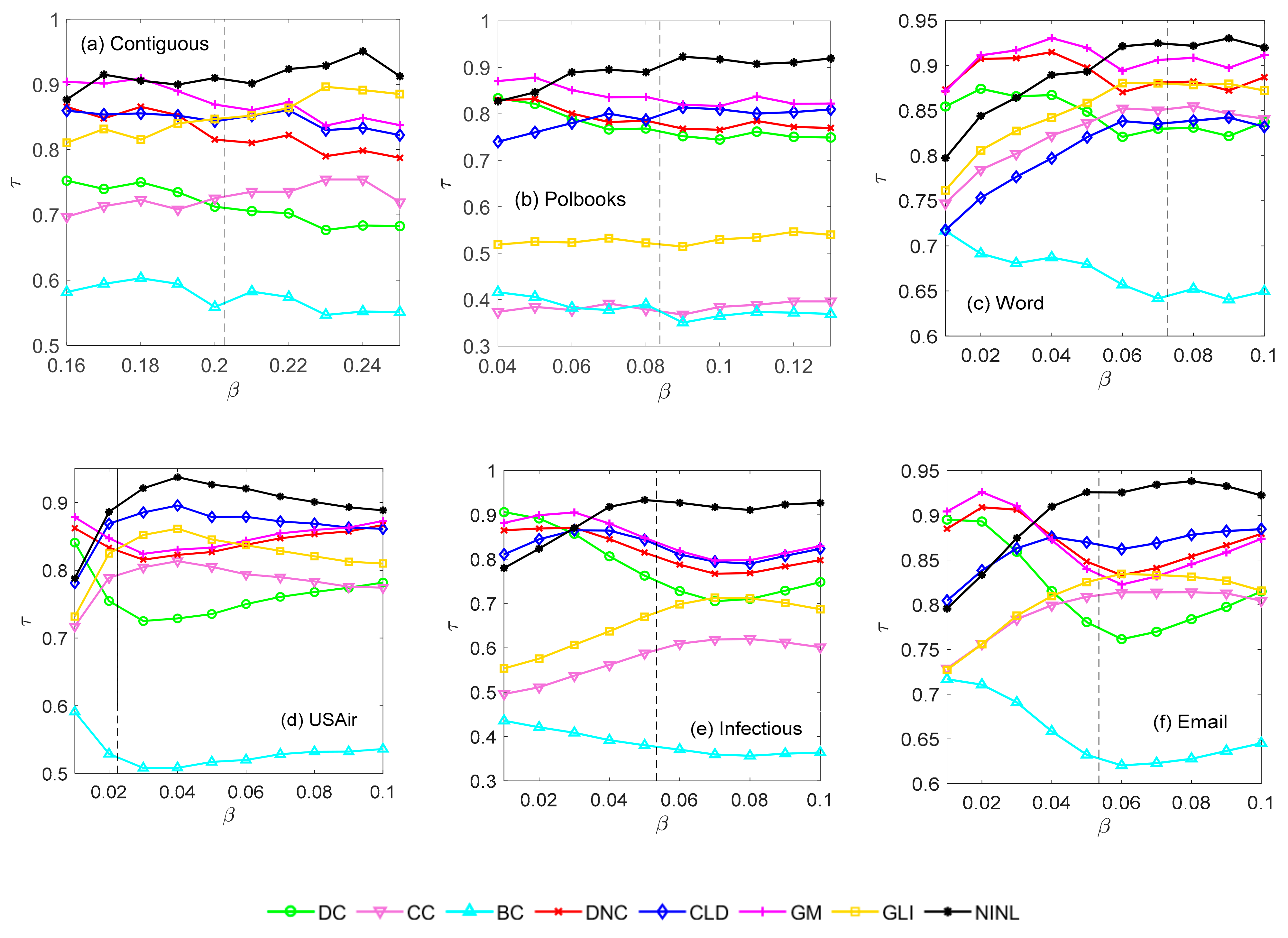
4.2.3. Recognition Effect of Each Method under a Certain Range of Propagation Probability
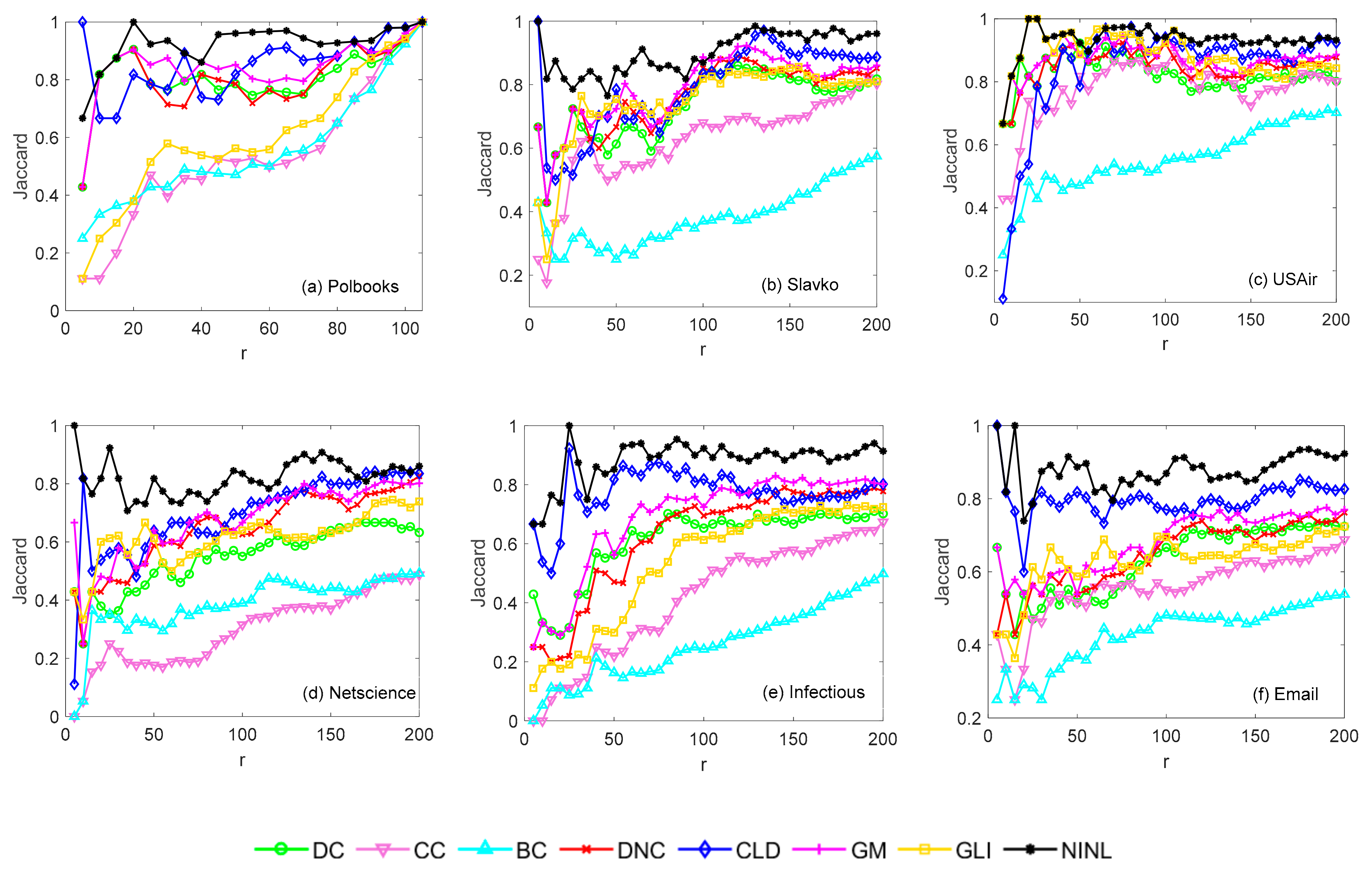
4.2.4. Recognition Effect of Each Method under a Certain Percentage of Ranking Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pawan, K.; Ravins, D. Formalising and detecting community structures in real world complex networks. J. Syst. Sci. Complex. 2021, 34, 180–205. [Google Scholar]
- Robitaille, A.L.; Webber, Q.M.R.; Turner, J.W.; Wal, E.V. The problem and promise of scale in multilayer animal social networks. Curr. Zool. 2021, 67, 113–123. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Jing, R.Z. Characterization of delay propagation in the air traffic network. J. Air Transp. Manag. 2021, 94, 102075. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Y.; Zhang, G.Q.; Wang, G.Y. A novel functional network based on three-way decision for link prediction in signed social networks. Cognit. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Nguyen, T.; Le, H.; Quinn, T.P.; Nguyen, T.; Venkatesh, S. GraphDTA: Predicting drug–target binding affinity with graph neural networks. Bioinformatics 2021, 37, 1140–1147. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef]
- Borgatti, S.P. Centrality and network flow. Soc. Netw. 2005, 27, 55–71. [Google Scholar] [CrossRef]
- Hwang, W.; Cho, Y.; Zhang, A.; Cho, Y.R.; Hwang, W. Bridging Centrality: Identifying Bridging Nodes in Scale-free Networks. In Proceedings of the Twelfth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’06), Philadelphia, PA, USA, 20–23 August 2006. [Google Scholar]
- Lü, L.Y.; Zhang, Y.C.; Yeung, C.H.; Zhou, T. Leaders in social networks, the Delicious case. PLoS ONE 2011, 6, e21202. [Google Scholar] [CrossRef] [Green Version]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef] [Green Version]
- Lü, L.Y.; Zhou, T.; Zhang, Q.M.; Stanley, H.E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 440–442. [Google Scholar] [CrossRef] [Green Version]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Phys. A 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Ahmed, I.; Mohamed, E.H. Density centrality: Identifying influential nodes based on area density formula. Chaos Solitons Fractals 2018, 114, 69–80. [Google Scholar]
- Li, Z.; Ren, T.; Ma, X.Q.; Zhou, T. Identifying influential spreaders by gravity model. Sci. Rep. 2019, 9, 355–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.T.; Zhang, R.S.; Hu, R.J.; Yang, F.; Yao, Y.; Yuan, Y.B. Identifying and ranking influential spreaders in complex networks by combining a local-degree sum and the clustering coefficient. Int. J. Mod. Phys. B 2018, 32, 1850118. [Google Scholar] [CrossRef]
- Sheng, J.F.; Dai, J.Y.; Wang, B.; Duan, G.H.; Long, J.; Zhang, J.K.; Guan, K.R.; Hu, S.; Chen, L.; Guan, W.H. Identifying influential nodes in complex networks based on global and local structure. Phys. A 2020, 541, 123262. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Hu, M.; Huang, T.Y. Influential nodes identification in complex networks based on global and local information. Chin. Phys. B 2020, 29, 664–670. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A.; Jalili, M.; Fasaei, M.S.K. Finding influential nodes in social networks based on neighborhood correlation coefficient. Knowl. Based Syst. 2020, 194, 105580. [Google Scholar] [CrossRef]
- Yan, X.L.; Cui, Y.P.; Ni, S.J. Identifying influential spreaders in complex networks based on entropy weight method and gravity law. Chin. Phys. B. 2020, 29, 664–672. [Google Scholar] [CrossRef]
- Babu, M.; Marimuthu, S.; Joy, M.; Nadaraj, M.; Jeyaseelan, L. Forecasting COVID-19 epidemic in India and high incidence states using SIR and logistic growth models. Clin. Epidemiol. Glob. Health 2021, 9, 26–33. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar]
- Contiguous USA Network Dataset—KONECT. 2017. Available online: http://konect.cc/networks/contiguous-usa (accessed on 5 July 2021).
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Blagus, N.; Šubelj, L.; Bajec, M. Self-similar scaling of density in complex real-world networks. Phys. A 2012, 391, 2794–2802. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gleiser, P.M.; Danon, L. Community structure in jazz. Adv. Complex Syst. 2003, 6, 565–573. [Google Scholar] [CrossRef] [Green Version]
- Batagel, V.; Mrvar, A. Pajek-program for large Network analysis. Connections 1998, 21, 47–57. [Google Scholar]
- Isella, L.; Stehlé, J.; Barrat, A.; Cattuto, C.; Pinton, J.F.; Broeck, W.V.D. What’s in a crowd? Analysis of face-to-face behavioral networks. J. Theor. Biol. 2011, 271, 166–180. [Google Scholar] [CrossRef] [Green Version]
- Guimerà, R.; Danon, L.; Díaz, G.A.; Giralt, F.; Arenas, L. Self-similar community structure in a network of human interactions. Phys. Rev. E 2003, 68, 065103. [Google Scholar] [CrossRef] [Green Version]
- Datasets. Available online: https://github.com/Ismileo/Datasets (accessed on 19 July 2021).
- Newman, M.E.J. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [Green Version]
- Castellano, C.; Pastor-Satorras, R. Thresholds for epidemic spreading in networks. Phys. Rev. Lett. 2010, 105, 218701. [Google Scholar] [CrossRef] [Green Version]
- Knight, W.R. A computer method for calculating kendall’s tau with ungrouped data. J. Am. Stat. Assoc. 1966, 61, 436–439. [Google Scholar] [CrossRef]
- Lorentz, J.; Bolboacă, S.-D. Pearson versus Spearman, Kendall’s Tau Correlation Analysis on Structure-Activity Relationships of Biologic Active Compounds. Leonardo J. Sci. 2006, 5, 179–200. [Google Scholar]
- Amirkhani, D.; Bastanfard, A. An objective method to evaluate exemplar-based inpainted images quality using Jaccard index. Multimed. Tools. Appl. 2021, 80, 26199–26212. [Google Scholar] [CrossRef]
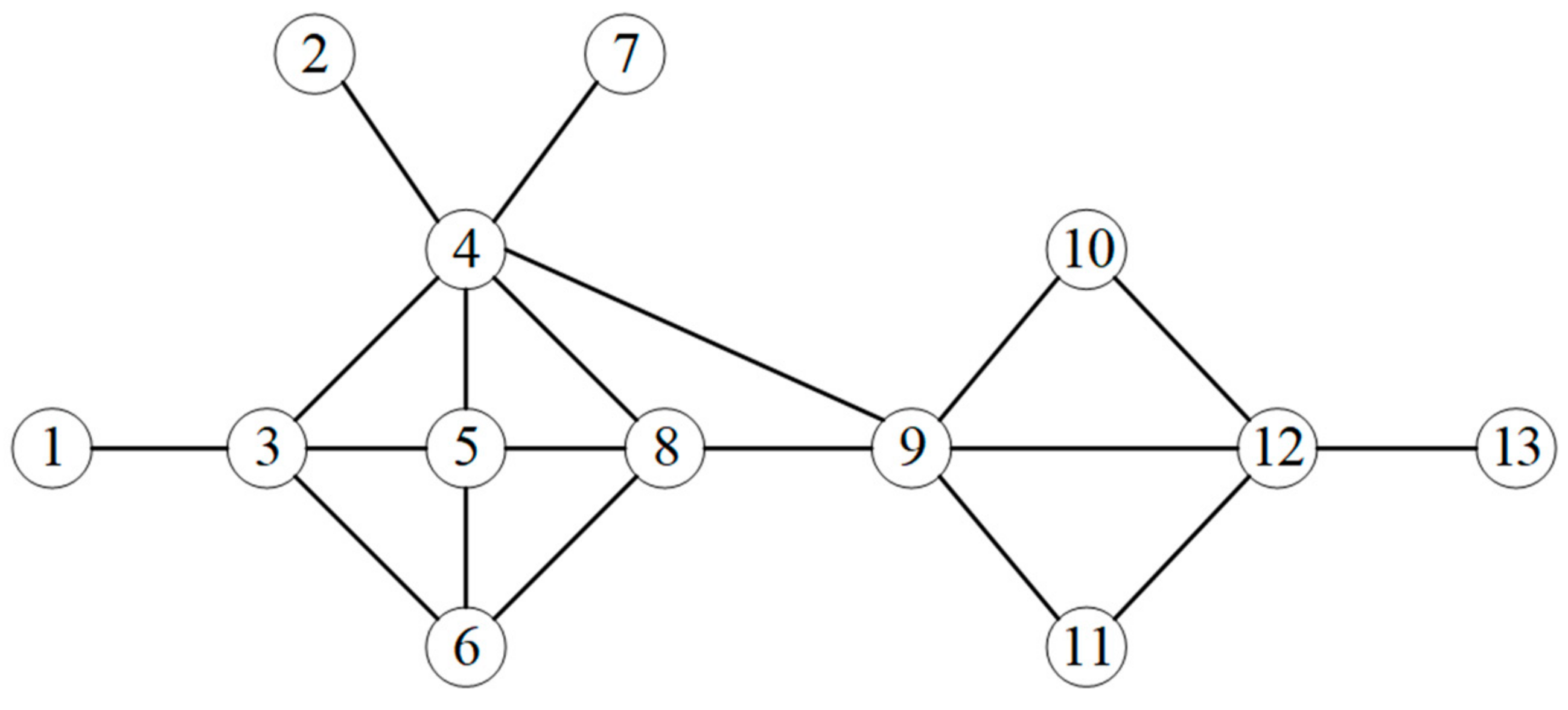

| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NINL0 | 29 | 37 | 37 | 38 | 37 | 37 | 37 | 38 | 38 | 37 | 37 | 37 | 24 |
| NINL1 | 37 | 38 | 141 | 224 | 150 | 112 | 38 | 150 | 187 | 75 | 75 | 136 | 37 |
| NINL2 | 141 | 224 | 523 | 704 | 627 | 441 | 224 | 673 | 660 | 323 | 323 | 374 | 136 |
| NINL3 | 523 | 704 | 1913 | 2931 | 2341 | 1823 | 704 | 2432 | 2397 | 1034 | 1034 | 1442 | 374 |
| Networks | n | m | kmax | <k> | D | L | C | r |
|---|---|---|---|---|---|---|---|---|
| Contiguous | 49 | 107 | 8 | 4.367 | 11 | 4.163 | 0.497 | 0.2334 |
| Dolphins | 62 | 159 | 12 | 5.129 | 8 | 3.357 | 0.259 | −0.0436 |
| Polbooks | 105 | 441 | 25 | 8.4 | 7 | 3.079 | 0.488 | −0.1279 |
| Word | 112 | 425 | 49 | 7.589 | 5 | 2.536 | 0.173 | −0.1293 |
| Jazz | 198 | 2742 | 100 | 27.697 | 6 | 2.235 | 0.618 | 0.0202 |
| Slavko | 324 | 2218 | 58 | 13.691 | 7 | 3.054 | 0.466 | 0.2473 |
| USAir | 332 | 2126 | 139 | 12.807 | 6 | 2.738 | 0.625 | −0.2079 |
| Netscience | 379 | 914 | 34 | 4.823 | 17 | 6.042 | 0.741 | −0.0817 |
| Infectious | 410 | 2765 | 50 | 13.488 | 9 | 3.631 | 0.456 | 0.2258 |
| 1133 | 5451 | 71 | 9.622 | 8 | 3.606 | 0.220 | 0.0782 |
| Networks | βth | β | τDC | τCC | τBC | τDNC | τCLD | τGM | τGLI | τNINL |
|---|---|---|---|---|---|---|---|---|---|---|
| Contiguous | 0.2027 | 0.20 | 0.7126 | 0.7253 | 0.5587 | 0.8155 | 0.8435 | 0.8690 | 0.8469 | 0.9099 |
| Dolphin | 0.1470 | 0.15 | 0.7721 | 0.6187 | 0.5389 | 0.8355 | 0.7916 | 0.8731 | 0.8355 | 0.9344 |
| Polbooks | 0.0838 | 0.09 | 0.7518 | 0.3679 | 0.3505 | 0.7679 | 0.8139 | 0.8198 | 0.5141 | 0.9229 |
| Word | 0.0726 | 0.08 | 0.8311 | 0.8549 | 0.6523 | 0.8822 | 0.8388 | 0.9086 | 0.8784 | 0.9218 |
| Jazz | 0.0259 | 0.03 | 0.8069 | 0.7080 | 0.4569 | 0.8175 | 0.8655 | 0.8505 | 0.8937 | 0.9322 |
| Slavko | 0.0466 | 0.05 | 0.7719 | 0.7128 | 0.3625 | 0.8234 | 0.8538 | 0.8411 | 0.7938 | 0.9305 |
| USAir | 0.0225 | 0.03 | 0.7251 | 0.8043 | 0.5081 | 0.8157 | 0.8854 | 0.8243 | 0.8522 | 0.9211 |
| Netscience | 0.1247 | 0.13 | 0.5955 | 0.3292 | 0.3048 | 0.7724 | 0.7980 | 0.7788 | 0.6950 | 0.8395 |
| Infectious | 0.0534 | 0.06 | 0.7281 | 0.6095 | 0.3707 | 0.7877 | 0.8105 | 0.8186 | 0.6984 | 0.9273 |
| 0.0535 | 0.06 | 0.7615 | 0.8138 | 0.6203 | 0.8330 | 0.8622 | 0.8226 | 0.8345 | 0.9255 |
| Word Network | USAir Network | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank | DC | CC | BC | DNC | CLD | GM | GLI | NINL | Φ | Rank | DC | CC | BC | DNC | CLD | GM | GLI | NINL | Φ |
| 1 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 1 | 118 | 118 | 118 | 118 | 109 | 118 | 118 | 118 | 261 |
| 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 261 | 261 | 8 | 261 | 131 | 261 | 261 | 261 | 118 |
| 3 | 44 | 52 | 44 | 52 | 52 | 52 | 52 | 52 | 52 | 3 | 255 | 67 | 261 | 255 | 112 | 255 | 255 | 255 | 255 |
| 4 | 52 | 44 | 52 | 44 | 44 | 44 | 44 | 44 | 44 | 4 | 152 | 255 | 201 | 182 | 299 | 182 | 182 | 182 | 182 |
| 5 | 105 | 28 | 10 | 105 | 51 | 105 | 105 | 105 | 105 | 5 | 182 | 201 | 47 | 152 | 118 | 152 | 152 | 152 | 230 |
| 6 | 10 | 105 | 80 | 10 | 105 | 10 | 25 | 51 | 10 | 6 | 230 | 182 | 182 | 230 | 255 | 230 | 230 | 230 | 176 |
| 7 | 25 | 10 | 105 | 28 | 22 | 25 | 51 | 10 | 25 | 7 | 166 | 47 | 255 | 166 | 176 | 166 | 67 | 112 | 152 |
| 8 | 28 | 27 | 28 | 25 | 55 | 51 | 28 | 26 | 51 | 8 | 67 | 166 | 152 | 67 | 147 | 67 | 166 | 166 | 147 |
| 9 | 51 | 25 | 2 | 51 | 25 | 28 | 26 | 25 | 28 | 9 | 112 | 248 | 313 | 112 | 261 | 112 | 112 | 67 | 67 |
| 10 | 2 | 26 | 29 | 26 | 32 | 26 | 10 | 55 | 55 | 10 | 201 | 112 | 13 | 201 | 301 | 147 | 147 | 147 | 166 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Wang, L. Identifying Influential Nodes in Complex Networks Based on Node Itself and Neighbor Layer Information. Symmetry 2021, 13, 1570. https://doi.org/10.3390/sym13091570
Zhu J, Wang L. Identifying Influential Nodes in Complex Networks Based on Node Itself and Neighbor Layer Information. Symmetry. 2021; 13(9):1570. https://doi.org/10.3390/sym13091570
Chicago/Turabian StyleZhu, Jingcheng, and Lunwen Wang. 2021. "Identifying Influential Nodes in Complex Networks Based on Node Itself and Neighbor Layer Information" Symmetry 13, no. 9: 1570. https://doi.org/10.3390/sym13091570
APA StyleZhu, J., & Wang, L. (2021). Identifying Influential Nodes in Complex Networks Based on Node Itself and Neighbor Layer Information. Symmetry, 13(9), 1570. https://doi.org/10.3390/sym13091570





