The Multiple Dimensions of Networks in Cancer: A Perspective
Abstract
:1. Introduction: Networks in Cancer
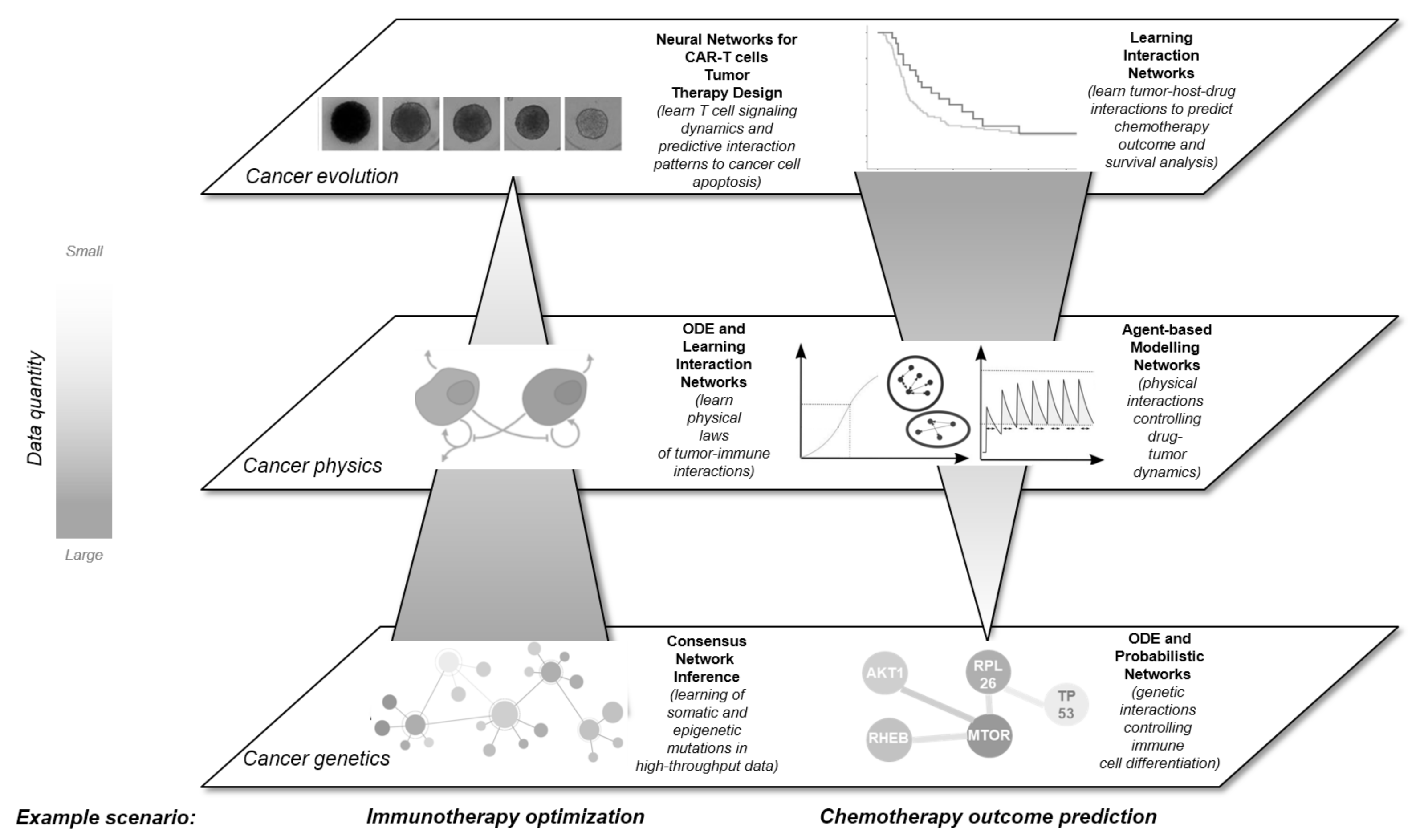
2. A Multidimensional View on Networks in Cancer
2.1. Network Approaches in Cancer Genomic Research
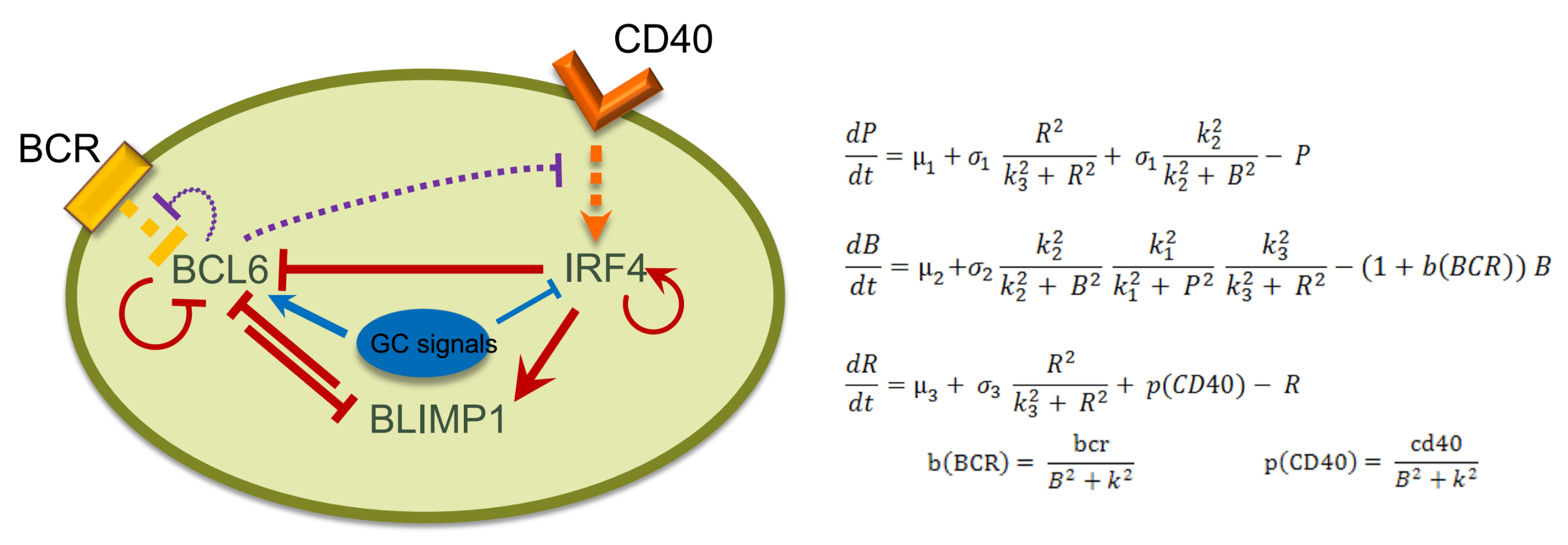
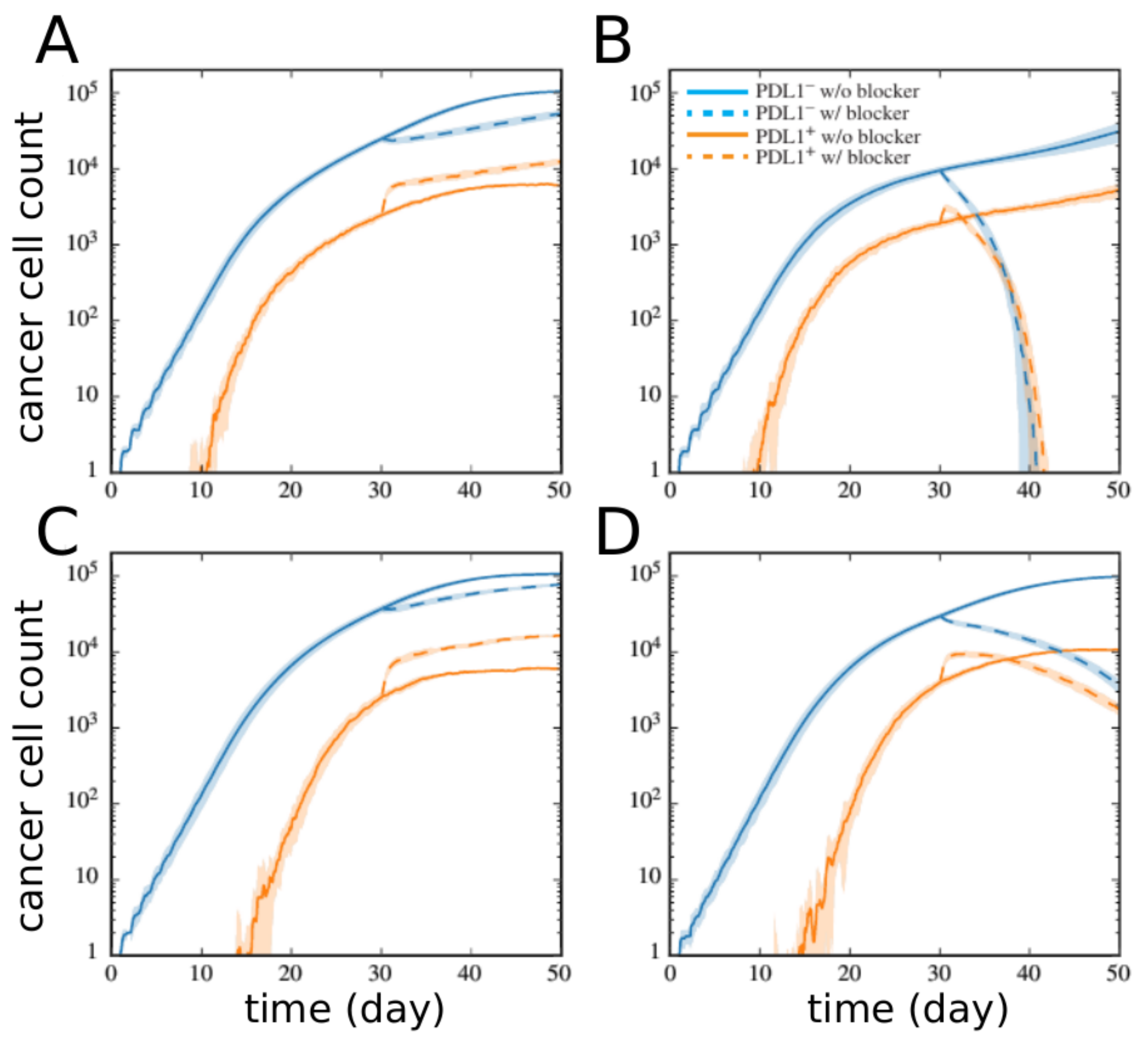
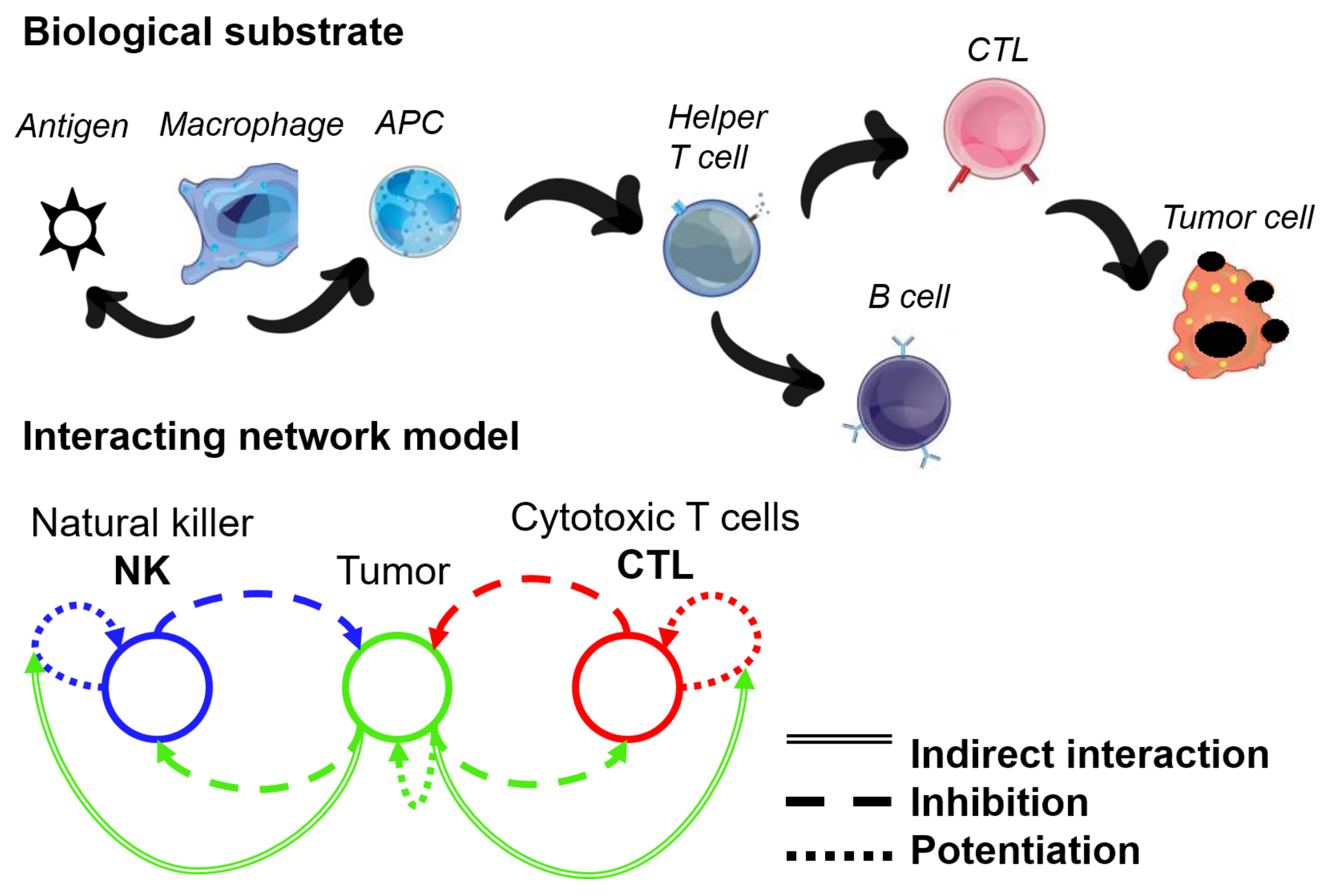
2.2. Network Approaches for Cancer Immunotherapy Optimisation
2.3. Network Approaches in Mechanistic Modelling
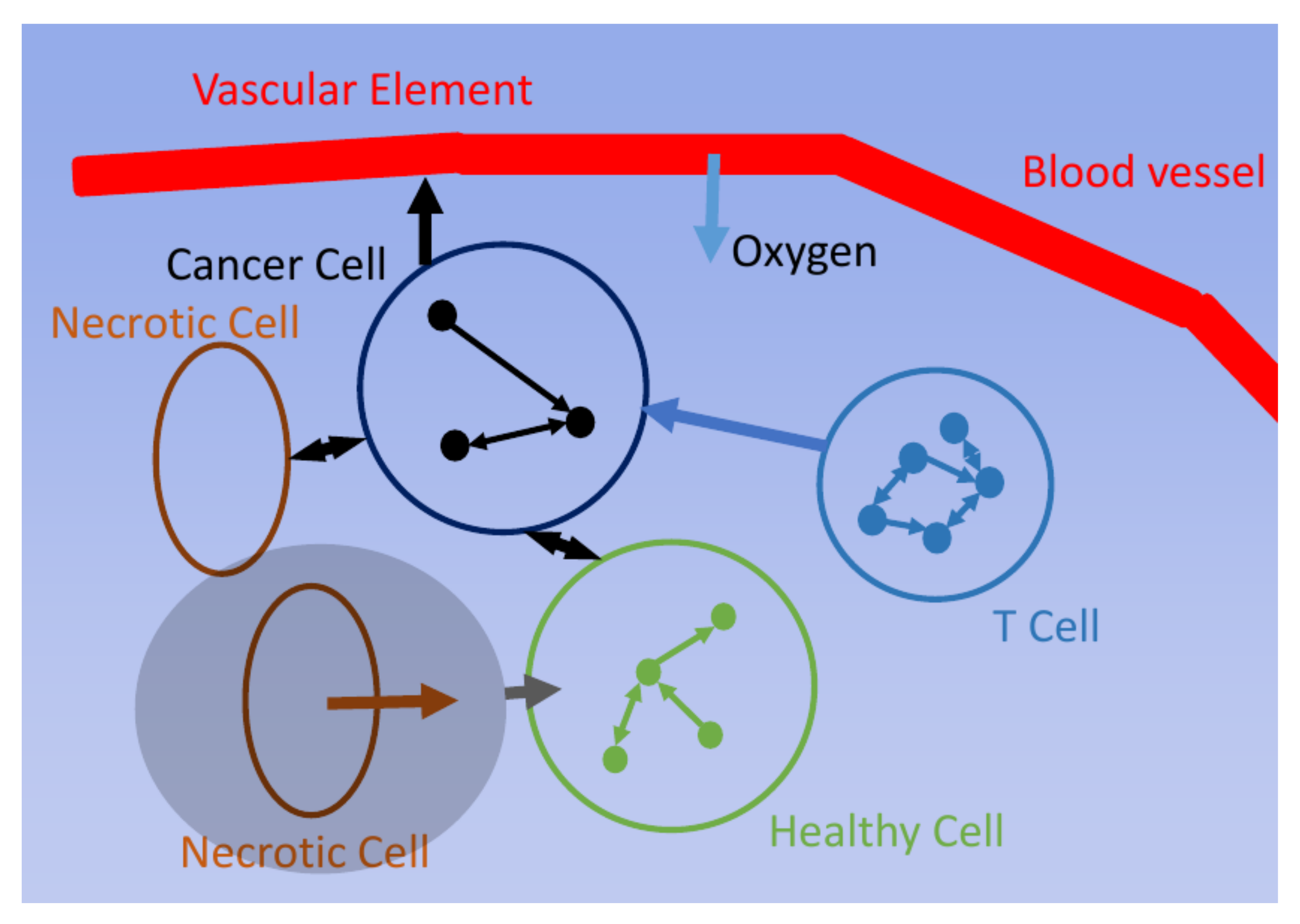
2.3.1. Continuum Modelling
2.3.2. Discrete Modelling
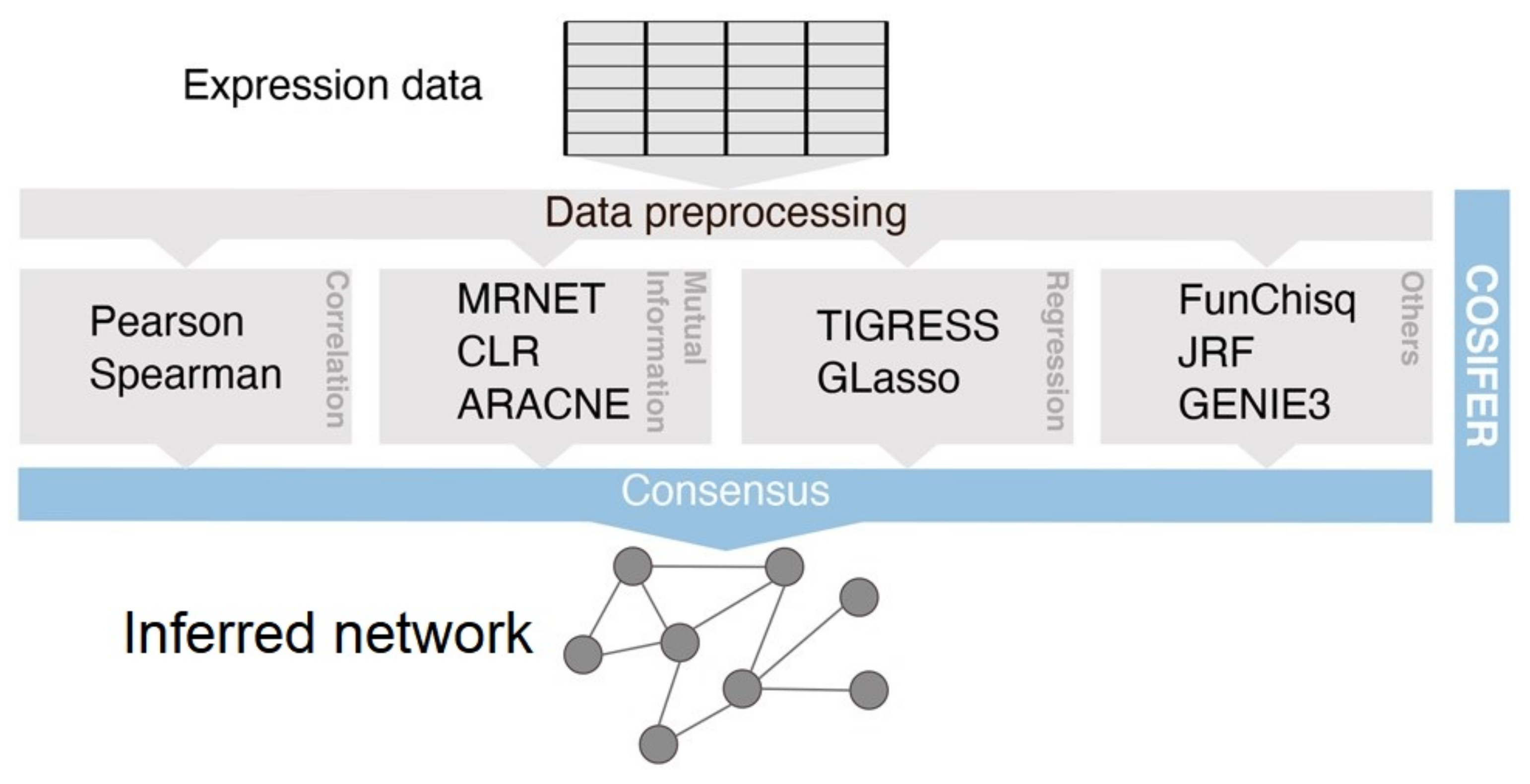
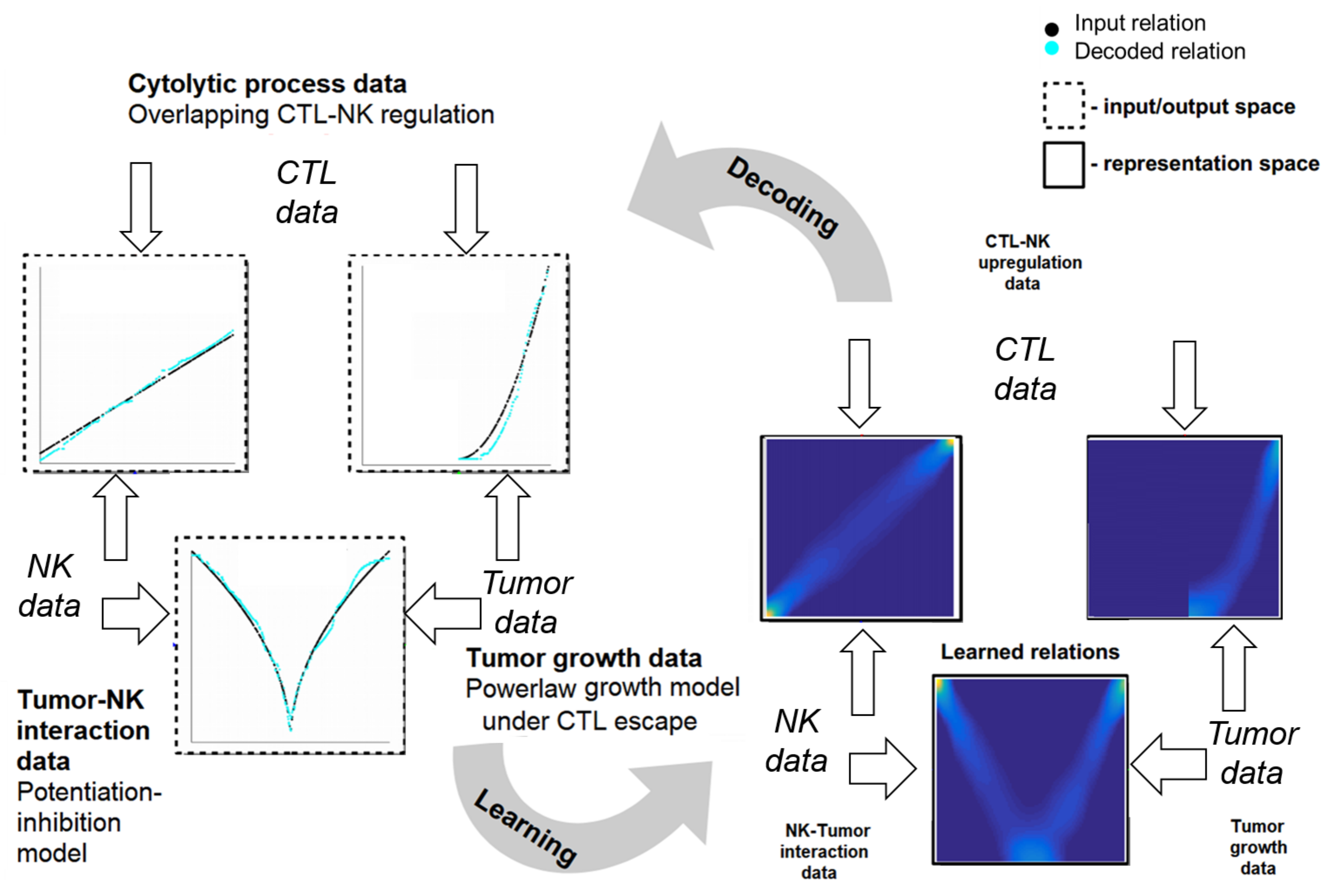
2.4. Learning Mechanistic Interaction Networks
2.4.1. Grounding the Learning Mechanistic Interaction Networks
2.4.2. Instantiations of Learning Mechanistic Interaction Networks
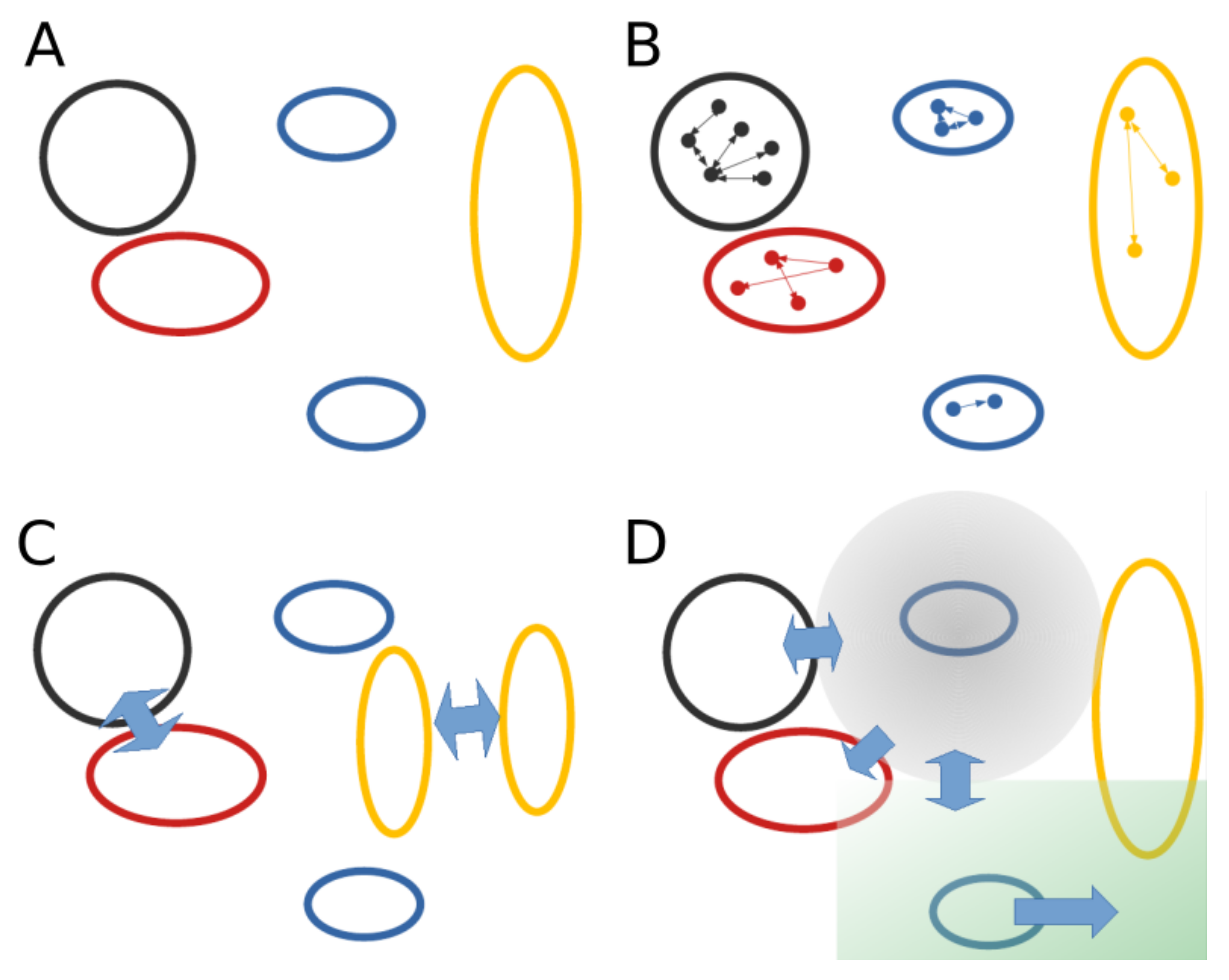
3. Unifying the Dimensions
- enable the investigation of fundamental mathematical, physical and biological principles derived from experimental data;
- fuse data from different sources, such as genetics, imaging, pathology, and mammography, to capture patterns at multiple scales to characterise tumour evolution;
- predict a tumour’s evolution after a specific treatment in a personalised manner, such as immunotherapy or conventional drug administration; and
- alleviate over-treatment, where a patient receives treatments or invasive procedures that might not be necessary.
4. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Global Cancer Observatory. Available online: https://gco.iarc.fr/ (accessed on 21 August 2021).
- Alexandrov, L.B.; Nik-Zainal, S.; Wedge, D.C.; Aparicio, S.A.J.R.; Behjati, S.; Biankin, A.V.; Bignell, G.R.; Bolli, N.; Borg, A.; Børresen-Dale, A.L.; et al. Signatures of mutational processes in human cancer. Nature 2013, 500, 415–421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esteller, M. Cancer epigenomics: DNA methylomes and histone-modification maps. Nat. Rev. Genet. 2007, 8, 286–298. [Google Scholar] [CrossRef] [PubMed]
- Vogelstein, B.; Papadopoulos, N.; Velculescu, V.E.; Zhou, S.; Diaz, L.A.; Kinzler, K.W. Cancer Genome Landscapes. Science 2013, 339, 1546–1558. [Google Scholar] [CrossRef] [PubMed]
- Bauer, R.; Kaiser, M.; Stoll, E. A computational model incorporating neural stem cell dynamics reproduces glioma incidence across the lifespan in the human population. PLoS ONE 2014, 9, e111219. [Google Scholar] [CrossRef] [Green Version]
- ICGC Data Portal. Available online: https://dcc.icgc.org/ (accessed on 21 August 2021).
- Lawrence, M.S.; Stojanov, P.; Mermel, C.H.; Garraway, L.A.; Golub, T.R.; Meyerson, M.; Gabriel, S.B.; Lander, E.S.; Getz, G. Discovery and saturation analysis of cancer genes across 21 tumor types. Nature 2014, 505, 495–501. [Google Scholar] [CrossRef] [Green Version]
- Garraway, L.A.; Lander, E.S. Lessons from the cancer genome. Cell 2013, 153, 17–37. [Google Scholar] [CrossRef] [Green Version]
- Creixell, P.; Reimand, J.; Haider, S.; Wu, G.; Shibata, T.; Vazquez, M.; Mustonen, V.; Gonzalez-Perez, A.; Pearson, J.; Sander, C.; et al. Pathway and Network Analysis of Cancer Genomes. Nat. Methods 2015, 12, 615–621. [Google Scholar] [CrossRef]
- Vidal, M.; Cusick, M.E.; Barabási, A.L. Interactome Networks and Human Disease. Cell 2011, 144, 986–998. [Google Scholar] [CrossRef] [Green Version]
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Kellis, M.; Collins, J.J.; Stolovitzky, G. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar] [CrossRef] [Green Version]
- Manica, M.; Bunne, C.; Mathis, R.; Cadow, J.; Ahsen, M.E.; Stolovitzky, G.A.; Martínez, M.R. COSIFER: A Python package for the consensus inference of molecular interaction networks. Bioinformatics 2020, 37, 2070–2072. [Google Scholar] [CrossRef]
- Butte, A.J.; Kohane, I.S. Unsupervised knowledge discovery in medical databases using relevance networks. Proc. AMIA Symp. 1999, 711––715. [Google Scholar]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Dalla Favera, R.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5, e8. [Google Scholar] [CrossRef]
- Meyer, P.E.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-theoretic inference of large transcriptional regulatory networks. EURASIP J. Bioinform. Syst. Biol. 2007, 2007, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [Green Version]
- Haury, A.C.; Mordelet, F.; Vera-Licona, P.; Vert, J.P. TIGRESS: Trustful inference of gene regulation using stability selection. BMC Syst. Biol. 2012, 6, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Song, M. Deciphering Interactions in Causal Networks without Parametric Assumptions. arXiv 2013, arXiv:1311.2707. [Google Scholar]
- Petralia, F.; Song, W.M.; Tu, Z.; Wang, P. New Method for Joint Network Analysis Reveals Common and Different Coexpression Patterns among Genes and Proteins in Breast Cancer. J. Proteome Res. 2016, 15, 743–754. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring Regulatory Networks from Expression Data Using Tree-Based Methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Lefebvre, C.; Rajbhandari, P.; Alvarez, M.J.; Bandaru, P.; Lim, W.K.; Sato, M.; Wang, K.; Sumazin, P.; Kustagi, M.; Bisikirska, B.C.; et al. A human B-cell interactome identifies MYB and FOXM1 as master regulators of proliferation in germinal centers. Mol. Syst. Biol. 2010, 6, 377. [Google Scholar] [CrossRef]
- Li, Z.; Ivanov, A.A.; Su, R.; Gonzalez-Pecchi, V.; Qi, Q.; Liu, S.; Webber, P.; McMillan, E.; Rusnak, L.; Pham, C.; et al. The OncoPPi network of cancer-focused protein–protein interactions to inform biological insights and therapeutic strategies. Nat. Commun. 2017, 8, 14356. [Google Scholar] [CrossRef]
- Rai, A.; Pradhan, P.; Nagraj, J.; Lohitesh, K.; Chowdhury, R.; Jalan, S. Understanding cancer complexome using networks, spectral graph theory and multilayer framework. Sci. Rep. 2017, 7, 41676. [Google Scholar] [CrossRef] [Green Version]
- Khatri, P.; Drăghici, S. Ontological analysis of gene expression data: Current tools, limitations, and open problems. Bioinformatics 2005, 21, 3587–3595. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, A.; Tamayo, P.; Mootha, V.K.; Mukherjee, S.; Ebert, B.L.; Gillette, M.A.; Paulovich, A.; Pomeroy, S.L.; Golub, T.R.; Lander, E.S.; et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 2005, 102, 15545–15550. [Google Scholar] [CrossRef] [Green Version]
- Draghici, S.; Khatri, P.; Tarca, A.L.; Amin, K.; Done, A.; Voichita, C.; Georgescu, C.; Romero, R. A systems biology approach for pathway level analysis. Genome Res. 2007, 17, 1537–1545. [Google Scholar] [CrossRef] [Green Version]
- Martinez, M.R.; Corradin, A.; Klein, U.; Alvarez, M.J.; Toffolo, G.M.; di Camillo, B.; Califano, A.; Stolovitzky, G.A. Quantitative modeling of the terminal differentiation of B cells and mechanisms of lymphomagenesis. Proc. Natl. Acad. Sci. USA 2012, 109, 2672–2677. [Google Scholar] [CrossRef] [Green Version]
- Korkut, A.; Wang, W.; Demir, E.; Aksoy, B.A.; Jing, X.; Molinelli, E.J.; Babur, O.; Bemis, D.L.; Onur Sumer, S.; Solit, D.B.; et al. Perturbation biology nominates upstream–downstream drug combinations in RAF inhibitor resistant melanoma cells. eLife 2015, 4, e04640. [Google Scholar] [CrossRef]
- Arkin, A.; Ross, J.; McAdams, H.H. Stochastic Kinetic Analysis of Developmental Pathway Bifurcation in Phage Lambda-Infected Escherichia coli Cells. Genetics 1998, 149, 1633–1648. [Google Scholar] [CrossRef]
- Rodríguez Martínez, M.; Soriano, J.; Tlusty, T.; Pilpel, Y.; Furman, I. Messenger RNA fluctuations and regulatory RNAs shape the dynamics of a negative feedback loop. Phys. Rev. E 2010, 81, 031924. [Google Scholar] [CrossRef] [Green Version]
- Thomas, M.J.; Klein, U.; Lygeros, J.; Rodríguez Martínez, M. A Probabilistic Model of the Germinal Center Reaction. Front. Immunol. 2019, 10, 689. [Google Scholar] [CrossRef] [Green Version]
- Pélissier, A.; Akrout, Y.; Jahn, K.; Kuipers, J.; Klein, U.; Beerenwinkel, N.; Rodríguez Martínez, M. Computational Model Reveals a Stochastic Mechanism behind Germinal Center Clonal Bursts. Cells 2020, 9, 1448. [Google Scholar] [CrossRef] [PubMed]
- Chaves, M.; Albert, R.; Sontag, E.D. Robustness and fragility of Boolean models for genetic regulatory networks. J. Theor. Biol. 2005, 235, 431–449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; Zhang, W. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002, 18, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Chaves, M.; Sontag, E.D.; Albert, R. Methods of robustness analysis for Boolean models of gene control networks. IEE Proc. Syst. Biol. 2006, 153, 154–167. [Google Scholar] [CrossRef] [Green Version]
- Fumiã, H.F.; Martins, M.L. Boolean Network Model for Cancer Pathways: Predicting Carcinogenesis and Targeted Therapy Outcomes. PLoS ONE 2013, 8, e69008. [Google Scholar] [CrossRef] [Green Version]
- Béal, J.; Montagud, A.; Traynard, P.; Barillot, E.; Calzone, L. Personalization of Logical Models With Multi-Omics Data Allows Clinical Stratification of Patients. Front. Physiol. 2019, 9, 1965. [Google Scholar] [CrossRef]
- Eduati, F.; Jaaks, P.; Wappler, J.; Cramer, T.; Merten, C.A.; Garnett, M.J.; Saez-Rodriguez, J. Patient-specific logic models of signaling pathways from screenings on cancer biopsies to prioritize personalized combination therapies. Mol. Syst. Biol. 2020, 16, e8664. [Google Scholar] [CrossRef]
- Vanunu, O.; Magger, O.; Ruppin, E.; Shlomi, T.; Sharan, R. Associating Genes and Protein Complexes with Disease via Network Propagation. PLoS Comput. Biol. 2010, 6, 9. [Google Scholar] [CrossRef] [Green Version]
- Hofree, M.; Shen, J.P.; Carter, H.; Gross, A.; Ideker, T. Network-based stratification of tumor mutations. Nat. Methods 2013, 10, 1108–1115. [Google Scholar] [CrossRef]
- Oskooei, A.; Manica, M.; Mathis, R.; Martínez, M.R. Network-based Biased Tree Ensembles (NetBiTE) for Drug Sensitivity Prediction and Drug Sensitivity Biomarker Identification in Cancer. Sci. Rep. 2019, 9, 15918. [Google Scholar] [CrossRef]
- Manica, M.; Cadow, J.; Mathis, R.; Rodríguez Martínez, M. PIMKL: Pathway-Induced Multiple Kernel Learning. Npj Syst. Biol. Appl. 2019, 5, 1–8. [Google Scholar] [CrossRef]
- Axenie, C.; Kurz, D. GLUECK: Growth pattern learning for unsupervised extraction of cancer kinetics. In Machine Learning and Knowledge Discovery in Databases, Proceedings of the ECML2020—Applied Data Science and Demo Track, Ghent, Belgium, 14–18 September 2020; Dong, Y., Ifrim, G., Mladenić, D., Saunders, C., Van Hoecke, S., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 171–186. [Google Scholar]
- Axenie, C.; Kurz, D. Tumor Characterization using Unsupervised Learning of Mathematical Relations within Breast Cancer Data. In Proceedings of the International Conference on Artificial Neural Networks 2020, Bratislava, Slovakia, 15–18 September 2020; pp. 838–849. [Google Scholar]
- Massafra, R.; Bove, S.; Lorusso, V.; Biafora, A.; Comes, M.C.; Didonna, V.; Diotaiuti, S.; Fanizzi, A.; Nardone, A.; Nolasco, A.; et al. Radiomic Feature Reduction Approach to Predict Breast Cancer by Contrast-Enhanced Spectral Mammography Images. Diagnostics 2021, 11, 684. [Google Scholar] [CrossRef]
- Axenie, C.; Kurz, D. CHIMERA: Combining Mechanistic Models and Machine Learning for Personalized Chemotherapy and Surgery Sequencing in Breast Cancer. In Proceedings of the International Symposium on Mathematical and Computational Oncology 2020, San Diego, CA, USA, 8–10 October 2020; pp. 13–24. [Google Scholar]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333–337. [Google Scholar] [CrossRef]
- Shalapour, S.; Karin, M. Immunity, inflammation, and cancer: An eternal fight between good and evil. J. Clin. Investig. 2015, 125, 3347–3355. [Google Scholar] [CrossRef] [Green Version]
- Jackson, H.J.; Rafiq, S.; Brentjens, R.J. Driving CAR T-cells forward. Nat. Rev. Clin. Oncol. 2016, 13, 370–383. [Google Scholar] [CrossRef]
- Park, J.H.; Rivière, I.; Gonen, M.; Wang, X.; Sénéchal, B.; Curran, K.J.; Sauter, C.; Wang, Y.; Santomasso, B.; Mead, E.; et al. Long-Term Follow-up of CD19 CAR Therapy in Acute Lymphoblastic Leukemia. N. Engl. J. Med. 2018, 378, 449–459. [Google Scholar] [CrossRef]
- Rafiq, S.; Hackett, C.S.; Brentjens, R.J. Engineering strategies to overcome the current roadblocks in CAR T cell therapy. Nat. Rev. Clin. Oncol. 2020, 17, 147–167. [Google Scholar] [CrossRef]
- Konstorum, A.; Vella, A.T.; Adler, A.J.; Laubenbacher, R.C. A mathematical model of combined CD8 T cell costimulation by 4-1BB (CD137) and OX40 (CD134) receptors. Sci. Rep. 2019, 9, 10862. [Google Scholar] [CrossRef] [Green Version]
- Wertheim, K.Y.; Puniya, B.L.; La Fleur, A.; Shah, A.R.; Barberis, M.; Helikar, T. Multi-Approach and Multi-Scale Model of CD4+ T Cells Predicts Switch-Like and Oscillatory Emergent Behaviors in Inflammatory Response to Infection. bioRxiv 2020. [Google Scholar] [CrossRef]
- Bouchnita, A.; Bocharov, G.; Meyerhans, A.; Volpert, V. Hybrid approach to model the spatial regulation of T cell responses. BMC Immunol. 2017, 18. [Google Scholar] [CrossRef] [Green Version]
- Mayer, A.; Zhang, Y.; Perelson, A.S.; Wingreen, N.S. Regulation of T cell expansion by antigen presentation dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 5914–5919. [Google Scholar] [CrossRef] [Green Version]
- Meyer-Hermann, M.; Mohr, E.; Pelletier, N.; Zhang, Y.; Victora, G.D.; Toellner, K.M. A Theory of Germinal Center B Cell Selection, Division, and Exit. Cell Rep. 2012, 2, 162–174. [Google Scholar] [CrossRef] [Green Version]
- Mehta, P.; Schwab, D.J. An exact mapping between the variational renormalization group and deep learning. arXiv 2014, arXiv:1410.3831. [Google Scholar]
- Weber, A.; Born, J.; Rodríguez Martínez, M. TITAN: T Cell Receptor Specificity Prediction with Bimodal Attention Networks. arXiv 2021, arXiv:2105.03323. [Google Scholar]
- Dlamini, Z.; Francies, F.Z.; Hull, R.; Marima, R. Artificial intelligence (AI) and big data in cancer and precision oncology. Comput. Struct. Biotechnol. J. 2020, 18, 2300–2311. [Google Scholar] [CrossRef]
- Enderling, H.; AJ Chaplain, M. Mathematical modeling of tumor growth and treatment. Curr. Pharm. Des. 2014, 20, 4934–4940. [Google Scholar] [CrossRef] [Green Version]
- Heindl, A.; Sestak, I.; Naidoo, K.; Cuzick, J.; Dowsett, M.; Yuan, Y. Relevance of spatial heterogeneity of immune infiltration for predicting risk of recurrence after endocrine therapy of ER+ breast cancer. JNCI J. Natl. Cancer Inst. 2018, 110, 166–175. [Google Scholar] [CrossRef]
- Gallaher, J.A.; Enriquez-Navas, P.M.; Luddy, K.A.; Gatenby, R.A.; Anderson, A.R. Spatial heterogeneity and evolutionary dynamics modulate time to recurrence in continuous and adaptive cancer therapies. Cancer Res. 2018, 78, 2127–2139. [Google Scholar] [CrossRef] [Green Version]
- Gatenby, R.A.; Gawlinski, E.T. A reaction-diffusion model of cancer invasion. Cancer Res. 1996, 56, 5745–5753. [Google Scholar]
- Ghaffarizadeh, A.; Heiland, R.; Friedman, S.H.; Mumenthaler, S.M.; Macklin, P. PhysiCell: An open source physics-based cell simulator for 3-D multicellular systems. PLoS Comput. Biol. 2018, 14, e1005991. [Google Scholar] [CrossRef] [Green Version]
- Breitwieser, L.; Hesam, A.; de Montigny, J.; Vavourakis, V.; Iosif, A.; Jennings, J.; Kaiser, M.; Manca, M.; Di Meglio, A.; Al-Ars, Z.; et al. BioDynaMo: A general platform for scalable agent-based simulation. bioRxiv 2021, 2020-06. [Google Scholar] [CrossRef]
- Kaul, H.; Ventikos, Y. Investigating biocomplexity through the agent-based paradigm. Brief. Bioinform. 2015, 16, 137–152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Metzcar, J.; Wang, Y.; Heiland, R.; Macklin, P. A review of cell-based computational modeling in cancer biology. JCO Clin. Cancer Inform. 2019, 2, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-de Aledo, P.; Vladimirov, A.; Manca, M.; Baugh, J.; Asai, R.; Kaiser, M.; Bauer, R. An optimization approach for agent-based computational models of biological development. Adv. Eng. Softw. 2018, 121, 262–275. [Google Scholar] [CrossRef]
- Macnamara, C.K. Biomechanical modelling of cancer: Agent-based force-based models of solid tumours within the context of the tumour microenvironment. Comput. Syst. Oncol. 2021, 1, e1018. [Google Scholar]
- Bauer, R.; Clowry, G.; Kaiser, M. Creative destruction: A basic computational model of cortical layer formation. Cereb Cortex 2021, 31, 3237–3253. [Google Scholar] [CrossRef] [PubMed]
- Gorochowski, T.E. Agent-based modelling in synthetic biology. Essays Biochem. 2016, 60, 325–336. [Google Scholar] [PubMed] [Green Version]
- Mogilner, A.; Manhart, A. Agent-based modeling: Case study in cleavage furrow models. Mol. Biol. Cell 2016, 27, 3379–3384. [Google Scholar] [CrossRef] [Green Version]
- Tracy, M.; Cerdá, M.; Keyes, K.M. Agent-based modeling in public health: Current applications and future directions. Annu. Rev. Public Health 2018, 39, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Bauer, R.; Zubler, F.; Hauri, A.; Muir, D.R.; Douglas, R.J. Developmental origin of patchy axonal connectivity in the neocortex: A computational model. Cereb. Cortex 2014, 24, 487–500. [Google Scholar] [CrossRef] [Green Version]
- De Montigny, J.; Iosif, A.; Breitwieser, L.; Manca, M.; Bauer, R.; Vavourakis, V. An in silico hybrid continuum-/agent-based procedure to modelling cancer development: Interrogating the interplay amongst glioma invasion, vascularity and necrosis. Methods 2021, 185, 94–104. [Google Scholar] [CrossRef]
- Jalalimanesh, A.; Haghighi, H.S.; Ahmadi, A.; Soltani, M. Simulation-based optimization of radiotherapy: Agent-based modeling and reinforcement learning. Math. Comput. Simul. 2017, 133, 235–248. [Google Scholar] [CrossRef]
- Hadjicharalambous, M.; Wijeratne, P.A.; Vavourakis, V. From tumour perfusion to drug delivery and clinical translation of in silico cancer models. Methods 2021, 185, 82–93. [Google Scholar] [CrossRef]
- Gong, C.; Milberg, O.; Wang, B.; Vicini, P.; Narwal, R.; Roskos, L.; Popel, A.S. A computational multiscale agent-based model for simulating spatio-temporal tumour immune response to PD1 and PDL1 inhibition. J. R. Soc. Interface 2017, 14, 20170320. [Google Scholar] [CrossRef] [Green Version]
- Le, D.T.; Uram, J.N.; Wang, H.; Bartlett, B.R.; Kemberling, H.; Eyring, A.D.; Skora, A.D.; Luber, B.S.; Azad, N.S.; Laheru, D.; et al. PD-1 blockade in tumors with mismatch-repair deficiency. N. Engl. J. Med. 2015, 372, 2509–2520. [Google Scholar] [CrossRef] [Green Version]
- Cristini, V.; Koay, E.; Wang, Z. An Introduction to Physical Oncology: How Mechanistic Mathematical Modeling Can Improve Cancer Therapy Outcomes; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Werner, B.; Scott, J.G.; Sottoriva, A.; Anderson, A.R.; Traulsen, A.; Altrock, P.M. The cancer stem cell fraction in hierarchically organized tumors can be estimated using mathematical modeling and patient-specific treatment trajectories. Cancer Res. 2016, 76, 1705–1713. [Google Scholar] [CrossRef] [Green Version]
- Chamseddine, I.M.; Rejniak, K.A. Hybrid modeling frameworks of tumor development and treatment. Wiley Interdiscip. Rev. Syst. Biol. Med. 2020, 12, e1461. [Google Scholar] [CrossRef] [Green Version]
- Nia, H.T.; Munn, L.L.; Jain, R.K. Physical traits of cancer. Science 2020, 370. [Google Scholar] [CrossRef]
- Kondylakis, H.; Axenie, C.; Bastola, D.K.; Katehakis, D.G.; Kouroubali, A.; Kurz, D.; Larburu, N.; Macía, I.; Maguire, R.; Maramis, C.; et al. Status and recommendations of technological and data-driven innovations in cancer care: Focus group study. J. Med. Internet Res. 2020, 22, e22034. [Google Scholar] [CrossRef]
- Nia, H.T.; Liu, H.; Seano, G.; Datta, M.; Jones, D.; Rahbari, N.; Incio, J.; Chauhan, V.P.; Jung, K.; Martin, J.D.; et al. Solid stress and elastic energy as measures of tumour mechanopathology. Nat. Biomed. Eng. 2016, 1, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Griffon-Etienne, G.; Boucher, Y.; Brekken, C.; Suit, H.D.; Jain, R.K. Taxane-induced apoptosis decompresses blood vessels and lowers interstitial fluid pressure in solid tumors: Clinical implications. Cancer Res. 1999, 59, 3776–3782. [Google Scholar] [PubMed]
- Rouvière, O.; Melodelima, C.; Dinh, A.H.; Bratan, F.; Pagnoux, G.; Sanzalone, T.; Crouzet, S.; Colombel, M.; Mège-Lechevallier, F.; Souchon, R. Stiffness of benign and malignant prostate tissue measured by shear-wave elastography: A preliminary study. Eur. Radiol. 2017, 27, 1858–1866. [Google Scholar] [CrossRef] [PubMed]
- Nathanson, S.D.; Nelson, L. Interstitial fluid pressure in breast cancer, benign breast conditions, and breast parenchyma. Ann. Surg. Oncol. 1994, 1, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. PLoS Comput. Biol. 2014, 10, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Ben-Shmuel, A.; Biber, G.; Barda-Saad, M. Unleashing Natural Killer Cells in the Tumor Microenvironment–The Next Generation of Immunotherapy? Front. Immunol. 2020, 11, 275. [Google Scholar] [CrossRef] [Green Version]
- Uzhachenko, R.V.; Shanker, A. CD8+ T lymphocyte and NK cell network: Circuitry in the cytotoxic domain of immunity. Front. Immunol. 2019, 10, 1906. [Google Scholar] [CrossRef] [Green Version]
- Markowetz, F.; Troyanskaya, O.G. Computational identification of cellular networks and pathways. Mol. BioSyst. 2007, 3, 478–482. [Google Scholar] [CrossRef]
- Cornish, A.J.; Markowetz, F. SANTA: Quantifying the functional content of molecular networks. PLoS Comput. Biol. 2014, 10, e1003808. [Google Scholar] [CrossRef] [Green Version]
- Haeno, H.; Gonen, M.; Davis, M.B.; Herman, J.M.; Iacobuzio-Donahue, C.A.; Michor, F. Computational modeling of pancreatic cancer reveals kinetics of metastasis suggesting optimum treatment strategies. Cell 2012, 148, 362–375. [Google Scholar] [CrossRef] [Green Version]
- Benzekry, S. Artificial intelligence and mechanistic modeling for clinical decision making in oncology. Clin. Pharmacol. Ther. 2020, 108, 471–486. [Google Scholar] [CrossRef]
- Vaghi, C.; Rodallec, A.; Fanciullino, R.; Ciccolini, J.; Mochel, J.P.; Mastri, M.; Poignard, C.; Ebos, J.M.L.; Benzekry, S. Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors. PLoS Comput. Biol. 2020, 16, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Volk, L.D.; Flister, M.J.; Chihade, D.; Desai, N.; Trieu, V.; Ran, S. Synergy of nab-paclitaxel and bevacizumab in eradicating large orthotopic breast tumors and preexisting metastases. Neoplasia 2011, 13, 327–338. [Google Scholar] [CrossRef] [Green Version]
- Benzekry, S.; Lamont, C.; Weremowicz, J.; Beheshti, A.; Hlatky, L.; Hahnfeldt, P. Tumor growth kinetics of subcutaneously implanted Lewis Lung carcinoma cells. PLoS Comput. Biol. 2019. [Google Scholar] [CrossRef]
- Simpson-Herren, L.; Lloyd, H.H. Kinetic parameters and growth curves for experimental tumor systems. Cancer Chemother. Rep. 1970, 54, 143–174. [Google Scholar]
- Tan, G.; Kasuya, H.; Sahin, T.T.; Yamamura, K.; Wu, Z.; Koide, Y.; Hotta, Y.; Shikano, T.; Yamada, S.; Kanzaki, A.; et al. Combination therapy of oncolytic herpes simplex virus HF10 and bevacizumab against experimental model of human breast carcinoma xenograft. Int. J. Cancer 2015, 136, 1718–1730. [Google Scholar] [CrossRef]
- Edgerton, M.E.; Chuang, Y.L.; Macklin, P.; Yang, W.; Bearer, E.L.; Cristini, V. A novel, patient-specific mathematical pathology approach for assessment of surgical volume: Application to ductal carcinoma in situ of the breast. Anal. Cell. Pathol. 2011, 34, 247–263. [Google Scholar] [CrossRef]
- Burstein, H.J.; Polyak, K.; Wong, J.S.; Lester, S.C.; Kaelin, C.M. Ductal carcinoma in situ of the breast. N. Engl. J. Med. 2004, 350, 1430–1441. [Google Scholar] [CrossRef] [Green Version]
- Franks, S.; Byrne, H.; King, J.; Underwood, J.; Lewis, C. Modelling the early growth of ductal carcinoma in situ of the breast. J. Math. Biol. 2003, 47, 424–452. [Google Scholar] [CrossRef]
- Franks, S.; Byrne, H.; Underwood, J.; Lewis, C. Biological inferences from a mathematical model of comedo ductal carcinoma in situ of the breast. J. Theor. Biol. 2005, 232, 523–543. [Google Scholar] [CrossRef]
- Smith, J.; Martin, L. Do cells cycle? Proc. Natl. Acad. Sci. USA 1973, 70, 1263–1267. [Google Scholar] [CrossRef] [Green Version]
- Marx, J. How cells cycle toward cancer. Science 1994, 263, 319–322. [Google Scholar] [CrossRef]
- Cristini, V.; Lowengrub, J. Multiscale Modeling of Cancer: An Integrated Experimental and Mathematical Modeling Approach; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Macklin, P.; Edgerton, M.E.; Thompson, A.M.; Cristini, V. Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 2012, 301, 122–140. [Google Scholar] [CrossRef] [Green Version]
- Benzekry, S.; Lamont, C.; Barbolosi, D.; Hlatky, L.; Hahnfeldt, P. Mathematical Modeling of Tumor–Tumor Distant Interactions Supports a Systemic Control of Tumor Growth. Cancer Res. 2017, 77, 5183–5193. [Google Scholar] [CrossRef] [Green Version]
- Axenie, C.; Kurz, D. PRINCESS: Prediction of Individual Breast Cancer Evolution to Surgical Size. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), Rochester, MN, USA, 28–30 July 2020; pp. 457–462. [Google Scholar]
- Coffey, J.C.; Wang, J.; Smith, M.; Bouchier-Hayes, D.; Cotter, T.; Redmond, H. Excisional surgery for cancer cure: Therapy at a cost. Lancet Oncol. 2003, 4, 760–768. [Google Scholar] [CrossRef]
- Pusztai, L.; Foldi, J.; Dhawan, A.; DiGiovanna, M.P.; Mamounas, E.P. Changing frameworks in treatment sequencing of triple-negative and HER2-positive, early-stage breast cancers. Lancet Oncol. 2019, 20, e390–e396. [Google Scholar] [CrossRef]
- Afghahi, A.; Timms, K.M.; Vinayak, S.; Jensen, K.S.; Kurian, A.W.; Carlson, R.W.; Chang, P.-J.; Schackmann, E.; Hartmann, A.-R.; Ford, J.M.; et al. Tumor BRCA1 reversion mutation arising during neoadjuvant platinum-based chemotherapy in triple-negative breast cancer is associated with therapy resistance. Clin. Cancer Res. 2017, 23, 3365–3370. [Google Scholar] [CrossRef] [Green Version]
- Killelea, B.K.; Yang, V.Q.; Mougalian, S.; Horowitz, N.R.; Pusztai, L.; Chagpar, A.B.; Lannin, D.R. Neoadjuvant chemotherapy for breast cancer increases the rate of breast conservation: Results from the National Cancer Database. J. Am. Coll. Surg. 2015, 220, 1063–1069. [Google Scholar] [CrossRef]
- Reid-Lawrence, S.; Tan, A.R.; Mayer, I.A. Optimizing Adjuvant and Neoadjuvant Chemotherapy for Triple-Negative Breast Cancer. In Triple-Negative Breast Cancer; Springer: Cham, Switzerland, 2018; pp. 83–94. [Google Scholar]
- Loibl, S.; Treue, D.; Budczies, J.; Weber, K.; Stenzinger, A.; Schmitt, W.D.; Weichert, W.; Jank, P.; Furlanetto, J.; Klauschen, F.; et al. Mutational diversity and therapy response in breast Cancer: A sequencing analysis in the Neoadjuvant GeparSepto trial. Clin. Cancer Res. 2019, 25, 3986–3995. [Google Scholar] [CrossRef] [Green Version]
- Fisher, B.; Gunduz, N.; Saffer, E.A. Influence of the Interval between Primary Tumor Removal and Chemotherapy on Kinetics and Growth of Metastases. Cancer Res. 1983, 43, 1488–1492. [Google Scholar]
- Pauli, C.; Hopkins, B.D.; Prandi, D.; Shaw, R.; Fedrizzi, T.; Sboner, A.; Sailer, V.; Augello, M.; Puca, L.; Rosati, R.; et al. Personalized in vitro and in vivo cancer models to guide precision medicine. Cancer Discov. 2017, 7, 462–477. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Deng, Z.; Wang, H.; Ma, W.; Zhou, C.; Zhang, S. Repeated cycles of 5-fluorouracil chemotherapy impaired anti-tumor functions of cytotoxic T cells in a CT26 tumor-bearing mouse model. BMC Immunol. 2016, 17, 29. [Google Scholar] [CrossRef] [PubMed]
- Kessler, D.A.; Austin, R.H.; Levine, H. Resistance to chemotherapy: Patient variability and cellular heterogeneity. Cancer Res. 2014, 74, 4663–4670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Navin, N.E. Tumor evolution in response to chemotherapy: Phenotype versus genotype. Cell Rep. 2014, 6, 417–419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henke, E.; Nandigama, R.; Ergün, S. Extracellular matrix in the tumor microenvironment and its impact on cancer therapy. Front. Mol. Biosci. 2020, 6, 160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurz, D.; Axenie, C. PERFECTO: Prediction of Extended Response and Growth Functions for Estimating Chemotherapy Outcomes in Breast Cancer. In Proceedings of the 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Seoul, Korea, 16–19 December 2020; pp. 609–614. [Google Scholar]
- She, Y.; Jin, Z.; Wu, J.; Deng, J.; Zhang, L.; Su, H.; Jiang, G.; Liu, H.; Xie, D.; Cao, N.; et al. Development and validation of a deep learning model for non–small cell lung cancer survival. JAMA Netw. Open 2020, 3, e205842. [Google Scholar] [CrossRef] [PubMed]
- Benzekry, S.; Pasquier, E.; Barbolosi, D.; Lacarelle, B.; Barlési, F.; André, N.; Ciccolini, J. Metronomic reloaded: Theoretical models bringing chemotherapy into the era of precision medicine. Semin. Cancer Biol. 2015, 35, 53–61. [Google Scholar] [CrossRef]
- Amoroso, N.; Pomarico, D.; Fanizzi, A.; Didonna, V.; Giotta, F.; La Forgia, D.L.; Latorre, A.; Monaco, A.; Pantaleo, E.; Petruzzellis, N.; et al. A Roadmap towards Breast Cancer Therapies Supported by Explainable Artificial Intelligence. Appl. Sci. 2021, 11, 4881. [Google Scholar] [CrossRef]
- Simone, G.; Bianchi, M.; Giannarelli, D.; Daneshmand, S.; Papalia, R.; Ferriero, M.; Guaglianone, S.; Sentinelli, S.; Colombo, R.; Montorsi, F.; et al. Development and external validation of nomograms predicting disease-free and cancer-specific survival after radical cystectomy. World J. Urol. 2015, 33, 1419–1428. [Google Scholar] [CrossRef]
- He, Y.; Liu, H.; Wang, S.; Zhang, J. A nomogram for predicting cancer-specific survival in patients with osteosarcoma as secondary malignancy. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Zlotnik, A.; Abraira, V. A general-purpose nomogram generator for predictive logistic regression models. Stata J. 2015, 15, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Jalali, A.; Alvarez-Iglesias, A.; Roshan, D.; Newell, J. Visualising statistical models using dynamic nomograms. PLoS ONE 2019, 14, e0225253. [Google Scholar] [CrossRef]
- Zhong, B.Y.; Ni, C.F.; Ji, J.S.; Yin, G.W.; Chen, L.; Zhu, H.D.; Guo, J.H.; He, S.C.; Deng, G.; Zhang, Q.; et al. Nomogram and artificial neural network for prognostic performance on the albumin-bilirubin grade for hepatocellular carcinoma undergoing transarterial chemoembolization. J. Vasc. Interv. Radiol. 2019, 30, 330–338. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, K.; Hellmayr, C.; Liu, W.; Markowetz, F. Reconstructing evolving signalling networks by hidden Markov nested effects models. Ann. Appl. Stat. 2014, 8, 448–480. [Google Scholar] [CrossRef] [Green Version]
- Achim, T.; Florian, M. Structure Learning in Nested Effects Models. Stat. Appl. Genet. Mol. Biol. 2008, 7, 1–28. [Google Scholar]
- Castro, M.A.; Wang, X.; Fletcher, M.N.; Meyer, K.B.; Markowetz, F. RedeR: R/Bioconductor package for representing modular structures, nested networks and multiple levels of hierarchical associations. Genome Biol. 2012, 13, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Letort, G.; Montagud, A.; Stoll, G.; Heiland, R.; Barillot, E.; Macklin, P.; Zinovyev, A.; Calzone, L. PhysiBoSS: A multi-scale agent-based modelling framework integrating physical dimension and cell signalling. Bioinformatics 2019, 35, 1188–1196. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Axenie, C.; Bauer, R.; Martínez, M.R. The Multiple Dimensions of Networks in Cancer: A Perspective. Symmetry 2021, 13, 1559. https://doi.org/10.3390/sym13091559
Axenie C, Bauer R, Martínez MR. The Multiple Dimensions of Networks in Cancer: A Perspective. Symmetry. 2021; 13(9):1559. https://doi.org/10.3390/sym13091559
Chicago/Turabian StyleAxenie, Cristian, Roman Bauer, and María Rodríguez Martínez. 2021. "The Multiple Dimensions of Networks in Cancer: A Perspective" Symmetry 13, no. 9: 1559. https://doi.org/10.3390/sym13091559
APA StyleAxenie, C., Bauer, R., & Martínez, M. R. (2021). The Multiple Dimensions of Networks in Cancer: A Perspective. Symmetry, 13(9), 1559. https://doi.org/10.3390/sym13091559







