Time–Frequency Extraction Model Based on Variational Mode Decomposition and Hilbert–Huang Transform for Offshore Oil Platforms Using MIMU Data
Abstract
:1. Introduction
2. A VMD–HHT Approach for Extracting Time–Frequency–Energy Characteristics of Dynamic Responses
2.1. Hilbert–Huang Transform
2.2. Variational Mode Decomposition
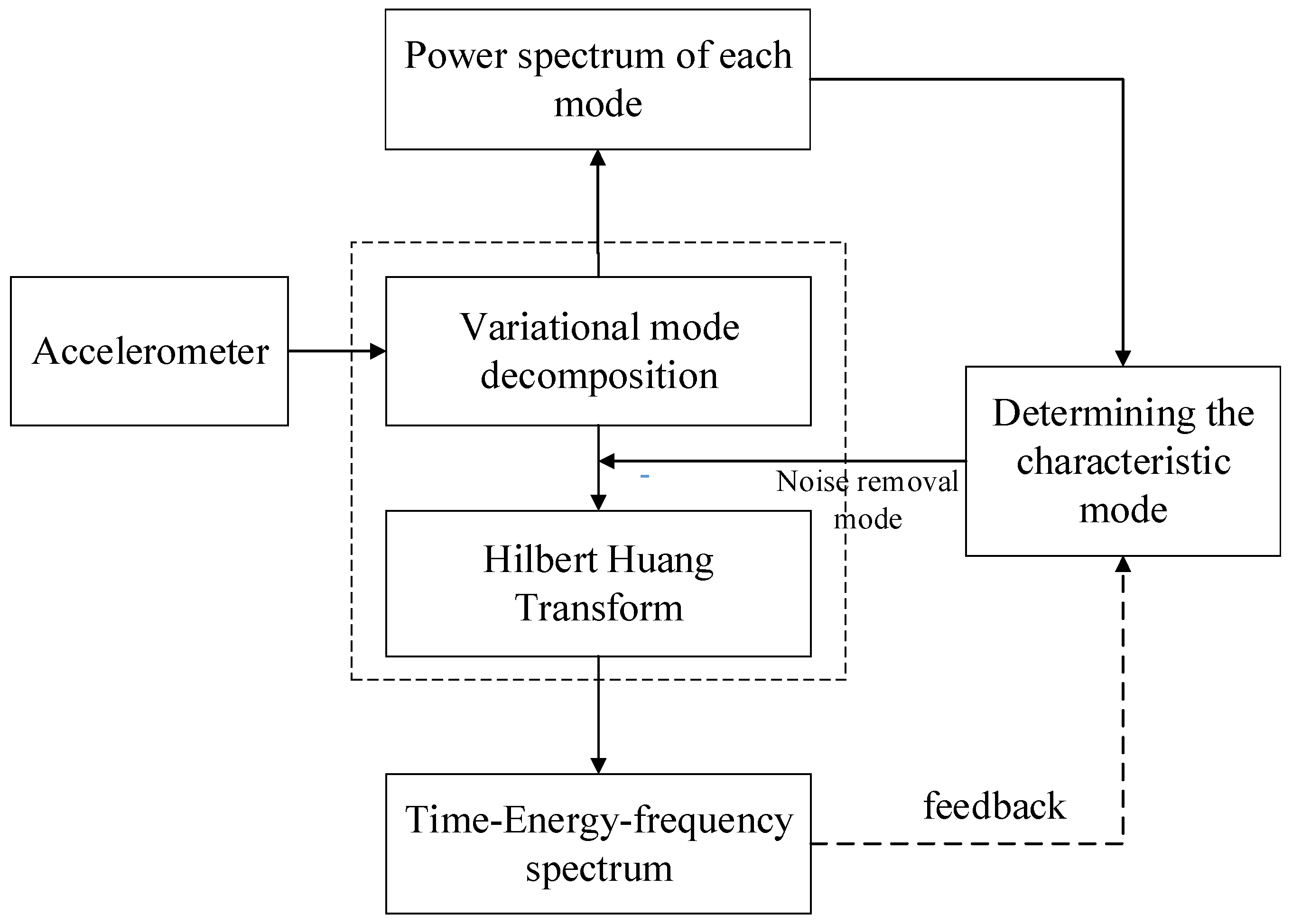
2.3. VMD–HHT Model
3. Dynamic Responses Monitored by MIMU
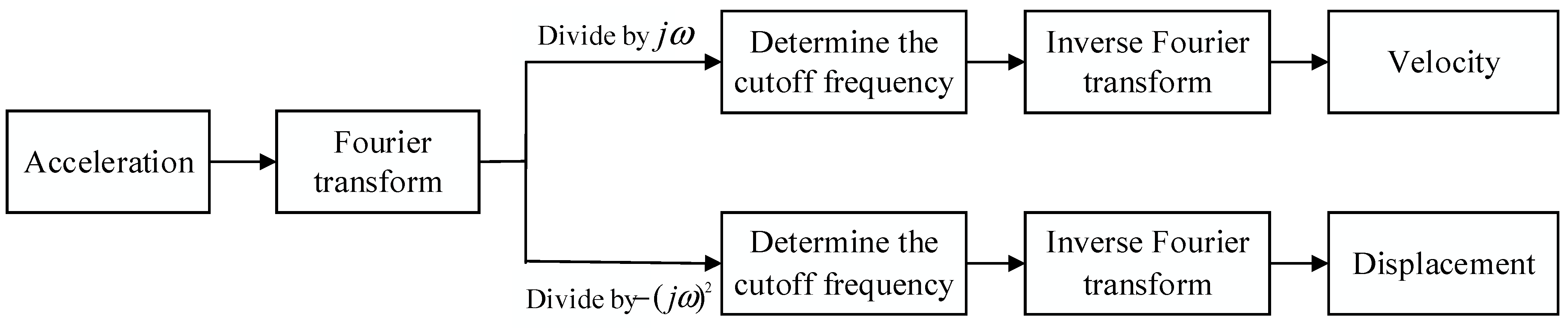
3.1. Accelerometer-Derived Displacement Reconstruction
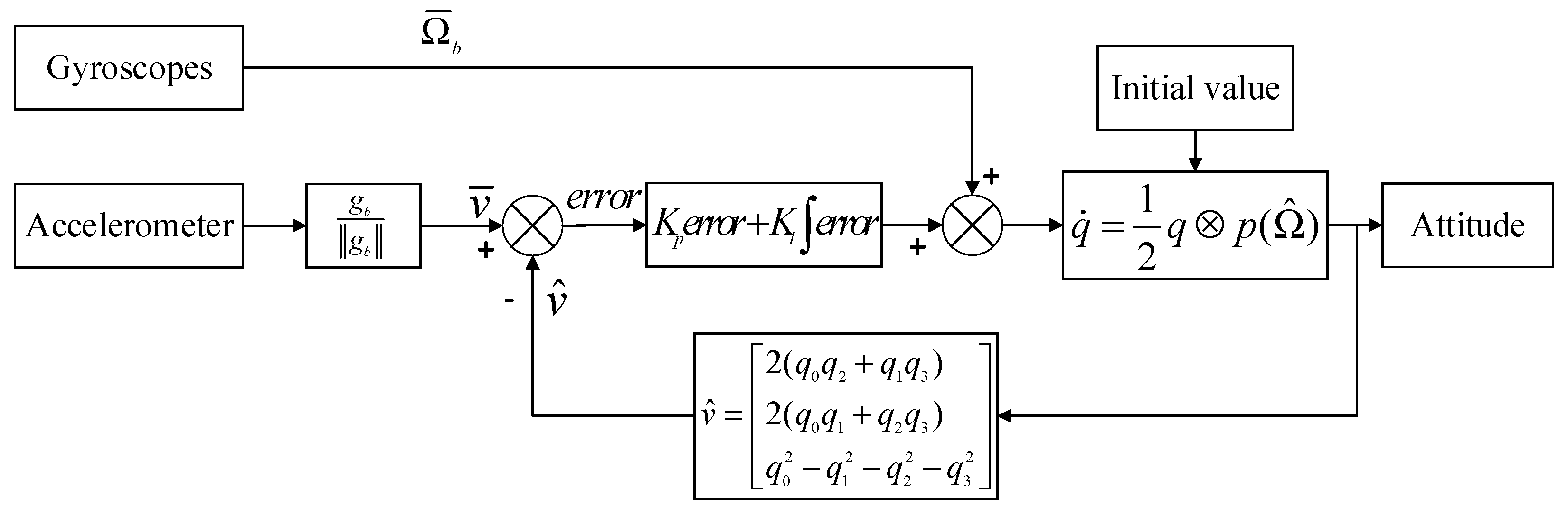
3.2. Gyro-Derived Torsion Reconstruction
- (1)
- The accelerometer is normalized to a single vector .
- (2)
- The acceleration data in the geographical coordinate system are converted to the carrier coordinate system, and the estimation in the carrier coordinate system is given bywhere is quaternions.
- (3)
- The deviation between the acceleration estimation and the measurements by accelerometer is the error item between the integrated torsion angle of the gyroscope and the torsion angle measured by the accelerometer. The value can be expressed by the cross product.
- (4)
- The corrected torsion angle can be obtained based on a PI controller using the results from the previous step,where is the torsion angle obtained by gyro integration, while and are the PI control param.
- (5)
- The quaternion differential equation can be solved by using the corrected torsion angle (See Formula (8)), and the quaternion can be updated to calculate the theoretical estimation of the accelerometer (transfer to Equation (2)).
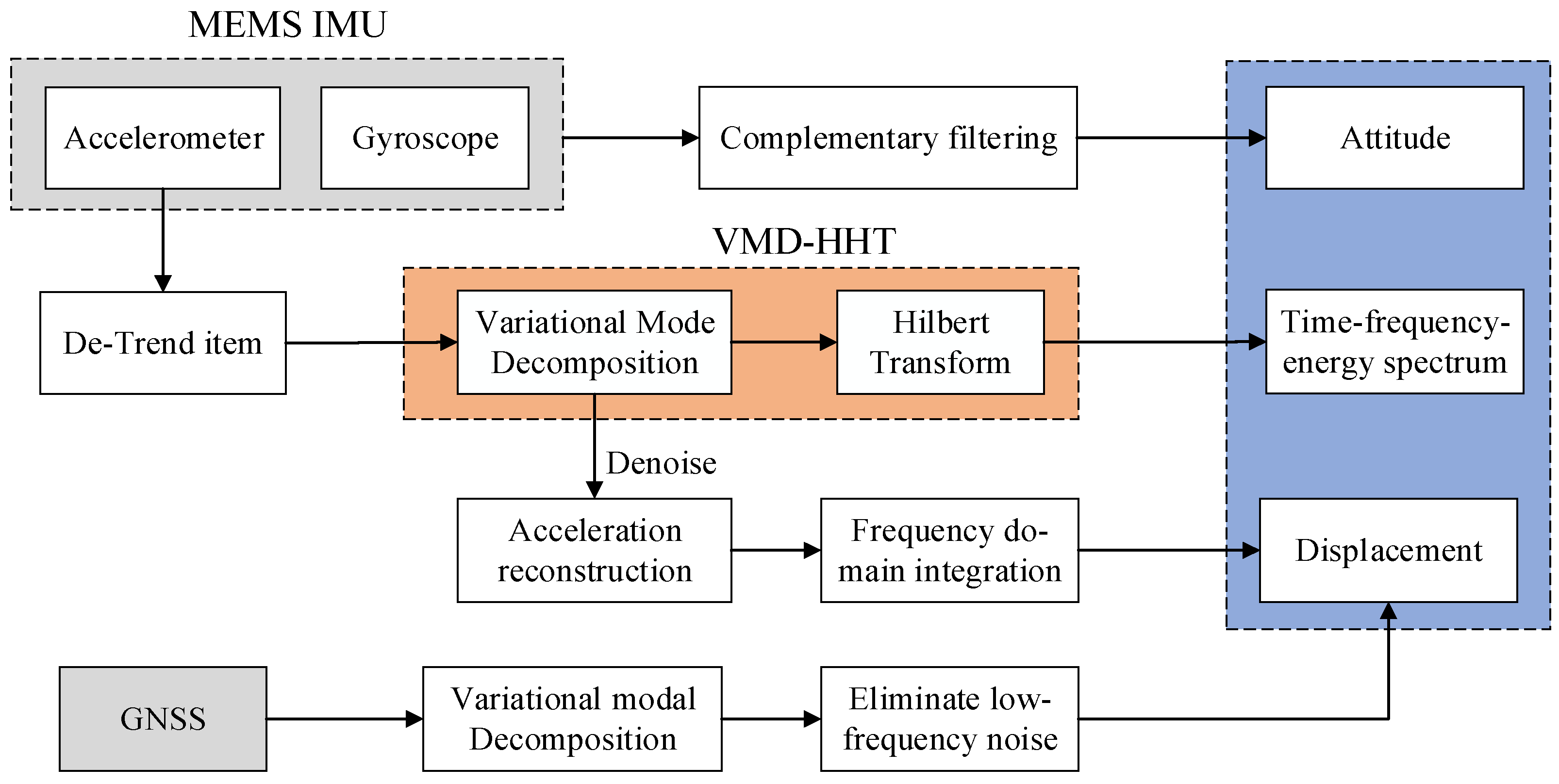
3.3. The Schematic to Monitor Dynamic Responses Based on VMD–HHT Characteristic Extraction Model
4. Simulation Shaking-Table Tests
4.1. Simulation Shaking Table
4.2. Data Collection
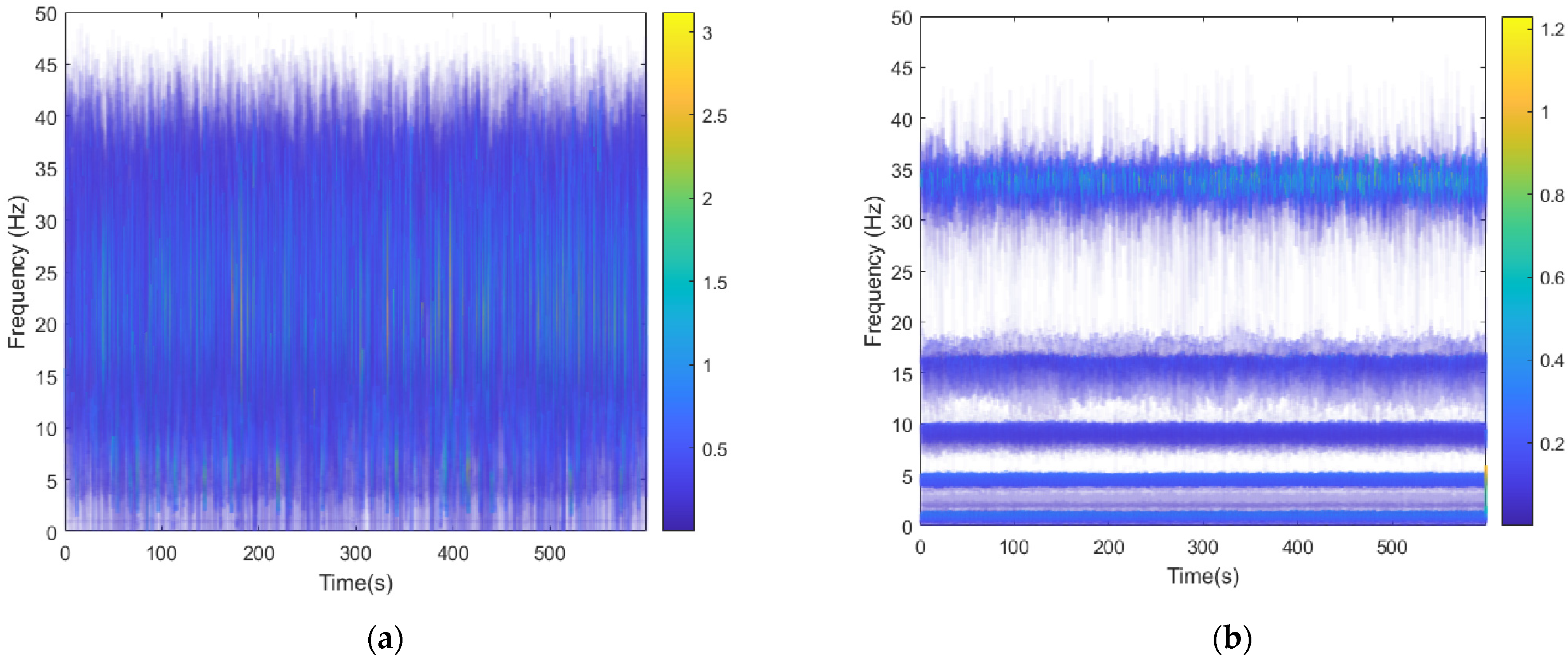
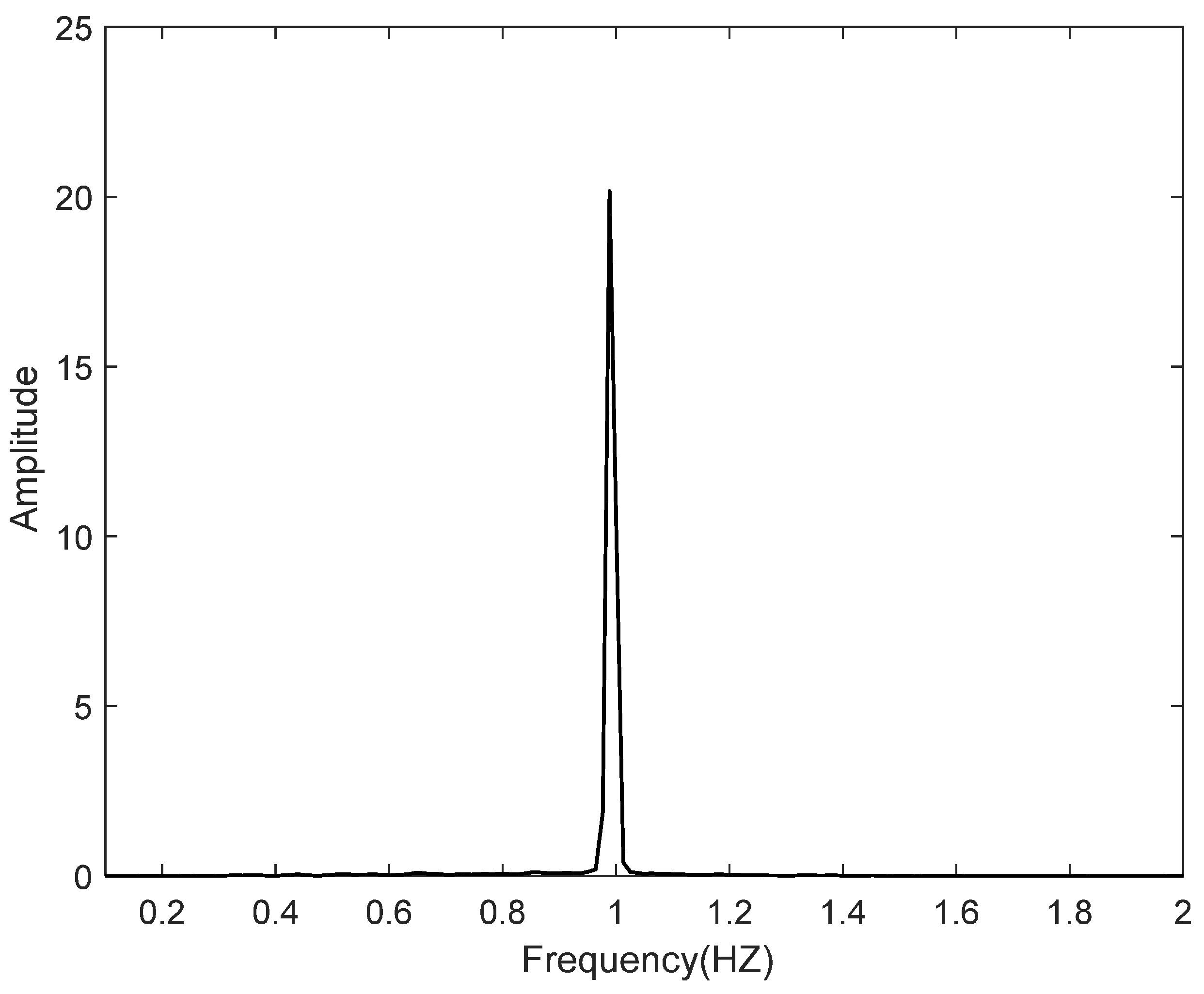
4.3. Comparison of PSD, HHT, and VMD–HHT
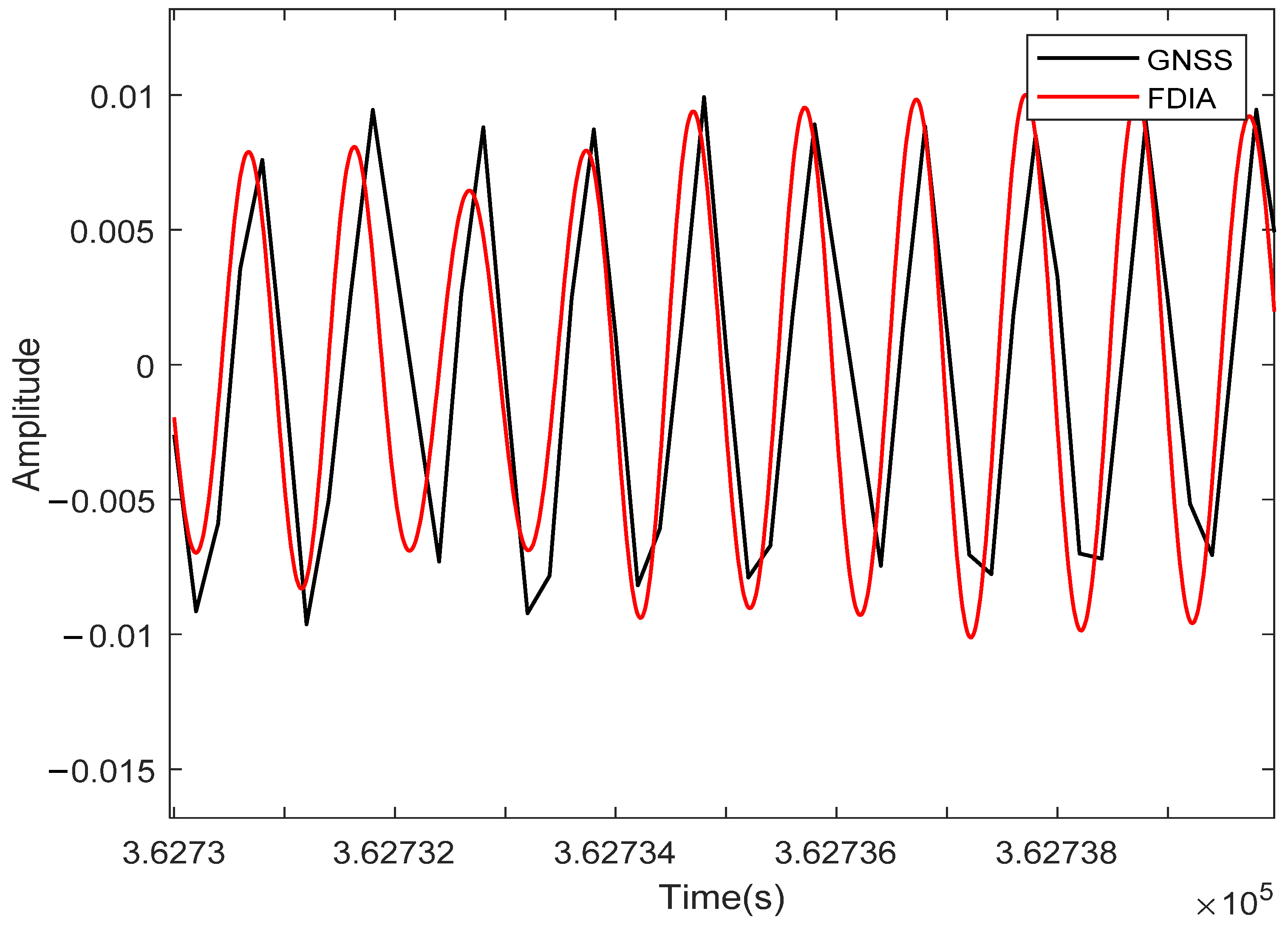
4.4. Reconstruction of Dynamic Displacement Using FDIA Based on the VMD–HHT Model and GPS
5. Trial Analysis of CB4A Offshore Oil Platform
5.1. Equipment for Monitoring Dynamic Responses
5.2. Data Acquisition
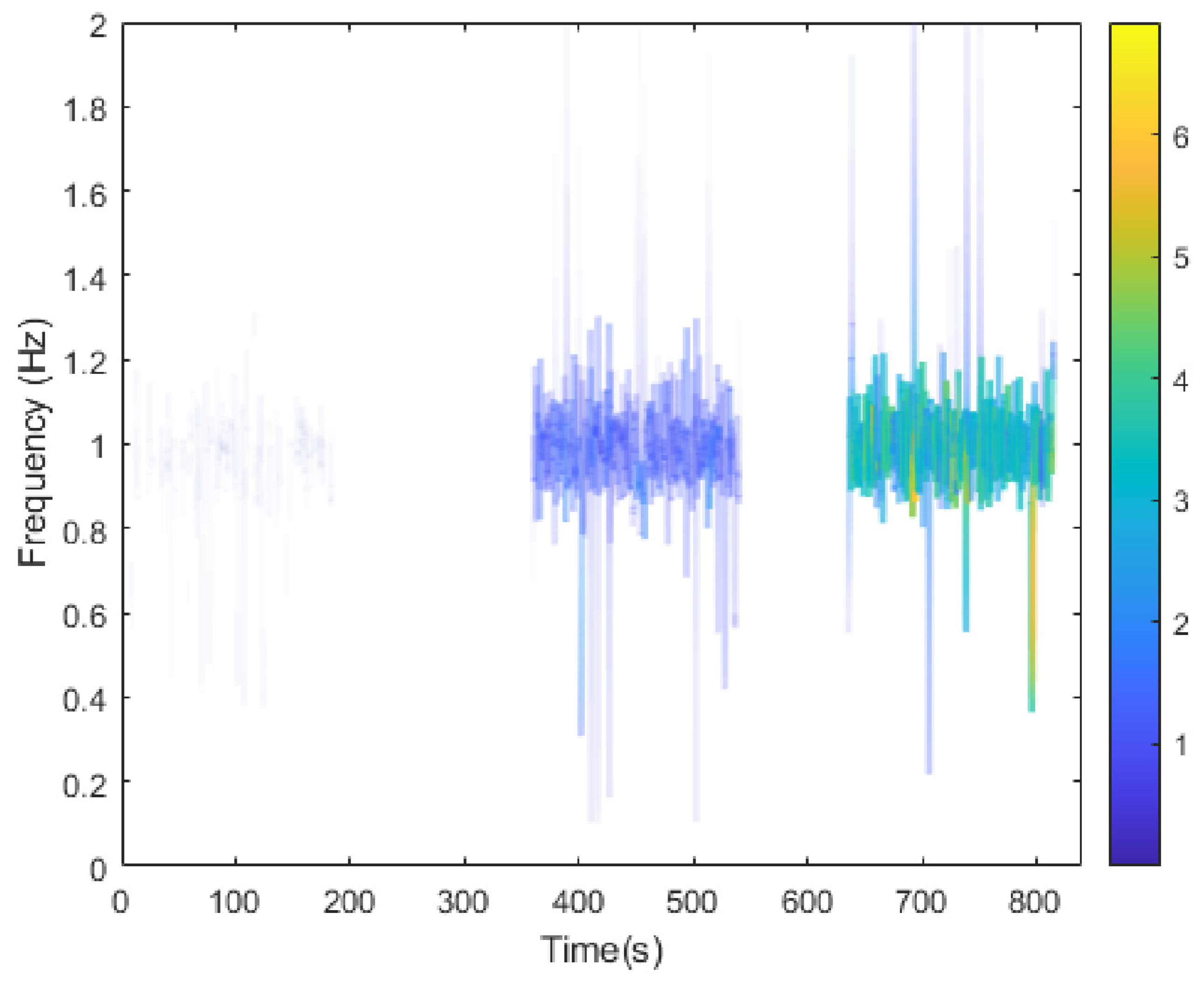
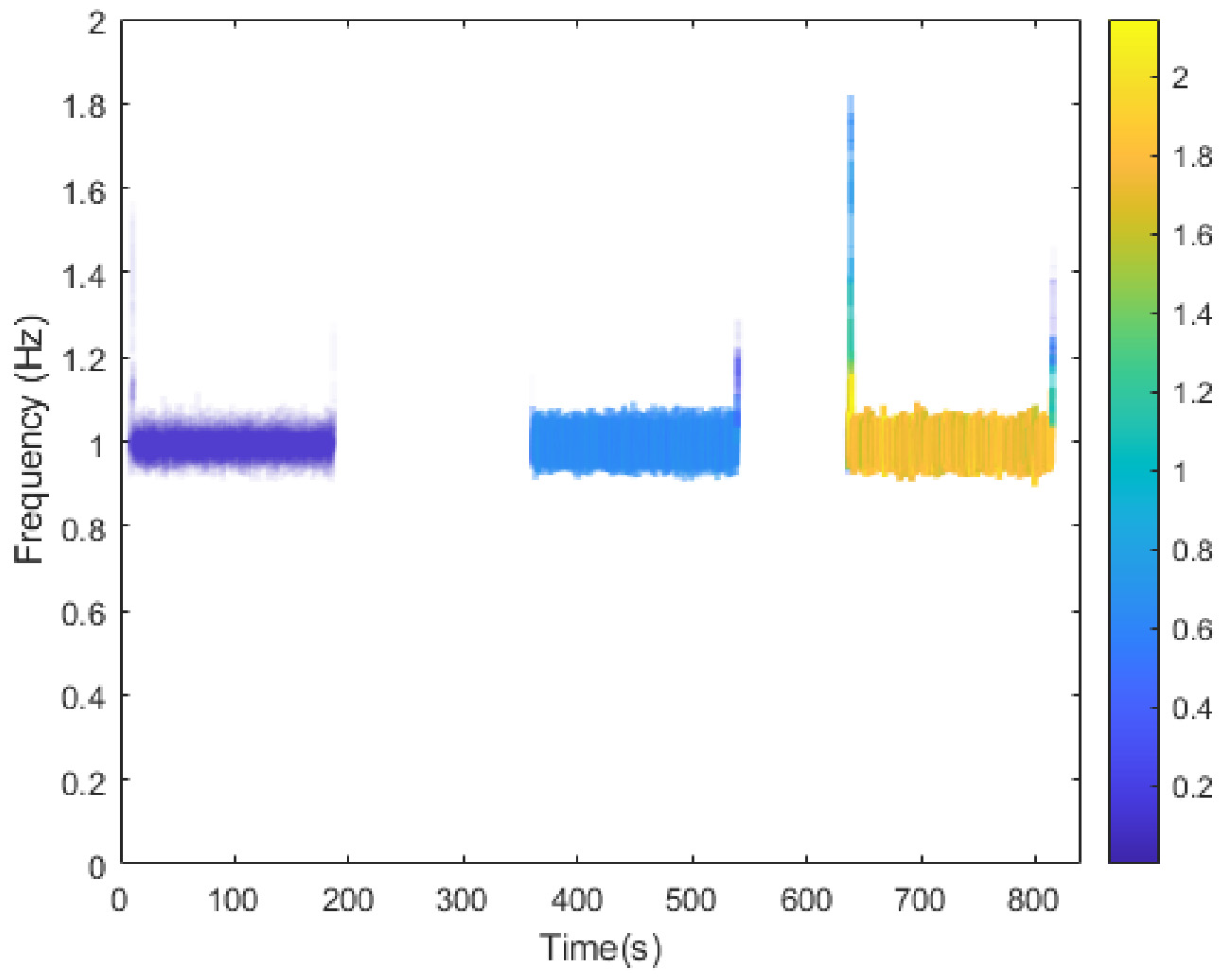
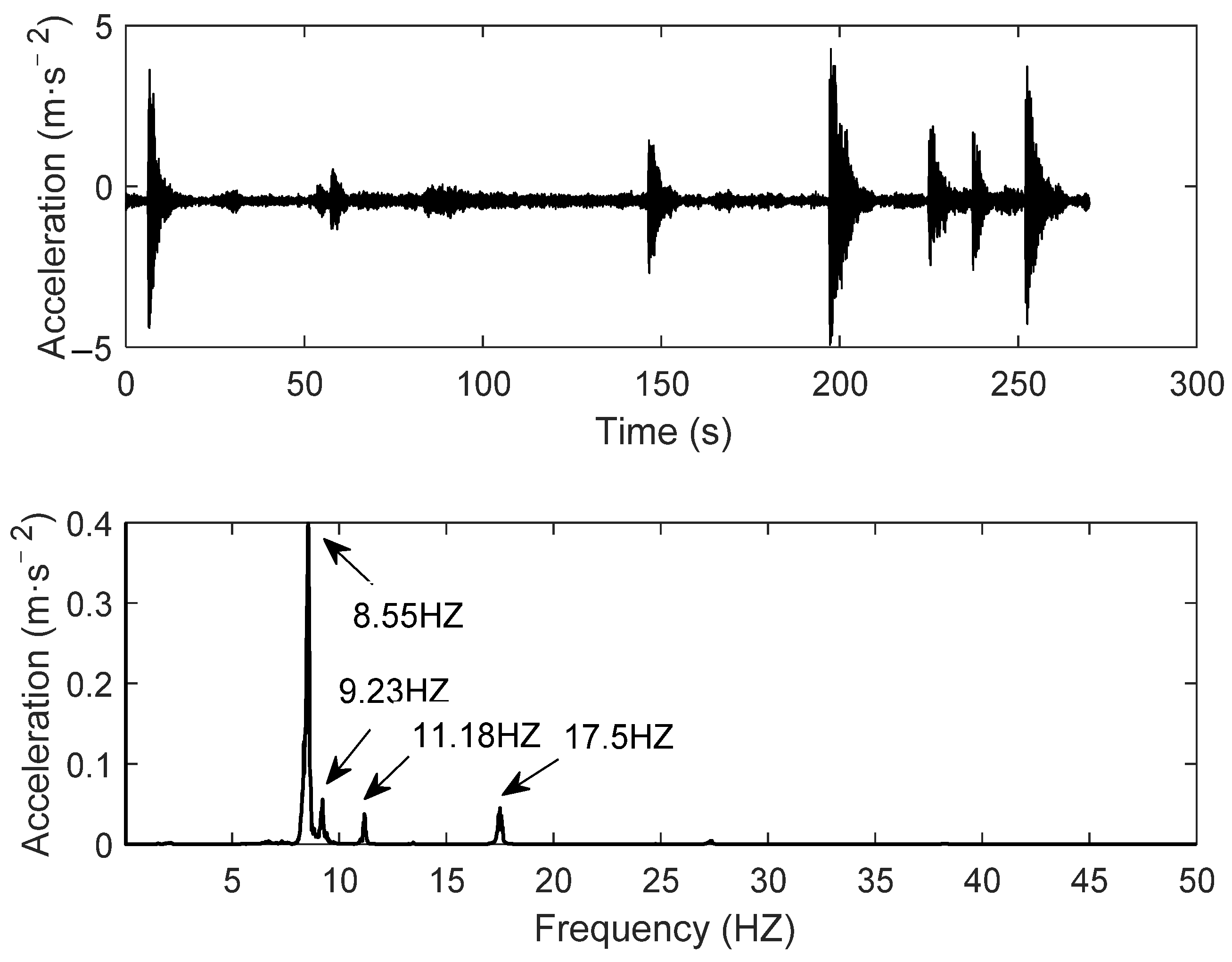
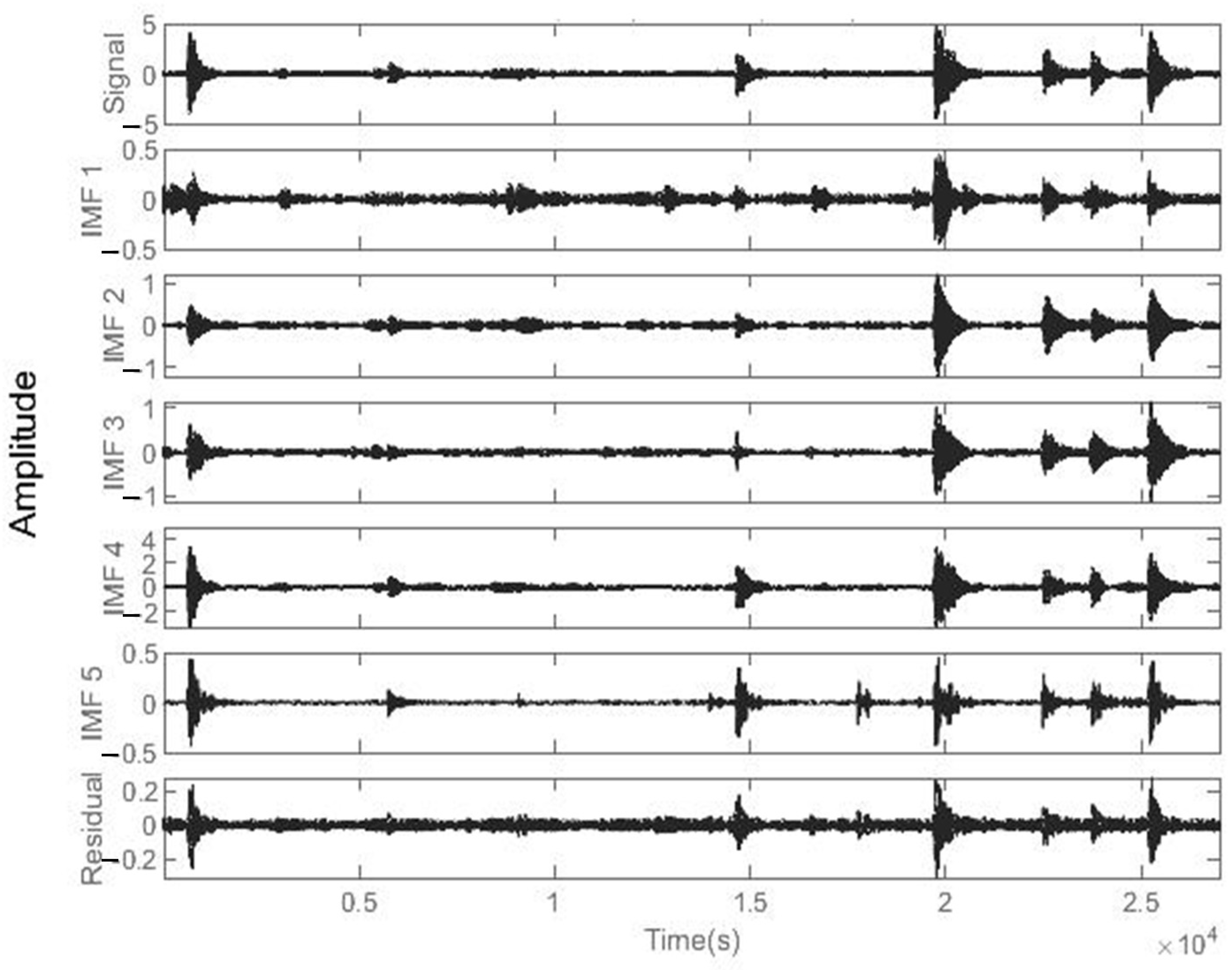
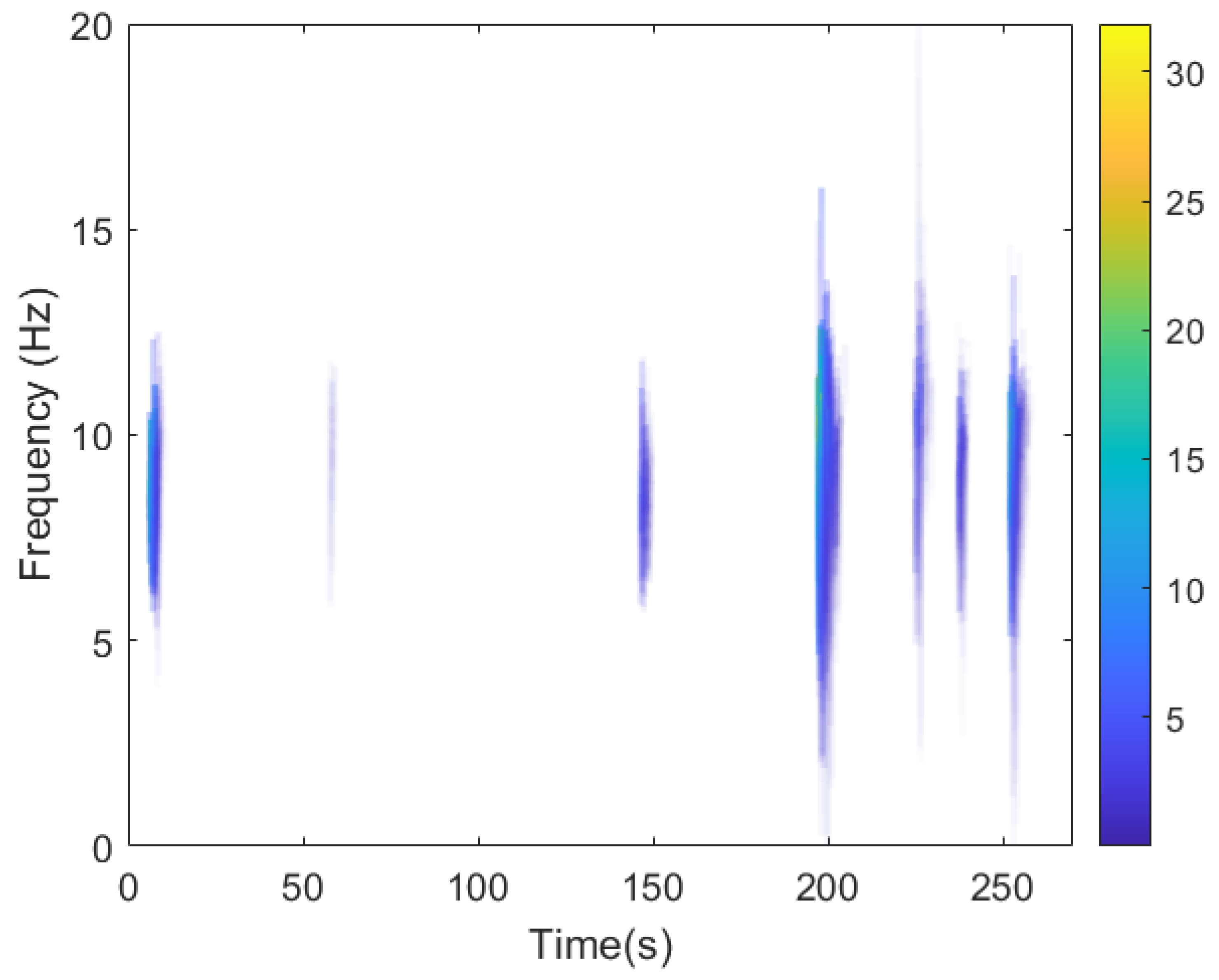
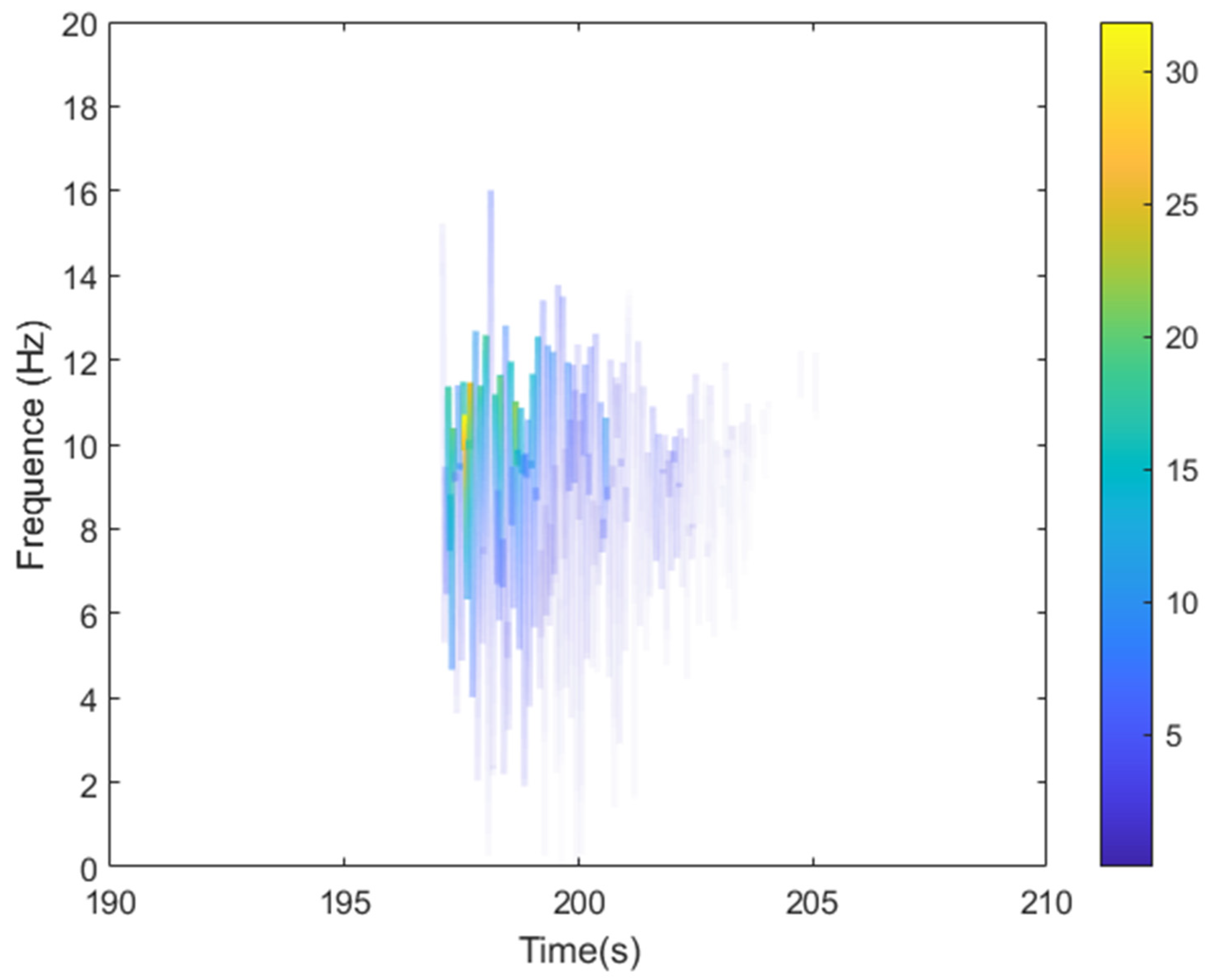
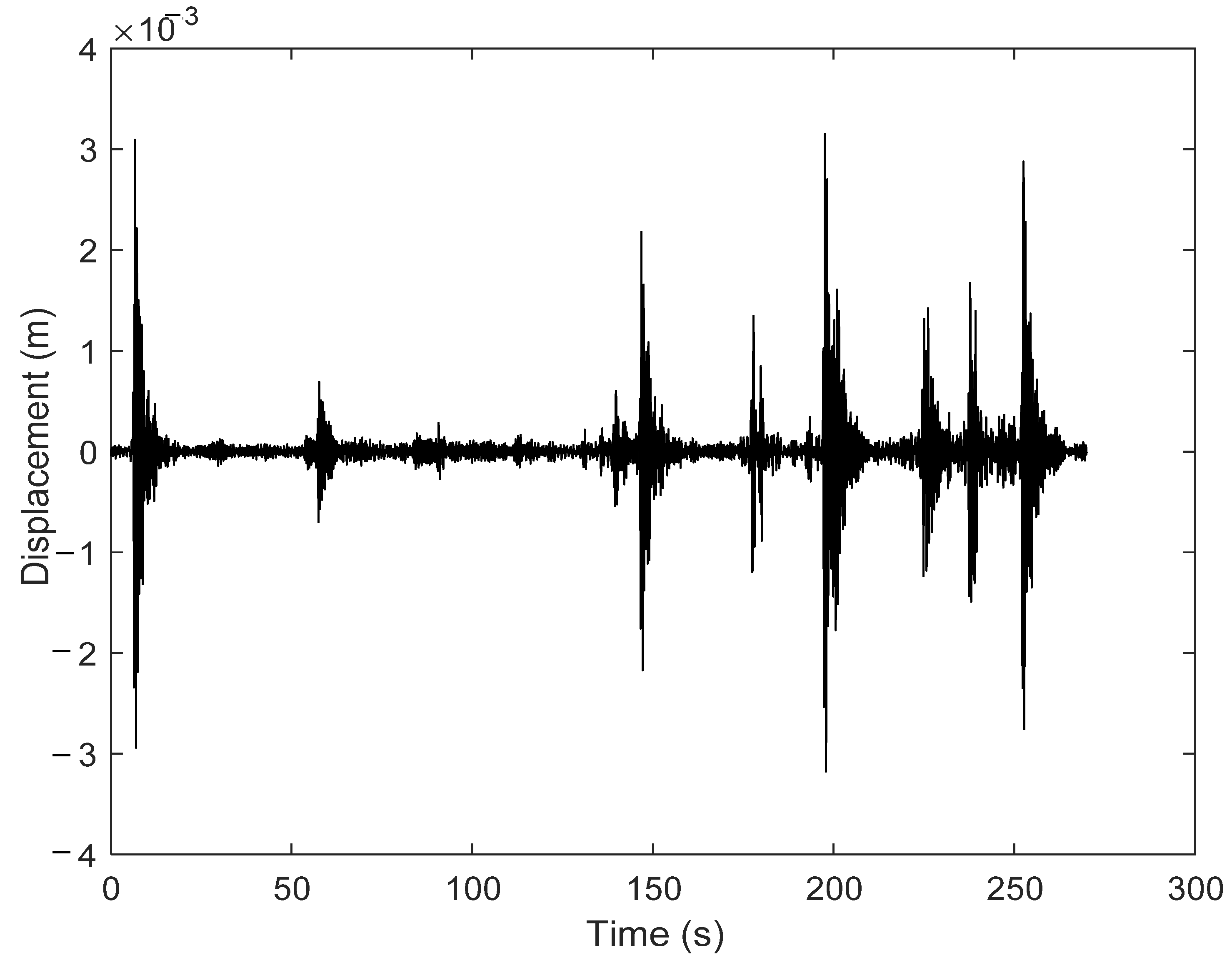
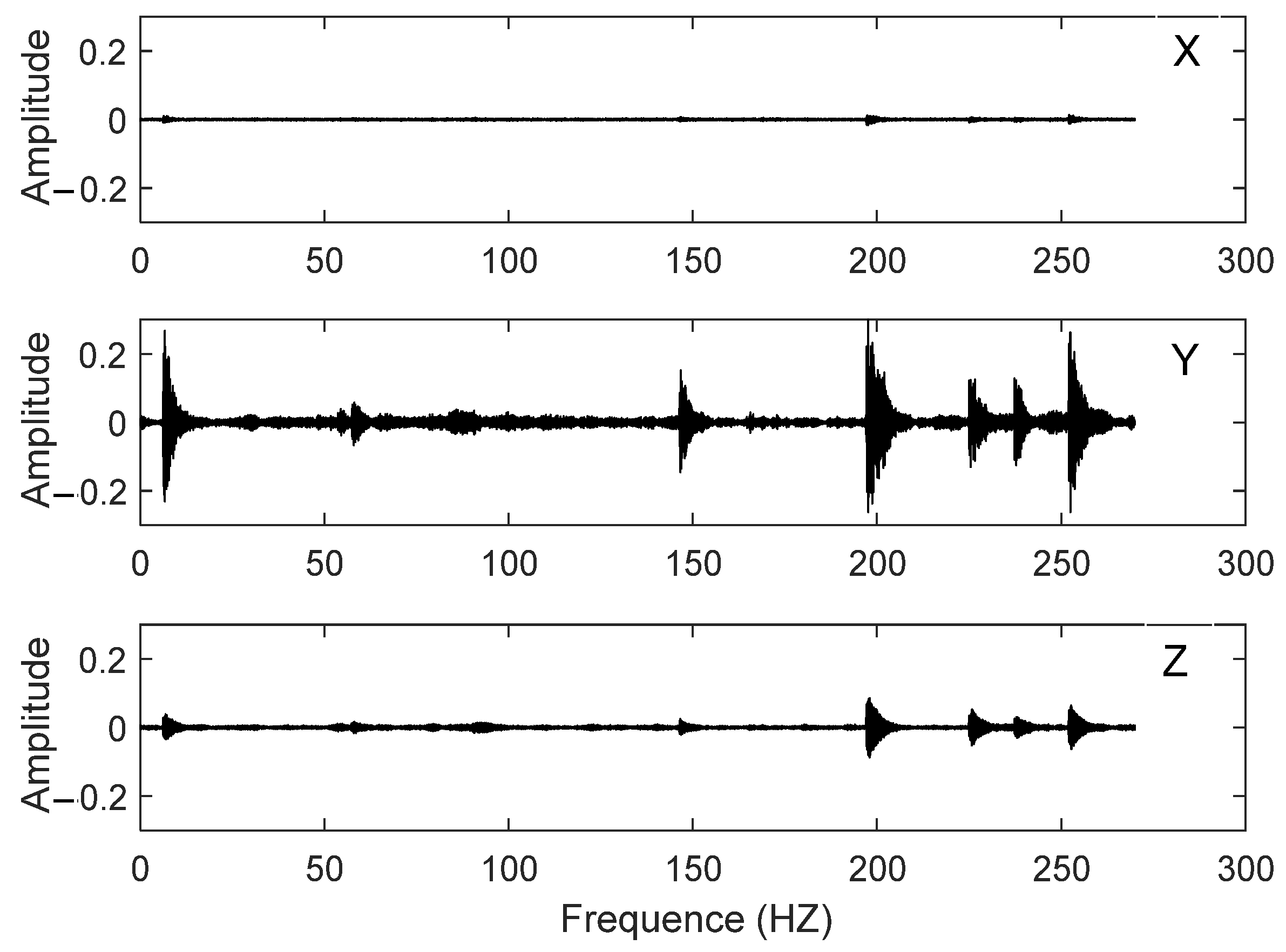
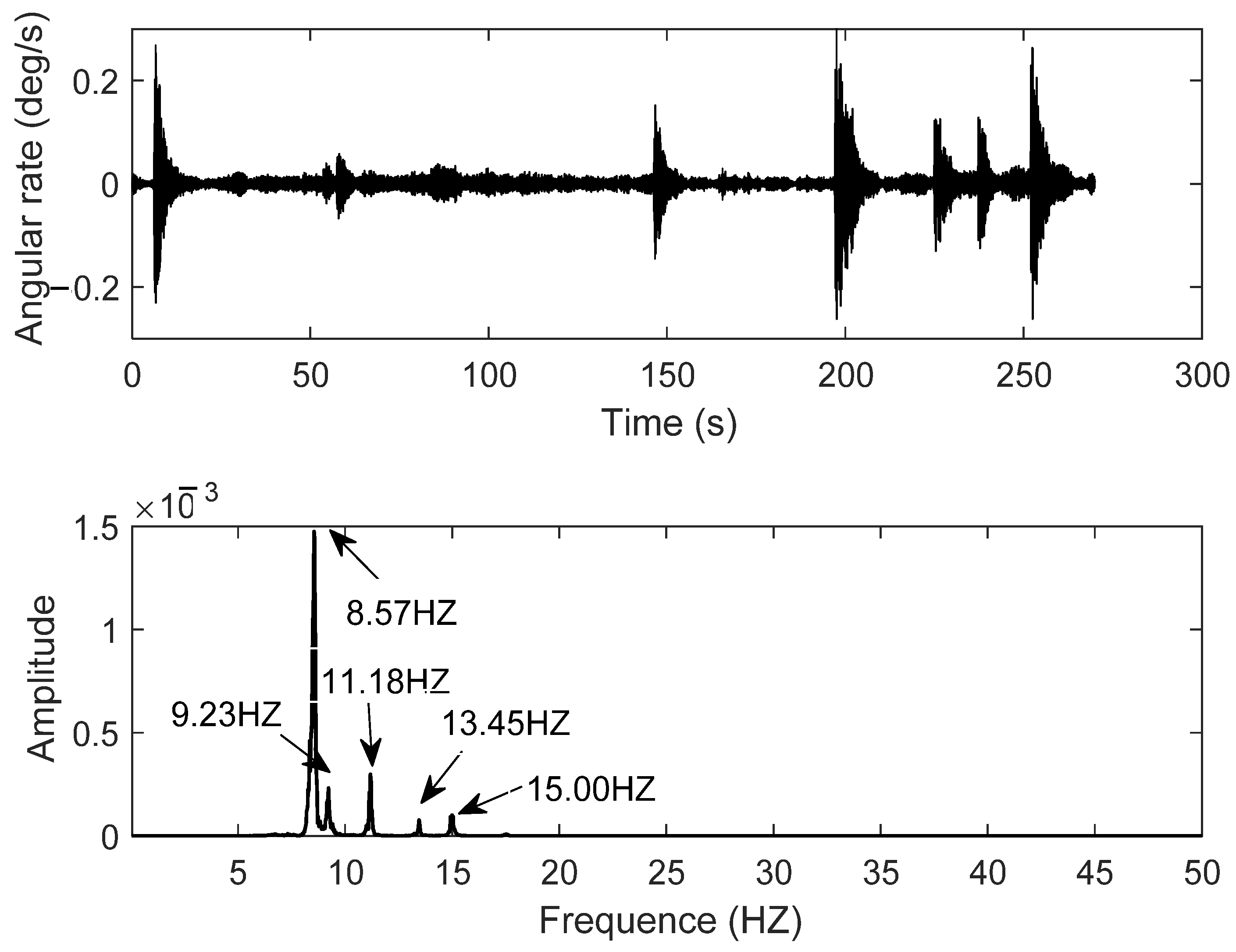
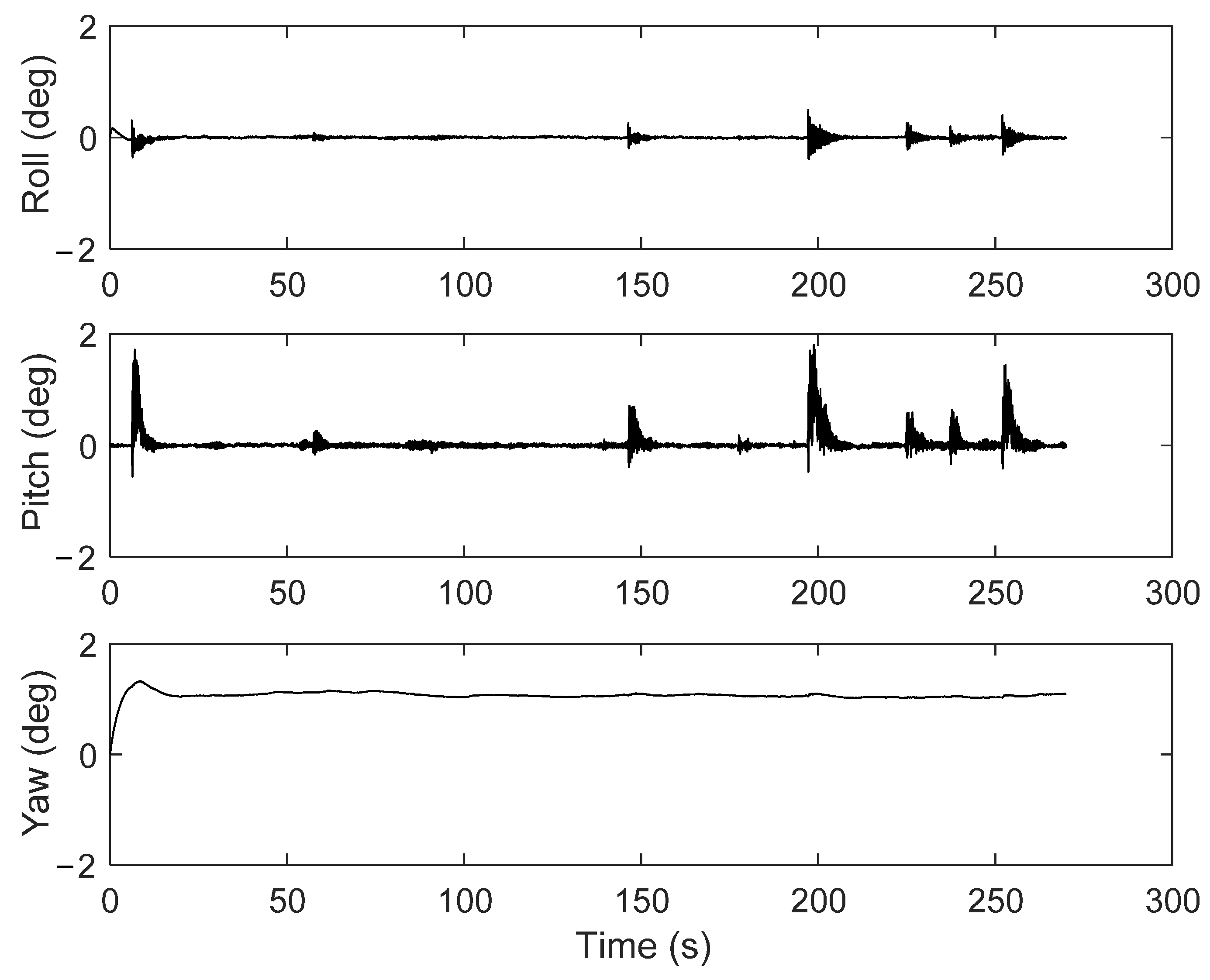
5.3. Dynamic Responses Time–Frequency Extraction
5.4. Reconstruction of Dynamic Displacement Based on VMD–HHT Using Accelerometer
5.5. Evaluation of the Torsion Angle Based on Mahony Complementary Filter Using MIMU
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.F.; Wang, N. Comprehensive safety assessment method for offshore platform in different application scenarios. Energy Energy Conserv. 2021, 1, 198–200. [Google Scholar]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Hu, G.S. Digital Signal Processing: Theory, Algorithm and Implementation; Tsinghua University Press: Beijing, China, 2012. [Google Scholar]
- Mateo, C.; Talavera, J. Short-time Fourier transform with the window size fixed in the frequency domain. Digit. Signal Process. 2018, 77, 13–21. [Google Scholar] [CrossRef]
- Debnath, L.; Shah, F.A. Wavelet Transforms and Their Applications; Birkhäuser: Boston, MA, USA, 2015. [Google Scholar]
- Wang, D.J.; Xiong, Y.L. A precise kinematic single epoch positioning algorithm using moving window wavelet denoising. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 779–785. [Google Scholar]
- Yi, C.; Lv, Y.; Xiao, H. Multi-sensor signal denoising based on matching synchro squeezing wavelet transform for mechanical fault condition assessment. Meas. Sci. Technol. 2018, 29, 045104. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, C.; Zhang, J. Denoising method of deformation monitoring data based on variational mode decomposition. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 784–791. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Chan, W.S.; Xu, Y.L.; Ding, X.L. An integrated GPS–accelerometer data processing technique for structural deformation monitoring. J. Geod. 2006, 80, 705–719. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Rehman, N.; Park, C.; Huang, N.E. EMD via MEMD: Multivariate noise-aided computation of standard EMD. Adv. Adapt. Data Anal. 2013, 5, 1350007. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Zhang, M.; Yu, Q. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Shrivastava, Y.; Singh, B. A comparative study of EMD and EEMD approaches for identifying chatter frequency in CNC turning. Eur. J. Mech. 2019, 73, 381–393. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Niu, Y.; Xiong, C. Analysis of the dynamic characteristics of a suspension bridge based on RTK-GNSS measurement combining EEMD and a wavelet packet technique. Meas. Sci. Technol. 2018, 29, 85–103. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Gao, J. EMD-wavelet based stochastic error reducing model for GPS/INS integrated navigation. J. Southeast Univ. 2012, 42, 406–412. [Google Scholar]
- Song, J.G.; Zhao, C.X.; Lin, S.H. Decomposition of seismic signal based on Hilbert-Huang transform. In Proceedings of the 2011 International Conference on Business Management and Electronic Information, Guangzhou, China, 13 May 2011; pp. 840–843. [Google Scholar]
- Zhou, Y.; Chen, W.; Gao, J. Application of Hilbert–Huang transform based instantaneous frequency to seismic reflection data. J. Appl. Geophys. 2012, 82, 68–74. [Google Scholar] [CrossRef]
- Huang, N.E. Hilbert-Huang Transform and Its Applications, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar]
- Shi, C.; Niu, Y.J.; Wei, N. Application of the HHT-EEMD approach in analysis of GPS height time series. J. Geod. Geodyn. 2018, 38, 661–667. [Google Scholar]
- Mou, Z.; Niu, X.; Wang, C. A precise feature extraction method for shock wave signal with improved CEEMD-HHT. J. Ambient Intell. Humaniz. Comput. 2020, 3, 1–12. [Google Scholar] [CrossRef]
- Luo, Y.Y.; Yao, Y.B.; Huang, C. Deformation feature extraction and analysis based on improved variational mode decomposition. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 612–619. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, M.; Guan, L.; Gao, Y. UAV torsion angle measurement based on enhanced mahony complementary filter. IEEE Int. Conf. Mechatron. Autom. 2018, 545–550. [Google Scholar]









| Equipment | Performance | |
|---|---|---|
| GNSS | Signal Tracking | BDS: B1/B2; GPS:L1/L2 GLONASS: L1/L2; GALILEO:E1/E5b |
| RTK (RMS) | Horizontal: 8 mm + 1 ppm Vertical: 15 mm + 1 ppm | |
| Updating Frequency | 5 Hz | |
| Accelerometer | Dynamic Range | |
| Bias Stability | ||
| Noise Density | ||
| Updating Frequency | 100 Hz | |
| Index Item | Gyroscope | Accelerom |
|---|---|---|
| Standard full range | ±450 °/s | ±20 g |
| Initial bias error (one year) | 0.2 °/s | 5 mg |
| In-run bias stability | 10 °/h | 15 µg |
| Bandwidth (−3 dB) | 415 Hz | 375 Hz |
| Noise density | 0.01 °/s/√Hz | 60 µg/√Hz |
| g-sensitivity (calibrated) | 0.003 °/s/g | N/A |
| Nonorthogonality | 0.05 deg | 0.05 deg |
| Nonlinearity | 0.01% | 0.1% |
| Tracking Signal | BDS B1/B2/B3 |
| GPS L1/L2/L5 | |
| GLONASS /L1/L2 | |
| GALILEO E1/E5a/E5b | |
| QZSS L1/L5 | |
| SBAS L1 | |
| Single(RMS) | Plane: 1.5 m; Altitude: 3 m |
| DGPS(RMS) | Plane: 0.4 m; Altitude: 0.8 m |
| RTK(RMS) | Plane: 8 mm + 1 ppm Altitude: 15 mm + 1 ppm |
| Sampling rate | 5 Hz |
| Collision | First | Second | Third | Fourth | Fifth | Sixth | Seventh | Eighth |
|---|---|---|---|---|---|---|---|---|
| Time | 15:34:37 | 15:35:28 | 15:36:00 | 15:36:58 | 15:37:30 | 15:37:51 | 15:38:17 | 15:38:46 |
| GPS Period | 200094.6 | 200145.6 | 200177.6 | 200235.6 | 200267.6 | 200290.8 | 200314.6 | 200343.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, X.; Li, W.; Liu, F.; Hancock, C. Time–Frequency Extraction Model Based on Variational Mode Decomposition and Hilbert–Huang Transform for Offshore Oil Platforms Using MIMU Data. Symmetry 2021, 13, 1443. https://doi.org/10.3390/sym13081443
Wang J, Liu X, Li W, Liu F, Hancock C. Time–Frequency Extraction Model Based on Variational Mode Decomposition and Hilbert–Huang Transform for Offshore Oil Platforms Using MIMU Data. Symmetry. 2021; 13(8):1443. https://doi.org/10.3390/sym13081443
Chicago/Turabian StyleWang, Jian, Xu Liu, Wen Li, Fei Liu, and Craig Hancock. 2021. "Time–Frequency Extraction Model Based on Variational Mode Decomposition and Hilbert–Huang Transform for Offshore Oil Platforms Using MIMU Data" Symmetry 13, no. 8: 1443. https://doi.org/10.3390/sym13081443
APA StyleWang, J., Liu, X., Li, W., Liu, F., & Hancock, C. (2021). Time–Frequency Extraction Model Based on Variational Mode Decomposition and Hilbert–Huang Transform for Offshore Oil Platforms Using MIMU Data. Symmetry, 13(8), 1443. https://doi.org/10.3390/sym13081443








