Abstract
Optical vortices are beams of laser light with screw symmetry in their wavefront. With a corresponding azimuthal dependence in optical phase, they convey orbital angular momentum, and their methods of production and applications have become one of the most rapidly accelerating areas in optical physics and technology. It has been established that the quantum nature of electromagnetic radiation extends to properties conveyed by each individual photon in such beams. It is therefore of interest to identify and characterize the symmetry aspects of the quantized fields of vortex radiation that relate to the beam and become manifest in its interactions with matter. Chirality is a prominent example of one such aspect; many other facets also invite attention. Fundamental CPT symmetry is satisfied throughout the field of optics, and it plays significantly into manifestations of chirality where spatial parity is broken; duality symmetry between electric and magnetic fields is also involved in the detailed representation. From more specific considerations of spatial inversion, amongst which it emerges that the topological charge has the character of a pseudoscalar, other elements of spatial symmetry, beyond simple parity inversion, prove to repay additional scrutiny. A photon-based perspective on these features enables regard to be given to the salient quantum operators, paying heed to quantum uncertainty limits of observables. The analysis supports a persistence in features of significance for the material interactions of vortex beams, which may indicate further scope for suitably tailored experimental design.
1. Introduction
The arrival of laser sources in the mid-twentieth century heralded the development of technology with a new capacity to produce beams of light of unprecedented directionality and collimation, spurring major progress in the emerging science of quantum optics. In quantum terms, laser light is primarily characterized by a strongly peaked population distribution of very well-defined modes of propagating radiation, whose quanta are photons. Major advances [1,2,3,4] introduced the concept of azimuthally structured light, leading to the conclusion that such photons might individually and separably convey observable attributes of the specific modes to which they belonged [5,6,7]. That discovery, and its experimental proof, has proved an especially rich ground of research in connection with the particular form of structure known as an optical vortex, or twisted light, usually associated with a helicoidal wavefront [8,9,10,11,12]. It had already been quickly established that vortex photons could produce novel mechanical effects, initially described as optical spanners [13,14,15]—a term signifying a wrench-like delivery of torque, alluding to the well-established term optical tweezers for optical nanomanipulation [16,17]. Subsequently, attention has increasingly focused on other attributes of structured light, especially in connection with an enhanced information capacity in channels for optical communication and data handling [18,19,20,21,22], and in distinctive forms of spectroscopic interaction [23,24]; in both connections, quantum aspects of the radiation become prominent [25].
For any essentially paraxial beam (signifying an idealized approximation of laser light with a beam waist much larger than the reduced wavelength, λ/2π), the angular momentum (AM) that it conveys can be represented as a sum of spin and orbital parts: SAM and OAM respectively. Based on such a simple partitioning, the former proves to be associated with polarization alone. At the photon level, only circular polarization states offer sharp quantum values, as such radiation states are eigenfunctions of both the SAM and Hamiltonian operators [26]. A separately quantized orbital angular momentum was originally conceived in an essentially classical formulation as a facet of an azimuthal phase, manifest in specifically structured beams [1]. For paraxial beams propagating with a phasor structure , where is a topological charge and φ the azimuthal angle about the beam axis, it was shown that the densities of OAM along the propagation direction, jz, and energy density, w, must satisfy the condition
where ω is the circular frequency of the radiation (assuming a plane polarization with no SAM). The result is consistent with an orbital angular momentum per photon. However, it emerges that the partition of optical AM into spin and orbital components is not unique, as is evidenced by the separate quantum operators lacking conformity to the correct commutation relations for unique and independent definitions [3,27].
Optical beams with the phasor structure entail a wavefront comprising intertwined helicoidal surfaces. Recognition of this clearly chiral character in the vortex optical field has led to numerous highly rewarding investigations into the potential interplay of material and optical chirality [25,28,29,30,31,32,33,34,35,36,37,38]. Pursuing the quantum principles of optical vortex interactions has recently introduced a new and broader focus on spatial symmetry, as individual photon-matter coupling events prove to be sensitive to the detailed form of the optical modes to which the photons belong. Such features are also very evident in atoms, both in spectroscopic and optical force studies [39].
In each connection, attention has begun to focus on the spatial variations of measurements across, or within, the transverse profile of vortex light. Here, not only do new symmetry principles come into play, but quantum aspects including uncertainty also become significant considerations. Any localized measurement associated with the creation or annihilation of individual photons—such as absorption leading to a spectroscopic transition—are fundamentally compromised by the preclusion of a position operator for any relativistic quantum particle [26,40]. Quantum uncertainty also obviates the precise positional registration of any individual photon’s angular momentum [41]. It is now appreciated that optical modes with marginally different directions of propagation cannot be discriminated with arbitrary precision [42]. The core of an optical vortex is not a precise singularity; it has an effectively finite width [43,44].
This paper aims to systematize these symmetry features, to explain their mathematical origin and their physical significance. While the quantum features of optical polarization have recently been the subject of a comprehensive survey [45], such aspects of wavefront-vortex or vector-vortex beams have yet to be addressed with the same level of scrutiny. Polarization features are separable from the wavefront structure, only for states of uniform polarization, and then only in the paraxial approximation. This is a topic that has advanced considerably in the fifteen years since the applicability to studies of chiral matter was first reviewed [46]. Detailed analysis can now elicit clear principles for the symmetry classification of optical vortex modes and their fields, revealing features of far greater intricacy than spatial parity alone.
2. Electrodynamics and Quantum Features of Structured Light
2.1. Field Operator Symmetries
Since photons cannot be localized, we can quickly dispense with any notion that these quanta might themselves be meaningfully categorized in terms of spatial or temporal parity. Even for their classical wave counterparts, and the optical modes for their representation, there are fundamental differences in the symmetry aspects of the constituent electric and magnetic fields, E and B respectively, for freely propagating light—although confined radiation may conform to mode-specific rules. For example, a linearly polarized standing wave in a laser cavity may have either even or odd spatial inversion symmetry, according to whether it supports an even or odd number of half-wavelengths between its end-mirrors.
At the outset, it is important to recognize that the symmetry properties of specific optical modes need not conform to the symmetries of the fundamental quantum field operators; it will become clear how this is so, in the analysis that follows. Significantly, in the quantum cast of electrodynamics, it is possible to exploit the fundamental, unequivocal symmetry of the field operators which, as we shall see below, entail summing over any complete set of modes. The fundamental symmetries are parities with respect to charge, space, and time inversion, respectively represented by , , and . In the form of their product, fundamental symmetry is satisfied throughout the field of optics [47,48]; the reader interested in broader aspects including violation beyond the sphere of optics is referred to a useful review [49]. For each of the three symmetries individually, the pertinent symmetry group Z2 has eigenvalues of ±1 denoting even or odd parity. Charge conjugation has little relevance for the interactions of structured light, and in considering the spatial parity of propagating light at a measurement instant in time we can focus on alone.
The constraints on observables specifically imposed by temporal symmetry are the same for any closed system, including freely propagating light. Indeed, this contrasts with the behaviour of open systems exhibiting gain or damping [50,51,52,53,54] that are associated with time-dependent expectation values. In the present paper, the focus is to be on the intrinsic symmetry properties of optical vortices, which are distinct eigenmodes of the unperturbed radiation Hamiltonian, rather than their interactions in dissipative or active media—for the latter, see also the fuller discussion in reference [55] and the citations given therein. A general discussion of symmetry in quantum electrodynamical interactions—including multipolar forms of coupling and key observables in optically dissipative effects such as dichroism in absorption—has been given in another recent article [56].
To address symmetry aspects at the photon level it is expedient to exhibit the key electrodynamic equations in generic quantum form, applicable to various forms of structured light—wavefront-vortex beams in particular. In quantum form, each optical field acquires the status of a position-dependent operator. Adopting the Coulomb gauge, which dictates zero divergence in the vector potential A, it is most appropriate to develop a detailed theory in terms of transverse (solenoidal) electric and magnetic fields, and B, respectively, developed as expansions in any complete set of electromagnetic modes [57]. B is itself pure solenoidal, irrespective of the gauge; the transverse label is unnecessary. These fields are rigorously related to the vector potential:
These equations represent conditions on A, though they are not sufficient to fully define it (for it is a gauge-dependent quantity, and not an observable). It follows that the quantum field operators and B have specific and opposite signatures for space and time parity: is odd and B even with respect to inversion ; both have the opposite signatures under . It is as a result of this difference that chiroptical effects (those that discriminate the handedness of chiral matter) are most commonly manifest in light-matter interactions entailing an interference of electric and magnetic coupling with light [55,58,59,60].
Before proceeding further, duality symmetry is also worth observing. In source-free space, it is possible to purposely cast theory in a form that respects the Heaviside-Lamor duality transformation. One of the less widely appreciated implications of Noether’s theorem [61] is a rotation in (E, cB) space [62,63], whose implementation is equivalent in physical effect to a local coordinate rotation of π/2 in physical 3D space, about an axis defined by the local Poynting vector. To such an end, it is possible to cast equations in terms of another adjunct vector field, C (representing one of a potentially cascading sequence), through the relation [64], using the non-zero curl as an alternative basis for representing electromagnetic properties [65]. However, C and its kind again represent incompletely defined, gauge-dependent properties, and it emerges that all quantifiable expressions for all observables may correctly be secured without their involvement.
2.2. Quantised Fields and Mode Expansions
Each of the electromagnetic fields can be cast as a Fourier series, entailing summation over any complete set of radiation modes—the latter defined by wave-vector and polarization [66]. It is convenient to adopt Ω as a generic label for any such mode, each of which is associated with five degrees of spatial freedom, configuration space . For conventional plane waves, three of these degrees of freedom are commonly associated with Cartesian components of the wave-vector kΩ (with wave number kΩ). Perhaps surprisingly, quantum aspects of radiation are quite commonly cast in terms of plane-wave descriptions, despite the intrinsic lack of physicality associated with their infinite transverse extent. However, for vortex structured beams such a representation is clearly inadmissible, and with a mapping the wave-vector space is typically redefined in terms of , signifying partition into axial and transverse (angular and radial) functions. Here, are integers, the former designating a topological charge and the latter a secondary index denoting a form of radial distribution [67]; in the well-studied case of Laguerre-Gaussian optical beams, signify the degree and order of an associated Laguerre polynomial that tempers a Gaussian radial distribution. For Bessel beams, denotes the order of a Bessel function of the first kind, and the secondary index is redundant [68].
In all cases, the other two degrees of freedom in relate to the polarization η, where they may, for example, be mapped by stereographic projection to co-ordinates on the Poincaré sphere denoting a major axis of polarization and a degree of ellipticity. These degrees of freedom provide the well-known polarization basis for binary basis information, due to the orthogonality in polarization of states that occupy diametrically opposite positions on the Poincaré sphere. (For vector vortex beams with transversely structured polarization, two transverse degrees of freedom are harnessed by polarization, signifying a loss of freedom in the wave-vector space. This is manifest in the observation that combinations, i.e., physical superpositions, of vortex modes can deliver vortex polarization structures, and vice versa, as discussed later.)
Generalizing the procedure for developing a quantum representation of optical vortex fields [69], the fields and B, which represent observables, can be cast as Hermitian quantum operators. Their explicit time dependence can be secured from the Heisenberg equations of motion, as indicated in the following. On expansion in terms of any appropriate and complete set of modes Ω, the operator representations of these operators, and the vector potential, at a position r take the following forms, conveniently expressed in terms of cylindrical coordinates ;
suppressing for simplicity the explicit inclusion of Gouy factors. In these two expressions, the equation for the electric field is cast in terms of eΩ, the complex polarization vector, and aΩ, the corresponding photon annihilation operator; the counterpart term featuring the creation operator is the Hermitian conjugate written as h.c. Also, is a mode normalization factor incorporating V−1/2, where V is the quantization volume V, such that the number of photons in this volume is given by ; is a dimensionless radial distribution function. The electric and magnetic fields both satisfy the time-independent Helmholtz equation:
where kΩ = ω/c.
The above field operators are expressed in the Schrödinger representation, in which time-dependence is developed in the state functions, not the operators. The standard temporal phase factors associated with each of the “positive and negative” frequency terms are readily retrieved using the Heisenberg equations of motion for the creation and annihilation operators:
with . Hence, the annihilation operator terms shown explicitly in Equations (3)–(5) carry a temporal factor exp(−iωt), the conjugate being associated with the creation operator held in the Hermitian conjugate terms. As presented, time reversal is wrought by complex conjugation of variables and Hermitian conjugation of operators. Accordingly, exchanging the exhibited terms with their conjugates preserves the sign for , but reverses it for B. Under the inversion operation , which spatially inverts polarization, wave-vectors, and position vectors, the electric field has odd spatial parity, and is therefore formally representable as a polar vector; the magnetic field is represented by an axial vector (a pseudovector).
2.3. Linear Momentum Density
The quantum operator for the Poynting vector, signifying the local density of linear momentum, is given by [70]:
where ε0 is the vacuum permittivity; the second term is included to ensure Hermiticity of the operator, since the operators and B do not commute [71]. Hence, P is clearly odd in both time and space, as befits linear momentum. Its local direction serves to identify the local normal to the optical wavefront surface. The Poynting vector is not, however, anchored in the physical 3D space of linear dimensions—although, as an expression of linear momentum density, it can indeed be defined at any point or region within that space. Momentum cannot be graphically represented by a vector portrayed in physical space—only in reciprocal (momentum) space.
Through its definition as the curl of the vector potential, the magnetic field B is intrinsically transverse with respect to the local Poynting vector. For a given mode, represent a right-handed orthogonal set and their components may be used to define a locally orthogonal triad of axes, of Cartesian or cylindrical form, for example. In structured light the local Poynting vector is not simply identifiable with the direction of beam propagation [72]—its orientation may vary across the beam as illustrated in Figure 1. Exact calculations of the Poynting trajectories for both LG and Bessel beams in fact exhibit a subtle difference between surfaces of hyperboloid and cylindrical form [73]. Both and B then have components parallel to the beam axis, and a component pointing inwards. Their relative magnitudes are locally determined, at a radial displacement ρ from the beam axis, by an angle expressed as follows [42]:
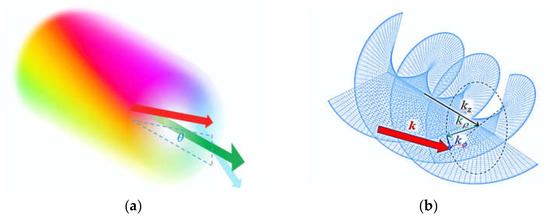
Figure 1.
(a) Phasor structure of an = 1, p = 0 LG beam, cycling as it propagates; hue denotes the phase, colour intensity the level of irradiance; the latter vanishes along the propagation axis (green arrow) at the phase singularity. The orientation of the local wave-vector (normal to the wavefront surface) is azimuth-dependent, as indicated at positions of opposite phase by red and blue arrows. (b) = 3, p = 0 LG beam, showing the mutually orthogonal disposition of the cylindrical components of a local wave-vector.
In consequence, both the electric and magnetic field vectors have components that are locally longitudinal, as well as counterparts of conventional transverse character, with respect to the propagation direction.
2.4. Quantum Uncertainty
Interesting features emerge in the differential resolution of an LG mode at radially distinct locations. It is useful to define a parameter , such that δg serves as a measure of the resolving distinguishability of modes Ω, Ω′ differing only in the directions of local wave-vectors k and k′ of the same magnitude k, across a range of radial distances . It has been shown that close to the beam axis the distinguishability scales as k2 −1, i.e., inversely proportional to the topological charge . However, for positions remote from the beam axis, the resolution limit scales with k −12 ρ −3, quadratic in [42].
The infinitesimal singularity at the core of a vortex beam is a classical concept; the quantum formulation is essentially consistent with an effectively paraxial cylindrical core, but limits on positional precision may be more generally regarded as a facet of quantum uncertainty on photon number within any small, confined 3D volume [43]. Quantum uncertainty may prove significant in developments that, in order to harness quadrupole interactions, depend on the high phase gradient near the core; whereas the classical lower bound of intensity on the axis is zero due to a precise phase singularity, quantum effects may always provide for a finite residual intensity even in that region. Indeed, a long-established quantum uncertainty principle concerns the number of photons and its potential phase resolution within a given volume; the following definitive statement is commonly cited [74]:
(although defining a quantum operator for the phase is well-known to be extremely problematic [75,76,77]). While achieving enhanced information content per photon can be exploited for data transmission at low values of the topological charge, there is an ultimate trade-off, where increasing the topological charge ceases to deliver any advantage [78].
The paraxial approximation is defensible only if allowance is made for an effective indistinguishability of photons with small differences in propagation direction, within a quantization volume V. If we consider two modes Ω and Ω′ of the same indices (, p) but with small local differences in wave-vector direction, then developing the commutation equation in terms of cylindrical coordinates (see Figure 1b), we find [42]:
In the special case Ω = Ω′, integration over reciprocal space recovers the standard result, for photons of the same mode, signifying the identification of the photon as an integer-spin entity, a boson. As such, every photon interaction with matter has to engage one or more of the creation and annihilation operators. Notably, since these shift operators are not Hermitian, we cannot use the Cauchy-Schwartz inequality to secure from the above commutation property any corresponding quantum uncertainty relation. However, the result correctly reflects the fact that modes with very marginally different directions of propagation cannot be discriminated with arbitrary precision.
The physical implication for photon propagation is that it is not resolvably rectilinear, within any volume of linear dimensions significantly smaller than the optical wavelength. This is, indeed, consistent with position-momentum uncertainty. However, this does not admit any notion of an interplay of population between modes with marginally different wave-vector, such as might be formulated in terms of a superposition of offset mode states with time-varying coefficients. The lack of any quantum interaction to modify such mode occupancy by the corresponding creation and annihilation of photons of similar wave-vector is an insurmountable obstacle, serving to dispatch any notion of an optical vortex as a continuously reforming vector bundle of plane waves.
One key aspect of the above discussion needs to be emphasized. Optical vortex modes generally have cylindrical screw or hyperboloidal screw axial symmetry; the phase and amplitude uncertainty of the component electromagnetic fields cannot compromise the transverse spatial symmetry properties of those fields. This conclusion is comprehensively vindicated in all experiments demonstrating the orbital angular momentum of vortex beams and their interference patterning. This will allow us to proceed with a detailed analysis of those spatial symmetries, in Section 4. First, however, the crucial aspect of angular momentum operators needs to be addressed.
3. Angular Momentum Quantization
3.1. Quantum Operators
The total angular momentum J of any finite beam is given by the following volume integral:
which is a constant of motion for free-space propagation. Its familiar manifestation as spin angular momentum (SAM)—failing to represent the entirety of angular momentum in the case of optical vortices—is expressible as
For plane-wave or essentially paraxial beams of light (beam-waist , the wavelength) and adopting a circular polarization basis for the mode expansions, (3) and (4), an explicit evaluation of Equation (13) produces the following result:
where is the unit vector in the z-direction of beam propagation, and is the number of photons of L/R handedness C within the measurement volume. For these states of pure circular polarization the result for the SAM can be written as per photon, with for left/right handedness. Circular polarizations are the only basis states that are eigenstates of both the S operator defined by Equation (13), and the radiation Hamiltonian. Any other polarization state may be resolved into a fractionally weighted superposition of these two circular polarizations, equivalent to a rotation of the basis space on the Poincaré sphere.
The total angular momentum can be written as J = S + L, where L is an orbital angular momentum (OAM) given by [26]:
The OAM result, again for plane-wave/paraxial light, is per photon, consistent with the result secured in the foundational theory [1]. In contrast to the SAM, the OAM is unequivocally quantized in integer values with no upper bound. It is a global property signifying the rotations of phase distributions within twisted optical modes, with extremely wide-ranging applications [79].
Although the compartmentalization of optical angular momentum into spin and orbital components facilitates separation of wave-vector and polarization structures, only a paraxial approximation affords this definitive separation [26,80,81,82], and only here can unit spin be uniquely associated with states of circular polarization. More generally, with the definition (13), optical SAM comprises not just conventional longitudinal spin angular momentum about the beam axis but also transverse spin. This is another consequence of non-zero longitudinal field components [83]; those field components and transverse spin are both neglected in the paraxial approximation [84,85]. In fact neither it nor the orbital AM operator satisfies the proper form of necessary quantum operator commutation [3,27]: instead, the following relations apply, where subscript indices denote Cartesian components, ε denotes the Levi-Civita antisymmetric tensor, and repeated indices require summation:
Note, in particular, the full commutability amongst components of optical spin, which contrasts markedly with its material counterpart that renders it impossible, in matter, to resolve quantum angular momentum components about distinguishable axes.
3.2. Conservation of Angular Momentum
The separability of orbital and spin angular momentum, to an extent compromised by the existence of transverse components when non-paraxial conditions apply, produces an interplay of spin and orbital angular momentum [86,87,88,89] whose effects become especially evident through interactions of sharply focused beams with matter [81,90,91,92,93,94]. When the corresponding individual operators for spin and orbital angular momentum no longer have sharp eigenvalues, measurements of either kind within the beam profile can only reveal a distribution, whose non-integer expectation values of the spin and orbital components, expressible as [87,89]:
with θ as given by Equation (9).
To achieve complete conversion between fully quantized spin and orbital angular momentum, there is now a wide variety of well-proven methods involving propagation of the vortex light through purpose-made optics. For example, AM interconversion may be purposely achieved at the focus of a high numerical aperture lens or on propagation through optical components that play an equally passive role, the conversion process conserving the total angular momentum in the radiation field [95,96,97]. In active media, OAM may exchange with the material system, as for example through coupling with plasmonic excitations in metallic nanostructures [98]: orbital angular momentum may also undergo transduction in systems having a rotational degree of freedom, as has been shown in both optically linear and nonlinear interactions [99,100]. In conventional nonlinear optics, parametric conversion processes (those that are coherent, elastic, and conserve linear momentum) also fully exhibit and conserve OAM—a principle that was first established in the doubling of topological charge in second harmonic generation. Indeed, in processes leading to higher harmonics, each output conveys an OAM equal to its harmonic number [69,101,102,103].
4. Spatial Symmetry Aspects of Optical Vortices
We have seen that an optical vortex signifies a beam with a helicoidal wavefront structure, exemplified by the LG modes in which they are most frequently created. Such a beam with topological charge is, at any instant in time, an intrinsically chiral structure with a screw axis rotating by 2π/ over a repeat distance of one wavelength. Elements of transverse spatial symmetry in such beams are readily identifiable, as has long been evident from the characteristic patterning observed in the interference of vortex modes [104,105,106,107,108]; the position-dependence of the orientation in such features reflects the propagative twist. The mode sums of Equations (4) and (5) embrace, for each mode with a specific topological charge , also the corresponding mode with charge , of opposite handedness: changing the sign is equivalent to space inversion. However, there are more detailed intricacies to consider. In the following we first address aspects of optical helicity and chirality, then turning attention to broader issues of spatial symmetry.
4.1. Polarisation States, Chirality, and Helicity
First, we note that similar remarks can be made about circular polarizations—again, since polarizations of opposite handedness are accommodated in the mode summations. In fact, the polarization sum can be effected over a state basis represented by any pair of diametrically opposite positions on the Poincaré sphere—which are always of opposite helicity. The quantitative measure of optical helicity is a scalar quantity κ, defined as the volume integral, over a discrete 3D element of space, of a scalar product between the vector potential and magnetic field [59,109,110]:
For freely propagating light this is a conserved quantity [111,112,113], as follows from the dual electric-magnetic symmetry of Maxwell’s equations [114]. In fact, using the relation χ = ck2κ for monochromatic (not necessarily paraxial) light [115], the flow of chirality satisfies the following continuity equation [59,116,117,118]:
where the spatial integration is taken, and is the optical chirality;
In terms of photon numbers, the optical helicity reduces to
where, once again, is the number of photons of L/R handedness C in the appropriate element of 3D space. Here, it should again be emphasized, this is an exact relation for paraxial light; higher order corrections due to longitudinal fields enter the result when the beam waist is less than around one wavelength [119].
Noting the link that exists between angular momentum and helicity—compare the above with Equation (14)—it is important above all to note that such a connection exists for light purely as a result of its propagating character [38,59,109,116,118]. There is no such connection for stationary matter. Accordingly, whereas angular momentum is conserved in interactions between light and matter, in the light-matter system as a whole, there is no such conservation of helicity/chirality. Indeed, there is no quantum operator for such a property in matter, and even to systematize measures of molecular chirality is a challenge. Lacking a fundamental principle of universal application, only ad hoc heuristic methods provide any basis for quantitative categorization [120].
Thus, although in some instances of chiroptical effect, such as single-photon circular dichroism [35,121], optical helicity proves to be proportional to the circular differential, there can be no connection at the level of quantum mechanism between such observables and the beam properties of optical helicity, chirality density, or chirality flow. There is no physical sense in which chirality can be said to be conferred between matter and radiation. A chiral molecule will often manifest circular differential effects of opposite sign in different wavelength regions.
4.2. Cylindrical and Rotational Symmetry
However, there are other more interesting attributes of symmetry to explore. Chiral systems are necessarily of low symmetry: although they may possess few symmetry elements, the only elements necessarily precluded by chirality are inversion, reflection, and rotation-inversion elements. For matter itself, chirality thus signifies a lack of any improper rotation axes: the operations of the relevant point group or space group to which it belongs can contain no inversion, mirror reflection, or other rotation-reflection symmetry elements [122]. These conditions are encapsulated by a preclusion of Sn symmetry elements for all integers n, where the Schoenflies symbol Sn signifies invariance under reflection with rotation about a perpendicular axis through an angle 2π/n. As is well known, the operation of spatial inversion represented by the parity operator is exactly equivalent to mirror reflection in any plane, followed by π rotation about the normal to the chosen plane of reflection. (Regarding planar surfaces or interfaces, the sole requirement is a lack of reflection symmetry in any plane perpendicular to the surface).
As we have seen, for monochromatic radiation there is an implicit time-dependence that is separable, enabling us to focus on 3D symmetry. In consequence of the helical structure, the group theoretical representation of any attribute of an OAM state can only be one of the pure rotation groups. Consider a paraxial representation of a generalized optical vortex beam specified by wave number k, polarization η, and topological charge , propagating in the z-direction. For generality we can also anticipate a radial dependence characterized by an index p. We sustain consideration of the Rayleigh range, z ≪ zR, where . With the standard phasor decomposition of Equation (3), the local electric field at a position in cylindrical coordinates can be represented as follows:
where
Here, in common terminology the scalar field is termed the phase, and the complex field exponential (or cis function) may be referred to as a positional phasor. It is also useful to define a phasor gradient vector field;
Equally, θ′ is the gradient of θ.
The phasor defined by Equation (23) is a feature of not just the electric field but also the magnetic field B. Field gradients prove to play a significant role in a wide range of quadrupole and higher multipole interactions [39,123,124,125,126,127,128,129,130,131,132]. In molecular or dielectric materials, and especially those with a chiral structure, electronic transitions may be mediated by more than one type of multipole, and through involvement of the azimuthal phasor in twisted light, the electric quadrupole form of coupling in particular introduces a range of new and interesting features. For example, it can introduce a capacity for discriminating physical media of left- or right-handed structure, as for example in angle-resolved Raman scattering of vortex light to resolve optically active molecular enantiomers [24,133,134].
In optics, the direct connection in physical significance between the phase and phase factor, and the mapping between the two, can lead to a blurring of distinction in their description. However, a clear difference in the form of their gradient fields invites closer attention to their symmetry properties. The wavefront of a vortex beam is itself chiral; it lacks any inversion, reflection, or rotation-reflection symmetry, and within the span of a wavelength it has only screw-axis (rotation-translation) symmetry. However, the temporal separability means that significant symmetry elements are nonetheless present in the phase and phasor gradient fields. The most obvious feature, for a beam of topological charge , is an azimuthal phase distribution of symmetry. Indeed, this is a property that can be directly exploited in directly launching such a beam through the electronic decay of an exciton state of exactly the same symmetry [135,136,137].
Before discussing the more detailed intricacies of these features, a caveat is appropriate: in the structure of any vortex beam, different attributes of the light may exhibit different elements of symmetry. The symmetry properties of the electromagnetic fields may be separable from those of the wavefront—the latter representing the shape of a surface whose normal determines the direction of the local Poynting vector. The polarization vector field may have a 3D chiral structure in certain kinds of “vector vortex” beam, but for the present we consider more well-known cases where the polarization vector is a constant, separable and independent of the wavefront shape. For paraxial beams the symmetry of each property is that of a transverse cross-section of the beam. Regarding the spatial symmetry aspects of the phasors, noting that spatial inversion is equivalent to reflection followed by π rotation, it is expedient to consider specifically reflection in the beam-transverse, (x,y) plane.
To begin with parity inversion, it is evident that for the phasor , a scalar as defined by Equation (23), both ± cases of the longitudinal factor, exp(±ikz), are trivially eigenfunctions of with even parity: the directions of both z and the wave-vector change on spatial inversion: here, of course, there is no effect within the (x,y) plane.
Now consider the azimuthal part, exp(±iϕ), again using the principle that spatial inversion is equivalent to reflection and π rotation. For clarity, we can apply first to ϕ, then to . For ϕ, reflection in the (x,y) plane makes no difference, but the rotation that shifts ϕ → ϕ + π will either change the sign of exp(±iϕ) if is an odd integer, or leave it unchanged if is even. This is immediately obvious in the phase diagrams in Figure 2. Recognising the scalar property of the phasor thus reveals a pseudoscalar character for the topological charge ; it is a scalar of odd parity under : in-plane reflection and rotation by π has the same effect as space inversion. Thus, exp (±iϕ) is also invariant under , so that the parity signatures of the and B fields in each twisted mode, under , are those of the parent operators. The same applies, of course, to and parity signatures.
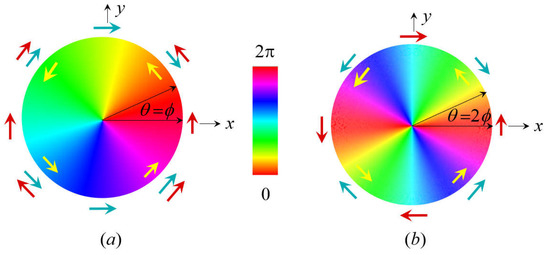
Figure 2.
(a) Colour-continuum representation of the phasor Φ for a vortex at z = 0: (a) topological charge = 1, where phase θ = ϕ; (b) = 2, phase θ = 2ϕ (ϕ = 0 as usual designating the notional x-axis). The phase gradient field, indicated by yellow arrows (twice the magnitude in the latter case), is constant in θ. Any shift ϕ →ϕ + π imparts a change of sign to the phasor in (a), as for all cases of odd ; the same shift in (b) retains the sign, as is true for all even values of . The vector field of the phasor gradient varies non-uniformly in direction, its real and imaginary parts (respectively represented by blue and red arrows) having signs either parallel or antiparallel to the phase gradient, according to the quadrant in (a), and the octant in (b).
This ensures that for twisted light, just as for other beams lacking OAM, an interference of electric and magnetic couplings can engender a chirally differential effect, irrespective of the odd or even nature of [35]. The conclusion is vindicated by the earlier observation that the OAM per photon is : angular momentum is invariably a property that is even under , and this requires that both and change sign on space inversion. Equally, this conclusion tallies with the observation that changing the sign of alone inverts the handedness of the wavefront.
However, the above analysis also reveals other intriguing aspects of spatial symmetry, beyond the simple issue of global parity under . Such features can be readily recognized from the illustrations in Figure 2. Consider (a), representing a mode of unit topological charge arbitrarily depicted for the (x, y) plane at z = 0. At any given radial distance ρ from the origin, the phase gradient θ′1 is a constant irrespective of the azimuthal angle ϕ. This signifies that its Cartesian components in the transverse plane change sign on π/2 rotation about the beam axis. As a property of the beam it has the properties of the irreducible representation (irrep) A2 in the point group C∞v symmetry, being invariant under arbitrary rotations, and antisymmetric under reflections in any vertical plane [138].
There is no such symmetry for the phase factor gradient Φ′1, whose complex value changes non-uniformly around any ring, so that C∞ cylindrical rotation symmetry is absent. Consider rotation by π radians about the z axis: the real part of Φ′1 is symmetric under C2 rotation in the (x, z) plane, and antisymmetric for C2 rotation in the (y, z) plane; for the imaginary part of Φ′1, the converse applies. These characteristics mark out Re(Φ′1) as transforming under the irrep B2 of the dihedral point group D2, whilst Im(Φ′1) transforms under irrep B3.
The rapidity of change in both elements of the phasor gradient field clearly increases with . For = 2, as shown in Figure 1b, the phase gradient θ′2 is once again invariant under cylindrical rotations and antisymmetric under reflections; it, too, belongs to the irrep A2 in the point group C∞v. Here, however, the symmetry representations under the operations of the D2 point group are A for Re (Φ′2) and B1 for Im (Φ′2). Note the difference in behaviour of both the real and imaginary parts, under C2(z) rotation, exhibited by these differing values of .
In fact, since the effect of reflection in the (x, y) plane is trivial, the above analysis can be more simply expressed by considering, instead of the pure-rotation subgroups of the three-dimensional special orthogonal group SO (3), those of its 2D counterpart, subgroups of SO (2) (circular symmetry). Note that the quantum mechanical rotation operator, for each of the symmetries identified above, is directly related to the phasor as defined by Equation (23):
Accordingly, we can generalize to topological charge of arbitrary value > 2 by observing that the phasor itself has pure rotational symmetry and no other element; it transforms under symmetry operations of the Schoenflies point group as the totally symmetric irreducible representation A [139]; its real and imaginary parts individually admit additional symmetry elements and transform as separate representations of the higher symmetry pure rotation group [139]. For the real and imaginary parts of the gradient field , those irreducible representations obviously interchange. Table 1 and Table 2 show specifically the transformation behaviour and irreducible representations of salient properties, for odd and even values of . Note that in the latter case, the vector nature of the gradient field imparts different representations to the real part of the phasor and the imaginary part of its gradient, just as we saw for = 2.

Table 1.
Irreducible representations of the point group and salient symmetry operations for the real and imaginary parts of the azimuthal phasor of a paraxial optical vortex, and of its vector gradient field for odd topological charge; m denotes any positive integer number of rotations.

Table 2.
Irreducible representations for even topological charge ; all other details as in Table 1.
5. Conclusions
The understandable focus in the majority of studies, on the spatial properties of helicity and angular momentum in vortex light, has lent an emphasis to measures and implications of beam chirality. Whilst chirality signifies a lack of symmetry under the operation of space inversion , it does not preclude aspects of rotational symmetry closely linked to the corresponding generator of axial rotations, well-known to be manifest in petal-like interference structures. However, beyond the established context of experimentation designedly based on beam interference, such patterning also arises in studies that focus on the nature of light-matter interactions—as for example in spectroscopic investigations. At this quantum level, just as with molecules, there is far more to spatial symmetry than just parity, where the interactions of structured beams are concerned.
The results for spatial symmetry, here reported for the first time, will be important for applications in which light-matter interactions are studied across a limited section of a vortex beam; several protocols for experiments of this kind have recently been proposed [25,134]. This contrasts with most studies that collect signals from the whole transverse cross-section of the beam, where azimuthal integration over the phasor and its gradient field clearly give results that average to zero. Laser studies of phenomena such as the attenuated transmission of twisted light in probing turbid or structurally complex media [140,141], where locally inhomogeneous light scattering and absorption take place, may benefit from the differential response that can be identified in different transverse sectors of the beam. It is interesting to surmise whether such effects might also play into the retention or loss of information content in the propagation of twisted beams suffering the effects of atmospheric turbulence, a feature of keen interest to the optical vortex community [142,143,144,145,146].
This article has dwelt on the quantum and symmetry aspects of optical vortices whose chiral structure owes its origin to a helicoidal wavefront; polarization aspects have largely concerned only the special cases of uniform circular polarization. Although beyond the scope of the present analysis, it will be interesting to develop and further explore counterpart principles for vector-vortex modes whose polarization varies within the beam cross-section [147,148,149]—including Poincaré states whose profiles may include a distribution of polarizations spanning the whole surface in a Poincaré sphere representation [105,150,151,152]. The generation and properties of such modes commonly involve an intricate interplay of OAM and polarization features [153,154]; for such modes, further aspects of symmetry arise, such as the Poincaré-Hopf indices for interference singularities producing a distribution of intensity nulls [155]. However, the fully-fledged quantum field theory for the nanoscale light-matter interactions of such beams has yet to be developed; that level of analysis represents the next edge of ongoing research.
To finally conclude, it is interesting to observe more broadly the realm of applications that has already arisen from the development of optical vortices, through the strongly active synergism of theory and experiment. As previously noted, the topological charge of an optical vortex can have either positive or negative values; it is only technical limitations that place any upper bound on its magnitude, and values of up to several hundred have in fact been experimentally achieved. This capacity represents the basis for developments in a surprisingly large range, exploiting quantum aspects of the high-level modal symmetry associated with beam phase and transverse structure, as well as the quantized orbital angular momentum [156]. Some of the fields showing special promise include quantum computing and cryptography, optical communications, micro-rheology, materials characterization, nanofabrication, and bioimaging: a very brief summary follows.
Structured beams in general offer enhanced bandwidth for optical information transfer and exciting opportunities to expand the scope of quantum computing. Exploiting the quantum aspects of twisted light itself represents an inviting new basis for enhanced cryptography [21], through the implementation of high-dimensional generalizations of the familiar qubit states [22]. There are highly interesting optical communication opportunities [157,158], with much of the current focus being the challenge of propagation through scattering or turbulent media [159,160,161]. Meanwhile, directly exploiting the orbital angular momentum of vortex beams finds microscale optomechanical applications in microparticle sorting [162], non-contact motorized lab-on-a-chip fluidics [163,164], and confined space rheology [165], while the application of vortex beams in the field of nanolithography has been shown to afford new top-down methods for directly fabricating chiral nanostructures [32,166]. The chirality intrinsically associated with such beams is of further interest for the additional dimension it can offer as a spectroscopic tool, where it is used as a probe of media ranging from chiral compounds [25,119], to plasmonic, nano- and meta-materials [34,167,168], and magnetic media [169], and in studies on free atoms [170,171]. Yet in highly complex, structurally heterogeneous, and strongly attenuating media, vortex beams still exhibit novel attributes [140], including a capacity for enhanced depth imaging, even extending to the analysis of brain tissue [141]. There is a truly phenomenal growth in the list of applications and every indication that this expansion is likely to remain a strongly continuing trend.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The author gratefully acknowledges helpful comments from David Bradshaw and Kayn Forbes, as well as from anonymous referees.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular-momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Van Enk, S.J.; Nienhuis, G. Spin and orbital angular momentum of photons. Europhys. Lett. 1994, 25, 497–501. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K.; Allen, L.; Padgett, M.J. The production of multiringed Laguerre-Gaussian modes by computer-generated holograms. J. Mod. Opt. 1998, 45, 1231–1237. [Google Scholar] [CrossRef]
- Berkhout, G.C.G.; Lavery, M.P.J.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef] [PubMed]
- Galvez, E.J.; Coyle, L.E.; Johnson, E.; Reschovsky, B.J. Interferometric measurement of the helical mode of a single photon. New J. Phys. 2011, 13, 053017. [Google Scholar] [CrossRef]
- O’Sullivan, M.N.; Mirhosseini, M.; Malik, M.; Boyd, R.W. Near-perfect sorting of orbital angular momentum and angular position states of light. Opt. Express 2012, 20, 24444–24449. [Google Scholar] [CrossRef] [PubMed]
- Santamato, E. Photon orbital angular momentum: Problems and perspectives. Fortschr. Phys. 2004, 52, 1141–1153. [Google Scholar] [CrossRef]
- Andrews, D.L. Structured Light and its Applications: An Introduction to Phase-Structured Beams and Nanoscale Optical Forces; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2008. [Google Scholar]
- Torres, J.P.; Torner, L. Twisted Photons: Applications of Light with Orbital Angular Momentum; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Bliokh, K.Y.; Nori, F. Spatiotemporal vortex beams and angular momentum. Phys. Rev. A 2012, 86, 033824. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Babiker, M.; Power, W.L.; Allen, L. Light-induced torque on moving atoms. Phys. Rev. Lett. 1994, 73, 1239–1242. [Google Scholar] [CrossRef] [PubMed]
- Power, W.L.; Allen, L.; Babiker, M.; Lembessis, V.E. Atomic motion in light-beams possessing orbital angular-momentum. Phys. Rev. A 1995, 52, 479–488. [Google Scholar] [CrossRef]
- Simpson, N.B.; Allen, L.; Padgett, M.J. Optical tweezers and optical spanners with Laguerre-Gaussian modes. J. Mod. Opt. 1996, 43, 2485–2491. [Google Scholar] [CrossRef]
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef]
- Jones, P.H.; Maragò, O.M.; Volpe, G. Optical Tweezers: Principles and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Vallone, G.; D’Ambrosio, V.; Sponselli, A.; Slussarenko, S.; Marrucci, L.; Sciarrino, F.; Villoresi, P. Free-space quantum key distribution by rotation-invariant twisted photons. Phys. Rev. Lett. 2014, 113, 060503. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Mirhosseini, M.; Magaña-Loaiza, O.S.; O’Sullivan, M.N.; Rodenburg, B.; Malik, M.; Lavery, M.P.J.; Padgett, M.J.; Gauthier, D.J.; Boyd, R.W. High-dimensional quantum cryptography with twisted light. New J. Phys. 2015, 17, 033033. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Tu, J.J.; Birman, J.L. Raman scattering using vortex light. J. Phys. Chem. Solids 2015, 77, 117–121. [Google Scholar] [CrossRef]
- Forbes, K.A. Raman optical activity using twisted photons. Phys. Rev. Lett. 2019, 122, 103201. [Google Scholar] [CrossRef] [PubMed]
- Forbes, K.A.; Andrews, D.L. Orbital angular momentum of twisted light: Chirality and optical activity. J. Phys. Photonics 2021, 3, 022007. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1995. [Google Scholar]
- van Enk, S.J.; Nienhuis, G. Commutation rules and eigenvalues of spin and orbital angular-momentum of radiation-fields. J. Mod. Opt. 1994, 41, 963–977. [Google Scholar] [CrossRef]
- Andrews, D.L.; Dávila Romero, L.C.; Babiker, M. On optical vortex interactions with chiral matter. Opt. Commun. 2004, 237, 133–139. [Google Scholar] [CrossRef]
- Araoka, F.; Verbiest, T.; Clays, K.; Persoons, A. Interactions of twisted light with chiral molecules: An experimental investigation. Phys. Rev. A 2005, 71, 055401. [Google Scholar] [CrossRef]
- Van Veenendaal, M.; McNulty, I. Prediction of strong dichroism induced by x rays carrying orbital momentum. Phys. Rev. Lett. 2007, 98, 157401. [Google Scholar] [CrossRef] [PubMed]
- Löffler, W.; Broer, D.; Woerdman, J. Circular dichroism of cholesteric polymers and the orbital angular momentum of light. Phys. Rev. A 2011, 83, 065801. [Google Scholar] [CrossRef]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using optical vortex to control the chirality of twisted metal nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef] [PubMed]
- Lowney, J.; Roger, T.; Faccio, D.; Wright, E.M. Dichroism for orbital angular momentum using parametric amplification. Phys. Rev. A 2014, 90, 053828. [Google Scholar] [CrossRef]
- Wu, T.; Wang, R.; Zhang, X. Plasmon-induced strong interaction between chiral molecules and orbital angular momentum of light. Sci. Rep. 2015, 5, 18003. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Optical orbital angular momentum: Twisted light and chirality. Opt. Lett. 2018, 43, 435–438. [Google Scholar] [CrossRef]
- Samlan, C.T.; Suna, R.R.; Naik, D.N.; Viswanathan, N.K. Spin-orbit beams for optical chirality measurement. Appl. Phys. Lett. 2018, 112, 031101. [Google Scholar] [CrossRef]
- Alpeggiani, F.; Bliokh, K.Y.; Nori, F.; Kuipers, L. Electromagnetic helicity in complex media. Phys. Rev. Lett. 2018, 120, 243605. [Google Scholar] [CrossRef]
- Woźniak, P.; De Leon, I.; Höflich, K.; Leuchs, G.; Banzer, P. Interaction of light carrying orbital angular momentum with a chiral dipolar scatterer. Optica 2019, 6, 961–965. [Google Scholar] [CrossRef]
- Babiker, M.; Andrews, D.L.; Lembessis, V.E. Atoms in complex twisted light. J. Opt. 2019, 21, 013001. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. Why photons cannot be sharply localized. Phys. Rev. A 2009, 79, 032112. [Google Scholar] [CrossRef]
- Franke-Arnold, S.; Barnett, S.M.; Yao, E.; Leach, J.; Courtial, J.; Padgett, M. Uncertainty principle for angular position and angular momentum. New J. Phys. 2004, 6, 103. [Google Scholar] [CrossRef]
- Andrews, D.L.; Forbes, K.A. Quantum features in the orthogonality of optical modes for structured and plane-wave light. Opt. Lett. 2018, 43, 3249–3252. [Google Scholar] [CrossRef]
- Berry, M.; Dennis, M. Quantum cores of optical phase singularities. J. Opt. A Pure Appl. Opt. 2004, 6, S178. [Google Scholar] [CrossRef]
- Barnett, S.M. On the quantum core of an optical vortex. J. Mod. Opt. 2008, 55, 2279–2292. [Google Scholar] [CrossRef]
- Goldberg, A.Z.; de la Hoz, P.; Björk, G.; Klimov, A.B.; Grassl, M.; Leuchs, G.; Sánchez-Soto, L.L. Quantum concepts in optical polarization. Adv. Opt. Photon. 2021, 13, 1–73. [Google Scholar] [CrossRef]
- Andrews, D.; Davila Romero, L.; Babiker, M. Twisted laser beams and their optical interactions with chiral matter. In Trends in Chemical Physics Research; Linke, A.N., Ed.; Nova Science Pub Inc.: Hauppauge, NY, USA, 2006; pp. 155–176. [Google Scholar]
- Greenberg, O. Why is CPT Fundamental? Found. Phys. 2006, 36, 1535–1553. [Google Scholar] [CrossRef]
- Kaplan, A.D.; Tsankov, T.D. CPT invariance in classical electrodynamics. Eur. J. Phys. 2017, 38, 065205. [Google Scholar] [CrossRef]
- Lehnert, R. CPT symmetry and its violation. Symmetry 2016, 8, 114. [Google Scholar] [CrossRef]
- Bender, C.M. Introduction to PT-symmetric quantum theory. Contemp. Phys. 2005, 46, 277–292. [Google Scholar] [CrossRef]
- Peřina, J., Jr.; Lukš, A.; Kalaga, J.K.; Leoński, W.; Miranowicz, A. Nonclassical light at exceptional points of a quantum PT-symmetric two-mode system. Phys. Rev. A 2019, 100, 053820. [Google Scholar] [CrossRef]
- Arkhipov, I.I.; Miranowicz, A.; Minganti, F.; Nori, F. Liouvillian exceptional points of any order in dissipative linear bosonic systems: Coherence functions and switching between and anti- symmetries. Phys. Rev. A 2020, 102, 033715. [Google Scholar] [CrossRef]
- Downing, C.A.; Zueco, D.; Martin-Moreno, L. Chiral current circulation and PT symmetry in a trimer of oscillators. ACS Photonics 2020, 7, 5401–5414. [Google Scholar] [CrossRef]
- Ding, L.; Shi, K.; Zhang, Q.; Shen, D.; Zhang, X.; Zhang, W. Experimental determination of P T-Symmetric exceptional points in a single trapped ion. Phys. Rev. Lett. 2021, 126, 083604. [Google Scholar] [CrossRef]
- Andrews, D.L. Quantum formulation for nanoscale optical and material chirality: Symmetry issues, space and time parity, and observables. J. Opt. 2018, 20, 033003. [Google Scholar] [CrossRef]
- Andrews, D.L. Symmetries, conserved properties, tensor representations, and irreducible forms in molecular quantum electrodynamics. Symmetry 2018, 10, 298. [Google Scholar] [CrossRef]
- Power, E.A. Introductory Quantum Electrodynamics; American Elsevier Pub. Co.: New York, NY, USA, 1965. [Google Scholar]
- Barron, L.D. Molecular Light Scattering and Optical Activity; Cambridge University Press: Cambridge, UK, 2004; Volume 2. [Google Scholar]
- Coles, M.M.; Andrews, D.L. Chirality and angular momentum in optical radiation. Phys. Rev. A 2012, 85, 063810. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Leeder, J.M.; Coles, M.M.; Andrews, D.L. Signatures of material and optical chirality: Origins and measures. Chem. Phys. Lett. 2015, 626, 106–110. [Google Scholar] [CrossRef]
- Noether, E. Invariante variationsprobleme. Nachr. d. König. Gesellsch. d. Wiss. zu Göttingen, Math-Phys. Klasse 1918, 235–257. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Cameron, R.P.; Barnett, S.M. Electric–magnetic symmetry and Noether’s theorem. New J. Phys. 2012, 14, 123019. [Google Scholar] [CrossRef]
- Barnett, S.M.; Cameron, R.P.; Yao, A.M. Duplex symmetry and its relation to the conservation of optical helicity. Phys. Rev. A 2012, 86, 013845. [Google Scholar] [CrossRef]
- Lock, M.P.E.; Andrews, D.L.; Jones, G.A. On the nature of long range electronic coupling in a medium: Distance and orientational dependence for chromophores in molecular aggregates. J. Chem. Phys. 2014, 140, 044103. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L. Photon-based and classical descriptions in nanophotonics: A review. J. Nanophoton. 2014, 8, 081599. [Google Scholar] [CrossRef]
- Karimi, E.; Boyd, R.W.; de la Hoz, P.; de Guise, H.; Řeháček, J.; Hradil, Z.; Aiello, A.; Leuchs, G.; Sánchez-Soto, L.L. Radial quantum number of Laguerre-Gauss modes. Phys. Rev. A 2014, 89, 063813. [Google Scholar] [CrossRef]
- Simon, D.S. Bessel beams, self-healing, and diffraction-free propagation. In A Guided Tour of Light Beams, 2nd ed.; IOP Publishing: Bristol, UK, 2020; pp. 5-1–5-22. [Google Scholar]
- Dávila Romero, L.C.; Andrews, D.L.; Babiker, M. A quantum electrodynamics framework for the nonlinear optics of twisted beams. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S66–S72. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. II. Maxwell fields in the vicinity of a molecule. Phys. Rev. A 1983, 28, 2663–2670. [Google Scholar] [CrossRef]
- Craig, D.P.; Thirunamachandran, T. Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions; Dover Publications: Mineola, NY, USA, 1998. [Google Scholar]
- Allen, L.; Padgett, M.J. The Poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density. Opt. Commun. 2000, 184, 67–71. [Google Scholar] [CrossRef]
- Berry, M.; McDonald, K. Exact and geometrical optics energy trajectories in twisted beams. J. Opt. A Pure Appl. Opt. 2008, 10, 035005. [Google Scholar] [CrossRef]
- Heitler, W. The Quantum Theory of Radiation; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Barnett, S.; Pegg, D. Phase in quantum optics. J. Phys. A Math. Gen. 1986, 19, 3849. [Google Scholar] [CrossRef]
- Pegg, D.T.; Vaccaro, J.A.; Barnett, S.M. Quantum-optical phase and canonical conjugation. J. Mod. Opt. 1990, 37, 1703–1710. [Google Scholar] [CrossRef]
- Barnett, S.M.; Vaccaro, J.A. The Quantum Phase Operator: A Review; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Coles, M.M. An upper bound on the rate of information transfer in optical vortex beams. Laser Phys. Lett. 2018, 15, 095202. [Google Scholar] [CrossRef]
- Andrews, D.L.; Babiker, M. The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bekshaev, A.Y.; Soskin, M.; Vasnetsov, M.V. Paraxial Light Beams with Angular Momentum; Nova Science: New York, NY, USA, 2008. [Google Scholar]
- Nieminen, T.A.; Stilgoe, A.B.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Angular momentum of a strongly focused Gaussian beam. J. Opt. A Pure Appl. Opt. 2008, 10, 115005. [Google Scholar] [CrossRef]
- Zangwill, A. Modern Electrodynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Forbes, K.A.; Green, D.; Jones, G.A. Relevance of longitudinal fields of paraxial optical vortices. J. Opt. 2021, 23, 075401. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Neugebauer, M.; Bauer, T.; Aiello, A.; Banzer, P. Measuring the transverse spin density of light. Phys. Rev. Lett. 2015, 114, 063901. [Google Scholar] [CrossRef]
- Barnett, S.M.; Allen, L. Orbital angular momentum and nonparaxial light beams. Opt. Commun. 1994, 110, 670–678. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Alonso, M.A.; Ostrovskaya, E.A.; Aiello, A. Angular momenta and spin-orbit interaction of nonparaxial light in free space. Phys. Rev. A 2010, 82, 063825. [Google Scholar] [CrossRef]
- Bekshaev, A.; Bliokh, K.Y.; Soskin, M. Internal flows and energy circulation in light beams. J. Opt. 2011, 13, 053001. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Courtial, J.; Padgett, M.J. Limit to the orbital angular momentum per unit energy in a light beam that can be focussed onto a small particle. Opt. Commun. 2000, 173, 269–274. [Google Scholar] [CrossRef]
- Volyar, A.V.; Shvedov, V.G.; Fadeeva, T.A. The structure of a nonparaxial Gaussian beam near the focus: II. Optical vortices. Opt. Spectrosc. 2001, 90, 93–100. [Google Scholar] [CrossRef]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.; McGloin, D.; Chiu, D.T. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, P.B.; Neto, P.A.M.; Nussenzveig, H.M. Angular momentum of focused beams: Beyond the paraxial approximation. Phys. Rev. A 2009, 79, 033830. [Google Scholar] [CrossRef]
- Sheppard, C.J. Focusing of vortex beams: Lommel treatment. J. Opt. A Pure Appl. Opt. 2014, 31, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodríguez-Herrera, O.G.; Lara, D.; Dainty, C. Spin-to-orbital angular momentum conversion in focusing, scattering, and imaging systems. Opt. Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, F.; De Leon, I.; Schulz, S.A.; Upham, J.; Karimi, E.; Boyd, R.W. Optical spin-to-orbital angular momentum conversion in ultra-thin metasurfaces with arbitrary topological charges. Appl. Phys. Lett. 2014, 105, 101905. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Gu, M. Angular momentum-reversible near-unity bisignate circular dichroism. Laser Photon. Rev. 2018, 12, 1700255. [Google Scholar] [CrossRef]
- Kaviani, H.; Ghobadi, R.; Behera, B.; Wu, M.; Hryciw, A.; Vo, S.; Fattal, D.; Barclay, P. Optomechanical detection of light with orbital angular momentum. Opt. Express 2020, 28, 15482–15496. [Google Scholar] [CrossRef]
- Xiong, H.; Huang, Y.-M.; Wu, Y. Laguerre-Gaussian optical sum-sideband generation via orbital angular momentum exchange. Phys. Rev. A 2021, 103, 043506. [Google Scholar] [CrossRef]
- Dholakia, K.; Simpson, N.B.; Padgett, M.J.; Allen, L. Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 1996, 54, R3742–R3745. [Google Scholar] [CrossRef]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys. Rev. A 1997, 56, 4193–4196. [Google Scholar] [CrossRef]
- Gariepy, G.; Leach, J.; Kim, K.T.; Hammond, T.J.; Frumker, E.; Boyd, R.W.; Corkum, P.B. Creating high-harmonic beams with controlled orbital angular momentum. Phys. Rev. Lett. 2014, 113, 153901. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Padgett, M.J.; Babiker, M. The orbital angular momentum of light. Prog. Opt. 1999, 39, 291–372. [Google Scholar]
- Galvez, E.J.; Khadka, S.; Schubert, W.H.; Nomoto, S. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre–Gauss and polarization modes of light. Appl. Opt. 2012, 51, 2925–2934. [Google Scholar] [CrossRef]
- Khajavi, B.; Galvez, E.J. Determining topological charge of an optical beam using a wedged optical flat. Opt. Lett. 2017, 42, 1516–1519. [Google Scholar] [CrossRef]
- Pan, S.; Pei, C.; Liu, S.; Wei, J.; Wu, D.; Liu, Z.; Yin, Y.; Xia, Y.; Yin, J. Measuring orbital angular momentums of light based on petal interference patterns. OSA Contin. 2018, 1, 451–461. [Google Scholar] [CrossRef]
- Lan, B.; Liu, C.; Rui, D.; Chen, M.; Shen, F.; Xian, H. The topological charge measurement of the vortex beam based on dislocation self-reference interferometry. Phys. Scr. 2019, 94, 055502. [Google Scholar] [CrossRef]
- Barnett, S.M.; Allen, L.; Cameron, R.P.; Gilson, C.R.; Padgett, M.J.; Speirits, F.C.; Yao, A.M. On the natures of the spin and orbital parts of optical angular momentum. J. Opt. 2016, 18, 064004. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I. A conformally invariant derivation of average electromagnetic helicity. Symmetry 2019, 11, 1427. [Google Scholar] [CrossRef]
- Lipkin, D.M. Existence of a new conservation law in electromagnetic theory. J. Math. Phys. 1964, 5, 696–700. [Google Scholar] [CrossRef]
- Fushchich, W.; Nikitin, A. The complete sets of conservation laws for the electromagnetic field. J. Phys. A Math. Gen. 1992, 25, L231–L233. [Google Scholar] [CrossRef]
- Anco, S.C.; Pohjanpelto, J. Classification of local conservation laws of Maxwell′s equations. Acta Appl. Math. 2001, 69, 285–327. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Nori, F. Dual electromagnetism: Helicity, spin, momentum and angular momentum. New J. Phys. 2013, 15, 033026. [Google Scholar] [CrossRef]
- Philbin, T.G. Lipkin’s conservation law, Noether’s theorem, and the relation to optical helicity. Phys. Rev. A 2013, 87, 043843. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Characterizing optical chirality. Phys. Rev. A 2011, 83, 021803. [Google Scholar] [CrossRef]
- Nienhuis, G. Conservation laws and symmetry transformations of the electromagnetic field with sources. Phys. Rev. A 2016, 93, 023840. [Google Scholar] [CrossRef]
- Crimin, F.; Mackinnon, N.; Götte, J.B.; Barnett, S.M. Optical helicity and chirality: Conservation and sources. Appl. Sci. 2019, 9, 828. [Google Scholar] [CrossRef]
- Forbes, K.A.; Jones, G.A. Optical vortex dichroism in chiral particles. Phys. Rev. A 2021, 103, 053515. [Google Scholar] [CrossRef]
- Natarajan, R.; Basak, S.C. Numerical characterization of molecular chirality of organic compounds. Curr. Comp. Aid. Drug Des. 2009, 5, 13–22. [Google Scholar] [CrossRef]
- Andrews, D.L.; Coles, M.M. Measures of chirality and angular momentum in the electromagnetic field. Opt. Lett. 2012, 37, 3009–3011. [Google Scholar] [CrossRef] [PubMed]
- Ladd, M. Symmetry of Crystals and Molecules; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Babiker, M.; Bennett, C.R.; Andrews, D.L.; Dávila Romero, L.C. Orbital angular momentum exchange in the interaction of twisted light with molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef]
- Lloyd, S.; Babiker, M.; Yuan, J. Quantized orbital angular momentum transfer and magnetic dichroism in the interaction of electron vortices with matter. Phys. Rev. Lett. 2012, 108, 074802. [Google Scholar] [CrossRef] [PubMed]
- Lembessis, V.E.; Babiker, M. Enhanced quadrupole effects for atoms in optical vortices. Phys. Rev. Lett. 2013, 110, 083002. [Google Scholar] [CrossRef]
- Mondal, P.K.; Deb, B.; Majumder, S. Angular momentum transfer in interaction of Laguerre-Gaussian beams with atoms and molecules. Phys. Rev. A 2014, 89, 063418. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Mukherjee, A. High-multipole excitations of hydrogen-like atoms by twisted photons near a phase singularity. J. Opt. 2016, 18, 074013. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef]
- Sakai, K.; Yamamoto, T.; Sasaki, K. Nanofocusing of structured light for quadrupolar light-matter interactions. Sci. Rep. 2018, 8, 7746. [Google Scholar] [CrossRef]
- Schulz, S.-L.; Peshkov, A.; Müller, R.; Lange, R.; Huntemann, N.; Tamm, C.; Peik, E.; Surzhykov, A. Generalized excitation of atomic multipole transitions by twisted light modes. Phys. Rev. A 2020, 102, 012812. [Google Scholar] [CrossRef]
- Forbes, K.A. Nonlinear chiral molecular photonics using twisted light: Hyper-Rayleigh and hyper-Raman optical activity. J. Opt. 2020, 22, 095401. [Google Scholar] [CrossRef]
- Bougouffa, S.; Babiker, M. Atom trapping and dynamics in the interaction of optical vortices with quadrupole-active transitions. Phys. Rev. A 2020, 101, 043403. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Spin-orbit interactions and chiroptical effects engaging orbital angular momentum of twisted light in chiral and achiral media. Phys. Rev. A 2019, 99, 023837. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Enhanced optical activity using the orbital angular momentum of structured light. Phys. Rev. Res. 2019, 1, 033080. [Google Scholar] [CrossRef]
- Coles, M.M.; Williams, M.D.; Saadi, K.; Bradshaw, D.S.; Andrews, D.L. Chiral nanoemitter array: A launchpad for optical vortices. Laser Photon. Rev. 2013, 7, 1088–1092. [Google Scholar] [CrossRef]
- Williams, M.D.; Coles, M.M.; Saadi, K.; Bradshaw, D.S.; Andrews, D.L. Optical vortex generation from molecular chromophore arrays. Phys. Rev. Lett. 2013, 111, 153603. [Google Scholar] [CrossRef]
- Williams, M.D.; Coles, M.M.; Bradshaw, D.S.; Andrews, D.L. Direct generation of optical vortices. Phys. Rev. A 2014, 89, 033837. [Google Scholar] [CrossRef]
- Kettle, S.F.A. Symmetry and Structure: Readable Group Theory for Chemists; Wiley: Chichester, UK, 2008. [Google Scholar]
- Ludwig, W.; Falter, C. Symmetries in Physics: Group Theory Applied to Physical Problems; Springer Science & Business Media: Berlin, Germany, 2012; Volume 64. [Google Scholar]
- Wang, W.; Gozali, R.; Shi, L.; Lindwasser, L.; Alfano, R. Deep transmission of Laguerre–Gaussian vortex beams through turbid scattering media. Opt. Lett. 2016, 41, 2069–2072. [Google Scholar] [CrossRef]
- Shi, L.; Lindwasser, L.; Wang, W.; Alfano, R.; Rodríguez-Contreras, A. Propagation of Gaussian and Laguerre-Gaussian vortex beams through mouse brain tissue. J. Biophotonics 2017, 10, 1756–1760. [Google Scholar] [CrossRef]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.; Padgett, M.J.; Boyd, R.W. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef]
- Gu, Y. Statistics of optical vortex wander on propagation through atmospheric turbulence. J. Opt. Soc. Am. A 2013, 30, 708–716. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Rodenburg, B.; Malik, M.; Boyd, R.W. Free-space communication through turbulence: A comparison of plane-wave and orbital-angular-momentum encodings. J. Mod. Opt. 2014, 61, 43–48. [Google Scholar] [CrossRef]
- Li, L.; Xie, G.; Ren, Y.; Ahmed, N.; Huang, H.; Zhao, Z.; Liao, P.; Lavery, M.P.; Yan, Y.; Bao, C. Orbital-angular-momentum-multiplexed free-space optical communication link using transmitter lenses. Appl. Opt. 2016, 55, 2098–2103. [Google Scholar] [CrossRef][Green Version]
- Li, L.; Zhang, R.; Liao, P.; Cao, Y.; Song, H.; Zhao, Y.; Du, J.; Zhao, Z.; Liu, C.; Pang, K. Mitigation for turbulence effects in a 40-Gbit/s orbital-angular-momentum-multiplexed free-space optical link between a ground station and a retro-reflecting UAV using MIMO equalization. Opt. Lett. 2019, 44, 5181–5184. [Google Scholar] [CrossRef]
- Norrman, A.; Friberg, A.T.; Leuchs, G. Vector-light quantum complementarity and the degree of polarization. Optica 2020, 7, 93–97. [Google Scholar] [CrossRef]
- Wang, J.; Castellucci, F.; Franke-Arnold, S. Vectorial light–matter interaction: Exploring spatially structured complex light fields. AVS Quantum Sci. 2020, 2, 031702. [Google Scholar] [CrossRef]
- Hu, X.-B.; Perez-Garcia, B.; Rodríguez-Fajardo, V.; Hernandez-Aranda, R.I.; Forbes, A.; Rosales-Guzmán, C. Free-space local nonseparability dynamics of vector modes. Photonics Res. 2021, 9, 439–445. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef] [PubMed]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Xin, Y. Generation of full Poincare beams on arbitrary order Poincare sphere. Curr. Opt. Photonics 2017, 1, 631–636. [Google Scholar]
- Woźniak, W.A.; Kurzynowski, P.; Popiołek-Masajada, A. Polarization vortices as a superposition of orthogonal phase vortices. Opt. Commun. 2019, 441, 155–159. [Google Scholar] [CrossRef]
- Saito, S. Poincaré rotator for vortexed photons. Front. Phys. 2021, 9, 646228. [Google Scholar] [CrossRef]
- Freund, I. Polarization flowers. Opt. Commun. 2001, 199, 47–63. [Google Scholar] [CrossRef]
- Boyd, R.W.; Padgett, M.J. Quantum mechanical properties of light fields carrying orbital angular momentum. In Optics in Our Time; Al-Amri, M.D., El-Gomati, M.M., Zubairy, M.S., Eds.; Springer: Cham, Switzerland, 2016; pp. 435–454. [Google Scholar]
- Xie, G.; Li, L.; Ren, Y.; Huang, H.; Yan, Y.; Ahmed, N.; Zhao, Z.; Lavery, M.P.J.; Ashrafi, N.; Ashrafi, S.; et al. Performance metrics and design considerations for a free-space optical orbital-angular-momentum-multiplexed communication link. Optica 2015, 2, 357–365. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Tyler, G.A.; Boyd, R.W. Influence of atmospheric turbulence on the propagation of quantum states of light carrying orbital angular momentum. Opt. Lett. 2009, 34, 142–144. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; McDuffie, S.; Najjar, M.A.M.; Rafsanjani, S.M.H.; Korotkova, O. Mitigation of atmospheric turbulence with random light carrying OAM. Opt. Commun. 2019, 446, 178–185. [Google Scholar] [CrossRef]
- Lavery, M.P.; Peuntinger, C.; Günthner, K.; Banzer, P.; Elser, D.; Boyd, R.W.; Padgett, M.J.; Marquardt, C.; Leuchs, G. Free-space propagation of high-dimensional structured optical fields in an urban environment. Sci. Adv. 2017, 3, e1700552. [Google Scholar] [CrossRef]
- Bobkova, V.; Stegemann, J.; Droop, R.; Otte, E.; Denz, C. Optical grinder: Sorting of trapped particles by orbital angular momentum. Opt. Express 2021, 29, 12967–12975. [Google Scholar] [CrossRef]
- Bianchi, S.; Vizsnyiczai, G.; Ferretti, S.; Maggi, C.; Di Leonardo, R. An optical reaction micro-turbine. Nat. Commun. 2018, 9, 1–6. [Google Scholar]
- Shen, Z.; Xiang, Z.; Wang, Z.; Shen, Y.; Zhang, B. Optical spanner for nanoparticle rotation with focused optical vortex generated through a Pancharatnam–Berry phase metalens. Appl. Opt. 2021, 60, 4820–4826. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Syubaev, S.; Zhizhchenko, A.; Kuchmizhak, A.; Porfirev, A.; Pustovalov, E.; Vitrik, O.; Kulchin, Y.; Khonina, S.; Kudryashov, S. Direct laser printing of chiral plasmonic nanojets by vortex beams. Opt. Express 2017, 25, 10214–10223. [Google Scholar] [CrossRef] [PubMed]
- Brullot, W.; Vanbel, M.K.; Swusten, T.; Verbiest, T. Resolving enantiomers using the optical angular momentum of twisted light. Sci. Adv. 2016, 2, e1501349. [Google Scholar] [CrossRef]
- Wang, S.; Deng, Z.-L.; Cao, Y.; Hu, D.; Xu, Y.; Cai, B.; Jin, L.; Bao, Y.; Wang, X.; Li, X. Angular momentum-dependent transmission of circularly polarized vortex beams through a plasmonic coaxial nanoring. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar]
- Sirenko, A.; Marsik, P.; Bernhard, C.; Stanislavchuk, T.; Kiryukhin, V.; Cheong, S.-W. Terahertz vortex beam as a spectroscopic probe of magnetic excitations. Phys. Rev. Lett. 2019, 122, 237401. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Solyanik, M. Circular dichroism of twisted photons in non-chiral atomic matter. J. Opt. 2017, 19, 105401. [Google Scholar] [CrossRef]
- Solyanik-Gorgone, M.; Afanasev, A.; Carlson, C.E.; Schmiegelow, C.T.; Schmidt-Kaler, F. Excitation of E1-forbidden atomic transitions with electric, magnetic, or mixed multipolarity in light fields carrying orbital and spin angular momentum. J. Opt. Soc. Am. B 2019, 36, 565–574. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).