1. Introduction
In this paper, all graphs to be considered are finite, simple, and undirected. We write to define the set of consecutive integers , for any positive integers . We denote two isomorphic graphs G and H with . The degree of vertex x of G, denoted by , is the number of vertices in G adjacent to x.
Let
G be a graph with the vertex set
and the edge set
. An
edge-magic total labeling (or EMT labeling for short) of a graph
G is a bijection
with the property that there exists a constant
k such that
, for any edge
. Then,
G is said to be
edge-magic (EMT) and
k is called a
magic sum. This notion was defined by Kotzig and Rosa [
1], who called it
magic valuation, and later rediscovered by Ringel and Lladó [
2]. In [
2], Ringel and Lladó conjectured that all trees are EMT. Since then, numerous papers associated with EMT labeling have been published.
In 1998, Enomoto et al. [
3] introduced a special case of EMT labeling with the extra property that
. It is called a
super edge-magic total labeling (SEMT labeling). A graph
G that admits an SEMT labeling is said to be
super edge-magic (SEMT). An SEMT labeling has a significant role in graph labeling because it is related to other types of labelings. Figueroa-Centeno et al. [
4] found relationships between SEMT and well-known labelings such as harmonious, sequential, and cordial labelings. Bača et al. [
5] established the relationship between SEMT and EMT labelings and
-edge-antimagic vertex labeling. Other relationships and comprehensive surveys about SEMT and EMT graphs can be found in [
6,
7,
8,
9].
The next Lemma states a necessary and sufficient condition of an SEMT graph. We frequently use this condition to construct SEMT labelings of some graphs.
Lemma 1 ([4]).A graph G is SEMT if and only if there exists a bijective function such that the set consists of consecutive integers. In such a case, f extends to an SEMT labeling of G with magic sum , where . In [
3], Enomoto et al. presented a necessary condition for an SEMT graph as stated in the following.
Lemma 2 ([3]).If a graph G with order p and size q is SEMT, then . We call an SEMT graph with the maximum number of edges given by Lemma 2 a
maximal SEMT graph. In [
10], Macdougall and Wallis provide some properties of maximal SEMT graphs and construct some particular maximal SEMT graphs such as triangulations of
v-cycle, generalized prisms, and graphs with large cliques. Sugeng and Xie [
11] presented a construction to extend any non-maximal SEMT graph into a maximal SEMT graph by utilizing the adjacency matrix. Thus, it is interesting to ask the question of which other graphs are maximal SEMT.
Subsequently, Gutiérrez and Lladó [
12] generalized the notion of EMT and SEMT into
H-(super)magic labelings in 2005. Let
G be a graph where each edge belongs to at least one subgraph isomorphic to a given graph
H. In this case,
G admits an
H-covering. An
H-magic labeling of G is a bijection
with the property that there exists a positive integer
k such that
, for every subgraph
of
G isomorphic to
H. The
H-magic labeling
g of
G with the extra property that
is called
H-supermagic labeling of
G. A graph
G is an
H-magic or
H-supermagic if it has an
H-magic labeling or
H-supermagic labeling, respectively.
While working with
H-magic graphs, we found labelings of graphs which are simultaneously
H-magic and
F-magic, for two non isomorphic graphs
F and
H. For instance,
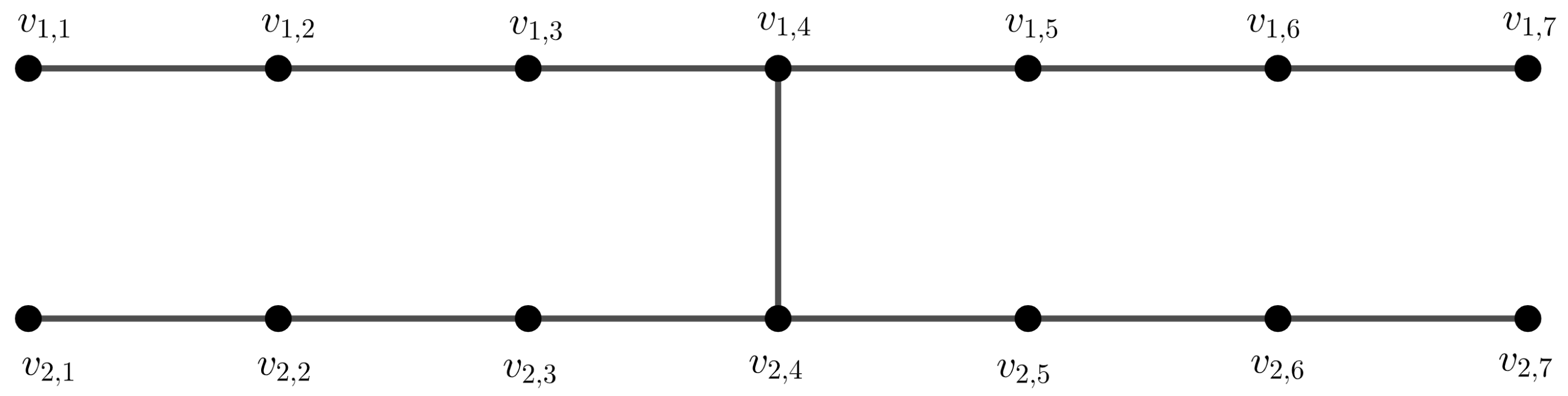
Figure 1 shows an example of a ladder
which is
-magic and
-magic, for any
, at the same time [
13]. This leads us to generalize the concept of
H-magic with two or more non-isomorphic covers.
Given two non-isomorphic graphs F and H, let G be a graph admitting an F-covering and H-covering simultaneously. An -simultaneously-magic labeling of G, denoted by -sim-magic labeling, is a bijective function with the property that there exist two positive integers and (not necessarily the same) such that and , for each subgraph of G isomorphic to F and each subgraph of G isomorphic to H. In such a case that , we call f an -simultaneously-supermagic labeling, denoted by -sim-supermagic labeling. The graph G is said to be -sim-magic or -sim-supermagic if it has an -sim-magic labeling or -sim-supermagic labeling, respectively. By the definition of these notions, the construction of -sim-(super)magic labelings of graphs can enlarge the collection of graphs that are known to be F-(super)magic and H-(super)magic.
In [
13], we established the existence of a
-sim-supermagic labeling of a join product graph
and a
-sim-supermagic labeling of a Cartesian product graph
where
H is isomorphic to a ladder or an even cycle. We also presented the relationship between an
labeling of a tree
T not isomorphic to a star and a
-sim-supermagic of the Cartesian product
.
Since SEMT and EMT labelings are known to be related to other well-known graph labelings, in this paper we focus on the study of -sim-(super)magic labelings; in particular for a graph H that is isomorphic to a path, a star, or a cycle. We denote a path on n vertices by and a cycle on n vertices by . A star is a tree on vertices with one vertex, called the center, having degree n and the remaining vertices having degree one.
An automorphism of a graph G is a permutation of preserving adjacency. A graph G is said to be vertex-transitive if, for any two vertices u and w, there is an automorphism of G that maps u to w and it is said to be edge-transitive if, for any two edges u and w, there is an automorphism of G that maps u to w. If G is both vertex-transitive and edge-transitive, G is said to be symmetric. Recall that a cycle is symmetric; a star is edge-transitive but not vertex-transitive; and a path on at least 4 vertices is neither vertex-transitive nor edge-transitive. In other words, in this paper we study -sim-(super)magic labelings for three classes of graphs H with varied symmetry.
Some of our results enlarge the collection of known (S)EMT and
H-(super)magic graphs. To show this, in
Section 2 we list some necessary or sufficient conditions for a graph to be
H-(super)magic, for
H isomorphic to a path, a star, or a cycle.
To recognize whether a graph is not
-sim-(super)magic, we determine
forbidden subgraphs for
-sim-(super)magic graphs. In
Section 3,
Section 4 and
Section 5 some forbidden subgraphs for
-sim-(super)magic labelings, where
H is isomorphic to a path, a star, or a cycle, are presented. In those sections, we say that
G is
H-free if
G does not contain
H as a subgraph.
Additionally, in
Section 3, we characterize
-sim-(super)magic graphs of small order and establish sufficient conditions for
-sim-(super)magic graphs. In
Section 4, we characterize
-(super)magic graphs. In
Section 5, we characterize
-(super)magic graphs of order
by establishing a relation between (S)EMT and
-(super)magic labelings and construct some cycles with chords that are
-(super)magic. Our constructions subsequently extend known maximal SEMT graphs and cycle-(super)magic graphs. In
Section 5, we present sufficient conditions for an SEMT graph with order
m to be
-sim-(super)magic for
.
3. -Sim-Supermagic Labelings
In this section, we provide the collection of forbidden subgraphs and characterize a -sim-supermagic graph.
Let
and
be two integers. We denote the edge sets of a path
and a cycle
as
and
, respectively. An
-tadpole is a graph obtained by joining the end vertex
of
to the vertex
of
.
Figure 6 shows the
-tadpole graph.
We denote the star with
n pendant edges as
. Consider the star
with three pendant edges denoted by
. We define
as a subdivision of the star
by replacing the edge
with a path on
n vertices and the remaining edges by paths on three vertices.
Figure 7 illustrates the subdivided star
.
In [
19], Maryati et al. introduced a subgraph-amalgamation. For
, let
be a collection of graphs
s where each
contains
as a fixed subgraph and let
be the collection of
s. The
H-amalgamation of
, denoted by
, is a graph constructed from identifying the
of each
. If
is isomorphic to a given graph
G, we write the
H-amalgamation as
.
Let
be an
-tadpole containing a subgraph
isomorphic to
; let
be a path
, whose edge set is
, containing a subgraph
isomorphic to
; and
.
Figure 8 illustrates the
-tadpole,
.
The next theorem stated forbidden subgraphs of -sim-(super)magic graphs.
Theorem 8. If G is -sim-(super)magic, then G is H-free where
- 1 .
, for any and ;
- 2 .
, for any ;
- 3 .
, for any ;
- 4 .
, for any ;
- 5 .
-tadpole, for any and ;
- 6 .
-tadpole, , for any and .
Proof. The case where , for any and , is an immediate consequence of Theorems 1 and 2; and the case where , for any , is an immediate consequence of Theorem 3. The rest of the cases are proven as follows.
Case 3. , for any .
Suppose that
G is a
-sim-(super)magic graph and
G is not
-free. Let
f be a
-sim-(super)magic labeling of
G. Consider two subgraphs isomorphic to
with edges
and
. Since
G is
-magic,
By eliminating
in both sides of Equation (
1), we have
However, . This clearly forces , a contradiction.
Case 4. , for any .
Assume to the contrary that G is -sim-(super)magic and G contains as a subgraph. Let f be a -sim-(super)magic labeling of G. Consider a subgraph H isomorphic to . Label the vertex set and the edge set . There exist two paths isomorphic to with edges and . As f is a -sim-(super)magic labeling, we have Thus, we obtain , a contradiction.
Case 5. -tadpole, for any and .
Suppose that G is -sim-(super)magic and contains -tadpole as a subgraph. Let f be a -sim-(super)magic labeling of G. Next, let k be an arbitrary positive integer with . Consider a subgraph H isomorphic to -tadpole. Denote the vertex set and the edge set . Consider two paths isomorphic to with edges and . Since G is -sim-(super)magic, . As a result, we have , a contradiction.
Case 6. -(tadpole), , for any and .
Assume to the contrary that G is -sim-(super)magic and contains a subgraph isomorphic to -(tadpole), . Let f be a -sim-(super)magic labeling of G. Then, let m be an arbitrary positive integer with . Consider a subgraph H of G isomorphic to -(tadpole), . Denote the vertex set and the edge set . Consider two paths isomorphic to with edges and . As G is -sim-(super)magic, we have
. Thus, we have , a contradiction. □
We remark that if G is -sim-(super)magic, then is the longest path of G. Notice that, for , contains as a subgraph. By Theorem 8, such graphs are not -sim-supermagic. The converse of Theorem 8 is not true as shown in the following example.
Example 1. The graph is not -sim-(super)magic for any integer .
Proof. Suppose that there exists a -sim-(super)magic labeling on . Let be the set of the internal vertex label in a for . Clearly . For each edge , the -weight, . Thus, the -weight of is for every . Consequently, should be a constant for every , a contradiction. □
Problem 1. What are the other forbidden subgraphs of -sim-(super)magic graph?
As a consequence of Theorem 8 where , for any integer , we have the following two results.
Corollary 2. Let be a positive integer and G be a graph that admits -covering. If G is -sim-(super)magic, then .
Corollary 3. Let be a positive integer and G be a graph that admits -covering. If G is -sim-(super)magic, then G is -free for any .
By the previous two corollaries, Theorem 8, and Example 1, we have the following corollaries.
Corollary 4. Let and G be a graph that admits -covering. If G is -sim-(super)magic, then G is a forest. In particular, if G is -sim-(super)magic, then G is a tree.
Let
be a positive integer. In [
12], it is proved that the star
is
-supermagic for each
. Moreover, the
-supermagic labeling of
in [
12] is also an SEMT labeling of
. Combining with Example 1 and Corollary 4, we obtain the following.
Corollary 5. A graph G is -sim-(super)magic if and only if G is isomorphic to the star for any positive integer .
A
caterpillar is a graph derived from a path
,
, where the vertex
is adjacent to
leaves,
. A special case of caterpillars when
,
, and
is called a
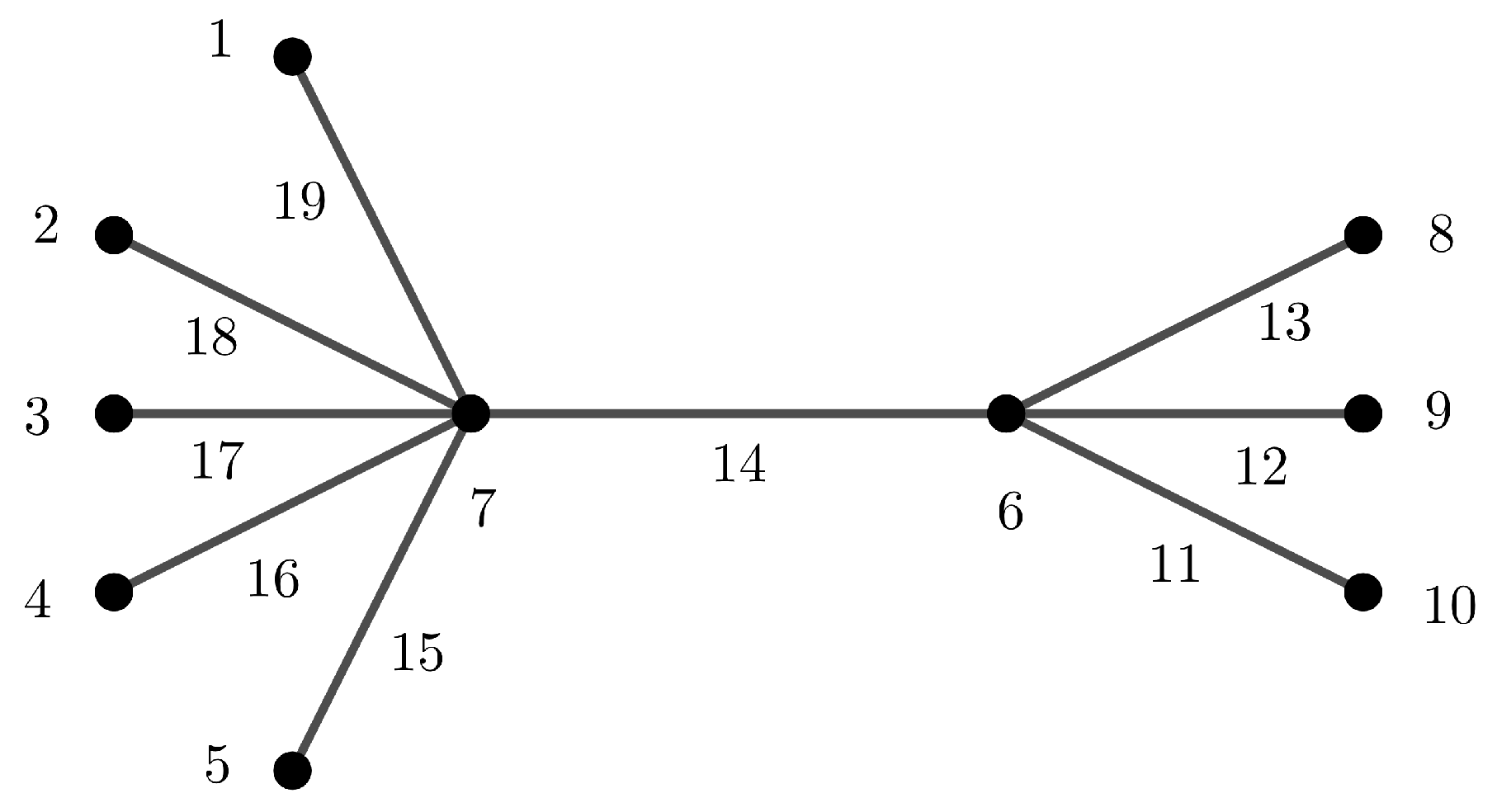
double star . An illustration of the double star
and a
-sim-supermagic labeling on
can be seen in
Figure 9. Since Kotzig and Rosa [
1] have proved that all caterpillars are SEMT, utilizing Corollary 4, we have the following.
Corollary 6. A connected graph G is -sim-(super)magic if and only if G is isomorphic to a double star for any two positive integers m and n.
Problem 2. Characterize -sim-(super)magic graphs for any .
We conclude this section by presenting sufficient conditions for an (S)EMT graph to be -sim-(super)magic.
Lemma 3. Let k and n be two positive integers. Let G be a graph of order at least that admits -covering. Let be the family of all subgraphs of G isomorphic to and let be the sum of all internal vertices labels in for every . If f is an (S)EMT labeling in G such that is constant, for each , then G is -sim-(super)magic.
Proof. Let
be the magic sum of the labeling. Let
be two positive integers in
. Consider two arbitrary paths
and
in
. Thus,
. Hence, we have the following:
As a result, the sum of all edges and vertices labels associated to a subgraph of G isomorphic to is a constant. Therefore, G is a -(super)magic. Since f is simultaneously SEMT and -(super)magic, G is -sim-(super)magic. □
As an immediate consequence of Lemma 3, we have the following special cases of caterpillars that are
-sim-magic. The
broom is defined as a graph isomorphic to the caterpillar
where
and
. The
double broom is a graph isomorphic to the caterpillar
where
,
, and
.
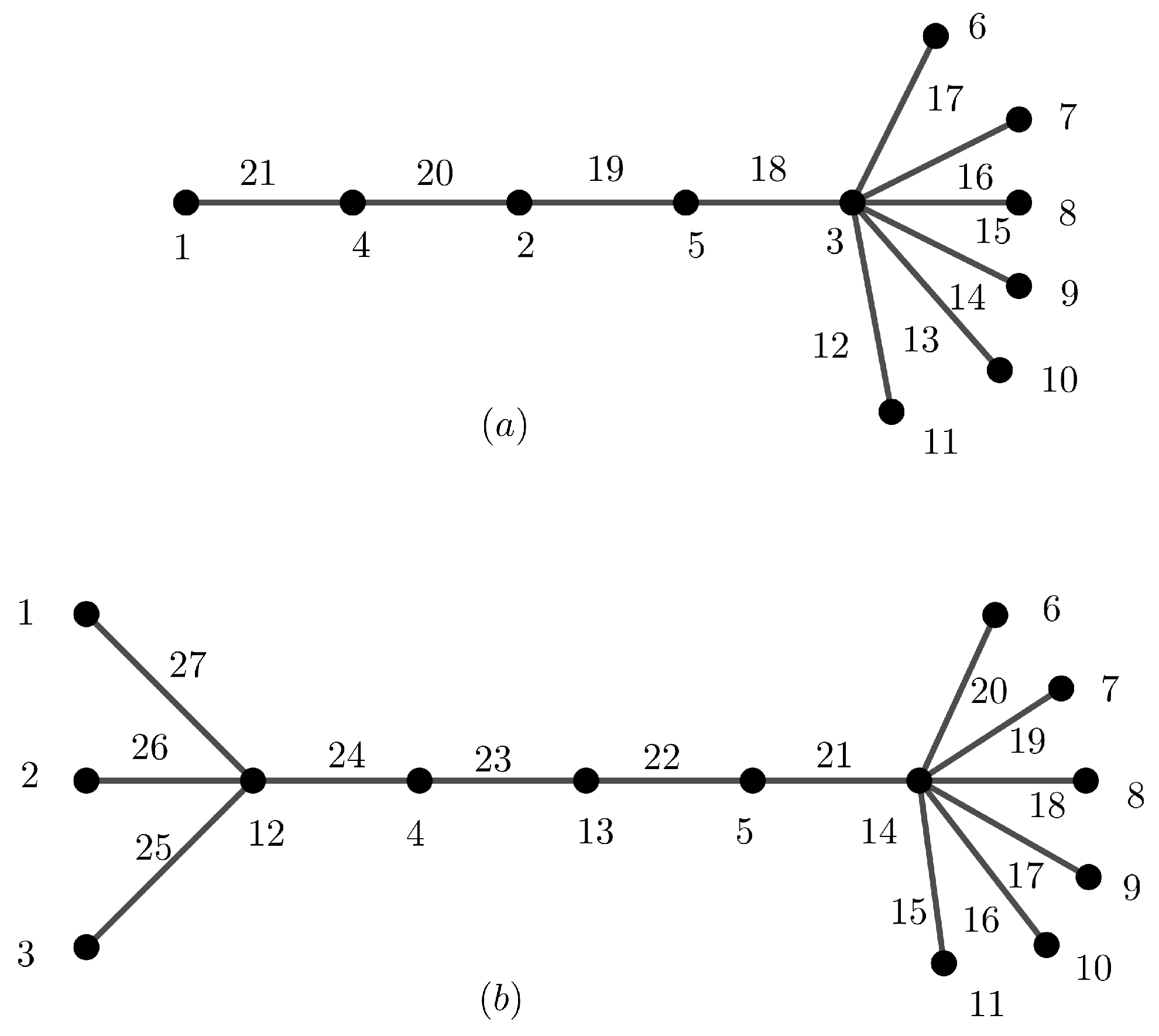
Figure 10 illustrates the broom
and the double broom
.
Corollary 7. Let and m be three positive integers at least two and . The broom and the double broom are -sim-magic.
Proof. It is known that all caterpillars are edge magic [
1]. Moreover, all subgraphs isomorphic to
have the same internal vertices. This completes the proof. □
Figure 10 illustrates
-sim-supermagic labelings of the broom
and the double broom
for
and
, respectively.
4. A -Sim-Supermagic Labelings
In this section, we characterize -sim-(super)magic graphs. Clearly, necessary conditions of -magic graphs in Theorem 4 and Corollary 1 are also necessary conditions of -sim-(super)magic graphs. In the following Lemma, we strengthen the degree condition of Corollary 1 for -sim-(super)magic graphs.
Lemma 4. Let be a positive integer and G be a -sim-(super)magic. Then, there is only one vertex x of G with .
Proof. Suppose that there are two vertices
v and
w in
such that
and
. Let
f be a
-sim-(super)magic labeling of
G. Hence, there exist two positive integers
and
such that each edge
satisfies
and each subgraph
H of
G isomorphic to
satisfies
. Consider two arbitrary stars with center
v and
w that are isomorphic to
as
and
. Thus,
As a result, we have , a contradiction. □
Recall that Gutiérrez and Lladó [
12] proved the following theorem. The labeling in the proof of the theorem will be utilized to characterize
-sim-supermagic graphs.
Theorem 9 ( [
12]).
The star is -supermagic for any . Proof. Denote the vertex set of by , where is the maximum degree vertex, and the edge set of by . Define a bijection with and , for any , and . Thus, . We can verify that (constant) for every subgraph H of isomorphic to . Therefore, is -supermagic for each . □
Now we are ready to characterize -sim-supermagic graphs.
Theorem 10. Let be a positive integer. A graph G is -sim-supermagic if and only if G is isomorphic to the star for .
Proof. (⇐) First, we prove that, for , the star is -sim-supermagic. Recall the -supermagic labeling of in the proof of Theorem 9, where (constant), for each edge in . Hence, is -sim-supermagic for .
Conversely, we prove that if G is -sim-supermagic, then G is isomorphic to the star for . Clearly, a connected graph G with order two and three is isomorphic to and , respectively. Then, consider G with order at least four. Suppose to the contrary that G is not isomorphic to any star . Let e be an arbitrary edge in G. Suppose that e belongs to , a subgraph isomorphic to , where e is incident with c, the center of . Since G is not isomorphic to a star, there exists another edge which is not incident with c. Since G admits -covering, then belongs to a subgraph that is isomorphic to where the center is not c, a contradiction by Lemma 4. □
We remark that by considering , we can derive another proof of Corollary 5 from Theorem 10.
5. A -Sim-Supermagic Labelings
In this section, we list some forbidden subgraphs and some -sim-(super)magic graphs. We start by presenting results for -sim-(super)magic graphs of order n by considering the relation between two well-known magic labelings: (S)EMT and -(super)magic.
Lemma 5. Let G be a graph of order n admitting a covering. If G is (S)EMT then G is -(super)magic.
Proof. Let f be an EMT labeling of G. Thus, there exists a positive integer such that for each edge in . Denote as the set of vertices in G. Define a bijection with for all V(G). Consider an arbitrary subgraph C isomorphic to . Since the label of each vertex x is counted twice in , then , a constant. Therefore, G is -(super)magic. □
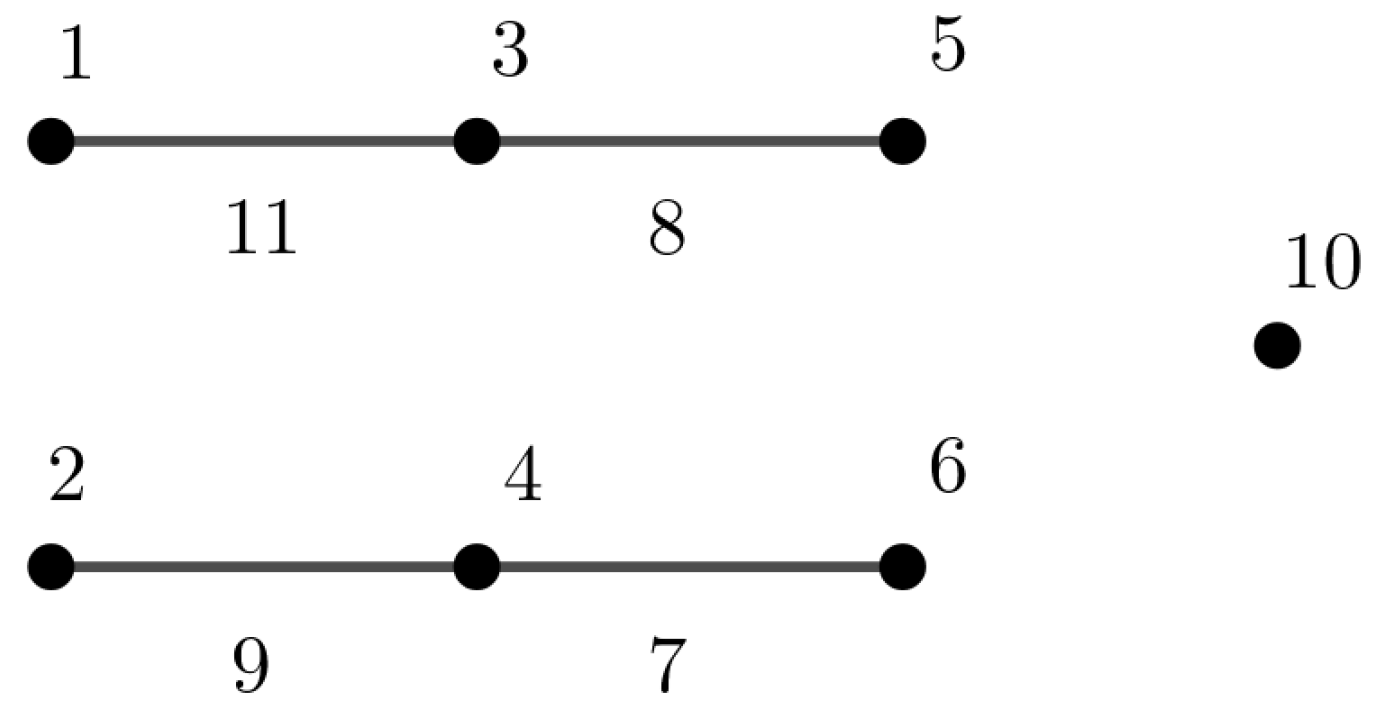
The converse of Lemma 5 is not true since
is
-(super)magic, although it is known that
is neither EMT [
1,
3] nor SEMT [
3] (See
Figure 11). However, it is clear that we have the following necessary and sufficient condition for a graph of order
n to admit a
-sim-(super)magic labeling.
Corollary 8. Let G be a graph order n admitting a covering. G is (S)EMT if and only if G is -sim-(super)magic.
It is known that the complete graph
is EMT if and only if
[
1]. Since each pair of vertices in
are adjacent, the number of subgraphs of
isomorphic to
is the number of
n-cycles in the symmetric group
, which is
Thus, the number of subgraphs of
and
isomorphic to
and
is 24 and 120, respectively.
Corollary 9. Let be a positive integer. A complete graph is -sim-magic if and only if or .
Proof. (⇐) Recall the known EMT labeling
f in
for
or 6 [
1]. By Lemma 5,
f is a
-magic labeling. This gives
as
-sim-magic for
or 6.
(⇒) Conversely, it is immediately known from the fact that
is not EMT according to Kotzig and Rosa [
1]. □
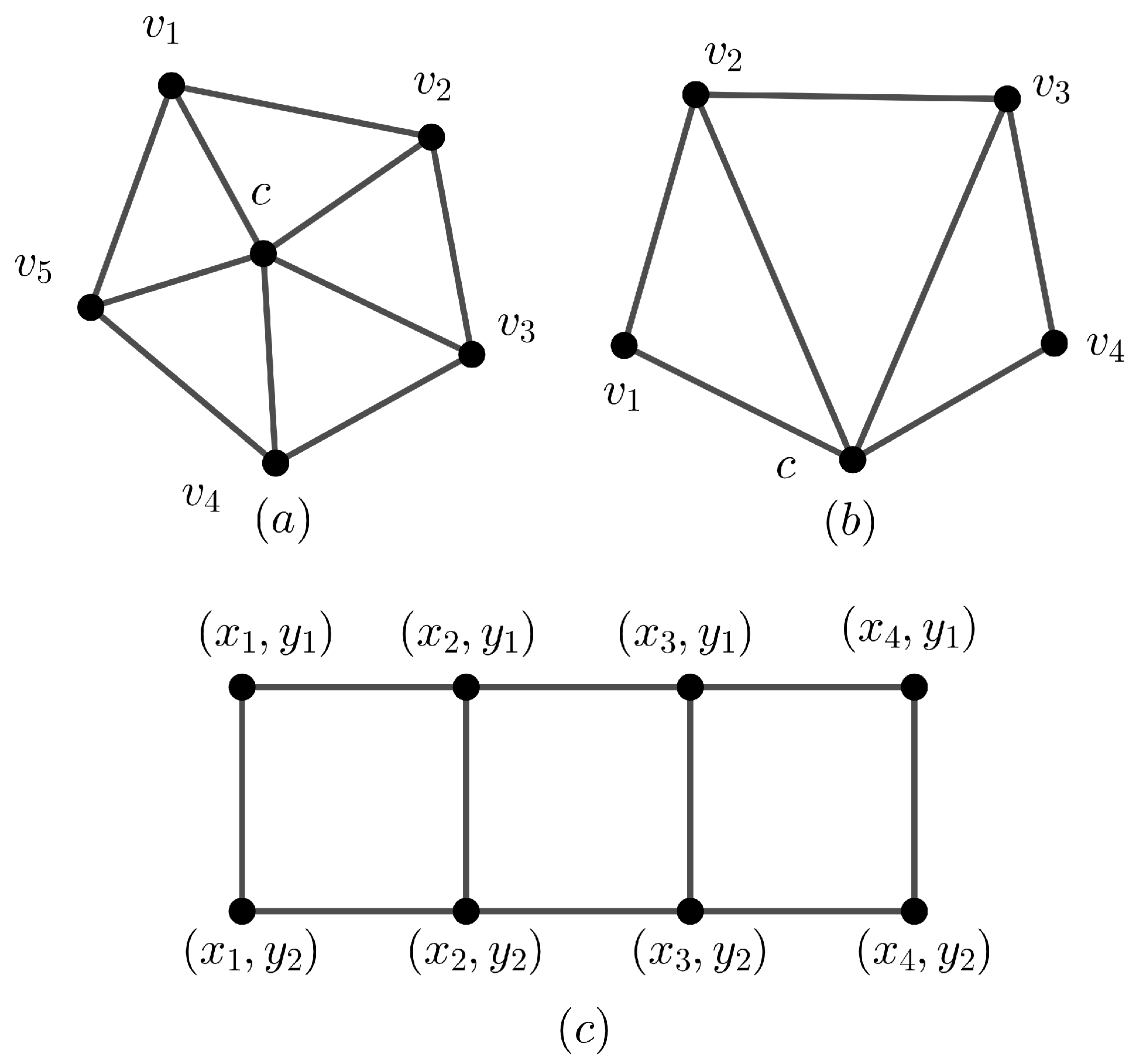
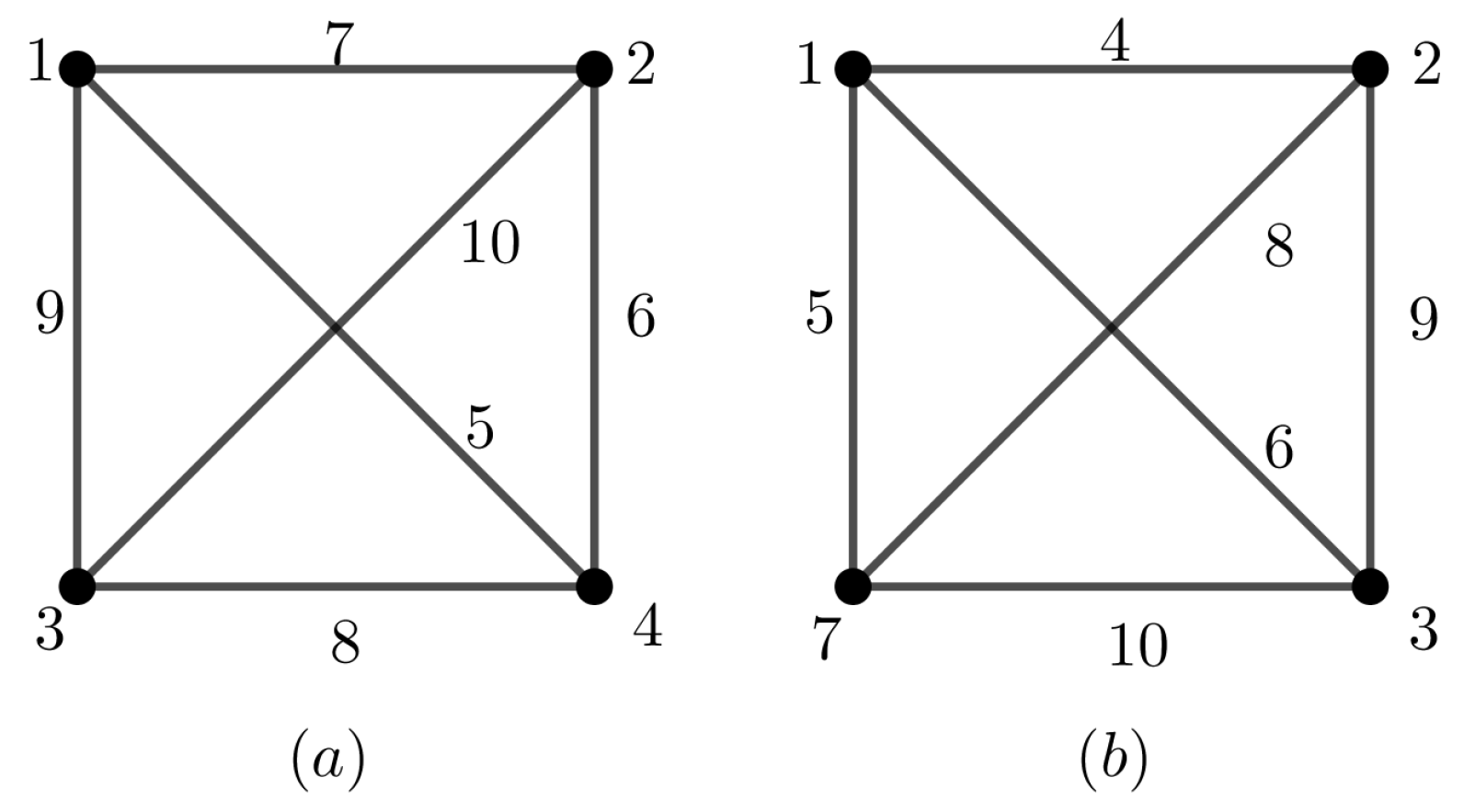
Figure 12 shows
-sim-supermagic and
-sim-supermagic graphs.
Kotzig and Rosa [
1] proved that the complete bipartite graph
is EMT for all
m and
n. Philips et al. [
20] constructed an EMT labeling of the wheel
for
or 2(mod 4). By Lemma 5, we have the following Corollary.
Corollary 10. Let be a positive integer.
- 1 .
is -sim-magic;
- 2 .
is -sim-magic for or 2(mod 4).
In the next two theorems, we consider a -sim-supermagic labeling of a cycle with chords. A chord is an edge joining two non-adjacent vertices in a cycle. An n-power of graph is a graph with the vertex set and any two vertices are adjacent when their distance in G is at most n. Recall from Lemma 2 that is not SEMT, so it is if we remove at most two edges from . Thus, it is interesting to construct a maximal SEMT graph, where the number of edges is equal to the upper bound of inequality in Lemma 2, from .
Let be a positive integer and be the vertex set of the cycle . Let be the set of three edges in . We define the cycle with chords where the vertex set is and the edge set is . It is clear that admits a -covering for every odd integer and we have the following theorem.
Theorem 11. Let be an odd integer. A cycle with chords is -sim-supermagic.
Proof. Let be the vertex set of . Define a bijection as , for . Thus, for each edge , we have
- 1 .
, for each ;
- 2 .
;
- 3 .
, for and .
Consequently, and the set consists of consecutive integers. By Lemma 1, is SEMT and f is the SEMT labeling with magic sum . By Lemma 5, f is also a -supermagic labeling of . This concludes that is -sim-supermagic. □
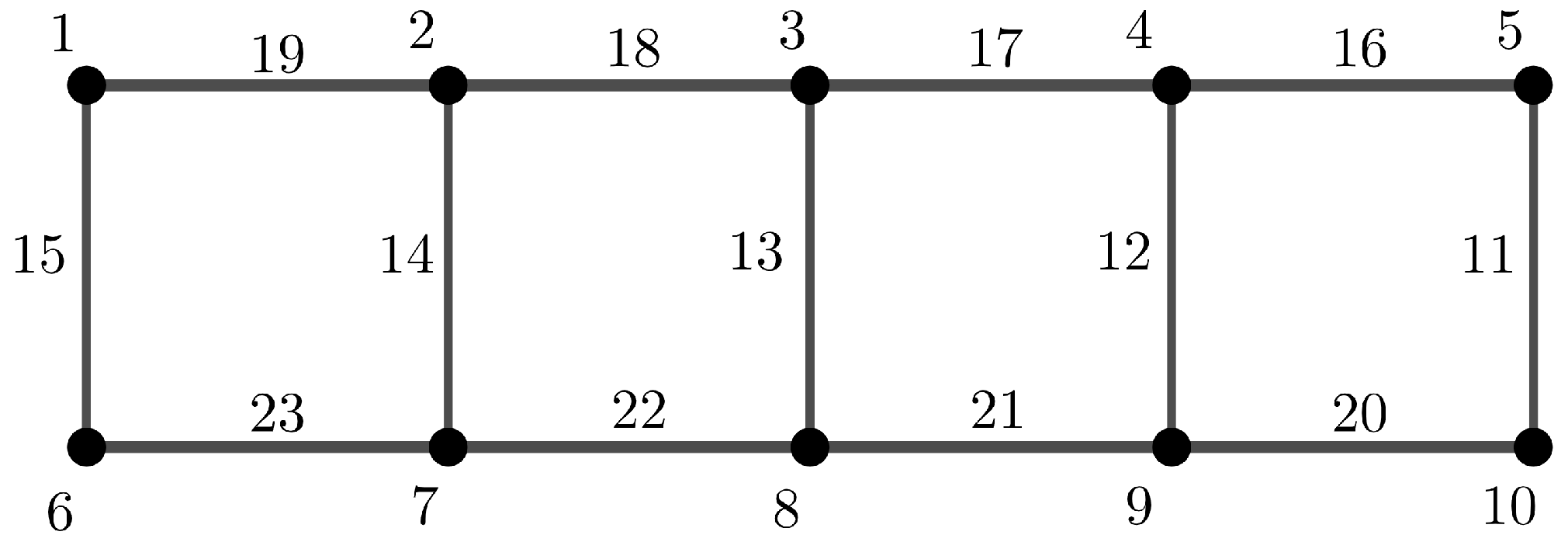
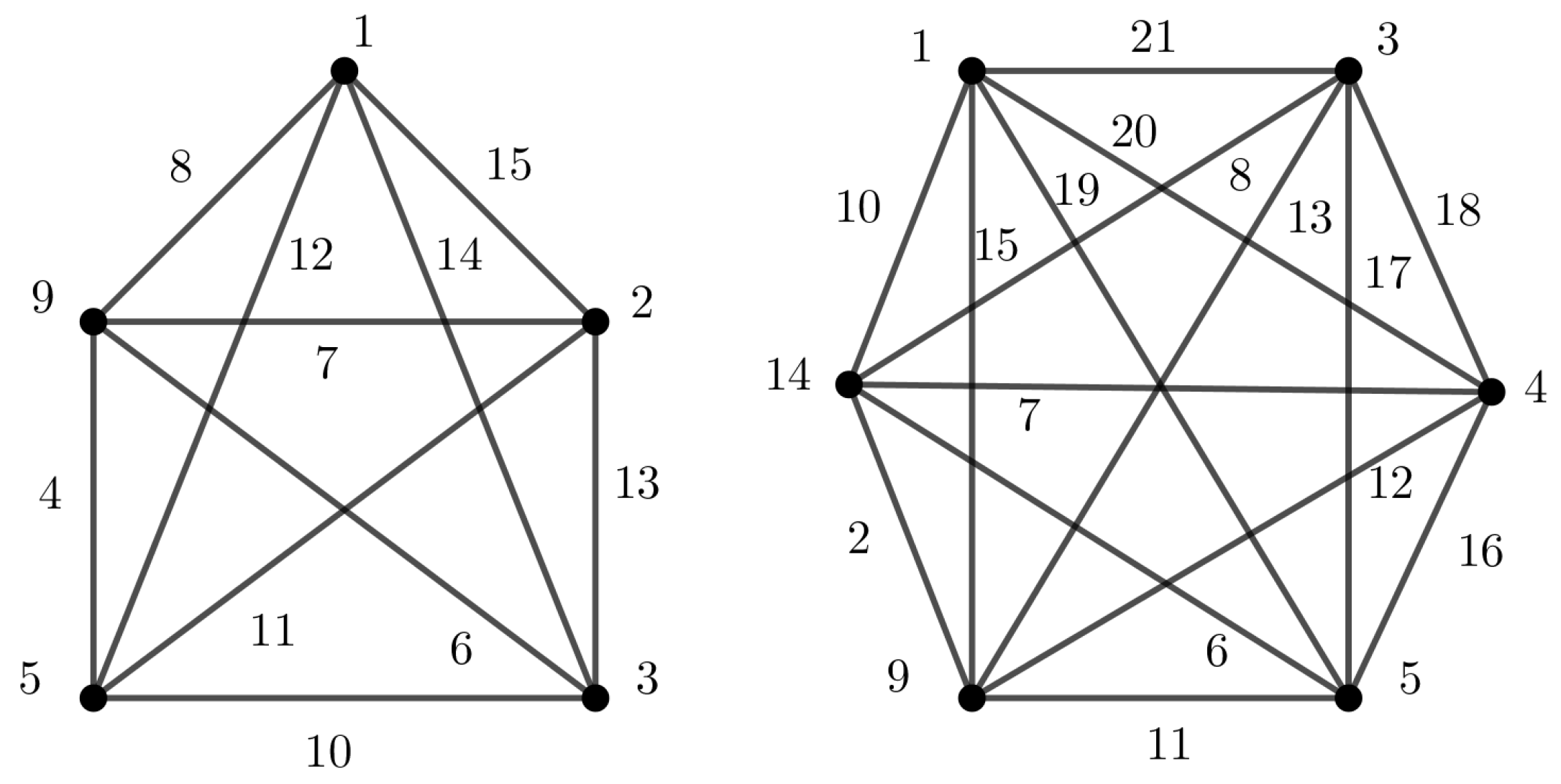
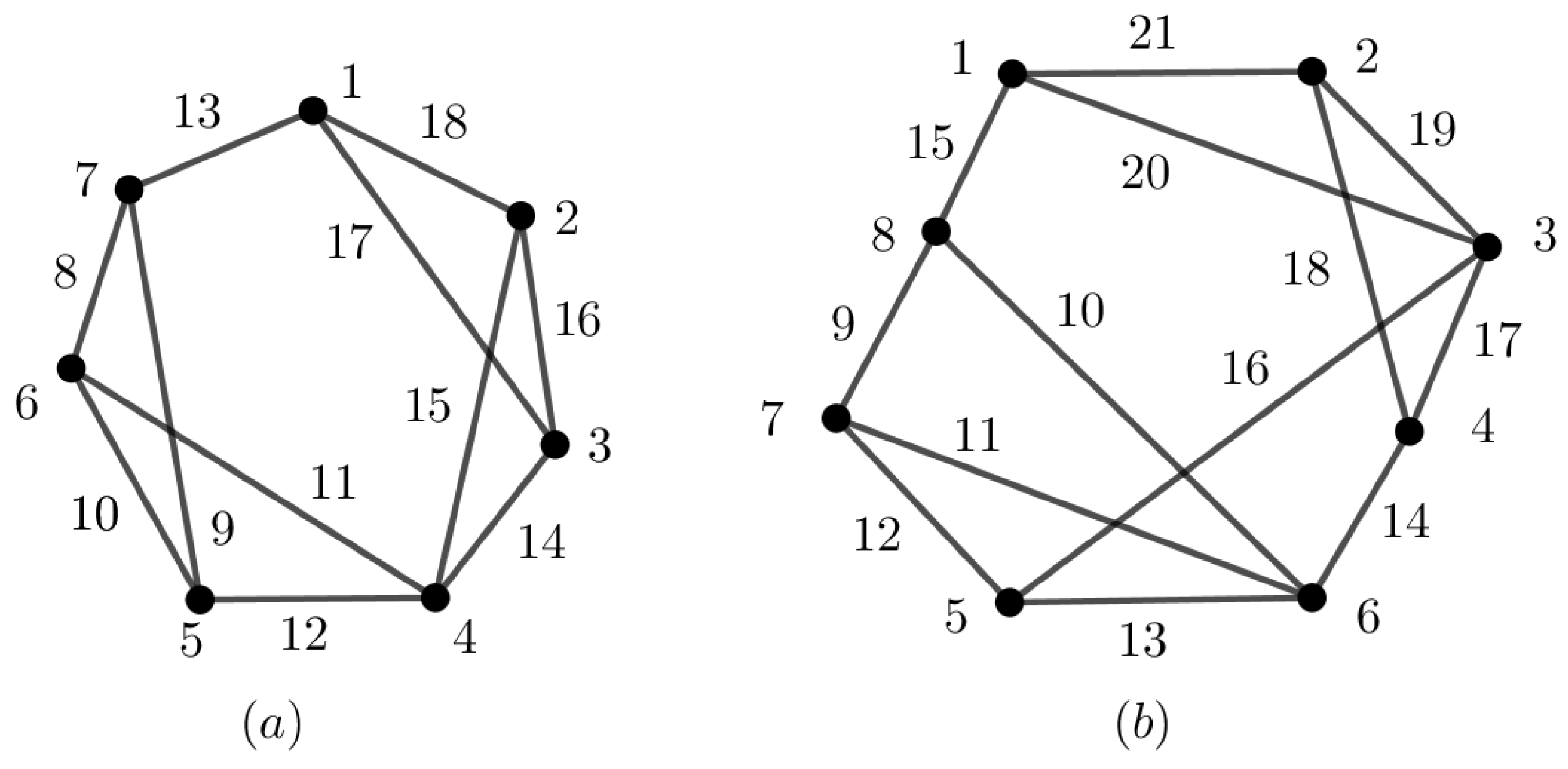
Figure 13a illustrates a
-sim-supermagic labeling of
.
Let be an even integer. Let . We define the cycle with chords as a graph where the vertex set is and the edge set is . Such a cycle with chords admits -covering for each an even integer.
Theorem 12. Let be an even integer. A cycle with chords is -sim-supermagic.
Proof. Let be the vertex set of . Define a bijection as follows.
, for every and ;
;
.
For each , we have
, for each and ;
;
;
, for each , and ;
;
;
.
It can be counted that and the set consists of consecutive integers. By Lemma 1, is SEMT and f is the SEMT labeling with magic sum . By Lemma 5, f is also a -supermagic labeling of . This concludes that is -sim-supermagic. □
Figure 13b shows a
-sim-supermagic labeling of cycle with chords
.
In addition to maximal SEMT graphs construction, we remark that Theorems 11 and 12 also enlarge the classes of graphs known to be -supermagic and SEMT.
Notice that up to Theorem 12 we only consider -sim-supermagic graphs of order n. Therefore, it is interesting to ask whether an (S)EMT graph G of order n can admit a -(super)magic labeling, for . We start by presenting some forbidden subgraphs of -sim-(super)magic graphs, for .
Theorem 13. If G is -sim-(super)magic, then G is H-free, where
- 1 .
, for any ;
- 2 .
, for any .
Proof. Suppose that G is -sim-(super)magic and G is not H-free. Then, G contains a subgraph that is isomorphic to H. Let f be a -sim-(super)magic labeling of G, such that there exist two positive integers and , satisfying and , for each edge and for each subgraph C isomorphic to , respectively. We consider the following two cases.
Case 1. .
Consider a subgraph
of a graph
G. Denote the vertices in
by
such that the edge set is
. There are two cycles
and
isomorphic to
with
and
. Then,
or
Since for each edge , . Hence, , a contradiction.
Case 2. .
Consider a subgraph
of a graph
G. Denote the vertices in
by
such that the edge set is
. There are two cycles
and
isomorphic to
with
and
. Then
or
Thus and . Hence, , a contradiction. □
The converse of Theorem 13 is not true. Consider
m copies of isomorphic cycles of order
n,
. It is clear that
admits
-covering and is
H-free, for
H isomorphic to the forbidden subgraphs in Theorem 13. However
is SEMT if and only if
m and
n are odd [
21], and so
, for even
, is not
-sim-supermagic. Therefore, the two subgraphs in Theorem 13 are not the only forbidden subgraphs of
-sim-supermagic graphs.
Problem 3. What are the other forbidden subgraphs of -sim-(super)magic graphs?
In the following lemma, we state sufficient conditions for an (S)EMT graph to be a -sim-(super)magic graph.
Lemma 6. Let and be two positive integers. Let G be a graph order at least that admits -covering. Let be the family of all subgraph of G isomorphic to and be the sum of all vertices labels in , for each . If f is an (S)EMT labeling in G such that is constant, for every , then G is -sim-(super)magic.
Proof. Let
as the magic sum of the labeling. Let
be two positive integers in
. Consider two arbitrary cycles
and
in
. Thus,
. Hence, we have that
Hence, the sum of all edges and vertices labels associated to a subgraph of G isomorphic to is a constant. Therefore, G is a -(super)magic for each . Since f is simultaneously an (S)EMT and -(super)magic, G is -sim-(super)magic. □
Consequently, by Lemma 6, we have the following corollary.
Corollary 11. Let be an odd integer. The disjoint copies of cycle on 3 vertices, , is -sim-supermagic.
Proof. Recall an SEMT labeling of
, for odd
m, from [
21]. We denote
and
and
and
and define
Let
be a subgraph of
isomorphic to
and
be the sum of all vertices labels in
. Hence, for
, we have
and, for
, we have
Therefore, is constant for . By Lemma 6, is -sim-supermagic. □