Abstract
This article takes an approach to creating a machine learning model for the oil and gas industry. This task is dedicated to the most up-to-date issues of machine learning and artificial intelligence. One of the goals of this research was to build a model to predict the possible risks arising in the process of drilling wells. Drilling of wells for oil and gas production is a highly complex and expensive part of reservoir development. Thus, together with injury prevention, there is a goal to save cost expenditures on downtime and repair of drilling equipment. Nowadays, companies have begun to look for ways to improve the efficiency of drilling and minimize non-production time with the help of new technologies. To support decisions in a narrow time frame, it is valuable to have an early warning system. Such a decision support system will help an engineer to intervene in the drilling process and prevent high expenses of unproductive time and equipment repair due to a problem. This work describes a comparison of machine learning algorithms for anomaly detection during well drilling. In particular, machine learning algorithms will make it possible to make decisions when determining the geometry of the grid of wells—the nature of the relative position of production and injection wells at the production facility. Development systems are most often subdivided into the following: placement of wells along a symmetric grid, and placement of wells along a non-symmetric grid (mainly in rows). The tested models classify drilling problems based on historical data from previously drilled wells. To validate anomaly detection algorithms, we used historical logs of drilling problems for 67 wells at a large brownfield in Siberia, Russia. Wells with problems were selected and analyzed. It should be noted that out of the 67 wells, 20 wells were drilled without expenses for unproductive time. The experiential results illustrate that a model based on gradient boosting can classify the complications in the drilling process better than other models.
1. Introduction
Today, the use of machine learning (ML) capabilities in the oil and gas industry is becoming a central topic in various research centers and universities in the modern world. ML algorithms can provide practical solutions for analyzing and leveraging big historical data. ML technology has long been successfully used in computer science, engineering, mathematics, physics and astronomy, neuroscience, and medicine [1,2,3,4,5,6,7,8,9,10].
However, for the oil and gas industry, the use of such technologies has significantly increased in recent years [11,12,13,14,15,16,17,18]. An important task in the development of the oil and gas industry in the coming years is to increase the efficiency of producing oil and gas and drilling wells, and the main impetus to the introduction of methods of ML was the fall in oil prices. Oil and gas companies have concentrated on resource efficiency, optimizing their production processes [19,20,21,22,23,24,25,26,27,28,29,30].
This challenge should be solved at the expense of the overall development of fundamental and applied research and the rapid introduction of the results obtained. In drilling, one of the main issues in improving the quality of well construction is a reduction in the number and severity of problems, which is closely related to the use of modern computer–mathematical methods and computer technology. The use of such tools will help to identify wells with problems during drilling and further determine the symmetry or asymmetry of the well placement. The use of a symmetrical arrangement is advisable when operating a reservoir with fixed oil-bearing contours, i.e., with an equal distribution of the reservoir energy. The placement of wells on an asymmetric grid is distinguished according to the density of the grid, according to the rate of well commissioning, and according to the order in which wells are commissioned.
It is worth noting that the use of high-performance data analysis software is not a novelty for the oil industry. Since the 1990s, technologies for the collection and analysis of well data have been widely used. However, large capital expenditures on the implementation of these tools scared off many companies since their implementation could not be financially justified.
Currently, one of the main challenges facing the oil and gas industry is to improve the efficiency of well drilling.
The requirements of the practice of drilling deep oil and gas wells require a wide range of requirements for the theory of machine learning. In this case, the theory should be defined as a normal process at the time of origin, and during development, considering any problem as an integral part of the drilling processes. It is desirable that a theoretical description of drilling problems (DPs) allows not only judging them at a qualitative level but also quantifying the interrelation of their essential variables. Several years ago, these tasks seemed laborious.
Existing works were aimed at improving the drilling process using methods of artificial intelligence (AI).
Zhan and colleagues [31], in their work, used a nonparametric system of fuzzy inferences to predict the state of the rotary steerable system (RSS) by forecasting the state of the RSS in real time based on the operating mode and drilling parameters. This method allows reducing the cost of repair and maintenance of the drilling equipment.
Wang [32] presented an approach that uses multilayer neural network modeling to predict nonlinear optimization of DPs. The proposed model can not only predict the pump pressure, as the desired parameter, but can also ensure the impact of each input parameter in this model.
The mechanism of damage to drilling equipment is usually accompanied by several successive incidents that contribute to the loss of efficiency. Consequently, recognition, classification, elimination of breakdowns, and calculation of the remaining useful life are impossible without constant monitoring of the health of the system. Therefore, Camci and colleagues [33], with the help of the hidden Markov model, created a model capable of monitoring the current state of the mechanism, through signals sent by sensors. In particular, this model has shown excellent results for diagnosing the condition of drill bits.
At present, methods of programming neural networks for solving problems in various fields have been widely used. An artificial neural network is an interconnected group of nodes, similar to our brain system [34]. For example, Lind and Kabirova [35] used the neural programming method to predict possible problems that may arise when drilling wells, based on information about the oil field reserves. The results obtained showed the effectiveness of the neural network application for solving this problem.
A Bayesian neural network was used in the work by Al-yami and Schubert [36]. The method used allowed creating a system for making expert decisions in drilling. This method can be used to train young engineers. The system can also provide advice during all stages of well construction. This advice can be on well completion, monitoring of drilling and cementing of wells, selection of drilling fluids, etc.
Drilling engineers are always looking for methods to predict unexpected drilling situations and to improve the associated parameters accordingly. The prediction of the drilling rate is given high priority because of its impact on the optimization of various parameters, which directly reduces costs. Jahanbakhshi and colleagues used a neural network to predict the rate of penetration (ROP) [37]. The type of rock, mechanical properties of the formation, hydraulics, the type of bit and its features, and rotor speed were chosen as input parameters. Monazami and colleagues [38], in their article, also used a neural network to estimate the ROP. The authors considered this method as the most useful tool in forecasting in comparison with the currently available procedures. The model allows the drilling crew to assess the ROP not only at the planning stage but also during drilling. The results of this work showed that neural programming for the quality of ROP prediction is superior to conventional methods. Amer and colleagues [39] used the method of backpropagation to predict the ROP, which showed its success in their work.
Gidh and colleagues [40] also used an artificial neural network to develop a program to optimize drilling parameters. The result of this work was a model capable of choosing the optimal ROP and weight on the bit to extend the life of the bit. This model selects the necessary drilling parameters based on the expected characteristics of the rock on which the drilling will take place. Further, all parameters were adjusted for the relevant conditions.
In another publication, the ROP, together with the specific mechanical energy found by Rashidi and colleagues [41], was used to calculate the bit wear in real time. Between the specific mechanical energy and the weight on the bit, a linear relationship was obtained. Based on the analysis of a vast number of experiments, the authors believe that this model can become a valuable tool in the analysis of bit wear in real time.
Valisevich and colleagues [42], using an artificial neural network, created a model optimizing the development of bits in real time. All this led to an increase in the drilling speed, and a decrease in bit wear during drilling.
Another application of neural networks was presented by Dashevskiy and colleagues [43]. This work allowed simulating a nonlinear drilling system with a minimal error share by monitoring its dynamic behavior. The authors achieved the primary aim of the work—the use of neural networks for the intelligent control of drilling in dynamics.
GirirajKumar and colleagues [44], for an improvement in drilling, suggested using an optimally tuned proportional–integral–differential (PID) controller in high-performance drilling systems. The primary aim of their work was to obtain a stable, reliable, and controlled system by tuning the PID controller, using the optimization algorithm for swarm intelligence. The results of their work showed that tuning the PID controller using RI (swarm intelligence) provides a smaller overshoot.
Using a neural network, Lind and colleagues created an algorithm for predicting the loss of drilling fluids [45]. This system allows one to receive a recommendation for the selection of drilling fluids.
Static training methods for predicting torque and friction in real time were applied by Hegde and colleagues [46]. They considered algorithms such as regression, random forest, and the support vector method. These methods can be used to predict DPs and take appropriate measures to eliminate them. For example, an unexpected change in the value of torque may be a sign of a complication.
Another common complication—the instability of the walls of the well—with the help of a neural network, was predicted by Okpo and colleagues [47]. The program developed by the authors was used to predict the geomechanical parameters of the formation. The model was developed in a Neuroph Studio, and the platform of the neural network was Java and Netbeans IDE. The main advantage of this model is its simplicity and open-source code.
Unrau and colleagues [48], using an ML method, improved the existing alarm system on a drilling rig. The standard alarm systems used for drilling can register too many false alarms that significantly affect the drilling process. The ML algorithm proposed by the authors can be used to reduce false alarms while maintaining the efficiency of the alarm system. The model successfully detects kicks and loss.
As noted above, the integration of AI methods in a drilling process has great practical importance.
A DP is a violation of the continuity of the technological process of the construction of a well, requiring, for its liquidation, carrying out special works not planned in the project. In the process of drilling oil and gas wells, due to phenomena of a geological nature, there are, from time to time, problems in the technological process. This could be loss of drilling mud and fluid, kicks, or a stuck drill and casing columns [49].
Drilling crews constantly face a lot of difficult situations, the exits from which can be very expensive, and even impossible. A drill string may be stuck, by pressing against the wall of the well during a draw-down, or as a result of key seating. To eliminate these problems, additional efforts will be required to free the drill string. Sometimes, these efforts can fail. Then, drilling a side track is required [50].
Making a decision to eliminate these problems is a complex process. The damage from complications consists of the time spent for the elimination of DPs, and costs for materials and energy. To minimize the risks of drilling problems, work is being carried out to minimize vibrations of the bottom of the drilling assembly [51]; a mathematical model of a screw downhole motor (SDM)–drilling string (DS) system is being developed, which allows predicting the range of DS self-oscillations and boundaries of rotational and translational wave disturbances for the case of string modeling as a heterogeneous rod when drilling directionally straight sections of a well [52]. Thus, preventing problems and accordingly minimizing the risks of their occurrence are an actual problem today.
The aim of this work was to find a learning algorithm to recognize and classify DPs while drilling wells. Of the eight methods of ML, gradient boosting (GB) was chosen. This algorithm showed a high-performance precision, recall, and F-score (see below). This learning algorithm, based on historical data from previously drilled wells, classifies the DPs better than other algorithms. Such a decision support system will help engineers to intervene in the drilling process and prevent high expenses due to unproductive time and equipment repair. Another significant plus is worth noting. That is, the algorithm, in addition to the classification of DPs, accurately determines the standard drilling mode. This minimizes the possibility of triggering false alarms, which will also save drilling time. False alarms are also one of the problems when drilling wells which take up a significant amount of time and money.
2. Existing Methodologies
In order to create a program that classifies the problems in the drilling process, the main methods of ML with which the calculation was performed were considered. These methods have shown successful applicability in solving problems in various industries.
2.1. Logistic Regression
Logistic regression is a statistical technique for analyzing a dataset that has one or more independent variables that determine the outcome. The outcome is measured using a dichotomous variable (which has only two possible outcomes). It is used to predict the binary outcome (1/0, Yes/No, True/False) given a set of explanatory variables [53].
It is worth noting that this method is based on fairly strong probabilistic assumptions, which have several interesting consequences. First, the linear classification algorithm turns out to be the optimal Bayesian classifier. Secondly, the forms of the activation function (it is the sigmoid function) and the loss function are uniquely determined. Thirdly, an interesting additional possibility arises, along with the classification of the object, to obtain numerical estimates of the probability of problems belonging to each of the classes [54].
2.2. Naive Bayesian Classifier
A naive Bayesian classifier is a simple probabilistic classifier based on the application of Bayes’ theorem with strict (naive) assumptions about independence.
In other words, a naive Bayesian classifier assumes that the presence of a particular feature in a class is not related to the presence of any other feature. For example, circulation loss can be detected by the following signs: the fluid flow from the well decreases, the level in the tanks decreases, and the outlet pressure decreases. Even if these parameters are dependent on each other or on the presence of other parameters, a naive Bayesian classifier will consider all of these properties independently of each other to create the likelihood that well loss is occurring [55].
Depending on the exact nature of the probabilistic model, naive Bayesian classifiers can be trained very effectively. In many practical applications, the maximum likelihood method is used to estimate the parameters for naive Bayesian models. In other words, one can work with a naive Bayesian model not believing in Bayesian probability and not using Bayesian methods [56].
2.3. Method K-Nearest Neighbors
The method of k-nearest neighbors is a metric algorithm for automatic classification of objects. The main principle of the method of nearest neighbors is that the object is assigned to the class that is the most common among the neighbors of this element.
Neighbors are taken based on a set of objects whose classes are already known, and, based on the key value for this method, the value of k is calculated, in order to find which class is the most numerous among them. Each object has a finite number of attributes.
It is assumed that there is a certain set of objects with an already existing classification [57].
In the learning process, the algorithm simply remembers all the feature vectors and the corresponding class labels. When working with real data, i.e., observations whose class labels are unknown, the algorithm calculates the distance between the new observation vector and the ones previously stored. Then, k-nearest vectors are selected, and the new object belongs to the class that owns most of them.
2.4. Decision Tree
Decision trees are a simple and widely used classification method. This method applies a simple idea to solve a problem. Decision trees ask thoughtful questions about the attributes of a test record. Each time the tree receives a response, the next question is asked until a conclusion is drawn about the class label of the record [58].
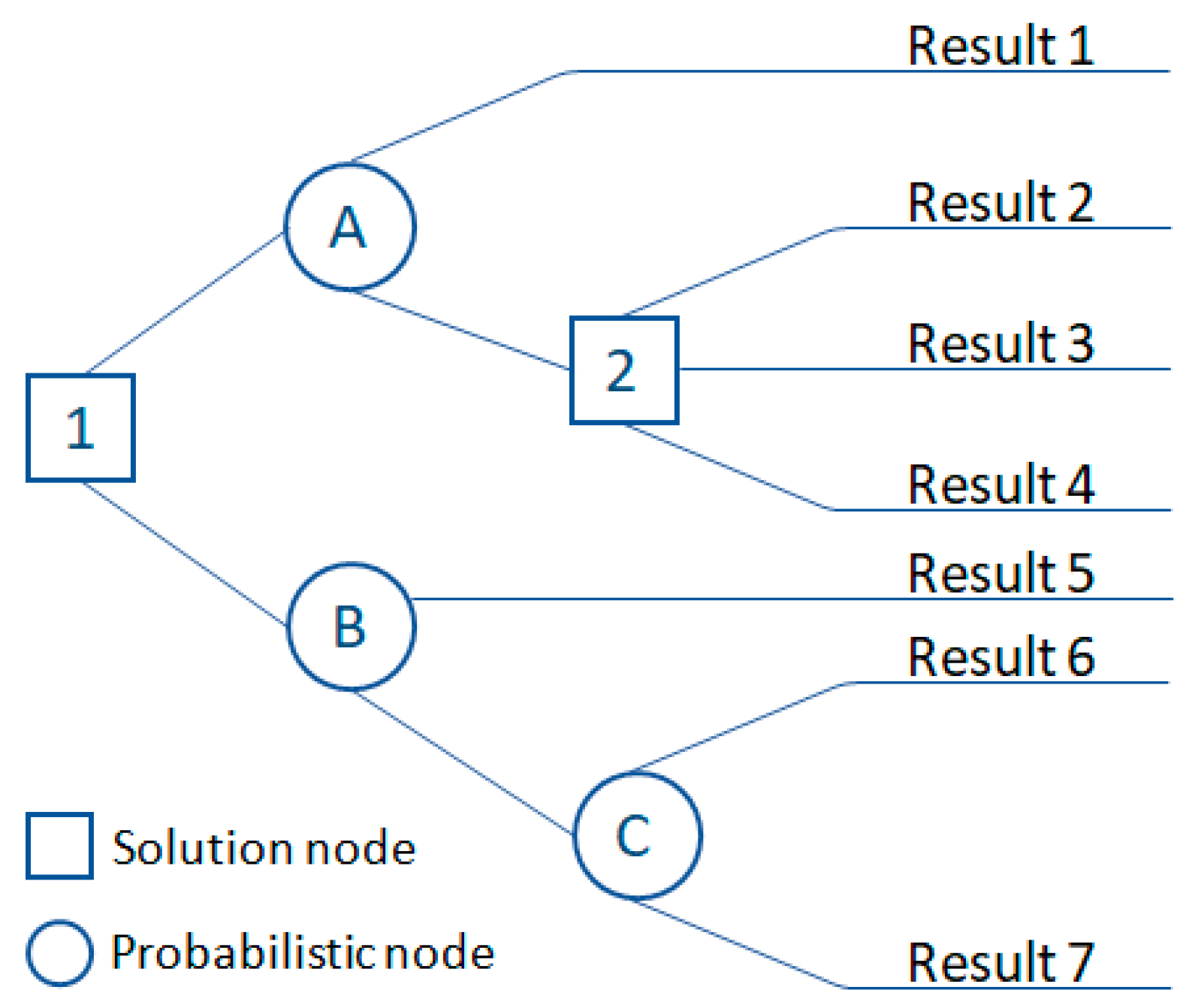
A decision tree is a graphical method that describes solutions and their possible outcomes. Decision trees consist of three types (Figure 1):
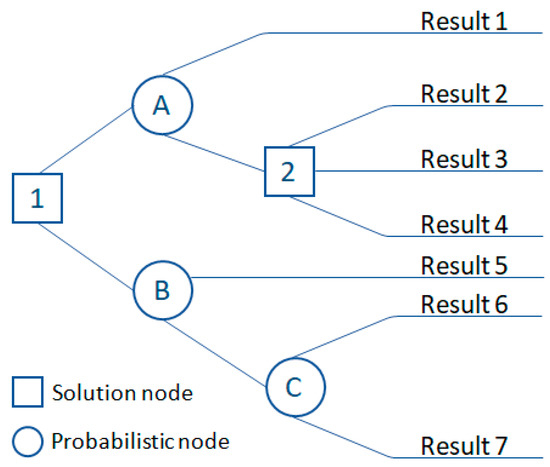
Figure 1.
Decision tree diagram.
- Decision node: This is often represented by squares that show what can be conducted. The lines coming out of the square show all the available options available on the node.
- Probability knot: This is often represented by circles showing random results. Exodus odds are events that can occur but are beyond the control of the manager.
- Closing node: This is represented by triangles or lines that do not have additional solution nodes or random nodes. Terminal nodes represent the final outcomes of the decision process.
2.5. Support Vector Machine
The support vector method is a set of similar algorithms of the form “learning with the teacher”, used for classification problems and regression analysis. This method belongs to the family of linear classifiers. A special property of the support vector method is a continuous decrease in the empirical classification error and an increase in the gap. Therefore, this method is also known as the classifier method with the maximum gap.
The basic idea of the method of support vectors is the translation of the original vectors into a space of higher dimension, and the search for a separating hyperplane with the maximum gap in this space. Two parallel hyperplanes are constructed on both sides of the hyperplane that separates the classes. The separating hyperplane is a hyperplane that maximizes the distance to two parallel hyperplanes. The algorithm works under the assumption that the greater the difference or the distance between these parallel hyperplanes, the smaller the average classifier error [59].
2.6. Random Forest
A random forest is a set of decision trees. In regression problems, their answers are averaged, and in classification problems, a decision is made by voting on the majority.
The method is based on the construction of a large number (assembly) of decision trees, each of which is constructed from a sample obtained from the initial training sample using a sample with a return. In contrast to the classical algorithms for constructing decision trees, in the method of random forests, when building each tree in the stages of vertex splitting, only a fixed number of randomly selected attributes of the training sample are used, and a complete tree is built, i.e., each sheet. The tree contains observations of only one class. Classification is carried out by voting classifiers, defined by individual trees, and regression estimation by averaging the regression estimates of all trees. It is known that the accuracy of ensembles of classifiers essentially depends on the variety of classifiers that make up the ensemble, or, in other words, on how correlated their decisions are. That is, the more diverse the classifiers of an ensemble, the higher the probability of a correct classification [60].
2.7. Gradient Boosting
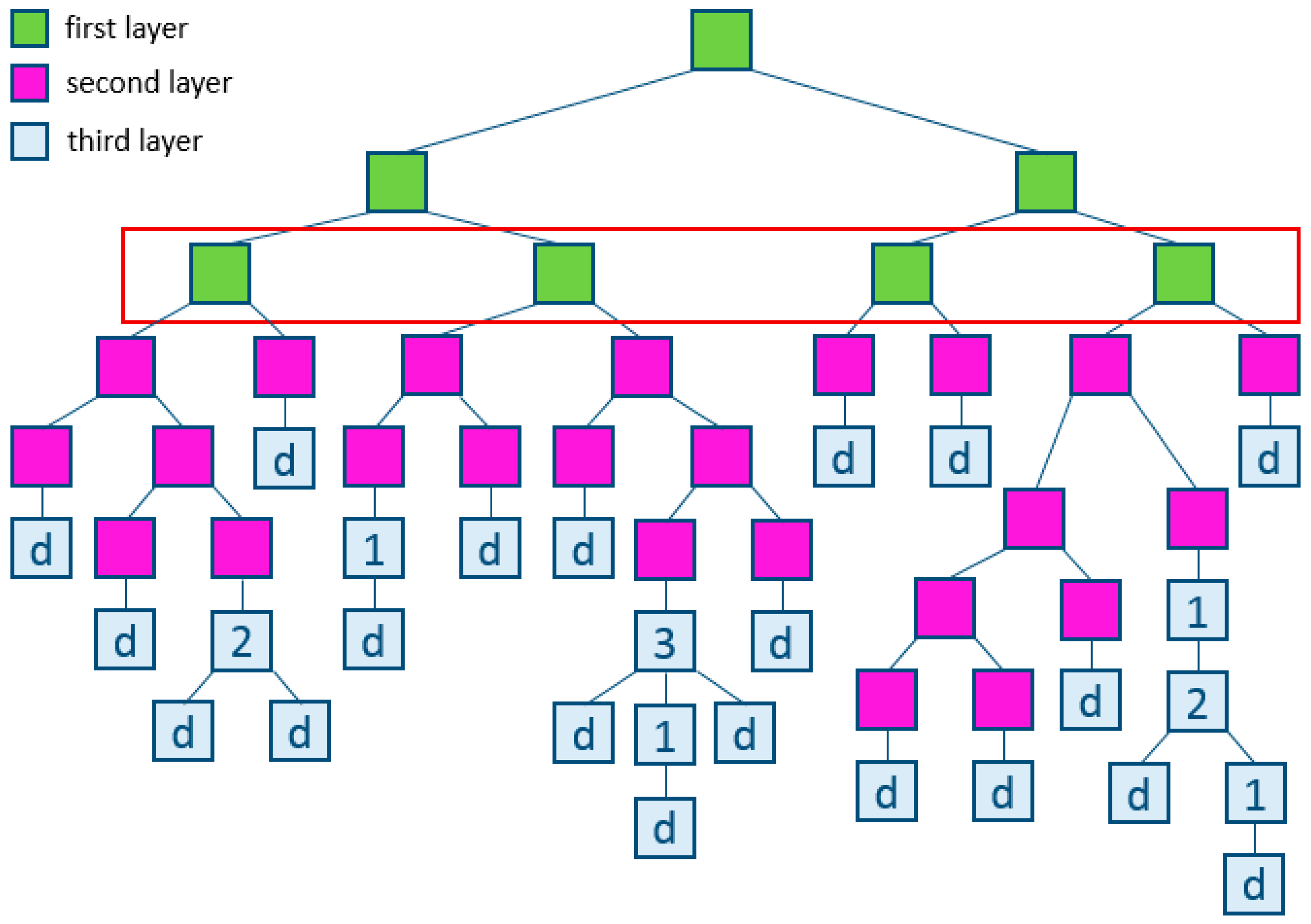
Boosting is a procedure for the sequential construction of a composition of ML algorithms, where each subsequent algorithm seeks to compensate for the shortcomings of the composition of all previous algorithms. Boosting is a «greedy» algorithm for composing the final algorithms (Figure 2).
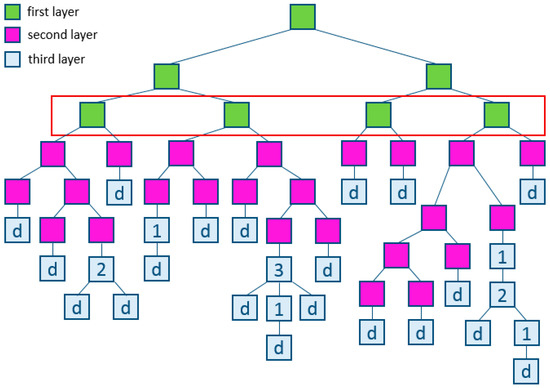
Figure 2.
Example of gradient boosting.
Boosting over decision trees is considered one of the most effective methods in terms of the quality of classification. In many experiments, there was an almost unlimited reduction in the error rate on an independent test sample, as the composition was increased. Moreover, the quality of the test sample often continued to improve even after achieving an unmistakable recognition of the entire training sample. This overturned the ideas that existed for a sufficiently long time that it is necessary to limit the complexity of the algorithms in order to increase the generalizing ability. With the example of boosting, it became clear that a good quality can have arbitrarily complex compositions, if properly tuned.
Subsequently, the booster phenomenon received a theoretical justification. It turned out that weighted voting does not increase the effective complexity of the algorithm but only smooths out the answers of the basic algorithms. Quantitative estimates of the generalization of the boosting capacity are formulated in terms of indentation. The effectiveness of the boost is explained by the fact that as the basic algorithms are added, the indentation of the learning objects increases. Additionally, the booster continues to expand classes, even after achieving an unmistakable classification of the training sample (Figure 2) [61,62].
2.8. Neural Network
An artificial neural network is a mathematical model, as well as a software or hardware implementation, built on the principle of the organization and functioning of biological neural networks—the nerve cell networks of a living organism. This concept arose when studying the processes occurring in the brain, and when trying to simulate these processes. The first such attempt was the neural networks of McCulloch and Pitts [63]. After the development of learning algorithms, the resulting models began to be used for practical purposes: in forecasting problems, for pattern recognition, in control tasks, etc.
A neural network is a system capable of changing its structure under the influence of external factors. An artificial network is trained on input data. During the training, the internal parameters of the artificial neural network are adjusted to the input data, which makes it possible to isolate patterns in the data or to solve problems of prediction, classification, and clustering. When using an artificial neural network for data analysis, the researcher solves several problems: what learning algorithm to use, what is the network configuration, etc. The required internal parameters are found automatically, according to the chosen algorithm and configuration [63].
2.9. Evaluation of the Quality of Machine Learning Methods
Metrics are used to evaluate model quality and compare algorithms. Before moving to the metrics, we need to introduce an important concept for describing these metrics in terms of classification errors—the confusion matrix.
Having two classes and an algorithm that predicts the belonging of each object to one of the classes, the classification error matrix will look similar to that shown in Table 1.

Table 1.
Metrics by model.
In Table 1, “y’” is the answer of the algorithm on the object, and “y” is the true label of the class on this object.
Thus, classification errors are of two types: false negative (FN) and false positive (FP).
2.10. Precision, Recall, and F-Score
Recall demonstrates the ability of the algorithm to detect a given class, and precision demonstrates the ability to distinguish this class from other classes.
To assess the quality of the models used to classify the complications in the drilling process, the widely used precision, recall, and F-score metrics were used.
where TP—positive observation which was expected to be positive; FN—observation is positive, but it was predicted negatively; FP—observation is negative, but it was predicted positively.
There are several different ways to combine precision and recall in an aggregated quality criterion. The F-score is an average harmonic of precision and recall:
where β, in this case, determines the weight of accuracy in the metric, and for β = 1, this is the average harmonic (with a factor of 2, meaning that in the case of precision = 1 and recall = 1, we have = 1); the F-score reaches a maximum for completeness and accuracy of one, and is close to zero if one of the arguments is close to zero.
The sklearn library in Python has a convenient function metric, classification_report, which returns the recall, precision, and F-score for each of the classes, as well as the number of instances of each class [64].
3. Given Data
As initial data, reports on drilling 67 wells were assessed. Many of the wells have had DPs that have led to rig downtime and loss of productive drilling time. The analysis of the total time spent on drilling all wells showed that about 10.33% of this time was unproductive operating time.
It is worth noting that 10.33% is an important value, considering that the average cost per hour of drilling varies from RUB 15,000 to 55,000. Additionally, in this database, there is a well in which the unproductive time was 50% of the total operating time.
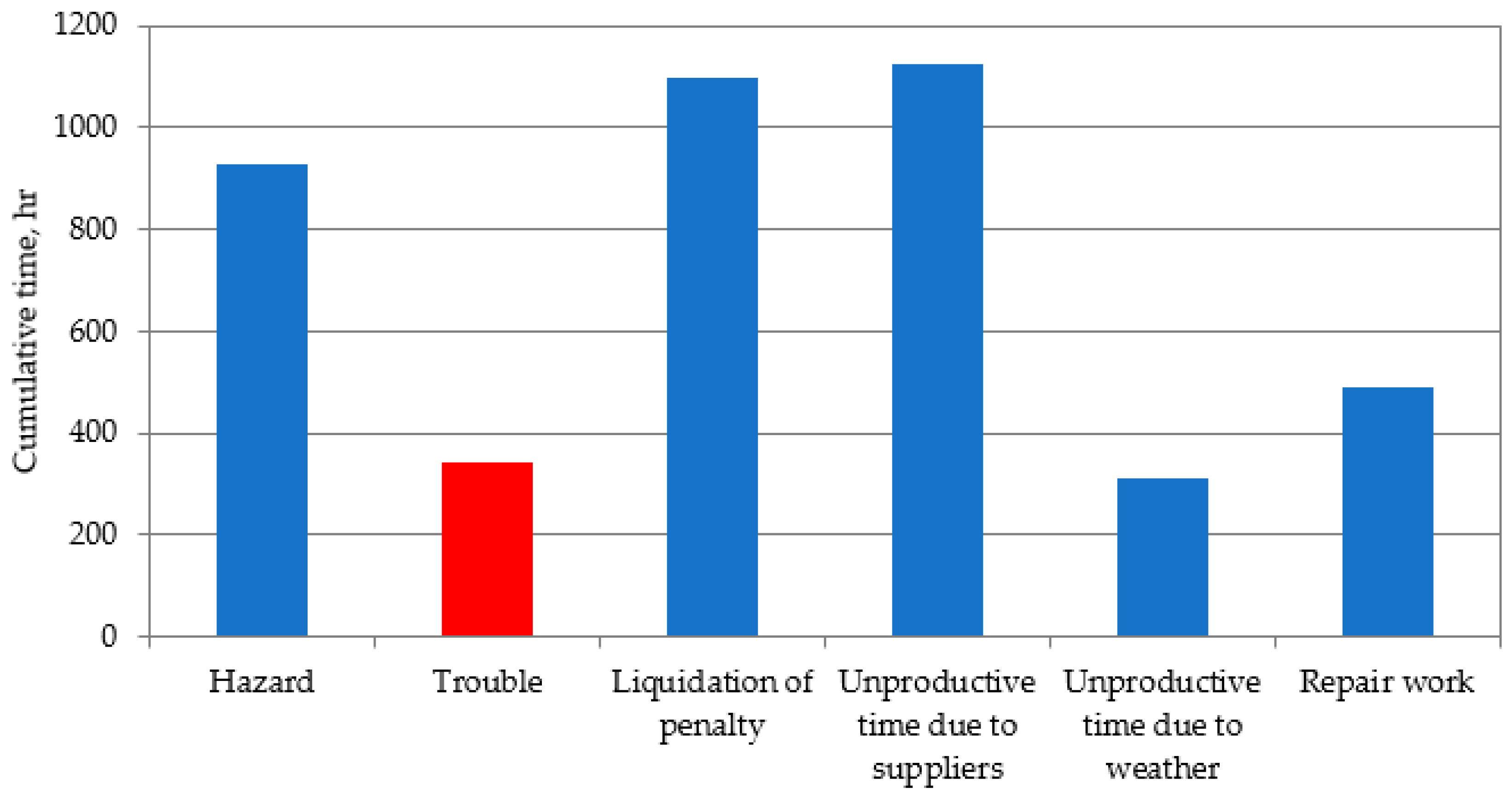
The main causes of unproductive drilling time at one specific field are shown in Figure 3. The greatest losses of time were due to rig downtime in waiting for contractors and equipment. Then, there is unproductive time due to the liquidation of penalties (unscheduled work, redrilling due to the fault of the contractor, etc.). In this project, we are interested in the trouble (DPs) that arises during the drilling process. This includes kicks, loss of circulation, and borehole instability.
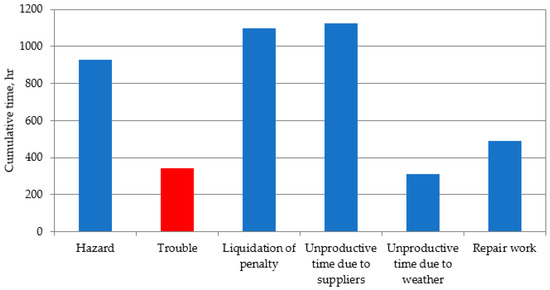
Figure 3.
Distribution of non-productive time in field.
Wells with problems were identified and analyzed. It should be noted that out of 67 wells, 20 wells were drilled without expenses for unproductive time. The most common problem is related to the seizure that occurs when the casing runs down. It is worth noting that in this project, calculations were made for complications arising directly during drilling. For three wells, trouble arose during drilling, and detailed records are available.
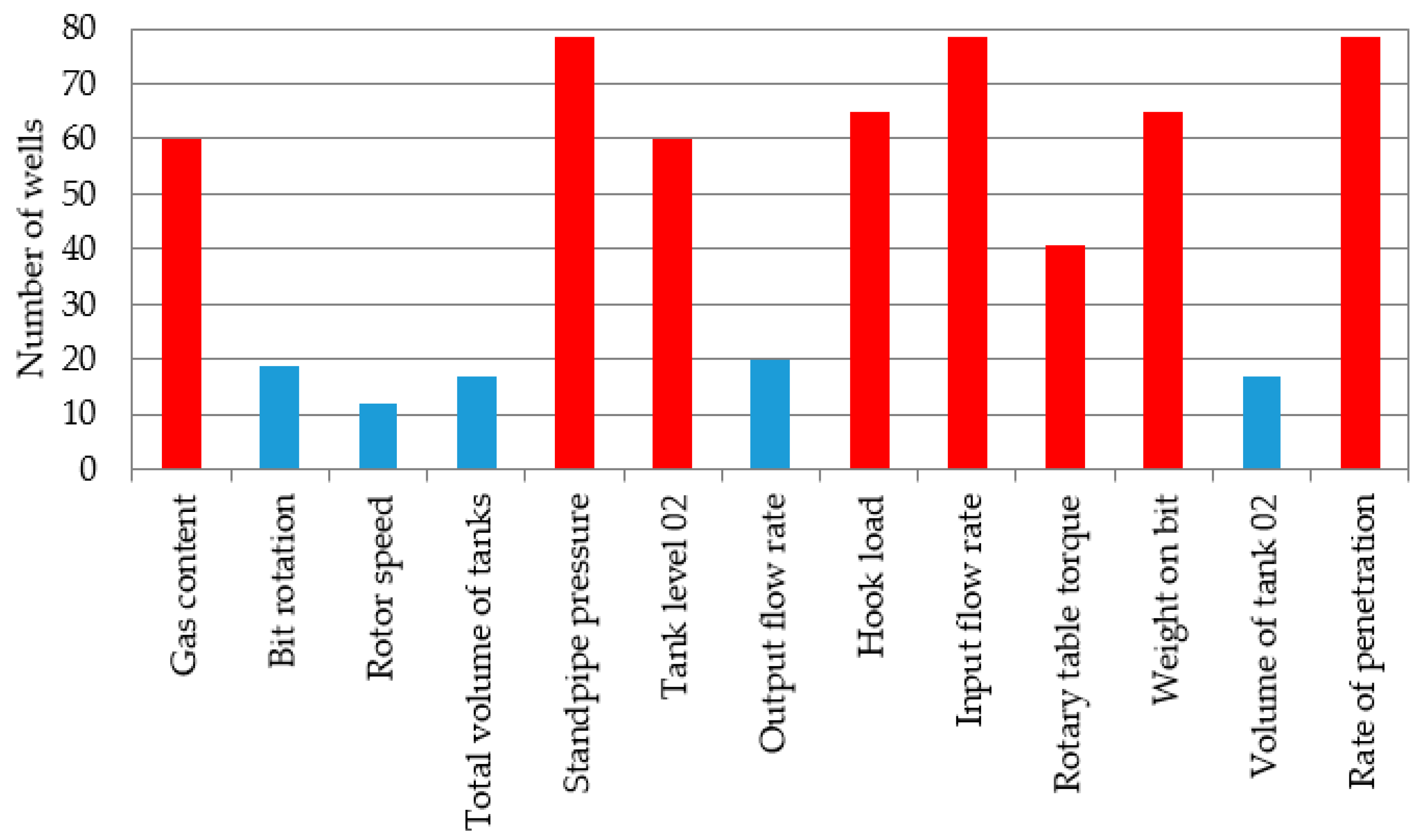
For further analysis, all drilling parameters that were recorded for each well were considered. The analysis of the data showed that not all the wells from the sample have the same number of corresponding recorded drilling parameters. Some wells recorded the minimum number of parameters. We would like to note that drilling reports were provided for 67 wells, but the files with the recorded drilling parameters were provided for 78 wells. Therefore, data representing 78 wells were analyzed. For a wide analysis of the drilling parameters recorded on the wells, reports from 78 wells were taken into account. It can be seen from Figure 4 that only eight parameters are the most commonly reported for all wells; these are highlighted in red. Additionally, these parameters will be used as input parameters for the classification of complications.
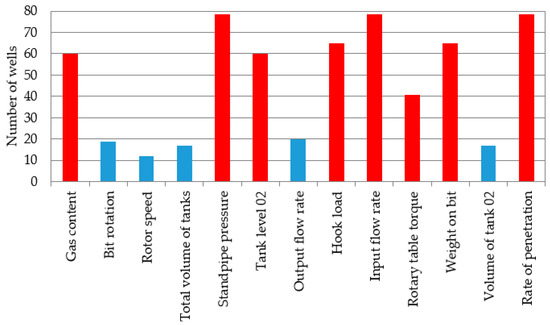
Figure 4.
Drilling parameters analyzed for wells.
After the work was conducted, for the three wells in which the DPs were plotted, the recorded drilling parameters were plotted. The graphs were constructed using the Python programming language, Figure 5, Figure 6 and Figure 7.
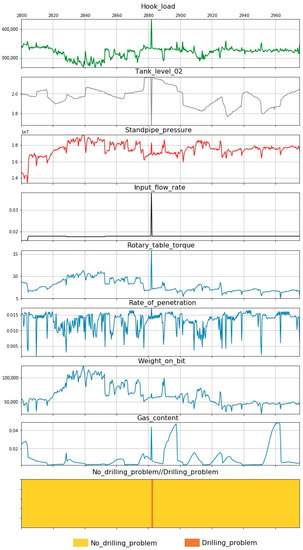
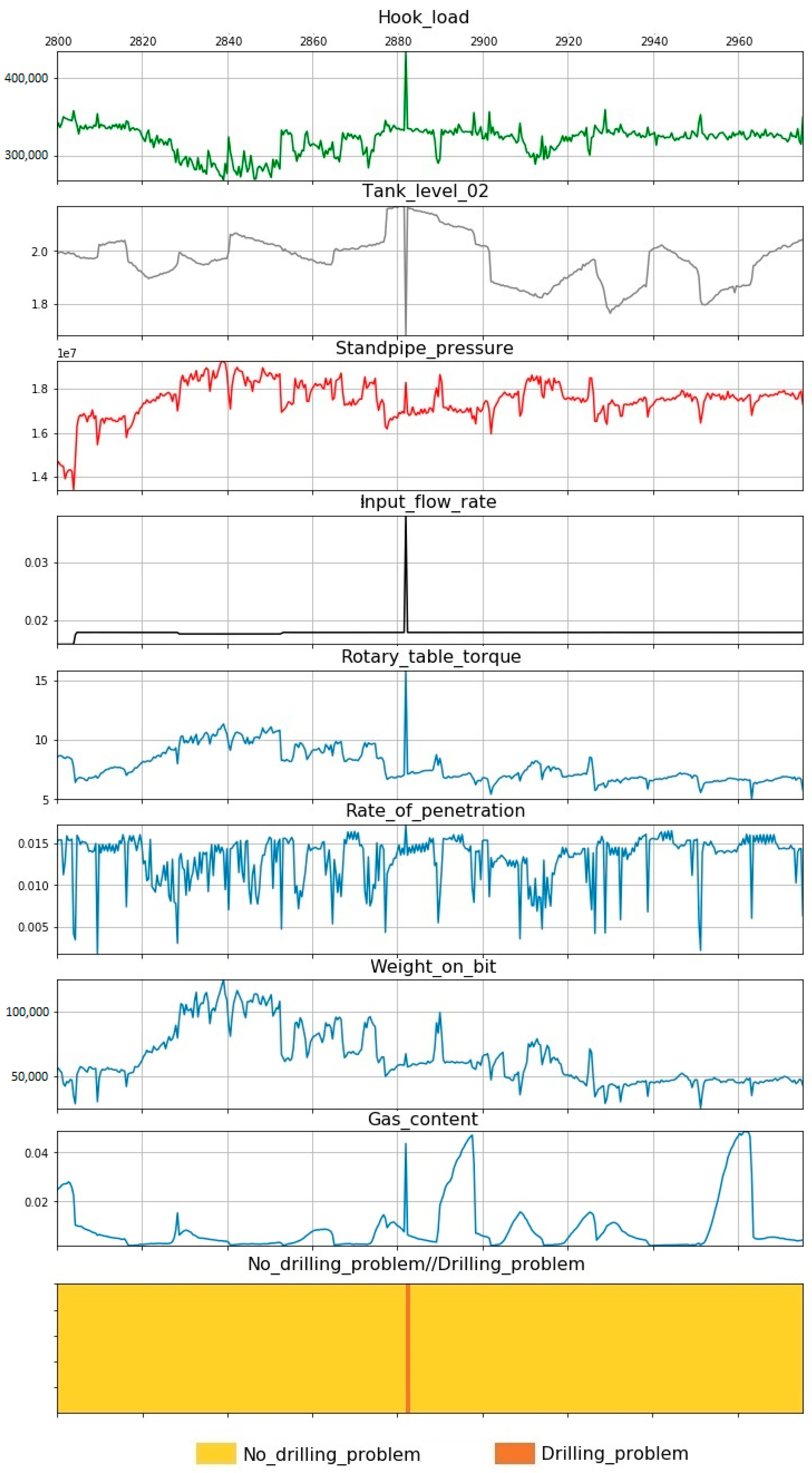
Figure 5.
Drilling problem at well 1—borehole instability, drilling parameters versus time.
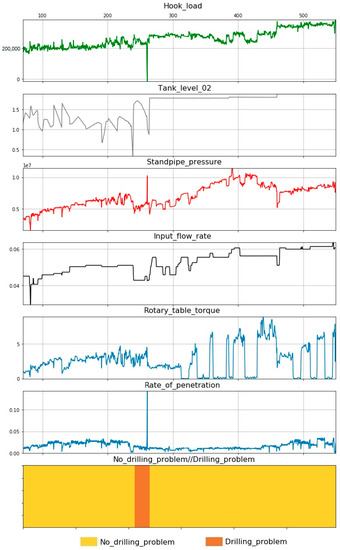
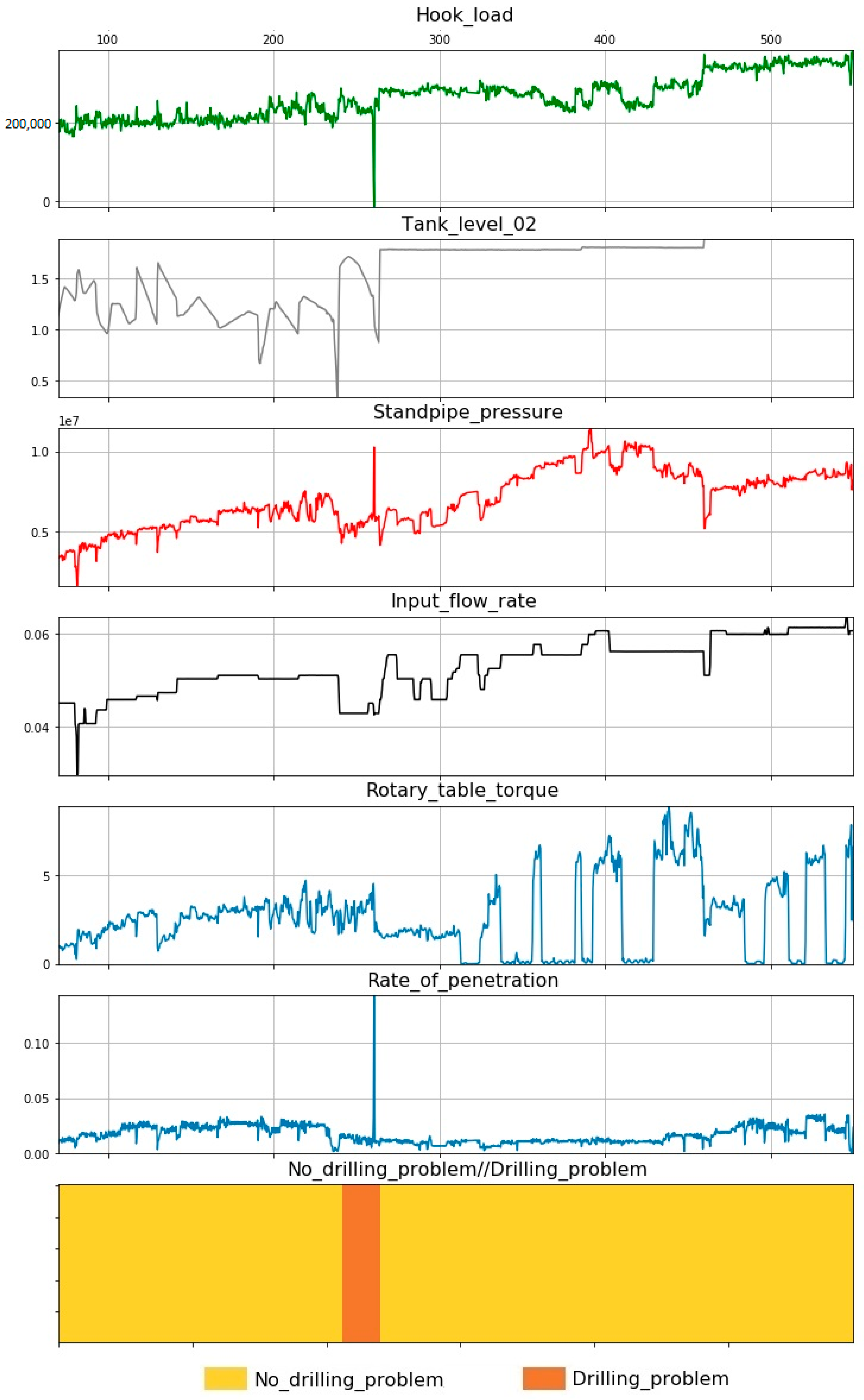
Figure 6.
Drilling problem at well 2—circulation loss, drilling parameters versus time.
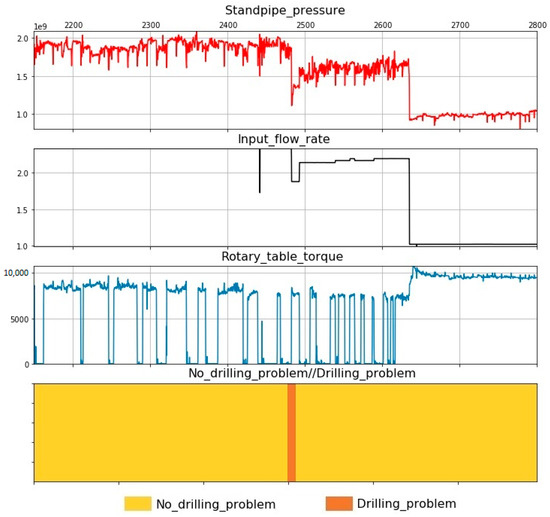
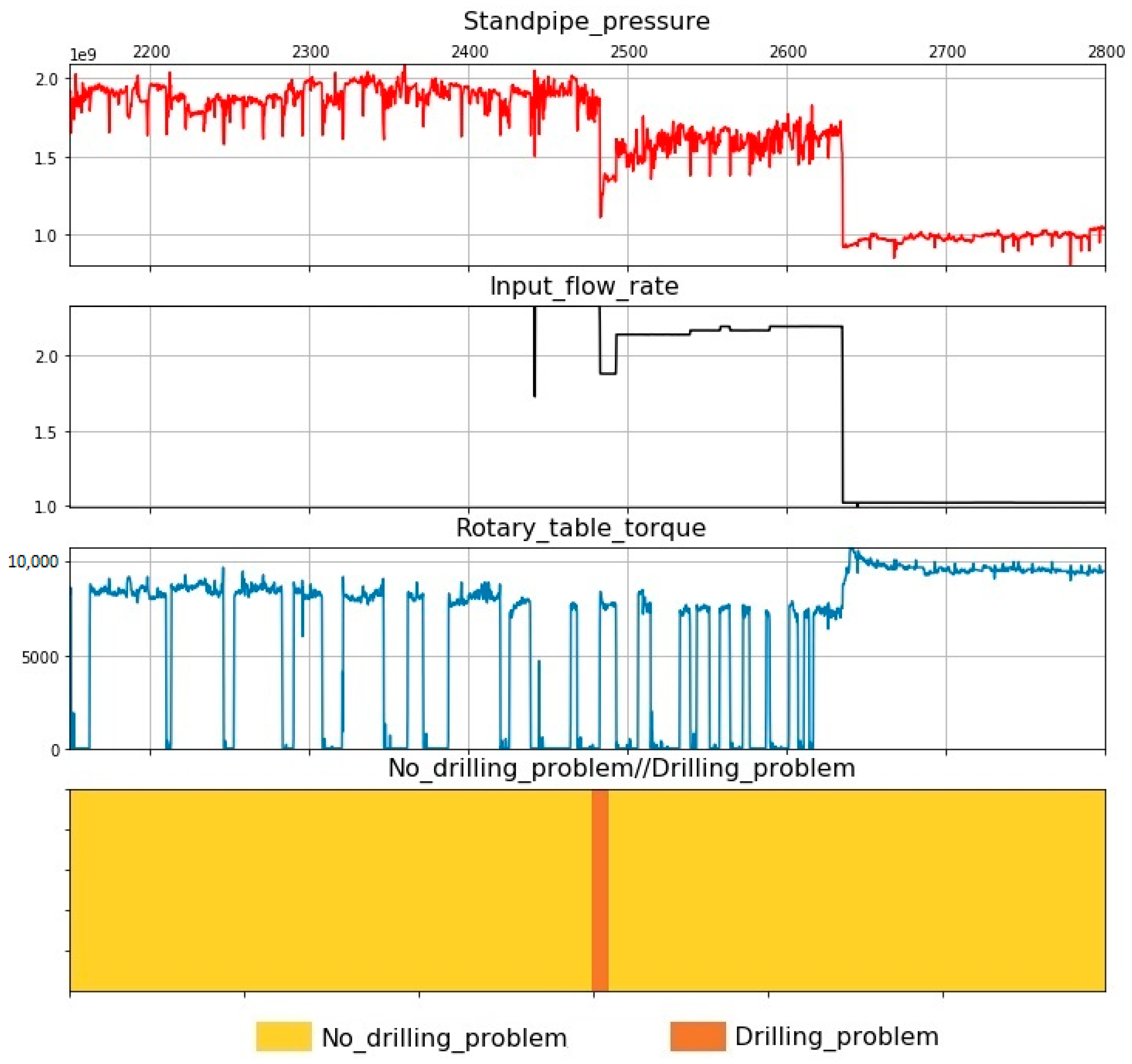
Figure 7.
Drilling problem at well 3—circulation loss, drilling parameters versus time.
Well 1. The DP was associated with borehole instability due to technical water entering at a depth of 2882 m (Figure 5). It can be noted that this problem was accompanied by steep changes in drilling parameters. In particular, the value of the hook load, rotary table torque, etc., steeply increased. To eliminate this problem, the drilling crew spent 231 hours working on it.
Well 2. During well drilling, in the interval 239–263 m, the drilling fluid was lost at a volume of 40 m3 (Figure 6). A total of 7.1 hours of unproductive time were spent on solving this problem. It is worth noting that the graph clearly shows that during the loss, circulation significantly decreased the level of the fluid capacity to mud tank № 2. A mud tank is an open-top container, typically made of square steel tubes and steel plates, to store drilling fluid on a drilling rig. They are also called mud pits, as they were once simple pits in the ground.
Well 3. When drilling to 2493 m, the drilling fluid was lost. The total loss was 55 m3 (Figure 7). To eliminate the complication, colmatage fluid was injected. The total time taken to combat the DP was 27.9 hours. This well is one of those that did not record the complete list of required drilling parameters.
4. Results
According to the algorithms of machine training given in the previous chapter, calculations were performed to classify (forecast) the problems in the drilling process. For calculations, the Python programming language and the scikit-learn library were used.
The percentage of training and test samples among the data was set as 65/35%, respectively. The training sample is a sample based on which the chosen algorithm adjusts the dependency model. The test sample is the sample by which the accuracy of the model used is checked. The following drilling parameters were used as input parameters:
- Standpipe pressure;
- Tank level 02;
- Input flow rate;
- Hook load;
- Rotary table torque;
- Rate of penetration;
- Weight on bit;
- Gas content.
As a result of the calculations, the following metrics were obtained, for the subsequent detection of the most accurate model.
Table 2 shows that the following algorithms of machine learning (ML) have the highest values of the metrics: decision tree; random forest; gradient boosting (GB).

Table 2.
Metrics by model.
Next, we considered the number of correct and incorrect assumptions in the calculation of algorithms. Table 3 presents the case for situations where there are no problems while drilling, and in Table 4, the classification of problems while drilling is shown. The goal is to see how the algorithm can misclassify the drilling process. “Right” is the number of correctly predicted values; “False” is the number of misplaced predictions when drilling without a problem being recognized. From the data presented, it can be seen that the greatest number of correct and accurate classifications of situations is obtained using the ML method of gradient boosting (GB). GB allowed, with the lowest number of errors, classifying the complication from the available dataset.

Table 3.
Accuracy of prediction of a normal situation.

Table 4.
Accuracy of prediction of a problem situation.
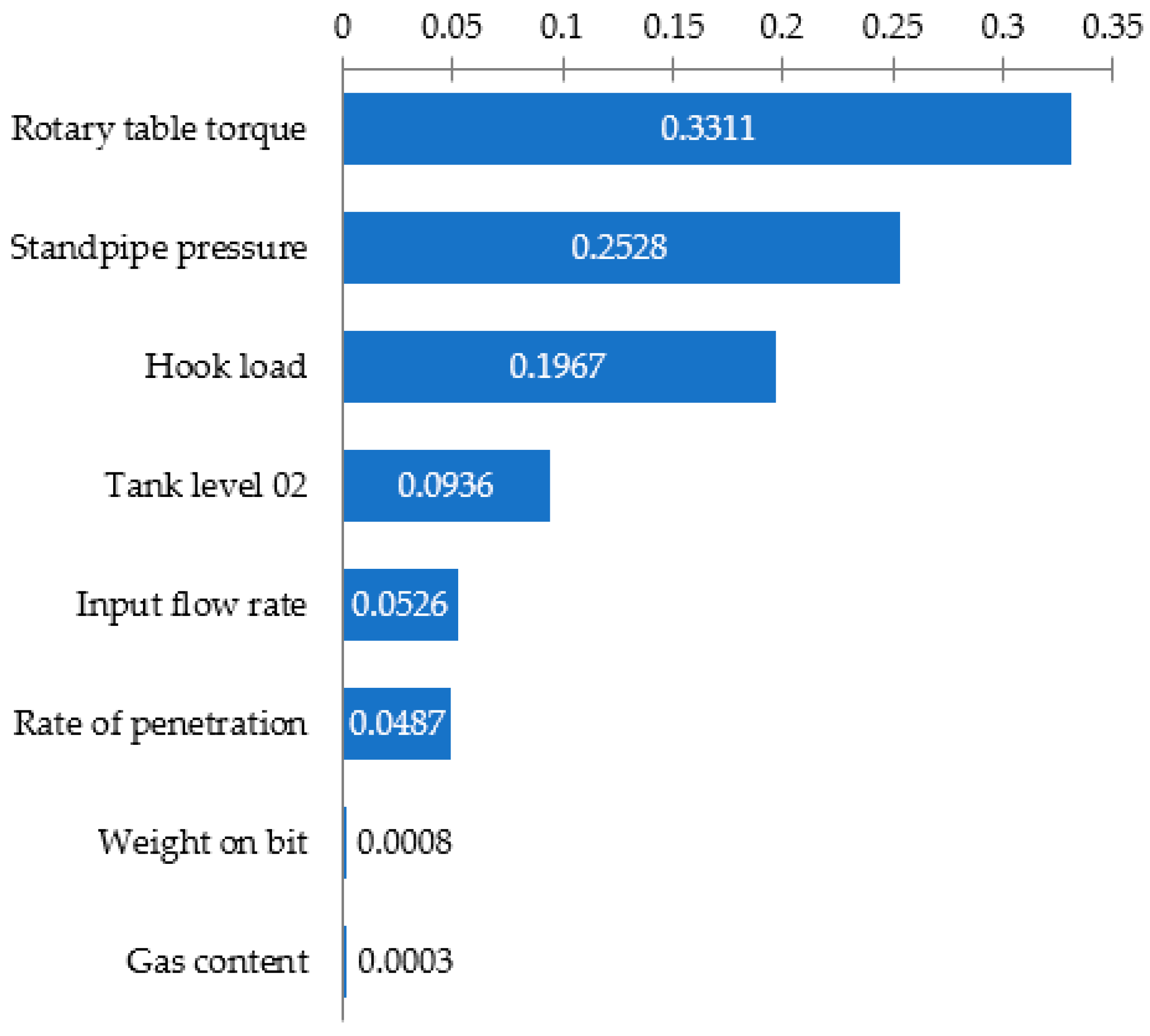
Then, a sensitivity analysis was performed (Figure 8), when the drilling parameters were removed from the gradient boosting, in turn, by their weight coefficients from the smallest to the largest. This allowed understanding how many parameters at the input are needed in this situation for the correct operation of gradient boosting. It was established that when the parameters such as “Gas content”, “Weight on bit”, and “Rate of penetration” are removed from the model, the system classifies the drilling problems with the same accuracy. Accordingly, it can be concluded that this algorithm, in the event of an emergency situation, can classify drilling problems according to the five available parameters without a loss of accuracy: “Rotary table torque”, “Standpipe pressure”, “Hook load”, “Tank level 02”, and “Input flow rate”.
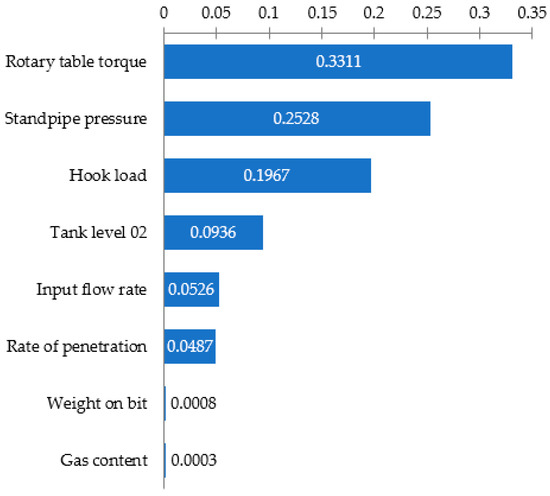
Figure 8.
Feature importance for gradient boosting.
5. Discussion
Based on the results of this work, an algorithm of gradient boosting is capable of recognizing and classifying complications in the process of drilling wells better than other algorithms. This algorithm has the highest value of the test metrics and the greatest number of correct and accurate classifications. The algorithm returned the correct prediction of a normal situation 3917 times out of 3917, and the correct prediction of a problem situation 42 times out of 45. It can be argued that using the gradient boosting algorithm while drilling wells will help, in terms of time, in assisting with the drilling process and prevent high expenses for rig downtime and equipment repair. The program will signal a possible problem. It is worth noting that in this work, we did not use too much initial data. Therefore, it is recommended to increase the efficiency of the model, in order to test it on a higher number of initial data.
Worth noting is another significant plus. The algorithm, in addition to the classification of DPs, accurately determines the standard drilling mode (without problem). This minimizes the possibility of triggering false alarms, which will also save drilling time. False alarms are also one of the problems when drilling wells, which take up a significant amount of time and money. Additionally, if new technologies are introduced by companies in oil and gas production, this will allow businesses to save their costs. For example, in the construction of a drilling rig that reaches hundreds of millions of dollars, even a 5% reduction in planning time can have a significant positive impact on the company’s profits [65].
Nybø [66,67] solved a similar problem. In this work, a hybrid system was developed that includes a physical model and AI. Together, they allow one to recognize the problems when drilling much better than individually. Additionally, in this paper, the problem of the small number of studies on the introduction of methods of ML in the drilling sector was addressed. The authors of this work are also convinced that this integration of machines and people will significantly increase the efficiency of drilling wells.
Based on the results of the analysis using eight algorithms, it can be seen that the logistic regression and support vector method show metrics equal to zero for the recognition of complications. Perhaps these values are associated with the small number of initial data of complications. Therefore, these algorithms show such poor results. As noted above, for further work, it is recommended to experiment with a much larger number of initial data.
6. Conclusions
In trying to avoid the problems in the drilling process, their classification and timely elimination remain an urgent problem to date. The aim of this work was to create a program capable of recognizing and classifying drilling problems (DPs). Following the results of this work, the following achievements were made:
- Based on the literature review, a wide application of AI in drilling was shown, from the creation of training programs to the prediction of the rate of penetration.
- During the analysis of the initial data, wells with problems that were encountered during drilling were identified. To model the presented DPs, a computer model was set up.
- During the analysis of the drilling reports, a list of the main parameters was compiled, which participated as input for the model: standpipe pressure; tank level; input flow rate; hook load; rotary table torque; rate of penetration; weight on bit; gas content.
- Of the eight methods of machine learning (ML), the GB method was chosen. This algorithm showed a high-performance precision, recall, and F-score.
- For the GB method, the parameters that make the greatest contribution to the operation of the algorithm were established using the feature importation parameter. These are the rotary table torque, standpipe pressure, and hook load.
- During the GB analysis, it was established that in the case of removing parameters such as gas content, the model continued to work without changing the accuracy of the classification of the DPs.
- Although the ultimate goal of this work was to teach the program to classify the problems in the drilling process, in the future, it is necessary to consider the possibility of predicting the drilling problems in real time, for example, using time series. Such a model will avoid problems, preventing high costs.
- In the future, it is necessary to train the algorithm on a larger number of data on wells with problems. This will expand the application of the program and elucidate how to classify various types of drilling problems.
- It will be useful to test the model by specifying not only drilling parameters but also geophysical logging data, on the input. This will allow models to take into account such a parameter as lithology. Depending on the different rocks, the log data will show the different behaviors of the curves.
- It is also recommended to use geomechanical parameters of the formation as input data. These data will allow predicting possible problem areas of the well in advance that are prone to collapse.
Author Contributions
Conceptualization, A.G. and I.B.; formal analysis, S.S.; investigation, A.G.; methodology, A.G. and S.I.; project administration, A.G. and S.I.; resources, I.B. and O.T.G.; software, A.G.; supervision, O.T.G.; validation, A.G.; visualization, S.S.; writing—original draft, S.I.; writing—review and editing, I.B. and O.T.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to their storage in private networks.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AI | Artificial intelligence |
| DPs | Drilling problems |
| GB | Gradient boosting |
| ML | Machine learning |
| PID | Proportional–integral–differential |
| ROP | Process rate of penetration |
| RSS | Rotary steerable system |
References
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.T. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 1999, 292, 195–202. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.M.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, H.; Engelbrecht, J.; Brunak, S.; Heijne, G.V. Identification of prokaryotic and eukaryotic signal peptides and prediction of their cleavage sites. Protein Eng. 1997, 10, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Engergy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Almeida, T.L.P.; Passos, B.A.F.; Costa, J.L.S.; Andrade, A.J.N. Identifying clay mineral using angular competitive neural network: A machine learning application for porosity estimative. J. Pet. Sci. Eng. 2021, 200, 108303. [Google Scholar] [CrossRef]
- Hajizadeh, Y. Machine learning in oil and gas; a SWOT analysis approach. J. Pet. Sci. Eng. 2019, 176, 661–663. [Google Scholar] [CrossRef]
- Hanga, K.M.; Kovalchuk, Y. Machine learning and multi-agent systems in oil and gas industry applications: A survey. Comput. Sci. Rev. 2019, 34, 100191. [Google Scholar] [CrossRef]
- Nima, M.; Hamzeh, G.; David, A.W.; Mohammad, M.; Shadfar, D.; Sina, R.; Alireza, S.; Amirafzal, K.S. A geomechanical approach to casing collapse prediction in oil and gas wells aided by machine learning. J. Pet. Sci. Eng. 2021, 196, 107811. [Google Scholar]
- Mohamed, L.; Mohamed, S.; Sofiène, T. Detection and sizing of metal-loss defects in oil and gas pipelines using pattern-adapted wavelets and machine learning. Appl. Soft Comput. 2017, 52, 247–261. [Google Scholar]
- Sina, R.; Mohammad, M.; Hamzeh, G.; David, A.W.; Nima, M.; Jamshid, M.; Shadfar, D. Determination of bubble point pressure & oil formation volume factor of crude oils applying multiple hidden layers extreme learning machine algorithms. J. Pet. Sci. Eng. 2021, 202, 108425. [Google Scholar]
- Hao, C.; Chao, Z.; Ninghong, J.; Ian, D.; Shenglai, Y.; Yong, Z.Y. A machine learning model for predicting the minimum miscibility pressure of CO2 and crude oil system based on a support vector machine algorithm approach. Fuel 2021, 290, 120048. [Google Scholar]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A.; Potapov, A.V. Evaluation of bulk material behavior control method in technological units using dem. CIS Iron Steel Rev. 2020, 20, 3–6. [Google Scholar] [CrossRef]
- Litvinenko, V.S.; Tsvetkov, P.S.; Molodtsov, K.V. The social and market mechanism of sustainable development of public companies in the mineral resource sector. Eurasian Min. 2020, 2020, 36–41. [Google Scholar] [CrossRef]
- Kamatov, K.A.; Buslaev, G.V. Solutions for drilling efficiency improvement in extreme geological conditions of Timano-Pechora region. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 26 October 2015; pp. 1–10. [Google Scholar]
- Charfeddine, L.; Barkat, K. Short-and long-run asymmetric effect of oil prices and oil and gas revenues on the real GDP and economic diversification in oil-dependent economy. Energy Econ. 2020, 86, 104680. [Google Scholar] [CrossRef]
- Aleksandrova, T.; Aleksandrov, A.; Nikolaeva, N. An investigation of the possibility of extraction of metals from heavy oil. Miner. Process. Extr. Metall. Rev. 2017, 38, 92–95. [Google Scholar] [CrossRef]
- Nevskaya, M.A.; Seleznev, S.G.; Masloboev, V.A.; Klyuchnikova, E.M.; Makarov, D.V. Environmental and business challenges presented by mining and mineral processing waste in the Russian Federation. Minerals 2019, 7, 445. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Leusheva, E.; Morenov, V.; Li, L.; Jiang, G.; Fang, C.; Zhang, L.; Zheng, S.; Yu, Y. Influence of polymer reagents in the drilling fluids on the efficiency of deviated and horizontal wells drilling. Energies 2020, 13, 4704. [Google Scholar] [CrossRef]
- Gang, H.; Zhaoqiang, X.; Guorong, W.; Bin, Z.; Yubing, L.; Ye, L. Forecasting energy consumption of long-distance oil products pipeline based on improved fruit fly optimization algorithm and support vector regression. Energy 2021, 224, 120153. [Google Scholar]
- Yurak, V.V.; Dushin, A.V.; Mochalova, L.A. Vs sustainable development: Scenarios for the future. J. Min. Inst. 2020, 242, 242–247. [Google Scholar] [CrossRef]
- Kondrasheva, N.K.; Rudko, V.A.; Kondrashev, D.O.; Gabdulkhakov, R.R.; Derkunskii, I.O.; Konoplin, R.R. Effect of delayed coking pressure on the yield and quality of middle and heavy distillates used as components of environmentally friendly marine fuels. Energy Fuels 2019, 33, 636–644. [Google Scholar] [CrossRef]
- Kondrasheva, N.K.; Rudko, V.A.; Ancheyta, J. thermogravimetric determination of the kinetics of petroleum needle coke formation by decantoil thermolysis. ACS Omega 2020, 5, 29570–29576. [Google Scholar] [CrossRef] [PubMed]
- Seçkin, K.; Aytaç, A.; Stelios, B.; Wasim, A. A new forecasting model with wrapper-based feature selection approach using multi-objective optimization technique for chaotic crude oil time series. Energy 2020, 212, 118750. [Google Scholar]
- Hebert, D.; Misiti, A. The Growing Role of Artificial Intelligence in Oil and Gas. Available online: https://insights.globalspec.com/article/2772/the-growing-role-of-artificial-intelligence-in-oil-and-gas (accessed on 23 April 2021).
- Zhan, S.; Rodiek, J.; Heuermann-Kuehn, L.E.; Baumann, J. Prognostics health management for a directional drilling system. In Proceedings of the Prognostics and System Health Management Conference, Shenzhen, China, 24–25 May 2011; pp. 1–7. [Google Scholar]
- Wang, Y. Drilling Hydraulics Optimization Using Neural Networks; University of Louisiana at Lafayette Press: Lafayette, LA, USA, 2015. [Google Scholar]
- Camci, F.; Chinnam, R.B. Dynamic bayesian networks for machine diagnostics: Hierarchical hidden Markov models vs. competitive learning. In Proceedings of the International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; pp. 1–6. [Google Scholar]
- Yang, Z.R.; Yang, Z. Comprehensive Biomedical Physics, 1st ed.; Elsevier Science & Technology: Stockholm, Sweden, 2004. [Google Scholar]
- Lind, Y.B.; Kabirova, A.R. Artificial neural networks in drilling troubles prediction. In Proceedings of the SPE Russian Oil and Gas Exploration & Production Technical Conference and Exhibition, Moscow, Russia, 14–16 October 2014; pp. 1–7. [Google Scholar]
- Al-yami, A.S.H.; Schubert, J. Systems and Methods for Expert Systems for Well Completion using Bayesian Decision Models (BDNs), Drilling Fluids Types, and Well Types. Available online: https://hdl.handle.net/1969.1/177120 (accessed on 23 April 2021).
- Jahanbakhshi, R.; Keshavarzi, R.; Jafarnezhad, A. Real-time prediction of rate of penetration during drilling operation in oil and gas wells. In Proceedings of the Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; pp. 1–9. [Google Scholar]
- Monazami, M.; Hashemi, A.; Shahbazian, M. Drilling rate of penetration prediction using artificial neural network: A case study of one of Iranian southern oil fields. J. Oil. Gas. Bus. 2012, 6, 21–31. [Google Scholar]
- Amer, M.M.; Dahab, A.S.; El-Sayed, A.H. An ROP predictive model in nile delta area using artificial neural networks. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017; pp. 1–11. [Google Scholar]
- Gidh, Y.; Purwanto, A.; Bits, S. Artificial neural network drilling parameter optimization system improves ROP by predicting/managing bit wear. In Proceedings of the SPE Intelligent Energy International, Utrecht, The Netherlands, 27–29 March 2012; pp. 1–13. [Google Scholar]
- Rashidi, B.; Hareland, G.; Nygaard, R. Real-time drill bit wear prediction by combining rock energy and drilling strength concepts. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 3–6 November 2008; pp. 1–9. [Google Scholar]
- Valisevich, A.; Ruzhnikov, A.; Bebeshko, I.; Moreno, R.; Zhentichka, M.; Bits, S. Drillbit optimization system: Real-time approach to enhance rate of penetration and bit wear monitoring. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 26–28 October 2015; pp. 1–14. [Google Scholar]
- Dashevskiy, D.; Dubinsky, V.; Macpherson, J.D. Application of neural networks for predictive control in drilling dynamics. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; pp. 1–9. [Google Scholar]
- GirirajKumar, S.M.; Jayaraj, D.; Kishan, A.R. PSO based tuning of a PID controller for a high-performance drilling machine. Int. J. Comput. Appl. 2010, 1, 12–18. [Google Scholar] [CrossRef]
- Lind, Y.B.; Samsykin, A.V.; Galeev, S.R. Information and analytical system for prevention of drilling fluid loss. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 26–28 October 2015; pp. 1–12. [Google Scholar]
- Hegde, C.; Wallace, S.; Gray, K. Real Time prediction and classification of torque and drag during drilling using statistical learning methods. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, VA, USA, 13–15 October 2015; pp. 1–13. [Google Scholar]
- Okpo, E.E.; Dosunmu, A.; Odagme, B.S. Artificial neural network model for predicting wellbore instability. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2–4 August 2016; pp. 1–10. [Google Scholar]
- Unrau, S.; Torrione, P.; Hibbard, M.; Smith, R.; Olesen, L.; Watson, J. Machine learning algorithms applied to detection of well control events. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017; pp. 1–10. [Google Scholar]
- Shchepetov, O.A. System classification of failures in drilling. Vestn. Astrakhan State Tech. Univ. Ser. Manag. Comput. Sci. Inform. 2009, 2, 36–42. [Google Scholar]
- Aldred, W.; Plumb, D.; Bradford, I.; Cook, J.; Gholkar, V.; Cousins, L.; Minton, R.; Fuller, J.; Goraya, S.; Tucker, D. Managing drilling risk. Oilfield Rev. 1999, 11, 2–19. [Google Scholar]
- Dvoynikov, M.V. Research on technical and technological parameters of inclined drilling. J. Min. Inst. 2017, 223, 86–92. [Google Scholar]
- Litvinenko, V.S.; Dvoynikov, M.V. Methodology for determining the parameters of drilling mode for directional straight sections of well using screw downhole motors. J. Min. Inst. 2020, 41, 105–112. [Google Scholar] [CrossRef]
- Logistical Regression for Kettles: Detailed Explanation. Available online: https://www.machinelearningmastery.ru/logistic-regression-for-dummies-a-detailed-explanation-9597f76edf46/ (accessed on 2 July 2021).
- Vorontsov, K.V. Lectures on Linear Classification Algorithms; Moscow Institute of Physics and Technology Press: Moscow, Russia, 2009. [Google Scholar]
- Commonly Used Machine Learning Algorithms (with Python and R Codes). Available online: https://www.analyticsvidhya.com/blog/2017/09/common-machine-learning-algorithms/ (accessed on 2 July 2021).
- Ray, S. Easy Steps to Learn Naive Bayes Algorithm with Codes in Python and R. Available online: https://www.analyticsvidhya.com/blog/2017/09/naive-bayes-explained/ (accessed on 23 April 2021).
- Piryonesi, S.M.; Tamer, E.E. Role of data analytics in infrastructure asset management: Overcoming data size and quality problems. J. Transp. Eng. Part B Pavements 2020, 146, 1–7. [Google Scholar] [CrossRef]
- Decision Tree Classifier. Available online: http://mines.humanoriented.com/classes/2010/fall/csci568/portfolio_exports/lguo/decisionTree.html (accessed on 2 July 2021).
- Vorontsov, K.V. Lectures on the Support Vector Machine; Moscow Institute of Physics and Technology Press: Moscow, Russia, 2007. [Google Scholar]
- Chistyakov, S.P. Random forest. Proc. Karelian Res. Cent. Russ. Acad. Sci. 2013, 1, 117–136. [Google Scholar]
- Vorontsov, K.V. Mathematical Methods of Learning by Precedents: A Course of Lectures; Moscow Institute of Physics and Technology Press: Moscow, Russia, 2009. [Google Scholar]
- Matthew, M. More Steps to Mastering Machine Learning with Python. Available online: http://www.kdnuggets.com/2017/03/seven-more-steps-machine-learning-python.html (accessed on 23 April 2021).
- McCulloch, U.S.; Pitts, V. Logical Calculus of Ideas Relating to Nervous Activity; Foreign Literature Publishing House: Moscow, Russia, 1956. [Google Scholar]
- Labintcev, E. Metrics in the Problems of Machine Learning. Available online: https://habrahabr.ru/company/ods/blog/328372/ (accessed on 23 April 2021).
- Nelson, A. Driving Efficiency in the Oil and Gas Industry. Available online: https://biarri.com/driving-efficiency-oil-gas-industry/ (accessed on 23 April 2021).
- Nybø, R. Efficient Drilling Problem Detection; Norwegian University of Science and Technology Press: Trondheim, Norway, 2009. [Google Scholar]
- Nybø, R.; Sui, D. Closing the integration gap for the next generation of drilling decision support systems. In Proceedings of the SPE Intelligent Energy Conference & Exhibition, Utrecht, The Netherlands, 1–3 April 2014; pp. 1–10. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).