Abstract
Let G be a graph with no isolated vertex and let be the open neighbourhood of . Let be a function and for every . We say that f is a strongly total Roman dominating function on G if the subgraph induced by has no isolated vertex and for every . The strongly total Roman domination number of G, denoted by , is defined as the minimum weight among all strongly total Roman dominating functions f on G. This paper is devoted to the study of the strongly total Roman domination number of a graph and it is a contribution to the Special Issue “Theoretical Computer Science and Discrete Mathematics” of Symmetry. In particular, we show that the theory of strongly total Roman domination is an appropriate framework for investigating the total Roman domination number of lexicographic product graphs. We also obtain tight bounds on this parameter and provide closed formulas for some product graphs. Finally and as a consequence of the study, we prove that the problem of computing is NP-hard.
1. Introduction
Let G be a simple graph with no isolated vertex. Given a vertex , and denote the open neighbourhood and the closed neighbourhood of v in G, respectively. The order, minimum degree and maximum degree of G will be denoted by , and , respectively. As usual, given a set and a vertex , the external private neighbourhood and the internal private neighbourhood of v with respect to D is defined to be and , respectively.
Domination in graphs is a classical research topic that has experienced rapid growth since its introduction. A set is said to be a dominating set of G if for every . Let be the set of dominating sets of G. The domination number of G is defined to be the following.
We define a -set as a set with . The same agreement will be assumed for optimal parameters associated with other characteristic functions or sets of a graph. For more information on domination and its variants in graphs, we suggest the books [1,2,3,4].
An important domination variant in graph, which may be the most studied, is the total domination number. A total dominating set of G is a set such that for every . Let be the set of total dominating sets of G. The total domination number of G is defined to be the following.
More information on total domination in graphs can be found in the works [5,6,7]. Let G be a graph with no isolated vertex and a function. For every , we define . We will use the unified notation to identify the function f with the subsets , , associated with it. Given a set , we define and, particularly, we define the weight of f as One of the domination topics widely studied by research is the Roman domination, which is a domination variant arising from some historical roots coming from the ancient Roman Empire [8]. A function is a Roman dominating function on G if for every vertex . The Roman domination number of G denoted by is the minimum weight among all Roman dominating functions on G. For more information on Roman domination in graphs, we suggest the referenced works [9,10,11,12].
One of the classical variants of Roman domination is the so-called total Roman domination. This article deals precisely with this style of domination. A total Roman dominating function (TRDF) on a graph G with no isolated vertex is a Roman dominating function such that . The minimum weight among all TRDFs on G is the total Roman domination number of G and is denoted as . This concept was introduced in 2013 by Liu and Chang [13] and formally presented and deeply studied three years later by Abdollahzadeh Ahangar et al. [14]. Subsequently, several researchers have continued with the study of this parameter. For instance, in [15,16,17], some combinatorial results were presented. In [18,19,20,21], constructive characterizations in trees related with this domination parameter were provided. In [22,23,24,25], studies of the total Roman domination number on graph products were carried out. In particular, we want to highlight the following closed formula provided in [25] for the case of lexicographic product graphs.
For any graph G with no isolated vertex and any nontrivial graph H, the total Roman domination number of the lexicographic product graph is given by the following [25]:
where As it can be observed, the authors [25] showed that the behavior of depends on two domination parameters of graphs, namely the well-known total domination number and the incipient parameter . In that regard, the authors exposed some results on this last parameter and they raised the challenge of conducting a detailed study of the topic.
In this paper, we continue with the study of this novel parameter although it will be carried out by considering a different approach. In Section 2 we define a new variant of total Roman domination, namely strongly total Roman domination number and denoted by . We then show that this variant is an appropriate framework to investigate the parameter of a graph. Section 3 is devoted to providing closed formulas for some product graphs. As a consequence of the study, we conclude this section by showing that the problem of computing is NP-hard. Finally, in Section 4 we obtain tight bounds on the strongly total Roman domination number of a graph and we discuss the tightness of these bounds.
We assume that the reader is familiar with the basic concepts and terminology of graph domination. If this is not the case, then we suggest the textbooks [1,4]. For the remainder of the article, definitions will be introduced whenever a concept is required.
2. Strongly Total Roman Dominating Functions
The concept of a total Roman dominating function on a graph is associated with the “total domination” property, i.e., this kind of functions requires that each vertex has a neighboring vertex with a positive label assigned to it. However, some vertices have a “special property”, which in some cases others do not have. In particular, vertices with label zero must always have a neighbor with label two, but it is not always the case that a vertex with label one satisfies this property. In relation to the above situation, we introduce a “stronger” version of the standard total Roman domination below.
A strongly total Roman dominating function (STRDF) on a graph G with no isolated vertex is a total Roman dominating function with the additional property that is a dominating set of G. The minimum weight among all STRDFs on G is the strongly total Roman domination number of G and is denoted .
To illustrate this concept, we consider the graph G shown in Figure 1. For this example, .
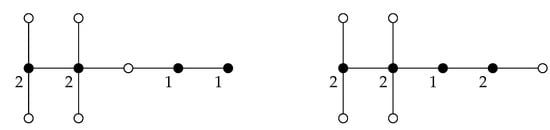
Figure 1.
The function on the left is a -function, while the function on the right is a -function.
Now, we proceed to show that this new domination variant is an appropriate framework to investigate the parameter .
Theorem 1.
For any graph G with no isolated vertex,
Proof.
Let be a -function. By definition we have that and . Therefore, the following obtains.
On the other side, let such that , and . Notice that the function , defined by , and , is a STRDF on G. Hence, , which completes the proof. □
To end this section and as a consequence of previous theorem, we show the basic results given in [25] for the strongly total Roman domination number.
Theorem 2.
Ref. [25] For any graph G with no isolated vertex,
Furthermore,
- (i)
- if and only if there exists a -function such that is dominating set of G.
- (ii)
- if and only if there exists a -set that contains some -set.
3. Exact Formulas for Some Graph Products and Computational Complexity
In order to show the tightness of several bounds and relationships, in this section we obtain the strongly total Roman domination number concerning a well-know families of graphs. We emphasize that we will use the notation , , and for complete graphs, star graphs, complete bipartite graphs and the wheel graphs of order n, respectively.
The join graph of the graphs G and H is the graph with vertex set and edge set .
Theorem 3.
For any graphs G and H,
Proof.
We first notice that . Now, we observe that if and only if or . Therefore, by Theorem 2 we deduce that if and only if or , which completes the proof. □
The following corollary is an immediate consequence of the theorem above.
Corollary 1.
The following equalities hold for any integer .
- (i)
- (ii)
- If such that , then
Let G be a graph with no isolated vertex and H is any graph. The corona product graph is defined as the graph obtained from G and H, by taking one copy of G and copies of H and joining by an edge every vertex from the ith-copy of H with the ith-vertex of G. Next, we study the strongly total Roman domination number of any corona product graph.
Theorem 4.
For any graph G with no isolated vertex and any graph H,
Proof.
First, we notice that . Hence, Theorem 2 leads to the equality Therefore, the proof is complete. □
Let G be a graph with no isolated vertex and H a nontrivial graph. The lexicographic product of G and H is the graph for which the vertex set is and two vertices are neighbors if and only if or and .
Theorem 5.
Ref. [26] For any graph G with no isolated vertex and any nontrivial graph H,
We next show that the strongly total Roman domination number and the total Roman domination number coincide for lexicographic product graphs.
Theorem 6.
For any graph G with no isolated vertex and any nontrivial graph H,
Proof.
If , then the result immediately follows by applying Equation (1) and Theorems 2 and 5, i.e., we have the following.
From this moment on, we assume that . By Equation (1) and Theorems 1 and 2 we deduce that . We only need to prove that . Let be a -function and a -set. Notice that the function , defined by , and , is a STRDF on . Hence, which completes the proof. □
As shown in [27], the general optimization problem of computing the total domination number of a graph with no isolated vertex is NP-hard. Therefore, by Theorem 6 (considering the case ) we immediately obtain the analogous result for the strongly total Roman domination number.
Theorem 7.
The problem of computing the strongly total Roman domination number of a graph with no isolated vertex is NP-hard.
4. Primary Combinatorial Results
The first result of this section provides bounds for the strongly total Roman domination number in terms of the order of a graph. For this purpose, we need to recall the following well-known result.
Theorem 8.
Ref. [5] If G is a connected non-complete graph of order at least three, then G has a -set D such that every vertex satisfies or is adjacent to a vertex satisfying .
Theorem 9.
For any connected graph G of order at least three,
Furthermore,
- (i)
- if and only if .
- (ii)
- if and only if .
Proof.
The lower bound is straightforward. Now, we proceed to prove the upper bound. If G is isomorphic to a complete graph, then , as desired. From this moment, we assume that G is different of a complete graph. Let D be a -set which satisfies Theorem 8 and . Now, we consider the following sets.
Let us define as a function of minimum weight among all functions on G satisfying the following conditions.
- (a)
- .
- (b)
- .
- (c)
- for every vertex .
By (a), it is straightforward that . By (b) and (c) we deduce that every vertex in has a neighbor in . Now, let . By definition, and thus Theorem 8 results in . Hence, by (b). This implies that . Therefore, is a STRDF on G and thus .
We only need to prove that . Let . By definition, we have that and . Hence, by (a) and (c) we deduce that . Thus, the minimality of results in and it is straightforward that . Therefore, the following
is as required. Hence, the proof of the upper bound is complete.
We then proceed to prove (i). By Theorem 2 we deduce that if and only if . Hence, (i) follows.
Finally, we proceed to prove (ii). If , then Theorem 2 leads to . Conversely, if , then by (i) we deduce that . Thus, Theorem 2 results in . Therefore, (ii) follows. □
The upper bound above is tight. For instance, it is achieved for the graph G given in Figure 1. Moreover and as an immediate consequence of Theorems 2 and 9, it is also achieved for the graphs G with . This family is defined in [14].
We continue by providing additional upper bounds. As shown in Theorem 2, the strongly total Roman domination number is bounded from above by . Since , the next result improves this upper bound for any graph G with no isolated vertex. We need to introduce the following result.
Theorem 10.
Ref. [9] Let be a -function on a graph G with no isolated vertex such that is minimum. Then the following conditions hold.
- (a)
- for every vertex .
- (b)
- for any two different vertices .
Theorem 11.
For any graph G with no isolated vertex,
Proof.
Let be a -function such that is minimum. Hence, conditions (a) and (b) of Theorem 10 are satisfied. Now, we consider a function of minimum weight among all functions on G such that the following conditions are satisfied:
- (i)
- .
- (ii)
- for every vertex .
- (iii)
- for every vertex .
We proceed to prove that is a STRDF on G. By definitions of f and , it is straightforward that . Now, let . By (i) we deduce that . Moreover, if , then because . Otherwise, if , then (ii) results in . Hence, , which implies that is a STRDF on G, as desired. Thus, .
Now, let D be a -set. Hence, for every . In addition, notice that for every . Thus, by (ii) and (iii), conditions (a) and (b) of Theorem 10 and the minimality of , we deduce that From the inequalities above we obtain
Therefore, the proof is complete. □
The bound above is tight. For instance, it is achieved for any graph such that . In this case, Theorem 3 results in .
The following characterization is an immediate consequence of Theorem 11 and the well-known inequality .
Theorem 12.
Let G be a graph with no isolated vertex. Then if and only if and .
From Theorem 4 and the fact that we deduce that for any graph with no isolated vertex and any nontrivial graph . This previous equality chain shows that the condition is a necessary condition but is not sufficient to satisfy .
We continue the study by providing a new upper bound, which improves the classical inequality . We need to introduce some concepts and tools. For any -set D, let be a set of minimum cardinality such that . Observe that is not necessarily a -set. For instance, for the graph G given in Figure 2 we have that and . However, the set D of black-colored vertices is the only -set; moreover, the only dominating set that is a subset of D is D itself.
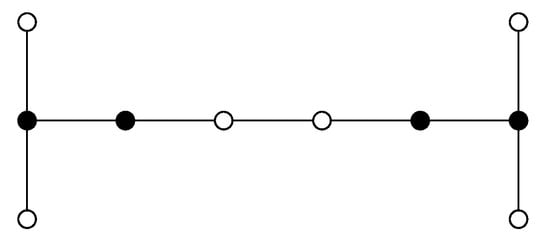
Figure 2.
The set of black-colored vertices is the only -set.
We define as the kernel of D. The maximum cardinality among all kernels from all -sets D is the kernel of G and it is denoted by . For instance, and also if , then .
Theorem 13.
For any graph G with no isolated vertex,
Proof.
Let D be a -set such that . Let be the set such that . Notice that the function , defined by , and , is a STRDF on G. Hence,
Therefore, the proof is complete. □
The following result provides a necessary condition for the graphs G satisfying .
Theorem 14.
Let G be a graph of order at least three with no isolated vertex. If , then for every -set D and .
Proof.
If there exist a -set D and a vertex such that , then because . Hence, and Theorem 13 results in , which completes the proof. □
The following results provide lower bounds for the strongly total Roman domination number in terms of order, maximum degree and total domination number of a graph.
Theorem 15.
For any graph G with every component of order at least three,
Proof.
Let be a -function. As , we deduce that
Now, it is easy to deduce that because . Hence,
Therefore, we deduce that which completes the proof. □
In order to show a class of graphs satisfying the equality in the previous bound, we consider the corona product graphs . For these graphs we obtain that
because by Theorem 4, , and .
In [15], the authors showed that for any graph G with no isolated vertex. The following result is a direct consequence of this previous inequality and Theorems 2, 5 and 15.
Theorem 16.
For any graph G with no isolated vertex,
Furthermore, if , then the previous bound is achieved.
The next theorem shows another relationship between our parameter and the order, maximum degree and total domination number of a graph. This result improves the bound given in the previous theorem whenever .
Theorem 17.
For any graph G with no isolated vertex,
Proof.
Let be a -function. As , we deduce that
Now, notice that the following is the case:
From previous inequality chains we deduce the following:
Therefore, , as desired. □
The bound above is tight. For instance, it is achieved for any graph G such that .
5. Conclusions and Open Problems
In this article we introduced the concept of strongly total Roman domination number and showed that this parameter is an appropriate framework to study the total Roman domination number of lexicographic product graphs. Moreover, we obtained new tight bounds and provided exact formulas for some product graphs. As a consequence of this study, we showed that the problem of computing is NP-hard.
We next propose some open problems which we consider to be interesting:
- (i)
- Since the optimization problem of finding is NP-hard, it would be interesting to compute the value of this parameter for other families of graphs.
- (ii)
- We propose the problem of characterizing the graphs satisfying the following equalities:
- (a)
- ;
- (b)
- ;
- (c)
- .
Author Contributions
The work was organized and led by A.C.M. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs: Volume 2: Advanced Topics; Chapman & Hall/CRC Pure and Applied Mathematics, Taylor & Francis: Abingdon, UK, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Henning, M.A. Topics in domination in graphs. In Developments in Mathematics; Springer: Cham, Switzerland, 2020; Volume 64. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Henning, M.A. Structures of domination in graphs. In Developments in Mathematics; Springer: Cham, Seitzerland, 2021; Volume 66. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Henning, M.A. Graphs with large total domination number. J. Graph Theory 2000, 35, 21–45. [Google Scholar] [CrossRef]
- Henning, M. A survey of selected recent results on total domination in graphs. Discret. Math. 2009, 309, 32–63. [Google Scholar] [CrossRef] [Green Version]
- Henning, M.; Yeo, A. Total Domination in Graphs. Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Stewart, I. Defend the Roman Empire! Sci. Am. 1999, 281, 136–138. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Dreyer, P.A., Jr.; Hedetniemi, S.M.; Hedetniemi, S.T. Roman domination in graphs. Discret. Math. 2004, 278, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Chambers, E.W.; Kinnersley, B.; Prince, N.; West, D.B. Extremal problems for Roman domination. SIAM J. Discret. Math. 2009, 23, 1575–1586. [Google Scholar] [CrossRef] [Green Version]
- Chellali, M.; Jafari Rad, N.; Sheikholeslami, S.M.; Volkmann, L. Roman Domination in Graphs. In Topics in Domination in Graphs. Developments in Mathematics; Springer: Cham, Switzerland, 2020; Volume 64. [Google Scholar]
- Henning, M.A. A characterization of Roman trees. Discuss. Math. Graph Theory 2002, 22, 325–334. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chang, G.J. Roman domination on strongly chordal graphs. J. Comb. Optim. 2013, 26, 608–619. [Google Scholar] [CrossRef]
- Abdollahzadeh Ahangar, H.; Henning, M.A.; Samodivkin, V.; Yero, I.G. Total Roman domination in graphs. Appl. Anal. Discret. Math. 2016, 10, 501–517. [Google Scholar] [CrossRef] [Green Version]
- Abdollahzadeh Ahangar, H.; Amjadi, J.; Sheikholeslami, S.M.; Soroudi, M. On the total Roman domination number of graph. Ars Combin. 2020, 150, 225–240. [Google Scholar]
- Cabrera Martínez, A.; Cabrera García, S.; Carrión García, A. Further results on the total Roman domination of graphs. Mathematics 2020, 8, 349. [Google Scholar] [CrossRef] [Green Version]
- Pushpam, P.R.L.; Sampath, P. On total Roman domination in graphs. In Theoretical Computer Science and Discrete Mathematics; Lecture Notes in Comput. Sci.; Springer: Cham, Switzerland, 2017; Volume 10398, pp. 326–331. [Google Scholar]
- Cabrera Martínez, A.; Martínez Arias, A.; Menendez Castillo, M. A characterization relating domination, semitotal domination and total Roman domination in trees. Commun. Comb. Optim. 2021, 6, 197–209. [Google Scholar]
- Amjadi, J.; Nazari-Moghaddam, S.; Sheikholeslami, S.M.; Volkmann, L. Total Roman domination number of trees. Australas. J. Combin. 2017, 69, 271–285. [Google Scholar]
- Cabrera García, S.; Cabrera Martínez, A.; Hernández Mira, F.A.; Yero, I.G. Total Roman {2}-domination in graphs. Quaest. Math 2021, 44, 411–434. [Google Scholar] [CrossRef] [Green Version]
- Amjadi, J.; Sheikholeslami, S.M.; Soroudi, M. On the total Roman domination in trees. Discuss. Math. Graph Theory 2019, 39, 519–532. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Cabrera García, S.; Carrión García, A.; Hernández Mira, F.A. Total Roman domination number of rooted product graphs. Mathematics 2020, 8, 1850. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Kuziak, D.; Peterin, I.; Yero, I.G. Dominating the direct product of two graphs through total Roman strategies. Mathematics 2020, 8, 1438. [Google Scholar] [CrossRef]
- Campanelli, N.; Kuziak, D. Total Roman domination in the lexicographic product of graphs. Discret. Appl. Math. 2019, 263, 88–95. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Rodríguez-Velázquez, J.A. Closed formulas for the total Roman domination number of lexicographic product graphs. ARS Math. Contemp. 2021, in press. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Rodríguez-Velázquez, J.A. Total protection of lexicographic product graphs. Dis. Math. Graph Theory 2020, in press. [Google Scholar] [CrossRef] [Green Version]
- Laskar, R.; Pfaff, J.; Hedetniemi, S.; Hedetniemi, S. On the algorithmic complexity of total domination. SIAM J. Alg. Discr. Meth. 1984, 5, 420–425. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).