Identification of the Domain of the Sturm–Liouville Operator on a Star Graph
Abstract
:1. Introduction
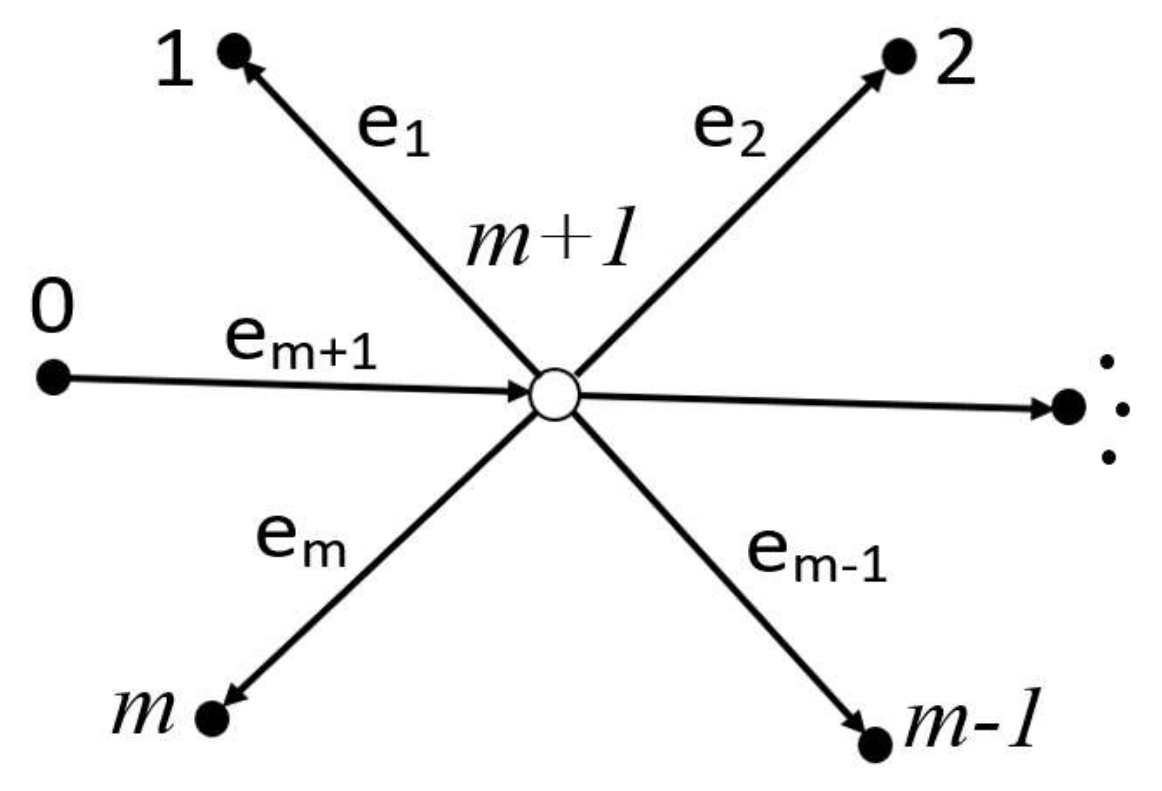
2. Solution of the Cauchy Problem for the Sturm–Liouville Equation on a Star Graph
3. Construction of a Biorthogonal System of Solutions for a Set of Boundary Conditions
4. An Equivalent Set of Boundary Forms That Have an Integral Form
5. Selection of Canonical Problems and the Statement of the Inverse Problem
6. A Uniqueness Theorem for Recovering Boundary Functions
7. Refinement of the Uniqueness Theorem in the Case of Boundary Value Problems
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Borg, G. Eine Umkehrung der Storm-Liouvillshen Eigenwertaufgabe. Bestimmung der Differentialgleichung durch die Eigenwerte. Acta Math. 1945, 78, 1–96. [Google Scholar] [CrossRef]
- Levitan, B.M.; Gasymov, M.G. Determination of a differential equation by two of its spectra. Russ. Math. Surv. 1964, 19, 1–63. [Google Scholar] [CrossRef]
- Plaksina, O.A. Inverse problems of spectral analysis for the Storm-Liouville operators with nonseparated boundary conditions. Acta Math. 1988, 59, 1–23. [Google Scholar] [CrossRef]
- Yurko, V. Inverse problems for differential pencils on A-graphs. J. Inverse Ill-Posed Probl. 2017, 25, 819–828. [Google Scholar] [CrossRef]
- Kanguzhin, B.E.; Dairbaeva, G.; Madibaiuly, Z. Uniqueness of the restoration of boundary conditions differential operator on a set of spectra. J. Math. Mech. Comput. Sci. 2019, 104, 44–49. [Google Scholar] [CrossRef]
- Kanguzhin, B.E.; Dairbaeva, G.; Madibaiuly, Z. Identification of boundary conditions of a differential operator. J. Math. Mech. Comput. Sci. 2019, 103, 82–93. [Google Scholar] [CrossRef]
- Kanguzhin, B.E. Recovering of two-point boundary conditions by finite set of eigenvalues of boundary value problems for higher order differential equations. UFA Math. J. 2020, 12, 22–29. [Google Scholar] [CrossRef]
- Liu, D.-Q.; Yang, C.-F. Inverse spectral problems for Dirac operators on a star graph with mixed boundary conditions. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Sadovnichii, V.; Sultanaev, Y.T.; Akhtyamov, A. The inverse problem of recovering the coefficients of a differential equations on a graph. J. Inverse Ill-Posed Probl. 2020, 28, 727–738. [Google Scholar] [CrossRef]
- Zhapsarbaeva, L.K.; Kanguzhin, B.E.; Seitova, A.A. Asymptotics of the eigenvaluesof the double differentiation operator with Birkhoff-regular boundary conditions on a star graph. Mat. Zhurnal 2018, 18, 107–124. [Google Scholar]
- Ao, S.I.; Gelman, L. Electrical Engineering and Applied Computing; Springer Science+Business Media: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Ranganathan, K. A Textbook of Graph Theory; Springer Science+Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Solomyak, M. Schrodinger operators on homogeneous metric trees: Spectrum in gaps. Rev. Math. Phys. 2002, 14, 421–468. [Google Scholar] [CrossRef] [Green Version]
- Nurakhmetov, D.; Jumabayev, S.; Aniyarov, A.; Kussainov, R. Symmetric Properties of Eigenvalues and Eigenfunctions of Uniform Beams. Symmetry 2020, 12, 2097. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanguzhin, B.; Aimal Rasa, G.H.; Kaiyrbek, Z. Identification of the Domain of the Sturm–Liouville Operator on a Star Graph. Symmetry 2021, 13, 1210. https://doi.org/10.3390/sym13071210
Kanguzhin B, Aimal Rasa GH, Kaiyrbek Z. Identification of the Domain of the Sturm–Liouville Operator on a Star Graph. Symmetry. 2021; 13(7):1210. https://doi.org/10.3390/sym13071210
Chicago/Turabian StyleKanguzhin, Baltabek, Ghulam Hazrat Aimal Rasa, and Zhalgas Kaiyrbek. 2021. "Identification of the Domain of the Sturm–Liouville Operator on a Star Graph" Symmetry 13, no. 7: 1210. https://doi.org/10.3390/sym13071210
APA StyleKanguzhin, B., Aimal Rasa, G. H., & Kaiyrbek, Z. (2021). Identification of the Domain of the Sturm–Liouville Operator on a Star Graph. Symmetry, 13(7), 1210. https://doi.org/10.3390/sym13071210





