Abstract
The allocation of products on shelves is an important issue from the point of view of effective decision making by retailers. In this paper, we investigate a practical shelf space allocation model which takes into account the number of facings, capping, and nesting of a product. We divide the shelf into the segments of variable size in which the products of the specific types could be placed. The interconnections between products are modelled with the help of categorizing the products into specific types as well as grouping some of them into clusters. This results in four groups of constraints—shelf constraints, shelf type constraints, product constraints, position allocation constraints—that are used in the model for aesthetic symmetry of a planogram. We propose a simulated annealing algorithm with improvement and reallocation procedures to solve the planogram profit maximization problem. Experiments are based on artificial data sets that have been generated according to real-world conditions. The efficiency of the designed algorithm has been estimated using the CPLEX solver. The computational tests demonstrate that the proposed algorithm gives valuable results in an acceptable time.
1. Introduction
The retail shelf space allocation problem (SSAP) is well known in the various literature. This study investigates the retailer’s task to sell different products and to allocate them on limited shelf space. The aim is to determine the right shelf and shelf segment to place the product and the appropriate amount of shelf space assigned to each product in order to maximize the retailer’s profit. The shelf space allocation process from the retailer’s point of view is based on two factors. On the one hand, they must allocate products on suitable shelves. On the other hand, they must consider customer preferences because product demand and customers’ shopping loyalty and satisfaction are influenced by the proximity of interchangeable products and by the physical position of the shelf on which products are placed [1,2].
In retail stores, the retailers’ goal to maximize the profit from selling products is achieved with the help of planograms. Planograms are the graphic representation of physical products’ arrangements on store shelves that help the retailer to figure out the right position of the product on the shelf and to set its number of facings. Very frequently, planograms are used to promote symmetry and aesthetics, which in turn improve customer satisfaction with shopping. The available shelf space is a limited resource in the small local stores as well as in the large hypermarkets. Hence, the right shelf space planning and merchandising rules allow retailers to increase achieved profit and improve customer satisfaction [1,3].
SSAPs incorporate concerns such as assortment selecting, inventory management, development of price, replenishment, and supply chain management [1,2]. Talking about principles of retail SSAPs and their role in sales generation, there are five aspects that influence the profit and sales: the location of the shelves, products, items within product categories, secondary product locations (off-shelf), and point-of-purchase materials (banners, posters, brochures) [4]. Zhang and Rajaram [5] paid attention to inventory management strategies and developed an optimization model which combines space dedication with space sharing for basic products considering assortment planning and replenishment scheduling. In contrast, Urban [6] classified the backroom and the showroom inventories and included them into the model. Hübner and Schaal [7] embodied into the optimization model in-store replenishment actions.
A considerable number of articles have been written in the last three decades on assortment selection and SSAPs. However, experimental studies of space elasticities are limited in the literature. Furthermore, such variables are costly and difficult to evaluate or obtain from a real store. In many studies, different approaches are used to solve the SSAP. Numerous pieces of research model the SSAP without elasticity parameters, explaining that elasticity parameters affect sales to a small degree, while others include them in their models generating such parameters with normal or uniform distribution.
Difficulty in the SSAP occurs as a result of the inclusion of the space elasticity effects in the demand function, which are difficult and expensive to estimate and non-linear by nature. Furthermore, SSAP models that can be suitable to real stores are difficult to prepare either because of their simplicity and lack of practical constraints or due to their complexity and difficulty in parameters estimation requirements.
Czerniachowska and Hernes [8] compared linear and non-linear profit functions with space elasticity parameters. They showed that the resulting total profit in the retailers’ SSAP with vertical position effects significantly differ in these two profit functions. Additionally, the SSAP is difficult to be solved because of existing many intercorrelated decision processes. As the variety of the product displayed on the shelves increases, space and cross-space elasticities significantly grow and diversify. Therefore, SSAP becomes more complex [9].
The aim of the paper is to develop the novel SSAP model and to implement simulated annealing for solving it. The proposed approach is mainly characterized by:
- Dividing the shelf into the segments of variable size (which could be enlarged or reduced) and allocating the products on different horizontal shelf segments. To the best of our knowledge, this is the first model which considers vertical shelf levels (e.g., pallet, low-level, eye-level) and horizontal shelf segments (e.g., aisle, local, convenience) of flexible size for aesthetic symmetry.
- Differentiating shelf segments of a symmetrical planogram based on the customer traffic flow (e.g., segments situated near the aisle at the beginning or at the end of a planogram).
- Specifying shelf segments dedicated for the specific product types (e.g., local and convenience segments) which could be situated in arbitrary place of a planogram.
- Grouping similar products into clusters with the intention to place them one next to the other on the shelf for making the comparison of the products by customers easier.
- Considering two orientation possibilities (front or side) to allocate products on shelves.
- Incorporation of capping and nesting parameters.
This research adopts the capping and nesting allocation parameters used in another model with vertical shelf levels based on the product prices by Czerniachowska and Hernes [10,11]. Cappings mean allocation of items on top of each other, such as light rectangular cartoons. Nestings mean the allocation of the products inside each other, such as plates or glasses. These parameters significantly reduce the shelf space for product exposure. Hence, in our research, we enhance the SSAP model with capping and nesting parameters which tend to be profitable enough.
The paper makes the following contributions:
- Presenting a practical retail SSAP model with above mentioned characteristics.
- Adjusting the simulated annealing (SA) algorithm for solving the retail SSAP.
- The enhancement of the well-known SA hyper-heuristic with solution improvement and product reallocation procedures which enables to get more profitable solution within the small number of iterations.
In this research, SA was implemented because SA hyper-heuristic is an efficient and effective technique for solving optimization problems. It is widely applied in business, management decisions, and solving scientific and engineering problems. The SA concept is easy to understand and implement.
Compared to GA, SA is a single-solution-based algorithm, while GA is a population-based algorithm. Because we developed the solution improvement procedure, which increases the solution quality, we expect that SA would be faster than other population-based metaheuristics such as GA.
Generally, SA has only an exploitation function, while GA has both exploration and exploitation, but GA generates lots of solutions based on the population size. This significantly increases computational time. Next, multiple constraints checking and intermediary result correction are needed in each standard GA operation, such as selection, crossover, and mutation. This also increases the processing time in the case of a complicated SSAP model.
Last but not least, we found different GA implementations in SSAP research literature. However, retail literature has significantly fewer of studies where SA is investigated. This research presents the evaluation of SA with regard to multiconstrained SSAPs. Of course, the solution method selection depends on the nature of the problem.
The paper is organized as follows. The related works are collected in Section 2. Problem description and its mathematical model are given in Section 3. SA hyper-heuristic is presented in Section 4. Next, in Section 5, the results of computational experiments are outlined. The article is concluded in Section 6.
2. Related Works
2.1. Visual Attention to Product
The aesthetic appeal of the shelf assortment draws customers’ attention. Products that evoke social approval, tactile satisfaction, self-expression, the affirmation of being unique and intellectual motivation encourage great involvement from customers. Customers find interesting, high-involvement products to be more attractive than low-involvement ones [12].
Djamasbi et al. [13] put the main stress on customers’ visual stimulation and deployment of visual attention. Larger products are more noticeable than smaller ones. Products with brighter colors are more attractive to customers than darker ones. Products allocated at eye level attract more attention than those located at the bottom shelves.
The results of Huang et al. [14] demonstrate the positive impact of product advertisements. With the enormous marketing potential, customers become more loyal to a certain product, spending more time in front of the shelf and actively examining such a product, which results in carefully performed purchasing decisions.
Desrochers and Nelson [15] noticed that customers’ purchasing decisions depend on product categorization, appropriate associations, and visual presentation on the shelf. Furthermore, Valenzuela and Raghubir [16] postulated that the bottom shelves are purposeful for basic products or cheaper brands, although impulse or more expensive products should be placed on the top shelves.
According to Ngo and Byrne [17], customers scan planogram shelves from the top left to the bottom right corner following a Z-shaped path. Desrochers and Nelson [15] studied the influence of customer behavior on buying decisions and suggested that customers’ decisions are stimulated by appropriate product classification and prior allocation of products in another subcategory. Anic et al. [18] concluded that customers’ buying behaviors strictly depend on store traffic directions and suggested that retailers should include traffic flow merchandising rules while adjusting shelf space.
2.2. Assortment Decisions
With the increasing amount of assortment offered in retail stores and optimization of merchandising rules, retail stores can offer consumers more convenience while shopping and a wider diversity of products, thus improving their satisfaction. Due to the continuous changing of consumer habits, many vendors have invested in visual merchandising at the store to seize potential opportunities in retail shopping.
Assortment planning means determining the most profitable product to maximize sales and improve brand recognition. This is an extremely important and inductive task for retailers [19,20]. Moreover, such factors as seasons changing, new products presentation, advertising, and changes in consumer tastes stimulate retailers to periodically look over store assortment [20].
Generally, in retail stores, the displayed assortment must incorporate product categories related to fast-moving goods, i.e., “basic” products or high-sales product categories that are usually sold at a low margin (e.g., bread, salt, milk, eggs). The rest of the store assortment ordinarily includes impulsive product categories, which may be purchased quickly without prior planning [21].
Product substitution is a key component in the assortment planning process, which is determined by the customers’ consent to select another product with similar parameters if their preferred one is out of stock. Kök et al. [22] differentiated between three main types of customer substitution: stock-out based substitution, assortment-based substitution, and assortment involving substitution.
Furthermore, Kök et al. [21] synthesize several modeling strategies for assortment planning and related issues. They provided a unified modelling method for assortment and inventory planning but do not incorporate concepts such as restricted shelf space or space elasticity, which are important to shelf space planning.
It can be summarized that a typical assortment selection is based on the category, brand, and price of the products. Customers compare different alternative products displayed on shelves and make choices about which product to put into the basket. There is no unique method of assortment planning which can take into account all the marketing variables and implications of operational decisions because of the limited data available and the complexity of the assortment planning task.
2.3. Shelf Space Allocation Decisions
The primary goal of SSAP studies is to propose how to optimize the utilization of limited retail shelf space allowing the retailer to obtain as much profit as possible. Shelf management is the strategy that resolves how products should be displayed on the shelves and what amount of space is required for each product.
Shelf space is important for retailers and has been referred to as the most limited retailer’s resource [9,23,24,25]. The ultimate goal of shelf space planning is to maximize profit by assigning products to shelves while keeping limited shelf space and allocation constraints in view—such as product quantities, inventory, and other operational costs. This planning issue is allocating a retail store’s limited shelf space among the various products to be presented. This includes the concerns of how much shelf space to give to each product, which eventually correlates to the number of each product, where to place each product on the vertical shelf, where to place each product on the horizontal shelf, and what brands to place next to each other [26].
Silver (1981) [26] concluded that one of the major factors which directly affect the amount of sales is the decisions of the retailers on the shelf space allocation. Moreover, correct shelf space allocation decisions and good visual merchandising not only attract customers’ attention but also motivate customers to make future buying choices.
The research results by Drèze et al. [27] showed that allocating a product on shelves at eye level significantly increases sales. In contrast, changes in the shelf space assigned to a product have a lesser impact on sales.
Some literature streams concern aesthetic effects and categorising products into families based on different characteristics [3,28].
Bianchi-Aguiar et al. [3] differentiated macro and micro levels of space planning steps. The macro-level is strategic, and it concerns determining the space for product categories and shelf types. The micro-level is tactical, and it encompasses assigning particular goods within each category. Because retailers are unlikely to modify the architecture of the shelves during product redistribution, shelf-related decisions (e.g., shelf height and depth, number of levels per shelf) are normally supplied as inputs to the modelling techniques following macro space planning.
Russell and Urban [28] developed two models which allow to categorise product on shelves and to group them into families. The first model for small instances determines the product placement on shelves, ensures the boundaries and spans, multi-shelf spans of product families. The second one for large instances does not point out the precise location of the product on the shelf, but it ensures that each family is placed on vertically or horizontally adjacent shelves.
2.4. Solution Approaches
Since SSAP is almost always NP-hard, advanced heuristics and meta-heuristics is used. Such algorithms allow the achievement of a satisfactory near-optimal solution but do not promise globally optimal value [1].
Previous studies have emphasized different evolutionary approaches [29,30]. Pinto and Soares [30] proposed a decision support system that uses an evolutionary framework to solve SSAP. They also present an integration of sales forecasting models for different product categories. Esparcia-Alcázar and Martínez-García [29] studied a linear SSAP called the ‘product-to-shelf allocation problem’ in the previous work. Their goal was to find the length of the shelf for each product taking into consideration standard retailer’s requirements, similarity requirements between groups and relation of products within groups. They proposed an evolutionary methodology for this problem.
Many researchers reported SA hyper-heuristic to solve complex SSAP [31,32,33,34].
Bai and Kendall [31] formulated the SSAP as a non-linear product profit function and demonstrated it as an extension of the multi-knapsack problem. They proposed SA hyper-heuristic algorithm with the usage of low-level heuristics. Furthermore, Bai et al. [34] proposed a two-dimensional display shelf space allocation model. They proposed iterative allocation based on gradient and SA hyper-heuristic learning method.
Nierop et al. [33] studied the relation between stock-keeping units (SKU) sales and SKU marketing performance on shelf allocation. They proposed SA algorithm to find the increases in retailer’s profits if products have proper shelf location.
Borin et al. [31] proposed a model which integrates shelf space allocation, assortment and inventory mechanisms. They presented a heuristic approach based on a SA hyper-heuristic and tested it on small problem sizes with known optimal values, as well as on large problem sizes without known optimal values.
A series of recent studies indicated the usability of genetic algorithm [6,10,35,36,37,38,39].
Hwang et al. [35] presented a gradient search heuristic and genetic algorithm to solve the retailer’s problem, taking into account brands selling on multi-level shelves. It is considered that the vertical location effects of the shelves where the product is exposed have a significant impact on sales.
Hansen et al. [38] studied the effects of vertical and horizontal location of the products and product cross-elasticity. He examined heuristics and meta-heuristics for decision models with facing-dependent demand and proposed a genetic algorithm for improving retail shelf allocation decisions.
Ghazavi and Lofti [39] studied a combined demand function that simulates customers’ shopping paths, taking into consideration shelf level, shelf space, and store’s zones. They proposed an exact algorithm, a meta-heuristic such as a genetic algorithm and a hybrid genetic algorithm with an imperialist competitive approach.
Urban [6] theorized inventory-control models, product assortment models, and space-shelf allocation models, extending them into a constrained environment. He developed a greedy heuristic and genetic algorithm.
Esparcia-Alcazar et al. [36,37] studied product to shelf allocation problem, which differs from SSAP. They formulated it as a mixed-integer quadratic assignment problem and proposed a genetic algorithm to obtain an efficient result.
Czerniachowska and Hernes [10] applied a genetic algorithm for solving the SSAP with vertical position and price effects. In their model, the bottom shelves were dedicated to cheaper products; the top shelves were for placing more expensive products. Cheaper products could be allocated on higher shelves if there is available space, but the expensive products must not be placed on lower shelves.
The literature review also shows the existence of other artificial algorithms. For example, recent research by Ozcan and Esnaf [40] presented a heuristic approach on the basis of an artificial bee colony algorithm using the model with regard to space and cross elasticity as shelf space decision factors.
3. Problem Model
Based on business tasks, space allocation is performed within a given category. A planogram is multi-shelved; each shelf usually allows allocating predefined package types, package weights or package sizes of the products.
To begin with, the sets and iterators used in this research are given in Table 1. The list of variables used in this research is shown in Table 2. Decision variables used in this research are described in Table 3.

Table 1.
List of sets and iterators used in the analysis.

Table 2.
List of parameters used in the analysis.

Table 3.
List of decision variables used in the analysis.
The problem can be formulated as follows. We are given a planogram, which consists of one fixture. A fixture consists of shelves. Parameters such as the shelf length , the shelf height , and the shelf depth are set for each shelf. A pallet is the lowest shelf and is set aside on the floor.
Suppose that for appropriate product placement based on their position constraints, a shelf is partitioned into segments, each with the defined width . In the current research, we suppose that the shelf center is the whole shelf except outside segments near the first and the last aisles. On a planogram, the first and the last aisle segments are symmetrical but differ on the direction of the customer traffic flow. The binary parameters for shelf segments are defined. Among them are: which means if the segment is used for convenience products, which shows if the segment is used for local products. It is clear that a segment can be situated either near the aisle or in the center of the planogram. Moreover, a segment may be used for convenience or local products, or both of them. Never mind if the convenience and local segments are symmetrical on a planogram or not; allocation of them must be both functional and pleasing to the customer’s eye. These segments may be allocated between the general products creating loose symmetry on a planogram.
Convenience products, in most cases, are purchased with minimum endeavor and without deliberating to buy them as an attachment to the goal product. For example, if somebody buys meat, often one can see bouillon and meat flavored dish spices on the related planogram. On the fresh planogram with vegetables, one can see salad dressing and seasoning as attrition for the vegetables.
In contradiction to convenience products, local products are not subsumed into the particular products assortment in all stores but vary in each store. The particular store assortment is generally conveyed from the main template planogram. Contradictory, local products are on the decision of each store where planogram is exposed, they can be adjoined to the assembled planogram.
The binary parameters which indicate shelf properties are defined. Among them are: which expresses if a shelf is a pallet (for big heavy packages of products), means if a shelf is for fast-moving products or at a lower level (for example for presentation of the products for kids), denotes if a shelf is at eye level (for brand products), means the shelf where a local segment is situated, means the shelf where convenience segment is situated, is used for all shelves because in each shelf centre segments are situated, and also used for all shelves because the first and the last aisle segments are situated on each shelf. To make it clear, on each shelf, there are the first and the last segments which correspond to customer traffic flow. The central part of the shelf (in which customers spend more time) combines all shelf segments which are not near the aisles, but local and convenience segments exist on only one shelf of a planogram.
The left and right coordinates of the shelf segments are calculated as follows:
| —for a pallet segment; | |
| —for low-level segment; | |
| —for eye-level segment; | |
| —for local segment; | |
| —for convenience segment; | |
| —for shelf center segment; | |
| —for first aisle segment; | |
| —for last aisle segment. |
Suppose that we are given of products. The product has various parameters. Among them are: width , height , and depth . The retailer can define minimum and maximum numbers of facings. Each product has a supply limit that specifies the maximum availability of the product quantity. The product can have capping or nesting characteristics or neither of them.
The total number of product items equals the sum of facings , cappings , and nestings numbers of a product. Based on the product package, the minimum and maximum side cappings per facing group may be set for each product on the shelf. The number of facings in one group that must be placed on a shelf to support the cappings above must be at least . Additionally, the minimum and maximum number of nestings of one facing of the product may be also set for each product on the shelf. and signify the maximum possible additional number of products that can be placed above facings without destroying them and so that additional products do not fall off the shelf. Similarly, the number of shelves where product can be placed may be restricted by the retailer. The minimum and maximum numbers of shelves for product allocation define this behavior. Unit profit characterizes the profit parameter of the product. For all products, its main front orientation is available, but for some products also can be placed on side orientation . For front oriented product, its width is the space parameter; for side orientated products, its depth is the space parameter. Cluster products indicate products grouped in clusters in order to be placed on one shelf.
Binary parameters define the properties of the product: means that the product must or must not be allocated on a pallet, shows that the product must be allocated at lower level, indicates that the product must be allocated at eye level, denotes that the product must be allocated on the shelf assigned for local products, signifies that the product must be allocated on the shelf for convenience products, shows that the product must be allocated in the center of the shelf, and identify that the product must be allocated near the first or the last aisles.
In the current research, we call specific segment any of the local, convenience, center, or aisle segments. We call the product specific if it is tagged at least by one of the parameters . All specific products must be placed in the corresponding specific segments. The rest regular products may also be placed in the specific segments if there is free space there. However, the pallet products cannot be placed on other shelves, and similarly, not pallet products cannot be placed on the pallet.
For correct product assignment to segments, they are marked by 8 tags and divided on each shelf into three subsets: subset is before the specific segment, subset is inside the specific segment, subset is after the specific segment. The specific segment is flexible, so it can be reduced or extended. The position of it is float, so it can be moved slightly left or right. Nevertheless, the center of each tagged specific product must be placed between the original left and right segment borders.
In the current research, we consider that there out-of-stock situations are not to occur, and that all products can be physically allocated on the shelf defined to them. We do nottake into account the number of facings in the vertical dimension. We take into account the height of the product, we use it for capping and nesting calculations. We do not use it for calculating the number of facings in the vertical dimension as we analyze only one visible product row on a planogram. The shelf depth is used for deciding on the product orientation. In practice, the lower shelves are deeper, the higher shelves are shallower. The shelf depth is also measured for one front facings row. There is one local and one convenience segment on a planogram.
In this research, the interconnections between products are presented in the following ways:
- representing local products,
- representing convenience products,
- grouping come products into clusters.
In this research, the constraints are grouped into four categories:
- the shelf constraints;
- the product constraints;
- multi-shelves constraints
- shelf segment constraints.
The goal in this SSAP is to define the number of facings , cappings , and nestings of a product allocated to the shelf on its front or side orientation with regard to the mentioned constraints. Next, assign each product to the subset of the tag (i.e., subsets before , after or inside the specific shelf segment) on the shelf . The criteria function is the retailer’s profit maximization.
The model can then be formulated as follows
subject to:
3.1. Shelf Constraints
Constraint (2) keeps the shelf length within bounds. Constraint (3) makes sure that the product’s height does not exceed the shelf height limit. It is supposed that the capped products are orientated to the customer on that side that their widths (depth) achieve an extra height of the facing of a product in the front (side) orientation. The equation is used for omitting the division by 0 cases if there is no product on the shelf. Constraint (4) restricts the shelf depth.
3.2. Product Constraints
Constraints (5) and (6) define the lower and upper bound of a number of shelves where the product should be placed. Constraint (7) restricts the maximum supply of a product. Constraints (8) and (9) determine the lower and upper bound of product facings. Constraints (10) and (11) represent the lower and upper bound of side cappings per position. Constraints (12) and (13) guarantee the lower and upper bound of side nestings per position.
3.3. Multi-Shelves Constraints
Constraints (14) and (15) restrict that only one orientation (front or side) is possible. Constraint (16) guarantee the same product orientation for a product on all shelves for the multi-shelf products. Constraint (17) defines the possibility of side orientation for some products. The next two constraints ensure better product visibility in rectangular blocks on multiple shelves so that the product to be placed on the neighbor shelf (constraint (18)) and with the number of facings of it must be the same (constraint (19)). Constraint (20) ensures that products grouped in the same cluster must be allocated on the shelf together.
3.4. Shelf Segment Constraints
The occupied space temporary variables could be presented as
Constraint (24) ensures tags compatibility. Constraint (25) shows that non-specific product is assigned to the subset A or B if it is placed on a pallet, low-level or eye-level shelf. The same is for local and convenience shelves (constraint (26)). Constraint (27) ensures that specific products are assigned to the subset C if it is placed on the shelf. The next two constraints refer to non-specific products on the central segments (constraint (28)) and aisle segments (constraint (29)) and assign them to subsets A or B.
Constraint (30) ensures the size of the segments of the shelf center position. We suppose that the center of a product is within the local shelf segment on the shelf. The first part of the constraint (30) describes what is analyzed if there is extra free space on a shelf; the second part of the constraint shows the general allocation situation when the shelf is almost filled. Specific products from the subset are placed on the shelf inside the specific shelf segment in such a way that the center coordinate of each product stays between the specific segment borders. Because of this, the products from this subset may exceed the subset borders but no more than . In this case, the maximal extended width of the specific segment receives the following coordinates . The rest non-specific products are assigned to the subsets and . The reducing and enlarging method for these segments is similar to the case with the subset . Constraints (31) and (32) indicate that aisle products can be allocated near the first (constraint (31)) and the last (constraint (32)) aisle. The first and the last aisles are symmetrical but invite a different number of customers because of the direction of the traffic flow. We suppose that the center of a product is within the first (constraint (31)) or the last (constraint (32)) shelf segment on the shelf. The maximal enlargement of the first aisle segment is , and in case of the last aisle segment.
3.5. Relationship Constraints
Relationship constraints regulate the connection between binary decision variables and integer decision variables. Constraints (33) and (34) ensure that if the product is placed on the shelf, it has the positive number of facings assigned in front of side orientation (constraint (34)), and the width occupied by the product on the shelf concerning front of side orientation is positive (constraint (33)). Constraint (35) ensures that if the product is placed on the shelf, it is assigned to one of the subsets (, , or ). Constraint (36) ensures that if the number of cappings is assigned, the number of facings must also be assigned for this product. Constraint (37) ensures that if the number of nestings is assigned, the number of facings must also be assigned for this product.
3.6. Decision Variables
The binary decision variable (38) shows if the product is placed on the shelf . Integer decision variables (39)–(41) indicate the number of facings, cappings and nestings of the product on the shelf . The binary decision variables (42) and (43) defines that the front or side orientation is selected for the product. The binary decision variable (44) signifies that the product is assigned to the subset of the appropriate type on the shelf .
In our research, the objective is to maximize the total profit of the planogram fixture.
4. Simulated Annealing Approach
Simulated annealing (SA) is a local search technique for reaching the global optimum of a given function. This is a hyper-heuristic that is inspired by a physical cooling material process in which the temperature slowly decreases in order to minimize material defects. SA operates with an optimization problem objective function on behalf of the energy of a material. It is used for problems in which an approximate global optimum is more valuable than the local optimum in the predefined time [41].
In the beginning, the initial solution is generated. At each iteration, a new neighbor solution is created with the goal of improving the value of the objective function. In the current research, we make an attempt to maximize the profit function. The SA algorithm accepts all new solutions that are better than the current one and accepts worse solutions with a certain probability in order to escape from the local optima and have the opportunity to find more possible solutions. Metropolis probability [42] is used to decide if a worse solution should be accepted. It is defined by , where is called a “cost function” and coincides with the free energy of the metal annealing process. In this case, the temperature parameter is used to guide the opportunity to move to a worse solution. SA starts from the established high temperature, next on each iteration, it repeatedly reduces it according to the annealing schedule until the temperature achieves its minimum or other stopping criteria are met. In this research, we use the maximum number of iterations without improvement as additional stopping criteria for large instances.
SA is a powerful and valuable tool in a variety of optimization problems. Nevertheless, one of its drawbacks is its sensitivity to the number of parameters and problem instance. For this reason, the researcher should perform many experiments with the aim to correctly tune the problematic parameters ([31,32,33,34,41,43,44]).
In the proposed approach, only regular products with undefined at the beginning shelf are processed in terms of finding shelf for them and adjusting the number of facings, cappings, and nestings. For local and convenience products, only adjusting the number of facings, cappings, and nestings are applied. Because there is only one local and one convenience segment on a planogram, the shelf where such products could be placed is one. Also, such products must be assigned to the subset C). This means that we have already found the shelf for them. Therefore, the algorithm processes other products for which the shelf is undefined yet. Disregard the fact that the aisle products are not regular; they also need the shelf to be found for them because each shelf could have the first and the last aisle segments. The same is for center products because the shelf center segments exist on all shelves.
The proposed approach processes cluster products in the following way. The algorithm checks if the cluster products are on the same shelf and perform appropriate movements to set them on the same shelf. Once the shelves have been defined, the algorithm tries to find the number of facings, cappings, and nestings.
To begin with, the following parameters must be defined (Table 4).

Table 4.
List of parameters used in the algorithm.
- Initial Phase
Determine the starting temperature by multiplying the shelf width into the number of products . Initialize a number of iterations without improvement with zero, as well as the last total profit . Initialize the initial solution : (1) allocate pallet products on the pallet shelf (because they cannot be placed on another shelf) with the exact algorithm; (2) next assign convenience and local products to the shelf where the corresponding segments exist; (3) randomly assign the rest products to all shelves (except the pallet). Set minimum values of facings, cappings, and nestings to the product. If the initial solution with assigned lower bound values does not fit the constraints, destroy it, and repeat initialization.
The heuristics rules are the following. There are three main priority rules: (1) highest unit profit of the product; (2) lowest width of the product; (3) ratio of the product profit divided by the occupied shelf width. Create a new solution applying these heuristics in a way that:
- consider or not consider facings/cappings/nestings already on the shelf;
- allow or not allow to select the same product more than once in the next iteration;
These give 12 heuristics. Add random selection rule as the last heuristics.
- 2.
- Iterative Phase
While the temperature exceeds its lower bound, select the heuristic rule and generate the solution based on it. At first, generate a solution increasing the numbers of facing, cappings, and nestings times in the previous solution , next correct these numbers based on one of the heuristic rules selected randomly. Use each heuristic (the maximum possible number of heuristics is ) for solution generation, simultaneously moving to the next iteration, but select the heuristic for later processing steps from the generated ones randomly.
Apply improvement procedure for it and get the set of improved solutions. Calculate the total profit for each one and leave the solution with the highest total profit . Apply reallocation procedure for the improved solution with the highest total profit. Calculate the total profit for it. Calculate the profit of the current solution and evaluate it, selecting the solution with the highest profit to the next step in this procedure.
If the received solution has a higher profit than the previous solution , replace s with x. If the received solution do not exceed the profit of the previous solution , take it, replacing s with x corresponding to the probability . Therefore, for the next iteration, select all better solutions and select some worse solutions according to the Metropolis probability [41]. Otherwise, leave the previous solution without changes.
Reduce the current temperature.
- 3.
- Termination Criteria
The algorithm stops when the temperature decreases to or the number of iterations without improvement exceeds its predefined value . The last stopping criteria was used only for large instances.
In the current research, the SA based algorithm works as follows (Algorithms 1 and 2).
In the proposed approach, the improvement procedure performs as follows. We incorporate the improvement technique [10] for making solution on any SA iteration’s more profitable. In their research, they applied it in any GA iteration. Clearly, such strategies might be used on other metaheuristic approaches on other SSAP models. The method includes three improvement variations: increasing shelf ratio, increasing shelf profit, reducing free shelf space. The main idea is to find the products on other shelves that could add more profit if they were placed on the current shelf. Next, select the less profitable products on the current shelf and move them to the shelf where they could increase the overall profit. The shelf ratio is the total profit of products, including facings, cappings, and nestings on the shelf divided by the shelf length.
| Algorithm 1. Pseudocode of the general steps of the proposed SA algorithm |
| 1: Define heuristics rules . 2: Define a maximum temperature . 3: Set a starting temperature . 4: Initialise the number of iterations without improvement . 5: Initialise the last profit . 6: Initialise the initial solution , the total profit is . 7: Save current solution as the best solution , . 8: while (){ 9: for (;;) 10: { 11: Randomly select the heuristic rule . 12: Generate a new solution based on the selected , 13: . 14: Calculate . 15: If (){ 16: Set 17: }else{ 18: Increase 19: } 20: Set 21: If () 22: { 23: Save current solution as the best solution , . 24: } 25: If (){ 26: Set . 27: } 28: } 29: Set . 30: Set . 31:} |
| Algorithm 2. Pseudocode of the iterative solution generation |
| 1: { 2: Generate solution increase the number of facings, cappings and nestings times in the previous solution . 3: Correct (reduce) the number of facings, cappings, and nestings in the solution according to , with regard to all constraints, the total profit is . 4: Improve the solution , the total profit is . 5: Reallocate products in the solution , the total profit is . 6: Set the new solution as the solution with the highest profit, 7: , 8: 9: if (){ 10: Set solution , . 11: } else { 12: Set . 13: Generate a random uniformly in range [0,1]. 14: if (){ 15: Set solution , . 16: } 17: } 18: Return 19: } |
Perform the appropriate products movement between shelves according to the three mentioned rules. Swap products between shelves in order to:
- increase shelf ratio of the current or other shelf;
- increase shelf profit of the current or other shelf;
- reduce free shelf space of the current or other shelf.
The following cases could appear:
- the product could be profitable if it is placed on the current shelf;
- the product is not profitable being placed on the current shelf;
- the product could be profitable if it is placed on another shelf;
- the product is not profitable being placed on another shelf.
The reallocation procedure performs swapping products between the shelves and changing the number of facings, cappings, and nestings of product. When moving products to other shelves, only the appropriate shelves are considered. This means that convenience and local products do not change their shelves as the corresponding segments do not exist on other shelves. Increasing and reducing the number of facings is performed, either considering cappings and nestings or not. This means that in some cases while reducing facings, we must also reduce cappings and nestings. If not, cappings could fall off the shelf, and nestings cannot stay on the shelf without a base facing below.
Pallet products are not processed iteratively by SA. They are allocated once with the exact algorithm at the beginning.
5. Results
The goal of the computational experiments was to evaluate the quality of the SA algorithm, which was developed to solve the SSAP. Because of the lack of real-world data due to trade secrets, several simulated data sets for the problem were prepared. Twenty-five problem instances with different problem sizes were tested. The structure of the experimental data represents the retailer’s problem. Suppose that there are five stores where planograms with different lengths must be set. In each store, different shelf space is available for the products, but the same set of products must be allocated on the shelves. Hence five product planogram sets were initialized.
- Set 1—There are 10 products that must be placed on 4 shelves on the planogram. The shelf lengths in each store are 250 cm, 375 cm, 500 cm, 625 cm, 750 cm.
- Set 2—There are 20 products that must be placed on 4 shelves on the planogram. The shelf lengths in each store are 250 cm, 375 cm, 500 cm, 625 cm, 750 cm.
- Set 3—There are 30 products that must be placed on 4 shelves on the planogram. The shelf lengths in each store are 250 cm, 375 cm, 500 cm, 625 cm, 750 cm.
- Set 4—There are 40 products that must be placed on 4 shelves on the planogram. The shelf lengths in each store are 250 cm, 375 cm, 500 cm, 625 cm, 750 cm.
- Set 5—There are 50 products that must be placed on 4 shelves on the planogram. The shelf lengths in each store are 250 cm, 375 cm, 500 cm, 625 cm, 750 cm.
The impact of shelf space availability, shelf capacity and shelf feasibility on the algorithm’s performance is taken into consideration in this research. Due to the fact that each product has minimal and maximal values of facings, cappings and nestings, the usable shelf space must be larger than the minimal shelf space required if all products were to be placed with their minimal possible values of facings, cappings, and nestings values.
The following parameters were determined for each product: facings LB/UB, cappings LB/UB, nestings LB/UB, shelves LB/UB, supply limit, pallet products, eye-level products, low-level products, aisle products, shelf centre products, convenience products, local products, shelf length, shelf height, and shelf weight. The lower bound of product facings is no less than 1. This suggests that each product from the set must be allocated on the planogram. Cappings/nestings values indicate that some products may be capped, others may be nested whilst others can neither be capped nor nested. Pallet product parameters indicate whether products from the set must be placed on a pallet. Otherwise, products must be placed on ordinary shelves rather than a pallet. Eye-level and low-level parameters suggest whether products must be placed on analogous-type shelves. Aisle, shelf center, convenience and local product parameters indicate whether products must be placed inside the analogous shelf segments. In other words, the center position of the product must be set between the left and the right bounds of the analogous shelf segment.
The SA solutions were compared to the CPLEX ones, whose solving time was limited to the time in which SA finds the solution. Therefore, the solution time of SA and the solver are equal in the first case. In the second case, CPLEX solving time was limited to 5 min. There are no results for the case with 50 products on 250 cm because they do not satisfy the LB limits.
- The computational experiments were performed in Visual C# 2015.
- Language: Visual C# 2015
- Microsoft Visual Studio Community 2015
- Version 14.0.25431.01 Update 3
- Microsoft .NET Framework
- Version 4.6.01055
- IBM ILOG CPLEX Optimization Studio Version 12.7.1.0 was used to find the optimal or feasible solution.
The following SA parameters were selected:
- number of heuristics ;
- maximum number of iterations ;
- maximum number of iterations without improvement not used for 10 and 20 products;
- maximum number of iterations without improvement for 30, 40, and 50 products;
- minimum temperature ;
- coefficient of increase of the numbers of facings, cappings, and nestings ;
the number of products to be moved and paired used in the improvement procedure: 5 by 4 (for 10 products), 6 by 4 (for 20 products), 6 by 3 (for 30 products), 4 by 2 (for 40 products), 4 by 2 (for 50 products).
Table 5 shows the solution quality of the SA algorithm. 10 tests were performed for each instance in order to evaluate the SA algorithm. The best solution providing the maximum total profit was selected from all the test sets.

Table 5.
Quality of the SA solution compared to the CPLEX solver
Two columns of Table 5 report a comparison of SA and CPLEX solution quality with the same time restraints. This means that CPLEX solver solution time was restricted to the time in which SA finds the solution. It can be observed that SA was better in 9 out of 24 cases, being better than the CPLEX solution on average by approximately 11.26%, but the CPLEX was better than SA on average by approximately 11.50%. Changing time to 5 min does not change the CPLEX solution quality significantly (the last two columns of Table 5). There is the same number of tests (i.e., 9 tests) in which SA solution was better than the CPLEX one. On average SA was better than the CPLEX by approximately 10.69%, but the CPLEX was better than SA on average by approximately 11.59%. For a set of 30 the SA was better than the CPLEX up to 24%, which proves the necessity of SA implementation.
Table 6 shows the SA computational time. It can be seen that the solution time varies from 0.02 min (1 s) for the small instance of 10 products on the 500 cm shelves to 227.10 min for the large 50 products instance on 750 cm shelves. The average solution time for 20 and 30 products equals a few minutes; for 10 products, the average time is even less than a minute. For 40 products, the average time is about an hour. For 50 products, the average time is more than 1.5 h.

Table 6.
Computational time of the SA algorithm
It could be noted that the computational size increases significantly with the increase in the number of products. However, the computational time does not differ so much if we allocate the same number of products on different shelf lengths.
Interesting results are reported in the last two columns. Because SA accepts the worse solution with a given probability, there is the possibility that once the solution has been destroyed, it would not be improved even in the last iteration. We have 3 such cases from 24 tests. Therefore, in our proposed SA we always save the best solution, and if in the last iteration the solution is worse, we replace it with the previously saved better solution. The last column reports the number of solutions in which the solution was the best in the last iteration from all 10 tests performed for each instance. It could be observed that in only 9 instances, the solution has not been getting worse while performing iterations. In the rest tests, we did not receive the highest improvement in the last iteration. This proves the usefulness of the second termination criteria parameter , which helps to save time.
The obtained results have been statistically analysed in PQStat 1.8.2.164. We have assumed the significance level equal 0.05. We have checked the profit SA and profit CPLEX. Statistics Friedman test gives p-value < 0.000001. By comparing the p-value of Friedman’s test with the significance level 0.05, we find that total planogram profit is not the same in the SA and CPLEX solutions (Table 7 and Figure 1).

Table 7.
Friedman ANOVA, trend test algorithm.
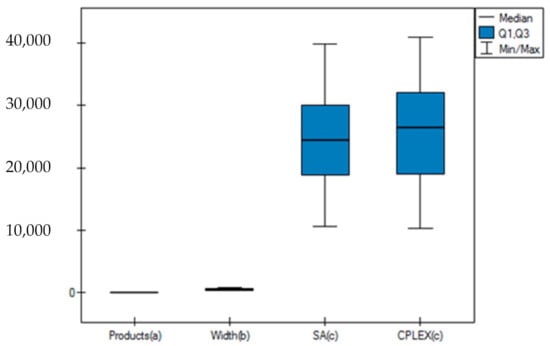
Figure 1.
Friedman ANOVA, trend test.
6. Conclusions
The SSAP attempts to find the best combination of product displays in order to optimize profitability. Because shelf resources are limited, decisions on the right product at the appropriate place with the proper space allocation are required.
In this paper, the problem of shelf space allocation with the aim of maximizing the total planogram fixture profit was studied. The idea of the research was motivated by the aesthetic appeal of symmetrical planograms and by the real business tasks of the retailers whose choices are important and challenging. Planograms have traditionally aided retailers in improving customer experience and making shopping easier by promoting product balance, symmetry, and visual attractiveness. Decisions are made for the number of facings of products on the shelves to regulate the profit; therefore, retailers need a mechanism that helps them to make a choice on how to get the highest possible profit. The objective of this paper was to propose a practical SSAP mathematical model and to develop an efficient solution algorithm based on simulated annealing for it. The model uses four types of constraints related to shelving, product, multi-shelf allocation, and segment, which influence the retailer’s decisions. To the best of our knowledge, the retailers’ tasks and constraints are diversified by the real-life problems, but most articles examine the standard set of constraints on the SSAP. Therefore, in this research, we tried to analyze different constraints simultaneously.
This paper outlined a SA hyper-heuristic algorithm to solve the SSAP. The problem was also solved by using CPLEX solver, the solution time of which was restricted to the SA algorithm time and to a constant time limit which equals 5 min. We performed the computational experiments on the artificial experimental data showing that the same product sets must be allocated in different stores, where planograms vary in their lengths. The SA algorithm performance for various data sets was also evaluated. The obtained results have been analyzed statistically. It was found that with a significance level 0.05 that the results obtained by SA and CPLEX solvers are not the same. The developed algorithm is expected to be useful in the retail industry considering shelf space allocation of the products in stores.
The SSAP is an extension of the multi-knapsack problem and is classified as NP-hard; therefore, it is difficult to be solved optimally in a reasonable time. As a consequence, heuristic and metaheuristic approaches are applied to find the appropriate solution. Various heuristic approaches are widely used to solve shelf space allocation or related problems and are also raised in the literature. In this research, we therefore turn our attention to the implementation of the SA algorithm, efficiently of which we compare to the CPLEX solver. The novel solution techniques such as improvement and reallocation procedures were added to the main SA. Therefore, the number of iterations in which the solution was found is relatively low.
The experimental results showed that the developed SA based approach is effective for providing good results at a reasonable solution time for various large-sized SSAPs. SA, investigated in this research, gives high-quality results in feasible time for miscellaneous problem instances. In 9 test cases from 24, the proposed SA was better than the CPLEX solver, both within the same as SA time limit and the 5 min time limit. Changing the CPLEX time limit does not generate other quality solutions. Unfortunately, the computational time increases extremely with the increase of the number of products—e.g., from 1 s for the 10 products up to 3 h 47 min for 50 products. However, the computational time does not noticeably differ if one set of products are allocated on different shelf lengths.
The main limitations of the proposed approach are:
- Considering a planogram of a single product category.
- Absence of time-dependent variables in the proposed model.
- Lack of defining the product positioning for all, not only specific products.
The limitations of our SSAP model point to some future areas of research. The first one is to optimize the product groups (not only for cluster products) rather than individual products. Next, the future model could incorporate supply chain decisions, schedule and delivery costs of the products from warehouses to stores. Finally, the current algorithm assigns products to the appropriate shelf or shelf segment. This means the physical possibility of product allocation without giving the accurate row or column. Therefore, some sorting or grouping methods could be applied as an extension of the method in the next research with the defining of the product position on the shelf or the restrictions to the surrounding products could be made. These considerations could be taken into account in future research.
The main implication of the presented research for science is that the developed model extends shelf space allocation models by constraints based on retailers’ requirements and customers’ buying decisions. The main implication of the presented research for practice is the possibility of using its results by the retailers who make product judgments or profit estimation while allocating products on planogram shelves. Additionally, the SA improving method provides results for retail-specific category management problem, which could be applied in other heuristics and metaheuristics. SA is an up-and-coming approach while dealing with combinatorial optimization tasks.
Author Contributions
Conceptualization, K.C. and M.H.; Methodology, K.C.; Software, K.C.; Validation, K.C. and M.H.; Formal analysis, K.C.; Investigation, K.C.; Resources, K.C. and M.H.; Data curation, K.C.; Writing—original draft preparation, K.C.; Writing—review and editing, M.H.; Visualization, K.C.; Supervision, M.H.; Project administration, M.H.; Funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education in Poland under the program “Regional Initiative of Excellence” 2019–2022 project number 015/RID/2018/19, total funding amount 10,721,040.00 PLN.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hübner, A. Retail Category Management: Decision Support Systems for Assortment, Shelf Space, Inventory and Price Planning; Springer: Berlin/Heidelberg, Germany, 2011; Volume 656. [Google Scholar]
- Hübner, A.; Schaal, K. A shelf-space optimisation model when demand is stochastic and space-elastic. Omega 2017, 68, 139–154. [Google Scholar] [CrossRef]
- Bianchi-Aguiar, T.; Hübner, A.; Carravilla, M.A.; Oliveira, J.F. Retail shelf space planning problems: A comprehensive review and classification framework. Eur. J. Oper. Res. 2021, 289, 1–16. [Google Scholar] [CrossRef]
- Buttle, F. Retail space allocation. Internat. J. Phys. Distrib. Mater. Manag. 1984, 14, 3–23. [Google Scholar]
- Zhang, W.; Rajaram, K. Managing limited retail space for basic products: Space sharing vs. space dedication. Eur. J. Oper. Res. 2017, 263, 768–781. [Google Scholar] [CrossRef] [Green Version]
- Urban, T.L. An inventory-theoretic approach to product assortment and shelf-space allocation. J. Retail. 1998, 74, 15–35. [Google Scholar] [CrossRef]
- Hübner, A.; Schaal, K. Effect of replenishment and backroom on retail shelf-space planning. Bus. Res. 2017, 10, 123–156. [Google Scholar] [CrossRef] [Green Version]
- Czerniachowska, K.; Hernes, M. Optimization Models for the Shelf Space Allocation Problem with Vertical Position Effects. In Proceedings of the 36th IBIMA Conference, Granada, Spain, 4–5 November 2020. [Google Scholar]
- Kim, G.; Moon, I. Integrated planning for product selection, shelf-space allocation, and replenishment decision with elasticity and positioning effects. J. Retail. Consum. Serv. 2021, 58, 102274. [Google Scholar] [CrossRef]
- Czerniachowska, K.; Hernes, M. A genetic algorithm for the shelf-space allocation problem with vertical position effects. Mathematics 2020, 8, 1881. [Google Scholar] [CrossRef]
- Czerniachowska, K.; Hernes, M. A heuristic approach to shelf space allocation decision support including facings, capping, and nesting. Symmetry 2021, 13, 314. [Google Scholar] [CrossRef]
- Flores, W.; Chen, J.-C.V.; Ross, W.H. The effect of variations in banner ad, type of product, website context, and language of advertising on Internet users’ attitudes. Comput. Hum. Behav. 2014, 31, 37–47. [Google Scholar] [CrossRef]
- Djamasbi, S.; Siegel, M.; Tullis, T. Generation Y, web design, and eye tracking. Int. J. Hum. Comput. St. 2010, 68, 307–323. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-Y.; Chou, C.-J.; Lin, P.-C. Involvement theory in constructing bloggers’ intention to purchase travel products. Tour. Manag. 2010, 31, 513–526. [Google Scholar] [CrossRef]
- Desrochers, D.M.; Nelson, P. Adding consumer behavior insights to category management: Improving item placement decisions. J. Retail. 2006, 82, 357–365. [Google Scholar] [CrossRef]
- Valenzuela, A.; Raghubir, P. Center of Orientation: Effect of Vertical and Horizontal Shelf Space Product Position. ACR N. Am. Adv. 2009, 36, 100–103. [Google Scholar]
- Ngo, D.C.L.; Byrne, J.G. Application of an aesthetic evaluation model to data entry screens. Comput. Hum. Behav. 2001, 17, 149–185. [Google Scholar] [CrossRef]
- Anic, I.-D.; Radas, S.; Lim, L.K.S. Relative effects of store traffic and customer traffic flow on shopper spending. Int. Rev. Retail. Distrib. Consum. Res. 2010, 20, 237–250. [Google Scholar] [CrossRef]
- Daruka, G.P.; Palekar, U.S. Application of column generation techniques to retail assortment planning. In Integer Programming: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2005; pp. 221–251. [Google Scholar] [CrossRef]
- Flamand, T.; Ghoniem, A.; Haouari, M.; Maddah, B. Integrated assortment planning and store-wide shelf space allocation: An optimisation-based approach. Omega 2018, 81, 134–149. [Google Scholar] [CrossRef]
- Kök, A.G.; Fisher, M.L.; Vaidyanathan, R. Assortment planning: Review of literature and industry practice. In International Series in Operations Research and Management Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 223, pp. 175–236. [Google Scholar] [CrossRef]
- Kök, A.G.; Fisher, M.L.; Vaidyanathan, R. Assortment planning: Review of literature and industry practice. Retail supply chain management. In Retail Supply Chain Management. International Series in Operations Research and Management Science; Springer: Boston, MA, USA, 2008; Volume 122, pp. 99–153. [Google Scholar] [CrossRef]
- Irion, J.; Lu, J.C.; Al-Khayyal, F.; Tsao, Y.C. A piecewise linearisation framework for retail shelf space management models. Eur. J. Oper. Res. 2012, 222, 122–136. [Google Scholar] [CrossRef]
- Geismar, H.N.; Dawande, M.; Murthi, B.P.S.; Sriskandarajah, C. Maximizing Revenue Through Two-Dimensional Shelf-Space Allocation. Prod. Oper. Manag. 2015, 24, 1148–1163. [Google Scholar] [CrossRef]
- Yu, V.F.; Maglasang, R.; Tsao, Y.C. A reduced variable neighborhood search-based hyperheuristic for the shelf space allocation problem. Comput. Ind. Eng. 2020, 143, 106420. [Google Scholar] [CrossRef]
- Silver, E.A. Operations Research and Inventory Management: A Review and Critique. Oper. Res. 1981, 29, 628–645. [Google Scholar] [CrossRef]
- Drèze, X.; Hoch, S.J.; Purk, M.E. Shelf management and space elasticity. J. Retail. 1994, 70, 301–326. [Google Scholar] [CrossRef] [Green Version]
- Russell, R.A.; Urban, T.L. The location and allocation of products and product families on retail shelves. Ann. Oper. Res. 2010, 179, 131–147. [Google Scholar] [CrossRef]
- Esparcia-Alcázar, A.I.; Martínez-García, A.I. Linear Shelf Space Allocation Using a Multi Objective Evolutionary Algorithm. Technical Report ITI-SAC-027. 2008, pp. 1–23. Available online: https://pdfs.semanticscholar.org/e768/f366d4c7cb4009e5d937eb177710003a38f8.pdf (accessed on 29 June 2021).
- Pinto, F.; Soares, C. Space allocation in the retail industry: A decision support system integrating evolutionary algorithms and regression models. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2013; pp. 531–546. Available online: https://link.springer.com/chapter/10.1007/978-3-642-40994-3_34 (accessed on 29 June 2021).
- Borin, N.; Farris, P.W.; Freeland, J.R. A Model for Determining Retail Product Category Assortment and Shelf Space Allocation. Decis. Sci. 1994, 25, 359–384. [Google Scholar] [CrossRef]
- Bai, R.; Kendall, G. An investigation of automated planograms using a simulated annealing based hyper-heuristic. Oper. Res. Comput. Sci. Interfaces Ser. 2005, 32, 87–108. [Google Scholar]
- Van Nierop, E.; Fok, D.; Franses, P.H. Interaction between shelf layout and marketing effectiveness and its impact on optimising shelf arrangements. Mark. Sci. 2008, 27, 1065–1082. [Google Scholar] [CrossRef]
- Bai, R.; van Woensel, T.; Kendall, G.; Burke, E.K. A new model and a hyper-heuristic approach for two-dimensional shelf space allocation. 4OR 2013, 11, 31–55. [Google Scholar] [CrossRef]
- Hwang, H.; Choi, B.; Lee, M.J. A model for shelf space allocation and inventory control considering location and inventory level effects on demand. Int. J. Prod. Econ. 2005, 97, 185–195. [Google Scholar] [CrossRef]
- Esparcia-Alcazar, A.I.; Lluch-Revert, L.; Sharman, K.C.; Albarracin-Guillem, J.M.; Palmer-Gato, M.E. Towards an evolutionary tool for the allocation of supermarket shelf space. In Proceedings of the eighth annual conference on genetic and evolutionary computation, Woshington, DC, USA, 8–12 July 2006; pp. 1653–1660. [Google Scholar]
- Esparcia-Alćazar, A.I.; Lluch-Revert, L.; Sharman, K.; Albarracín-Guillem, J.M.; Palmer-Gato, M.E. An Evolutionary Algorithm for the Product to Shelf Allocation Problem. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; IEEE, 2006. [Google Scholar] [CrossRef]
- Hansen, J.M.; Raut, S.; Swami, S. Retail Shelf Allocation: A Comparative Analysis of Heuristic and Meta-Heuristic Approaches. J. Retail. 2010, 86, 94–105. [Google Scholar] [CrossRef]
- Ghazavi, E.; Lotfi, M.M. Formulation of customers’ shopping path in shelf space planning: A simulation-optimisation approach. Expert Syst. Appl. 2016, 55, 243–254. [Google Scholar] [CrossRef]
- Ozcan, T.; Esnaf, S. A heuristic approach based on artificial bee colony algorithm for retail shelf space optimisation. In Proceedings of the 2011 IEEE Congress on Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 95–101. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Otten, R.H.J.M.; van Ginneken, L.P.P.P. The Annealing Algorithm; Kluwer: Boston, MA, USA, 1989. [Google Scholar]
- Ingber, L. Simulated Annealing: Practice Versus Theory. Math. Comput. Model. 1993, 18, 29–57. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).