Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization
Abstract
1. Introduction
2. Theoretical Description
3. Results and Discussion
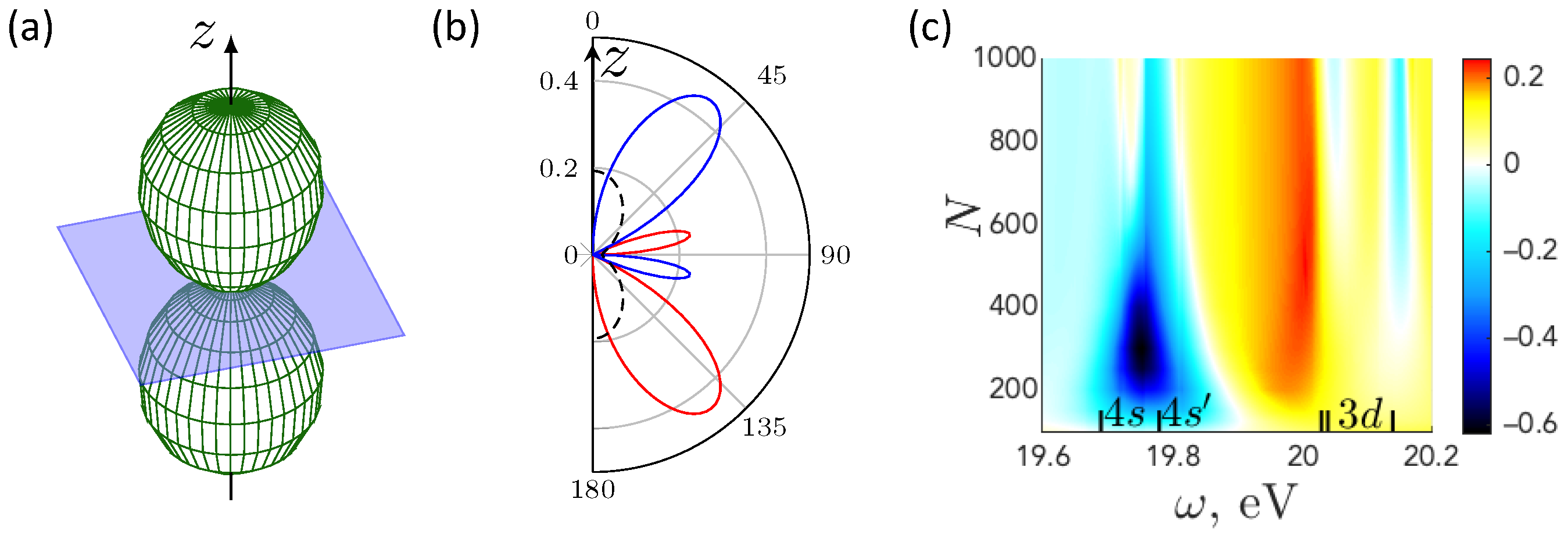
3.1. Photoelectron Spin Polarization in Two-Photon Ionization
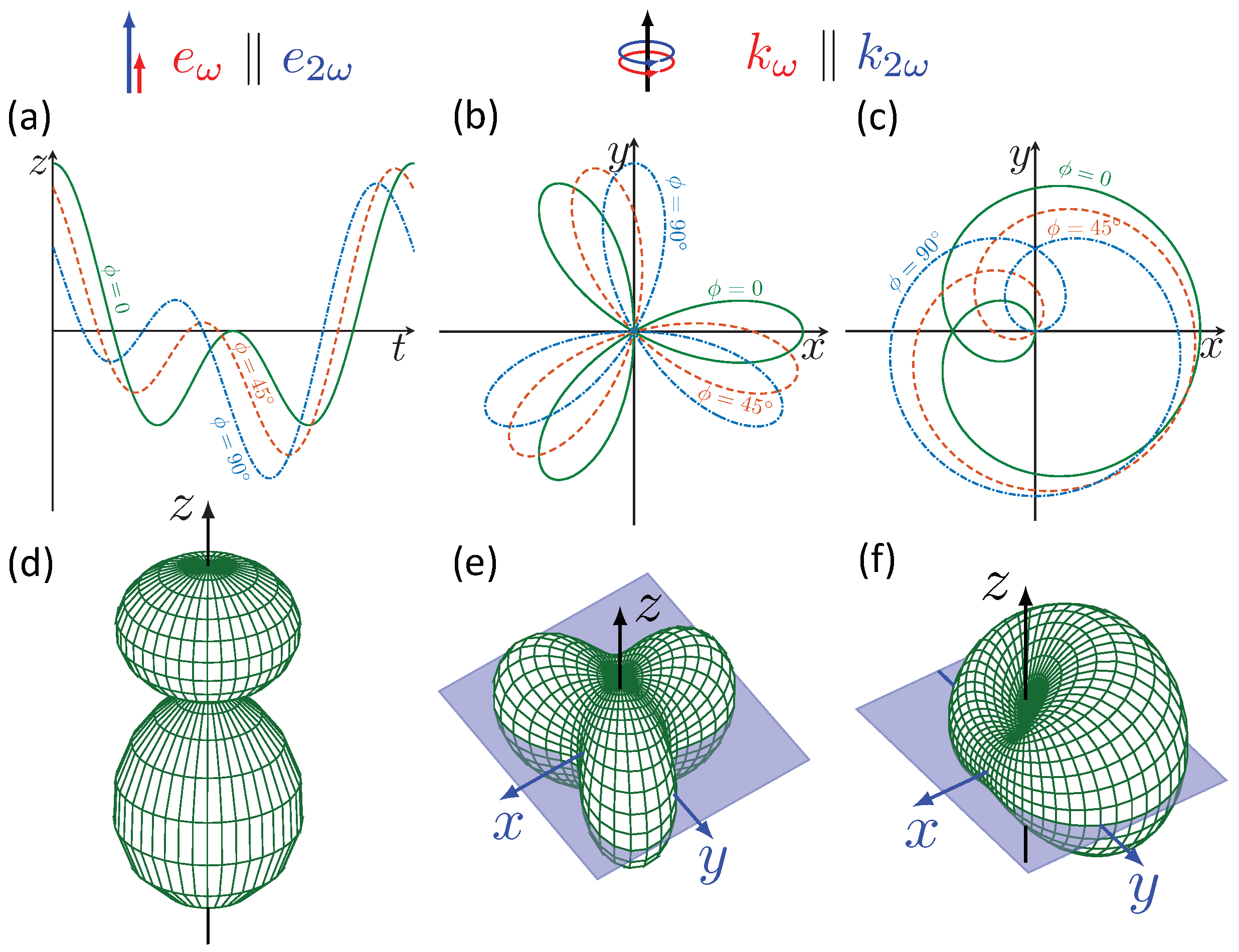
3.2. Parallel Polarization Vectors
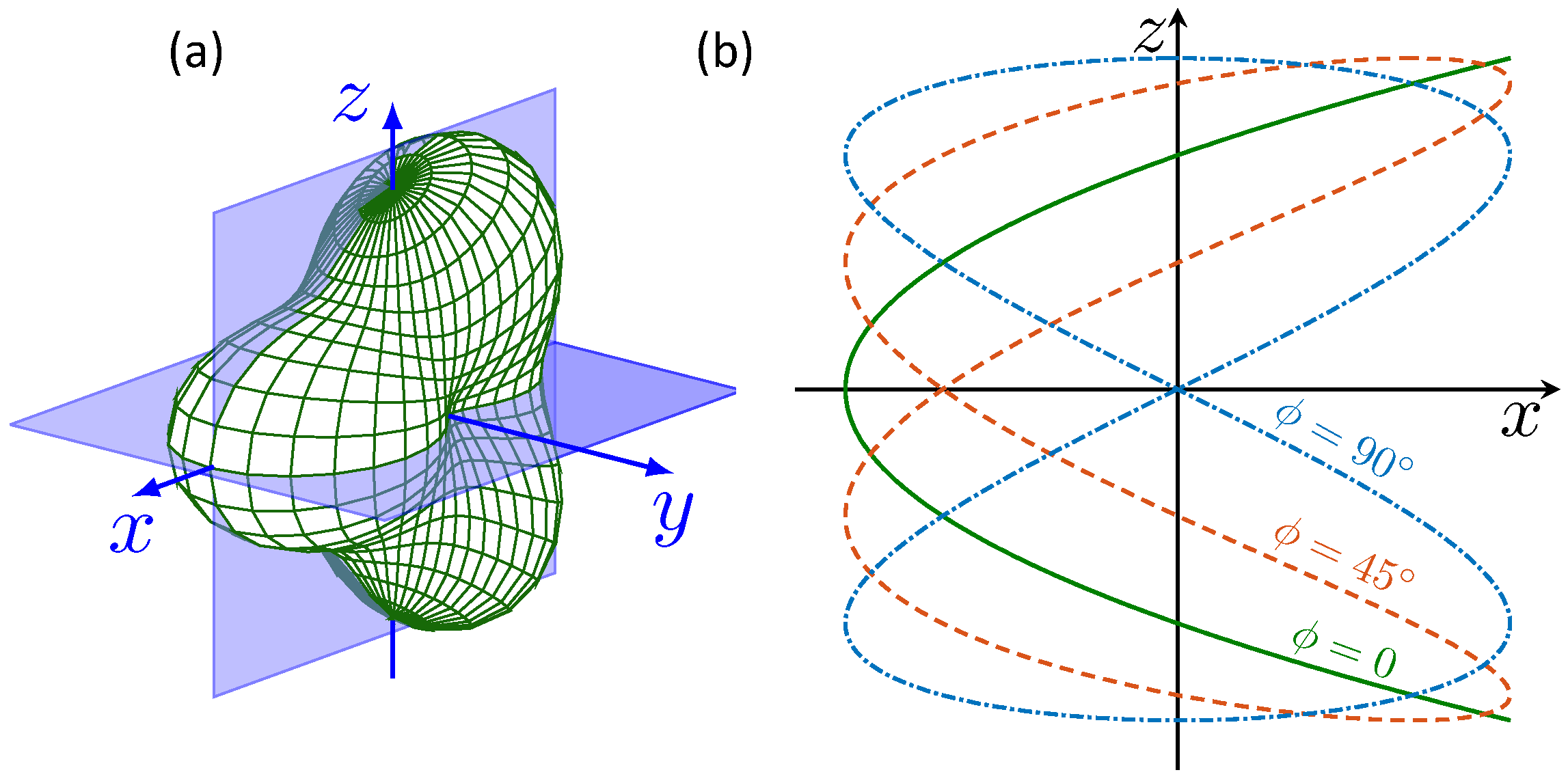
3.3. Orthogonal Polarization Vectors
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Statistical Tensor Formalism
- (a)
- For fields polarized in the same direction.
- (b)
- For fields polarized in orthogonal directions.
Appendix B. Atomic Model
- (a)
- odd CSFs: ; ; ; ; .
- (b)
- even CSFs: ; ; ; ; .
| State | E, eV | Leading Configurations |
|---|---|---|
| 16.67 | ||
| 16.85 | ||
| 19.69 | ||
| 19.78 | ||
| 20.03 | ||
| 20.04 | ||
| 20.14 | ||
| 20.57 | ||
| 20.66 | ||
| 20.70 | ||
| 20.71 | ||
| 20.81 | ||
| 20.95 | ||
| 21.01 | ||
| 21.02 | ||
| 21.04 | ||
| 21.11 |
References
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.; von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.; Treger, D. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef]
- Rougemaille, N.; Schmid, A. Magnetic imaging with spin-polarized low-energy electron microscopy. Eur. Phys. J. Appl. Phys. 2010, 50, 20101. [Google Scholar] [CrossRef]
- Johnson, P.D. Spin-polarized photoemission. Rep. Prog. Phys. 1997, 60, 1217–1304. [Google Scholar] [CrossRef]
- Heinzmann, U.; Dil, J.H. Spin-orbit-induced photoelectron spin polarization in angle-resolved photoemission from both atomic and condenced matter targets. J. Phys. Condens. Matter 2012, 24, 173001. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.; Qian, T.; Ding, H. Angle-resolved photoemission spectroscopy and its application to topological materials. Nat. Rev. Phys. 2019, 1, 609–626. [Google Scholar] [CrossRef]
- Fano, U. Spin Orientation of Photoelectrons Ejected by Circularly Polarized Light. Phys. Rev. 1969, 178, 131–136, ibid 184, 250, 1969 Erratum. [Google Scholar] [CrossRef]
- Lubell, M.S.; Raith, W. Polarization Effect in Photoionization of Cesium. Phys. Rev. Lett. 1969, 23, 211–214. [Google Scholar] [CrossRef]
- Kessler, J.; Lorenz, J. Experimental Verification of the Fano Effect. Phys. Rev. Lett. 1970, 24, 87–88. [Google Scholar] [CrossRef]
- Cherepkov, N. Spin Polarization of Atomic and Molecular Photoelectrons. In Advances in Atomic and Molecular Physics; Bates, D., Bederson, B., Eds.; Academic Press: Cambridge, MA, USA, 1983; Volume 19, pp. 395–447. [Google Scholar] [CrossRef]
- Cherepkov, N. Spin polarisation of photoelectrons ejected from unpolarised atoms. J. Phys. B At. Mol. Opt. Phys. 2001, 12, 1279. [Google Scholar] [CrossRef]
- Cherepkov, N. Spin polarisation of electrons ejected from unpolarised atoms by unpolarised and linearly polarised light. J. Phys. B At. Mol. Opt. Phys. 1978, 11, L435. [Google Scholar] [CrossRef]
- Barth, I.; Smirnova, O. Spin-polarized electrons produced by strong-field ionization. Phys. Rev. A 2013, 88, 013401. [Google Scholar] [CrossRef]
- Milošević, D.B. Possibility of introducing spin into attoscience with spin-polarized electrons produced by a bichromatic circularly polarized laser field. Phys. Rev. A 2016, 93, 051402. [Google Scholar] [CrossRef]
- Milošević, D.B. Atomic and Molecular Processes in a Strong Bicircular Laser Field. Atoms 2018, 6, 61. [Google Scholar] [CrossRef]
- Liu, M.M.; Shao, Y.; Han, M.; Ge, P.; Deng, Y.; Wu, C.; Gong, Q.; Liu, Y. Energy- and Momentum-Resolved Photoelectron Spin Polarization in Multiphoton Ionization of Xe by Circularly Polarized Fields. Phys. Rev. Lett. 2018, 120, 043201. [Google Scholar] [CrossRef]
- Baranova, N.B.; Zel’dovich, B.Y. Physical effects in optical fields with nonzero average cube <E3> ≠ 0. J. Opt. Soc. Am. B 1991, 8, 27–32. [Google Scholar] [CrossRef]
- Yin, Y.Y.; Chen, C.; Elliott, D.S.; Smith, A.V. Asymmetric photoelectron angular distributions from interfering photoionization processes. Phys. Rev. Lett. 1992, 69, 2353–2356. [Google Scholar] [CrossRef]
- Goetz, R.E.; Koch, C.P.; Greenman, L. Quantum Control of Photoelectron Circular Dichroism. Phys. Rev. Lett. 2019, 122, 013204. [Google Scholar] [CrossRef]
- Prince, K.C.; Allaria, E.; Callegari, C.; Cucini, R.; Ninno, G.D.; Di Mitri, S.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Coherent control with a short-wavelength free-electron laser. Nat. Photonics 2016, 10, 176–179. [Google Scholar] [CrossRef]
- Callegari, C.; Grum-Grzhimailo, A.N.; Ishikawa, K.L.; Prince, K.C.; Sansone, G.; Ueda, K. Atomic, molecular and optical physics applications of longitudinally coherent and narrow bandwidth Free-Electron Lasers. Phys. Rep. 2021, 904, 1–59. [Google Scholar] [CrossRef]
- You, D.; Ueda, K.; Gryzlova, E.V.; Grum-Grzhimailo, A.N.; Popova, M.M.; Staroselskaya, E.I.; Tugs, O.; Orimo, Y.; Sato, T.; Ishikawa, K.L.; et al. New Method for Measuring Angle-Resolved Phases in Photoemission. Phys. Rev. X 2020, 10, 031070. [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Popova, M.M.; Grum-Grzhimailo, A.N. Spin polarization of photoelectrons in bichromatic extreme-ultraviolet atomic ionization. Phys. Rev. A 2020, 102, 053116. [Google Scholar] [CrossRef]
- Hübner, J.; Rühle, W.W.; Klude, M.; Hommel, D.; Bhat, R.D.R.; Sipe, J.E.; van Driel, H.M. Direct Observation of Optically Injected Spin-Polarized Currents in Semiconductors. Phys. Rev. Lett. 2003, 90, 216601. [Google Scholar] [CrossRef]
- Stevens, M.J.; Smirl, A.L.; Bhat, R.D.R.; Najmaie, A.; Sipe, J.E.; van Driel, H.M. Quantum Interference Control of Ballistic Pure Spin Currents in Semiconductors. Phys. Rev. Lett. 2003, 90, 136603. [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Popova, M.M.; Grum-Grzhimailo, A.N.; Staroselskaya, E.I.; Douguet, N.; Bartschat, K. Coherent control of the photoelectron angular distribution in ionization of neon by a circularly polarized bichromatic field in the resonance region. Phys. Rev. A 2019, 100, 063417. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; Dover Publications: Mineola, NY, USA, 1961. [Google Scholar]
- Balashov, V.V.; Grum-Grzhimailo, A.N.; Kabachnik, N.M. Polarization and Correlation Phenomena in Atomic Collisions. A Practical Theory Course; Physics of Atoms and Molecules, Kluwer Academic/Plenum Publishers: New York, NY, USA; Boston, MA, USA; Dordrecht, The Netherland; London, UK; Moscow, Russia, 2000. [Google Scholar] [CrossRef]
- Nakajima, T.; Lambropoulos, P. Electron spin-polarization in one-, two- and three-photon ionization of xenon. Europhys. Lett. 2002, 57, 25. [Google Scholar] [CrossRef]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Jacobs, V.L. Polarization phenomena in multiphoton ionization of atoms. J. Phys. B Atom. Molec. Phys. 1973, 6, 1461–1472. [Google Scholar] [CrossRef]
- Dill, D. Resonances in Photoelectron Angular Distributions. Phys. Rev. A 1973, 7, 1976–1987. [Google Scholar] [CrossRef]
- Devons, S.; Goldfarb, L.J.B. Angular Correlations. In Kernreaktionen III/Nuclear Reactions III; Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1957; Volume 42, Chapter 5; pp. 362–554. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure. An MCHF Approach; Institute of Physics Publishing: Bristol, UK, 1997. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.8); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020. Available online: https://physics.nist.gov/asd (accessed on 21 April 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popova, M.M.; Gryzlova, E.V.; Kiselev, M.D.; Grum-Grzhimailo, A.N. Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization. Symmetry 2021, 13, 1015. https://doi.org/10.3390/sym13061015
Popova MM, Gryzlova EV, Kiselev MD, Grum-Grzhimailo AN. Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization. Symmetry. 2021; 13(6):1015. https://doi.org/10.3390/sym13061015
Chicago/Turabian StylePopova, Maria M., Elena V. Gryzlova, Maksim D. Kiselev, and Alexei N. Grum-Grzhimailo. 2021. "Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization" Symmetry 13, no. 6: 1015. https://doi.org/10.3390/sym13061015
APA StylePopova, M. M., Gryzlova, E. V., Kiselev, M. D., & Grum-Grzhimailo, A. N. (2021). Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization. Symmetry, 13(6), 1015. https://doi.org/10.3390/sym13061015







