A Hopf Algebra on Permutations Arising from Super-Shuffle Product

Abstract

In this paper, we first prove that any atom of a permutation obtained by the super-shuffle product of two permutations can only consist of some complete atoms of the original two permutations. Then, we prove that the super-shuffle product and the cut-box coproduct on permutations are compatible, which makes it a bialgebra. As this algebra is graded and connected, it is a Hopf algebra.

1. Introduction

The concept of Hopf algebra was derived from the study of algebraic topology and algebraic groups in the 1940s and 1950s [1,2,3]. The structure of Hopf algebras is relatively stable and has many properties worth studying, such as commutativity, cocommutativity, and free and cofree properties [4,5,6]. With the further study of these properties, many new Hopf algebra structures have been discovered, especially in algebraic combinatorics, such as Hopf algebra on permutations [6,7,8], Hopf algebra on graphs [9], Hopf algebra on trees [6,10], and Hopf algebra on the symmetric functions [11,12]. In recent years, they have been gradually applied to many subjects, such as free Lie algebras [13,14], Lie superalgebras [15,16], Clifford algebras [17,18,19], Drinfeld-Jimbo quantum groups [20], the Jacobian Conjecture for free metabelian algebras [21,22] and even nonlinear control theory [23].

In 1995, Malvenuto and Reutenauer [24] studied a pair of Hopf algebra on permutations, where one of the products ${\star }^{\prime }$ is essentially the shuffle product ш in [25]. The shuffle product’s ш is classic and has been studied by many teams recently. However, the product ${\star }^{\prime }$ is not commutative on permutations. In 2020, Zhao and Li [26] introduced a new shuffle product ${\text{ш}}_G$ on permutations based on the global descents, which makes it commutative. Then, they defined a deconcatenation coproduct $\Delta$ and proved that $(KS,{\text{ш}}_G,\mu ,\Delta ,\nu )$ is a graded connected bialgebra and, hence, a Hopf algebra [27]. Moreover, they figured out its dual Hopf algebra $(KS,{\text{ш}}_G^{*},\mu ,{\Delta }^{*},\nu )$ and a closed-formula of its antipode [28].

The symmetric group on a set X, denoted as $Sym\left(X\right)$, is a group of all bijections from X to itself, which is widely applied to many areas, such as algebraic number theory [29] and substochastic matrices [30,31,32,33]. In combinatorics, a permutation of degree n is an arrangement of n elements. The symmetric group of degree n, denoted by $S_n$, contains all permutations of $\left[n\right]=\{1,2,\dots ,n\}$. Let $K{S}_n$ be the vector space spanned by $S_n$ over field K, where $S_n$ is the symmetric group of degree n. Define $KS:={⨁}_{n\ge 0}K{S}_n$, where $S_0=\left\{ϵ\right\}$ and $ϵ$ is the empty permutation. Then, $KS$ is graded, and its nth component is $K{S}_n$.

In 2014, Vargas [34] defined the super-shuffle product $\underline{\text{ш}}$ on permutations, interpolating between the products ⋆ and ${\star }^{\prime }$ given in [24], and a coproduct ${\Delta }_{\diamond }$, called the cut-box coproduct in our paper. He also put forward that the super-shuffle product $\underline{\text{ш}}$ is commutative and associative on permutations and claimed that $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a graded connected bialgebra and, hence, a Hopf algebra. However, he did not provide a proof.

In 2018, Bergeron, Ceballos, and Pilaud [35] gave a new concept of gaps on permutations in $S_n$. In 2020, Aval, Bergeron, and Machacek [36] introduced global ascents of permutations and the standard factorization of a permutation given by global ascents. Then, the cut-box coproduct ${\Delta }_{\diamond }$ of a permutation can be reinterpreted as using the tensor notation at one of its global ascents. In this paper, we prove that any atom of a permutation obtained by the super-shuffle product of two permutations can only consist of some complete atoms of the original two permutations, see Lemma 1. The main work of this paper is to prove that $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a bialgebra.

In Section 2, we recall some important definitions and notations on Hopf algebras and permutations. In Section 3, we introduce the definition of a super-shuffle product $\underline{\text{ш}}$ and reinterpret the cut-box coproduct ${\Delta }_{\diamond }$ on permutations. We prove that ш and ${\Delta }_{\diamond }$ satisfy the compatibility condition in Section 4. Therefore, $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a Hopf algebra since it is graded and connected. Finally, a summarization can be found in Section 5.

2. Preliminaries

2.1. Basic Definitions

Here, we recall some basic definitions related to Hopf algebra, see [3] for more details. Let R be a commutative ring and B be an R-module.

Define a product $\pi :B{\otimes }_{R}B⟶B$ and a unit $\mu :R⟶B$, respectively, satisfying the diagrams in Figure 1.

Figure 1. Associative law and unit.

Then, $(B,\pi ,\mu )$ is an R-algebra.

The algebra B is graded if there is a direct sum decomposition $B={⨁}_{i\ge 0}{B}_i$ such that the product of homogeneous elements of degrees p and q is homogeneous of degree $p+q$, that is, $\pi (B_p\otimes B_q)\subseteq B_{p+q}$, and $\mu \left(R\right)\subseteq B_0$.

Define a coproduct $\Delta :B⟶B{\otimes }_{R}B$ and a counit $\nu :B⟶R$, respectively, satisfying the diagrams in Figure 2.

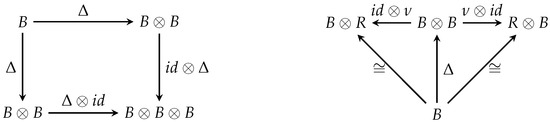
Figure 2. Coassociative Law and Counit.

Then, $(B,\Delta ,\nu )$ is an R-coalgebra.

The coalgebra B is graded if there is a direct sum decomposition $B={⨁}_{i\ge 0}{B}_i$ such that $\Delta \left(B_n\right)\subseteq ⨁(B_k\otimes B_{n-k})$ and $\nu \left(B_n\right)=0$ if $n\ge 1$.

If B is both an R-algebra and an R-coalgebra, and satisfies one of the following equivalent conditions:

(1) $\Delta$ and $\nu$ are algebra homomorphisms;

(2) $\pi$ and $\mu$ are coalgebra homomorphisms,

then we say the algebra and coalgebra structures on B are compatible and $(B,\pi ,\mu ,\Delta ,\nu )$ is an R-bialgebra.

If $B={⨁}_{i\ge 0}{B}_i$ is both a graded algebra and a graded coalgebra, and satisfies the compatibility condition, then we say B is a graded bialgebra.

If there exists a linear map $\theta :B⟶B$ satisfying

$$\pi \circ (\theta \otimes id)\circ \Delta =\mu \circ \nu =\pi \circ (id\otimes \theta )\circ \Delta ,$$

i.e., the diagram in Figure 3 commutes, then $\theta$ is an antipode. A bialgebra with an antipode is a Hopf algebra.

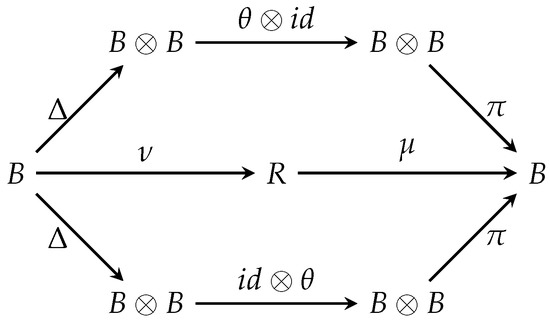
Figure 3. Antipode.

A bialgebra B over K is called graded connected if it is graded and satisfies $B_0=K{1}_B$, where K is a field. In 2008, Manchon [27] proved that any graded connected bialgebra admits a unique antipode and is a Hopf algebra.

2.2. Basic Notations

Now, we recall some basic notations on permutations; see [34,36] for more details.

Let $S_n$ be the symmetric group of degree n, which consists of all the permutations of degree n. A permutation $\omega$ in $S_n$ is a rearrangement of $\left[n\right]:=\{1,2,\dots ,n\}$, denoted by $\omega ={\omega }_1\cdots {\omega }_i{\omega }_{i+1}\cdots {\omega }_n$ in one-line notation, where ${\omega }_i=\omega \left(i\right)\in \left[n\right]$. Let $S:={\uplus }_{n\ge 0}{S}_n$ be the disjoint union of $S_n$, where $S_0=\left\{ϵ\right\}$ and $ϵ$ is the empty permutation.

For a permutation $\omega ={\omega }_1{\omega }_2\cdots {\omega }_n$ in $S_n$ in one-line notation, the position in front of the first element ${\omega }_1$ is called gap 0 of $\omega$, the position between ${\omega }_i$ and ${\omega }_{i+1}$ is called gapi of $\omega$ for all $0<i<n$, and the position behind the last element ${\omega }_n$ is called gap n of $\omega$. For example, the gaps of permutation $321465\in S_6$ are the numbers in the circles: ${}_{\mathrm{⓪}}{3}_{\mathrm{①}}{2}_{\mathrm{②}}{1}_{\mathrm{③}}{4}_{\mathrm{④}}{6}_{\mathrm{⑤}}{5}_{\mathrm{⑥}}$.

For a gap $\gamma$ of $\omega$, if $\omega \left(\right[\gamma \left]\right)=\left[\gamma \right]$, then $\gamma$ is called a global ascent of $\omega$. The gaps 0 and n must be global ascents of any permutation of degree n. A nonempty permutation with no global ascents except 0 and n is called an indecomposable permutation or an atom. A portion of an atom is a nontrivial subsequence of k adjacent elements from an atom with m elements, where $0<k<m$. For example, permutations $321,312,21$, and 1 are all atoms. The portions of 321 can only be $3,2,1,32$, and 21.

A sequence of $\left[n\right]$ with length m is denoted by $a=a_1{a}_2\cdots a_m(1\le m\le n)$, where $a_i(1\le i\le m)$ are finitely distinct elements selected from $\left[n\right]$. When no element is selected, we have an empty sequence with length 0, also denoted by $ϵ$. Let $\mathrm{alph}\left(a\right)$ be the set consisting of all elements in a and $A_m$ be the set of all the sequences of length m. The standard form of sequence a in $A_m$ is a permutation in $S_m$, denoted by $\mathrm{st}\left(a\right)$, satisfying

$$\mathrm{st}\left(a_i\right)<\mathrm{st}\left(a_j\right)\iff a_i<a_j,$$

$$\mathrm{st}\left(a_i\right)>\mathrm{st}\left(a_j\right)\iff a_i>a_j.$$

For example, the standard form of sequence 432 is 321, i.e., $\mathrm{st}\left(432\right)=321$. The standard form of the empty sequence is the empty permutation, i.e., $\mathrm{st}\left(ϵ\right)=ϵ$.

Consider a permutation $\alpha \in S_n$. By putting boxes ⋄ at all global ascents except 0 and n, we find $\alpha ={\alpha }_1\diamond \cdots \diamond {\alpha }_l$, called the factorization of $\alpha$, where ${\alpha }_i$’s are sequences of $\left[n\right]$ and the sum of the length of all ${\alpha }_i$’s is n. For example, let $\alpha =2314657$, then its global ascents are $0,3,4,6,7$ and its factorization is $\alpha =231\diamond 4\diamond 65\diamond 7$, where ${\alpha }_1=231,{\alpha }_2=4,{\alpha }_3=65,$ ${\alpha }_4=7$.

By taking the standard form of each sequence ${\alpha }_i(1\le i\le l)$, we obtain $\alpha$’s standard factorization $\alpha =\mathrm{st}\left({\alpha }_1\right)\diamond \cdots \diamond \mathrm{st}\left({\alpha }_l\right)$. Each permutation has a unique standard factorization. Clearly, each $\mathrm{st}\left({\alpha }_i\right)(1\le i\le l)$ in the standard factorization of $\alpha$ is an atom. The number of atoms in $\alpha$ is called the length of $\alpha$, denoted as ${\left|\alpha \right|}_{\diamond }$, so ${\left|\alpha \right|}_{\diamond }=l$, which is always less than or equal to its degree n. From now on, the notation $\alpha ={\alpha }_1\diamond \cdots \diamond {\alpha }_l$ always expresses $\alpha$’s standard factorization. For example, the standard factorization of $\alpha =2314657$ is $\alpha =\mathrm{st}\left(231\right)\diamond \mathrm{st}\left(4\right)\diamond \mathrm{st}\left(65\right)\diamond \mathrm{st}\left(7\right)=231\diamond 1\diamond 21\diamond 1$, where ${\alpha }_1=231,{\alpha }_2=1,{\alpha }_3=21,{\alpha }_4=1$, and the length of $\alpha$ is ${\left|\alpha \right|}_{\diamond }={|231\diamond 1\diamond 21\diamond 1|}_{\diamond }=4$.

From a standard factorization to the original permutation, we renumber the numbers in the atoms from left to right. For example,

$$21\diamond 12\diamond 1\diamond 1=213456,$$

$$1\diamond 12\diamond 12\diamond 1=123456.$$

3. Super-Shuffle Product and Cut-Box Coproduct

In 2014, Vargas defined two operations on permutations—the super-shuffle product and cut-box coproduct as follows [34].

Define the cut-box coproduct ${\Delta }_{\diamond }$ on $KS$ by

$${\Delta }_{\diamond }\left(\alpha \right):=\sum _{i=0}^l{\alpha }_1\diamond \cdots \diamond {\alpha }_i\otimes {\alpha }_{i+1}\diamond \cdots \diamond {\alpha }_l,$$

for any permutation $\alpha ={\alpha }_1\diamond {\alpha }_2\diamond \cdots \diamond {\alpha }_l$.

Example 1.

For permutation 214356, its global ascents are $0,2,4,5,6$, and its standard factorization is $21\diamond 21\diamond 1\diamond 1$. Then,

$$\begin{array}{cc}\hfill {\Delta }_{\diamond }\left(214356\right)=& {\Delta }_{\diamond }(21\diamond 21\diamond 1\diamond 1)\hfill \\ \hfill =& ϵ\otimes 21\diamond 21\diamond 1\diamond 1+21\otimes 21\diamond 1\diamond 1+21\diamond 21\otimes 1\diamond 1\hfill \\ \hfill & +21\diamond 21\diamond 1\otimes 1+21\diamond 21\diamond 1\diamond 1\otimes ϵ\hfill \\ \hfill =& ϵ\otimes 214356+21\otimes 2134+2143\otimes 12\hfill \\ & +21435\otimes 1+214356\otimes ϵ.\hfill \end{array}$$

From above, in the coproduct of a permutation the tensor notation ⊗ can only appear in one of its global ascents.

The counit map on $KS$ is defined by $\nu :KS⟶K,\nu \left(ϵ\right)=1$ and $\nu \left(\alpha \right)=0$ for any $\alpha \in S_n,n\ge 1$.

Let $I,J\subseteq \left[n\right]$, and $\left[n\right]$ be the disjoint union of I and J, denoted by $I\uplus J=\left[n\right]$.

For a permutation $\omega ={\omega }_1\cdots {\omega }_n\in S_n$, let ${\omega }_I={\omega }_{i_1}\cdots {\omega }_{i_k}$ with $I=\{i_1<\cdots <i_k\}\subseteq \left[n\right]$.

Define super-shuffle product on $KS$ by

$$\alpha \underline{\text{ш}}\beta :=\sum _{\begin{array}{c}I\uplus J=[n+p]\\ st\left({\omega }_I\right)=\alpha ,st\left({\omega }_J\right)=\beta \\ alpha\left({\omega }_I\right)\uplus alpha\left({\omega }_J\right)=[n+p]\end{array}}\omega$$

for any $\alpha \in S_n$, $\beta \in S_p$.

Example 2.

Let $\alpha =12\in S_2,\beta =1\in S_1$.

$$\begin{array}{cc}\hfill 12\underline{\text{ш}}1=& 123+132+312\hfill \\ \hfill +& 132+123+213\hfill \\ \hfill +& 231+213+123.\hfill \end{array}$$

Here we color the elements of $\alpha$ red and the elements of $\beta$ blue, then the same numbers in $\alpha$ and $\beta$ are different. Thus, we can claim that all permutations in the super-shuffle product are distinct even if they are same. From now on, when we compute super-shuffle product of two permutations we will color them in different colors.

For $\alpha ={\alpha }_1\cdots {\alpha }_q\in S_q$, define ${\widehat{\alpha }}_i(1\le i\le q)$ to be the renumbering of ${\alpha }_i$ satisfying that, if $r\ne t$ and ${\alpha }_r<{\alpha }_t$, then ${\widehat{\alpha }}_r<{\widehat{\alpha }}_t$, for all $r,t\in \left[q\right]$.

Remark 1.

For $\alpha ={\alpha }_1\cdots {\alpha }_q\in S_q,\beta ={\beta }_1\cdots {\beta }_p\in S_p$. If $T:=\left\{{\widehat{\alpha }}_i\right|1\le i\le q\}\subseteq [q+p]$ and $\left\{{\widehat{\beta }}_j\right|1\le j\le p\}=[q+p]\backslash T$, then

$$\pi :={\widehat{\alpha }}_1\cdots {\widehat{\alpha }}_r{\widehat{\beta }}_1\cdots {\widehat{\alpha }}_t\cdots {\widehat{\beta }}_k\cdots {\widehat{\alpha }}_q{\widehat{\beta }}_s\cdots {\widehat{\beta }}_p$$

is a permutation in the super-shuffle product $\alpha \underline{\text{ш}}\beta$, where $0\le r\le q,r+1\le t\le q,1\le k\le s-1,1\le s\le p+1$. In particular, when $r=0$ the first element of π is ${\widehat{\beta }}_1$, and when $s=p+1$, the last element of π is ${\widehat{\alpha }}_q$.

Therefore, $\widehat{1}\widehat{2}\widehat{1}$ is one of permutations in $\{123,132,231\}$, $\widehat{1}\widehat{1}\widehat{2}$ is one of permutations in $\{132,123,213\}$, and $\widehat{1}\widehat{1}\widehat{2}$ is one of permutations in $\{312,213,123\}$.

Define the unit map $\mu :K⟶KS$ on $KS$ by $\mu \left(1\right)=ϵ$.

Define the relative shuffle product ${\text{ш}}_{\diamond }$ on $KS$ recursively by

$$\alpha {\text{ш}}_{\diamond }\beta ={\alpha }_1\diamond ({\alpha }_2\diamond \cdots \diamond {\alpha }_l{\text{ш}}_{\diamond }\beta )+{\beta }_1\diamond (\alpha {\text{ш}}_{\diamond }{\beta }_2\diamond \cdots {\beta }_k),$$

for $\alpha ={\alpha }_1\diamond \cdots \diamond {\alpha }_l$, $\beta ={\beta }_1\diamond \cdots \diamond {\beta }_k$ and $\alpha {\text{ш}}_{\diamond }ϵ=ϵ{\text{ш}}_{\diamond }\alpha =\alpha$.

For example,

$$(21\diamond 1){\text{ш}}_{\diamond }1=21\diamond 1\diamond 1+21\diamond 1\diamond 1+1\diamond 21\diamond 1=2134+2134+1324.$$

For $\alpha \in S_n$ and $\beta \in S_p$, the permutations obtained by $\alpha \underline{\text{ш}}\beta$ of degree $n+p$, which are the permutations obtained by $\alpha {\text{ш}}_{\diamond }\beta$ and some others with length less than ${\left|\alpha \right|}_{\diamond }+{\left|\beta \right|}_{\diamond }$.

For example, let $\alpha =12\in S_2,\beta =1\in S_1$, and then ${\left|\alpha \right|}_{\diamond }={|1\diamond 1|}_{\diamond }={2,\left|\beta \right|}_{\diamond }={1,\left|\alpha \right|}_{\diamond }+{\left|\beta \right|}_{\diamond }=3.$ Then,

$$12{\text{ш}}_{\diamond }1=(1\diamond 1){\text{ш}}_{\diamond }1=1\diamond 1\diamond 1+1\diamond 1\diamond 1+1\diamond 1\diamond 1=123+123+123,$$

$$12\underline{\text{ш}}1=\underset{12{\text{ш}}_{\diamond }1}{\underbrace{123+123+123}}+\underset{{\left|\pi \right|}_{\diamond }=2}{\underbrace{132+132+213+213}}+\underset{{\left|\pi \right|}_{\diamond }=1}{\underbrace{231+312}}.$$

4. The Hopf Algebra Arising from the Super-Shuffle

By the definition, we have that the super-shuffle product of any two permutations of degrees n and p is a sum of permutations of degree $n+p$. Therefore, $(KS,\underline{\text{ш}},\mu )$ is a graded algebra. Since ${\Delta }_{\diamond }\left(K{S}_n\right)\subseteq {⨁}_{k=0}^n(K{S}_k\otimes K{S}_{n-k}),\nu \left(K\right)=K{S}_0$, $(KS,{\Delta }_{\diamond },\nu )$ is a graded coalgebra.

Vargas [34] put forward that $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a graded bialgebra, and thus it is a graded Hopf algebra. However, there was no proof. Here, we give a proof.

Lemma 1.

Let $\sigma ={\sigma }_1\cdots {\sigma }_s$, $\rho ={\rho }_1\cdots {\rho }_t$ be any two nonempty permutations. If π is a permutation obtained by $\sigma \underline{\text{ш}}\rho$, then any atom of π can only consist of some complete atoms of σ and ρ.

Proof 

(Proof of Lemma 1). Equivalently, we will prove that any atom of $\pi$ does not contain any portion of atoms of $\sigma$ or $\rho$.

Let $\pi ={\pi }_1{\pi }_2\cdots {\pi }_{s+t}$ in one-line notation be a permutation obtained by $\sigma \underline{\text{ш}}\rho$ and $\mathrm{st}({\pi }_u\cdots {\pi }_v)$ is an atom of $\pi$, where $1\le u\le v\le s+t$.

Suppose ${\pi }_u\cdots {\pi }_v$ contains a portion of an atom from the original permutation $\sigma$. Let $\mathrm{st}({\sigma }_1\cdots {\sigma }_p)$ be the portion, where ${\sigma }_p\cdots {\sigma }_q$ is corresponding to the portion in the one-line notation of $\sigma$. Then neither ${\widehat{\sigma }}_{p-1}$ nor ${\widehat{\sigma }}_{q+1}$ is an element in ${\pi }_u\cdots {\pi }_v$.

Since ${\pi }_u\cdots {\pi }_v$ is an atom, we have $\pi \left(\right[u-1\left]\right)=[u-1]$ and $\pi \left(\right[v\left]\right)=\left[v\right]$. So, $\{{\widehat{\sigma }}_1,\dots ,{\widehat{\sigma }}_{p-1}\}\subseteq [u-1]$,$\{{\widehat{\sigma }}_p,\dots ,{\widehat{\sigma }}_s\}\subseteq [s+t]\backslash [u-1]$,$\{{\widehat{\sigma }}_1,\dots ,{\widehat{\sigma }}_q\}\subseteq \left[v\right]$ and $\{{\widehat{\sigma }}_{q+1},\dots ,{\widehat{\sigma }}_s\}$

$\subseteq [s+t]\backslash \left[v\right]$. By the definition of renumbering, $max\{{\sigma }_1,\dots ,{\sigma }_{p-1}\}<min\{{\sigma }_p,\dots ,{\sigma }_s\}$, $max\{{\sigma }_1,\dots ,{\sigma }_q\}<min\{{\sigma }_{q+1},\dots ,{\sigma }_s\}$ and $\{{\sigma }_1,\dots ,{\sigma }_s\}=\left[n\right]$. Thus, $\sigma \left(\right[p-1\left]\right)=[p-1]$ and $\sigma \left(\right[q\left]\right)=\left[q\right]$. Clearly, $\sigma \left(\right[k\left]\right)\ne \left[k\right]$ for all $p<k<q$. Therefore, $p-1$ and q are global ascents of $\sigma$, and there is no global ascent between p and $q-1$, i.e., $\mathrm{st}({\sigma }_p\cdots {\sigma }_q)$ is an atom in $\sigma$, contradiction to that $\mathrm{st}({\sigma }_p\cdots {\sigma }_q)$ is a portion.

Similarly, ${\pi }_u\cdots {\pi }_v$ cannot contain a portion of any atom from the original permutation $\rho$. □

Example 3.

For any permutation $\alpha =21$ and $\beta =1\diamond 1$,

$$\begin{array}{cc}\hfill 21\underline{\text{ш}}1\diamond 1=& 4312+4132+4123+1\diamond 432+1\diamond 423+1\diamond 2\diamond 43\hfill \\ \hfill & +4213+4123+4132+1\diamond 423+1\diamond 432+1\diamond 342\hfill \\ \hfill & +4123+4213+4231+2413+2431+2341\hfill \\ \hfill & +321\diamond 4+312\diamond 4+3142+1\diamond 32\diamond 4+1\diamond 342+1\diamond 432\hfill \\ \hfill & +312\diamond 4+321\diamond 4+3241+231\diamond 4+2341+2431\hfill \\ \hfill & +21\diamond 3\diamond 4+231\diamond 4+2341+321\diamond 4+3241+3421.\hfill \end{array}$$

In our example, the atoms of each permutation obtained by $21\underline{\text{ш}}1\diamond 1$ all consist of some complete atoms of $\alpha$ and $\beta$.

Theorem 1.

$(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a bialgebra.

Proof of Theorem 1.

We know that $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a graded algebra and a graded coalgebrae. It is easy to check that $\nu$ is an algebra homomorphism. Thus, to prove $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a graded bialgebra we only need to prove it satisfies the compatibility, i.e.,

$${\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)={\Delta }_{\diamond }\left(\alpha \right)\underline{\text{ш}}{\Delta }_{\diamond }\left(\beta \right),$$

for any $\alpha ={\alpha }_1\diamond \cdots \diamond {\alpha }_l$ and $\beta ={\beta }_1\diamond \cdots \diamond {\beta }_t$.

From Lemma 1, we have that any atom of a permutation $\pi$ obtained by $\alpha \underline{\text{ш}}\beta$ can only consist of some complete atoms from the original two permutations $\alpha$ and $\beta$.

Denote ${\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=x}$ as the sum of all items in ${\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)$ with x atoms from $\alpha$ on the left side of tensor notation ⊗, $0\le x\le l$. Hence, we have

$${\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)={\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=0}+{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=1}+{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){{|}_{i=2}+\cdots +{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)|}_{i=l},$$

where

$$\begin{array}{cc}\hfill {\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=x}=& {\alpha }_1\diamond \cdots \diamond {\alpha }_x\otimes ({\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}\beta )\hfill \\ \hfill & +({\alpha }_1\diamond \cdots \diamond {\alpha }_x\underline{\text{ш}}{\beta }_1)\otimes ({\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}{\beta }_2\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill & +({\alpha }_1\diamond \cdots \diamond {\alpha }_x\underline{\text{ш}}{\beta }_1\diamond {\beta }_2)\otimes ({\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}{\beta }_3\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill & +\cdots \hfill \\ \hfill & +({\alpha }_1\diamond \cdots \diamond {\alpha }_x\underline{\text{ш}}\beta )\otimes ({\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}ϵ)\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& \sum _{j=0}^t({\alpha }_1\diamond \cdots \diamond {\alpha }_x\underline{\text{ш}}{\beta }_1\diamond \cdots \diamond {\beta }_j)\otimes ({\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}{\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill =& ({\alpha }_1\diamond \cdots \diamond {\alpha }_x\otimes {\alpha }_{x+1}\diamond \cdots \diamond {\alpha }_l)\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t).\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill {\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)=& {\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=0}+{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){|}_{i=1}+{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right){{|}_{i=2}+\cdots +{\Delta }_{\diamond }\left(\alpha \underline{\text{ш}}\beta \right)|}_{i=l}\hfill \\ \hfill =& (ϵ\otimes {\alpha }_1\diamond \cdots \diamond {\alpha }_l)\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill & +({\alpha }_1\otimes {\alpha }_2\diamond \cdots \diamond {\alpha }_l)\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill & +({\alpha }_1\diamond {\alpha }_2\otimes {\alpha }_3\diamond \cdots \diamond {\alpha }_l)\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill & +\cdots \hfill \\ \hfill & +({\alpha }_1\diamond \cdots \diamond {\alpha }_l\otimes ϵ)\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill =& \left[\begin{array}{c}ϵ\otimes {\alpha }_1\diamond \cdots \diamond {\alpha }_l+{\alpha }_1\otimes {\alpha }_2\diamond \cdots \diamond {\alpha }_l\hfill \\ +\cdots +{\alpha }_1\diamond \cdots \diamond {\alpha }_l\otimes ϵ\hfill \end{array}\right]\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill =& \sum _{i=0}^l{\alpha }_1\diamond \cdots \diamond {\alpha }_i\otimes {\alpha }_{i+1}\diamond \cdots \diamond {\alpha }_l\underline{\text{ш}}\sum _{j=0}^t({\beta }_1\diamond \cdots \diamond {\beta }_j\otimes {\beta }_{j+1}\diamond \cdots \diamond {\beta }_t)\hfill \\ \hfill =& {\Delta }_{\diamond }\left(\alpha \right)\underline{\text{ш}}{\Delta }_{\diamond }\left(\beta \right).\hfill \end{array}$$

Hence, the cut-box coproduct ${\Delta }_{\diamond }$ is an algebra homomorphism, i.e., the super-shuffle product and the cut-box coproduct are compatible. Therefore, $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a bialgebra. □

Example 4.

Let $\alpha =12=1\diamond 1,\beta =1.$ Then,

$$\begin{array}{cc}\hfill {\Delta }_{\diamond }\left(12\underline{\text{ш}}1\right)=& {\Delta }_{\diamond }(231+213+123+132+123+213+123+132+312)\hfill \\ \hfill =& {\Delta }_{\diamond }\left[\begin{array}{c}231+21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+1\diamond 1\diamond 1\hfill \\ +21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+312\hfill \end{array}\right]\hfill \\ \hfill =& ϵ\otimes \left[\begin{array}{c}231+21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+1\diamond 1\diamond 1\hfill \\ +21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+312\hfill \end{array}\right]+1\otimes 1\diamond 1\hfill \\ \hfill & +1\otimes (21+1\diamond 1+21)+(21+1\diamond 1+21)\otimes 1\hfill \\ \hfill & +1\diamond 1\otimes 1+\left[\begin{array}{c}231+21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+1\diamond 1\diamond 1\hfill \\ +21\diamond 1+1\diamond 1\diamond 1+1\diamond 21+312\hfill \end{array}\right]\otimes ϵ\hfill \\ \hfill =& ϵ\otimes (1\diamond 1\underline{\text{ш}}1)+1\otimes (1\diamond 1)\hfill \\ \hfill & +1\otimes \left(1\underline{\text{ш}}1\right)+\left(1\underline{\text{ш}}1\right)\otimes 1\hfill \\ \hfill & +1\diamond 1\otimes 1+(1\diamond 1\underline{\text{ш}}1)\otimes ϵ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\Delta }_{\diamond }\left(12\right)\underline{\text{ш}}{\Delta }_{\diamond }\left(1\right)=& (ϵ\otimes 1\diamond 1)\underline{\text{ш}}(ϵ\otimes 1)+(1\otimes 1)\underline{\text{ш}}(ϵ\otimes 1)+(1\diamond 1\otimes ϵ)\underline{\text{ш}}(ϵ\otimes 1)\hfill \\ \hfill & +(ϵ\otimes 1\diamond 1)\underline{\text{ш}}(1\otimes ϵ)+(1\otimes 1)\underline{\text{ш}}(1\otimes ϵ)+(1\diamond 1\otimes ϵ)\underline{\text{ш}}(1\otimes ϵ)\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& \left(ϵ\underline{\text{ш}}ϵ\right)\otimes (1\diamond 1\underline{\text{ш}}1)+\left(1\underline{\text{ш}}ϵ\right)\otimes \left(1\underline{\text{ш}}1\right)+(1\diamond 1\underline{\text{ш}}ϵ)\otimes \left(ϵ\underline{\text{ш}}1\right)\hfill \\ \hfill & +\left(ϵ\underline{\text{ш}}1\right)\otimes (1\diamond 1\underline{\text{ш}}ϵ)+\left(1\underline{\text{ш}}1\right)\otimes \left(1\underline{\text{ш}}ϵ\right)+(1\diamond 1\underline{\text{ш}}1)\otimes \left(ϵ\underline{\text{ш}}ϵ\right).\hfill \end{array}$$

Thus, we have ${\Delta }_{\diamond }\left(12\underline{\text{ш}}1\right)={\Delta }_{\diamond }\left(12\right)\underline{\text{ш}}{\Delta }_{\diamond }\left(1\right).$

Corollary 1.

$(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a Hopf algebra.

Proof of Corollary 1.

From Theorem 1, we know $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a graded bialgebra. Since $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is graded and connected, $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a Hopf algebra. □

5. Conclusions

First, we proved that any atom of a permutation $\pi$ obtained by $\alpha \underline{\text{ш}}\beta$ can only consist of some complete atoms of $\alpha$ and $\beta$. Secondly, we proved that the super-shuffle product $\underline{\text{ш}}$ and the cut-box coproduct ${\Delta }_{\diamond }$ on $KS$ are compatible, and hence $(KS,\underline{\text{ш}},\mu ,{\Delta }_{\diamond },\nu )$ is a bialgebra; Finally, since this bialgebra is graded and connected, it is also a Hopf algebra.