The Brain and the New Foundations of Mathematics

Abstract

Many concepts in mathematics are not fully defined, and their properties are implicit, which leads to paradoxes. New foundations of mathematics were formulated based on the concept of innate programs of behavior and thinking. The basic axiom of mathematics is proposed, according to which any mathematical object has a physical carrier. This carrier can store and process only a finite amount of information. As a result of the D-procedure (encoding of any mathematical objects and operations on them in the form of qubits), a mathematical object is digitized. As a consequence, the basis of mathematics is the interaction of brain qubits, which can only implement arithmetic operations on numbers. A proof in mathematics is an algorithm for finding the correct statement from a list of already-existing statements. Some mathematical paradoxes (e.g., Banach–Tarski and Russell) and Smale’s 18th problem are solved by means of the D-procedure. The axiom of choice is a consequence of the equivalence of physical states, the choice among which can be made randomly. The proposed mathematics is constructive in the sense that any mathematical object exists if it is physically realized. The consistency of mathematics is due to directed evolution, which results in effective structures. Computing with qubits is based on the nontrivial quantum effects of biologically important molecules in neurons and the brain.

1. Introduction

The question of the foundations of mathematics has been discussed many times since its inception. A number of scientists, for example, considered set theory as such a foundation. However, at the present time, issues such as the following remain unresolved:

-

Why can we prove anything at all within the framework of mathematics?

-

Where do new mathematical concepts and structures come from?

-

Why do we consider inductive inference to be correct?

-

How do we manage to work with infinities in mathematics?

Mathematics itself cannot answer such questions. It is fundamentally important to consider the structure of the system (brain or computer) that operates with mathematical concepts. On the other hand, mathematics is a part of thinking as such and must obey some general laws.

Traditionally, human thinking is partially explained on the basis of a neural network paradigm, according to which a large number of neurons, connected with each other in a complex way, allow humans and animals to process information, recognize images and make decisions. At the same time, one of the problems of human and animal thinking is the acquisition of new knowledge. Previous works [1,2] show that the acquisition of new knowledge is contradictory, since the recognized image is not new, and the unrecognized image is not useful. To solve this problem, previous works [1,2] suggest that all behavioral programs are innate. It also agrees with the Chomskian innate, generative grammar. As a mechanism for the operation of such programs, nontrivial quantum effects of interaction between biologically important molecules are proposed [3,4,5].

This question is also closely related to the foundations of mathematics and logic. Indeed, if all the objects with which we work are innate, then the same applies to mathematical objects. However, there are an infinite number of mathematical objects, and any limited physical system (e.g., computer, brain) can store only a finite number of objects in memory and work with them. This property, as well as the presence of a number of other contradictions and paradoxes, entails the need to revise the foundations of mathematics.

This article is devoted to the formulation of new foundations of mathematics based on the concept of innate programs of behavior and thinking.

2. The Main Results of the Theory of Innate Behavioral Programs

In previous studies [1,2,6], a theory of innate behavior programs is proposed, within the framework of which the main problem of thinking is solved—the problem of knowledge acquisition. The main results of the theory can be described as follows:

• All human and animal behavior is innate. When we learn something or understand something, it means that we are using existing programs.
• Such innate programs allow behavior to respond flexibly to changes in the environment.

Thus, if the information is new, then it is useless; if it is useful, then it is not new (Figure 1).

3.

Behavioral programs are formed on the basis of genes in the process of ontogenesis.

Control of complex behaviors requires much more information than can be encoded in genes. An additional information resource can be the quantum effects of interactions between biologically important molecules, which also take place during the formation of the brain, as well as other organs (see, for example, [4,7]).

4.

As a result of the registration of the signal of the external environment by the receptors, it is memorized and recognized.

Memorizing the temporal and spatial ordering of the received signals is used by the organism to launch behavioral programs that are most appropriate for a given situation. If the received signal is not recognized (the image is new), then any a priori program, adequate for the given situation, cannot be launched.

5.

In the presence of uncertainty in the environment, innate programs do not start immediately, but after several repetitions, which makes it possible to reduce errors.

Another response to environmental uncertainty is trial and error, which allows the organism to find the most appropriate innate program.

6.

The transfer of experience from one organism to another occurs if the innate programs of behavior in both organisms are the same.

Thus, learning of animals and humans is only a method of finding the innate program of behavior that is most suitable for a given situation. New behavioral programs cannot arise in the learning process.

An important aspect of thinking is that we are aware of only part of the brain’s work. We are not aware of a significant part of the work associated, for example, with the work of ion channels, neuroreceptors and other intra- and inter-neuronal events. This property should play an important role in the construction of the foundations of mathematics.

3. Computer Proofs

Before considering the foundations of mathematics, let us consider how a computer (i.e., a system, the structure of which we know) can operate with mathematics. Naturally, regarding the human brain, we cannot say that we are fully aware of its structure and patterns of work.

One of the most important concepts in mathematics is a proof. What is a proof? One of the definitions is (see, for example, [8]):

A proof is a sequence of formulae each of which is either an axiom or follows from earlier formulae by a rule of inference.

At first glance, based on proofs in mathematics, new knowledge and new useful information arise. The answer to the question of what exactly happens as a result of a proof is closely related to the foundations of mathematics.

However, as a review of the literature on computer proofs shows, the computer can only select the appropriate proof from the proofs that are already available.

Herbrand proved a theorem [9] in which he proposed a method for automatic theorem proving. Robinson later [10] developed the principle of resolution for the same purpose. Applications for machine proofs are program analysis, deductive question-answer systems, problem-solving systems, and robot technology. Machine theorem proving means that the machine must prove that a certain formula follows from other formulas [11].

The problem in theorem proving is that the original formulas from which any other formulas are introduced must be known in advance. Only then can machine inference take place. In the general case, the list of these initial formulas is not known and cannot be formulated in the language of logic. In this case, machine inference is not applicable.

There are two opposite approaches in the development of automatic provers, human-oriented and machine-oriented (see, for example, [12,13]). Within the framework of the first, it is assumed that in the proof of the theorem, the system should repeat, as closely as possible, the human manner of reasoning. The second approach aims to build a logically rigorous chain that would connect the axioms and the required statement. Machine-oriented automatic proofers are mainly used for solving problems of computer science and industry.

For example, the program of Gowers and Ganesalingam [13] can prove a number of simple statements about metric spaces that the users can formulate in plain English. According to the authors, the human-oriented approach to automatic proof is more convenient to understand and use and, in many cases, may be more effective. One of the main problems of automatic provers is the so-called combinatorial explosion: the original problem leads to the need to solve several others, each of which can be decomposed into several simpler problems. A human in such a situation initially concentrates on one direction, but the mechanism of such behavior remains unknown.

Can a machine acquire human intuition? As discussed in the works [2,6], an attempt to program such a concept as “intuition” does not lead to success, since all variants of such “intuition” must also be programmed in advance. In this case, there is no need to talk about “intuition”.

The basis of a computer is a microprocessor—a device responsible for performing arithmetic, logical and control operations written in machine code. The microprocessor includes, in particular, an arithmetic logic unit. This unit, which, under the control of a control unit, is used to perform arithmetic and logical transformations (starting from elementary transformations) on data, in this case called operands. The length of the operands is usually called the size or length of the machine word. Figure 2 shows a diagram of an arithmetic logic unit that performs addition, subtraction, all logical functions and bit shifts on two four-bit operands.

Numbers in the computer can be represented in fixed-point and floating-point formats. In both cases, a corresponding number of memory cells (bits) are reserved for the number in advance. Elementary logical or arithmetic operations on bits are implemented using logical elements.

Notably, there is no fundamental difference between logic and mathematics (arithmetic) at the elementary level—both those and other operations are implemented on the same elements.

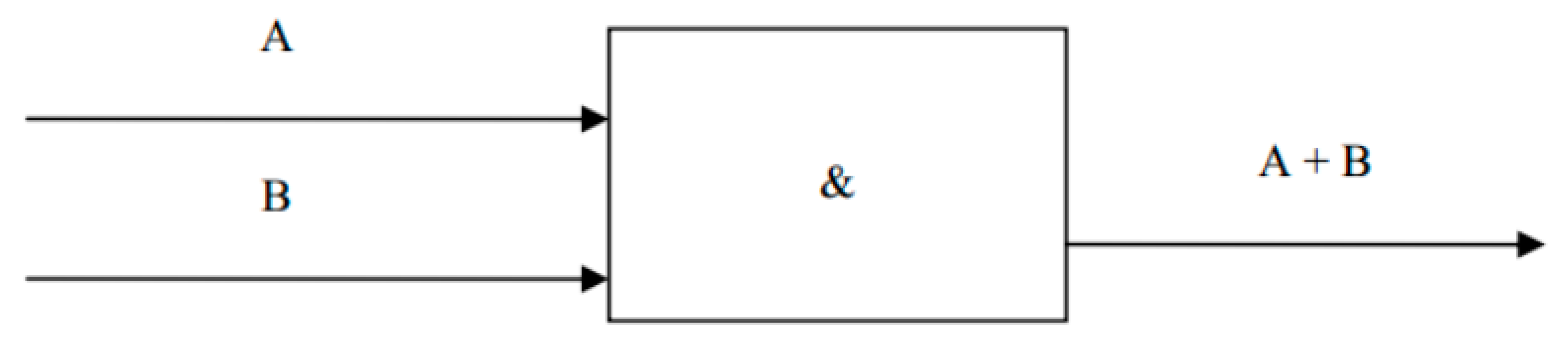
A logical element of a computer is a part of an electronic logical circuit that implements an elementary logical function. The logical elements of the computer operate with signals that are electrical impulses. In the presence of an impulse, the logical meaning of the signal is 1; in its absence, it is 0. Signals-values of the arguments arrive at the inputs of the logic element, and the signal - value of the function appears at the output.

For example, a logical AND circuit appears as follows (Figure 3):

Notably, this circuit (as well as other logic circuits) is preassembled to implement a certain logic function (in this case, the AND function) for all variants of input signals. In such a situation, for any input signals, the result of the circuit is predetermined by its structure. If we talk about the mathematical notation of this operation, then its result is known in advance.

Since a computer is simply a set of such elements connected in a certain manner, it is clear that at higher levels of the hierarchy of schemes, the results of operations (responses) are also known in advance. At the level of such circuits, a computer can use only elementary arithmetic operations.

How does a computer implement other (more advanced) mathematical operations on mathematical objects? An analysis of the operation of a computer shows that all these operations can also be realized only through elementary operations and in no other manner. Thus, what we call higher mathematics—set theory, topology, etc.—the computer can still realize only through elementary mathematics.

If the verification of the correctness of an arithmetic equality is not considered a proof, then we can say that in arithmetic there are no proofs at all.

Thus, the computer cannot prove anything. The computer can only choose such an output that corresponds to a specific input. This conclusion does not depend at all on what the element base of the computer is and can be attributed to all computer provers.

For the same reasons, it is understandable that a quantum computer does not prove anything in the sense in which a human does it. That is, as a result of computer proof, no new statements (which contain new knowledge) can arise.

A simplified calculation scheme on a quantum computer looks like this: a system of qubits is taken, on which the initial state is written. Then, the state of the system or its subsystems is changed by means of unitary transformations that perform certain logical operations. Finally, the value is measured, which is the result of computer work. The role of wires of a classical computer is played by qubits, and the role of logical blocks of a classical computer is played by unitary transformations.

The quantum system gives a result that is correct only with some probability. However, due to a small increase in operations in the algorithm, we can arbitrarily bring the probability of obtaining the correct result closer to unity. Basic quantum operations can be used to simulate the operation of ordinary logic gates that ordinary computers are made of. Therefore, quantum computers can solve any problem that can be solved on classical computers.

In the quantum case, a system of n qubits is in a state that is a superposition of all base states, so the change in the system affects all 2ⁿ base states simultaneously. In theory, the new scheme can work much (exponentially) faster than the classical scheme. In practice, for example, Grover’s quantum database search algorithm shows quadratic power gains versus classical algorithms.

Let a particle be placed in each register cell that can be in two possible states (see, for example, [15]):

$$|0\rangle \mathrm{and}|1\rangle .$$

The unit vector

$${\alpha }_0|0\rangle +{\alpha }_1|1\rangle$$

is called a qubit. A system of two qubits can be in the following state:

$${\alpha }_{00}|00\rangle +{\alpha }_{01}|01\rangle +{\alpha }_{10}|10\rangle +{\alpha }_{11}|11\rangle .$$

An example of an entangled (not achieved by tensor product) state is

$$\frac{1}{\sqrt{2}}\left(|00\rangle +|11\rangle \right).$$

For n cells one can write

$$\begin{gathered} |\psi \rangle ={\displaystyle \sum _{x=0}^{2^n-1}{\alpha }_x|x\rangle }, \\ |x\rangle =|\mathrm{010...01}\rangle . \end{gathered}$$

Computational quantum processes are unitary transformations. For example, the Walsh–Hadamard transform (see, for example, [16,17])

$$H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

transforms state

$$|0\rangle$$

into superposition of states:

$$\frac{1}{\sqrt{2}}|0\rangle +\frac{1}{\sqrt{2}}|1\rangle .$$

In such a manner, we can obtain a superposition of any states.

Access to calculation results—measurement—disturbs the state of the system. There exist one-, two- and three-qubit gates. Operations with qubits in a quantum computer are shown schematically in Figure 4.

Thus, in a quantum computer, as in a classical computer, there are no special operations of logical inference, abstraction, generalization, etc. All of them, in one way or another, are reduced to calculations in which there is no proof (in the sense of the definitions given above). Since quantum computers also deal only with computation, there are no quantum provers (in the sense of proving new theorems).

Thus, a computer (quantum or classical) does as follows:

searches for the correct statement from the list of available statements encoded in bits (qubits).

Moreover, there are no proofs (in the form in which they are understood in mathematics).

Alternatively, we can use another definition of proof, for example, in the form:

proof is an algorithm for finding the correct statement from a list of available statements.

However, such a definition differs significantly from the definition of proof used in mathematics and logic, first of all, in that in mathematics (logic), generally speaking, the entire list of statements is not known, from which we need to choose the correct one. As a result of the proof, we get something new; we acquire knowledge.

A human, at least at first glance, can prove a lot, for example, something that he did not know before. For example, often in mathematics, results are obtained that were not previously anticipated, which did not seem to be in our “lists”. That is, some theorems can be formulated earlier but proved later. Another variant is also possible: in the proof of the theorem, along the way, results that were not previously assumed at all can be obtained (also in the form of theorems). Clearly, this second variant is much more common, since in the process of development of mathematics, many more proofs were obtained compared to the number of statements that existed in mathematics in the early stages of its development.

Why does it seem to us that we can prove something and use more advanced branches of mathematics and more abstract concepts than a computer?

4. Foundations of Mathematics and Recognition-Explicit and Implicit Definitions

Compared to other sciences, mathematics is considered the most accurate, i.e., one in which everything is defined. The basis of mathematics is axioms and theorems, which can be obtained from axioms by means of proofs. Mathematical proofs are accepted as the most reliable, and it is believed that they can be completely trusted. At first glance, only the axioms (of which there are relatively few) contain a priori knowledge, while the knowledge obtained as a result of proving theorems seems new.

The question of the foundations of mathematics has been debated since its inception and use. One of the important questions in this context is the following: “What can be considered a rigorous mathematical proof?” There are several approaches to the foundations of mathematics (see, for example, [19,20,21]).

• Set-theoretic approach

Within the framework of this approach, it is proposed to consider all mathematical objects in the framework of set theory, for example, on the basis of the Zermelo–Fraenkel set theory. This approach has been predominant since the middle of the 20th century.

2.

Logicism

This approach presupposes a strict typification of mathematical objects, and many paradoxes (for example, in set theory) turn out to be impossible in principle.

3.

Formalism

This approach involves the study of formal systems based on classical logic.

4.

Intuitionism

Intuitionism assumes at the foundation of mathematics an intuitionistic logic, more limited in the means of proof, but more reliable. Intuitionism rejects proof by contradiction, many nonconstructive proofs become impossible, and many problems of set theory become meaningless (unformalizable). Constructive mathematics is close to intuitionism, according to which “to exist is to be built”.

From several competing projects for building new foundations of mathematics, which emerged almost simultaneously at the beginning of the 20th century, the leading project was the reorganization of all mathematics on the basis of set theory. Although set theory soon faced its own foundational crisis [22], it provided 20th-century mathematics a suitable language for formulating and proving theorems from a wide variety of areas of this science. Thus, despite intrinsic problems, set theory did serve as the basis for the unification and organization of mathematics in the 20th century.

Another direction that claims to be the foundations of mathematics at the present time is the theory of categories. Category theory was proposed in the 1940s by MacLane and Eilenberg as a useful language for algebraic topology [23].

According to the theory of categories [24], any given type of object should be considered together with the transformations of objects of this type into each other and into themselves. Since any object can be formally replaced by the identical transformation of a given object into itself, it is precisely the concept of transformation (or process) that is fundamental in this case, while the concept of an object plays only an auxiliary role.

For example, the category of topological spaces consists of all topological spaces and all continuous transformations of these spaces into each other and into themselves. Thus, element transformations and the elements themselves are equal.

As a third direction, actively developing at the present time, we can mention the homotopy type theory [25], which began to develop in 1980–1990s of the 20th century. Homotopy type theory is a logical-geometric theory, where the same symbols, symbolic expressions and syntactic operations with these expressions have both geometric and logical interpretations.

Notably, unlike most logical methods, homotopy type theory allows direct computer implementation (in particular, in the form of functional programming languages COQ and AGDA), which makes it promising in modern information technologies for representing knowledge [26,27].

However, within the framework of these theories, many concepts are still not fully defined.

Note that for the implementation of these and other areas of mathematics in any physical system, either numbers and their properties, or structures that must be recognized and encoded in bits (i.e., again, numbers) are used.

Thus, the main disadvantages of the foundations of mathematics are the following:

-

an attempt to explain mathematics from itself. However, mathematics cannot answer many questions. For example, why is proof possible at all?

-

Physical structures (computer, brain) that perform certain mathematical operations are not considered.

Why can mathematics prove at least something? Does this generate new knowledge? Part of the answer to the first question was trying to get metamathematics (the study of mathematics itself using mathematical methods), in particular—the proof theory. However, proof theory (see, for example, [28,29]) deals with somewhat different issues, for example, issues of provability and consistency. Moreover, many properties of mathematical objects are implicitly postulated in this theory.

Proof theory cannot answer the question of why a proof is possible at all.

The physical realization of all mathematical structures can play the role of metamathematics. At first glance, it seems that in physics, we use all the same mathematics to model physical structures. However, physics is closely related to the physical world that exists outside of us, not only with abstract concepts. This physical approach is not self-contained but rather is related to experiments. Thus, metamathematics is operations implemented in some physical structures (a set of qubits). This view is the opposite of Tegmark’s theory [30], in whose opinion all that is in the world is mathematics.

Let us discuss some of the main areas of mathematics and show that mathematical concepts are innate. On the other hand, we will show that many concepts in mathematics are not fully defined, which gives rise to paradoxes.

Mathematics is subdivided into elementary and advanced mathematics. These divisions study imaginary, ideal objects and relationships between them using formal language. The model of an object within the framework of mathematics does not consider all of its features but instead only the most necessary for the purposes of study (idealized). For example, when studying the physical properties of objects of the surrounding world, abstraction and generalization are used.

However, as shown in previous works [2,6], both abstraction and generalization should actually include a priori the ideal object that should be obtained as a result of these operations. This finding means that mathematical objects (as well as all other knowledge) are innate.

The primitive arithmetic L₀ is a system based on the language, in which there are operations of addition, multiplication, subtraction and division, i.e.,

$$L_0=\left\{+,\times ,-,÷\right\}.$$

In arithmetic, operations such as negation, implication, generality quantifier, mathematical induction (the basis of Peano arithmetic, see for example, [31]) and others are excluded. Nothing can be proven in L₀; one can only check by exhaustive search the solvability of the polynomial equation. In other words, only true statements are proved. As already shown above, then the concept of proof significantly changes its meaning, since it does not consist of obtaining new knowledge but rather in checking what has been obtained earlier.

Since multiplication and division can always be expressed in terms of addition, then this and only this language can be implemented on a computer or an arbitrary computing device.

The use of quantifiers already leads to the fact that the value is not completely determined. Quantifiers are not allowed in arithmetic. For example, the expression

$$\forall x$$

is undefined since all x values are undefined. That is, it assumed that we know what x is. It is just convenient to use, but it can actually lead to contradictions.

Algebra is a branch of mathematics that can be characterized as a generalization and extension of arithmetic; in this section, numbers and other mathematical objects are denoted by letters and other symbols, which allows us to write and study their properties in the most general form.

That is, arithmetic is implicitly extended in algebra. The term implicitly means that all the results of all algebra operations are not explicitly recorded somewhere. However, if we try to implement algebra on a computer, we will have to explicitly define the variables, i.e., write down all the numbers that these variables can be equal to and all the numbers that the operation on them can be equal to. Thus, in algebra, variables are not fully defined, and we only assume that we know everything about these variables.

Geometry deals with the mutual arrangement of bodies, which is expressed in contact or adherence to each other, the arrangement “between”, “inside” and so on; the size of bodies, that is, the concepts of equality of bodies, “larger” or “less”; and transformations of bodies. A geometric body is a collection of abstractions, such as “line”, “point” and others.

When exploring real objects, geometry only considers their shape and relative position, distracting from other properties of objects, such as density, weight, and color. This consideration allows us to go from spatial relations between real objects to any relations and forms that arise when considering homogeneous objects and are similar to spatial ones. What was said above in relation to algebra applies in full measure to geometry, i.e., that the geometric values are not fully defined. For example, we intuitively understand what a straight line is, but the coordinates of all the points that make up this line are not known to us.

When we talk about geometric objects (lines, bodies, etc.), they must be recognized in the sense that each object must correspond to an a priori standard and programs for working with it (see above). This standard and programs must be encoded in bits anyway. Only elementary arithmetic or logical operations are possible with bits.

In [6], some arbitrarily chosen theorems are considered (e.g., the Pythagorean theorem, the cosine theorem, the two policemen theorem, and the minimax theorem), and it is shown that as a result of proving any theorem, only a priori knowledge is used.

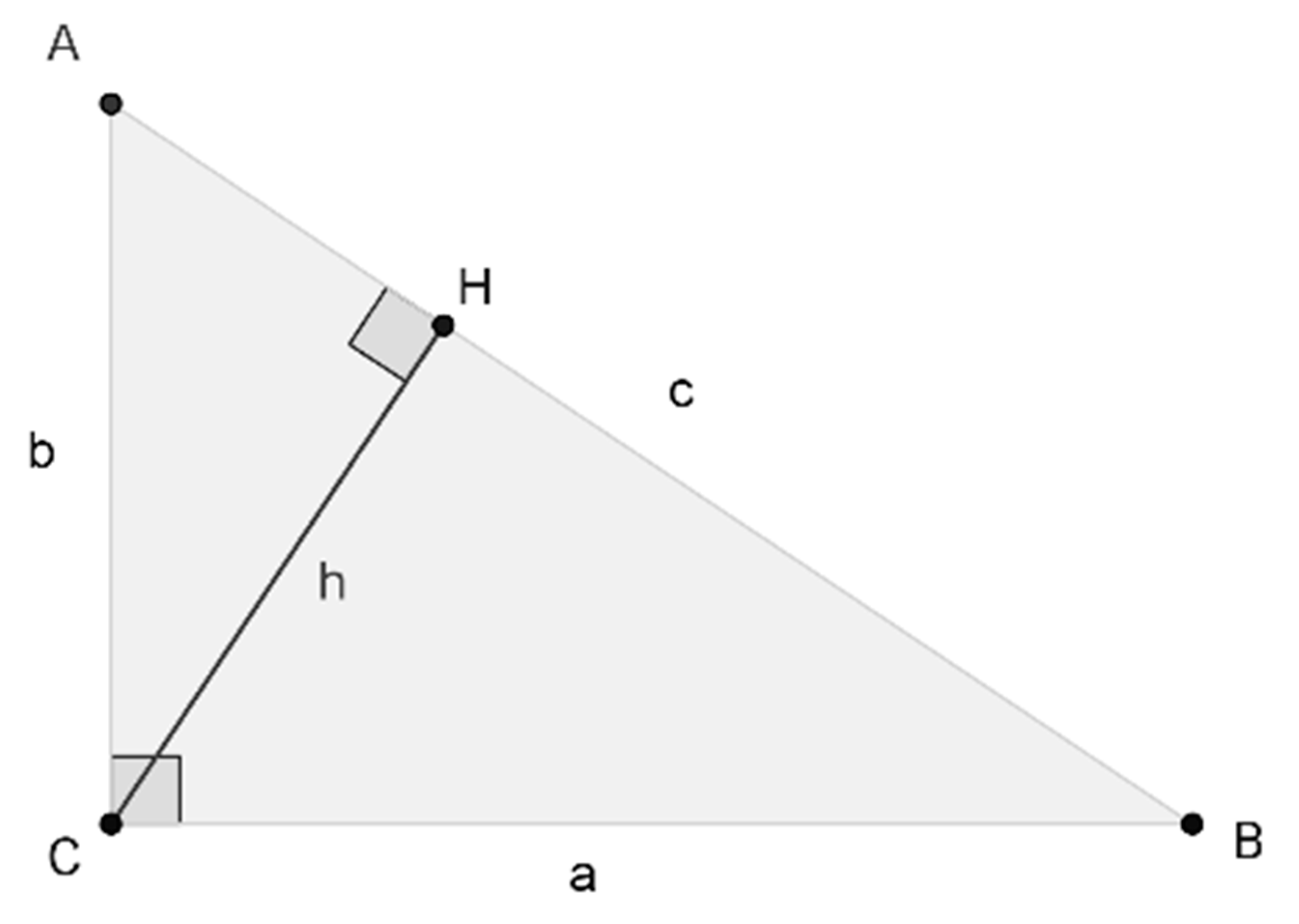
Consider, for example, the Pythagorean theorem, according to [6]. One of the proofs of the Pythagorean theorem is based on the similarity of triangles (Figure 5). Consider a triangle ABC with a right angle at vertex C with sides a, b and c opposite to vertices A, B and C.

If we draw the height CH, then by the similarity criterion by the equality of two angles, the triangles $\Delta ABC$, $\Delta ACH$ and $\Delta ABC$, $\Delta CBH$ turn out to be similar. Hence, a relationship follows:

$$\frac{a}{c}=\frac{\left|HB\right|}{a},\frac{b}{c}=\frac{\left|AH\right|}{b}.$$

Based on these proportions, we can obtain the following equalities:

$$a^2=c\left|HB\right|,b^2=c\left|AH\right|.$$

Adding term by term, we obtain

$$a^2+b^2=c\left|HB+AH\right|.$$

Finally, we obtain

$$a^2+b^2=c^2.$$

However, the very statement about such triangles is reduced simply to the properties of the numbers characterizing the sides and angles of the triangle. It is axiomatic that lines and angles can be assigned numbers. Further, the multiplication of the extreme terms of the proportions is also not at all obvious—it is again a consequence of the properties of numbers and operations on them. How do we know that if two angles in triangles are equal, then certain ratios are fulfilled for their sides? Thus, the Pythagorean theorem is simply a record of a priori knowledge about the properties of numbers.

Other geometric theorems can be considered similarly. For example, in [32,33], some trigonometric relationships were proved for double angles, arctangents, and the golden ratio in triangles.

To this end, it is necessary to add that concepts such as “triangle”, “angle”, and “vertex” are not defined. It is assumed that we know what they are. However, for these objects to be fully defined, it is necessary that all their values to be encoded somewhere. Otherwise, it is not known what they are; the objects remain incompletely defined. As will be shown below with the example of sets, it is incompletly defined objects that lead to paradoxes and contradictions. When the objects are completely correctly defined, there can be no contradictions.

It seems to us that our brain works with a segment and an angle as with whole objects, but we simply do not realize their bit codes.

Similar reasoning can be given for the cosine theorem, as well as for many other geometric theorems.

Geometry is closely related to sciences such as analytic geometry, topology, and algebraic geometry. All these sciences are based on all the same numbers encoded in qubits.

The mentioned theorems are not distinguished in any way from others; it can be shown that any other theorem is simply a record of some of the a priori knowledge about the properties of numbers.

Mathematical logic abstracts from meaning and judges about the relationship and transitions from one sentence (utterance) to another and the resulting conclusion from these sentences, not on the basis of their content but rather only on the basis of the form of the sequence of sentences (see, for example, [34]).

The use of mathematical methods in logic becomes possible when judgments are formulated in some exact language. Such precise languages have two sides: syntax and semantics. Syntax is a set of rules for constructing language objects (usually called formulas). Semantics is a set of conventions that describe our understanding of formulas (or some of them) and allow some formulas to be considered correct and others not.

Propositional calculus studies functions

$$f\left(p_1,\dots ,p_n\right),$$

where the variables, like the functions themselves, take one of two values:

$$\left\{1,0\right\},$$

which is equivalent to

$$\left\{\text{ture},\text{false}\right\}.$$

Variables called propositional, work with statements, including in the form of relations (predicates) of the type x < 3, x is an integer, etc. The characteristic functions of these relations are propositional variables p₁, …, p_n, taking values from {0,1}. Propositional variables are combined with each other using logical connectives into formulas that express any Boolean function.

Inference in propositional calculus is a finite sequence of formulas, each of which is either an axiom from the rules of inference, or a formula obtained from the previous ones as a result of applying modus ponens. The last formula in this sequence is called a theorem.

Note, however, that the formulas $f\left(p_1,\dots ,p_n\right)$ are not fully defined. For their complete definition, all values of the function must be written a priori somewhere for all values of the argument, i.e.,

$$f\left(0,\dots ,0\right)=1,f\left(0,\dots ,1\right)=1,\dots$$

In such a case, inference is simply a recognition of what is already known. If it seems to us that as a result of the application of the propositional calculus, something new has been obtained, then this only means that we have worked with an incompletely defined object. That is, some properties of such an object were implied.

Predicate calculus uses quantifiers $\forall ,\exists$ in first-order logic. Formulas can be true or false (see, for example, [34]).

As observed above, the use of quantifiers by themselves make the objects to which they refer not fully defined.

That is, the simplest logical operations are implemented based on physical circuits (for example, in a computer) and are fully defined. More complex logical operations (involving higher-order logic) are applied to objects that are not fully defined.

Thus, any calculations are possible only because the result is known in advance. The same can be said about arbitrary mathematical actions. That is, it is impossible to do without a stage of elementary operations, the result of which is known in advance, in any system, and not only in a computer system. It does not matter what the nature of these elementary operations is—it can be mechanics, current, or something else. The result of such operations is not only known in advance but rather is already built into the circuit in advance.

Mathematical thinking is possible only because its result is already known in advance, i.e., already implemented in some structures. We are surprised that we have discovered something only because we are not aware of part of the thought processes. However, that does not mean they do not occur.

Thus, an analysis of the foundations of mathematics shows the following:

-

a significant fraction of the concepts of mathematics are not fully defined. We are not aware of many properties of mathematical concepts. This leads to paradoxes and contradictions.

-

Truly constructive mathematics, in which all concepts are defined and somehow implemented in physical structures, is needed.

5. New Foundations of Mathematics: Accounting for Physical Realization

5.1. The Basic Axiom of Mathematics. D-Procedure. Maximum and Minimum Numbers

Based on the above conclusions, we can formulate the basic axiom of mathematics in the following form:

All mathematical structures and concepts have a physical carrier.

That is, all mathematical structures and objects have their own doi (digital object identifier), which is encoded in the form of bits (qubits) in the structure of the brain. We will assume that the calculations are based on physical interactions of qubits, organized in a certain manner. It will be shown below that quantum mechanics plays an important role in the functioning of the brain. In any case, classical computing is a special case of quantum computing.

Let us call a D-procedure the encoding of any mathematical objects and operations on them in the form of qubits. Accordingly, an object recorded on a physical medium in the form of qubits will be called digitalized.

Since the information capacity of any structure is limited (this is true even for the universe, see, for example, [35]), then there must be a maximum number Ω that can be written in such a structure. This number can be very (exponentially) large given the information capacity of the qubits. For example, this number can be represented as

$$\Omega =\exp \left(\exp \left(x\right)\right).$$

Here, x is responsible for the degrees of freedom of the brain and itself can be quite large (on the order of Avogadro’s number, which approximately characterizes the number of brain atoms).

Therefore, mathematical infinity is just a sign that we use when we mean a number greater than the maximum allowed. In this sense, all infinite numbers are equivalent.

At first glance, there is an obvious objection, such as:

$$\Omega +1>\Omega .$$

However, in fact, we cannot perform any operations with this number. It is impossible to prove or disprove anything connected with it, since the brain does not have the resources for this. That is, we can imagine that there is a number greater than the maximum (we can equate it to infinity), but we still cannot work with it.

Similarly, the minimum number can be written in the form

$${\Omega }^{-1}.$$

For similar reasons, it is impossible to write down a number less than the minimum, since the information capacity of the brain is not sufficient for this.

Objections similar to the one above apply to the minimum number. One can write the division of this number, for example, by two, and it seems that this number will necessarily be less than ${\Omega }^{-1}$. However, in reality, it will be just an overflow, i.e., it will be impossible to perform any operations with it. Thus, numbers less than the minimum should be set to zero.

Thus, all the numbers that the brain can operate are in the range of modules:

$${\Omega }^{-1}\le n\le \Omega .$$

These numbers can be plotted graphically (Figure 6):

In number theory, there are also large numbers, such as Skewes’ number,

$${10}^{{10}^{{10}^{34}}},$$

and others (for example, Graham’s number).

However, the use of a degree ladder of this type has yet to be proven. The fact that we use powers of the form

$${10}^{10}$$

still does not say anything about the possibility of an arbitrary build-up of degrees.

The proposed concept of the foundations of mathematics is close in spirit to the concept of It from bit, which was proposed by Wheeler in relation to physical objects. Its essence lies in the fact that any physical object can ultimately be represented as a collection of bits. Almost the same concept can be formulated in relation to thinking:

$$\mathit{\text{It from qubit}},$$

where by qubits we mean structured and connected qubits of the brain in a quite definite manner. Based on this basic axiom, new foundations of mathematics can now be formulated.

5.2. Set Theory: Russell’s and Banach–Tarski’s Paradoxes

As observed above, set theory is considered by many mathematicians to be the foundations of mathematics. However, the implementation of the concept of “set” in a computer system leads to difficulties, since it turns out that this concept is not fully defined.

If we try to define a set in a computer, then we will not be able to act otherwise than through numbers, since numbers are the basis of the computer’s work. A set is a number correlated with a number using some auxiliary characters, which are themselves encoded as numbers.

The set is closely related to recognition. When we say that there is a set to which roses, gladioli and asters belong, we mean that all these concepts are recognized, that is, there are mathematical standards for these concepts. In computer language, this means that each such word corresponds to a set of bits, the algorithms for which are known.

Let us denote

$$H_D$$

as the result of applying the D-procedure in relation to the set—a digitalized set. This value differs from the usual set H in that it is completely defined, i.e., all its elements together with their properties are explicitly written out in some physical structure, and no properties are implicitly implied.

The most famous set theory is the Zermelo–Fraenkel set theory (see, for example, [22,36]. However, even within the framework of this theory, many concepts are not fully defined, which leads to paradoxes.

What does it mean to “belong to the set”? This property seems to be self-evident and in some cases is not specified. However, to implement such a set and, in particular, to realize that an object belongs to it, one must actually do the following.

First, it is necessary to recognize the object, i.e., to compare it with a standard, which is in digital form and realized physically.

Second, the belonging operation cannot be implemented on a computer since it is absent in elementary arithmetic. Therefore, the set must be digitized, i.e., transformed into an ordered collection of zeros and ones. That is, it is necessary to perform the D-procedure.

After that, using arithmetic operations alone, one can determine whether a given element belongs to the set. In most cases, we are not aware of all these operations; therefore, within the framework of our consciousness, the set is not always fully defined. This uncertainty is the source of many logical paradoxes and paradoxes of mathematics in general.

Within the framework of the Zermelo–Fraenkel theory (see, for example, [22,36], the axiom of choice plays an important role. In any family Φ of nonempty sets, there is a choice function f that assigns to each

$$X\in \Phi$$

element

$$f\left(X\right)\in X.$$

Equivalent wording:

Zermelo’s theorem [37]. Any set X can be completely ordered, that is, introduce such an ordering relation under which any subset

$$A\subset X$$

will have minimal element

$$x^0\in A.$$

Zorn’s lemma [38]. If in a partially ordered set X any partially ordered subset is bounded from below, then X has a minimal element x*.

After the set is digitized, a sequence of qubits is formed. This sequence can always be ordered. However, this raises the question of the uniqueness of such an ordering and the uniqueness of the coding. Indeed, object can be encoded in different manners, depending on which pixel to start with. However, all these options are no different from each other, and they are equivalent. This property is widespread in physical systems (for example, when the energy level in the system is degenerate); however, it does not introduce any uncertainty and does not lead to paradoxes. We can agree in advance on the rules and procedure for coding. Thus, the axiom of choice is a consequence of the equivalence of physical states, the choice between which can be made randomly.

A consequence of the axiom of choice is the Banach–Tarski paradox [39]. The Banach–Tarski paradox is a theorem in set theory that states that a three-dimensional ball is equal to its two counterparts. Dividing the ball into a finite number of parts, we intuitively expect that by adding these parts together, we can obtain only solid figures, the volume of which is equal to the volume of the original ball. However, this is true only when the ball is divided into parts that have volume.

The essence of the paradox lies in the fact that in three-dimensional space, there are immeasurable sets that do not have volume if by volume we mean something that has the additivity property, and we assume that the volumes of two congruent sets coincide. Obviously, the “pieces” in the Banach–Tarski decomposition cannot be measurable (and it is impossible to implement such a decomposition by any means in practice).

As a result of the D-procedure, an unambiguous sequence of bits (qubits) is formed over a set of the “ball” type. Thus, the “pieces” will be measurable, and the Banach–Tarski paradox will not occur, because it is impossible to make two balls of the same radius from such an unambiguous sequence.

Within the framework of standard set theory, it is proven that the cardinalities of the sets of a segment and a square coincide (Cantor’s diagonal method, [40]). Let us show that, considering the physical realization of the sets, this conclusion is not correct. The points of the unit square have coordinates

$$x=0,{\alpha }_1,{\alpha }_2,\dots y=0,{\beta }_1,{\beta }_2,\dots .$$

The standard proof is based on the fact that in these sequences, each pair of coordinates can be associated with a point of a segment.

However, it is obvious that these sequences are finite in view of the finite memory of the computing device (brain). Wherein, they cannot be associated with the points of the segment since there are only half of the numbers in the record of the coordinates of the segment. They can be compared (as is carried out in mathematics) only by considering all these sequences to be infinite. However, the brain does not work with infinite numbers—when the maximum number Ω is exceeded, the infinity symbol appears, which means only one thing—that the number is greater than the maximum and nothing more. Such infinities can neither be compared nor added.

This conclusion also applies to cardinal arithmetic, in the framework of which the addition of the maximum numbers gives not the maximum number but rather infinity. That is, in fact, this number is simply not determined.

Thus, many paradoxes in mathematics are reduced to the fact that some concepts are not fully defined. Often the contradiction is inherent in the definitions themselves, i.e., some of them are incorrect. Consider, for example, Russell’s paradox.

Russell’s Paradox—is a set-theoretic paradox proposed in 1901 by Bertrand Russell, demonstrating the inconsistency of Frege’s logical system, which was an attempt to formalize Cantor’s set theory.

In informal language, the paradox can be described as follows. Let us agree to call a set “ordinary” if it is not its own element. For example, the set of all people is “ordinary” because the set itself is not a person. An example of an “unusual” set is the set of all sets, since it is itself a set, and therefore itself is its own element.

One can consider a set consisting only of all “ordinary” sets; such a set is called a Russell set. The paradox arises when trying to determine whether this set is “ordinary”, that is, whether it contains itself as an element. There are two possibilities.

• On the one hand, if the set is “ordinary”, it must include itself as an element, since it consists of all “ordinary” sets by definition. However, the set cannot be “ordinary”, since “ordinary” sets are those that do not include themselves.
• Thus, we assume that this set is “unusual”. However, it cannot include itself as an element since by definition, it should only consist of “ordinary” sets. However, if the set does not include itself as an element, then this is an “ordinary” set.

In any case, the result is a contradiction. A variation on Russell’s paradox is the Liar’s paradox. According to Russell [41], to say anything about statements, one must first define the very concept of “statement” while not using concepts that are not defined yet. Thus, it is possible to define statements of the first type that say nothing about statements. Then, we can define statements of the second type, which speak about statements of the first type, and so on. The statement “this statement is false” does not fall under any of these definitions and thus does not make sense.

Russell is quite right in thinking that the term “statement” itself must be defined. However, such a definition must be complete. To work with statements and draw some definite conclusions about statements in general, it is necessary to explicitly enumerate all possible statements somewhere. After such an operation, any such contradictions can no longer appear.

As observed above, the most famous approach to the axiomatization of mathematics is Zermelo–Fraenkel set theory, which arose as an extension of Zermelo’s theory [36]. The idea of Zermelo’s approach is that it is allowed to use only sets constructed from already constructed sets using a certain set of axioms. For example, in Zermelo set theory, it is impossible to construct the set of all sets. Thus, a Russell set cannot be built there either.

However, the point is not only to assert that something cannot be performed in some theory; rather, it is also desirable to substantiate it. The rationale is that a physical implementation of a mathematical structure, in particular a set, is needed. The physical realization of the set of all sets is impossible since it requires an infinite number of bits (qubits).

In the language of set theory, Russell’s paradox can be written as follows: let D be the set of all sets that are not elements of themselves,

$$D=\left\{x:x\notin x\right\},$$

then

$$D\in D\iff D\notin D.$$

That is, we come to a contradiction. However, this contradiction was already incorporated in the definition, since it is impossible to define such a set explicitly. This is just a flawed definition, not a paradox. This is the same as writing that x = 5 and x = 3. One equality excludes the other and is simply an incorrect notation. In the same way, there are incorrect records of the laws of physics or simply incorrect statements about physical quantities.

Thus, the set of all sets is not a definite object, the consequence of which is the paradox.

Thus, truly constructive mathematics is that all variables and actions in it are fully defined, i.e., all variants of these variables and actions on them are recorded on some physical medium. In this case, there is no need to imply anything. The fact that we often do not see these definitions explicitly does not mean that they do not exist. They are hardwired into the structure of the brain, but we are not realize of their existence.

In this formulation of the problem, the constructiveness of mathematics is ensured by physics, i.e., material carriers. In such mathematics, there is no proof or conclusion but rather only arithmetic operations.

Constructive mathematics believes that a mathematical object exists if it can be constructed according to some rule. Mathematics uses the abstraction of identification. Instead of an abstraction of identification (which in fact is not realizable), the basic axiom of mathematics, formulated above, should be reformulated as follows:

We can say that a mathematical object exists if it is physically implemented (encoded) somewhere.

5.3. Mathematical Logic, Geometry and Algebra

Above, the propositional calculus and predicate calculus were considered as parts of logic. However, the implementation of such logic on a computer consists only of zeros and ones and operations on them. Consequently, whatever concepts do exist in logic, they must all be recognized and stored in memory in the form of zeros and ones. Consequently, inference is nothing more than a computation—a transition from the initial data to the results of computations. When calculating, no new concepts can arise in principle—they are all explicitly embedded in the structure of the system that performs these calculations—the brain.

Often, we do not realize that one or another mathematical structure is based on numbers.

All geometric objects are a collection of pixels (small areas) in space. These pixels themselves are encoded in the qubit system in the form of zeros and ones.

Thus, when we say that thinking works with a geometric object as a whole (straight line, plane, angle, etc.), we simply do not realize that this object itself must be encoded somewhere.

That is, basic geometric concepts such as “point”, “angle”, “line”, “segment” and others after the D-procedure will be a collection of zeros and ones.

Algebra theorems are a consequence of the properties of numbers. When we say that algebra is a generalization of arithmetic, the term “generalization” in this case only means that all these numbers are written somewhere, but we do not realize this.

Let us show how abstraction works when considering the main theorem of algebra (see, for example, [42]). The main theorem of algebra is that an equation of the form

$$z^n+a_{n-1}{Z}^{n-1}+\dots a_0=0$$

always has at least one solution for n > 1. The consequence is that the equation has exactly n solutions on the complex plane.

We believe that we are working with abstract quantities such as z, a, but we do not realize that we are only actually working with numbers.

However, to prove something about the properties of this polynomial, it is necessary to know all the possible values of the quantities included in it. This means that the quantities z and a must be fully defined. Among their values are those that are the solution to the equation. The only question is now to find them.

Thus, after the D-procedure, all algebraic variables, as well as constants and parameters, are encoded in a set of qubits. In such a case, the proof is simply a search for the correct statement among all the valid statements.

The theory of groups, rings and algebra of logic can also be considered branches of algebra.

5.4. Calculus and Consistency of Mathematics

Consider the standard definition of a limit. The number sequence a_n at n → ∞ converges to the limit a

$${\lim }_{n\to \infty } a_n=a,$$

if for any ε > 0 one can specify N such that

$$\left|a_n-a\right|<\epsilon$$

for all n > N.

A numeric sequence with zero limit

$${\lim }_{n\to \infty } a_n=0$$

is called an infinitesimal quantity.

An addition to the standard analysis is the nonstandard analysis [43], which introduces hyperreal numbers. An important property of hyperreal numbers is that among them, there are infinitely small and infinitely large numbers, and they exist not as the limits of some functions or sequences (as in standard analysis) but rather as ordinary elements of the field.

However, as observed above, an infinitely small (as well as an infinitely large) value requires an infinitely large number of cells to record. Based on what was said above about the finiteness of the information capacity of the brain, we can conclude that infinitesimal numbers do not exist. Two numbers that differ by less than Ω⁻¹ are indistinguishable, and any number less than the minimum must be equal to zero. In this sense, they are all equivalent.

The derivative of the function f(x) at point x is the limit (see, for example, [44])

$$\frac{df}{dx}={\lim }_{\Delta x\to 0}\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}.$$

As a result of applying the D-procedure, a new definition of the derivative can be given as

$$\frac{df}{dx}={\left(\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}\right)}_{\Delta x={\Omega }^{-1}}.$$

Note that we are not realize that such minimum numbers exist (this also applies to maximum numbers). We think that there are no restrictions on how the brain works with numbers. Formally, such numbers can be written, but in reality, we cannot work with them, i.e., perform some operations on them.

The integral in standard analysis is defined as the sum limit (see, for example, [44]):

$${\lim }_{\Delta x_i\to 0}{\displaystyle \sum _{i=0}^{n-1}f\left({\xi }_i\right)\Delta x_i}={\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}.$$

According to the new definition, an integral is just a sum:

$${\displaystyle \sum _{i=0}^{\Omega }f\left({\xi }_i\right)\Delta x_i}={\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}.$$

We list other sections of mathematics, the foundations of which are close to the foundations of the sections considered to one degree or another:

Differential geometry, topology, differential equations, functional analysis and integral equations, theory of functions of a complex variable, partial differential equations, probability theory, calculus of variations and optimization methods.

Thus, all branches of mathematics as a result of the application of the D-procedure can be formulated on the basis of arithmetic alone. It is in this form that mathematics is used by the brain. It often seems to us that this or that mathematical concept is not reduced to arithmetic and is used by us as a whole. However, we often do not realize that in any case, it must be recorded in some type of physical structure.

Notably, the proposed approach is a significant change in the foundations of mathematics; however, it will practically not affect the results of calculations. The discreteness of the calculations, because any numbers must be implemented somewhere, introduces an additional error in the calculations, which is known from the example of computers. Discreteness of thinking in relation to mathematical structures will also lead to an error, but this error will be vanishingly small and will be much less than other types of errors.

Why is mathematics effective? Why do we believe that its foundations are consistent? It is impossible to explain these properties of mathematics on the basis of mutations and natural selection since mathematics is too complex and arose relatively recently. Calculations show [6,45,46] that not only advanced structures such as the brain that are capable of doing mathematics but also much simpler organisms could not have arisen in the process of undirected evolution. To solve the problem of the evolution of life, previous works [6,45,46,47] proposed a theory of directed evolution. A feature of directed evolution is that complex living structures naturally arose in the process of evolution, while randomness played a secondary role. Thus, the consistency of mathematics is ultimately due to the structure of the brain, the emergence of which at a certain stage in the evolution of life is a natural process.

5.5. Smale’s 18th Problem and Its Solution

The conclusions made on thinking and foundations of mathematics allow us to solve Smale’s 18th problem. According to Smale [48], this problem is formulated as follows:

What are the limits of intelligence, both artificial and human?

A limitation of both artificial and natural intelligence is the information capacity that can be stored and processed by a system of qubits. In this regard, artificial and natural intelligence are similar.

Common and most important in artificial and natural intelligence is that all behavioral programs are innate. Neither artificial nor natural systems can acquire knowledge, create new concepts, generalize, etc. When we think that we are getting new knowledge, we only choose certain programs from the a priori existing programs that most adequately correspond to the given external conditions. Artificial intelligence systems work in the same manner. There is no way to create a self-learning system (artificial or natural).

The difference between natural and artificial intelligence is that consciousness is present in natural intelligence as an additional controlling system. On the other hand, nontrivial quantum effects of interactions between biologically important molecules are currently not achieved artificially, which will hold back the development of artificial intelligence. This concept is the next level of technologies for controlling biologically important molecules (see below for possible experiments to test the proposed hypothesis). Controlling biologically important molecules (proteins, RNA, and DNA) at the atomic level will give the next significant leap in intelligence and possibly lead to some hybrid form of artificial and natural intelligence.

6. Physical Implementation of Mathematics and Thinking Processes: Nontrivial Quantum Effects in the Work of Neurons and the Brain

The foundations of mathematics suggested above require the brain to have very large computational power. As observed above, quantum mechanics allows this power to be realized. However, this raises a problem associated with the fact that at temperatures at which the brain operates, a rapid decoherence of a pure quantum state occurs, which significantly complicates the use of quantum operations.

6.1. Motivation for Using Quantum Mechanics to Model the Brain: Interaction between Biologically Important Molecules

The application of quantum mechanics to the work of the brain, according to [5], can be associated with three most important areas:

-

Ideas of Penrose [49,50,51,52] according to which collapse of the wave function is associated with the mental processes;

-

Quantum-like models and decision making [53,54,55,56,57,58,59,60,61,62];

-

Generalized Levinthal’s paradox and nontrivial quantum effects of interaction of proteins, RNA and DNA [3,4].

It is this latter motivation that seems to be the most important for explaining the foundations of mathematics based on the quantum effects of the brain.

In addition, previous works [63,64,65,66,67] can also be observed.

The model equations, according to [3,4], are presented in the following form:

$$i\hslash \frac{\partial \psi }{\partial t}=\widehat{H}\psi +\phi \psi ,$$

(1)

$$\frac{\partial \phi }{\partial t}=g\left(\phi ,\psi \right).$$

(2)

The first equation is the Schrödinger equation for a particle, which also contains the potential φ associated with the collective interaction of particles in addition to the usual Hamiltonian.

The second equation represents the dynamics of this many-particle potential. This special potential organizes collective effects so that protein folding and other processes are effective. The second equation can have trivial (zero) and nontrivial (nonzero) solutions. In the first case, we obtain the usual Schrödinger equation and, as a consequence, the known properties of motion and interaction of particles—diffusion, chemical reactions, viscosity, etc. However, in the presence of a nontrivial solution, additional possibilities appear (associated with an additional term in the Schrödinger equation) for the motion and interaction of particles. In particular, some states and spatial configurations of particles (biologically important molecules) may be forbidden.

6.2. Brain Editing, Slow and Fast Computing and Symmetry of the Brain

Any mathematical actions that the brain performs are ultimately determined by its structure. Two subsystems of information processing can be distinguished here: slow (e.g., neural networks, the formation of synaptic connections, and neurogenesis) and fast (e.g., intraneuronal information processing and the interaction of biologically important molecules). Let us consider the first subsystem.

Neural networks are constantly being reconfigured. As a result, the brain is able to adapt to the solution of arbitrary tasks. The main events at this level of the hierarchy are neurogenesis, creation of new synaptic connections, and strengthening (weakening) of existing synaptic connections.

The first information processing subsystem in the brain has been considered by many authors. Different parts of the brain are involved to one degree or another in the process of perception of the surrounding world and thinking. For example, in works [68,69,70,71,72,73,74,75,76,77,78,79], the role of the hypothalamus, amygdala, cerebral cortex and other regions of the brain is considered. Let us consider in this aspect only that part of the brain’s work that is associated with microglia.

For example, microglial cells perform immune functions—they “crawl” along tissue and “eat” anything suspicious. Microglial cells can divide and perform neural network editing functions. Note here that the operation of editing something implies a complex structure of the system that it is editing. In particular, the editing operation implies that microglial cells must orient themselves in the most complex three-dimensional structure of the brain, distinguishing not only some neurons from others but also distinguishing individual parts of the structure of each neuron. Microglial cells must perform all this very accurately; otherwise, the brain’s work will be disrupted.

How can cells do this type of work efficiently? As shown in [3], with respect to protein folding, efficient operation of proteins based on classical mechanisms of atomic interaction is impossible. The same applies to an even greater extent to the work of microglial cells. It was proposed that quantum interactions between proteins, RNA and DNA are responsible for the precise and efficient operation of these molecules (Equations (1) and (2)). Such interaction, in particular, implies long-range action, i.e., biologically important molecules must interact not only with the nearest atoms but also with rather distant molecules. In relation to microglial cells, this means that they not only have information about distant neurons but can also move directionally in accordance with this information.

We list some properties of microglia discovered relatively recently [80,81,82,83,84]:

-

Microglia destroy unnecessary synapses and also participate in the forgetting processes;

-

Microglia listen to neural activity in mice and actively disconnect little-used contacts;

-

Microglia are active during sleep;

-

Microglial cells are sensitive to norepinephrine. If its level is increased, microglia cease to bite off unnecessary synapses. This process participates in the editing of memory in sleep;

-

Abnormal activity of microglia can lead to schizophrenia;

-

In obesity, microglia eat dendritic spines on neurons, thereby reducing the number of potential connections;

-

Between neurons, there is an extracellular matrix, which occupies approximately 20% of the volume. The microglia eat up the synapse tunnel in the matrix. In this case, the intercellular matrix becomes viscous; and

-

Oligodendrocytes wrap axons with myelin. Microglia bite off pieces of myelin depending on the activity of the neuron.

Thus, microglial cells are an important part of thinking, in addition to neurons. Not only does every protein have a label according to which it finds its place in the cell but also every microglial cell has an even more complex label that marks its place among all other brain cells.

In previous studies [5,6], a quantum nonlocal model of the operation of neurons was proposed. The model is based on the fact that it is not sufficient for molecules to meet for a certain reaction between them to take place. It is also necessary that the conformational degrees of freedom also come to a certain state. Thus, for biologically important molecules, the equations of chemical kinetics represent only a rough approximation, which says nothing about the characteristic times of the processes. Let us introduce, according to [7] the variable ξ, which is responsible for the spatial position of the reacting molecules (x) and their internal degrees of freedom:

$$\xi =\xi \left(x_1,\dots x_n,{\alpha }_1,\dots ,{\alpha }_m\right).$$

Then, the kinetics of biochemical reactions will be determined by spatial coordinates and coordinates ξ, for which we can write the following master equation:

$$\frac{\partial p_n\left(\xi \right)}{\partial t}={\displaystyle \sum _m^{\max }{W}_{mn}{p}_m}-{\displaystyle \sum _m^{\max }{W}_{nm}{p}_n}.$$

Generally speaking W_mn can also depend on the coordinates of proteins, RNA and DNA inside and uotside the cell. In this case reaction-diffusion equation between substances u and v will be as follows:

$$\frac{\partial u\left(\xi \right)}{\partial t}=\gamma f\left(u,v,\xi \right)+D_u\Delta u.$$

According to [7], only at a certain value of the variable ξ corresponding to the native conformation of the macromolecule, can the reaction take place.

Thus, the system of Turing-type equations, considering the effects of long-range interaction, can be transformed into the following form:

$$\begin{gathered} \frac{\partial u\left({\xi }_u\right)}{\partial t}=\gamma f\left(u,v,{\xi }_u\right)+D_u\Delta u, \\ \frac{\partial v\left({\xi }_v\right)}{\partial t}=\gamma g\left(u,v,{\xi }_v\right)+D_v\Delta v, \\ \frac{\partial p_n\left({\xi }_u\right)}{\partial t}={\displaystyle \sum _m^{m_{\max }}{W}_{mn}\left({\xi }_u\right)p_m\left({\xi }_u\right)}-{\displaystyle \sum _m^{{\mathrm{m}}_{max}}{W}_{nm}\left({\xi }_u\right)p_n\left({\xi }_u\right)}, \\ \frac{\partial p_n\left({\xi }_v\right)}{\partial t}={\displaystyle \sum _m^{m_{max}}{W}_{mn}\left({\xi }_v\right)p_m\left({\xi }_v\right)}-{\displaystyle \sum _m^{m_{\max }}{W}_{nm}\left({\xi }_v\right)p_n\left({\xi }_v\right)}. \end{gathered}$$

System of equations [4] reflects the fact that the formation of synaptic connection between neurons depends not only on the nearest neighbors, but also on distant neurons.

In particular, the directed evolution of the strength of synaptic connections can be described on the basis of the following equation:

$$\frac{\partial p_n\left({\xi }_{X12}\right)}{\partial t}={\displaystyle \sum _m^{m_{\max }}{W}_{mn}\left({\xi }_{X12}\right)p_m\left({\xi }_{X12}\right)}-{\displaystyle \sum _m^{{\mathrm{m}}_{max}}{W}_{nm}\left({\xi }_{X12}\right)p_n\left({\xi }_{X12}\right)}.$$

Here, X is a set of innate behavioral programs. Indices 1 and 2 indicate to neurons between which synaptic contact is established.

The fast subsystem that performs computations includes the opening and closing of ion channels, changing the conformations of proteins, transporting and sorting proteins, transmitting signals from the cell nucleus, and reactions between biologically important molecules within a neuron.

One of the paths of information inside a neuron according to [63] is follows:

-

Actin filaments interact with the membrane and transmit the signal into the cell;

-

With the help of actin filaments the cytoskeleton can influence the membrane; and

-

G-proteins are used as carriers between the membrane and actin and tubulin.

In this manner, according to the authors, the cytoskeleton can influence the action potential. This influence can be seen as a fine-tuning of the potential that can allow more information to be stored and transported. This influence can be considered one of the mechanisms of the connection of biologically important molecules with an action potential. The coordinating center of such communication is the neuron nucleus.

Thus, the action potential is the coarsest computational process. At the next level, there is intraneuronal information processing (G-proteins, protein labels, neuroreceptors, nucleus, etc.). At an even more subtle level is the microscopic dynamics of the biologically important molecules themselves. All of these levels serve to fine tune coarser levels, allowing quantum computations with large amounts of data over complex mathematical structures.

Generally, thinking operations are based on quantum computing with qubits. However, we are not aware of the exponentially large number of states of these qubits.

Based on the proposed models, the calculation operators take the following form:

$${\widehat{P}}_1|010100\rangle ,{\widehat{P}}_2|010100\rangle \dots$$

These operators act on 1, 2, etc. qubits and are nonunitary.

Some mathematical structures can be simulated in the brain in an analog manner. In relation to quantum nontrivial effects, this means that some quantum physical structures have exactly such properties that allow one to model given mathematical concepts. This coding can significantly save the number of qubits. However, such properties can only be found experimentally.

Thus, all mathematical thinking is based on qubit arithmetic. The arrays of these qubits can be more subtly controlled using nontrivial quantum effects of interactions between biologically important molecules.

As an experimental test of possible quantum effects in the work of the brain, we can propose the study of the hidden symmetries of the brain. In particular, the hidden symmetries of the genome and proteome of neurons may contain important information about quantum computations performed with the participation of biologically important molecules.

There are multiple meanings of the term “symmetry” in relation to the brain. In neurology/neuroanatomy, it is often talked about “asymmetry” and lateralization between left and right cerebral hemispheres [85,86]. e.g., language is connected with the left hemisphere, spatial perception with the right hemisphere etc. In electrophysiology, one considers neuronal sensitivity to orientation of sensory inputs (e.g., vision) [87,88]. In physics of neural networks, one considers the appearance of phase transitions due to spontaneous symmetry breaking [89,90,91,92,93,94].

In previous studies [4,6], experiments that could confirm or deny the presence of nontrivial quantum effects in the work of neurons and the brain were proposed. These experiments are related to the possible study of reactions between biologically important molecules online, i.e., at very short times (femtoseconds) and with high resolution.

6.3. Non-Algorithmic Thinking and Free Will

Let us discuss the question of whether some non-algorithmic means can be used in mathematical thinking.

First, note that an algorithm is a broad concept. One of the definitions of the algorithm is:

a finite set of precisely specified rules for solving a certain class of problems or a set of instructions describing the order of actions of the executor to solve a specific problem.

Second, note that an algorithm is not necessarily a set of deterministic actions. There are probabilistic algorithms (see, for example, [95]) using random variables (for example, a random number generator, quantum algorithms).

There are two directions in non-algorithmicity: philosophical and mathematical. The mathematical direction is based on Gödel’s theorem, and the philosophical one is based on free will and the inaccuracy of human thinking.

There are algorithmically unsolvable problems, but this does not mean that there are non-algorithmic tools for solving such problems. It is quite possible that the problem simply does not have a solution, or that not everything in it is fully defined and is not realized by us.

A number of authors (see, for example, [49]) believe that mathematical truth is comprehended by mathematicians using non-algorithmic means (for example, according to Penrose this is collapse of the wave function). However, as was shown in [5], we are not aware of part of the brain’s actions (for example, this is opening and closing of ion channels), but of course this does not mean that they do not occur. Therefore, Penrose’s objection of non-algorithmicity is thereby removed. The fact that we are not aware of this process does not mean that it is not algorithmic.

Frequently, a concept such as free will is associated with non-algorithmic means. Free will is viewed in different ways within the framework of different philosophical trends (see, for example, [96]). However, in philosophy, free will is not precisely defined. It is possible that what seems to us to be the result of free choice is a consequence of the hidden work of algorithms.

If all our thinking is realized physically somewhere, then the question is not about whether mathematical thinking is completely algorithmic or not, but about what physics controls it. If what we call non-algorithmic (quasi-algorithmic) is implemented in certain physical structures (for example, in qubits associated with biologically important molecules), then this actually already means algorithmicity in the broad sense of the word, meaning, for example, that probability is the foundation of quantum mechanics. All algorithms based on quantum particles are probabilistic. Probability is today an irreducible cornerstone of quantum mechanics. If we assume that free will is based on such a probability, then the problem is solved.

There is also the term “quasi-algorithm”, which is used mainly in educational technologies (see, for example, [97,98]), but this term is also vaguely defined. Most likely, it implies free will and the uncertainty of human thinking.

Thus, the algorithmic basis of thinking does not contradict empirical facts and is internally consistent. In contrast, non-algorithmic (or quasi-algorithmic) thinking is imprecisely defined.

7. Conclusions

The new foundations of mathematics can be formulated as follows:

-

All mathematical and logical constructions exist only because they are based on physical media with certain laws of interaction (architecture).

-

Mathematics is based on arithmetic, the physical implementation of which is the interacting qubits of proteins and other molecules in the neurons of the brain.

-

All proofs in mathematics and logic represent a search for the correct statement among the already-existing statements.

-

The information capacity of the brain is finite, which entails the existence of the maximum number that the brain can process.

-

As a result of applying the D-procedure, any mathematical objects are converted into digital form, which avoids many mathematical paradoxes (Banach–Tarski, Russell and others).

-

Consciousness plays the role of a controlling system for thinking. However, we do not realize much of the work of the qubits.

-

The consistency of mathematics is due to the directed evolution of living systems, as a result of which effective structures arise.

As a further development of the proposed ideas, one can consider the search for hidden symmetries of the brain, the improvement of the quantum model of the operation of neuron qubits, as well as consideration of other branches of mathematics. In particular, a more rigorous substantiation of such concepts as provability, computability and consistency within the framework of the proposed model is interesting. As a result, it will be possible to formulate a new system of axioms instead of the Zermelo–Fraenkel theory.