Peakons of Novikov Equation via the Homotopy Analysis Method
Abstract
:1. Introduction
2. Mathematical Formulation and Implementation of HAM
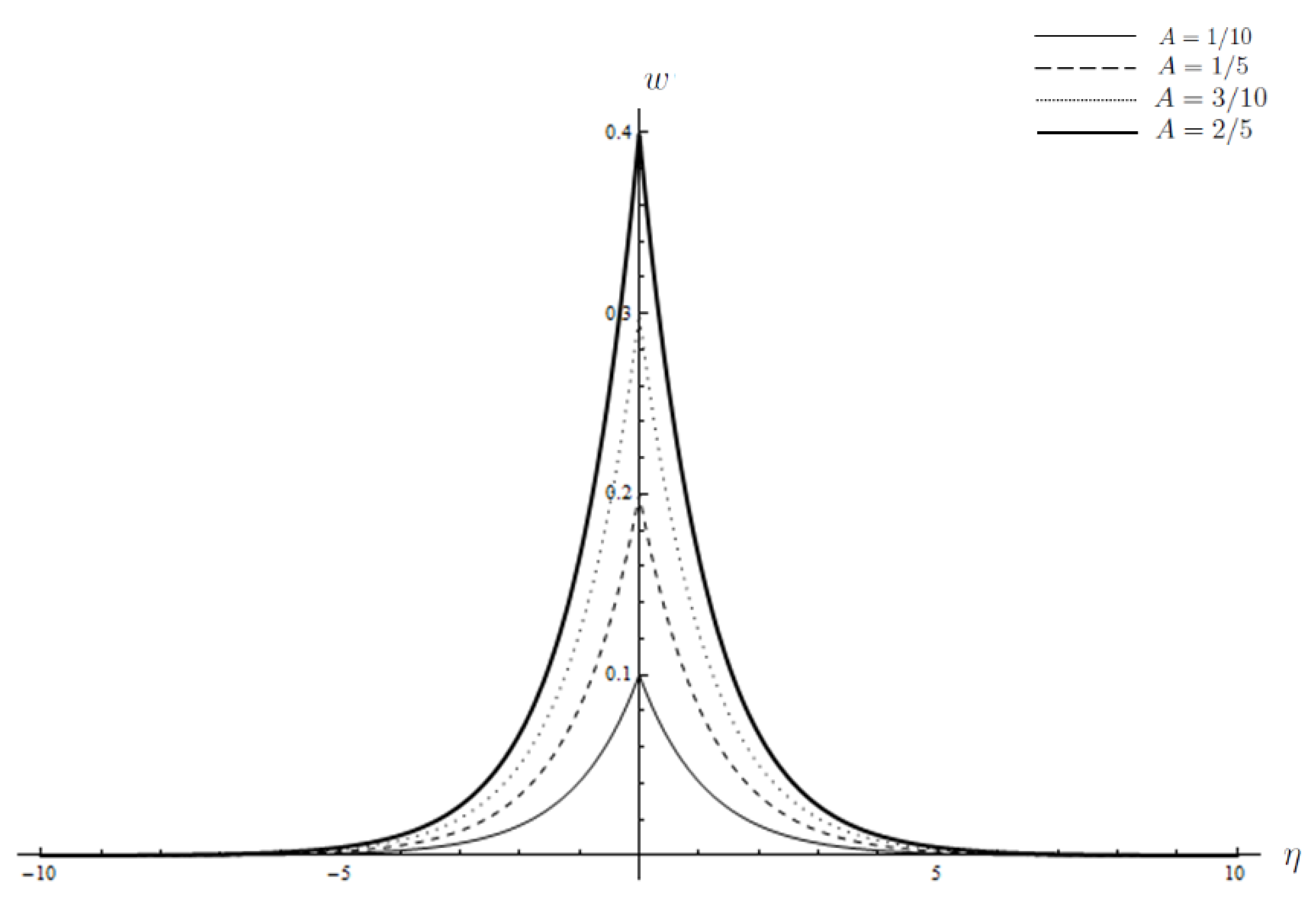
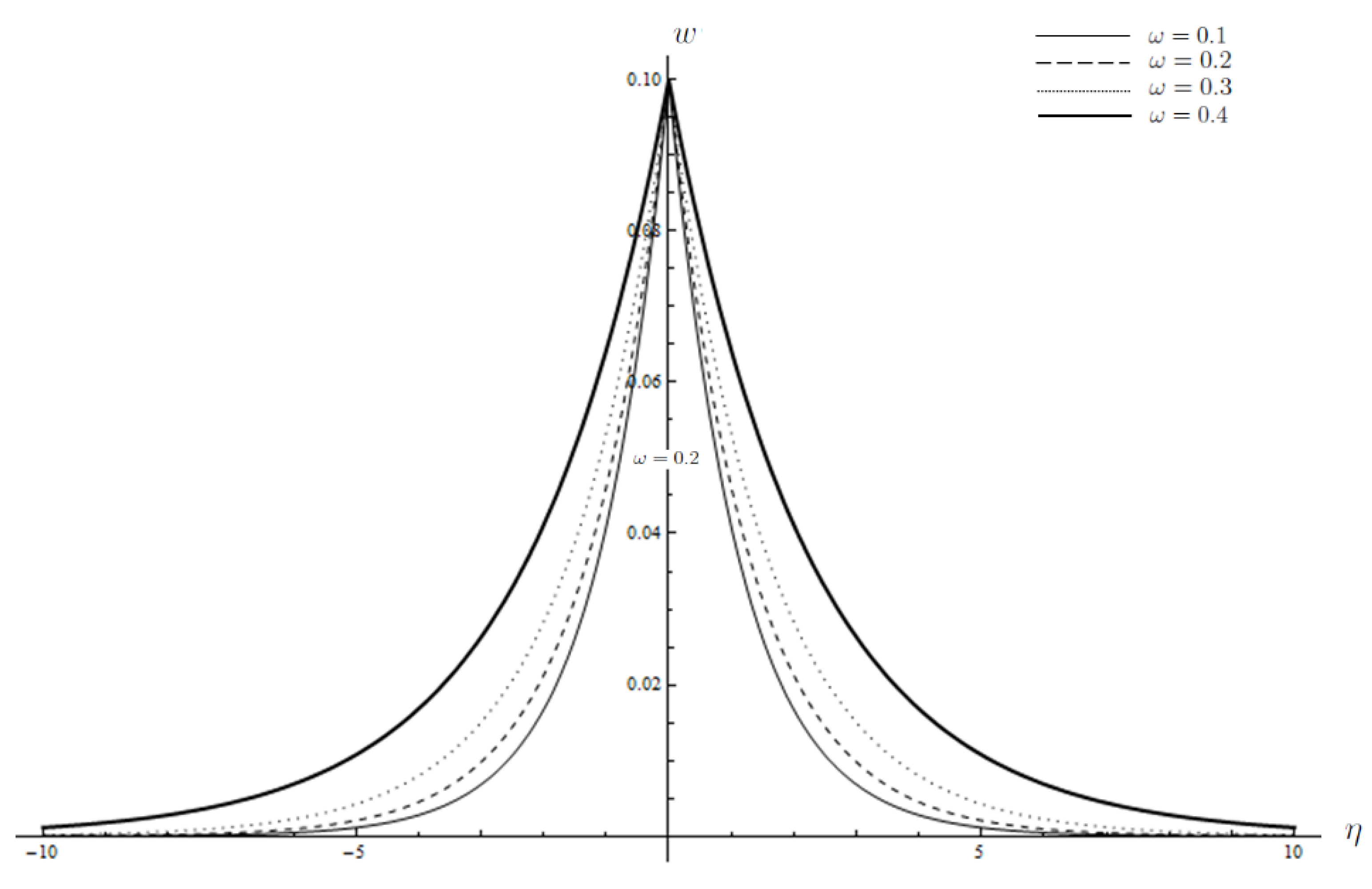
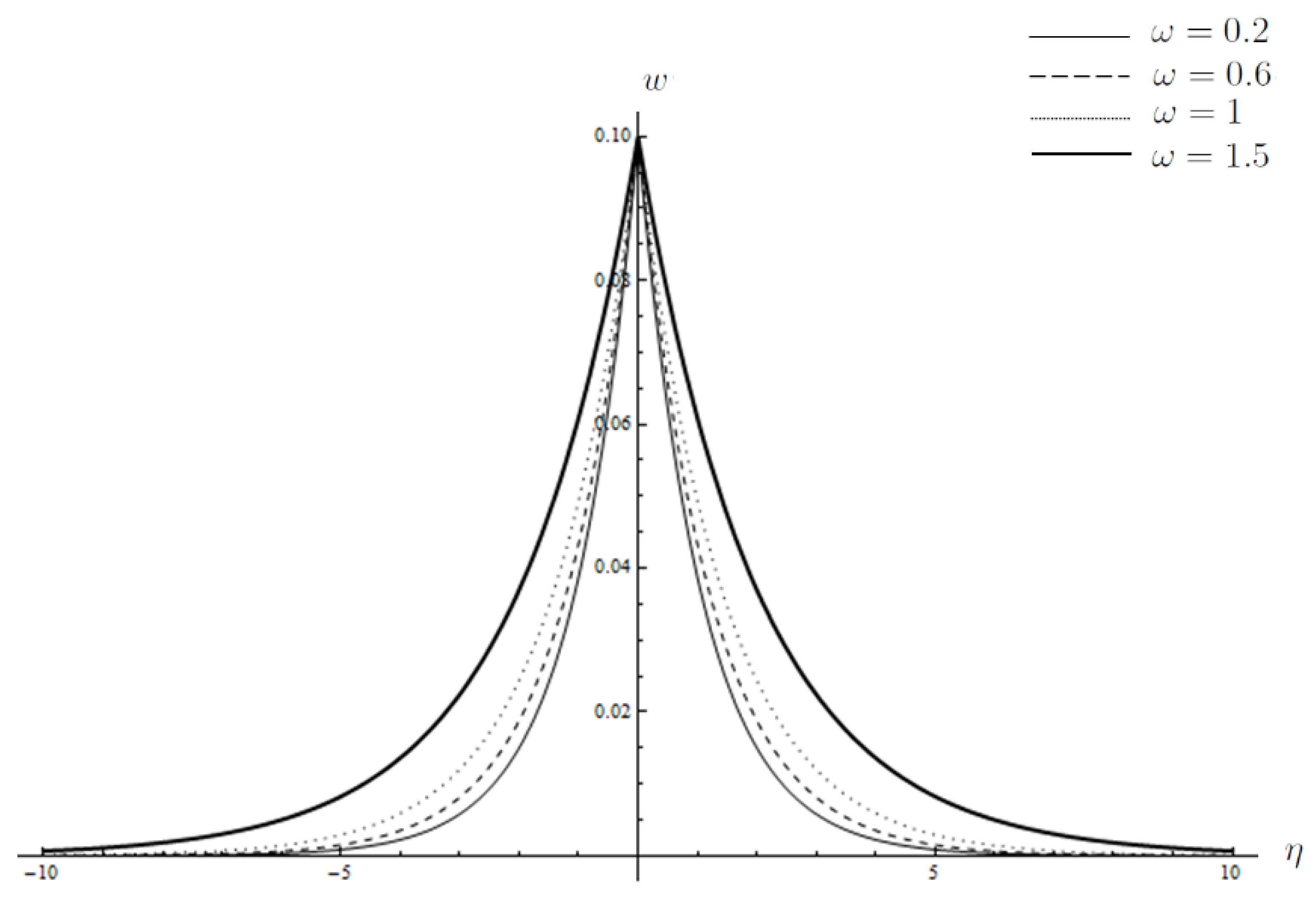
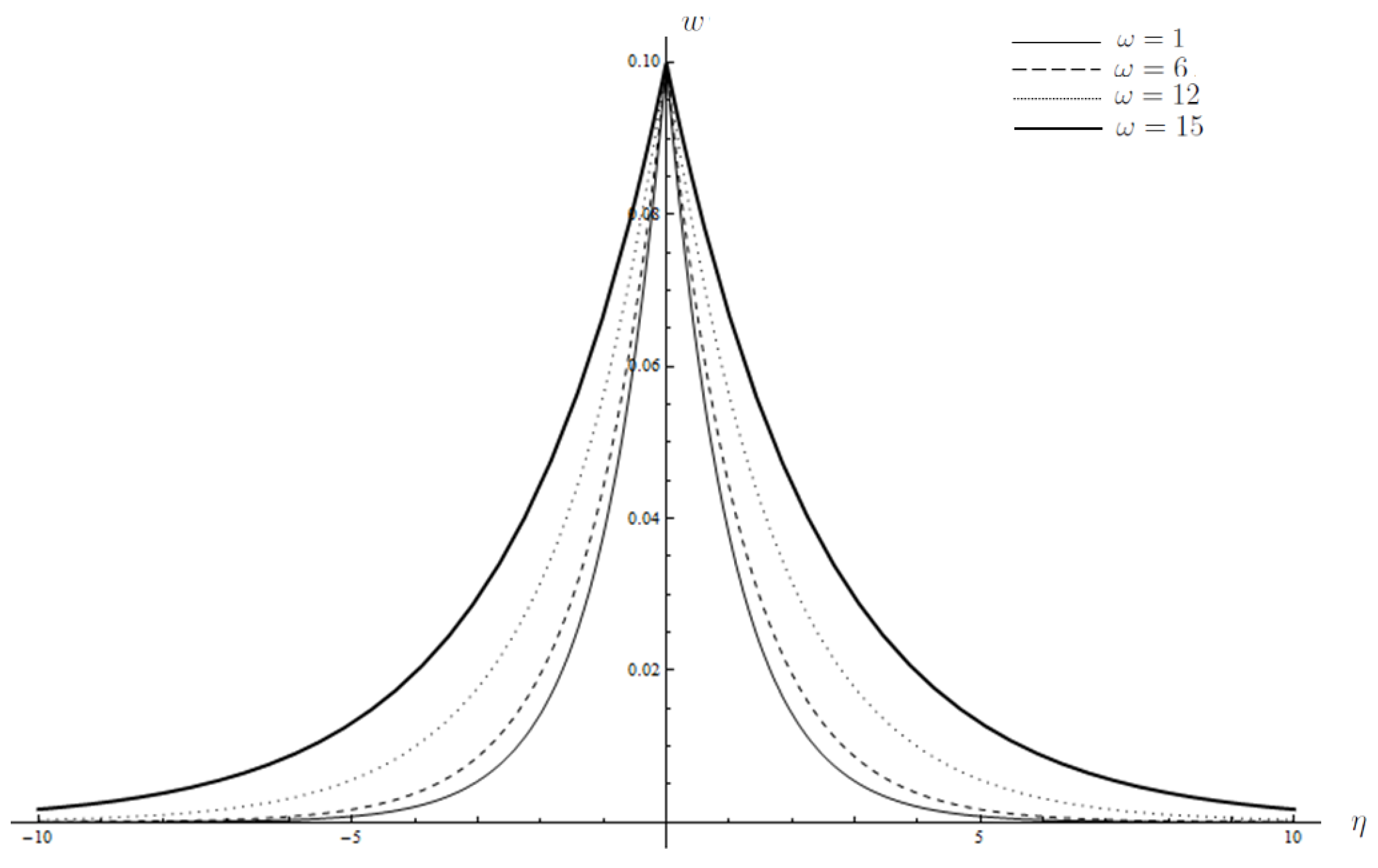
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| mKdV | modified KdV |
| CH | Camassa–Holm |
| DP | Degasperis–Procesi |
| NE | Novikov Equation |
| PDE(s) | Partial Differential Equation(s) |
| ADM | Adomian Decompostion Method |
| DTM | Differential Transform Method |
| HAM | Homotopy Analysis Method |
| BVP(s) | Boundary Value Problem(s) |
| DE | Differential Equation |
References
- Debnath, L. Nonlinear Partial Differential Equations for Scientists and Engineers, 3rd ed.; Birkhäuser: Basel, Switzerland, 2012. [Google Scholar]
- Camassa, R.; Holm, D.D. An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 1993, 71, 1661–1664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Degasperis, A.; Procesi, M. Asymptotic integrability. In Symmetry and Perturbation theory, Proceedings of the 2nd International Workshop (SPT 98), Universita di Roma “La Sapienza”, Rome, Italy, 16–22 December 1998; Degasperis, A., Gaeta, G., Eds.; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 1999; pp. 23–37. [Google Scholar]
- Novikov, V. Generalizations of the Camassa–Holm equation. J. Phys. A 2009, 42, 342002. [Google Scholar] [CrossRef]
- Hone, A.N.W.; Lundmark, H.; Szmigielski, J. Explicit multipeakon solutons of Novikov’s cubically nonlinear integrable Camassa–Holm type equation. Dyn. Partial Differ. Equ. 2009, 6, 253–289. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Qu, C. Stability of peakons for the Novikov equation. J. Math. Pures Appl. 2014, 101, 172–187. [Google Scholar] [CrossRef]
- Hone, A.N.W.; Wang, J.P. Integrable peakon equations with cubic nonlinearity. J. Phys. A. 2008, 41, 372002. [Google Scholar] [CrossRef]
- Bozhkov, Y.; Freire, I.L.; Ibragimov, N.H. Group analysis of the Novikov equation. Comput. Appl. Math. 2014, 33, 193–202. [Google Scholar] [CrossRef] [Green Version]
- Palacios, J.M. Asymptotic stability of peakons for the Novikov equation. J. Differ. Equ. 2020, 269, 7750–7791. [Google Scholar] [CrossRef]
- Grayshan, K. Peakon solutions of the Novikov equation and properties of the data-to-solution map. J. Math. Anal. Appl. 2013, 397, 515–521. [Google Scholar] [CrossRef] [Green Version]
- Ni, L.; Zhou, Y. Well-posedness and persistence properties for the Novikov equation. J. Differ. Equ. 2011, 250, 3002–3021. [Google Scholar] [CrossRef] [Green Version]
- Himonas, A.A.; Holliman, C. The Cauchy problem for the Novikov equation. Nonlinearity 2012, 25, 449–479. [Google Scholar] [CrossRef]
- Lai, S.; Ki, N.; Wu, Y. The existence of global strong and weak solutions for the Novikov equation. J. Math. Anal. Appl. 2013, 399, 682–691. [Google Scholar] [CrossRef]
- Tiğlay, F. The periodic Cauchy problem for Novikov’s equation. Int. Math. Res. Not. IMRN 2011, 2011, 4633–4648. [Google Scholar]
- Wu, X.; Yin, Z. Global weak solutions for the Novikov equation. J. Phys. A 2011, 44, 055202. [Google Scholar] [CrossRef]
- Jiang, Z.; Ni, L. Blow-up phenomenon for the integrable Novikov equation. J. Math. Anal. Appl. 2012, 385, 551–558. [Google Scholar] [CrossRef] [Green Version]
- Lundmark, H.; Shuaib, B. Ghostpeakons and characteristic curves for the Camassa–Holm, Degasperis–Procesi and Novikov Equations. SIGMA Symmetry Integr. Geom. Methods Appl. 2019, 15, 017. [Google Scholar] [CrossRef] [Green Version]
- Grayshan, K.; Himonas, A.A. Equations with peakon traveling wave solutions. Adv. Dyn. Syst. Appl. 2013, 8, 217–232. [Google Scholar]
- Himonas, A.A.; Holliman, C.; Kenig, C. Construction of 2-peakon solutions and ill-posedness for the Novikov equation. SIAM J. Math. Anal. 2018, 50, 2968–3006. [Google Scholar] [CrossRef]
- Artebrand, R.; Schroll, H.J. Numerical simulation of Camassa–Holm peakons by adaptive upwinding. Appl. Numer. Math. 2006, 56, 695–711. [Google Scholar] [CrossRef]
- Kalisch, H.; Lenells, J. Numerical study of traveling-wave solutions for the Camassa–Holm equation. Chaos Solitons Fractals 2005, 25, 287–298. [Google Scholar] [CrossRef]
- Xu, Y.; Shu, C.-W. A local discontinuous Galerkin method for the Camassa–Holm equation. SIAM J. Numer. Anal. 2006, 46, 1998–2021. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers. Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Nayfeh, A.H. Perturbation Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics. The Decomposition Method; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Hatami, M.; Ganji, D.D.; Sheikholeslami, M. Differential Transformation Method for Mechanical Engineering Problems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotoy Analysis Method; Chapman & Hall/CRC, CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Rebenda, J.; Šmarda, Z. Convergence analysis of an iterative scheme for solving initial value problem for multidimensional partial differential equations. Comp. Math. Appl. 2015, 70, 1772–1780. [Google Scholar] [CrossRef]
- Rebenda, J. Applications of differential transform to boundary value problems for delayed differential equations. AIP Conf. Proc. 2020, 2293, 340011. [Google Scholar]
- Liao, S.J.; Cheung, K.F. Homotopy analysis of nonlinear progressive waves in deep water. J. Engrg. Math. 2003, 45, 105–116. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.-Y.; Wu, W. Solving the nonlinear periodic wave problems with the Homotopy Analysis Method. Wave Motion. 2004, 41, 329–337. [Google Scholar] [CrossRef]
- Abbasbandy, S. Soliton solutions for the Fitzhugh-Nagumo equation with the homotopy analysis method. Appl. Math. Model. 2008, 32, 2706–2714. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Parkes, E.J. Solitary smooth hump solutions of the Camassa–Holm equation by means of the homotopy analysis method. Chaos Solitons Fractals 2008, 36, 581–591. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Liao, S.J. Solving solitary waves with discontinuity by means of the homotopy analysis method. Chaos Solitons Fractals 2005, 26, 177–185. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Zakaria, F.S. Soliton solutions for the fifth-order KdV equation with the homotopy analysis method. Nonlinear Dynam. 2008, 51, 83–87. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Parkes, E.J. Solitary-wave solutions of the Degasperis–Procesi equation by means of the homotopy analysis method. Int. J. Comput. Math. 2010, 87, 2303–2313. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.J. On peaked solitary waves of the Degasperis–Procesi equation. Sci. China Phys. Mech. Astr. 2013, 56, 418–422. [Google Scholar] [CrossRef]
- Liao, S.J. Chance and challenge: A brief review of homotopy analysis method. In Advances in the Homotopy Analysis Method; Liao, S., Ed.; World Sci. Publ.: Hackensack, NJ, USA, 2014; pp. 1–33. [Google Scholar]


| Order M | ||
|---|---|---|
| 2 | −0.0893854 | 5.38946 × |
| 4 | −0.0893718 | 2.77903 × |
| 6 | −0.0893686 | 1.43133 × |
| 8 | −0.0893678 | 7.3639 × |
| 10 | −0.0893676 | 3.78481 × |
| 12 | −0.0893676 | 1.94357 × |
| 14 | −0.0893676 | 9.97368 × |
| 16 | −0.0893676 | 5.11568 × |
| Order M | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2 | −0.0893676 | 5.44145 × | −0.178269 | 8.88994 × | −0.266163 | 2.58248 × | −0.352358 | 1.43883 × |
| 4 | −0.0893676 | 1.53232 × | −0.178268 | 6.4023 × | −0.266150 | 4.75746 × | −0.352252 | 2.63907 × |
| 6 | −0.0893676 | 3.215 × | −0.178268 | 3.43721 × | −0.266150 | 6.54017 × | −0.352250 | 3.6183 × |
| 8 | −0.0893676 | 5.62433 × | −0.178268 | 1.53888 × | −0.266150 | 7.5002 × | −0.352250 | 4.1407 × |
| 10 | −0.0893676 | 8.69982 × | −0.178268 | 6.09221 × | −0.266150 | 7.60614 × | −0.352250 | 4.19104 × |
| Order M | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2 | −0.0893676 | 5.44145 × | −0.0772860 | 1.39996 × | −0.0629260 | 1.45527 × | −0.0441163 | 1.65315 × |
| 4 | −0.0893676 | 1.53232 × | −0.0772860 | 2.78733 × | −0.0629260 | 1.37026 × | −0.0441162 | 1.55214 × |
| 6 | −0.0893676 | 3.215 × | −0.0772860 | 3.68153 × | −0.0629260 | 1.17036 × | −0.0441162 | 8.06038 × |
| 8 | −0.0893676 | 5.62433 × | −0.0772860 | 3.29652 × | −0.0629260 | 1.24233 × | −0.0441162 | 4.75567 × |
| 10 | −0.0893676 | 8.69982 × | −0.0772860 | 2.06995 × | −0.0629260 | 8.9394 × | −0.0441162 | 3.43156 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efstathiou, A.G.; Petropoulou, E.N. Peakons of Novikov Equation via the Homotopy Analysis Method. Symmetry 2021, 13, 738. https://doi.org/10.3390/sym13050738
Efstathiou AG, Petropoulou EN. Peakons of Novikov Equation via the Homotopy Analysis Method. Symmetry. 2021; 13(5):738. https://doi.org/10.3390/sym13050738
Chicago/Turabian StyleEfstathiou, Aggeliki G., and Eugenia N. Petropoulou. 2021. "Peakons of Novikov Equation via the Homotopy Analysis Method" Symmetry 13, no. 5: 738. https://doi.org/10.3390/sym13050738
APA StyleEfstathiou, A. G., & Petropoulou, E. N. (2021). Peakons of Novikov Equation via the Homotopy Analysis Method. Symmetry, 13(5), 738. https://doi.org/10.3390/sym13050738







