A New Generalization of the Generalized Inverse Rayleigh Distribution with Applications
Abstract
1. Introduction
2. The Beta Generalized Inverse Rayleigh Distribution
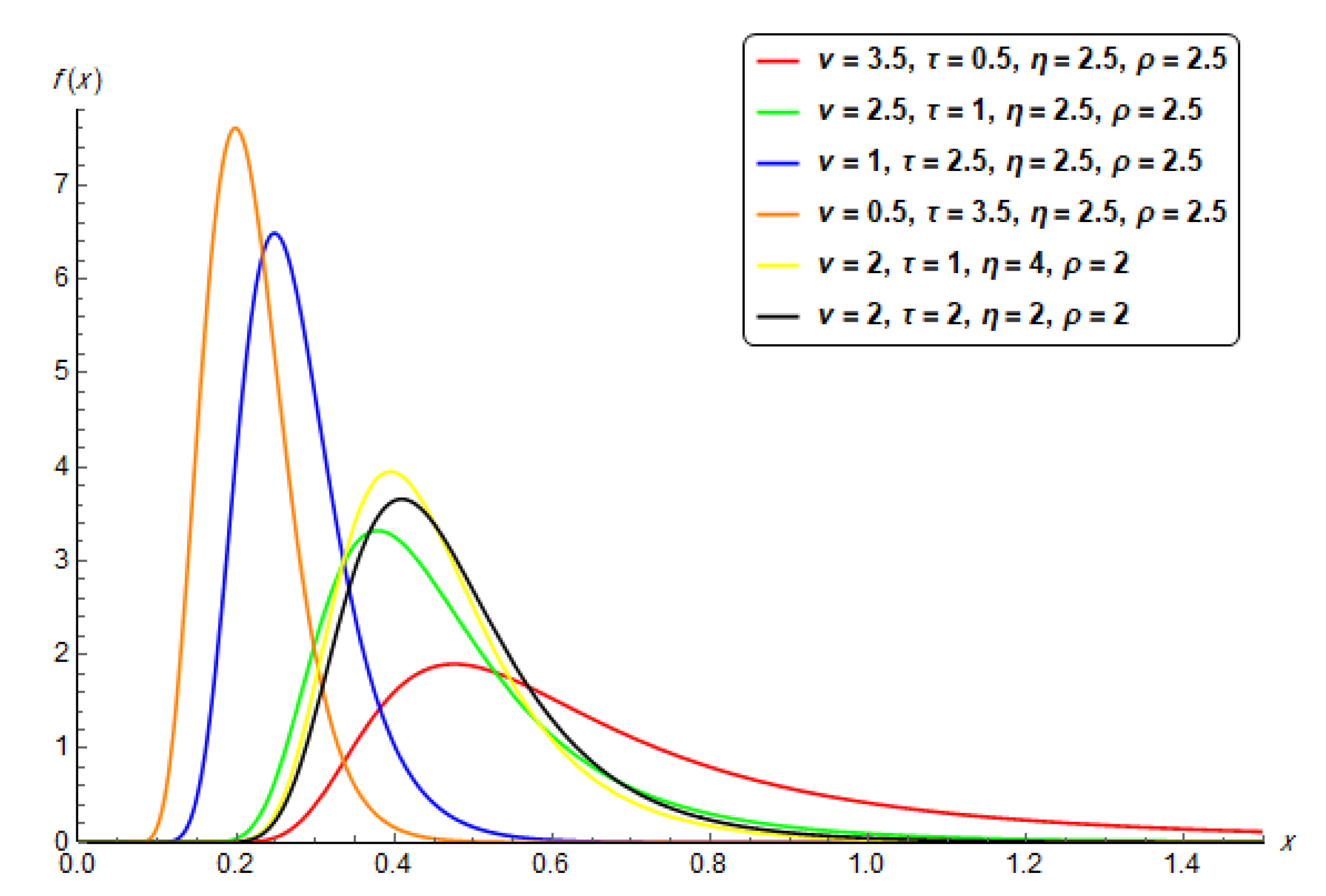
2.1. Probability Density Function of BGIRD
2.2. Cumulative Distribution Function of BGIRD
2.3. Mixture Representation
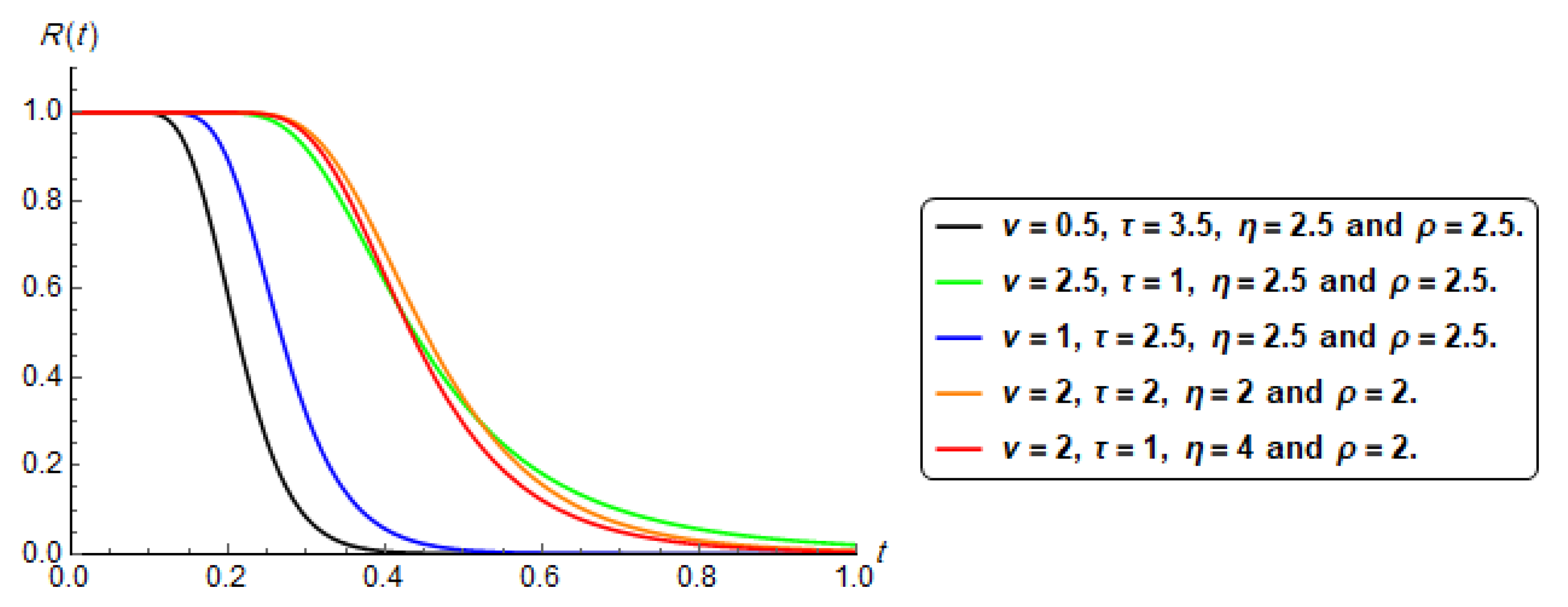
2.4. The Reliability Function
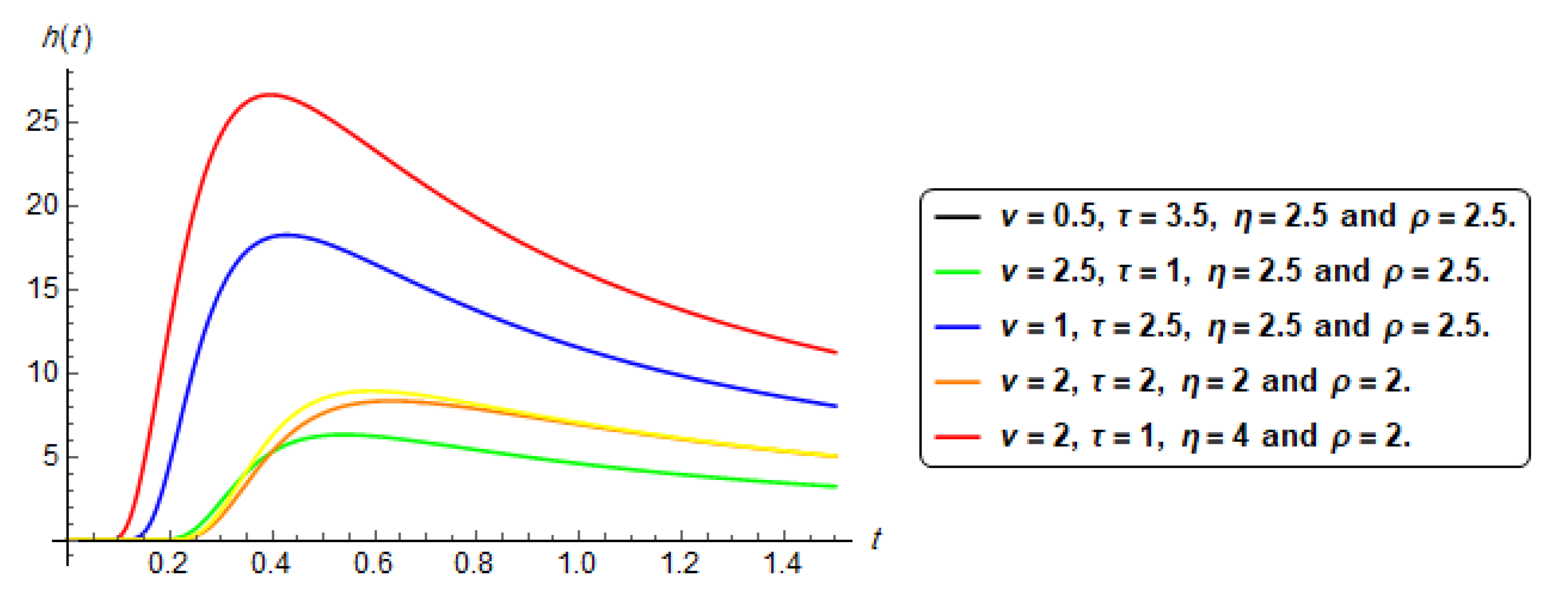
2.5. The Hazard Function
2.6. Special Sup-Models
- In particular, BGIRD becomes GIRD (, ) when and .
- The beta inverse Rayleigh distribution BIRD () is clearly a special case of BGIRD when = 1.
- IRD () can be obtained from (8) by making = 1.
- In addition, the exponentiated Rayleigh distribution ERD (, ) is a special case of BGIRD when = = 1 and the random variable Y = 1/X.
- If = = 1 and = 1 in Equation (8), the random variable Y = 1/X has the Rayleigh distribution ().
3. Statistical Properties
3.1. Quantile Function
3.2. Median
3.3. Mode
3.4. Moments
3.5. Harmonic Mean
3.6. Skewness and Kurtosis
3.7. Mean Deviations
3.7.1. The Mean Deviation about the Mean
3.7.2. The Mean Deviation about the Median
3.8. Rényi and Shannon Entropies
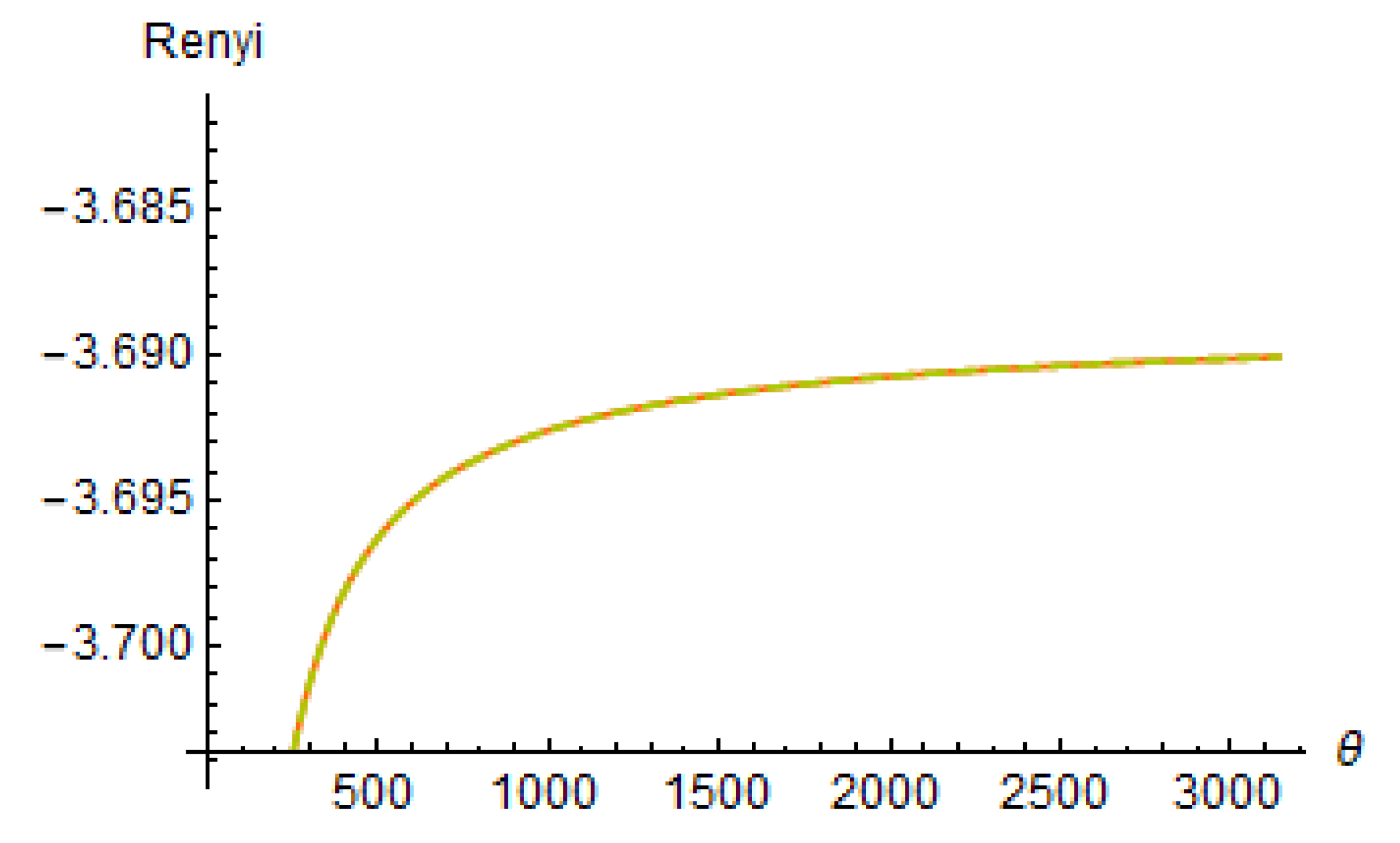
3.8.1. The Rényi Entropy for the BGIRD
3.8.2. The Shannon Entropy for the BGIRD
4. Order Statistics
5. Maximum Likelihood Estimation Method
6. Simulation Study
- From Table 2, we note that the MSEs of the ML estimates for BGIR(, , , ), , and decrease as the sample size increases which show consistency of the estimated parameters.
- According to the simulation results given in Table 2, as the sample size n increases, the ARBias is close to zero, the mean estimates tend to be closer to the true parameter values.
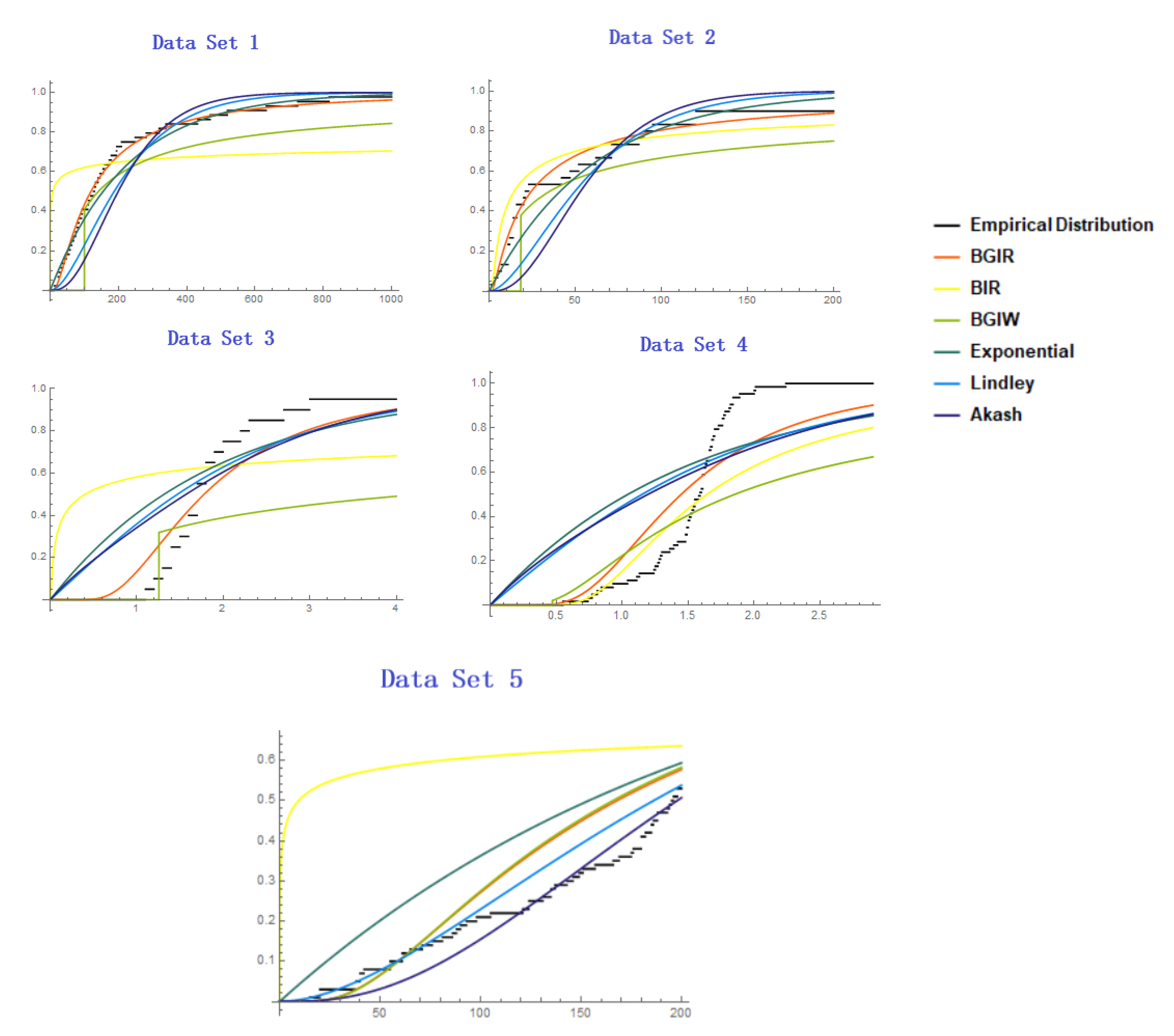
7. Application
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Appendix A
References
- Voda, V. On the inverse Rayleigh distributed random variable. Rep. Stat. Appl. Res. Jues 1972, 19, 13–21. [Google Scholar]
- Kumar, K.; Garg, R. Estimation of the parameters of randomly censored generalized inverted Rayleigh distribution. Int. J. Agric. Stat. Sci. 2014, 10, 147–155. [Google Scholar]
- Bakoban, R.A.; Abubaker, M.I. On the estimation of generalised inverted Rayleigh distribution with real data applications. Int. J. Electron. Commun. Comput. Eng. 2015, 6, 502–508. [Google Scholar]
- Bakoban, R.A.; Abubaker, M.I. Parameters estimation of the generalized inverted Rayleigh distribution based on progressive type II censoring. Adv. Appl. Stat. 2015, 47, 19–50. [Google Scholar]
- Bakoban, R.A.; Abubaker, M.I. Characterizations through the Generalized Inverted Rayleigh Distribution. Far East J. Theor. Stat. 2016, 52, 115–138. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-Normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Leao, J.; Saulo, H.; Bourguignon, M.; Cintra, R.; Rêgo, L.; Cordeiro, G. On some properties of the beta inverse Rayleigh distribution. Chil. J. Stat. 2013, 4, 111–131. [Google Scholar]
- Nekoukhou, V. The Beta-Rayleigh Distribution on the Lattice of Integers. J. Stat. Res. Iran 2015, 12, 205–224. [Google Scholar] [CrossRef]
- Bakoban, R.A.; Abu-Zinadah, H.H. The beta generalized inverted exponential distribution with real data applications. REVSTAT Stat. J. 2017, 15, 65–88. [Google Scholar]
- Khuri, A.I. Advanced Calculus with Applications in Statistics, 2nd ed.; Wiley: Princento, NJ, USA, 2003. [Google Scholar]
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics, 3rd ed.; Wiley: Princento, NJ, USA, 1962; Part 1. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. D 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Bain, L.J.; Engelhardt, M. Introduction to Probability and Mathematical Statistics, 2nd ed.; Brooks/Cole: Boston, MA, USA, 1992. [Google Scholar]
- Song, K.S. Rényi information, loglikelihood and an intrinsic distribution measure. J. Stat. Plan. Inference 2001, 93, 51–69. [Google Scholar] [CrossRef]
- David, H.A.; Nagaraja, H.N. Order Statistics, 3rd ed.; Wiley: Princento, NJ, USA, 2003. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 2nd ed.; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Shanker, R.; Hagos, F.; Sujatha, S. On Modeling of Lifetime Data using One-Parameter Akash, Lindley and Exponential Distributions. Biom. Biostat. Int. J. 2016, 3, 54–62. [Google Scholar] [CrossRef]
- Baharith, L.A.; Mousa, S.A.; Atallah, M.A.; Elgayar, S.H. The beta generalized inverse Weibull distribution. J. Adv. Math. Comput. Sci. 2014, 252–270. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
| Skewness | Kurtosis | Mean | Median | Mode | Harmonic Mean | ||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 2 | 1.5 | 0.13731 | 1.29818 | 0.637261 | 0.601615 | 0.545538 | 0.592602 |
| 2 | 2 | 2 | 2 | 0.13731 | 1.29818 | 0.477946 | 0.451212 | 0.409154 | 0.444451 |
| 2 | 2 | 0.5 | 2 | 0.31697 | 1.58531 | 1.42599 | 0.93221 | 0.60726 | 0.862293 |
| 2 | 2 | 1.5 | 2 | 0.162677 | 1.32328 | 0.543969 | 0.50147 | 0.439831 | 0.492135 |
| 2 | 2 | 5 | 2 | 0.0792963 | 1.25709 | 0.357224 | 0.349688 | 0.336093 | 0.346181 |
| 1 | 2 | 2 | 2 | 0.136143 | 1.29595 | 0.392529 | 0.368785 | 0.331165 | 0.360099 |
| 3 | 2 | 2 | 2 | 0.137703 | 1.29892 | 0.536444 | 0.507568 | 0.462275 | 0.501744 |
| 2 | 0.75 | 2 | 2 | 0.240794 | 1.4393 | 0.770942 | 0.63456 | 0.498165 | 0.616217 |
| 2 | 1 | 2 | 2 | 0.203663 | 1.37855 | 0.64575 | 0.566454 | 0.470633 | 0.553656 |
| 2 | 4 | 2 | 2 | 0.0921975 | 1.26287 | 0.387276 | 0.376634 | 0.35771 | 0.372261 |
| 1 | 1 | 1.5 | 0.5 | 0.24225 | 1.43601 | 2.46538 | 2.00588 | 1.53797 | 1.92415 |
| 1 | 1 | 1 | 1.5 | 0.30686 | 1.57048 | 3.54491 | 0.800748 | 0.54433 | 0.75225 |
| n | |||||||
|---|---|---|---|---|---|---|---|
| MLEs | 1.8771 | 2.1164 | 0.5575 | 1.9080 | 0.1219 | 1.0487 | |
| 10 | ARBias | 0.0614 | 0.0582 | 0.1149 | 0.0460 | 0.1977 | 0.1999 |
| MSE | 0.1384 | 0.1120 | 0.0204 | 0.0963 | 0.0056 | 0.1160 | |
| MLEs | 1.9092 | 2.0567 | 0.5353 | 1.9394 | 0.1348 | 0.9684 | |
| 20 | ARBias | 0.0454 | 0.0283 | 0.0706 | 0.0303 | 0.1130 | 0.1080 |
| MSE | 0.1217 | 0.0846 | 0.0133 | 0.0812 | 0.0032 | 0.0576 | |
| MLEs | 1.9511 | 2.0456 | 0.5190 | 1.9713 | 0.1412 | 0.9281 | |
| 30 | ARBias | 0.0244 | 0.0228 | 0.0381 | 0.0143 | 0.0708 | 0.0619 |
| MSE | 0.1191 | 0.0830 | 0.0064 | 0.0761 | 0.0019 | 0.0283 | |
| MLEs | 1.9430 | 2.0373 | 0.5131 | 1.9681 | 0.1447 | 0.9104 | |
| 50 | ARBias | 0.0285 | 0.0187 | 0.0261 | 0.0159 | 0.0477 | 0.0417 |
| MSE | 0.1160 | 0.0771 | 0.0057 | 0.0730 | 0.0014 | 0.0182 | |
| MLEs | 1.9714 | 2.0082 | 0.5049 | 1.9879 | 0.1490 | 0.8857 | |
| 100 | ARBias | 0.0143 | 0.0041 | 0.0098 | 0.0060 | 0.0191 | 0.0135 |
| MSE | 0.0373 | 0.0245 | 0.0019 | 0.0247 | 0.0005 | 0.0052 |
| Data | Model | MLEs | Statistics | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | −2 | |||||||
| Data 1 | BGIRD | 14.0184 | 74.0009 | 8.71669 | 0.15366 | 563.039 | 570.175 | 555.039 | |
| BIRD | 6899.62 | 4900.34 | 0.0543026 | 715.539 | 720.892 | 709.539 | |||
| BGIWD | 4938.59 | 0.001181 | 0.0862678 | 0.750759 | 39.904 | 576.569 | 585.49 | 566.569 | |
| Exponential | 0.004475 | 566.02 | 567.80 | 564.02 | |||||
| Lindley | 0.00891 | 581.16 | 582.95 | 579.16 | |||||
| Akash | 0.013423 | 611.93 | 613.71 | 609.93 | |||||
| Data 2 | BGIRD | 5.0833 | 14.4244 | 2.9408 | 0.1921 | 316.199 | 321.80 | 308.199 | |
| BIRD | 0.5395 | 9.6731 | 0.2074 | 330.41 | 333.21 | 326.41 | |||
| BGIWD | 4227.66 | 0.0013 | 0.0586 | 0.534319 | 40.7341 | 326.17 | 333.18 | 316.17 | |
| Exponential | 0.016779 | 307.26 | 308.66 | 305.26 | |||||
| Lindley | 0.033021 | 325.2 | 326.6 | 323.2 | |||||
| Akash | 0.050293 | 356.88 | 358.2 | 354.8 | |||||
| Data 3 | BGIRD | 17.5039 | 58.042 | 6.3644 | 0.3428 | 51.067 | 55.05 | 43.067 | |
| BIRD | 7569.7 | 5201.94 | 0.098989 | 133.896 | 136.883 | 127.896 | |||
| BGIWD | 2464.11 | 0.0015 | 0.0396 | 0.4256 | 29.545 | 109.587 | 114.566 | 99.5871 | |
| Exponential | 0.526316 | 67.67 | 68.67 | 65.67 | |||||
| Lindley | 0.816118 | 60.50 | 62.50 | 63.49 | |||||
| Akash | 1.156923 | 61.52 | 62.51 | 59.52 | |||||
| Data 4 | BGIRD | 21.0277 | 69.3754 | 9.45318 | 0.3144 | 102.438 | 111.01 | 94.4377 | |
| BIRD | 0.65579 | 0.808613 | 1.00416 | 115.251 | 121.681 | 109.251 | |||
| BGIWD | 37.7781 | 0.0052 | 0.174197 | 1.28585 | 2.63091 | 164.39 | 175.106 | 154.39 | |
| Exponential | 0.663647 | 179.66 | 181.80 | 177.66 | |||||
| Lindley | 0.996116 | 164.56 | 166.70 | 162.56 | |||||
| Akash | 1.355445 | 165.73 | 169.93 | 163.73 | |||||
| Data 5 | BGIRD | 12.0129 | 155.906 | 7.49802 | 0.205185 | 1285.79 | 1296.21 | 1277.79 | |
| BIRD | 19758 | 33641.7 | 0.0520308 | 1690.43 | 1698.24 | 1684.43 | |||
| BGIWD | 5.54157 | 1.93615 | 3.77834 | 0.629758 | 9.71891 | 1289.55 | 1302.57 | 1279.55 | |
| Exponential | 0.004505 | 1282.52 | 1285.12 | 1280.52 | |||||
| Lindley | 0.00897 | 1253.34 | 1255.95 | 1251.34 | |||||
| Akash | 0.013514 | 1257.83 | 1260.43 | 1255.83 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakoban, R.A.; Al-Shehri, A.M. A New Generalization of the Generalized Inverse Rayleigh Distribution with Applications. Symmetry 2021, 13, 711. https://doi.org/10.3390/sym13040711
Bakoban RA, Al-Shehri AM. A New Generalization of the Generalized Inverse Rayleigh Distribution with Applications. Symmetry. 2021; 13(4):711. https://doi.org/10.3390/sym13040711
Chicago/Turabian StyleBakoban, Rana Ali, and Ashwaq Mohammad Al-Shehri. 2021. "A New Generalization of the Generalized Inverse Rayleigh Distribution with Applications" Symmetry 13, no. 4: 711. https://doi.org/10.3390/sym13040711
APA StyleBakoban, R. A., & Al-Shehri, A. M. (2021). A New Generalization of the Generalized Inverse Rayleigh Distribution with Applications. Symmetry, 13(4), 711. https://doi.org/10.3390/sym13040711






