Abstract
We study the behaviour of a charge bound on a graphene annulus under the assumption that the particle can be treated as a massless Dirac electron. The eigenstates and relative energy are found in closed analytical form. Subsequently, we consider a large annulus with radius in the presence of a static magnetic field orthogonal to its plane and again the eigenstates and eigenenergies of the Dirac electron are found in both analytical and numerical form. The possibility of designing filiform currents by controlling the orbital angular momentum and the magnetic field is shown. The currents can be of interest in optoelectronic devices that are controlled by electromagnetic radiation. Moreover, a small radial force acts upon the annulus with a stretching effect. A linearly polarized electromagnetic field propagating in the orthogonal direction is added; the time evolution of the operators show that the acceleration of the electron is proportional to the rate of change of the spin of the particle.
1. Introduction
The origin of the mass of the electron, perpetual problem of theoretical physics, cannot be purely electromagnetic, as it would be infinite [1]. Modern field theory’s point of view pragmatically bypasses the question by using the renormalization concept and subtracting from the mass divergent terms [2]. Whatever the origin might be, the experimental fact is that the electron has a non vanishing mass that couples the left and right Weyl spinors in the relativistic Dirac equation so that the electron state is endowed of parity symmetry, but it is not eigenstate of the helicity operator. It is astounding that modern materials provide a way to study massless charges, albeit in an approximated fashion.
Graphene, a monolayer of carbon atoms arranged in an infinite pattern of hexagons, has a structure recalling a honeycomb. At low energy, the symmetry of the lattice permits the description of the electrons as massless charges, dubbed Dirac electrons, with velocity , where c is the speed of the light and [3,4,5]. Hence, the Dirac electron is described by the relativistic Dirac equation with and . Thus, present-day technology allows for the theoretical and experimental study of a massless particle, with states that are eigenstate of the helicity operator and that can interact with electromagnetic fields through its charge. Analytical solutions of the Dirac equations are very scarce, and it is remarkable that graphene in few cases permits solutions in a closed form that can be used as benchmarks for approximated or numerical calculations in complex problems [6,7,8,9,10,11]. These properties, together with a wealth of new effects, make the study of graphene very attractive.
Indeed, graphene is not an isolated example: new nano and mesoscopic materials present symmetries that, judiciously exploited, permit significant simplification in the study of complex systems by treating them as reduced dimensionality systems. These are materials with one (or two) spatial dimensions extending very much more than the other(s). The quantum modes pertaining to the small dimension(s) can only be populated by exciting them with a relative large energy and can often be neglected. For instance, fullerene, a spherical arrangements of 60 carbon atoms with radius ( is the Bohr radius), can be considered as a two-dimensional (2D) object [12,13,14,15] or even as a zero dimensional particle [4]. From graphene, it is possible to fabricate very long and narrow 2D strips and, by rolling, 2D tubes and cones.
In this paper, we deal with a Dirac electron bound in a two-dimensional annulus, the part of the plane between two circles of radius and () in the plane. Along , we set a static magnetic field and the propagation of a laser field of angular frequency . This might look like an artificial model, since the symmetry that is required for treating the electron as a massless particle requires an infinite lattice. Besides, the manufacture of a graphene annulus is rather difficult, and the Klein paradox obstructs the design of a potential trap [16]; several magnetic schemes have been proposed to bypass these drawbacks [4,6,7,17,18,19]. In our model, we adopt a very large annulus that should make the use of a massless electron in a finite piece of graphene acceptable; as a reward, analytical solutions are found.
To help in visualisation, we use a coherent notation: a vector is indicated by an arrow over the symbol and a matrix with the symbol , thus is the vector with the three standard Pauli matrices as components. A two-component spinor is marked with one dot below the symbol: ; a tilde below a letter () flags the operator. Always repeated indices imply summation.
2. Theory
In what follows, we make extensive use of the Heisenberg representation to find the time evolution of the operators relevant to the problem. Let be the Hamiltonian of the problem at hand, then, in the Heisenberg representation, the time evolution of the generic operator —which can be explicitly time dependent—is given by
the use of of this expression allows the finding of constants of motion by paying the price of using commutator algebra that, almost always, is straightforward.
2.1. Field Free Case
In order to understand what we should wait for, we start with the rather simple problem of the annulus in the absence of external fields. In this case, the Dirac equation for an electron with mass is
with ; and the left and right spinorial components of the Dirac spinor; the mass of the particle; and, the canonical momentum, which, in the absence of vector potential, is equal to the mechanical momentum . Coherently with our assumption, we set and ; hence, the equations for the two spinors decouple. Hereafter, we discuss always the left component alone and omit the superscript . Thus, the equation for the left spinor assumes the form of a standard Schrödinger equation
with Hamiltonian
2.1.1. Time Evolution of the Operators
Let be the angular momentum of the particle (throughout this paper, the traditional operators of the angular momenta are taken dimensionless). By use of the commutator
with the Levi–Civita symbol, it is easy to obtain
Let be the spin angular momentum operator; use of
gives the time evolution of the spin:
thus, and are not constant, but the total angular momentum is constant:
2.1.2. The Charge’s States
The constancy of the total angular momentum can be exploited for finding the general form of the spinor in the annulus. According to our 2D model, the motion along is forbidden; thus, working with cylindrical variables, we may write:
with
Equation (10) can be solved by the separation of the variables with the boundary conditions :
with solution
thus the general spinor is
We wish to solve the time independent Schrödinger equation . In plane circular variables, the Hamiltonian assumes the form
that, applied to the eigenstate (14) after some elementary algebra, gives:
this can be cast in the form of the Bessel equation
with
The most general solution for is
the boundary conditions give
with non-trivial solution for and only if the determinant of the coefficients vanishes:
The values of that satisfy this equality give the eigenstates. For any value of the orbital angular momentum m, there is an infinite number of zeros; thus, the eigenvalues are labelled by the indices m and n. From the physical point of view, n counts the number of nodes of the wave function between the borders of the annulus. In Table 1, we list a few eigenvalues ; the eigenenergy can be obtained from (18); thus, the knowledge of the experimental value of the Fermi velocity is not needed at this stage.

Table 1.
The selected values of in atomic units; the value of of the eigenenergy can be obtained by with and au. The values of the inner and outer radii of the annulus are and .
In Figure 1, we plot few eigenstates of the Dirac electron in the annulus for and several values of n. The eigenstates oscillate with decreasing amplitude toward the outer radius.
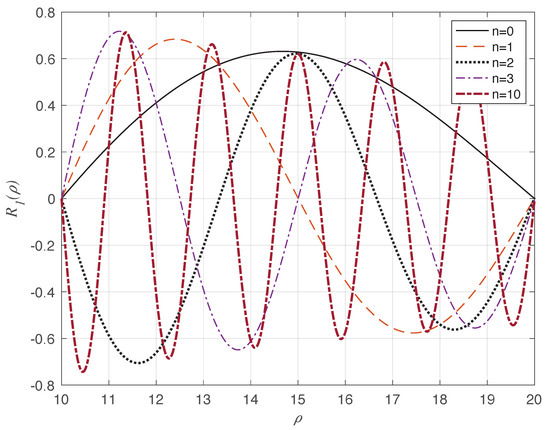
Figure 1.
(Color on line) Normalised wavefunction of the Dirac electron in the non-magnetized annulus for and different values of n as a function of in au.
In Figure 2, we show eigenfuctions for ; the behaviour of maintains the same characteristics than for , but the eigenstates are pushed toward the external part of the annulus.
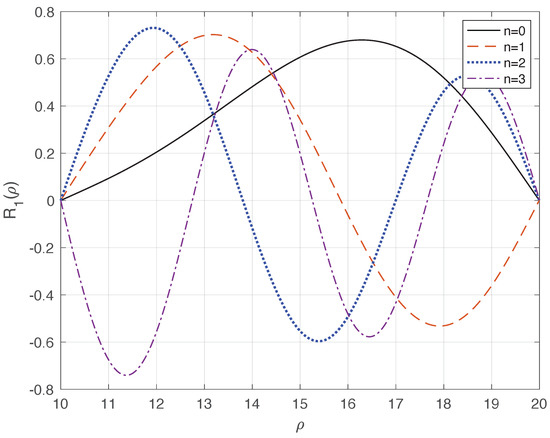
Figure 2.
(Color on line) Normalised wave functions of the Dirac electron in the non-magnetized annulus for and different values of n as a function of in au.
This feature is mostly evident in Figure 3, where we compare the eigenstates for with and : this is hardly surprising.
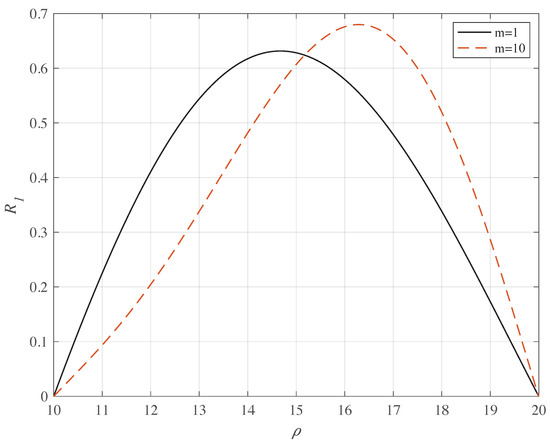
Figure 3.
(Color on line) Normalised wave functions of the Dirac electron in the non-magnetized annulus for and two different values of m as a function of in au.
3. Static Magnetic Field
The trapping of a Dirac electron within a region by an applied potential is made difficult by the Klein paradox, an epiphany of negative energy states. As mentioned in the Introduction, a plethora of schemes, requiring the presence of a magnetic field, has been advanced to overpass the problem. Rings and annuli are perfectly suitable to be used with a magnetic field because of their circular symmetry; they provide a fundamental environment for basic and applicative use [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].
Now, we discuss the problem of the annulus crossed by an orthogonal static magnetic field . The Hamiltonian for the left spinor can be rapidly obtained from Equation (4) with the usual substitution , where q is the charge (for the electron ) and the vector potential. Here, is the operator of the mechanical momentum; thus, the Hamiltonian is::
in quantum theory, the helicity is defined as the projection of the spin along the mechanical momentum, thus energy and helicity share the eingevectors. For convenience sake, in the following, the form
is used.
The time evolution of few relevant operators can be obtained via the Heisenberg equation. The commutator algebra is straightforward, but, occasionally, cumbersome. For example, the time evolution of the vector potential is
leading to
We list the time evolution of a few relevant operators in Table 2.

Table 2.
Time derivative of few operators. is the static magnetic field. For the spin two useful forms are listed.
The form that is assumed by is suggestive: a comparison with the force acting on a classical charge by a magnetic field
shows that, cum grano salis, the Pauli vector can be seen as the operator of the velocity; this vision is reinforced by the equation for . One important consideration can be still obtained from the rate equations and, specifically, from : the charge appears multiplied by the velocity factor ; thus, the magnetic force is decreased by the same factor. The magnetic forces acting on Dirac electrons are small. A rapid look to the table shows that the spin flip rate gives the acceleration. Even if it appears to be obvious, the equation for shows that the total angular momentum is constant along the external magnetic field. This conservation law is not true for and separately.
Solution
Setting
makes constant. Again, this can be exploited to obtain the general form of the spinor ;
By using cylindrical variables and the separation of the variables
we readily obtain the angular part:
i.e.,
thus the spinor is:
Lengthy algebra permits casting the Hamiltonian in cylindrical variables:
The time independent Schrödinger equation becomes:
where E is the energy of the eigenstate. The two coupled equations can be cast into one, for example, for :
that can be simplified with the substitution
(the parameter introduces into the problem a length scale absent in the non-magnetized annulus). The form of the differential equation becomes:
with
and the sign of the charge. The substitution
transforms the equation into the one of the confluent hypergeometric function
The equation
has two independent solutions that are generally indicated with and
(written in this form is always defined [36]).
In our case,
and
The most general solution is
with boundary conditions
that can be fulfilled if
A quick look to the expression for a in Equation (44) shows that the eigenenergies can be analytically found by setting
two indices are needed to list them: m, which gives the angular momentum, and n, which enumerates the energy at the chosen value of m. Thus
and, of course, and determine the value of . For checking purpose, a few values of are listed in Table 3.

Table 3.
Selected values of ; the inner and outer radia of the annulus are: and .
Many discontinuities and rapid oscillations between positive and negative values of the function
make the numerical solution of Equation (48) by finding the zeros of the equation difficult. Calculating to reach numerical converge is difficult and, thus, painstaking attention must be devoted to independent checks of the numerical results. The expression shown in Equation (49) is one of the main results of this work.
This discussion shows that x, as defined in (36), is the natural variable of the problem, but it is not a physically convenient one, as it contains, in its definition, the magnetic field ; to change the value of the magnetic field would affect the value of and thus making messy any regular study. In general one wants the dependence of the eigenenergies versus , and the plot of the eigenstates as a function of with fixed and . In the following, we show the eigenstates of the annulus in the presence of a magnetic field. We use large values of the radii of the annulus ( and ) to approximate the electron as a Dirac charge and let the magnetic field span over more than two orders of magnitude.
In Figure 4, the normalised wave function for and different values of m at au ( au T) is displayed. For small m, the wave functions are weakly dependent upon m; however, when m is large, the electron state peaks near the external edge of the annulus. Accordingly, we perceive the possibility of creating stationary filiform currents for and that is at the lowest possible energy. Figure 5 and Figure 6 show a few eigenstates for and .
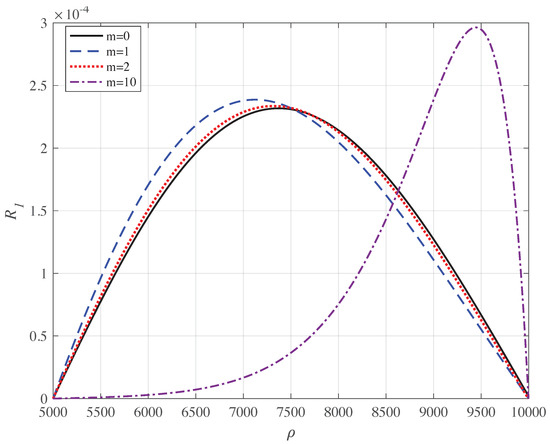
Figure 4.
(Color on line) Normalised wave function of the Dirac electron in the annulus for and different values of m as a function of in au; au. The energy of the states are: au, au, au, au.

Figure 5.
(Color on line) Normalised wavefunction of the Dirac electron in the annulus for and different values of n as a function of in au; au.; n gives the number of nodes between the borders of the ring. The energy of the states are: au, au, au, au.
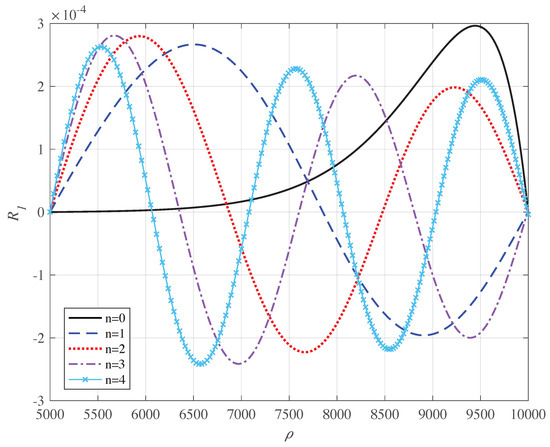
Figure 6.
(Color on line) Normalised wave function of the Dirac electron in the annulus as a function of in au for and different values of n au; n gives the number of nodes between the edges of the ring. The energy of the states are: au, au, au, au, au.
Figure 7 presents the distortions introduced by the magnetic field in the wave functions, showing a peculiar effect: by increasing the peak of the radial wave function moves inward and then outward. A large magnetic field confines the electron in the outer region of the annulus. Subsequently, it is possible, by using the orbital angular momentum m and the magnetic field as control knobs of an experiment, to produce filiform currents circulating in a reduced portion of the annulus. Such currents may be used in informatics technology [20,29,31,34,35,37,38,39,40,41,42]. Furthermore, an adiabatic increase of does not induce transition amongst the levels, but pushes the electron towards large .
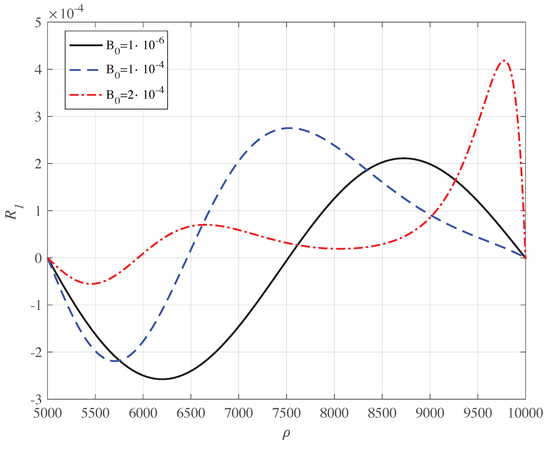
Figure 7.
(Color on line) Normalised wave function of the Dirac electron in the annulus as a function of in au for and different values of in au; here . The energy of the states are: au, au, au.
In Figure 8, we show versus for : in the range chosen here has an almost linear dependence upon . This linear dependence spans over more than 2 orders of and is somehow surprising; in fact, in Equation (44), enters the definition of the parameter a; the dependence of the functions and from a is highly non linear and it would hint a more structured pattern of the eigenenergy vs. .
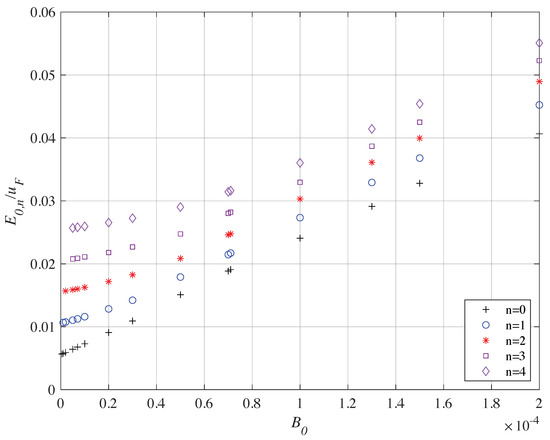
Figure 8.
(Color on line) Eigenenergies in au of the annulus as a function of the static magnetic field in au for few values of n with . The radia of the annulus are: and .
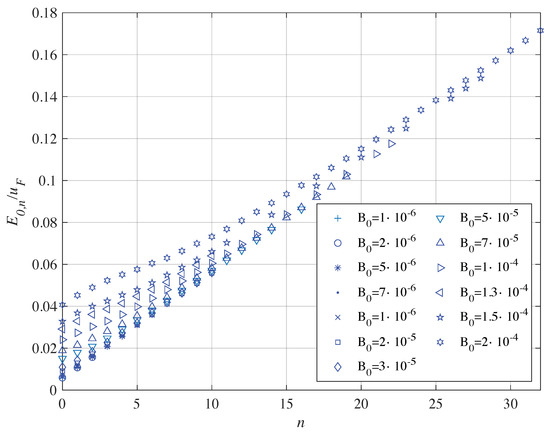
Figure 9.
Eigenenergies in au of the annulus vs. n at different values of the static magnetic field in au for . The radia of the annulus are: and .
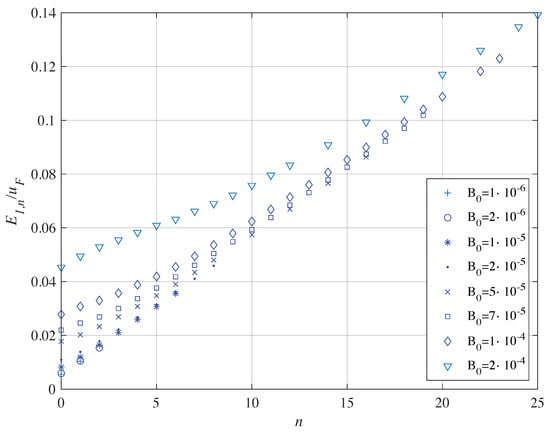
Figure 10.
Eigenenergies in au of the annulus as a function of n for several values of in au for . The radia of the annulus are: and .
The problems of convergence in the numerical calculation allow the determination of few eigenenergies at the lowest values of . The eigenenergies have almost a linear dependence upon n.
As is to be expected, the energy of the levels decreases by increasing the area of the annulus; thus, a radial stretching force F acts on the annulus. The force depends on the electron state on the annulus and acts on both the border circles. By keeping constant for the state when and , we get N.
The size of the annulus is important in the control of the shape of the eigenfunctions. In Figure 11, the eigenstates for are shown for a few selected values of the outer radius of the annulus. It is evident that the shape of qualitatively changes and the possibility of confining the electron in the external region of the annulus appears.
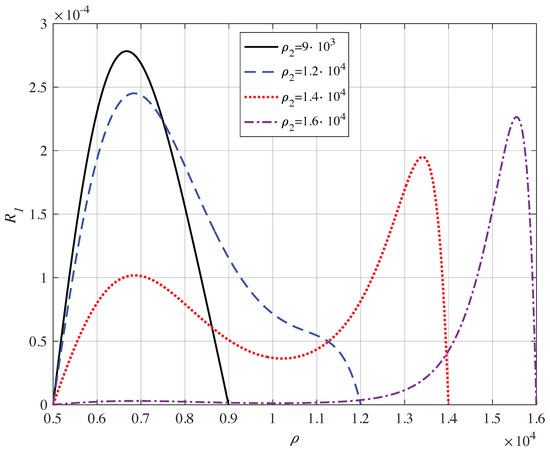
Figure 11.
(Color on line) Normalised eigenstates () as a function of the outer radius of the annulus; in the inset the in unit of the Bohr radius is given. The inner radius of the annulus is kept at: ; always au. The energy of the states are: au, au, au, au.
By giving an orbital angular momentum to the electron, a filiform current in the external border is created. Figure 12 shows this feature.
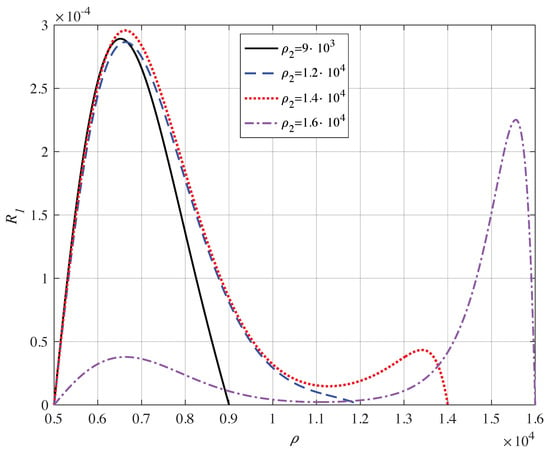
Figure 12.
(Color on line) Normalised eigenstates (, ) as a function of the outer radius of the annulus; in the inset the in unit of the Bohr radius is given. The inner radius of the annulus is kept at: ; always au. The energy of the states are: au, au, au, au.
4. Adding a Laser
It has been proven that electrons bound on a one-dimensional (1D) ring and acted upon by a strong laser field of frequency generate currents [22,30,43] and emit electromagnetic radiation with a broad spectrum of harmonics of [15,21,25,27,33,44]. Thus, it is proper to investigate the behaviour of a Dirac electron on an annulus shown by a laser field. Here, we consider a pulse propagating along , linearly polarized along and described by the vector potential
with describing the pulse profile. The electric and magnetic fields are:
with the chirp term given by
the effects of which are negligible in the case of adiabatic variation of the laser field. Moreover the dependence upon disappears, since the active particle is bound to move on the plane. The full vector potential is
and the full Hamiltonian
with the Hamiltonian of the magnetized annulus in Equation (22). If is a generic operator, then
The lengthy application of commutator algebra for the time derivatives of the operators produces Table 4.

Table 4.
Time derivative of few operators in the presence of a laser field.
The electric field now has a role in determining the change of the mechanical momentum , but the charge is not multiplied by the factor ; thus, the electric force is the dominant one. Moreover, the electric field causes periodic oscillations of the total angular momentum , which is not any more a constant of the motion.
Again, the Pauli’s matrices play the role of the velocity operator; thus, the acceleration is ruled by the spin flip . In classical physics, the spectrum that is emitted by an accelerated charge can be obtained from the Fourier transform of the acceleration . From the last equation in Table 4, we see that the parameter that is relevant to the spectrum is the quantum averaged dipole moment with the time dependent state of the Dirac electron. The application of a weak microwave field couples the annulus’ eigenstates and permits the fast excitation of the states with the possibility of rapid information exchange between storage and reading devices. From the theoretical point of view, the dipole matrix elements between the eigenstates and the relative selection rules are needed. The calculations are made difficult by the presence of the hypergeometric functions and . Currently, they are the object of a dedicated analysis and of a subsequent publication.
5. Conclusions and Comments
The special symmetry of a graphene layer permits the description of an electron as a massless charge, called Dirac electron, by means of the Dirac relativistic equation with the speed of the light that is replaced by the Fermi velocity, which, in graphene, is , even smaller than the average electron speed in the Hydrogen ground state (). This characteristic permits the theoretical and experimental study of massless charges interacting with fields.
In this paper, we study the response of a Dirac electron bound on a finite graphene annulus. The finiteness of the the annulus implies that, strictly speaking, the electron can no longer be considered to be massless and edge effects should be taken into consideration; to make these approximations less stringent, we consider a very large annulus with . We consider the annulus crossed by an orthogonal static magnetic field and solve the Dirac equation for the electron in closed form in terms of the two independent confluent hypergeometric functions. Detailed forms of the eigenstates and plots of their energy as a function of the parameter of the calculations are obtained. The energy of the levels is very small; for example, at au, au eV and au eV; thus, the levels can be coupled by microwaves, which, in terms of stability, are more easily handled than optical or near infrared photons. By tuning the angular momentum and the static magnetic field, the eigenstates and relative energy of the Dirac electron can be controlled and filiform currents circulating along the annulus can be created. Such currents are of interest in designing logical ports and memory mass storage that are relevant in electronic devices controlled by electromagnetic radiation.
The presence of a sinusoidal, linearly polarised, electromagnetic field propagating along the annulus axis induces spin flip, the rate of which is proportional to the electron acceleration and, via the Larmor formula, permits the determination of the spectrum that is emitted by the annulus driven by the external field.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maggiore, M. A Modern Introduction to Quantum Field Theory; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Sadowski, M.L.; Martinez, G.; Potemski, M.; Berger, C.; de Heer, W.A. Landau level spectroscopy of ultrathin graphite layers. Phys. Rev. Lett. 2006, 97, 266405. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Goerbig, M.O. Electronic properties of graphene in a strong magnetic field. Rev. Mod. Phys. 2011, 83, 1193. [Google Scholar] [CrossRef]
- Martino, A.D.; Dell’Anna, L.; Egger, R. Magnetic confinement of massless Dirac fermions in graphene. Phys. Rev. Lett. 2007, 98, 066802. [Google Scholar] [CrossRef] [PubMed]
- Eshghi, M.; Mehraban, H.; Azar, I.A. Eigenspectra and wave functions of the massless Dirac fermions under the nonuniform magnetic fields in graphene. Physica E 2017, 94, 106. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Portnoi, M.E. Quasi-exact solution to the Dirac equation for the hyperbolic-secant potential. Phys. Rev. A 2014, 89, 012101. [Google Scholar] [CrossRef]
- Liu, S.; Nurbawono, A.; Guo, N.; Zhang, C. Massless Dirac fermions in graphene under an external periodic magnetic field. J. Phys. Cond. Mat. 2013, 25, 395302. [Google Scholar] [CrossRef] [PubMed]
- Peres, N.M.R.; Rodrigues, J.N.B.; Stauber, T.; Dos Santos, J.L. Dirac electrons in graphene-based quantum wires and quantum dots. J. Phys. Cond. Mat. 2009, 21, 344202. [Google Scholar] [CrossRef] [PubMed]
- Masir, M.R.; Vasilopoulos, P.; Peeters, F.M. Magnetic Kronig–Penney model for Dirac electrons in single-layer graphene. New J. Phys. 2009, 11, 095009. [Google Scholar] [CrossRef]
- Cricchio, D.; Corso, P.P.; Fiordilino, E.; Orlando, G.; Persico, F. A paradigm of fullerene. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 085404. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E.; Persico, F. Electrons on a spherical surface: Physical properties and hollow spherical clusters. Phys. Rev. A 2012, 86, 013201. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Hutchison, C.; Witting, T.; Frank, F.; Weber, S.; Okell, W.A.; Fiordilino, E.; Cricchio, D.; Persico, F.; Zaïr, A.; et al. High-order harmonic generation in fullerenes using few-and multi-cycle pulses of different wavelengths. JOSA B 2013, 30, 7. [Google Scholar] [CrossRef]
- Castiglia, G.; Corso, P.P.; Cricchio, D.; Daniele, R.; Fiordilino, E.; Morales, F.; Persico, F. High-order-harmonic generation in dimensionally reduced systems. Phys. Rev. A 2013, 88, 033837. [Google Scholar] [CrossRef]
- Sakurai, J.J. Advanced Quantum Mechanics; Addison-Wesley Series in Advanced Physics; 1967; Available online: https://www.fisica.net/ebooks/quantica/Advanced%20Quantum%20Mechanics.pdf (accessed on 15 March 2021).
- Chen, H.-Y.; Apalkov, V.; Chakraborty, T. Fock-Darwin states of Dirac electrons in graphene-based artificial atoms. Phys. Rev. Lett. 2007, 98, 186803. [Google Scholar] [CrossRef] [PubMed]
- Downing, C.A.; Pearce, A.R.; Churchill, R.J.; Portnoi, M.E. Optimal traps in graphene. Phys. Rev. B 2015, 92, 165401. [Google Scholar] [CrossRef]
- Downing, C.A.; Portnoi, M.E. Massless Dirac fermions in two dimensions: Confinement in nonuniform magnetic fields. Phys. Rev. B 2016, 94, 165407. [Google Scholar] [CrossRef]
- Mailly, D.; Chapelier, C.; Benoit, A. Experimental observation of persistent currents in GaAs-AlGaAs single loop. Phys. Rev. Lett. 1993, 70, 2020. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.; Ceccherini, F. A numerical ab initio study of harmonic generation from a ring-shaped model molecule in laser fields. Laser Part. Beams 2001, 19, 85. [Google Scholar] [CrossRef]
- Barth, I.; Manz, J.; Shigeta, Y.; Yagi, K. Unidirectional electronic ring current driven by a few cycle circularly polarized laser pulse: Quantum model simulations for Mg-Porphyrin. J. Am. Chem. Soc. 2006, 128, 7043. [Google Scholar] [CrossRef]
- Moskalenko, A.S.; Matos-Abiague, A.; Berakdar, J. Nonequilibrium charge dynamics of light-driven rings threaded by a magnetic flux. Europhys. Lett. 2007, 78, 57001. [Google Scholar] [CrossRef]
- Zhu, Z.-G.; Berakdar, J. Photoinduced nonequilibrium spin and charge polarization in quantum rings. Phys. Rev. B 2008, 77, 235438. [Google Scholar] [CrossRef]
- Hinsche, N.F.; Moskalenko, A.S.; Berakdar, J. High-order harmonic generation by a driven mesoscopic ring with a localized impurity. Phys. Rev. A 2009, 79, 023822. [Google Scholar] [CrossRef]
- Fuhrer, A.; Lüscher, S.; Ihn, T.; Heinzel, T.; Ensslin, K.; Wegscheider, W.; Bichler, M. Energy spectra of quantum rings. Nature 2001, 413, 822. [Google Scholar] [CrossRef] [PubMed]
- Castiglia, G.; Corso, P.P.; Giovannini, U.D.; Fiordilino, E.; Frusteri, B. Laser driven structured quantum rings. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 115401. [Google Scholar] [CrossRef]
- Castiglia, G.; Corso, P.P.; Cricchio, D.; Giovannini, U.D.; Frusteri, B.; Fiordilino, E. Classical chaos and harmonic generation in laser driven nanorings. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 245601. [Google Scholar] [CrossRef]
- Khanzadi, H.; Salehani, H.K. Design of basic logic gates by triple quantum rings. J. Nanosci. Tech. 2016, 2, 119. [Google Scholar]
- Batra, K.; Joshi, H.; Prasad, V. Quantum ring states in magnetic field and delayed half-cycle pulses. Pramana 2016, 87, 29. [Google Scholar] [CrossRef]
- L-Badry, L.F.A. The electronic properties of concentric double quantum ring and possibility designing xor gate. Sol. St. Comm. 2017, 254, 15. [Google Scholar] [CrossRef]
- Fiordilino, E.; Frusteri, B. Defects in quantum ring to control high-harmonic spectrum. Laser Part. Beams 2017, 35, 126. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Tunable high harmonic pulses from nanorings swirled by optical vortices. Opt. Express 2017, 25, 27857–27873. [Google Scholar] [CrossRef] [PubMed]
- Cricchio, D.; Fiordilino, E. Laser driven quantum rings: One byte logic gate implementation. RSC Adv. 2018, 8, 3493. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E. Quantum ring in a magnetic field: High harmonic generation and not logic gate. Adv. Theory Simul. 2020, 2020, 2000070. [Google Scholar] [CrossRef]
- Riley, K.F.; Hobson, M.P.; Bence, S.J. Mathematical Methods for Physics and Engineering, 3rd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Matos-Abiague, A.; Berakdar, J. Emission spectrum of a mesoscopic ring driven by fast unipolar pulses. Phys. Lett. A 2004, 330, 113. [Google Scholar] [CrossRef]
- Moskalenko, A.S.; Matos-Abiague, A.; Berakdar, J. Revivals, collapses, and magnetic-pulse generation in quantum rings. Phys. Rev. B 2006, 74, 161303. [Google Scholar] [CrossRef]
- Maiti, S.K. NAND gate response in a mesoscopic ring: An exact result. Phys. Scr. 2009, 80, 055704. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, L.; Ji, R.; Yang, L.; Zhou, P.; Chen, H.; Ding, J.; Zhu, W.; Lu, Y.; Jia, L.; et al. Proof of concept of directed or/nor and and/nand logic circuit consisting of two parallel microring resonators. Opt. Lett. 2011, 36, 1650. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, L.; Yang, L. Electro-optic directed AND/NAND logic circuit based on two parallel microring resonators. Opt. Express 2012, 20, 16794. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E. Wavelet analysis and HHG in nanorings: Their applications in logic gates and memory mass devices. Nanoscale 2016, 8, 1968. [Google Scholar] [CrossRef] [PubMed]
- Barth, I.; Manz, J. Electric ring currents in atomic orbitals and magnetic fields induced by short intense circularly polarized π laser pulses. Phys. Rev. A 2007, 75, 012510. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E. Harmonic generation from nanorings driven by a two-color laser field. Laser Phys. Lett. 2014, 11, 066002. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).