The Magnetic Hooke-Newton Transmutation in Momentum Space
Abstract
1. Introduction
2. The Quadratic Conformal Image of the Equation for a Charge in the Uniform Magnetic Field in Momentum Space
3. The Magnetic Hooke-Newton Transmutation Due to the Action of an Effective Potential
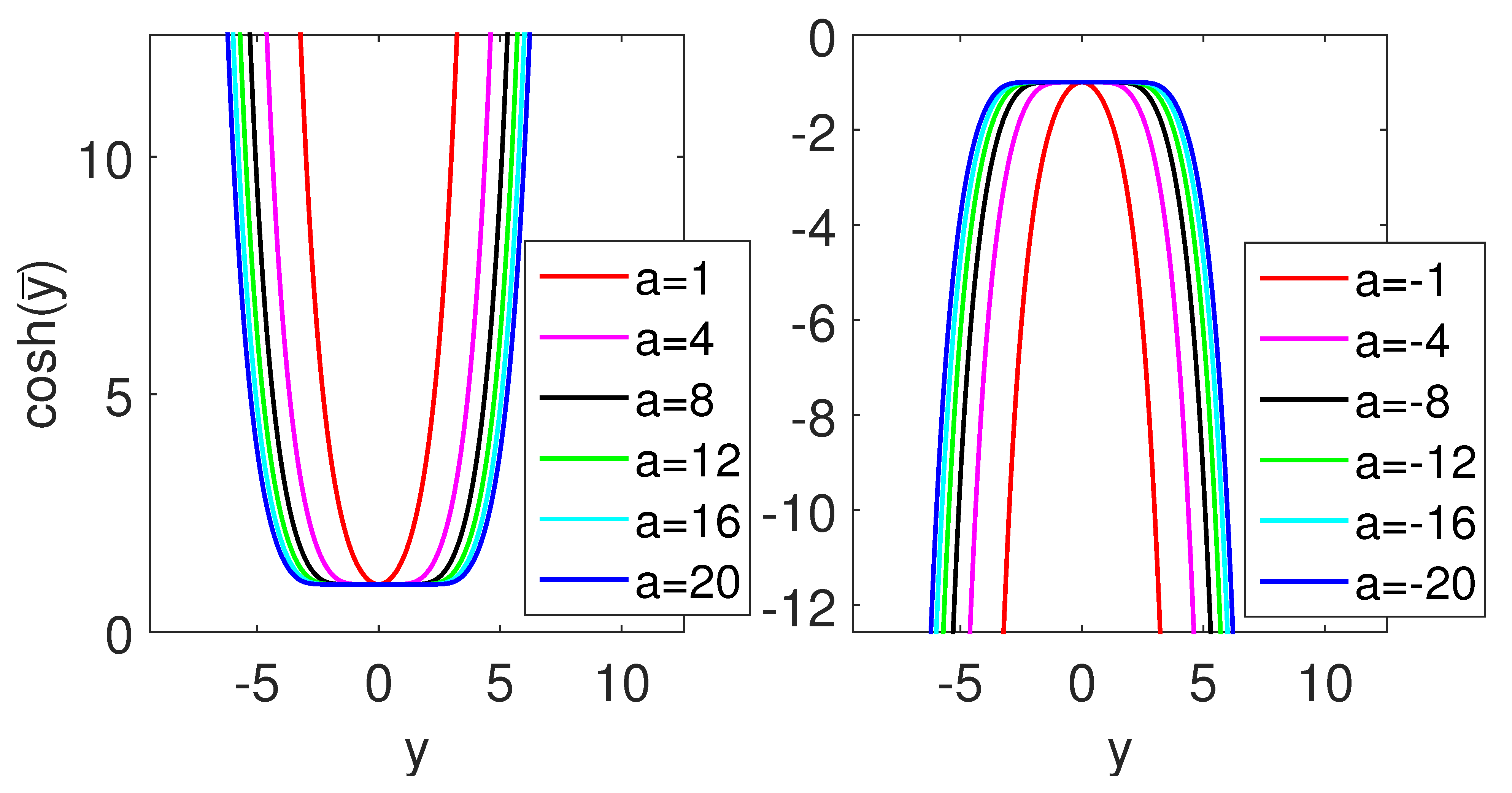
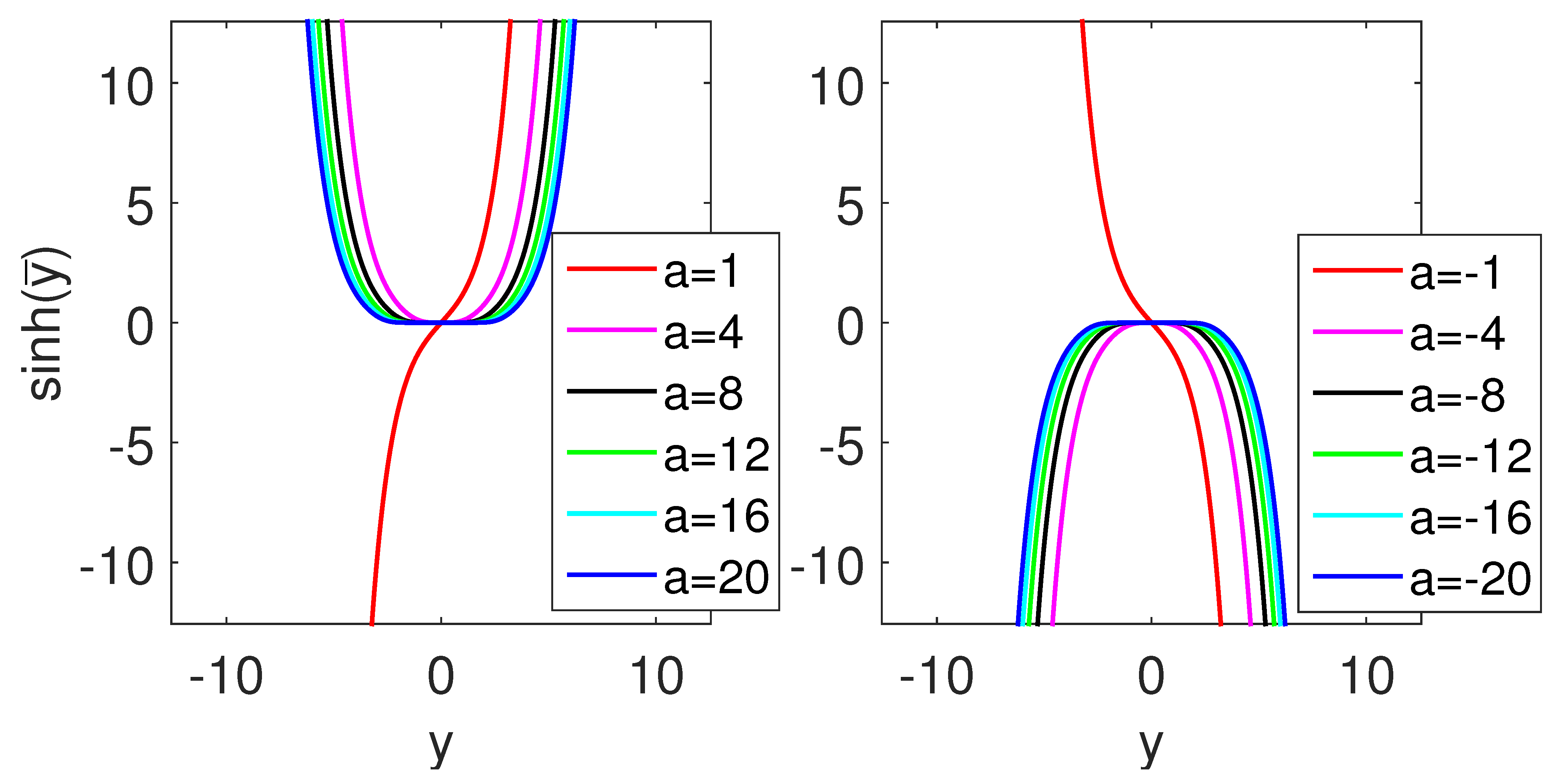
3.1. Bound State
3.2. Scattering State
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Conformal Structure of the Form-Invariant Line Element and the Effective Potential
References
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C.T. Acoustic cloaking and transformation acoustics. J. Phys. D Appl. Phys. 2010, 43, 113001. [Google Scholar] [CrossRef]
- Ni, X.; Wong, Z.-J.; Mrejen, M.; Wang, Y.; Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 2015, 349, 1310–1313. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Genov, D.A.; Sun, C.; Zhang, X. Cloaking of matter waves. Phys. Rev. Lett. 2008, 100, 123002–123004. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.-H. A mass-independent conformal quantum cloak. New J. Phys. 2017, 19, 113003. [Google Scholar] [CrossRef]
- Lin, D.-H. Transformation design method for quantum states. Phys. Rev. A 2012, 85, 053605. [Google Scholar] [CrossRef]
- Lin, D.-H. Form-invariant solution to quantum state on the sphere. J. Phys. Commun. 2020, 4, 085012. [Google Scholar] [CrossRef]
- Weigold, E.; McCarthy, I.E. Electron Momentum Spectroscopy; Kluwer Academic: New York, NY, USA, 1999. [Google Scholar]
- Lin, D.-H. Controlling matter waves in momentum space. Phys. Rev. A 2014, 90, 012709. [Google Scholar] [CrossRef]
- Lin, D.-H. Quantum states emerging from charged transformation-wave in a uniform magnetic field. Eur. Phys. J. D 2016, 70, 141. [Google Scholar] [CrossRef]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer: New York, NY, USA, 1966. [Google Scholar]
- Newton, I. Philosophiae Naturalis Principia Mathematica; Cambridge University Press: Cambridge, UK, 1687. [Google Scholar]
- Arnol’d, V.I. Huygens & Barrow, Newton & Hooke; Birkhäuser Verlag: Basel, Switzerland, 1990. [Google Scholar]
- Needham, T. Newton and the transmutation of force. Am. Math. Mon. 1993, 100, 119–137. [Google Scholar] [CrossRef]
- Leonhardt, U.; Philbin, T. Geometry and Light: The Science of Invisibility; Dover: New York, NY, USA, 2010. [Google Scholar]
- Lin, D.-H. The Hooke-newton transmutation system of magnetic force. J. Phys. Commun. 2018, 2, 065017. [Google Scholar] [CrossRef]
- Lin, D.-H. On the magnetic Hooke-newton transmutation of electrons. J. Phys. Commun. 2019, 3, 085014. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw Hill: New York, NY, USA, 1953. [Google Scholar]
- Lin, D.-H. On solutions of Coulomb system and its generalization to the Aharonov–Bohm effect. Ann. Phys. 2008, 323, 371–387. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken symmetries. Phys. Rev. 1962, 127, 965. [Google Scholar] [CrossRef]
- Gu, S.-J.; Yu, W.-C.; Lin, H.-Q. Construct order parameters from the reduced density matrix spectra. Ann. Phys. 2013, 336, 118–129. [Google Scholar] [CrossRef]
- Arraut, I. The Nambu-Goldstone theorem in nonrelativistic systems. Int. J. Mod. Phys. A 2017, 32, 1750127. [Google Scholar] [CrossRef]
- Dane, C.; Verdiyev, Y.A. Integrable systems of group SO(1,2) and Green’s functions. J. Math. Phys. 1996, 37, 39–60. [Google Scholar] [CrossRef]
- Flügge, S. Practical Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1971; Volume 2. [Google Scholar]
- Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Grosche, C. Path Integrals, Hyperbolic Spaces and Selberg Trace Formulae; World Scientific: Singapore, 2013. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.-H. The Magnetic Hooke-Newton Transmutation in Momentum Space. Symmetry 2021, 13, 608. https://doi.org/10.3390/sym13040608
Lin D-H. The Magnetic Hooke-Newton Transmutation in Momentum Space. Symmetry. 2021; 13(4):608. https://doi.org/10.3390/sym13040608
Chicago/Turabian StyleLin, De-Hone. 2021. "The Magnetic Hooke-Newton Transmutation in Momentum Space" Symmetry 13, no. 4: 608. https://doi.org/10.3390/sym13040608
APA StyleLin, D.-H. (2021). The Magnetic Hooke-Newton Transmutation in Momentum Space. Symmetry, 13(4), 608. https://doi.org/10.3390/sym13040608




