Let us recall the following two lemmas.
In general, the converse of the previous lemma does not hold. For example, the edge labeling of star with edge labels 1, 2, 3 is an irregular assignment with vertex weights 1, 2, 3, 6. However, this irregular labeling is not modular. If we label the edges of the star by labels 1, 2, 4, then we get a modular irregular assignment with modular vertex weights 0, 1, 2, 3, and .
The next statement gives a condition when an irregular assignment of a graph is also its modular irregular labeling.
The following theorem gives a lower bound of the modular irregularity strength.
Now, we give the precise value of the modular irregularity strength for fan graphs , for even.
Proof. Let . We have already mentioned that the fan graph admits an irregular assignment with edge labels and with vertex weights . From Lemma 6, it follows that the irregular assignment of is modular and
Let
. Suppose that there exists a modular irregular 3-labeling
of
. As the vertices
,
are either of degree 2 or 3, the weights of these vertices under any 3-labeling is at least 2 (this can be realizable only on a vertex of degree 2 as the sum of edge labels 1 + 1) and is at most 9 (this can be realizable only on a vertex of degree 3 as the sum of edge labels 3 + 3 + 3). As all the vertices must have distinct modular weights, we get that the weights of the vertices
,
, constitute the sequence of consecutive integers from 2 up to 9. Thus, the modular weight 1 can be obtained only by the centre
w. Moreover, it is easy to see that the weight of the centre cannot be 10 (must be at least 11 but at most 21). Thus,
. Then,
Since
and
, then Equation (
5) gives
which is a contradiction. Thus, there is no modular irregular 3-labeling for
.
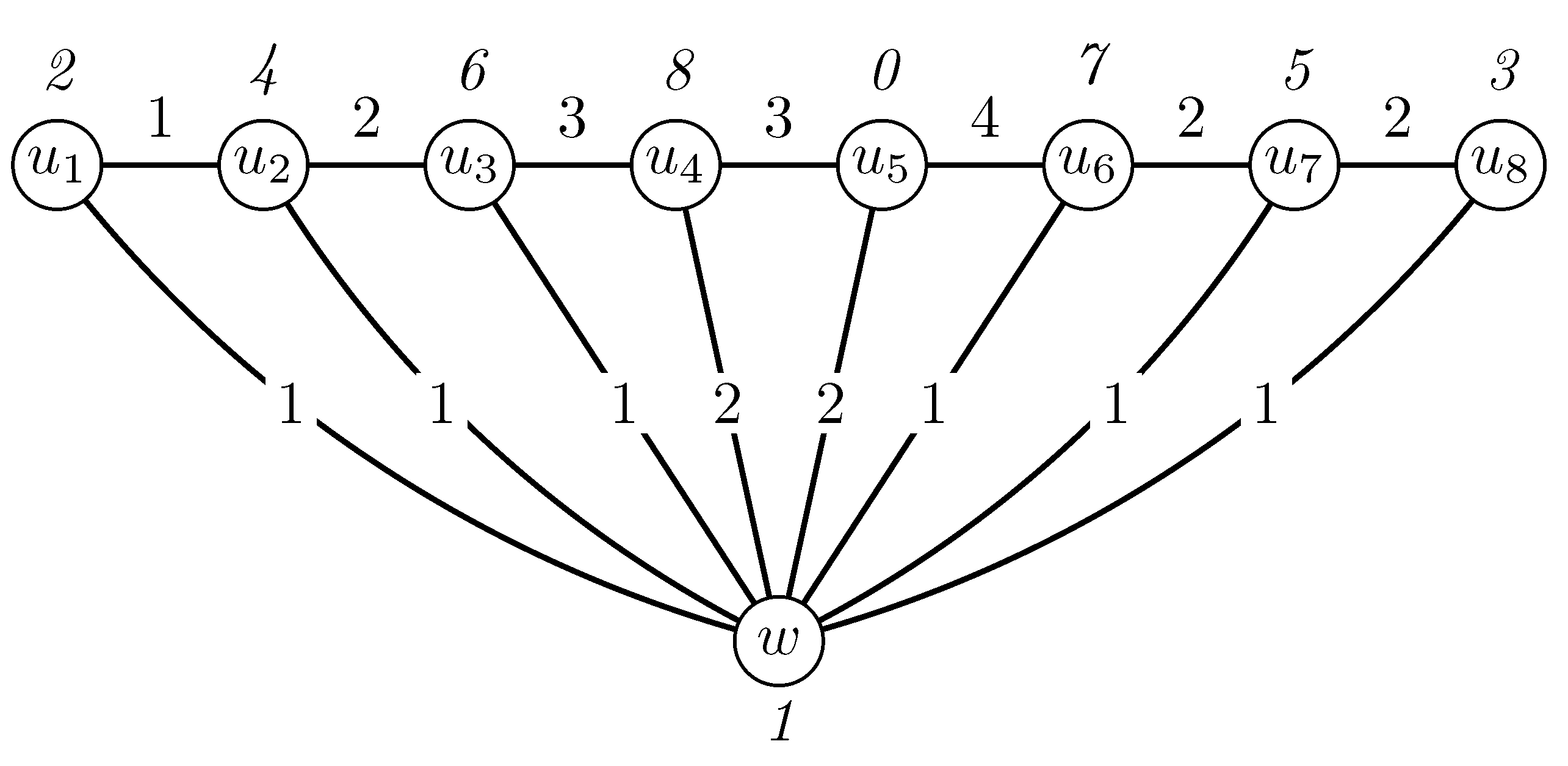
Figure 1 shows an example of a modular irregular 4-labeling of the fan graph
, where the modular weights are depicted in italic font.
Now, for let us distinguish the following three cases, according to n.
Case 1..
It is sufficient to consider the edge irregular
-labeling
defined by (
4). By Lemma 3, under the labeling
, the weights of all vertices
,
, successively assume values
, and by Lemma 4, the weight of the centre vertex is
. Since
, then
is an integer and
. This implies that the labeling
is a suitable modular irregular
-labeling.
Case 2..
Observe that under the labeling , by Lemma 4, the centre of admits the weight . Since , it follows that and the labeling is not modular irregular. Therefore, we need to modify the labeling .
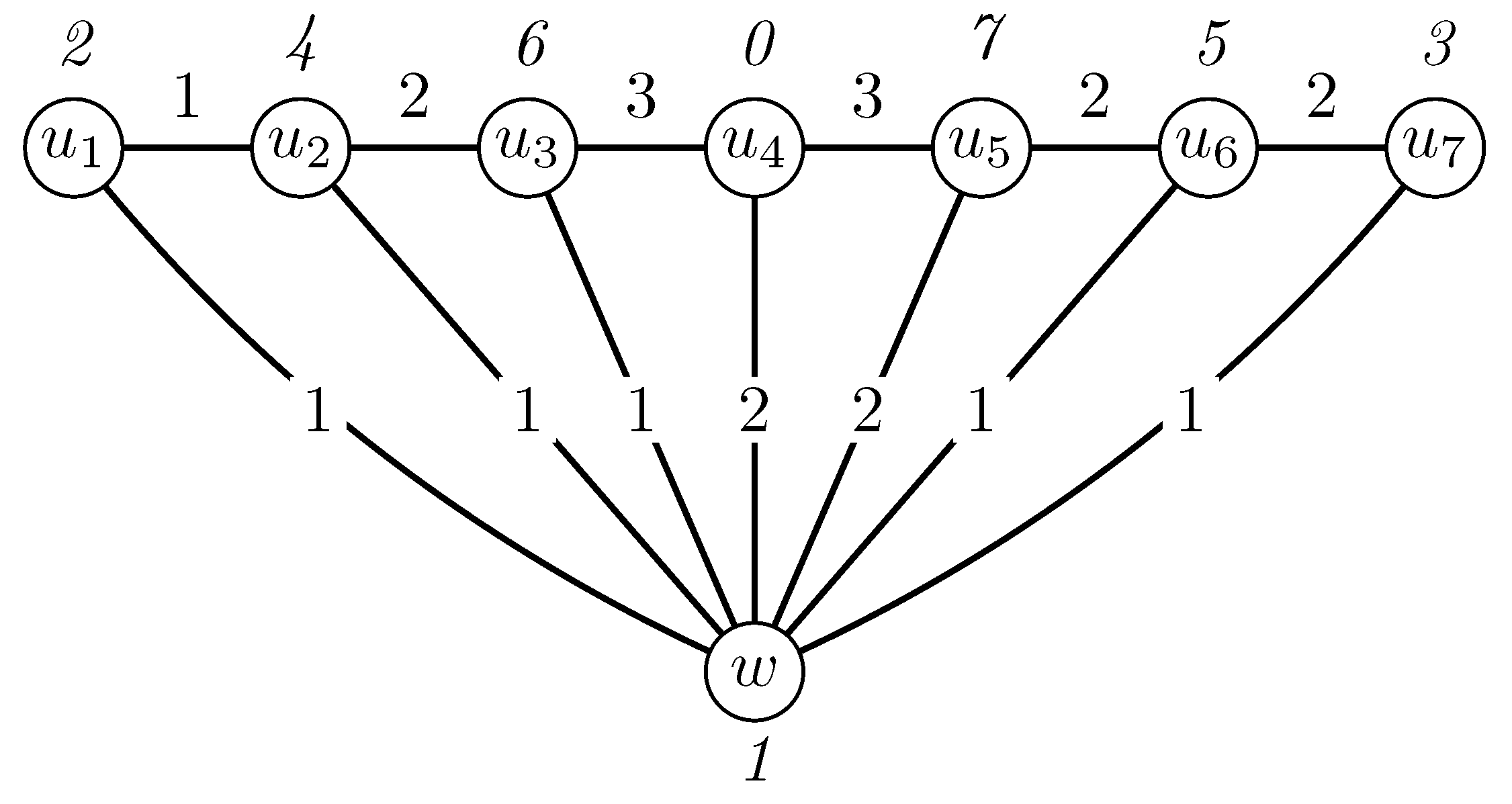
Figure 2 illustrates a modular irregular 3-labeling of the fan graph
, where the modular weights are depicted in italic font.
For
, we define an edge labeling
of
as follows:
One can see that decreasing the labels of the edges and , by one, and increasing the labels of the edges , and , by one has no effect on the weights of vertices , as they successively attain the values . We note that and
However, by increasing the labels of the edges
,
and
,
, the weight of the centre increases, and we have
Since is an integer, then . Thus, the labeling is a required modular irregular -labeling of .
Case 3., .
According to Lemma 4 we have that and it is not congruent to 1 . Our next goal is to modify the edge labeling such that the weights of vertices , , will not change but the weight of the centre decreases to a value congruent to one .
Therefore, for
, we construct an edge labeling
of
in the following way:
By direct computation we can see that increasing the labels of the edges , , and , by one and decreasing the labels of the edges , and , by one has no impact to weights of the vertices , and they preserve the values . Since and , it follows (applying Lemma 2) that all edge labels under the labeling are at most .
Decreasing the labels of the edges
,
and
,
, the weight of the centre decreases and we get
Because is an integer, . It proves that the labeling is a suitable modular irregular -labeling. □
An immediate consequence of the above theorem is the following statement.
Proof. It is a matter of routine checking to see that under the edge labeling
defined by (
4), for
n odd, the weights of the centre of
listed in Lemma 4 are not congruent to 1
. In order to preserve the property of the edge labeling
that the weights of all vertices
,
, form the set
, and to attain the weights of the centre congruent to one
, we will construct some appropriate modifications of the labeling
in a similar way as in the proof of Theorem 3.
Since we consider only n odd and moreover, , then we distinguish the following three cases according to the residue of n modulo 12.
Case 1..
From Theorem 1, it follows that and , , and . According to Lemma 6, we have that .
For
, we define an edge labeling
of
such that:
By a direct verification, we can detect that under the labeling
, all edge labels are at most
, the weights of the vertices
,
constitute a sequence of consecutive integers from 2 up to
, and the weight of the centre determined by Lemma 4 is increased by
. Consequently,
As is an integer, then .
Case 2..
Figure 3 depicts a modular irregular 3-labeling of the fan graph
. The modular weights are again illustrated using italic font.
For
, we define an edge labeling
of
in the following way:
We can see that the labeling
, as a modification of the labeling
, did not increase the largest values of the edges and has no effect on the weights of vertices
in
. The weight of the centre is reduced by
, and we get
Indeed, is an integer, and then .
Case 3..
For
, we define an edge labeling
of
as follows:
Again, it is readily seen that this modification of the labeling
has no impact on the weights of vertices
and to the largest values of the edges. Under the labeling
, the weight of the centre determined by Lemma 4 is decreased by
, and we have
Obviously, is an integer and . Thus, we arrive at the desired result. □