Abstract
Data hiding is a technique that embeds a secret message into a cover medium and transfers the hidden information in the secret message to the recipient. In the past, several data hiding methods based on magic matrix have used various geometrical shapes to transmit secret data. The embedding capacity achieved in these methods was often limited due to simple geometrical layouts. This paper proposes a data hiding scheme based on a double-layer octagon-shaped shell matrix. Compared to previous octagon-shaped data hiding methods, the proposed method embeds a total of 7 bits in each pixel pair, reaching an embedding capacity of 3.5 bits per pixel (bpp). Experimental results show that the proposed scheme has a higher embedding capacity compared to other irreversible data hiding schemes. Using the proposed method, it is possible to maintain the Peak Signal to Noise Ratio (PSNR) within an acceptable range with the embedding time less than 2 s.
1. Introduction
Data hiding technique, also called as steganography, embeds a secret message into a cover medium and transfers the information hidden in the secret message to the recipient. The term “steganos” in Greek means “hidden”, and “graphos,” “to write.” The earliest allusion to secret writing in the West with concrete evidence of intent appears in Homer’s Iliad [1,2,3,4]. From ancient times to the present, steganography includes invisible ink, micro-dots, character arrangement, digital signatures, covert channels, and spread spectrum communication, etc., and ensures that the information is less likely to be noticed and harder to retrieve when the message is transmitted. It makes the information transfer more secure and integrated. The main characteristics of data hiding techniques include security, imperceptibility, embedding capacity, and integrity. As it is very important to know how much secret data can be hidden in a cover image, embedding capacity is an important factor in evaluating the quality of a data hiding technique. The larger the hiding capacity, the more satisfied is the transmitting side to transmit a large chunk of secret data. Also, when the embedding capacity is large, the possibility of the transmission being intercepted by a malicious attacker becomes less and the security becomes high.
In the past, several data hiding methods have been proposed. For example, the method of least significant bits (LSB) substitution [5] proposed by Chang and Cheng in 2004. The limitation of this method was that it was easy to detect the hidden information, resulting in poor security. In 2006, Zhang and Wang proposed exploiting modification direction (EMD) [6] method. In 2010, Lee and Chen designed a modulus function [7] to embed secret data using a mapping process between the variant Cartesian product and each pixel group. The experimental results showed that Lee and Chen’s scheme achieved a high embedding capacity and a low distortion. In 2017, Lee et al. proposed an REMD [8] method using image interpolation and edge detection that achieved an embedding capacity of 3.01 bpp with an average image quality of 33 dB.
In the field of irreversible information hiding, the EMD method is an epoch-making method. It uses modular functions to reduce the computational cost of the information hidden in the carrier; therefore, this series of EMD methods also brings more novelty. Chang et al., in 2008, proposed a method using a reference matrix based on Sudoku, which made use of a pixel pair as coordinates of a Sudoku matrix to specify the value to embed a 9-ary secret digit into each pixel pair [9]. Chang et al., in 2014, proposed a turtle shell-based scheme (also called TS scheme) [10] for data hiding, in which a reference matrix was constructed based on a hexagon-shaped shell to embed three secret bits into each pixel pair of the cover image. Kurup et al. (2015) proposed a data hiding method based on octagon-shaped shells [11]. In 2017, Leng and Tseng introduced the reference matrix based on regular octagon-shape shells [12]. The further improvement in [13] achieved a higher payload of 3.5 bpp. In 2018, Lee and Wang proposed a magic signet hiding method [14], which randomly generated non-repetitive values of 0–15 in the signet to fill the reference matrix. Recently, in 2019, Zhang et al. proposed an efficient and adaptive data-hiding scheme based on a secure reference matrix [15]. The method was secure because of its large number of possible solutions (about 1078 solutions) for resisting attacks. In 2019, Chang and Liu proposed two enhanced real time turtle shell-based data hiding schemes [16]. Both the schemes mapped each cover pixel pair onto the original or altered the turtle shell matrix to find out its associate set for embedding secret data. Then, the cover pixel pair was modified with minimum distortion according to the associate set. In 2020, Nguyen et al. proposed a new data hiding approach to embed secret data based on an x-cross-shaped reference-affected matrix [17]. The reference matrix consisted of three parts: petal matrix, calyx matrix, and stamen matrix, which were combined for executing the embedding procedure. Using this method, it was found that the smooth regions were more suitable for embedding secret data due to the smaller difference between pixel values. Unlike the traditional EMD method, the above-mentioned methods used a reference matrix instead of the extraction function in the embedding and extraction procedures.
All the magic matrices-based schemes mentioned above embedded a single layer of secret data in the reference matrix. First, a pair of cover pixels were mapped on the x- and y-axes coordinates of the reference matrix, and then the coordinate positions were replaced with the secret data. However, this limited the embedding capacity. In order to overcome the limitation, this paper proposes a new scheme based on double-layer octagon-shaped shell matrix in which each cover pixel pair is able to carry 7-bit sub-streams of secret data.
This paper contributes to the related data hiding algorithms as follows.
- (1)
- The regular octagon-shaped shell method proposed in [12] carried only 5-bit of secret data for each pair of cover pixels. However, in our proposed scheme, additional 2-bits data was embedded in each cover pixel pair, leading to a higher embedding capacity of 3.5 bpp.
- (2)
- Peak signal to noise ratio (PSNR) and structural index similarity (SSIM) are two measuring tools that are widely used in image quality assessment. Especially in the steganography image, these two measuring instruments are used to measure the quality of imperceptibility. Based on the experimental analysis, results show that the average value of the stego-image quality had an acceptable value of 37dB on an average while SSIM values were between [0.9, 0.95]. We contend that our proposed method is more suitable for complex images to obtain a higher SSIM value. Also, as seen previously, the PSNR values remained stable for all the test images irrespective of their image texture.
- (3)
- Lastly, the computational cost in terms of embedding time is 1.82 s on an average.
2. Related Works
In 2006, Zhang and Wang proposed an epoch-making information hiding method, called the exploiting modification direction (EMD) method [6] in which a reference matrix M in the size of 256 × 256 was constructed based on a cross-shaped shell to embed secret data into each pixel pair of the cover image. In 2014, Chang et al. developed a data hiding scheme based on turtle-shaped shells [10] and then Leng [12] designed regular octagon-shaped shells for hiding secret data.
2.1. The EMD Embedding Method and the EMD Extensions
The exploiting modification direction (EMD) method [6] divided the to-be-hidden binary data into N pieces with L bits, and each secret piece is presented as a decimal value by D digital numbers in a (2n + 1)-ary notational system, where
where n is a parameter to determine how many pixels of cover image are used to hide one secret digit.
In the embedding phase, EMD method firstly uses pseudo-random generator to permute all pixels of cover image according to a secret key. After that, EMD method partitions the permuted pixels into a series of groups. The group is denoted as a vector Pn = (p1, p2, …, pn), which consists of n cover pixels. A weight vector Wn = (w1, w2, …, wn) = (1, 2, …, n) is defined. Therefore, the EMD method defines an embedding function f as weighted sum function modulo (2n + 1) for each group, a secret digit d can be carried by the n cover pixels, and at most one pixel is increased or decreased by one. f can be expressed as Equation (2):
After embedding a secret digit d, the group Pn is modified into Qn = (q1, q2, …, qn), which is defined according to following conditions:
- Qn = Pn = (p1, p2, …, pn), if d = f.
- When d ≠ f, computes s = d-f mod (2n + 1) and
Otherwise, , and . From the above properties, the EMD method at most modifies only one-pixel value in a group. That is why the EMD embedding scheme’s distortion induced in the stego-image is not great.
In the extracting phase, the secret digit can be extracted from stego-group Qn = (q1, q2, …, qn) by the following extraction function shown in Equation (3).
The EMD method provides a good quality of stego-image with an average PSNR value of more than 51 dB, and the theoretical maximal embedded rate of EMD method is 1.16 bpp for the best-case n = 2. For , the PSNR values of all test images averaged to 52.11 dB with embedding capacity of 1 bit per pixel (bpp).
To further improve the EMD scheme, several schemes based on magic matrix based (MMB) schemes have been proposed in the past few years. In 2010, Lee and Chen designed a modulus function [7] to embed secret data using a mapping process between the variant Cartesian product and each pixel group. The experimental results showed that Lee and Chen’s scheme achieved a high embedding capacity and a low distortion. The average PSNR was 51.157 dB when the embedding rate was 1 bit per grayscale pixel and the average PSNR was 31.847 dB when the embedding rate was 4 bpp with good security and absence of overflow/underflow. In 2017, Lee et al. proposed an REMD [8] method using image interpolation and edge detection that achieved an embedding capacity of 3.01 bpp with an average image quality of 33 dB.
2.2. Data Hiding Scheme Based on Turtle-Shaped Shells
In 2014, Chang et al. developed a data hiding scheme based on turtle-shaped shells, also called as TS scheme [10]. In their method, the secret data was represented in a binary format, 3 bits of which were embedded within every 2 pixels. Figure 1 presents a magic matrix M of size based on turtle-shaped shells. In the matrix M, two adjacent elements in the same row have a difference of 1, and two neighboring elements present in the same column have an alternating difference of 2 and 3.
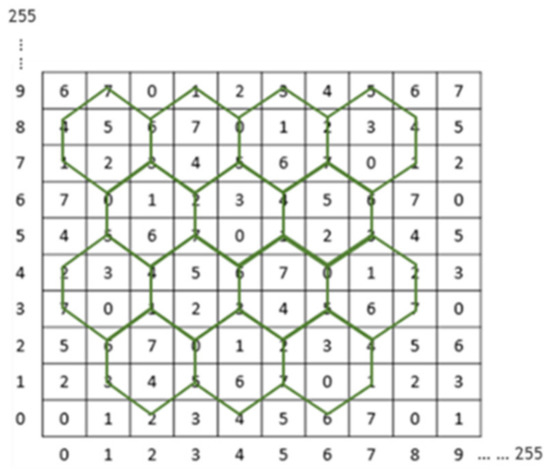
Figure 1.
Example of turtle-shaped shell.
Let m(,) and m(,) be two numbers in the magic matrix M, where (,) and (,) represent the pairs of cover pixels and stego pixels, respectively. This is before/after a 3-bit secret data has been concealed.
If the number m(,) falls in a turtle-shaped shell, then the secret number also can be found in the same turtle-shaped shell, such that . However, if is a number on the edge, then the number can be found in the surrounding three turtle shells. A calculation needs to be done to find the minimum distance between (,) and (,) under the condition that . Another special case occurs when the number is not located in any turtle-shaped shell. The solution, as shown in Figure 2, is to find the shortest distance between (,) and (,) so that the number equals the secret data .
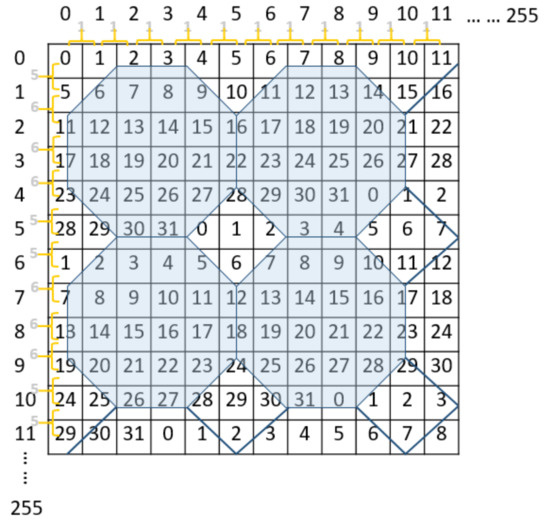
Figure 2.
An example of a reference matrix consisting of octagon-shaped shells.
The turtle shell-based method can obtain an average PSNR of 49.4 dB and an average embedding capacity of 1.5 bpp. The limitation of the turtle shell scheme [10] was that the embedding rate was limited.
2.3. The Regular Octagon-Shaped Shell Embedding Method
Kurup et al. (2015) proposed a data hiding method based on octagon-shaped shells [11], which also used a reference matrix. On average, the PSNR value obtained was 51.7 dB with an average embedding capacity of 2 bpp. In 2017, Leng and Tseng introduced the reference matrix based on regular octagon-shape shells [12] which achieved a payload of 2.5 bpp. The further improvement in [13] achieved the possible payload of 3.5 bpp.
As shown in Figure 2, Leng [12] constructed a reference matrix M in the size of 256 × 256 based on regular octagon-shaped shells for hiding secret data. The construction rules were as follows: In the same row of the reference matrix M, the value difference between two adjacent elements was set to “1”, and the value difference between two adjacent elements in the same column was set to “5”, followed by “6”, “6”, “6”, and “5” in repeated cycles. The reference matrix M composed of a number of contiguous regular octagon-shaped shells. Each regular octagon-shaped shell had a total of 32 numbers, ranging from 0–31. Once the transmission side constructed a reference matrix, the secret message was embedded into the cover image to obtain stego-image. A pair of pixels represented the values of x- and y-axes of the reference matrix coordinates, where each pixel pair corresponded to a 32-ary notational system value.
The data embedding process is presented as follows. In the reference matrix , assume that a secret binary stream S is embedded into a cover image I of size . The embedding procedure is described as follows:
Step 1: Convert the secret binary stream S into a sequence of 5 bits sub-streams , where n represents the number of 5-bit 32-ary digits.
Step 2: Divide the cover image I into non-overlapping pixel pairs (), . () are considered as the coordinates of the reference matrix M to specify the value of m().
Step 3: Embed a 5-bit secret digit into each pixel pair () to obtain a corresponding pixel pair (). Thereafter, the algorithm can be categorized into two cases.
Case 1: If m, it means that the current pixel pair () completely corresponds to the 5-bit secret digit, viz., m() = ; therefore () = (), directly skip to Step 4.
Case 2: If m() ≠ , it means that the current pixel pair cannot correspond to the 5-bit secret digit, viz., m() ≠ . Find the closest which is equal to , and then replace with in the cover image to hide the 5-bit secret digit such that () = . Find the closest based on the following rules:
Rule 1: If is an internal number, e.g., , find = within the octagon.
Rule 2: If is an edge number, e.g., , find = and closest to in the two involved octagons.
Rule 3: If is not included in any octagon, e.g., , find = within no limited range.
Step 4: Repeat Step 3 to embed the next 5-bit sub-stream into subsequent pixel pairs until the entire secret data S is hidden.
Finally, obtain the stego-image I’.
In the process of data extraction, the receiving side constructed a reference matrix by using the information composed in the matrix. According to the stego-image I’ and the reference matrix, the hidden pixel pairs were mapped to the coordinate positions of the reference matrix. In this way, the value of the coordinates of the reference matrix were extracted, which were the actual values of the secret data. Moreover, the data hiding based on octagon-shaped shell scheme greatly increases the embedding capacity under the acceptable image quality.
3. Proposed Scheme
This paper proposes a new scheme based on double-layer octagon-shaped shell matrix in which each cover pixel pair is able to carry 7-bit sub-streams of secret data, achieving an embedding capacity of 3.5 bpp. The following subsections present the construction of the double-layer octagon-shaped shell magic matrix, the embedding procedure, and the extraction procedure.
3.1. Construction of the Double-Layer Octagon-Shaped Shell Reference Matrix
In this section, we will construct a double-layer octagon-shaped shell reference matrix consisting of octagon-shaped shells for hiding secret data with high embedding capacity. The procedure can be divided into two parts. In the first part, we assign a 4-ary digit, referred to as type, to each octagon-shaped shell located at the top layer. In the second part, we assign a type attribute to each element at the bottom layer of the reference matrix.
Figure 2 shows the layout of octagon-shaped shells in the reference matrix. There are octagons as shown in Figure 3. For ease of explanation, the type matrix of the octagon-shaped shell is denoted as . The type matrix is constructed using the following rules: Firstly, the values of type in the same row change according to the gradient (ascent/descent) with a magnitude of “1”. Secondly, the values of the elements in the same column change according to the gradient (ascent/descent) with a magnitude of “2”. To demonstrate an example, we take four octagons near the origin (0, 0). First, we indicate their type values as {0, 1, 2, 3}, marked by red color in Figure 3. For example, ,, , . In this manner, we assign the four octagon-based type values {0, 1, 2, 3} to the whole octagons respectively.
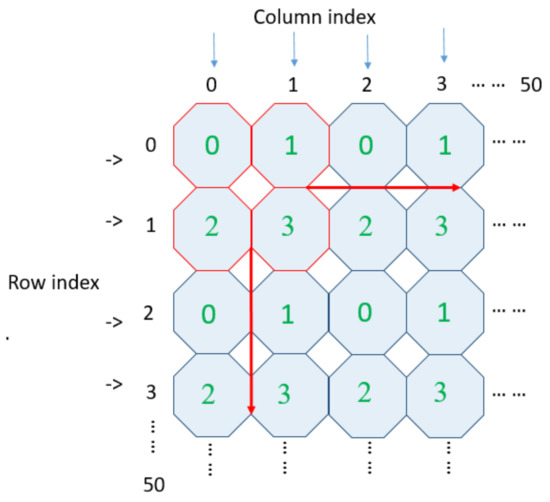
Figure 3.
An example of octagon types in reference matrix at the top layer.
For each element at the bottom layer of the reference matrix M, we assign an additional attribute, type, denoted as corresponding to each element Each type can be categorized into one of the following three cases, as shown in Figure 4a:

Figure 4.
Double-layer octagon-shaped shell reference matrix. (a) The top-layer octagon type; (b) Type attributes corresponds to matrix elements.
Case 1: Elements are only included in a regular octagon. For example, at the bottom layer is an internal number falling on a regular octagon with type assigned as . So, the type value of can be represented by as shown in Figure 4b.
Case 2: Elements are involved in two octagons. For example, at the bottom layer is also located on the edge adjacent to two octagons whose type codes are and at the top layer. The value of involves two octagons whose type value can be calculated from the values of two octagons and , using Equation (4), which is shown as follows. Accordingly, we obtain which is shown in Figure 4b.
Case 3: Elements are not involved in any octagon. The value of is assigned the type values based on the following rules:
Rule 1: For the element which is located at the origin, its type value is set as 0, viz., as shown in Figure 4b.
Rule 2: If the elements are located in the first column or the last column of the matrix, viz., or , their type values are equivalent to the values shifted to the right or left by one, viz., or for .
Rule 3: If the elements are located in the first row or last row of the matrix, viz., or , their type values are equivalent to the values when shifting down or moving up by one, viz., or .
Rule 4: If the elements are located in the middle of four octagons, e.g., in Figure 4a, their values can be calculated according to Equation (5), e.g., and , which are shown in Figure 4b.
Accordingly, each can be assigned a corresponding type value and a double-layer reference matrix is generated for hiding secret data.
In the process of embedding a secret message, a double-layer octagon-shaped shell reference matrix can be created, which can embed 7-bits of secret data into every non-overlapping pixel pair. The construction of the double-layer matrix is similar to the method of the one-layer regular octagon-shaped shells [12]. The difference here is that the construction information in the proposed method has more additional information to reveal about the second layer. The construction of the second layer matrix (i.e., the type matrix) can be calculated according to the above steps. The extra information of the second layer includes the value with the coordinate (0, 0) in , the construction rules of , and the algorithm for generating type matrix . The procedures for data embedding and extraction are described in detail in the following sections.
3.2. Data Embedding and Data Extraction Procedures
In this section, data embedding and extraction procedures of the proposed method are presented. Figure 5 shows the flow chart of the data embedding process. First, we divide the cover image into multiple non-overlapping pixel pairs (). The binary secret stream S is divided into 7-bit sub-steams , which are further converted into two numbers: 4-ary digit and 32-ary digit , respectively. The pair contains 4-ary and 32-ary numbers ( hidden in each pixel pair using the constructed double-layer reference matrix. When all the secret data is embedded, we get a stego-image. The detailed steps for data embedding and data extraction are described in the Algorithms 1 and 2.
| Algorithm 1. Data Embedding Algorithm. |
| Input: A cover image sized , the binary secret stream S with length L. |
| Output: A stego-image . |
| Step 1: Construct a one-layer reference matrix according to the rules described in Section 2. Thereafter, generate a double-layer reference matrix, assigning the type value corresponding to each matrix element according to the rules described in Section 3.1. |
| Step 2: Divide the cover image into non-overlapping pixel pairs () where . Consider as the coordinates of the matrix M to specify the value with the corresponding type ). |
| Step 3: Divide the secret message S into sub-streams of 7 bits, where . For each sub-stream , convert the first 2 bits into a 4-ary digit and the last 5 bits into a 32-ary digit , viz., where “||” denotes the string concatenation operator. |
| Step 4: Embed each sub-stream into each pixel pair () according to the following rules: Find the closest element m(u,v) by searching in a square of centered on , where and . Replace with such that the stego-pixel pairs , to embed the sub-stream consisting of and . |
| Step 5: Repeat Step 4 until all the sub-streams are embedded. Finally, obtain the stego-image I’. |
| Algorithm 2. Data Extraction Algorithm. |
| Input: A stego-image I′ sized . |
| Output: The binary secret stream S. |
| Step 1: Reconstruct the double-layer reference matrix where each matrix element corresponds to a type value , which is calculated according to the reules described in Section 3.1. |
| Step 2: Divide the stego-image I’ into non-overlapping pixel pairs, where . |
| Step 3: For each stego-pixel pair find two digits m in 32-ary format and in 4-ary format, respectively. The hidden secret data is , where and , respectively. |
| Step 4: Convert into binary bits of secret data. |
| Step 5: Repeat Steps 2–4 to extract all the sub-streams. Combine all the sub-streams to form the secret binary stream S. |

Figure 5.
Flowchart of data embedding procedure.
3.3. Example of Data Embedding and Data Extraction Procedures
We will take two cover pixel pairs () = and () = as examples to explain the embedding and extraction procedures based on the proposed method. The secret message of 14-bit stream to be embedded is . Figure 6 is the double-layer reference matrix related to the examples explained in this section. Figure 7 presents examples describing the data embedding process of the cover pixel pairs.
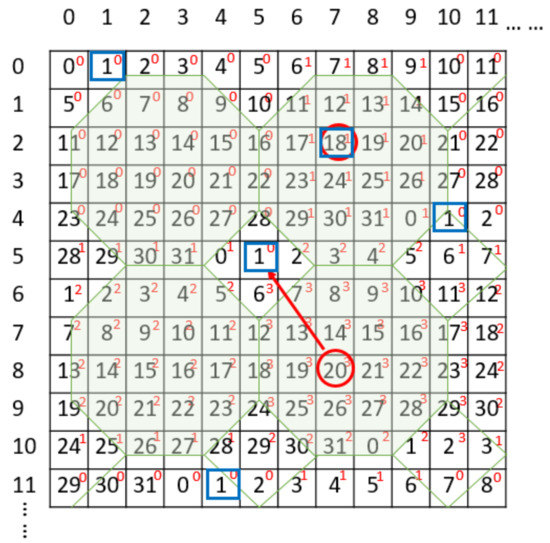
Figure 6.
Construction of double-layer octagon-shaped shell reference matrix.

Figure 7.
Examples describing data embedding of pixel pairs.
Assume that we want to hide the sub-stream “01 10010” in the first cover pixel pair . The sub-stream is first divided into two segments, namely and . Thereafter, we need to convert binary digits into decimal digits, which results in two numbers 1 and 18 after conversion in the 4-ary and 32-ary systems respectively. Since m and is shown in Figure 6, it is not necessary to change the cover pixel pair, and the secret message can be extracted at a later stage. Therefore, the stego-pixel pair is the same as the corresponding cover pixel pair () = as shown in Figure 7.
The second cover pixel pair is () = . The sub-stream to be hidden, is converted into decimal digits, which results in 0 and 1 in the 4-ary and 32-ary systems respectively. Marked by blue color in Figure 6, the location (5, 5) is closest to the location and satisfies at the top layer and at the bottom layer. Finally, the second cover pixel pair is replaced with the stego-pixel pair () = which is also shown in Figure 7.
A double-layer matrix is constructed according to the construction rules shown in Figure 6, on the receiving end. We then divide the stego-image into non-overlapping pixel pairs to embed the 7-bit secret message. Taking the first stego-pixel pair () = as an example, the values of and are obtained from at the top layer and and m at the bottom layer of the double-layer matrix, where is 1 and is 18 respectively. Moreover, 1 and 18 are converted into binary data “01” and “10010” in the 4-ary and 32-ary number systems respectively. Finally, we get the combined secret sub-stream “0110010”.
4. Experimental Results
Experiments were conducted using MATLAB R2017a to verify the performance of the proposed scheme. A total of six grayscale images were used from the University of Southern California-Signal and Image Processing Institute (USC-SIPI) image database [18] as shown in Figure 8. The size of each image was pixels. The binary secret stream S was generated randomly. The parameters of Embedding Capacity (EC), Peak Signal to Noise Ratio (PSNR), and Structural Similarity Index (SSIM) were used as evaluation parameters to validate the performance of the proposed method. EC is the amount of secret message per pixel that can be embedded in the image. If the number of secret messages embedded in the image is more and the image quality can be maintained to a certain standard, then the data hiding method is supposed to have high imperceptibility and high embedding capacity. PSNR is used to measure the quality of the image. If the value of this parameter is high, it means that the image quality is good, and the secret message hidden in stego-image cannot be perceived easily by the human eye. Refer to Equations (6) and (7) to calculate PSNR. Refer to Equation (8) to calculate the EC.

Figure 8.
Six grayscale test images; they should be listed as (a) Lena, (b) Baboon, (c) Peppers, (d) Boat, (e) Airplane, and (f) House.
( is the height of image, is the width of image, represents the cover image, and I′ represents the stego-image. MSE represents mean-square error, EC represents embedding capacity, and are the total number of secret bits that can be embedded).
In addition, the parameter of SSIM measures similarity between the original image and the stego image. This is in line with the human eye’s judgment of image quality. The higher the SSIM value, the higher will be the similarity between the original image and the stego image.
SSIM value is calculated using Equation (9) as shown below, where and are the average values of the original image and the stego image respectively; is the co-variation between the original and the stego images respectively; and and are the variation of the original image and the stego image respectively. and are constants.
A comparison of the proposed method with the other four methods is shown in Table 1. It can be observed that the proposed scheme obviously outperforms the other methods in terms of the embedding capacity and image quality. To be more precise, we can see that the proposed method has a higher embedding capacity (3.5 bpp) compared to the methods in [12,13,14,15,16,17,19,20], with an acceptable decrease in the image quality. Also, the image quality of the proposed method is better than that of [13] at the same embedding capacity of 3.5 bpp. Our proposed method outperforms in terms of PSNR with an average value of 36.91 dB compared to the average PSNR of 30.62 dB obtained in [13]. While [14,15,16,20] have higher average PSNR values of 44.12 dB, 46.37 dB, 46.84 dB, and 41.27 dB respectively, the embedding capacity of our proposed scheme is higher by 1.5 bpp.

Table 1.
Comparison of image quality (PSNR) and embedding capacity (EC).
As it can be seen in Table 2, we used six standard test images and set a fixed amount of embedding capacity to display changes in the PSNR for each image. For example, when the embedding capacity is bits, the average PSNR of each image remains at 38.09 dB. At the embedding capacity of bits, the PSNR remains at an average quality of 39.56 dB. Therefore, the PSNR value remains stable for each test image. The magnitude of the pixels change during the data embedding process, which depends on the constructed double-layer reference matrix and the embedding procedure. In other words, the image quality of the stego-image is independent of the cover image and it is possible to maintain the image quality within an acceptable range using the proposed method.

Table 2.
The PSNR values (dB) of the proposed method under various payloads (bits).
Table 3 shows the SSIM values of six standard test images at a fixed EC (3.5 bpp, which is 917,504 bits). Interestingly, the SSIM value for complex images such as Baboon is higher compared to the SSIM value for smooth images such as Airplane. This is a unique finding in our proposed method. Therefore, we contend that our proposed method is more suitable for complex images to obtain a higher SSIM value. Also, as seen previously, the PSNR values remains stable for all the test images irrespective of their image texture. To confirm this, we tested our proposed method on 50 additional test images using USC-SIPI database [18] and Kodak Image database [21] as shown in Figure 9.

Table 3.
The SSIM values for six standard test images at a fixed EC (3.5 bpp).
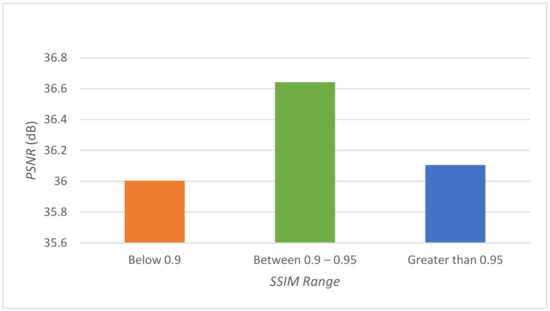
Figure 9.
Range of SSIM values for 50 standard test images.
Based on the experiment on 50 test images, the SSIM values can be categorized into three groups as shown in the Figure 9. It is evident from the figure that the images which obtain SSIM values between [0.90, 0.95] are the most suitable for the proposed method as these images show the highest PSNR value. The PSNR range obtained for SSIM values between [0.90, 0.95] is [34.085597, 36.941688] dB, which falls in the acceptable image quality range.
We also calculated the PSNR values for six standard test images at different EC (bpp) as shown in Figure 10 below. The figure clearly shows that as the embedding rate increases, the PSNR value decreases similar to the property of methods based on the magic matrix hiding methods of [12,13,14,15,16,17,19,20,22]. However, interestingly, the PSNR values for the test images do not have much difference from each other, which again shows the point that the PSNR values remains stable using our proposed method irrespective of the image texture.
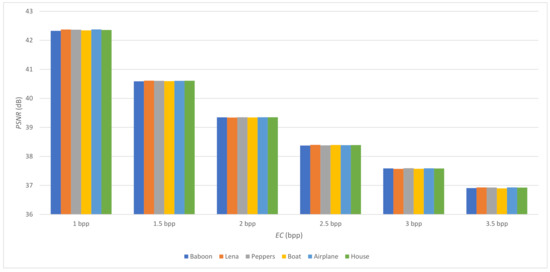
Figure 10.
The PSNR values for six standard test images at different EC (bpp).
Table 4 shows the comparison of EC (bpp), PSNR (dB), and embedding time (seconds) among Chang et al.’s turtle shell in a single-layer embedding, Leng and Tseng’s octagon-shaped shells scheme in a single-layer embedding, Xie et al.’s two-layer turtle shell matrix embedding, Shen et al.’s double-layer square magic matrix scheme, and the proposed method in a two-layer embedding using octagon-shaped shells. For simplicity, the representations [TS, 1, EC1.5], [Octagon, 1, EC2.5], [TS, 2, EC2.5], [Square, 2, EC2.5], [Ours, 2, EC3.5] stand for the methods exploiting Chang et al.’s turtle shell in a single-layer embedding [10] with EC = 1.5 bpp, Leng and Tseng’s octagon-shaped shells scheme in a single-layer embedding [12] with EC = 2.5 bpp, Xie et al.’s two-layer turtle shell matrix embedding [19] with EC = 2.5 bpp, Shen et al.’s double-layer square magic matrix scheme with EC = 2.5 bpp, and the proposed method in a two-layer embedding using octagon-shaped shells with EC = 3.5 bpp. As mentioned earlier, with regards to the information hiding method based on the magic matrix, under the same embedding capacity regardless of the image texture, the PSNR and SSIM values of all test images remain stable. Similarly, the execution time of each method also has this stable characteristic, which is presented in Table 4 and Figure 11.

Table 4.
Comparison of EC, PSNR values, and embedding time among Chang et al.’s turtle shell (TS) in a single-layer embedding, Leng’s octagon-shaped shells scheme in a single-layer embedding, Xie et al.’s two-layer turtle shell matrix embedding, Shen et al.’s double-layer square magic matrix scheme, and the proposed method in a two-layer embedding using octagon-shaped shells.
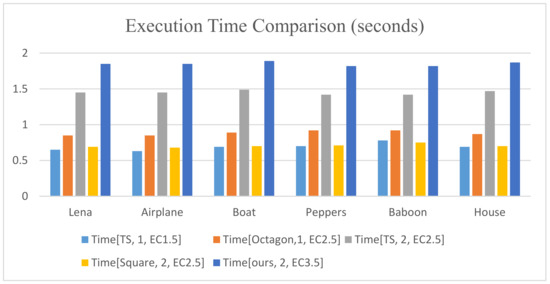
Figure 11.
Comparison of execution time of five methods with different embedding capacities.
Table 4 shows the comparison of EC (bpp), PSNR (dB), and embedding time (seconds) among Chang et al.’s turtle shell in a single-layer embedding, Leng’s octagon-shaped shells scheme in a single-layer embedding, Xie et al.’s two-layer turtle shell matrix embedding, Shen et al.’s double-layer square magic matrix scheme, and the proposed method in a two-layer embedding using octagon-shaped shells. For simplicity, the representations [TS, 1, EC1.5], [Octagon, 1, EC2.5], [TS, 2, EC2.5], [Square, 2, EC2.5], [Ours, 2, EC3.5] stand for the methods exploiting Chang et al.’s turtle shell in a single-layer embedding [10] with EC = 1.5 bpp, Leng and Tseng’s octagon-shaped shells scheme in a single-layer embedding [12] with EC = 2.5 bpp, Xie et al.’s two-layer turtle shell matrix embedding [19] with EC = 2.5 bpp, Shen et al.’s double-layer square magic matrix scheme with EC = 2.5 bpp, and the proposed method in a two-layer embedding using octagon-shaped shells with EC = 3.5 bpp. As mentioned earlier, the PSNR and SSIM values of all test images remain stable for the information hiding method based on the magic matrix, under the same embedding capacity regardless of the image texture. Similarly, the execution time of each method also shows stability, which is presented in Table 4 and Figure 11.
As seen in Figure 11, the method we proposed demonstrates maximum embedding capacity, and it also consumes the longest computation time. However, irrespective of the method, execution time of the maximum embedding capacity lies between 0.62 s and 1.90 s.
5. Conclusions
The steganography is used for covert communication in which secret data is hidden into a cover media, resulting in a stego-media. The key goal of steganography is to embed the maximum amount (capacity) of secret data to hide its existence with minimal distortion of the cover media. So, a data hiding methodology has to handle the tradeoff between “capacity” and “transparency/imperceptibility”. Inspired from the regular octagon-shaped shells data hiding method of Leng and Tseng [12], we proposed a steganographic method based on double-layer octagon-shaped shell matrix with high embedding capacity superior to the existing data hiding schemes.
In the regular octagon-shaped shells data hiding method, a 5-bit secret message could be embedded per pixel pair in the octagon-shaped shell matrix. In the double-layer octagon-shaped shells scheme proposed in this paper, we can further add 2 bits to enhance the embedding capacity. The digits of proposed reference matrix of the first layer are 2-bit data in the 4-ary number system, and the digits of second layer are 5-bit data in the 32-ary number system. Thus, each pixel pair can carry a total of 7-bit secret data, leading to a high embedding capacity of 3.5 bpp.
The experimental results verify that the proposed method is superior to the existing data hiding schemes in terms of embedding capacity, which was also able to maintain an acceptable visual quality of PSNR 37 dB on an average while SSIM values were between 0.9–0.95. We contend that our proposed method is more suitable for complex images to obtain a higher SSIM value as compared to other methods. Also, as seen previously, the PSNR values were stable for all the test images irrespective of their image texture. Moreover, the computation cost in terms of embedding time was 1.82 s on average.
In this article, there are two issues to be solved in the future.
- (1)
- The first point is the results in Table 3 are showing the proposed algorithm is insecure because of the obtained SSIM values with high EC. When SSIM = 0.95, most people will be satisfied with the visual image of the image. While SSIM is lower than 0.90, it means that the defect may be twice as much as 0.95, and the naked eyes may perceive the picture deterioration and cause insecurity. According to our experimental results, when the EC value reaches 3.5 bpp, approximately 10% of pictures will have an SSIM slightly below 0.9. The results under 0.95 should be the limit for increasing the EC.
- (2)
- From the experimental results in Figure 11, although the proposed method has a larger maximum embedding capability, it takes more time to implement information hiding than other methods. The execution time of the maximum embedding capacity was around 1.90 s. Therefore, in future, we will improvise the method showcased in paper [22] to develop another multi-layer information hiding method, in order to achieve better information hiding computational capabilities, making it more competitive in the real-time application environment.
Author Contributions
Conceptualization, C.-F.L.; Formal analysis, S.A. and Y.-H.L.; Funding acquisition, C.-F.L.; Methodology, C.-F.L. and Y.-H.L.; Project administration, C.-F.L. and J.-J.S.; Resources, C.-F.L. and J.-J.S.; Supervision, C.-F.L. and J.-J.S.; Validation, C.-F.L.; Visualization, J.-J.S.; Writing—original draft, Y.-H.L.; Writing—review & editing, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project of the Ministry of Science and Technology of the Republic of China under the Grants MOST 109-2221-E-324-022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
A total of six grayscale images were used from the University of Southern California-Signal and Image Processing Institute (USC-SIPI) image database [18].
Acknowledgments
This research was partially supported by the Ministry of Science and Technology of the Republic of China under the Grants MOST 109-2221-E-324-022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anderson, R.J.; Petitcolas, F.A.P. On the limits of steganography. IEEE J. Sel. Areas Commun. 1998, 16, 474–481. [Google Scholar] [CrossRef]
- Johnson, N.F.; Jajodia, S. Exploring steganography: Seeing the unseen. Computer 1998, 31, 26–34. [Google Scholar] [CrossRef]
- Saha, A.; Halder, S.; Kollya, S. Image steganography using 24-bit bitmap images. In Proceedings of the 14th International Conference on Computer and Information Technology (ICCIT 2011), Dhaka, Bangladesh, 22–24 December 2011; pp. 56–60. [Google Scholar] [CrossRef]
- Pitropakis, N.; Lambrinoudakis, C.; Geneiatakis, D.; Gritzalis, D. A Practical Steganographic Approach for Matroska Based High Quality Video Files. In Proceedings of the 2013 27th International Conference on Advanced Information Networking and Applications Workshops, Barcelona, Spain, 25–28 March 2013; pp. 684–688. [Google Scholar] [CrossRef]
- Chan, C.K.; Cheng, L.M. Hiding Data in Images by Simple LSB Substitution. Pattern Recognit. 2004, 37, 469–474. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wang, S.Z. Efficient Steganographic Embedding by Exploiting Modification Direction. IEEE Commun. Lett. 2006, 10, 781–783. [Google Scholar] [CrossRef]
- Lee, C.F.; Chen, H.L. A Novel Data Hiding Scheme Based on Modulus Function. J. Syst. Softw. 2010, 83, 832–843. [Google Scholar] [CrossRef]
- Lee, C.F.; Weng, C.Y.; Chen, K.C. An Efficient Reversible Data Hiding with Reduplicated Exploiting Modification Direction Using Image Interpolation and Edge Detection. Multimed. Tools Appl. 2017, 76, 9993–10016. [Google Scholar] [CrossRef]
- Chang, C.C.; Chou, Y.C.; Kieu, T.D. An Information Hiding Scheme Using Sudoku. In Proceedings of the 2008 3rd International Conference on Innovative Computing Information and Control, Dalian, China, 18–20 June 2008; pp. 17–22. [Google Scholar]
- Chang, C.C.; Liu, Y.; Nguyen, T.S. A Novel Turtle Shell Based Scheme for Data Hiding. In Proceedings of the 2014 Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kitakyushu, Japan, 27–29 August 2014; pp. 89–93. [Google Scholar] [CrossRef]
- Kurup, S.; Rodrigues, A.; Bhise, A. Data Hiding Scheme Based on Octagon Shaped Shell. In Proceeding of the 2015 International Conference on Advances in Computing, Communications and Informatics (ICACCI-2015), Kochi, India, 10–13 August 2015; pp. 1982–1986. [Google Scholar] [CrossRef]
- Leng, H.S.; Tseng, H.W. Maximizing the Payload of the Octagon-Shaped Shell-based Data Hiding Scheme. In Proceedings of the 2017 IEEE 8th International Conference on Awareness Science and Technology (iCAST), Taichung, Taiwan, 8–10 November 2017; pp. 45–49. [Google Scholar]
- Leng, H.S. Data Hiding Scheme Based on Regular Octagon-Shaped Shells. In Advances in Intelligent Information Hiding and Multimedia Signal Processing; Smart Innovation, Systems and Technologies; Springer: Cham, Switzerland, 2018; pp. 29–35. [Google Scholar]
- Lee, C.F.; Wang, Y.X. Secure Image Hiding Scheme Based on Magic Signet. J. Electron. Sci. Technol. (JEST) 2020, 18, 93–101. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, S.; Harn, L. An Efficient and Adaptive Data-Hiding Scheme Based on secure random matrix. PLoS ONE 2019, 14, e0222892. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Liu, Y. Fast Turtle Shell-Based Data Embedding Mechanisms with Good Visual Quality. J. Real-Time Image Process. 2019, 16, 589–599. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pan, J.S.; Ngo, T.G.; Dao, T.K. A Data Hiding Approach Based on Reference-Affected Matrix. In Advances in Intelligent Information Hiding and Multimedia Signal Processing; Smart Innovation, Systems and Technologies; Springer: Singapore, 2020; Volume 156, pp. 53–64. [Google Scholar]
- USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 28 July 2020).
- Xie, X.Z.; Lin, C.C.; Chang, C.C. Data Hiding Based on a Two-layer Turtle Shell Matrix. Symmetry 2018, 10, 47. [Google Scholar] [CrossRef]
- Xia, B.B.; Wang, A.H.; Chang, C.C.; Liu, L. An Image Steganography Scheme Using 3D-Sudoku. J. Inf. Hiding Multimed. Signal Process. 2016, 7, 836–845. [Google Scholar]
- True Color Kodak Images. Available online: http://r0k.us/graphics/kodak/ (accessed on 28 July 2020).
- Shen, J.J.; Lee, C.F.; Li, Y.H.; Agrawal, S. Image Steganographic Scheme Based on Doublelayer Magic Matrix. In Proceedings of the 2019 IEEE 10th International Conference on Awareness Science and Technology (iCAST), Morioka, Japan, 23–25 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).