The Exponentiated Fréchet Generator of Distributions with Applications
Abstract
1. Introduction
2. Exponentiated Fréchet-G Family
3. Special Models
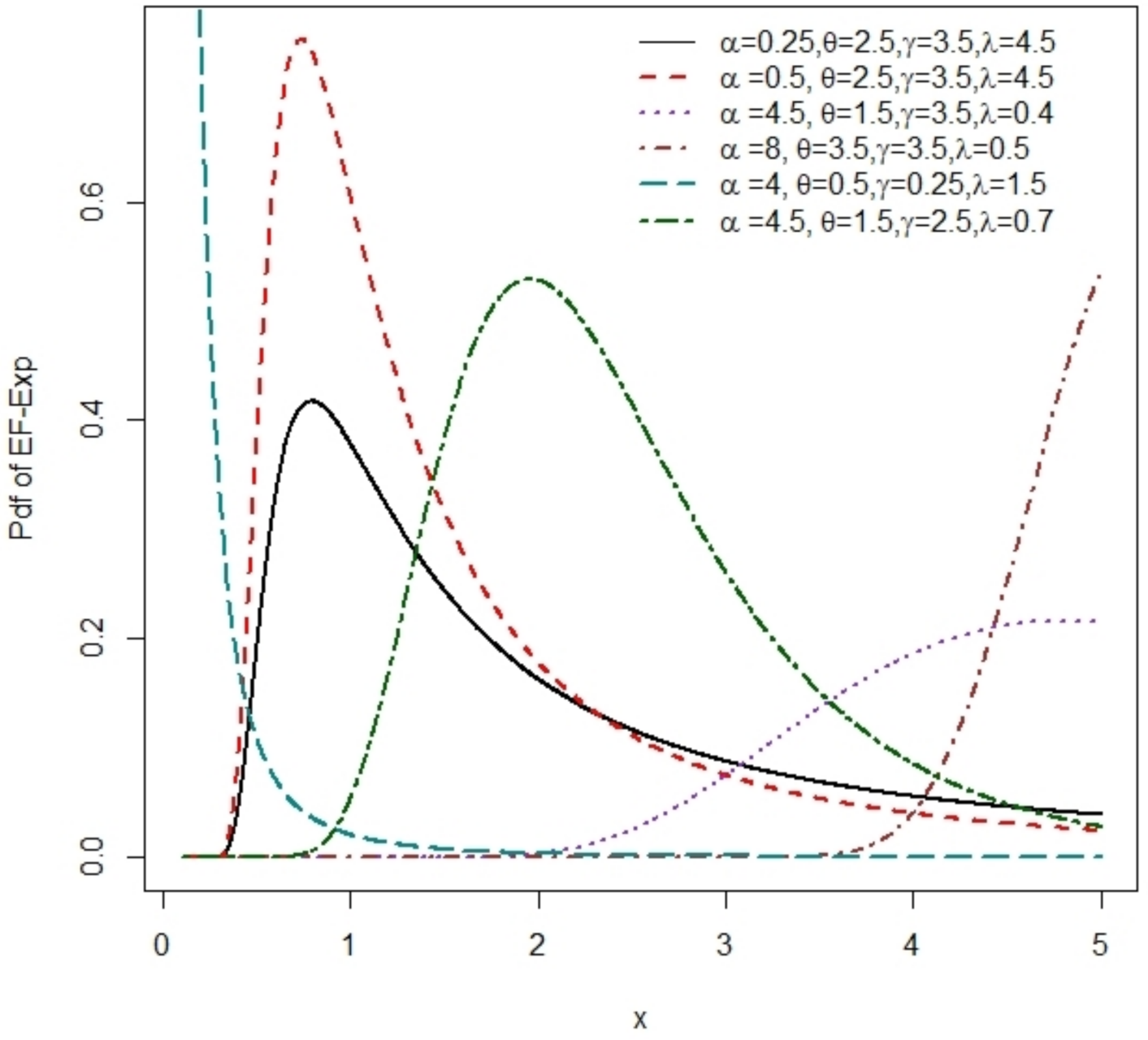
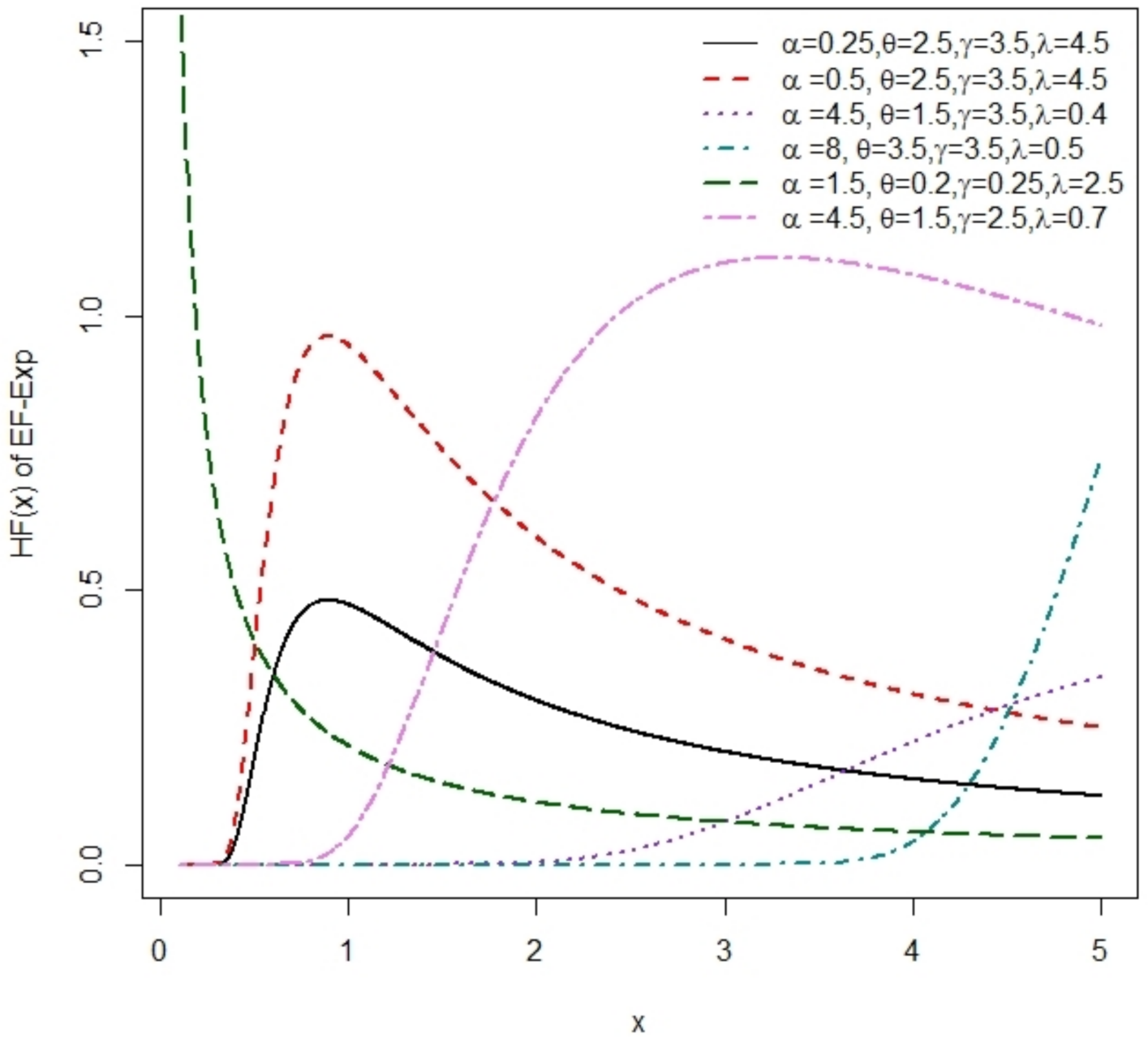
3.1. EF-Exponential Distribution
3.2. EF-Rayleigh Distribution
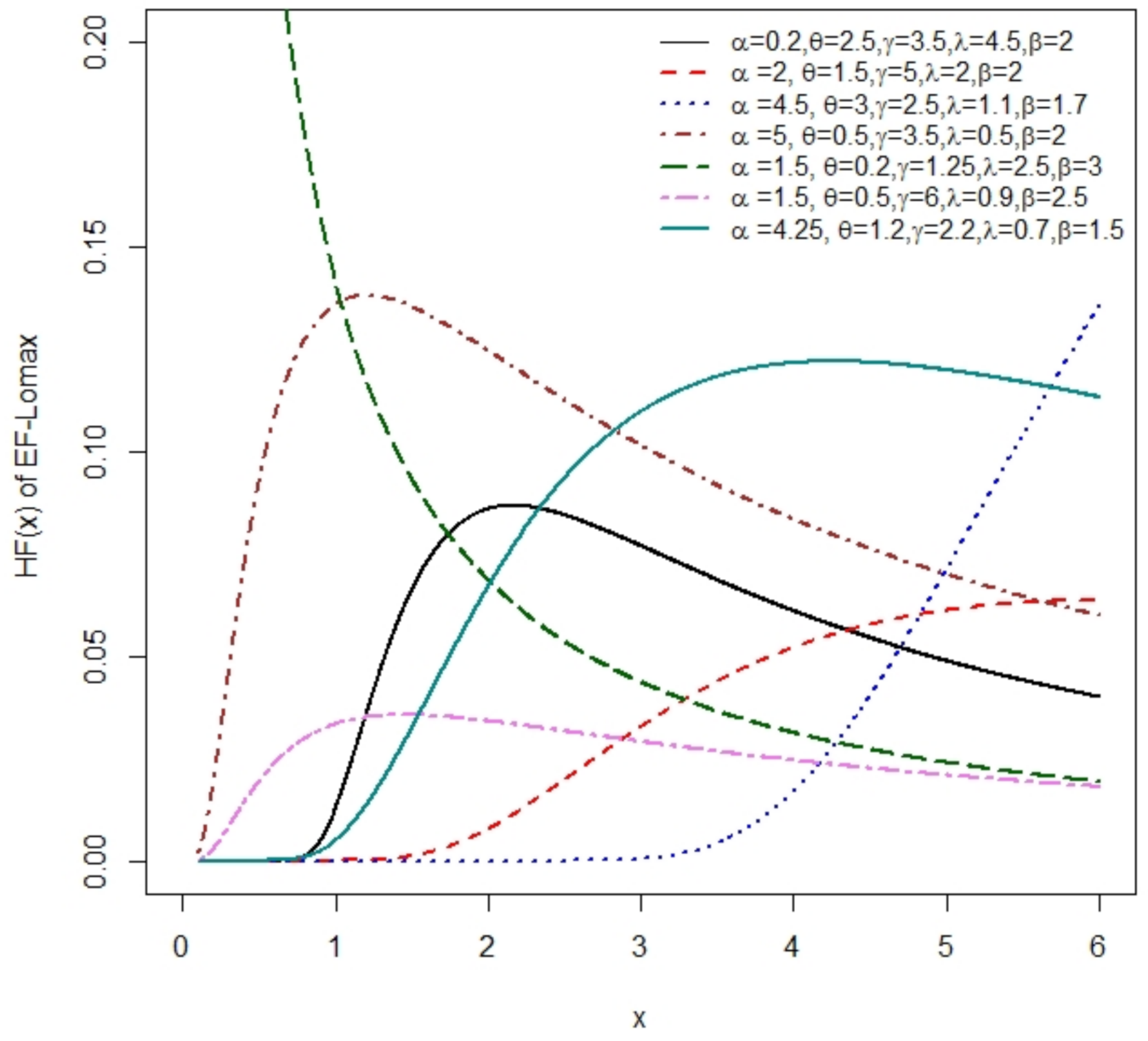
3.3. EF-Lomax Distribution
3.4. EF-Gompertz Distribution
4. Useful Expansion of the EF-G Density and Cumulative Functions
5. Mathematical Properties of EF-G
5.1. Quantiles of EF-G
5.2. Moment
5.3. Moment Generating Function (MGF)
5.4. Incomplete Moment
5.5. Rényi Entropy
5.6. Order Statistics
6. Estimation of the EF-G Parameters
7. Numerical Study
- Generate data from EF-Lomax by setting given by (9), where , such that
- Four sample sizes, , with the two sets of the true parameters ; the simulation for each sample size is considered over 1000 iterations.
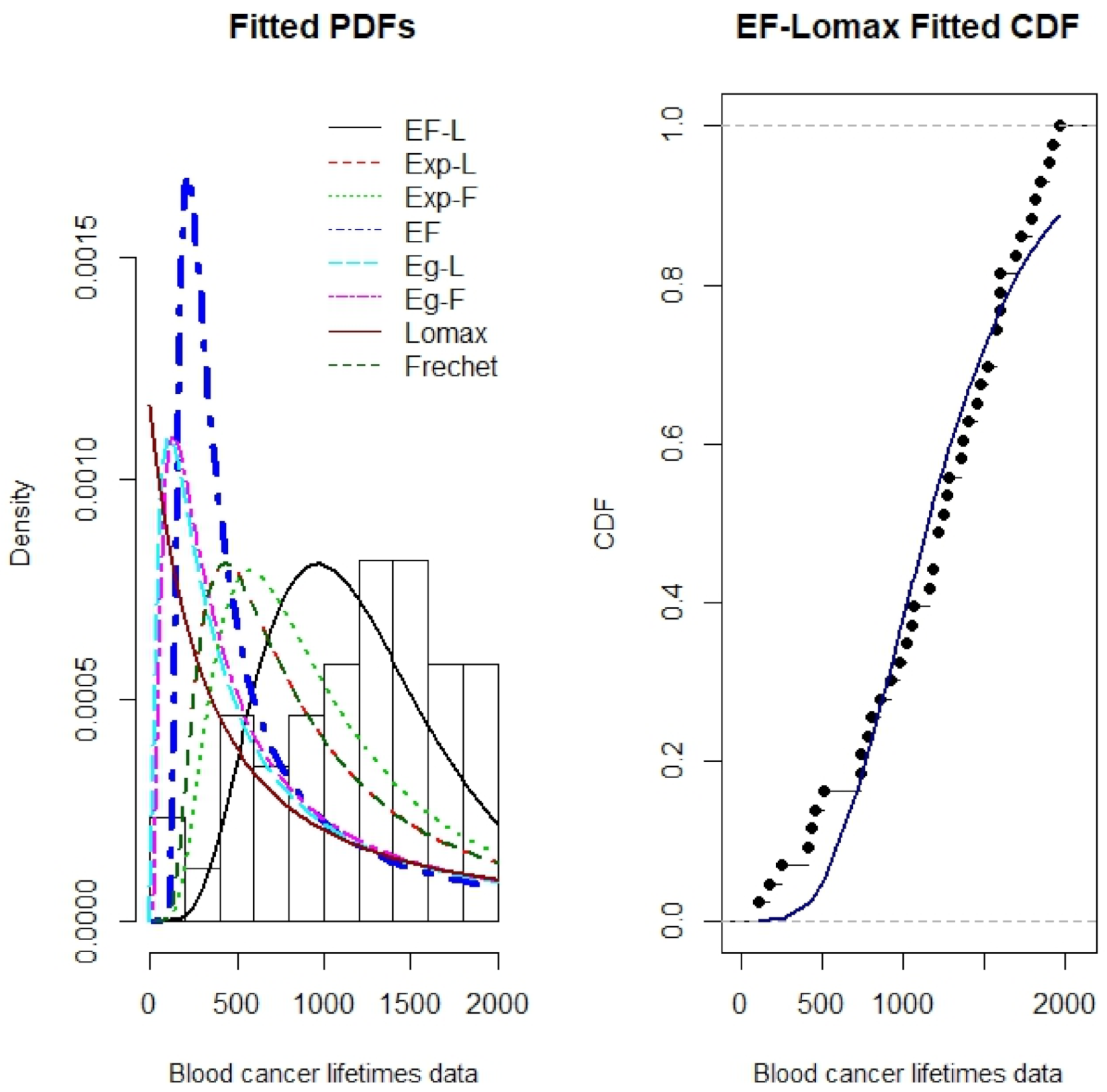
8. Applications
9. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. Appl. 2015, 2, 1. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Ghosh, I. On the Weibull-X family of distributions. J. Stat. Theory Appl. 2015, 14, 169–183. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Gomes-Silva, F.S.; Percontini, A.; de Brito, E.; Ramos, M.W.; Venâncio, R.; Cordeiro, G.M. The odd Lindley-G family of distributions. Austrian J. Stat. 2017, 46, 65–87. [Google Scholar] [CrossRef]
- Alizadeh, M.; Cordeiro, G.M.; Nascimento, A.D.; Lima, M.d.C.S.; Ortega, E.M. Odd-Burr generalized family of distributions with some applications. J. Stat. Comput. Simul. 2017, 87, 367–389. [Google Scholar] [CrossRef]
- Haq, M.; Elgarhy, M. The odd Fréchet-G family of probability distributions. J. Stat. Appl. Probab. 2018, 7, 189–203. [Google Scholar] [CrossRef]
- Nasiru, S. Extended odd Fréchet-G family of distributions. J. Probab. Stat. 2018, 2018. [Google Scholar] [CrossRef]
- Reyad, H.; Korkmaz, M.Ç.; Afify, A.Z.; Hamedani, G.; Othman, S. The Fréchet Topp Leone-G Family of Distributions: Properties, Characterizations and Applications. Ann. Data Sci. 2019, 1–22. [Google Scholar] [CrossRef]
- Bantan, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II power Topp-Leone generated family of distributions with statistical inference and applications. Symmetry 2020, 12, 75. [Google Scholar] [CrossRef]
- Almarashi, A.M.; Elgarhy, M.; Jamal, F.; Chesneau, C. The exponentiated truncated inverse Weibull-generated family of distributions with applications. Symmetry 2020, 12, 650. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The exponentiated Fréchet distribution. Interstat Electron. J. 2003, 14, 1–7. [Google Scholar]
- Nadarajah, S.; Kotz, S. The exponentiated type distributions. Acta Appl. Math. 2006, 92, 97–111. [Google Scholar] [CrossRef]
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; Imperial College Press: London, UK, 2000. [Google Scholar]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: Berlin, Germany, 2001; Volume 208. [Google Scholar]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M.M. The Zografos–Balakrishnan-G family of distributions: Mathematical properties and applications. Commun. Stat. Theory Methods 2015, 44, 186–215. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Ramires, T.G. A new generalized Weibull family of distributions: Mathematical properties and applications. J. Stat. Distrib. Appl. 2015, 2, 13. [Google Scholar] [CrossRef]
- Klakattawi, H.S. The Weibull-Gamma Distribution: Properties and Applications. Entropy 2019, 21, 438. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Kollia, G.D. A generalization of the Weibull distribution with application to the analysis of survival data. J. Am. Stat. Assoc. 1996, 91, 1575–1583. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biom. J. J. Math. Methods Biosci. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; da Cunha, D.C. The exponentiated generalized class of distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar] [CrossRef]
- Abouammoh, A.; Abdulghani, S.; Qamber, I. On partial orderings and testing of new better than renewal used classes. Reliab. Eng. Syst. Saf. 1994, 43, 37–41. [Google Scholar] [CrossRef]


| Set I: | , , , , ) | |||||
| MLE | 5.6117 | 4.2608 | 1.6915 | 1.7163 | 0.7071 | |
| RMSE | 1.1436 | 0.5609 | 0.6874 | 1.7537 | 0.6173 | |
| MLE | 5.9896 | 3.9999 | 1.8393 | 0.5624 | 0.2147 | |
| RMSE | 0.0532 | 0.0009 | 0.2317 | 0.3829 | 0.2857 | |
| MLE | 6.0055 | 4.0011 | 1.8249 | 0.5944 | 0.2132 | |
| RMSE | 0.1036 | 0.0027 | 0.2202 | 0.4450 | 0.2871 | |
| MLE | 5.9859 | 3.9998 | 1.8247 | 0.5682 | 0.2131 | |
| RMSE | 0.0313 | 0.0008 | 0.1957 | 0.3729 | 0.2870 | |
| Set II: | , , , , ) | |||||
| MLE | 2.1202 | 4.9756 | 3.1469 | 0.9955 | 0.9921 | |
| RMSE | 0.8809 | 0.0741 | 0.3350 | 0.5754 | 0.3170 | |
| MLE | 2.0336 | 4.9830 | 3.1185 | 0.9797 | 0.9694 | |
| RMSE | 0.7272 | 0.0564 | 0.2925 | 0.5133 | 0.2741 | |
| MLE | 1.9919 | 4.9937 | 3.1161 | 0.9771 | 0.9288 | |
| RMSE | 0.5142 | 0.0319 | 0.2187 | 0.3684 | 0.2300 | |
| MLE | 2.0072 | 4.9994 | 3.0832 | 1.0126 | 0.9033 | |
| RMSE | 0.4193 | 0.0202 | 0.1742 | 0.3217 | 0.2237 | |
| Distribution | Estimates | AIC | CAIC | K–S | |||
|---|---|---|---|---|---|---|---|
| EF-E | 12.01 | 2.35 | 2.25 | 0.01 | 922.91 | 923.32 | 0.0820 |
| Exp-E | 281.64 | 0.04 | - | - | 929.22 | 931.84 | 0.1082 |
| Exp-F | 0.12 | 5.05 | 184.57 | - | 956.37 | 960.29 | 0.1328 |
| EF | 5.79 | 173.48 | 2.80 | - | 924.99 | 928.92 | 0.0965 |
| EG-F | 95.69 | 0.20 | 24.35 | 47.56 | 959.72 | 964.95 | 0.1457 |
| Fréchet | 5.05 | 120.78 | - | - | 954.37 | 956.98 | 0.1328 |
| Exponential | 0.01 | - | - | - | 1192.96 | 1194.27 | 0.4929 |
| Distribution | Estimates | AIC | CAIC | K–S | ||||
|---|---|---|---|---|---|---|---|---|
| EF-L | 110.29 | 0.27 | 4.11 | 38.99 | 0.02 | 685.58 | 687.20 | 0.1754 |
| Exp-L | 12.57 | 0.003 | 1.94 | - | - | 699.04 | 699.66 | 0.2031 |
| Exp-F | 45.79 | 1.18 | 28.81 | - | - | 710.58 | 713.22 | 0.2602 |
| EF | 0.16 | 195 | 3.57 | - | - | 744.84 | 747.48 | 0.3834 |
| EG-L | 3.01 | 2.83 | 0.01 | 0.22 | - | 742.81 | 747.48 | 0.3235 |
| EG-F | 13.92 | 0.92 | 0.75 | 10.51 | - | 738.79 | 742.31 | 0.3463 |
| Lomax | 0.002 | 0.58 | - | - | - | 746.97 | 748.73 | 0.3275 |
| Fréchet | 1.18 | 717.98 | - | - | - | 708.57 | 710.34 | 0.2627 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baharith, L.A.; Alamoudi, H.H. The Exponentiated Fréchet Generator of Distributions with Applications. Symmetry 2021, 13, 572. https://doi.org/10.3390/sym13040572
Baharith LA, Alamoudi HH. The Exponentiated Fréchet Generator of Distributions with Applications. Symmetry. 2021; 13(4):572. https://doi.org/10.3390/sym13040572
Chicago/Turabian StyleBaharith, Lamya A., and Hanan H. Alamoudi. 2021. "The Exponentiated Fréchet Generator of Distributions with Applications" Symmetry 13, no. 4: 572. https://doi.org/10.3390/sym13040572
APA StyleBaharith, L. A., & Alamoudi, H. H. (2021). The Exponentiated Fréchet Generator of Distributions with Applications. Symmetry, 13(4), 572. https://doi.org/10.3390/sym13040572






