Vibration Analysis and Parameter Optimization of the Longitudinal Axial Flow Threshing Cylinder
Abstract
1. Introduction
2. Materials and Methods
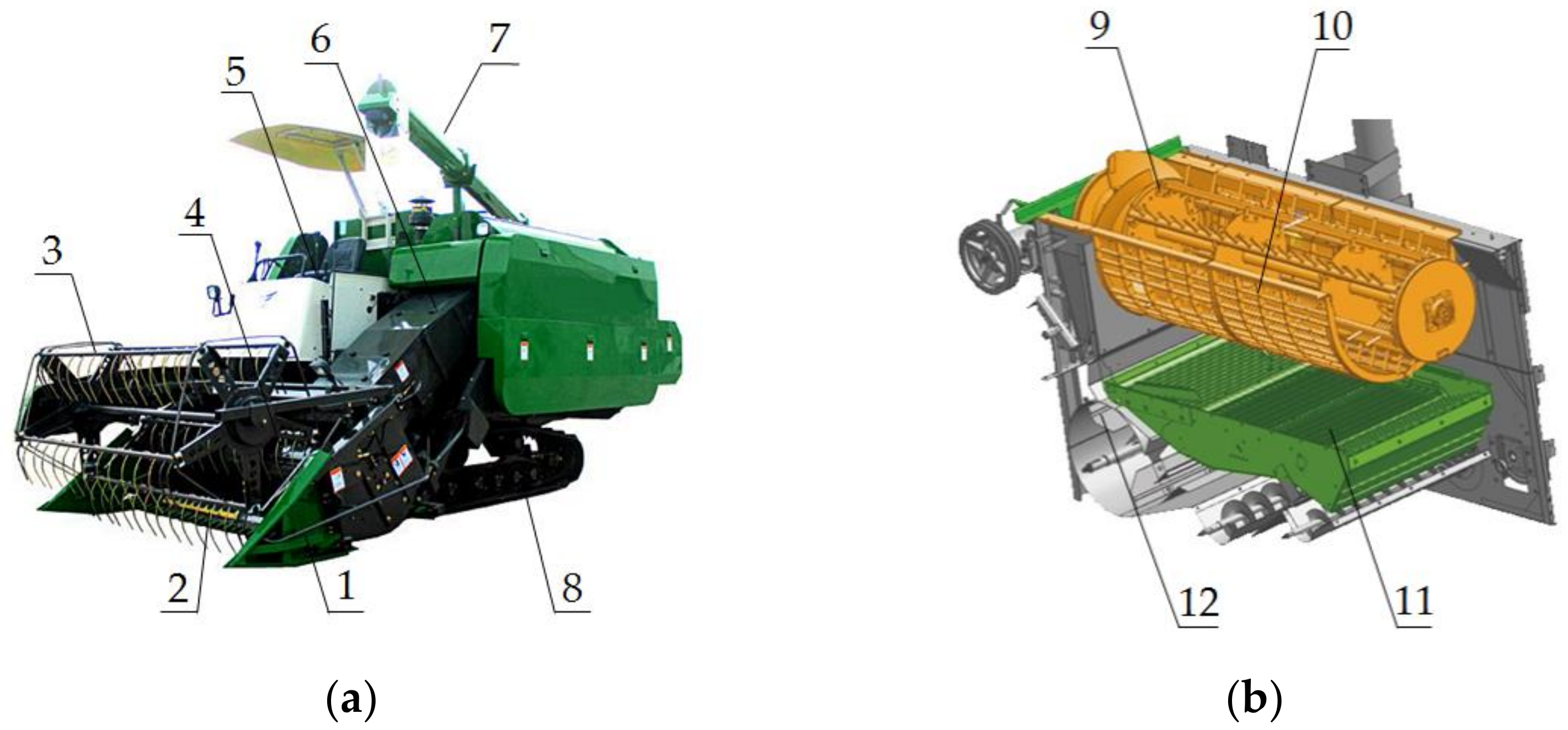
2.1. Structure and Working Process of a Full Feeding Rice Combine Harvester
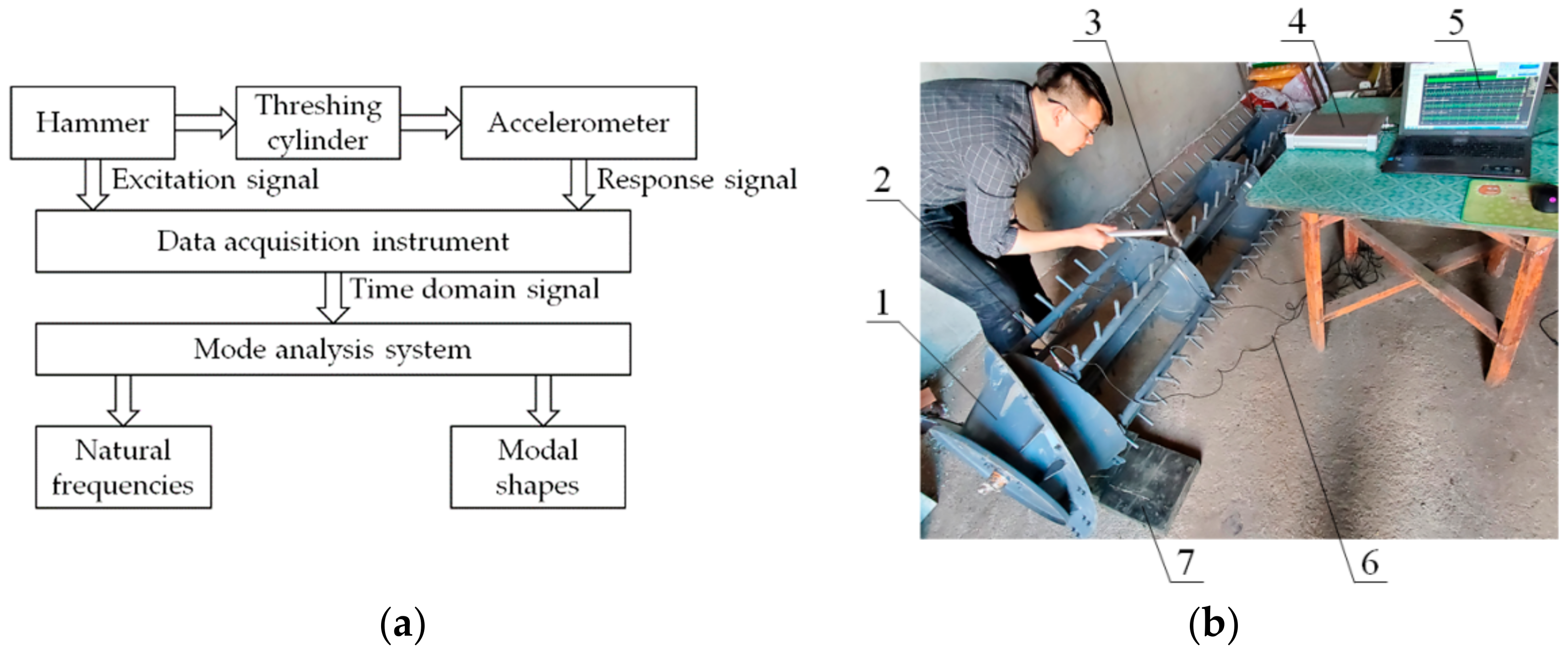
2.2. Modal Analysis and Test of Threshing Cylinder
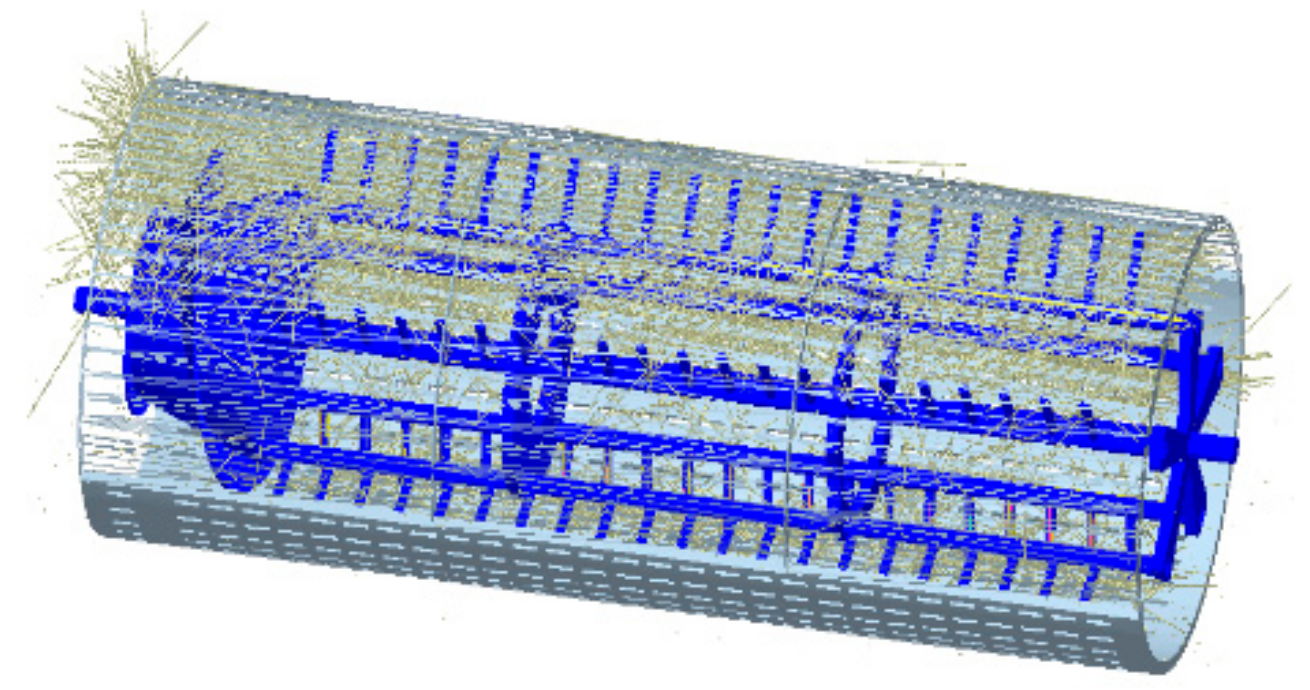
2.2.1. Free Modal Analysis of Finite Elements
2.2.2. Free Modal Test
2.2.3. Constrained Modal Analysis of Finite Element
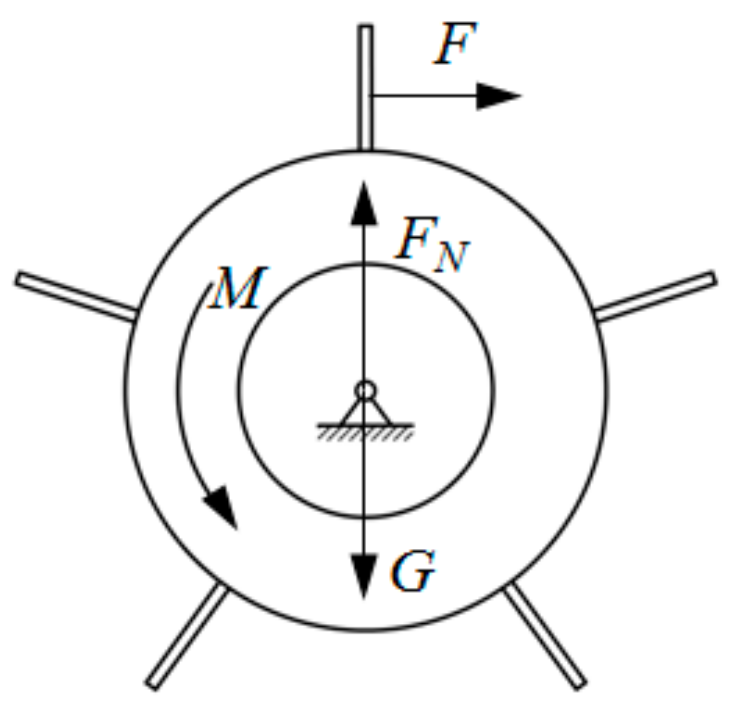
2.3. Analysis of Excitation Source
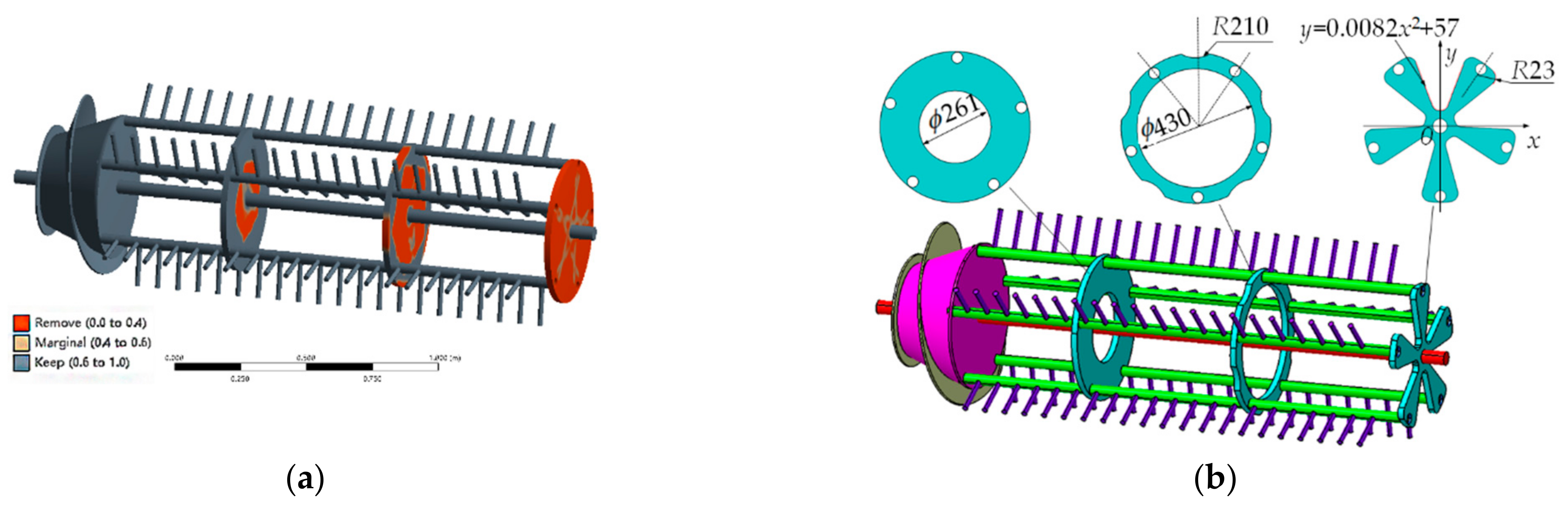
2.4. Optimization Design of Threshing Cylinder
2.4.1. Optimization Method
2.4.2. Test Design
2.5. Characteristic Analysis of Optimized Threshing Cylinder
2.5.1. Finite Element Analysis of Optimized Threshing Cylinder
2.5.2. Comparative Analysis of Field Experiment
3. Results and Discussion
3.1. Threshing Cylinder Vibrational Characteristic Analysis
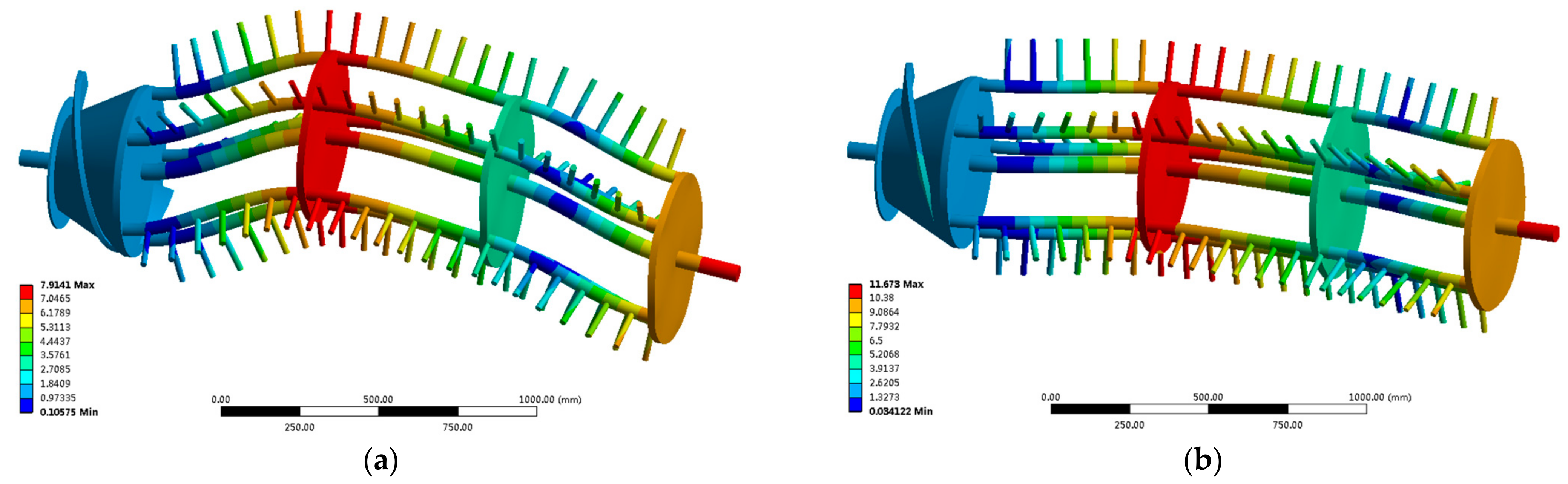
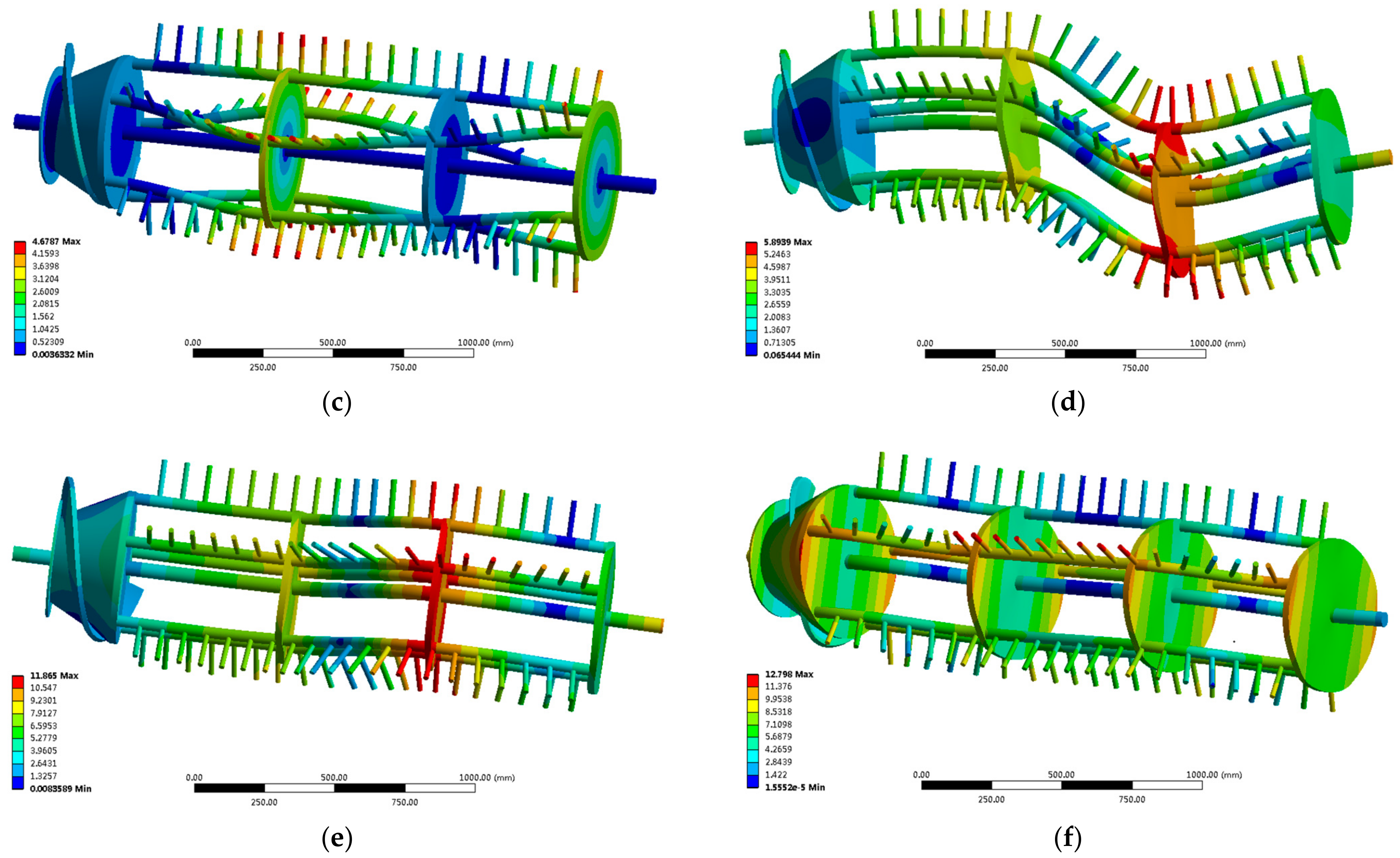
3.1.1. The Results of the Finite Element Free Modal Analysis
3.1.2. Comparison between Free Modal Analysis and Free Modal Test
3.1.3. The Results of the Finite Element Constrained Modal Analysis
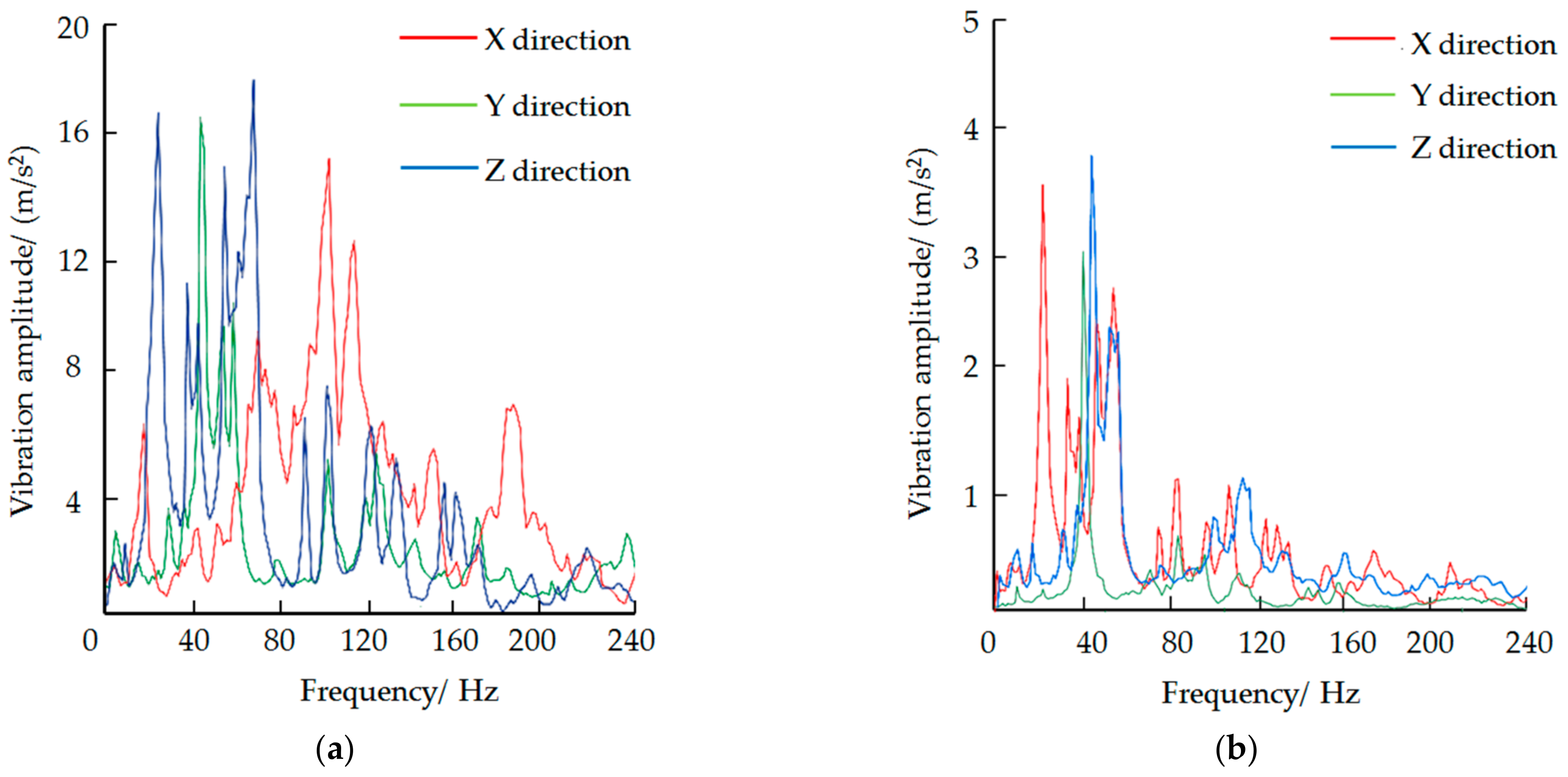
3.2. Resonance Analysis of Threshing Cylinder
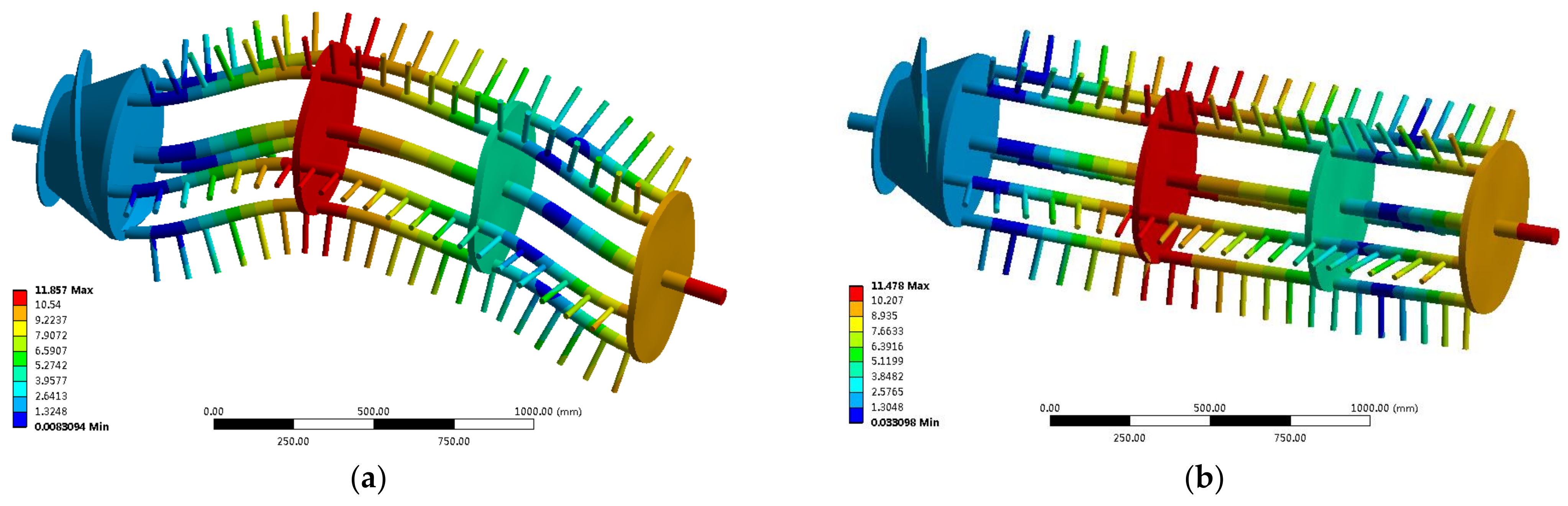
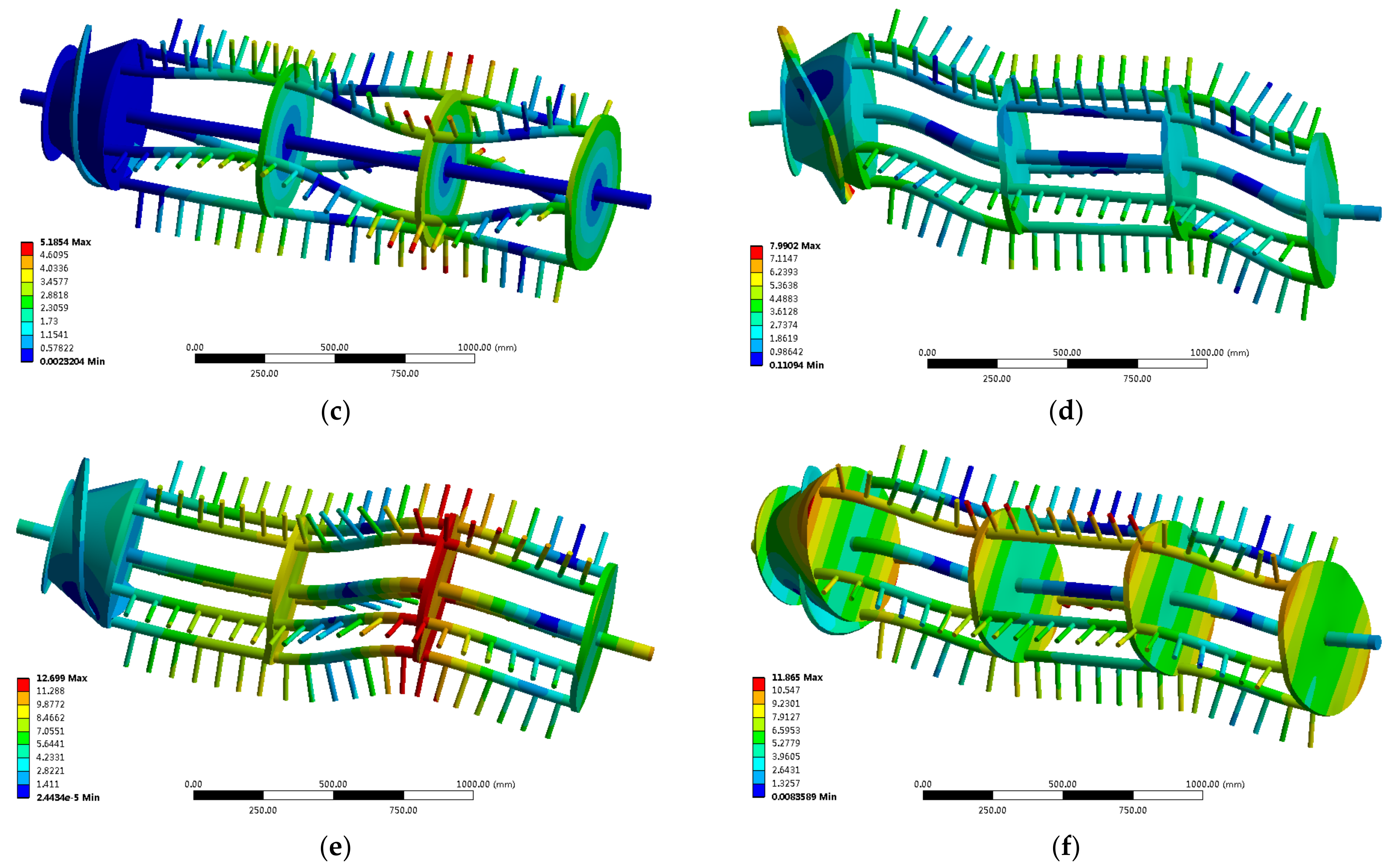
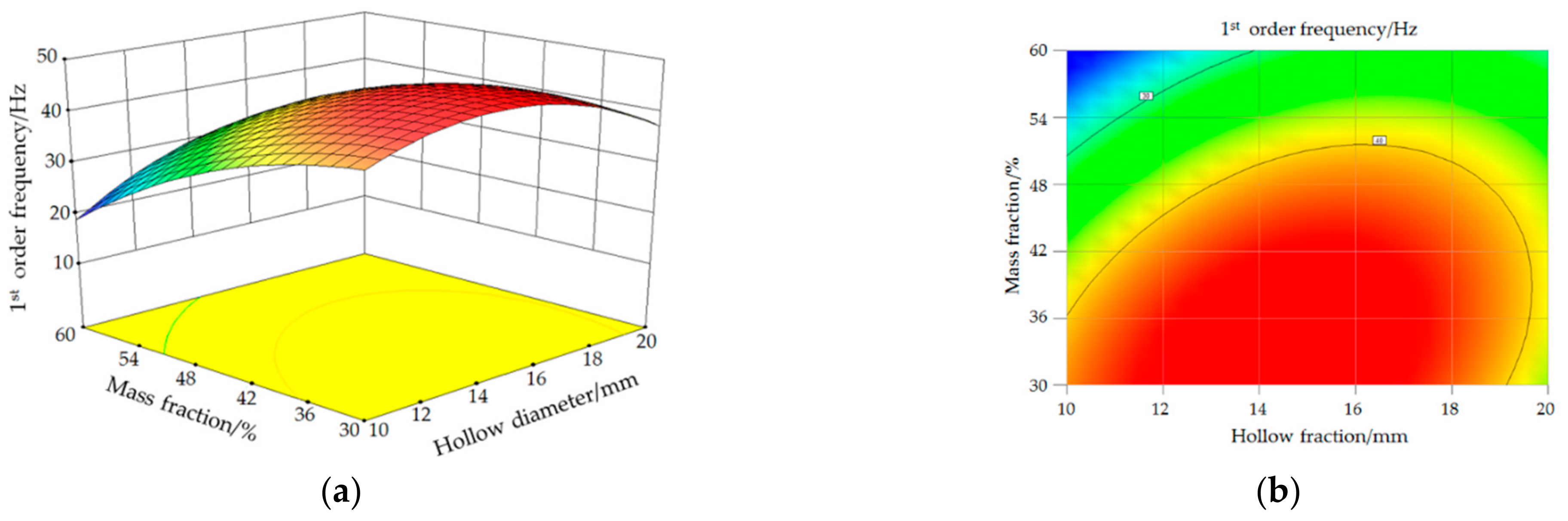
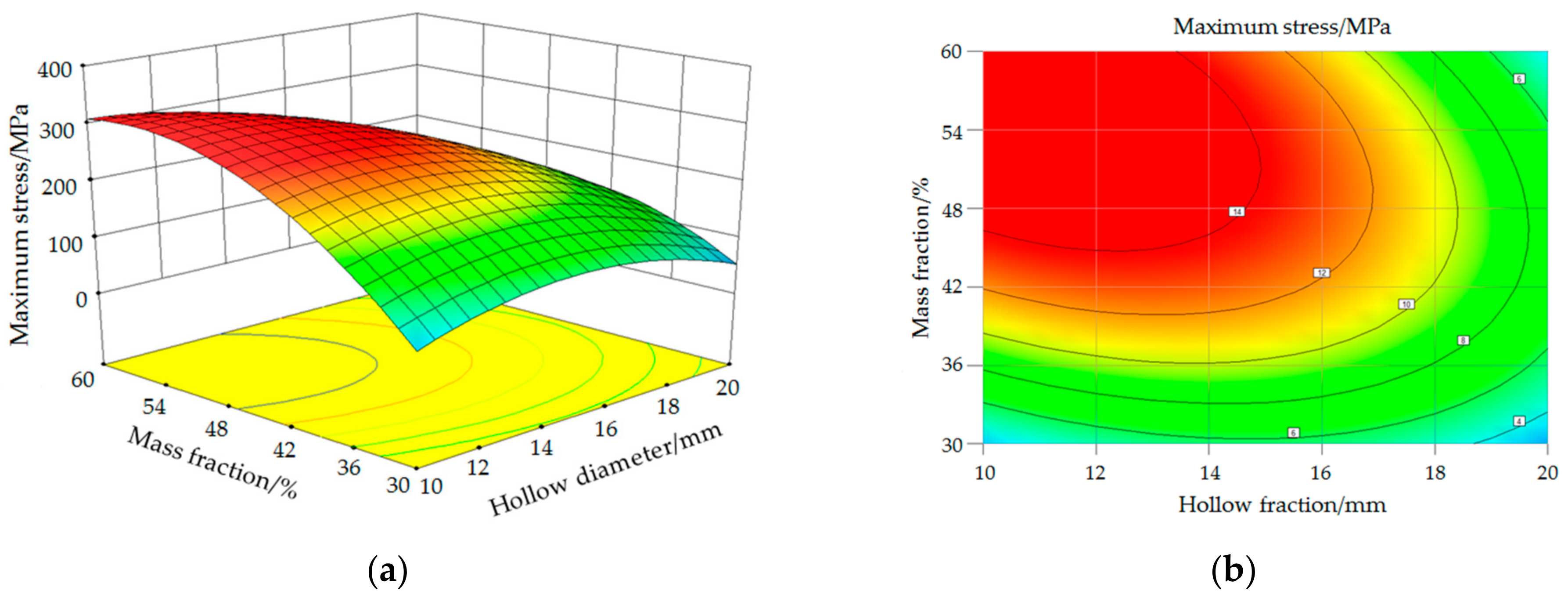
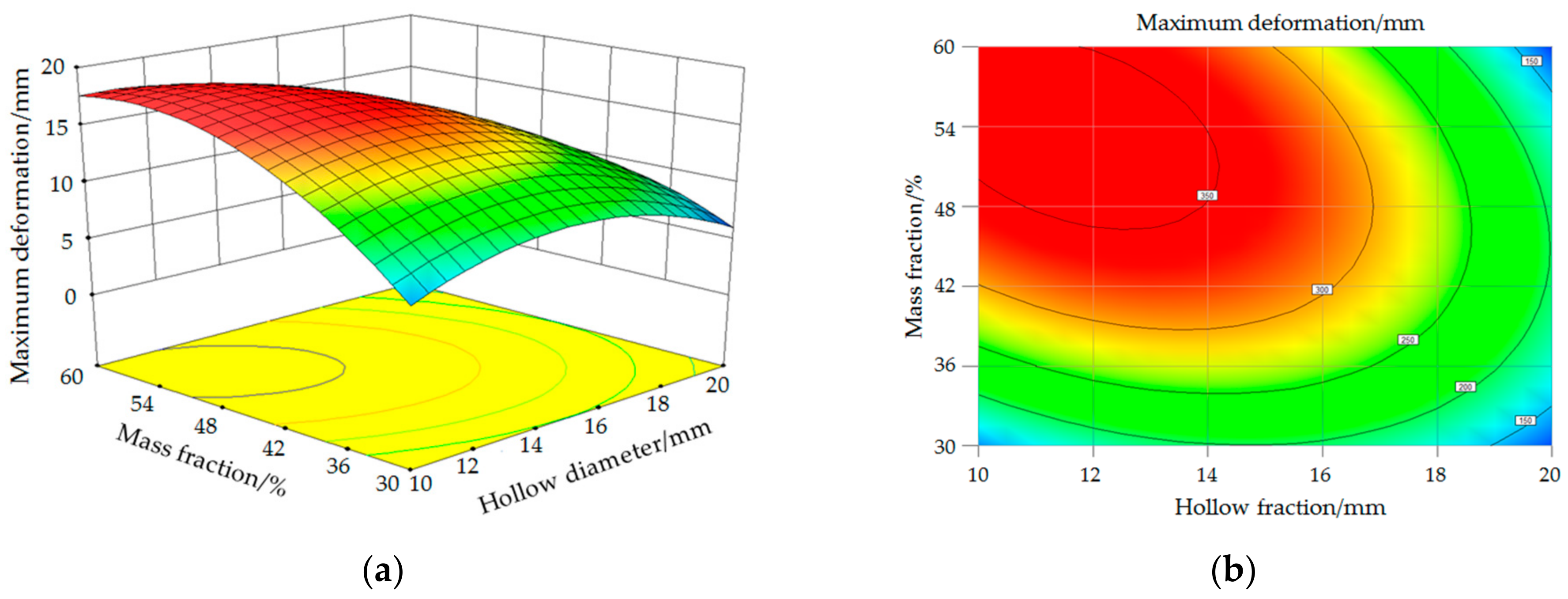
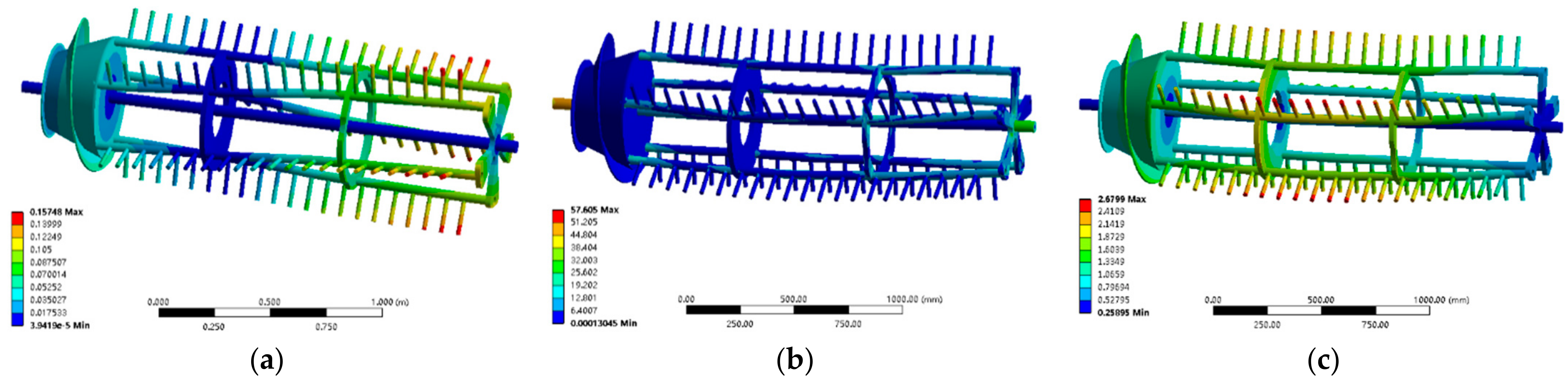
3.3. Analysis of the Results of Optimization Design
3.4. Analysis of Results of Threshing Cylinder Characteristics after Optimization
3.4.1. Finite Element Analysis Results of Threshing Cylinder after Optimization
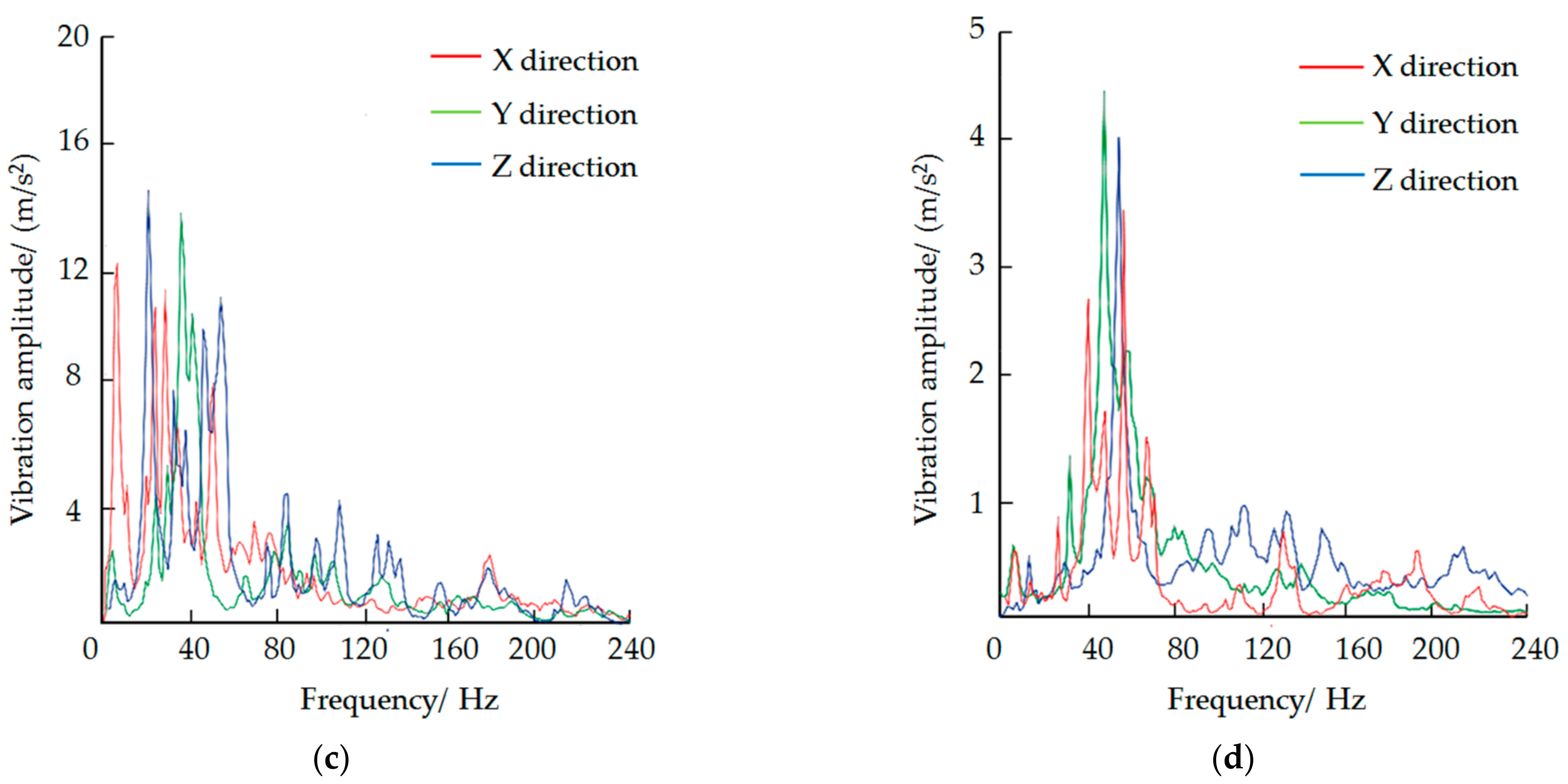
3.4.2. Comparative Analysis Results of Field Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choe, J.S.; Inoue, E.; Hashiguchi, K. Development of design theory on the tooth arrangement and the threshing drum for a large-sized and high-speed head-feeding combine. J. Fac. Agric. Kyushu Univ. 2000, 44, 377–384. [Google Scholar] [CrossRef]
- Kumar, A.; Mohan, D.; Patel, R.; Varghese, M. Development of grain threshers based on ergonomic design criteria. Appl. Ergon. 2002, 33, 503–508. [Google Scholar] [CrossRef]
- Su, Z.; Li, Y.; Dong, Y.; Tang, Z.; Liang, Z. Simulation of rice threshing performance with concentric and non-concentric threshing gaps. Biosyst. Eng. 2020, 197, 270–284. [Google Scholar] [CrossRef]
- Qian, Z.; Jin, C.; Zhang, D. Multiple frictional impact dynamics of threshing process between flexible tooth and grain kernel. Comput. Electron. Agric. 2017, 141, 276–285. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, C.; Li, H.; Qi, X.; Xiao, X.; Shi, X. Movement rules and screening characteristics of rice-threshed mixture separation through a cylinder sieve. Comput. Electron. Agric. 2018, 154, 320–329. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, Y.; Tang, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Xu, L.; Zhao, Z.; Tang, Z. Optimum design of an array structure for the grain loss sensor to upgrade its resolution for harvesting rice in a combine harvester. Biosyst. Eng. 2017, 157, 24–34. [Google Scholar] [CrossRef]
- Yao, Y.; Song, Z.; Du, Y.; Zhao, X.; Mao, E.; Liu, F. Analysis of vibration characteristics and its major influenced factors of header for corn combine harvesting machine. Trans. Chin. Soc. Agric. Eng. 2017, 33, 40–49. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.H. Experimental modal analysis and vibration monitoring of cutting tool support structure. Int. J. Mech. Sci. 1995, 37. [Google Scholar] [CrossRef]
- Komeili, M.; Menon, C. Resonance vibration of a thermally-actuated optical fiber with arbitrary periodic excitation: Analysis and optimization. Int. J. Mech. Sci. 2017, 123, 287–296. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Xu, L.; Hu, B.; Wang, R. Structural parameter optimization of combine harvester cutting bench. Trans. Chin. Soc. Agric. Eng. 2014, 30, 30–37. [Google Scholar] [CrossRef]
- Xie, X.; Ren, M.; Zhu, Y.; Zhang, Z. Simulation and experiment on lateral vibration transmission control of a shafting system with active stern support. Int. J. Mech. Sci. 2020, 170. [Google Scholar] [CrossRef]
- Viehmann, A.; Rinderknecht, S. Investigation of the driving comfort of the DE-REX powertrain based on vehicle measurements. IFAC-PapersOnLine 2019, 52, 103–108. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, L.; Ren, Y.; Li, Y.; Xiong, Z. Multi-objective optimization of active suspension system in electric vehicle with In-Wheel-Motor against the negative electromechanical coupling effects. Mech. Syst. Signal Process. 2019, 116, 545–565. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Taghizadeh-Alisaraei, A. Analysis of annoying shocks transferred from tractor seat using vibration signals and statistical methods. Comput. Electron. Agric. 2017, 141, 160–170. [Google Scholar] [CrossRef]
- Qin, W.; Shangguan, W.B.; Luo, G.; Xie, Z. A method for estimating mount isolations of powertrain mounting systems. J. Sound Vib. 2018, 426, 278–295. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Shuai, C.G.; Wang, F. Time-domain filtered-x-Newton narrowband algorithms for active isolation of frequency-fluctuating vibration. J. Sound Vib. 2016, 367, 1–21. [Google Scholar] [CrossRef]
- Elhewy, A.M.H.; Hassan, A.M.A.; Ibrahim, M.A. Weight optimization of offshore supply vessel based on structural analysis using finite element meth od. Alexandria Eng. J. 2016, 55, 1005–1015. [Google Scholar] [CrossRef][Green Version]
- Anthony, D.K.; Elliott, S.J. On reducing vibration transmission in a two-dimensional cantilever truss structure using geometric optimization and active vibration control techniques. J. Acoust. Soc. Am. 2001, 110, 1191–1194. [Google Scholar] [CrossRef]
- Sharafi, P.; Teh, L.H.; Hadi, M.N.S. Shape optimization of thin-walled steel sections using graph theory and ACO algorithm. J. Constr. Steel Res. 2014, 101, 331–341. [Google Scholar] [CrossRef]
- Rozvany, G.I.N. Topological optimization of grillages: Past controversies and new directions. Int. J. Mech. Sci. 1994, 36, 495–512. [Google Scholar] [CrossRef]
- Zhou, P.; Du, J.; Lü, Z. Simultaneous topology optimization of supporting structure and loci of isolators in an active vibration isolation system. Comput. Struct. 2018, 194, 74–85. [Google Scholar] [CrossRef]
- Van hoorickx, C.; Sigmund, O.; Schevenels, M.; Lazarov, B.S.; Lombaert, G. Topology optimization of two-dimensional elastic wave barriers. J. Sound Vib. 2016, 376, 95–111. [Google Scholar] [CrossRef]
- Rong, J.H.; Xie, Y.M.; Yang, X.Y.; Liang, Q.Q. Topology optimization of structures under dynamic response constraints. J. Sound Vib. 2000, 234, 177–189. [Google Scholar] [CrossRef]
- Park, J.; Wang, S. Noise reduction for compressors by modes control using topology optimization of eigenvalue. J. Sound Vib. 2008, 315, 836–848. [Google Scholar] [CrossRef]
- Maeda, Y.; Nishiwaki, S.; Izui, K.; Yoshimura, M.; Matsui, K.; Terada, K. Structural topology optimization of vibrating structures with specified eigenfrequencies and eigenmode shapes. Int. J. Numer. Methods Eng. 2006, 67, 597–628. [Google Scholar] [CrossRef]
- Wang, J.; Tang, H.; Zhou, W.; Yang, W.; Wang, Q. Improved design and experiment on pickup finger precision seed metering device. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2015, 46, 68–76. [Google Scholar] [CrossRef]
- Aenlle, M.L.; Brincker, R. Modal scaling in operational modal analysis using a finite element model. Int. J. Mech. Sci. 2013, 76, 86–101. [Google Scholar] [CrossRef]
- Petyt, M.; Lim, S.P. Finite element analysis of the noise inside a mechanically excited cylinder. Int. J. Numer. Methods Eng. 1978, 13, 109–122. [Google Scholar] [CrossRef]
- Laurent, C.; Bauerheim, M.; Poinsot, T.; Nicoud, F. A novel modal expansion method for low-order modeling of thermoacoustic instabilities in complex geometries. Combust. Flame 2019, 206, 334–348. [Google Scholar] [CrossRef]
- Nahvi, H.; Jabbari, M. Crack detection in beams using experimental modal data and finite element model. Int. J. Mech. Sci. 2005, 47, 1477–1497. [Google Scholar] [CrossRef]
- Datta, N.; Verma, Y. Analytical scrutiny and prominence of beam-wise rigid-body modes in vibration of plates with translational edge restraints. Int. J. Mech. Sci. 2018, 135, 124–132. [Google Scholar] [CrossRef]
- Sharifnia, M.; Akbarzadeh, A. A constrained assumed modes method for solution of a new dynamic equation for an axially moving beam. Comput. Math. Appl. 2016, 72, 2167–2180. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Karney, B.W.; Wang, Z.; Zhai, L. Virtual testing for modal and damping ratio identification of submerged structures using the PolyMAX algorithm with two-way fluid-structure Interactions. J. Fluids Struct. 2015, 54, 548–565. [Google Scholar] [CrossRef]
- Yao, Y.; Du, Y.; Zhu, Z.; Mao, E.; Song, Z. Vibration characteristics analysis and optimization of corn combine harvester frame using modal analysis method. Trans. Chin. Soc. Agric. Eng. 2015, 31, 46–53. [Google Scholar] [CrossRef]
- Jiang, Y.; Liao, Y.; Qin, C.; Guan, Z.; Liao, Q. Vibration analysis and improvement for frame of 4SY-2.9 typed rape windrower. Trans. Chin. Soc. Agric. Eng. 2017, 33, 53–60. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, Z.; Li, Y.; Wang, L. A research on the design of low-noise oil-pan based on FEM and BEM. Automot. Eng. 2013, 35, 364–368. [Google Scholar]
- Shu, G.; Liang, X. Identification of complex diesel engine noise sources based on coherent power spectrum analysis. Mech. Syst. Signal Process. 2007, 21, 405–416. [Google Scholar] [CrossRef]
- Jang, G.H.; Seo, C.H.; Lee, H.S. Finite Element Modal Analysis of an HDD Considering the Flexibility of Spinning Disk-Spindle, Head-Suspension-Actuator and Supporting Structure. In Proceedings of the Microsystem Technologies, Besançon, France, 7–9 June 2007; Volume 13, pp. 837–847. [Google Scholar]
- Ebrahimi, R.; Mirdamadi, H.R.; Ziaei-Rad, S. Operational modal analysis and fatigue life estimation of a chisel plow arm under soil-induced random excitations. Meas. J. Int. Meas. Confed. 2018, 116, 451–457. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Du, X.; Song, J.; Wang, J.; Zhang, F. Filling performance analysis and verification of cell-belt rice precision seed-metering based on friction and repeated filling principle. Trans. Chin. Soc. Agric. Eng. 2019, 35, 29–36. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Song, J.; Li, Y.; Ma, T. Experiment and discrete element model of rice seed based on 3D laser scanning. Trans. Chin. Soc. Agric. Eng. 2016, 32, 294–300. [Google Scholar] [CrossRef]
- Ariduru, S. Fatigue Life Calculation by Rainflow Cycle Counting Method. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2004. [Google Scholar]
- Gao, Z.; Xu, L.; Li, Y.; Wang, Y.; Sun, P. Vibration measure and analysis of crawler-type rice and wheat combine harvester in field harvesting condition. Trans. Chin. Soc. Agric. Eng. 2017, 33, 48–55. [Google Scholar] [CrossRef]
- Fraczek, J.; Złobecki, A.; Zemanek, J. Assessment of angle of repose of granular plant material using computer image analysis. J. Food Eng. 2007, 83, 17–22. [Google Scholar] [CrossRef]
- Wan, L.X.; Wu, J.; Shangguan, W.B. Modeling of dynamic properties for hydraulic engine mounts and optimized vibration control method of powertrain mounting systems. J. Vib. Shock 2008, 27, 4–7, 35. [Google Scholar] [CrossRef]
- Wang, C.Y.; He, L.; Li, Y.; Shuai, C.G. A multi-reference filtered-x-Newton narrowband algorithm for active isolation of vibration and experimental investigations. Mech. Syst. Signal Process. 2018, 98, 108–123. [Google Scholar] [CrossRef]
- Fukushima, T.; Inoue, E.; Mitsuoka, M.; Okayasu, T.; Sato, K. Collision vibration characteristics with interspace in knife driving system of combine harvester. Eng. Agric. Environ. Food 2012, 5, 115–120. [Google Scholar] [CrossRef]
- Feng, T.; Bakshi, S.; Gu, Q.; Yan, Z.; Chen, D. Design optimization of bottom-hole assembly to reduce drilling vibration. J. Pet. Sci. Eng. 2019, 179, 921–929. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Zhu, X.; Ma, S. Rotational speed control of threshing cylinder of oil sunflower combine harvester based on active disturbance rejection controller-dynamic matrix predictive. Trans. Chin. Soc. Agric. Eng. 2019, 35, 9–16. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| Overall dimension/(mm × mm × mm) | 5130 × 2470 × 2750 |
| Rated power/(kW) | 75 |
| Track width/(mm) | 450 |
| Header width/(mm) | 2000 |
| Ground clearance of chassis/(mm) | 672 |
| Threshing cylinder/(mm × mm) | Φ620 × 1960 |
| Sieve/(m2) | 1.24 |
| Reel diameter/(mm) | Φ900 |
| Feed rate/(t/h) | 16.2 |
| Working speed/(km/h) | 0~4.8 |
| Parameter | Values |
|---|---|
| Cylinder outer diameter/(mm × mm) | Φ620 × 1960 |
| Separating bar/(mm × mm) | Φ30 × 1800 |
| Nail tooth/(mm × mm) | Φ14 × 60 |
| Nail tooth spacing/(mm) | 40 |
| Fixing plate/(mm × mm) | Φ500 × 12 |
| Axis/(mm × mm) | Φ45 × 2150 |
| Order | Instrument | Parameter |
|---|---|---|
| 1 | Computer | / |
| 2 | INV3018C 8-channel 24-bit high precision data acquisition instrument | Parallel channel: 8 Maximum sampling frequency: 102.4 kHz A/D resolution: 24 bits |
| 3 | LC-2D force hammer | Measuring range: 0–2 kHz Charge reference sensitivity: 4 pC/N Linearity: <1% |
| 4 | AY100I piezoelectric acceleration sensor | Sensitivity: 100 mV/g Maximum frequency: 10,000 Hz Resolution: 0.0002 |
| 5 | DASP-10 Modal analysis system | / |
| Level | Hollow Diameter x1/mm | Mass Fraction x2/% |
|---|---|---|
| −1.414 | 8 | 23.8 |
| −1 | 10 | 30 |
| 0 | 15 | 45 |
| 1 | 20 | 60 |
| Material | Poisson Ratio | Shear Modulus/MPa | Density/kg·m−3 | Restitution Coefficient | Static Friction Coefficient | Dynamic Friction Coefficient |
|---|---|---|---|---|---|---|
| Grain | 0.33 | 2.60 | 1350 | 0.26 (Grain–Grain) | 0.93 (Grain–Grain) | 0.01 (Grain–Grain) |
| 0.23 (Grain–Straw) | 0.80 (Grain–Straw) | 0.01 (Grain–Straw) | ||||
| Straw | 0.42 | 1.00 | 100 | 0.20 (Straw–Straw) | 0.85 (Straw–Straw) | 0.01 (Straw–Straw) |
| 0.30 (Straw–Threshing cylinder) | 0.76 (Straw–Threshing cylinder) | 0.01 (Straw–Threshing cylinder) | ||||
| Threshing cylinder | 0.30 | 700 | 7850 | 0.50 (Grain–Threshing cylinder) | 0.52 (Grain–Threshing cylinder) | 0.01 (Grain–Threshing cylinder) |
| Order | Finite Element Free Modal Analysis | Modal Test | Error/% | ||
|---|---|---|---|---|---|
| Calculation Frequency/Hz | Modal Shape | Test Frequency/Hz | Modal Shape | ||
| 1 | 37.94 | Overall bending | 38.26 | Consistent | 0.84 |
| 2 | 45.38 | Overall bending | 44.10 | Consistent | 2.90 |
| 3 | 70.09 | Bending of separating bar and nail teeth deformation | 69.37 | Consistent | 1.04 |
| 4 | 93.87 | Overall bending | 98.45 | Consistent | 4.65 |
| 5 | 108.89 | Overall bending | 111.06 | Consistent | 1.95 |
| 6 | 133.71 | Overall torsion | 140.23 | Consistent | 4.65 |
| Rotating Parts | Speed/(r/min) | Theoretical Excitation Frequencies/(Hz) |
|---|---|---|
| Engine | 2200–2400 | 36.67–40 |
| Fan | 1050 | 17.50 |
| Tilt conveyor axis | 800 | 13.33 |
| Sieve axis | 450 | 7.50 |
| Screw pusher | 230 | 3.83 |
| Reel | 60 | 1.00 |
| Order | Test Factors | Performance Measures | |||
|---|---|---|---|---|---|
| Hollow Diameter x1/mm | Mass Fraction x2/% | First-Order Natural Frequency y1/Hz | Maximum Stress y2/MPa | Maximum Deformation y3/mm | |
| 1 | −1 (10) | −1 (30) | 43.64 | 107.32 | 2.37 |
| 2 | 1 (20) | −1 | 36.29 | 120.48 | 2.64 |
| 3 | 1 | −1 | 21.34 | 310.85 | 13.98 |
| 4 | 1 | 1 (60) | 29.68 | 106.43 | 2.97 |
| 5 | −1.414 (8) | 0 (45) | 24.15 | 321.40 | 13.23 |
| 6 | 1.414 (22) | 0 | 33.38 | 104.15 | 3.55 |
| 7 | 0 | −1.414 (23.8) | 44.90 | 112.66 | 0.36 |
| 8 | 0 | 1.414 (66.2) | 22.66 | 274.13 | 10.92 |
| 9 | 0 | 0 | 43.93 | 330.78 | 13.51 |
| 10 | 0 | 0 | 44.18 | 332.60 | 13.41 |
| 11 | 0 | 0 | 43.90 | 327.31 | 12.95 |
| 12 | 0 | 0 | 43.74 | 324.90 | 13.36 |
| 13 | 0 | 0 | 43.97 | 338.46 | 13.22 |
| 14 | 0 | 0 | 42.62 | 332.07 | 12.89 |
| 15 | 0 | 0 | 43.58 | 323.56 | 13.47 |
| 16 | 0 | 0 | 44.28 | 331.85 | 13.33 |
| Index | Source of Variance | Sum of Squares | Degree of Freedom | Mean Square Value | F-Value | p-Value |
|---|---|---|---|---|---|---|
| y1 | Model | 1120.93 | 5 | 224.19 | 89.10 | <0.0001 |
| Residual | 25.16 | 10 | 2.52 | |||
| Deviance | 23.29 | 3 | 7.76 | 29.06 | 0.0003 | |
| Error | 1.87 | 7 | 0.27 | |||
| y2 | Model | 152,700 | 5 | 30,545.74 | 55.25 | <0.0001 |
| Residual | 5528.31 | 10 | 552.83 | |||
| Deviance | 5367.24 | 3 | 1789.08 | 77.75 | <0.0001 | |
| Error | 161.07 | 7 | 23.01 | |||
| y3 | Model | 401.09 | 5 | 80.22 | 110.84 | <0.0001 |
| Residual | 7.24 | 10 | 0.72 | |||
| Deviance | 6.86 | 3 | 2.29 | 42.32 | <0.0001 | |
| Error | 0.38 | 7 | 0.054 |
| Peak Point | Measuring Point A | Peak Point | Measuring Point B | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X Direction | Y Direction | Z Direction | X Direction | Y Direction | Z Direction | ||||||||
| Frequency/Hz | Amplitude/(m/s2) | Frequency/Hz | Amplitude/(m/s2) | Frequency/Hz | Amplitude/(m/s2) | Frequency/Hz | Amplitude/(m/s2) | Frequency/Hz | Amplitude/(m/s2) | Frequency/Hz | Amplitude/(m/s2) | ||
| P1 | 112.50 | 15.42 | 42.86 | 16.18 | 72.15 | 18.00 | V1 | 8.15 | 12.18 | 40.02 | 13.98 | 20.54 | 15.22 |
| P2 | 119.46 | 12.80 | 55.40 | 10.20 | 28.60 | 16.85 | V2 | 38.27 | 11.23 | 42.75 | 10.20 | 52.20 | 10.18 |
| P3 | 76.45 | 9.06 | 48.92 | 9.76 | 45.26 | 15.57 | V3 | 32.80 | 10.15 | 38.27 | 5.60 | 43.63 | 9.12 |
| P4 | 185.00 | 7.48 | 120.10 | 5.12 | 40.20 | 11.44 | V4 | 50.58 | 8.67 | 83.00 | 3.85 | 32.06 | 7.75 |
| P5 | 20.40 | 6.15 | 100.53 | 4.83 | 42.55 | 9.80 | V5 | 20.00 | 5.80 | 100.25 | 2.27 | 38.70 | 6.96 |
| Q1 | 25.37 | 3.76 | 40.28 | 3.00 | 45.69 | 3.86 | W1 | 50.27 | 3.40 | 60.34 | 4.43 | 60.00 | 3.96 |
| Q2 | 52.70 | 2.88 | 83.65 | 0.66 | 56.80 | 2.27 | W2 | 40.00 | 2.76 | 68.70 | 2.31 | 112.55 | 1.02 |
| Q3 | 45.48 | 2.36 | 96.57 | 0.44 | 59.44 | 2.10 | W3 | 43.25 | 1.72 | 38.68 | 1.33 | 135.28 | 0.94 |
| Q4 | 38.55 | 1.86 | 76.84 | 0.37 | 113.20 | 1.17 | W4 | 70.58 | 1.46 | 71.25 | 1.17 | 150.30 | 0.77 |
| Q5 | 40.00 | 1.57 | 117.90 | 0.32 | 117.58 | 1.00 | W5 | 74.20 | 1.05 | 82.50 | 0.84 | 103.65 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xu, C.; Xu, Y.; Qi, X.; Liu, Z.; Tang, H. Vibration Analysis and Parameter Optimization of the Longitudinal Axial Flow Threshing Cylinder. Symmetry 2021, 13, 571. https://doi.org/10.3390/sym13040571
Wang J, Xu C, Xu Y, Qi X, Liu Z, Tang H. Vibration Analysis and Parameter Optimization of the Longitudinal Axial Flow Threshing Cylinder. Symmetry. 2021; 13(4):571. https://doi.org/10.3390/sym13040571
Chicago/Turabian StyleWang, Jinwu, Changsu Xu, Yanan Xu, Xin Qi, Ziming Liu, and Han Tang. 2021. "Vibration Analysis and Parameter Optimization of the Longitudinal Axial Flow Threshing Cylinder" Symmetry 13, no. 4: 571. https://doi.org/10.3390/sym13040571
APA StyleWang, J., Xu, C., Xu, Y., Qi, X., Liu, Z., & Tang, H. (2021). Vibration Analysis and Parameter Optimization of the Longitudinal Axial Flow Threshing Cylinder. Symmetry, 13(4), 571. https://doi.org/10.3390/sym13040571












