Abstract
Current approach to space-time coupling (STC) phenomena is given together with a complementary version of the STC concept that emphasizes the finiteness of the energy of the considered pulses. Manifestations of STC are discussed in the framework of the simplest exact localized solution of Maxwell’s equations, exhibiting a “collapsing shell”. It falls onto the center, continuously deforming, and then, having reached maximum compression, expands back without losing energy. Analytical solutions describing this process enable to fully characterize the field in space-time. It allowed to express energy density in the center of collapse in the terms of total pulse energy, frequency and spectral width in the far zone. The change of the pulse shape while travelling from one point to another is important for coherent control of quantum systems. We considered the excitation of a two-level system located in the center of the collapsing EM (electromagnetic) pulse. The result is again expressed through the parameters of the incident pulse. This study showed that as it propagates, a unipolar pulse can turn into a bipolar one, and in the case of measuring the excitation efficiency, we can judge which of these two pulses we are dealing with. The obtained results have no limitation on the number of cycles in a pulse. Our work confirms the productivity of using exact solutions of EM wave equations for describing the phenomena associated with STC effects. This is facilitated by rapid progress in the search for new types of such solutions.
1. Introduction
Emergence and development of ultrashort laser pulses [1,2] and ultrafast optics technology [3] stimulated the interest of researchers to laser pulses with the duration equal to few, one and even less periods of electromagnetic field [4,5,6,7]. Production, characterization and manipulation with these pulses are required by many applications in various branches of physics, chemistry, biology and medicine [8,9]. At the very beginning of the era of ultra-fast optics, it turned out that temporal pulse shaping changes its spatial spectrum (see for example [10] and references herein). In other words, it is not possible to control a beam in space and time independently. This is a manifestation of a linear optical effect, which is present not only in a dispersive medium, but also in empty space, and is called space-time coupling (STC).
STC is a fundamental property of real coherent EM beams. However, for pulses containing many periods of the field, STC is not important and is difficult to observe, whereas it is very important for few cycle pulses. Due to the wide range of research on ultrafast optics numerous papers, books and tutorials are devoted to STC. They often employ quite different and conflicting approaches to explanation and simulation of STC phenomenon.
This paper discusses two issues in which STC plays an important role. The first is what is the maximum energy density achieved in the center of a collapsing EM beam? The second: What is the efficiency of energy transfer of such a beam to a two-state quantum-mechanical system placed in the center? As was already mentioned above, STC is a very general property and therefore we use exact solutions of EM wave equations as a natural and reliable basis for STC theory and simulation. The results are valid for pulses of any duration from quasi-monochromatic to sub-period.
2. Materials and Methods
2.1. What Does the Concept of Spatio-Temporal Couplings Mean in the Theory of EM Waves?
Google Scholar indexes about twenty thousand papers on spatio-temporal couplings in EM pulses.
However, there is no generally accepted definition of the term (Wikipedia does not contain the article on this subject) and various authors explain it in different ways, for example: (a) in the language of formulas, it is said that the electric field of a beam cannot be represented by the product of functions of spatial and temporal coordinates [11] and (b) a beam whose temporal or spectral properties depend on space, or vice versa, is said to exhibit spatio-temporal couplings [12].
Our STC concept is closer to (b) and can be briefly formulated as follows: Any real pulse, that is, having a finite energy and obeying the equations of electromagnetic waves, has a temporal form that depends on coordinates, and its spatial forms are constantly changing. Such coupled variability is as fundamental property of EM pulses as the conservation laws of classical invariants: Energy, momentum, angular momentum, spin and Zeldovich invariants [13,14,15,16,17].
The most obvious consequence of STC is transformation of the temporal shape during travelling of a few cycle or subcycle beam. This is important in such problems as achievement of extreme laser field intensities [18] and manipulation of quantum systems with laser radiation [19,20]. It is easy to be convinced that plane waves and Gaussian beams cannot be used to simulate STC in these (and other) problems, as their energy is infinite. Fourier optics and superpositions of plane waves or Gaussian beams can be used. This certainly complicates the modeling [10].
At the same time, in the last three decades, the study of analytical solutions of Maxwell’s equations describing localized electromagnetic waves began, also largely due to the needs of ultrafast optics. They can be found in [4,13,18,21,22,23,24,25].
As is known [26,27], any EM wave can be constructed from linear transformations of solutions of the scalar wave equation:
However, formulas for exact solutions of Equation (1), as well as for Maxwell’s equations, are often rather complicated. Their study can be an independent task.
Nevertheless, the scalar wave equation allows us to explain the STC principle. In the case of spherical symmetry, Equation (1) takes the form:
Its solutions are traveling spherical waves [28]:
where is an arbitrary, fast-decreasing function. Their linear combination
has no singularity at [29,30] and can be used to construct the exact solution of Maxwell’s equations [24,31].
As is seen the scalar wave (4) describes a collapsing spherical shell, which is falling onto the center and then expanding back. This is a direct demonstration of the STC principal. Indeed, firstly, the variables and cannot be separated in two factors, with the product equal to Then, at each point while changes from to , the wave is continuously transformed from an incoming to an outcoming (reflected from the center) wave. As a result, the temporal shape strongly depends on the radius , giving at the center ():
For example, if , the pulse shape is a sequence of two bunches, incident (positive) and reflected (negative), separated at by an interval
If the radius is reduced, the shape of both bunches will change, and at the center the pulse (4) is transformed into (5). Then the interval is reduced to . The above scenario is illustrated in Figure 1 and is generally preserved for a vector field, but the calculations become more cumbersome. In the next Section, following [24,31], we present the results for the field of the simplest electromagnetic pulse corresponding to (4).
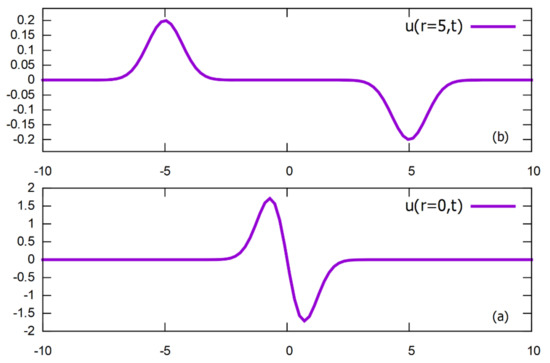
Figure 1.
(a) is the function and (b) is the function , if . Horizontally, the value of , vertically— in arbitrary units.
2.2. Exact Solutions of Free Space Electromagnetic Wave Equations with Finite Total Energy
Electromagnetic wave constructed from arbitrary solution of scalar wave Equation (1) has the following field structure (elementary derivation of (7) is given in [24,31] if we make the replacement , corresponding to duality transformation):
where is an arbitrary axial unit vector. If is spherically symmetric and has the form (4), expressions (7) demonstrate a collapsing vector electromagnetic pulse, which is very similar to a collapsing scalar shell, considered in the previous section. They are greatly simplified in near and far zones. In the far zone, when and ( is of the order of the pulse length) the pulse has the form of incoming wave falling onto the center:
where
In the center of the collapse zone, at the electric and magnetic wavefields are deduced from (7) and give:
Comparison of the fields in the near (11), (12) and far (8), (9) zones convincingly demonstrates STC. First, in the center, in contrast to (8), (9), only the electric field is nonzero and, secondly, its time dependence does not coincide with the shape of the incident beam and is transformed into its time derivative.
Knowing the fields, one can use the general formulas [27] to determine the electromagnetic energy density and then the total pulse energy [22,24,31]:
which, naturally, does not depend on time. The convergence of integral (13) is related to the assumption of rapid decay of the function f (x) (see (3) and (4)), which determines g(x) (see (8)–(10)).
Explicit expressions for the field of a light wave (7)–(12) allow comparing their characteristics in different regions of space. Namely, to predict the results of measuring the spectrum and shape of pulses at different positions of the detector. To do this, it is necessary to agree on the exact definitions of the compared quantities in the frequency and time domains.
Electric and magnetic fields in classical physics are real quantities. Therefore, the functions and all others proportional to them are real. In this case, physical intuition suggests the following natural definitions of pulse duration, frequency and line width [32]:
Note that (14)–(19) differ from the usual definitions of the moments of the complex Fourier transform used in quantum mechanics, and leading to the Heisenberg uncertainty relation. The difference is that 0 appears instead of as the lower frequency integration limit. As noted above, this is due to the reality of fields in classical physics. To establish the uncertainty relation, it was necessary for the first time in physics to turn to the properties of complex numbers (this circumstance was noted by D. Gabor [33]). In more detail than in this article, it is discussed in [31,32].
Thus, the field of a collapsing pulse (7), which is an exact solution of Maxwell’s equations, contains an arbitrary function , through which the total pulse energy and characteristics of its spectrum are expressed. This, along with accurate temporal and spectral characterization (14)–(19), ensures consistent accounting of STC effects.
The next two sections use a Sinusoidal–Gaussian (the word sinusoidal will be omitted in the rest of this article for brevity) function as the incident wave:
As will be seen further coefficients , and can be expressed in terms of pulse total energy and spectrum. This makes it possible to consider in a unified manner quasi-monochromatic and ultrashort pulses, including one- and sub-period.
2.3. Maximum Energy Density of a Collapsing EM Beam
Exact analytical pulse-like solutions of Maxwell’s equations are helpful for practical estimations and benchmarking the results of computer simulation as well as approximate models of EM beams widely used in many branches of physics, chemistry, biology and other fields. If we are talking about a few cycles and, often, femtosecond pulses, then STC can play a significant role. Evidently exact solutions of EM equations provide a rigorous approach to their accounting. This is demanded by various problems of ultrafast optics including formation of superstrong laser fields, for studying quantum electrodynamic effects, the use of femtosecond pulses in nonlinear optics, focusing, manipulation and control of laser radiation in the presence of spatiotemporal couplings, etc. (see [8,12,34] and references therein).
The above applies to the collapsing EM beam described by (7) and (4), especially since the latter contains an arbitrary function . It allows to estimate maximum energy density achievable with given pulse energy . The energy density at the center can be easily obtained using (11), (12):
Then dividing (21) by total pulse energy (13) yields:
Formula (22) as well as (21) and (13) is valid for arbitrary incident pulse shape function . For a Gaussian pulse shape (20) many expressions are simplified. Total energy is found by direct integration in (13):
Analysis of the time dependence for from (20) using Formula (21) shows that the maximum flux density at the center of the collapse is:
So, the energy density produced in the center of a collapsing EM pulse is proportional to the total pulse energy and depends on temporal shape of the incident pulse through parameters and , having the dimension of length. Formula (24) allows us to talk about laser beam engineering in the far zone to achieve the maximum field in the center [22].
For a quasi-monochromatic beam (with many periods of the light field), the Gaussian parameters and are evidently reduced to the central beam frequency and linewidth:
Then expression (24) takes on a simple and understandable form [31]:
where is the central wavelength. Formula (26) claims that in ultrashort pulses, with a decrease in the number of periods, an increasing fraction of the energy is concentrated in the volume . For few periods and sub-period pulses (small ), the situation must be analyzed on the basis of consistent application of definitions (14)–(19). This approach is implemented in the works [24,31].
For arbitrary number of time periods , the maximum available flux density as well as formulas for pulse shape parameters in time and frequency domains are given in the Appendix A.
2.4. Collapsing Shell: “Conventional or Strange Wave”?
In this Section, we will consider another property of the collapsing shell, which, as it turns out, goes beyond waves in free space. E.G. Bessonov in his works [35,36] published 40 and 30 years ago showed that the electric field vector of the far zone radiation produced by a charge moving in a finite space region satisfies condition (we use the letter instead of his for consistency with the works of subsequent authors):
Based on (27), he concluded that a bounded charge system cannot be a source of unipolar (single sign) waves and suggested using the value for classification of electromagnetic waves and description their properties. The waves obeying (27) he called “conventional” and the waves with (including unipolar waves) were called strange waves. Then in the same papers he considered several elementary processes to generate strange waves. This problem, especially in relation to unipolar pulses, is of fundamental and applied interest. The works [35,36] received a noticeable response in accelerator and microwave communities. Since then, several theoretical and experimental papers on e-beam and other sources of strange and unipolar waves have been published [37,38,39,40,41,42,43,44,45]. Interest in the topic increased sharply in the late 90s. Generation, application and study of unipolar pulses has become extremely relevant with the advent of the era of few cycle laser fields. The main findings of [35] were again analyzed and confirmed [46,47]. The parameter is now also used in a broader sense than the criteria given by Bessonov’s Formula (27). For characterization of strange waves which are not unipolar the authors of [48] introduced the degree of unipolarity:
Let us determine the place of the collapsing electromagnetic pulse in the above classification. Before answering the question posed in the title of the section, we note that the above-mentioned Bessonov’s works considered the radiation of a moving charge—Lienard–Wiechert potentials—the radiation field of a charge or a system of charges.
Nevertheless, it turns out that the relation is also fulfilled for an EM pulse collapsing in a vacuum. This is easy to verify by integrating in (7) over time. It leads, in accordance with (4), to the subtraction of two identical integrals. Therefore, the collapsing beam for which is a spherically symmetric function (4) also satisfies (27). So, in the above classification, this is a conventional wave.
To conclude this Section, there are two more remarks concerning Formula (27). First, it is also valid for the magnetic field of the collapsing spherical shell. Indeed, since in (7) is a time derivative, it is easy to see that the integral in (27) for , given by (7), vanishes for an arbitrary solution of the scalar wave Equation (1).
Secondly, according to Whittaker’s theorem “Only two solutions of the scalar wave equation are needed to represent an arbitrary electromagnetic field in empty space” [26,27]. The fields and are obtained as a result of the action of linear differential operators of the first order on these solutions. Hence it follows that if the solutions of the scalar wave equation that appear under the conditions of Whittaker’s theorem, or are used to construct the exact solution of Maxwell’s equations, are spherically symmetric, then the corresponding fields and satisfy condition (27). Finally, A.B. Plachenov showed that the condition (27) is satisfied by the fields of an arbitrary electromagnetic pulse if they decrease sufficiently rapidly in space and time [49]. A detailed consideration of this issue is beyond the scope of our work.
2.5. Excitation of a Two-Level Atom Placed at the Center of a Collapsing Beam
Returning to the principles of STC, discussed in Section 2.1, we can say that the manifestation of STC is a continuous change in the shape and spectrum of a propagating EM pulse. A consistent description of this effect is given by exact solutions of Maxwell’s equations corresponding to finite total pulse energy. The key words here are “finite total energy”. It is in this case that it is possible to unambiguously relate the characteristics of the EM pulse in different regions of space. For example, Formulas (24) and (26) relate the maximum energy density at the center of the collapse with the temporal shape of the pulse and its spectrum in the far zone.
As another instructive example, consider the efficiency of excitation of an atom by an EM finite-energy pulse. This formulation of the question is encountered in the problems of manipulating atoms with laser radiation that arise in chemistry, quantum optics, physics of trapped atoms and ions, trace elements and other fields [19]. The subtlety lies in the fact that the shape and spectrum of an incident pulse with a finite total energy in the far zone differs from that arriving at the point where the atom is located. This manifestation of the STC effect is again elegantly accounted for with the asymptotic expressions (8), (9) and (11), (12) of exact solution (7), (4) to Maxwell’s equations.
Let a two-level atom located at the center of the collapsing beam at be described by the probability amplitudes in the ground and excited states, so that the wave function of the atom has the form:
where and are the energies and wave functions of the system in the ground and excited states, respectively. Then the Schrödinger equation for the wave function (29) is reduced to a system of ordinary differential equations [19,50]:
where is the off-diagonal matrix element of the perturbation associated with the field of the incident electromagnetic pulse, which we take in the form:
where is the dipole moment of the atom, and is the field of the EM pulse at the point where the atom is.
Since this article deals with pulses with a finite total energy, it is clear, that
Assuming that at , the atom is in the ground state, let us consider the probability of its excitation by an EM pulse at . To do this, obviously, it is necessary to solve the system (30) with the initial conditions:
and calculate . Excitation efficiency is the ratio of the energy acquired by the atom
to the total energy of the incident pulse :
The value of naturally depends on the shape of the incident pulse , since both the numerator and denominator in (35), in accordance with (30), (31), (11) and (13), are defined in terms of .
Thus, to find the excitation efficiency , it is necessary to solve the system of equations (30) with the initial conditions (33). The explicit analytical solution of (30) is known only for several specific functions and is described by rather cumbersome expressions [19]. Therefore, in practice, one should focus on the numerical solution of problem (30) and (33). However, in the case of a weak field, the perturbation theory is valid:
and
Hence it follows that in the case of a small incident pulse energy of a collapsing pulse the excitation efficiency of an atom located in the center takes the form:
Formula (38) is obtained by substituting (11) into (31) and then into (36) and (35). It is seen that the value does not depend on the total pulse energy. It is it that can be considered a small parameter. Indeed, in accordance with (23) and (20), the total pulse energy determines the scale of the magnitude of the electromagnetic field, which is related to the perturbation theory used in deriving (37).
As in Section 2.3 (see (26)) for a Gaussian pulse (20), the excitation efficiency can be expressed in terms of the spectral parameters и of the incident pulse.
Accurate accounting of STC reveals some interesting effects for coherent pulse incident onto a quantum system. Firstly, the incident unipolar (or according to [5] half period) pulse:
after propagation to the center, as follows from Section 3 (see (11)), is transformed into one period [5] or, in terms of Section 2.2, Formula (27), conventional pulse:
Second, the presence of a quantum system at the focal point can in principle be used to unambiguously establish whether a pulse is one-period ( as in (27)) or half-period (, i.e., unipolar). To make sure of this, consider the transition amplitude (36) for small values of the transition frequency :
where is a perturbation proportional to the field acting on an atom. Accordingly, for the transition probability we obtain:
Thus, as seen from (42), the dependence of the transition probability on the resonance defect for unipolar () and conventional () pulses is fundamentally different. This difference makes it possible to judge the structure of ultrashort laser pulses. For experimental verification and usage, the quantum state engineering of trapped atomic particles developed in recent decades [51,52,53] can be proposed.
3. Results
- (a)
- The concept of space-time couplings of electromagnetic pulses is complemented by the important requirement of finiteness of total pulse energy.
- (b)
- The field of a collapsing electromagnetic beam is found in space and time basing on the exact solution of Maxwell’s equations in terms of the total energy, the spectrum and number of cycles in the incident pulse.
- (c)
- The excitation efficiency of a two-level quantum system placed in the center of a collapsing beam is found with a full account for space-time couplings.
- (d)
- The analysis showed that electromagnetic field distributions originated by solutions of scalar wave equation cannot be single sign (unipolar).
- (e)
- The method to experimentally distinguish between conventional and unipolar pulses is suggested.
4. Conclusions
STCs are usually associated with electromagnetic fields, which are described by functions with nonseparated spatial and temporal coordinates. In other words, fields that cannot be represented as the product of coordinate and temporal factors. At the same time, the opinion is often met that for practical purposes this does not matter. The latter is confirmed by wide application of plane waves, Gaussian beams, as well as fields in the form of products of the spatial and temporal (low- or sub-period) parts in various problems of laser and atomic physics, optics, including imaging and ultrafast optics. However, these approximations are not directly suitable for STC modeling. It is necessary to use functions with nonseparated spatial and temporal coordinates. Hope for the possibility of efficient and rigorous accounting of STC effects is given by exact analytical solutions of free space Maxwell’s equations. Their search and study are intensively developed after the works of R. W. Ziolkowski [54,55]. In this case, an important condition is the finiteness of the total pulse energy. A review and recent references on this subject are in [21,56,57].
In addition to the above, we consider STC as a definite property of any EM pulse possessing finite energy. This property is as fundamental, as the conservation laws of classical invariants: Total energy, momentum, angular momentum, spin and Zeldovich invariants [13,14,15,16,17]. Here it is appropriate to mention, following Bessonov, the formula of “conventional waves” (27), which says: Each of the projections of the electromagnetic field of a finite energy pulse at any point in space is a sign-variable function of time, the integral of which is zero.
The evident manifestation of STC is a continuous change in the shape and spectrum of a propagating EM pulse. This means that the space field distribution changes in time and vice versa: The observed pulse shape and spectrum change from point to point.
In this regard, if we consider the EM impulse as a material object, it is interesting to point out the discussion that has been going on for many years [58,59] around the painting “Rain, Steam and Speed—The Great Western Railway” (1844) by the brilliant English artist J.W.M. Turner, see Figure 2. It depicts [60] a steam locomotive—the fastest vehicle at the time—on the newly opened railway. “The feeling of speed is conveyed by the darker color of the locomotive in relation to the surrounding space, in which no object has a clear outline. Turner was almost not interested in the forms of the miracle of technology—the locomotive with its now seemingly old-fashioned tall pipe, he wanted to convey the movement … Lindsay [58], subtly noticed that the rapid movement of the locomotive is conveyed by the fact that it is made darker and clearer than anything else. The difference between them expresses the sequence of movement in time” [59]. Now we can assume, that depicting the most powerful and perfect technical creation in the picture, Turner, perhaps, expressed his presentiment of the physical picture of the structure of matter opening to humanity, part of which is a propagating electromagnetic pulse of finite energy, obeying the then still unknown Maxwell’s equations.

Figure 2.
“Rain, Steam and Speed—The Great Western Railway” (1844), J.W.M. Turner.
Our concept of STC naturally leads us in Section 2.3 and Section 2.5 to quantitative approach to analysis of STC effects based on exact solutions to Maxwell’s equations and accurate definitions of spectral parameters of real signals. This allows a unified description of quasi-monochromatic, few period and sub-period pulses.
In Section 2.3 and Appendix A, this approach is used for a detailed quantitative analysis of the structure of a collapsing electromagnetic shell. At the moment of collapse, in the center it takes the form of a ball, which, flying apart, again turns into a shell. Rigorous consideration of STC effects allows expressing the field at the center, including the maximum EM energy density, in terms of the frequency and linewidth of the incident radiation. In this way, it is possible to select the shape of the laser pulse in order to achieve the desired behavior of the electromagnetic field in the center.
In Section 2.5, taking STC effects into account, the efficiency of energy transfer of a collapsing electromagnetic pulse to a two-level atom located in the center is determined. In this case, the differences in the shape and spectrum of the pulse in the far and near zones can be especially important. For example, an incident half-period pulse transforms into a one-period pulse at the center, which significantly changes the excitation efficiency for a small energy level difference. This result opens the possibility of practically distinguishing between conventional and unipolar (strange) electromagnetic pulses.
Thus, there is reason to expect that the use of exact solutions of Maxwell’s equations can become an efficient, rigorous approach to the study of subtle and complex phenomena from STC to laser action on atoms and polyatomic objects. The further development of this direction will be facilitated by the search for more sophisticated and realistic exact solutions that correspond to the finite total pulse energy and thereby bring us closer to experiment.
The authors are indebted to N.V. Dyachkov, A.A. Gorbatsevich, V.I. Man’ko, A.B. Plachenov, I.E. Protsenko, I.V. Smetanin for valuable discussions and E.A. Rakhmanov, who took part in writing the Appendix A.
Author Contributions
Both authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Spectral Analysis of a Gaussian Pulse (20) Based on a “Real Signal” Definitions (14)–(19)
D. Gabor [33] and then I. Kay and R.F. Silverman [32] pointed out that the theory of the Fourier transform of complex functions and the associated Heisenberg uncertainty relation cannot be applied to the spectral analysis of classical signals that are real functions. This circumstance is critically important for ultrashort laser pulses, when the spectrum width and average frequency are comparable in magnitude. At the same time, for narrow-band signals, the effect does not manifest itself, and simpler formulas for the complex Fourier transform can be used as a rigorous approximation.
For reference, we give general formulas for pulse shape parameters in frequency () and time () domains calculated according to (14)–(19) for Gaussian function (20):
Formulas (A1)–(A6) are valid for arbitrary number N of electromagnetic field periods.
For quasi-monochromatic pulses when Formulas (A1)–(A6) easily yield (25):
whereas for sub-period pulses when one obtains:
in agreement with [31].
Now we can analyze the results of Section 2.3 in terms of physically significant and measurable quantities: Center frequency and line width (or, when convenient, N).
For example, the ratio of maximum flux density to the total pulse energy for an arbitrary number of field periods obviously follows from (23), (24) and (A1):
where . For large number of periods this yields (26).
References
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545. [Google Scholar] [CrossRef]
- Diels, J.; Rudolph, W. Ultrashort Laser Pulse Phenomena, 2nd ed.; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Weiner, A.M. Ultrafast optical pulse shaping: A tutorial review. Opt. Commun. 2011, 284, 3669–3692. [Google Scholar] [CrossRef]
- Feng, S.; Winful, H.G.; Hellwarth, R.W. Spatiotemporal evolution of focused single-cycle electromagnetic pulses. Phys. Rev. E 1999, 59, 4630. [Google Scholar] [CrossRef]
- Keldysh, L.V. Multiphoton ionization by a very short pulse. Phys. Usp. 2017, 60, 1187–1193. [Google Scholar] [CrossRef]
- Park, S.B.; Kim, K.; Cho, W.; Hwang, S.I.; Ivanov, I.; Nam, C.H.; Kim, K.T. Direct sampling of a light wave in air. Optica 2018, 5, 402–408. [Google Scholar] [CrossRef]
- Hwang, S.I.; Park, S.B.; Mu, J.; Cho, W.; Nam, C.H.; Kim, K.T. Generation of a single-cycle pulse using a two-stage compressor and its temporal characterization using a tunnelling ionization method. Sci. Rep. 2019, 9, 1613. [Google Scholar] [CrossRef] [PubMed]
- Nolte, S.; Schrempel, F.; Dausinger, F. Ultrashort Pusle Laser Technology; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar]
- Sun, H.; Fritz, A.; Dröge, G.; Neuhann, T.; Bille, J.F. Femtosecond-Laser-Assisted Cataract Surgery (FLACS). In High Resolution Imaging in Microscopy and Ophthalmology; Bille, J.F., Ed.; Springer: Cham, Switzerland, 2019; pp. 301–317. [Google Scholar]
- Frei, F.; Galler, A.; Feurer, T. Space-time coupling in femtosecond pulse shaping and its effects on coherent control. Chem. Phys. 2009, 130, 034302. [Google Scholar] [CrossRef]
- Jolly, S.W.; Gobert, O.; Quéré, F. Spatio-temporal characterization of ultrashort laser beams: A tutorial. Optica 2017, 4, 1298–1304. [Google Scholar] [CrossRef]
- Sainte-Marie, A.; Gobert, O.; Quéré, F. Controlling the velocity of ultrashort light pulses in vacuum through spatio-temporal couplings. Optica 2017, 4, 1298–1304. [Google Scholar] [CrossRef]
- Lekner, J. Theory of Electromagnetic Pulses; Morgan & Claypool Publishers: San Rafael, CA, USA, 2018. [Google Scholar]
- Zeldovich, Y.B. Number of quanta as an invariant of the classical electromagnetic field. Sov. Phys. Dokl. 1966, 10, 771. [Google Scholar]
- Bialynicki-Birula, I. Photon Wave Number. In Progress in Optics; Wolf, E., Ed.; Elsevier Science: New York, NY, USA, 1996; Volume 36, pp. 245–294. [Google Scholar]
- Feshchenko, R.M.; Vinogradov, A.V. On the number of photons in a classical electromagnetic field. J. Exp. Theor. Phys. 2018, 127, 274–278. [Google Scholar] [CrossRef]
- Feshchenko, R.M.; Vinogradov, A.V. On the number and spin of photons in classical electromagnetic fields. Phys. Scr. 2019, 94, 065501. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Korolev, K.Y.; Legkov, M.V. Exact analytical expression for the electromagnetic field in a focused laser beam or pulse. Proc. SPIE 2007, 6726, 672613. [Google Scholar]
- Shore, B.W. Manipulating of Quantum Structures with Laser Pulses; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Vitanov, N.V.; Shore, B.W. Designer evolution of quantum systems by inverse engineering. J. Phys. B At. Mol. Opt. 2016, 48, 174008. [Google Scholar] [CrossRef]
- Kiselev, A.P. Localized Light Waves: Paraxial and Exact Solutions of the Wave Equation (a Review). Opt. Spectrosc. 2007, 102, 603–622. [Google Scholar] [CrossRef]
- Gonoskov, I.; Aiello, A.; Heugel, S.; Leuchs, G. Dipole pulse theory: Maximizing the field amplitude from 4π focused laser pulses. Phys. Rew. A 2012, 86, 053836. [Google Scholar] [CrossRef]
- Hernández-Figueroa, H.E.; Zamboni-Rached, M.; Recami, E. Non-Diffracting Waves; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Artyukov, I.A.; Dyachkov, N.V.; Feshchenko, R.M.; Vinogradov, A.V. Energy density and spectrum of single-cycle and sub-cycle electromagnetic pulses. Quantum Electron. 2020, 50, 187–194. [Google Scholar] [CrossRef]
- So, I.A.; Plachenov, A.B.; Kiselev, A.P. Unidirectional Single-Cycle and Sub-Cycle Pulses. Opt. Spectrosc. 2020, 128, 2005–2006. [Google Scholar] [CrossRef]
- Bateman, H. The Mathematical Analysis of Electrical and Optical Wave-motion on the Basis of Maxwell’s Equations; Cambridge University Press: Cambridge, UK, 1915. [Google Scholar]
- Zangwill, A. Modern Electrodynamics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M.L. Solutions of Maxwell’s Equations in Free Space. In The Feynman Lectures on Physics; Addison-Wesley Pub. Co.: Boston, MA, USA, 1964; Volume 2, Chapter 20; p. 4. [Google Scholar]
- Tikhonov, A.N.; Samarskii, A.A. Equations of Mathematical Physics; Dover Publications: New York, NY, USA, 1963. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Spherical Waves. In Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987; p. 70. [Google Scholar]
- Artyukov, I.A.; Dyachkov, N.V.; Feshchenko, R.M.; Vinogradov, A.V. Collapsing EM wave—A simple model for nonparaxial, quasimonochromatic, single and half-cycle beams. Phys. Scr. 2020, 95, 064006. [Google Scholar] [CrossRef]
- Kay, I.; Silverman, R.A. On the Uncertainty Relation for Real Signals. Inf. Control 1957, 1, 64–75. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Elec. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Froula, D.H.; Palastro, J.P.; Turnbull, D.; Davies, A.; Nguyen, L.; Howard, A.; Ramsey, D.; Franke, P.; Bahk, S.-W.; Begishev, I.A.; et al. Flying focus: Spatial and temporal control of intensity for laser-based applications. Phys. Plasmas 2019, 26, 032109. [Google Scholar] [CrossRef]
- Bessonov, E.G. On a class of electromagnetic waves. Zh. Eksp. Teor. Fiz. 1981, 80, 852–858. [Google Scholar]
- Bessonov, E.G. Conventionally strange electromagnetic waves. Nucl. Instr. Meth. A 1991, 308, 135–139. [Google Scholar] [CrossRef]
- Shibata, Y.; Bessonov, E.G. Long Wavelength Broadband Sources of Coherent Radiation. arXiv 1997, arXiv:physics/9708023. [Google Scholar]
- Bratman, V.L.; Jaroszynski, D.A.; Samsonov, S.V.; Savilov, A.V. Generation of ultra-short quasi-unipolar electromagnetic pulses from quasi-planar electron bunches. Nucl. Instr. Meth. A 2001, 475, 436–440. [Google Scholar] [CrossRef]
- Alexeev, V.I.; Bessonov, E.G. Experiments on the generation of long wavelength edge radiation along directions nearly coincident with the axis of a straight section of the “Pakhra” synchrotron. NIM 2001, 173, 54–60. [Google Scholar] [CrossRef][Green Version]
- Schwarz, M.; Basler, P.; Borstel, M.V.; Müller, A.S. Analytic calculation of the electric field of a coherent THz pulse. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 050701. [Google Scholar] [CrossRef]
- Balal, N.; Bratman, V.L.; Savilov, A.V. Peculiarities of the coherent spontaneous synchrotron radiation of dense electron bunches. Phys. Plasmas 2014, 21, 023103. [Google Scholar] [CrossRef]
- Freund, F.T.; Herau, J.A.; Centa, V.A.; Scoville, J. Mechanism of unipolar electromagnetic pulses emitted from the hypocenters of impending earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 47–65. [Google Scholar] [CrossRef]
- Fedorov, V.M.; Ostashev, V.E.; Tarakanov, V.P.; Ul’yanov, A.V. High power radiators of ultra-short electromagnetic quasi-unipolar pulses. J. Phys. Conf. Ser. 2017, 830, 012020. [Google Scholar] [CrossRef]
- Naumenko, G.; Shevelev, M. First indication of the coherent unipolar diffraction radiation generated by relativistic electrons. JINST 2018, 13, C05001. [Google Scholar] [CrossRef]
- Naumenko, G.; Shevelev, M.; Popov, K.E. Unipolar Cherenkov and Diffraction Radiation of Relativistic Electrons. Phys. Part Nucl. Lett. 2020, 17, 834–839. [Google Scholar] [CrossRef]
- Kim, K.J.; McDonald, K.T.; Stupakov, G.V.; Zolotorev, M.S. A bounded source cannot emit a unipolar electromagnetic wave. arXiv 2000, arXiv:physics/0003064. [Google Scholar]
- Kim, K.J.; McDonald, K.T.; Stupakov, G.V.; Zolotorev, M.S. Comment on “Coherent Acceleration by Subcycle Laser Pulses”. Phys. Rev. Lett. 2000, 84, 3210. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, R.M.; Pakhomov, A.V.; Arkhipov, M.V.; Babushkin, I.; Tolmachev, Y.A.; Rosanov, N.N. Generation of unipolar pulses in nonlinear media. JETP Lett. 2017, 105, 408–418. [Google Scholar] [CrossRef]
- Plachenov, A.B. Paraxial beams and related solutions of the Helmholtz equation. In Proceedings of the International Conference DAYS ON DIFFRACTION, St. Petersburg, Russia, 25–29 May 2020. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, 3rd ed.; Pergamon Press: Oxford, UK, 1958. [Google Scholar]
- Jun, Y.; Kimble, H.J.; Katori, H. Quantum State Engineering and Precision Metrology Using State-Insensitive Light Traps. Science 2008, 320, 1734–1738. [Google Scholar]
- Cho, D.; Hong, S.; Lee, M.; Kim, T. A review of silicon microfabricated ion traps for quantum information processing. Micro Nano Syst. Lett. 2015, 3, 2. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Zhu, C.; Wang, Y.; Zhang, X.; Gao, K.; Zhang, W. Precision measurements with cold atoms and trapped ions. Chin. Phys. B 2020, 29, 093203. [Google Scholar] [CrossRef]
- Ziolkowski, R.W. Exact solutions of the wave equation with complex source locations. J. Math. Phys. 1985, 26, 861. [Google Scholar] [CrossRef]
- Ziolkowski, R.W. Localized Waves: Historical and Personal Perspectives. In Non-Diffracting Waves; Hernández-Figueroa, H.E., Recami, E., Eds.; John Wiley & Sons: New York, NY, USA, 2013; Chapter 2, see [23]. [Google Scholar]
- So, I.A.; Plachenov, A.B.; Kiselev, A.P. Simple unidirectional finite-energy pulses. Phys. Rev. A 2020, 102, 063529. [Google Scholar] [CrossRef]
- Zdagkas, A.; Papasimakis, N.; Savinov, V. Space-time nonseparable pulses: Constructing isodiffracting donut pulses from plane waves and single-cycle pulses. Phys. Rev. A 2020, 102, 063512. [Google Scholar] [CrossRef]
- Lindsay, J. J.M.W. Turner. His Life and Work; Cary, Adams & Mackay: London, UK, 1966. [Google Scholar]
- Nekrasova, E.A. Turner 1775–1851. Moscow, Russia. 1976. Available online: https://www.amazon.com/Nekrasova-Terner-1775-1851-Nekrasov-Turner/dp/B0718YYFZY (accessed on 22 March 2021).
- The National Gallery. Available online: https://www.nationalgallery.org.uk/paintings/joseph-mallord-william-turner-rain-steam-and-speed-the-great-western-railway (accessed on 22 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).