Abstract
A review of the mathematical and physical aspects of the Ermakov systems is presented. The main properties of Lie algebra invariants are extensively used. The two and tridimensional Ermakov systems are fully analyzed and the correspondent invariants found. Then, we go over quantization with special emphasis in the two dimensional case. An application to Nonlinear Optics is hereby developed. We also treat the so-called “one dimensional” case, which is easily solved in the classical case but offers special interest in the quantum realm, where one can find exactly the Feynman propagator. We finish with the stationary phase approximation which contains also some interesting features when compared with the exact solution. Some prospects for future research are also discussed.
1. Introduction
Determining exactly when the idea of Ermakov systems came into being remains a difficult task even today. Almost certainly the pioneer paper written by V. Ermakov in 1880 [1] is a kind of natural starting point, but even in that work, an Ermakov System lacks motivation in a well defined mathematical way. Here we have adopted a group theoretical point of view based in the conformal SO(2,1) invariance of a dynamical system whose functions depend just from the ratio of the coordinates. Relying in this point as the backbone of a definition of an Ermakov system we can do justice to both Ermakov and scientists that have done some work and contributed to this fascinating field of mathematical physics in the last 50 years.
There exist a wide range of papers dealing with the Ermakov systems. To name only a few the following references must be checked and read ([2,3,4,5,6,7]). The mentioned pieces of work deal with different generalizations and the Hamiltonian conditions of the Ermakov systems as well as the non-linear superposition techniques that may be defined in this context.
However, it seems necessary to begin with a clear definition of what an Ermakov System really is. The main idea relies on the motion of a non relativistic classical particle which always follows Newton’s Law but is not necessarily a Hamiltonian motion. Suppose that we confine ourselves to conformal motion, this means that the forces depend only upon ratios of the coordinates and not of the coordinates themselves. The most general set of forces to be included must necessarily contain the harmonic motion and an inverse cubic force because the equations of motion must be invariant under the conformal group ([8]). The geometric idea of conformal invariance is that the physical transformations depend only upon ratios of coordinates that conserve the angles instead the form of the trajectories. The natural generalization to a system of two particles reads [9]:
where
This system is not necessarily Hamiltonian but is -invariant (it shall be explicitly described in Equation (9)) and possesses the invariant quantity:
This invariant was derived by Ermakov in his original paper and generalized in a number of well-known papers (see [10,11,12,13,14]). It reduces to the inverse cubic case in one dimension just by trivially choosing:
In this case, Equation (1) will be the inverse cubic potential which we shall be treating at the end of this review, and (2) is the time dependent harmonic oscillator completely solved by Lewis and Riesenfeld in a widely-known paper (see [14]). However the equations of motion with arbitrary and still meet the requirements of being -invariant with the general Ermakov invariant given by the written in Equation (3).
In Section 2, Section 3, Section 4, Section 5 and Section 6, we shall present a review of previous result, including some of one of the authors. Ermakov systems in two and three dimensions are also considered. Section 7, Section 8 and Section 9 include original results related to aspects of quantum mechanics.
In order to establish symmetry properties of the Ermakov Systems and possible generalizations to a higher number of particles and coordinates, as well as to field theory, we move to the next section.
2. Symmetries of the Ermakov Systems
In searching for symmetries of the Ermakov system of differential equations, we just apply the Lie procedure described in well-known textbooks [15]. Let us perform the general scale transformation:
where time unavoidably scales as in order to cancel first derivatives in the equations of motion. The result of this transformation is:
If verifies the linear ordinary second order differential equation
then the system reduces to the simplified form:
The condition (4) on is not as restricted as it may seem at first sight as we shall discuss later on. Another interesting feature of the constraint is the following: Let us parametrize in the integral form:
which is called the quasilinear constraint. Simple substitution of this constraint for in (4), yields the following differential equation for :
whose general solution [10] is given by:
where and form a fundamental set of solutions of the linear Equation (4) and is the well-known Wronskian, given by:
As mentioned above, the solution of the constraint (6) in relies heavily on the solution of the constraint (4) in which is a linear differential equation. This shows that the Ermakov system is linearizable by virtue of the symmetry and its related Ermakov Invariant (3). If the Ermakov system possesses another invariant, this would make it algebraically solvable and the constraint would be uneccessary.
In looking for an additional invariant which would solve completely the mechanical problem, it is natural to look for the existence of a Hamiltonian. Remember that there is no indication whatsoever that an Ermakov system is, or should be Hamiltonian. In order to restrict ourselves to the Hamiltonian case, we should find the condition which leads an Ermakov system to posses a Hamiltonian. Taking polar coordinates in the equations of motion we have the transformation:
and then, the equations:
These equations of motion possess the set of symmetries given by the following infinitesimal generators [15]:
whose commutation relations are given by:
corresponding to the Lie group of finite transformations:
where are the parameters of the transformations. If a potential exists, it should verify that:
Using the condition:
We finally obtain that must be of the form:
if and only if the following relationship holds:
Using the above results one can easily prove that the Ermakov Invariant must read:
Or in another form:
A Hamiltonian in two dimensional polar coordinates can always be written in the general form:
Integrability is always dictated, in the Hamiltonian case, by separation of coordinates:
If , we recover the well-known case of radial symmetry with conserved angular momentum . In the case of a Hamiltonian Ermakov System, the separation of variables occurs in a very peculiar way as we deal with nonlinear differential equations. In fact, taking into account the expressions of (11) and (10), we easily see that there is a relationship among them given by:
As the functions and are arbitrary functions of , it is trivial to conclude that a Hamiltonian Ermakov System in two dimensions is always of the form:
possessing always an Ermakov Invariant:
Besides that, a Hamiltonian Invariant exists:
if and only if and satisfy:
3. Ermakov Systems in Three Dimensions
For a generalization of the Ermakov Systems to more than two spatial dimensions, we could in principle proceed in various ways [4] (see also [3]). We choose here to do it in a way which preserves the symmetry of the original dynamical system. Therefore we impose the set of equations to be invariant under the original S0(2,1) local symmetry and its natural extensions of second and third order. As a consequence of this condition, the equations must always display the general form:
In three dimensions the Ermakov Invariant does not always exist. However we can consider the case in which can be cast in the form:
Simple manipulation of (13c) leads to:
Then, an invariant can easily be constructed from (15), in the form:
Note however, that when , this invariant becomes the Ermakov Invariant (12) previously discussed in the two dimensional case. To follow this analogy we call, the generalized Ermakov Invariant. As it is expected, this is not the only Invariant than can be constructed in three dimensions. In fact, if now the conditions are:
then, from the first pair of equations of the Ermakov System, we easily obtain:
And using now the conditions (17), we arrive to:
The two dimensional limit is obtained when . The comparison between the definitions (14) and (17) yields in this case:
Thus and both invariants coalesce in just one invariant.
4. Hamiltonian Ermakov Systems in Three Dimensions
The three dimensional Ermakov system can be Hamiltonian only if:
The form of the potential necessarily is:
Taking into account all the previous statements, we are led to the unavoidable conclusion that:
So, the invariant (18) always exists if there is a generating and . If besides the equals the system is Hamiltonian and this Hamiltonian takes the form:
which clearly shows the existence of two invariants: and .
The much more restrictive condition:
yields the following Hamiltonian with three invariants: , , and :
It is natural to call the case with two invariants “Weak Ermakov System” while the case with three invariants shall be called “Strong Ermakov System”.
5. Examples of Ermakov Systems in Non-Linear Optics
The formalism just discussed will now be applied to the case of both the propagation of Gaussian light beams in nonlinear optical fibers [16] and the wave function of a Bose–Einstein condensate described for the Gross–Pitaevskii equation [17]. We shall fully develop only the first case. Suppose we set the experimental device such that the fiber goes along the -direction. The perpendicular plane to the propagation line is defined by the two coordinates and which describe the elliptical gaussian plane. The equation governing the behaviour of the beam inside the fiber is:
where is the proper frequency of vibration of the light beam and is the non-linear parameter which accounts for the interaction between the electric field of the laser beam and the fiber crystal. For elliptic gaussian beams, the form of the electric field carried by the laser is of the form:
with initial conditions given by:
In other words, the variables and are actually functions of , i.e.,
with initial conditions:
Inserting the form of the solutions and these boundary conditions into the non-linear Equation (21), we obtain the following set of equations for and :
where:
The form of the functions reads:
and the constants are defined in terms of the physical data as:
This two dimensional Ermakov System can be derived from a Hamiltonian of the form:
whilst the Ermakov Invariant remains:
It is straightforward but tedious to check that:
For reasons that will become clearer a little later, let us now proceed to define planar polar coordinates:
In these coordinates both the Invariant and the Hamiltonian take the form:
In the classical realm, it is trivial to see that the system is totally integrable as it can be reduced to quadratures. Trayectories can be obtained in various ways from the Hamiltonian expresion through quadratures involving only the radius .
6. Quantum Ermakov Systems: The Two Dimensional Case
Before going too much into detail, we would like to look for the eigenvectors and eigenvalues of the Ermakov Invariant:
In the angular coordinate representation:
since as we choose ℏ = 1,
Thus, we finally obtain for the eigenvalue equation of the Ermakov Invariant:
The range is divided into eight intervals. Although it may seem that we have many different shapes for the wells, we actually have only two classes of spectra:
.
Rounding up the interval: , we obtain Figure 1 for the equipotential lines which obviouly exhibits two axis of a discrete symmetry of the crystallographic type. One can actually identify these axis with the two () diagonals in the form shown by Figure 1.
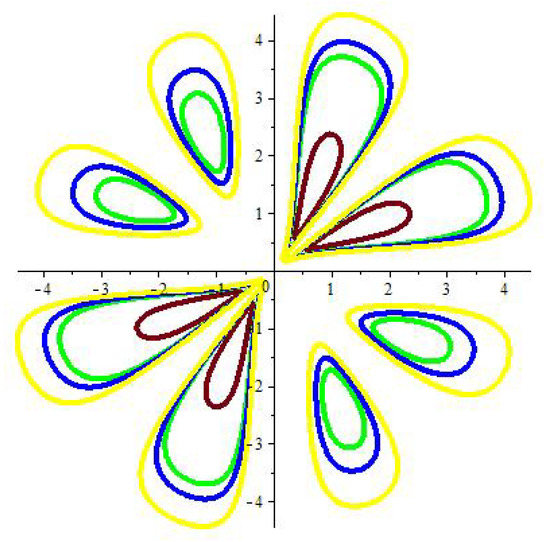
Figure 1.
{; }-axis. Equipotential curves in the Potential with at different energies. Brown E = 5, Green E = 9, Blue E = 10, and Yellow E = 12. Also and are both set to unity.
For the complete diagonalization of the Hamiltonian we proceed as follows. The energy eigenvalue equation is:
and the Hamiltonian operator has the already known form:
Since we know how to diagonalize , the states must be a direct product of two commuting operators: and .
The eigenstates of have already been found. The radial part is then reduced to:
It possesses a spectrum exactly valid for all values of the parameters and given by the expression:
and the radial wavefunctions are:
The total wavefunction is then:
7. Quantum Mechanics of the “One Dimensional” Ermakov System
In the last three sections some originals results are presented. We would like to motivate the reader by unifying all what has been said in the previous part of the review with ordinary classical and quantum mechanics of an elementary one dimensional system that retains as a symmetry the Lie Algebra and present notorious similarities with an Ermakov system in one dimension. Consider the one dimensional Schrödinger Equation. The potential is represented in Figure 2.
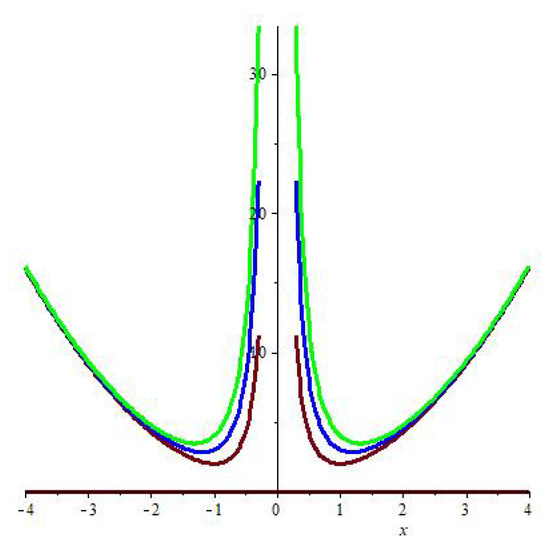
One can solve quite easily this equation. Solutions at the zero and infinity must be of the form:
We shall use henceforth some dimensions to compare them with the rest of the paper. The fundamental expressions are:
and now one obtains the following dimensionless equations for :
where has been defined as:
Let us now rewrite the equation for in the form, to be compared with the equation for the Associated Laguerre Equation:
The solution of the Associated Laguerre Equation (28) are the polynomials which take the form:
and the final normalized wave function is:
Actually it causes no surprise the similarity of these results with the ones describing the previous two dimensional case since both exhibit the -symmetry as it has been fully demonstrated and widely discussed by several authors (see references [9,18,19,20]).
8. The Feynman Propagator
As the potential exhibits a pure discrete spectrum (see Figure 2), we shall calculate the Feynman Propagator just with the help of the explicit form of its discrete eigenfunctions:
Now we shall use the Moeller Formula for the Associated Laguerre Polynomials which takes the form:
where is the Modified Bessel Function. In our case, the identification of the variables is quite straightforward:
Inserting this set of variables and constants into the propagator one obtains:
where
We have obtained the exact propagator for any value of . In fact taking the limit, one should recover the propagator of the harmonic oscillator which is a wel-kknown expression. We have only to take care of a simple fact that occurs in the index of the Modified Bessel Function. In the case the index can take two values = . For these values:
and we should take the average of these two functions:
The smooth limit for takes then the easy form
and z is:
One can finally write for the limit the expression:
which is the usual expression for the Feynman propagator of a harmonic oscillator.
9. The Stationary Phase Approximation
In this section we shall apply the method of the stationary phase approximation to the previous quantum system. One could ask themselves whether why such an approximate method should be applied to a quantum system whose exact solution is already known. The aim is to use this venerable approximation of semiclassical nature in order to compare the result with the previously exact result with the purpose of calibrate the goodness of the approximation. The classical Lagrangian is:
and the corresponding equations of motion are ():
The classical solution is easily found to be:
which for the reduces to the well-known solution of the classical harmonic oscillator:
Let us now calculate the action on the classical solution (31):
An easy but tedious calculation between the extremes and yields:
where
The action must be expressed in terms of the physical variables. That is to say in terms of {, } and the time difference . To do this we need to know as a function of the two extremes: , and also . We finally find the following expression:
Inserting (33) in the classical action (32), one clearly obtains the two following terms:
where:
and the second contribution is:
for and . trivially also is:
where the expression of is given by (33):
The interesting property of the classical action is that it is composed as the sum of very different contributions. The term is of a purely semiclassical nature. One should remember that in the limit , the action of the Harmonic Oscillator emerges solely from this term whereas the contribution (34) vanishes identically in this limit and has nothing to do with the classical limit. This leads us to consider this contribution as a purely quantal term. A numerical comparison can be made between the exact expression (29) by using for fixed values y and different values of T.
10. Conclusions
In this review we tried to unify all theoretical knowledge that is known about Ermakov Systems. Indeed many systems exhibiting the basic symmetries and properties hereby discussed can be treated along the same lines. The most remarkable example is that of Ermakov Systems of dimensions larger than three. We conjecture–with additional conditions similar to (14) and (17) in Section 4–that more weak Ermakov invariants can be found, i.e., three in the four dimensional cases, four in the five dimensional case, and so on. This hypothesis remains to be proved.
Many physical systems have appeared exhibiting the basic Ermakov properties [21]. The invariants eliminate one of the angular variables and substituting it with an Ermakov invariant. This is due to the symmetry SO(2,1) given by (8) although one should firstly to accommodate the representation of this Lie Algebra [22] to the variables of the real physical system. The important property of the SO(2,1) invariance must be always present regardless of the dimension. It is actually the basic symmetry of an Ermakov invariant in any dimension.
Author Contributions
The authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported in part by MICINN (Grant PID2019-106820RBC22) and Junta de Castilla y León (Grant SA256P18).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ermakov, V.P. Second order differential equations. Conditions of complete integrability. Univ. Izv. Kiev Ser. III 1880, 9, 1. [Google Scholar] [CrossRef]
- Athorne, C. Kepler-Ermakov problems. J. Phys. A Math. Gen. 1991, 24, L1385–L1389. [Google Scholar] [CrossRef]
- Cerveró, J.M.; Lejarreta, J.D. Ermakov Hamiltonians. Phys. Lett. A 1991, 156, 201–205. [Google Scholar] [CrossRef]
- Leach, P.G.L. Generalized Ermakov systems. Phys. Lett. A 1991, 158, 102–106. [Google Scholar] [CrossRef]
- Haas, F.; Goedert, J. Lie point symmetries for reduced Ermakov systems. Phys. Lett. 2004, A332, 25–34. [Google Scholar] [CrossRef][Green Version]
- Cariñena, J.F. A new approach to Ermakov systems and applications in quantum physics. Eur. Phys. J. Spec. Top. 2008, 160, 51–60. [Google Scholar] [CrossRef]
- Cariñena, J.F.; de Lucas, J. A nonlinear superposition rule for solutions of the Milne-Pinney equation. Phys. Lett. 2008, A372, 5385–5389. [Google Scholar] [CrossRef][Green Version]
- Wybourne, B.G. Classical Groups for Physicists; Wiley and Sons: Hoboken, NJ, USA, 1974. [Google Scholar]
- De Alfaro, V.; Fubini, S.; Furlan, G. Conformal invariance in quantum mechanics. Nuovo C. 1976, 34A, 569–612. [Google Scholar] [CrossRef]
- Pinney, E. The nonlinear differential equation y″ + p(x)y + cy−3 = 0. Proc. Am. Math. Soc. 1950, 1, 681. [Google Scholar] [CrossRef]
- Lewis, H.R. Classical and quantum systems with time-dependent harmonic-oscillator-type Hamiltonians. Phys. Rev. Lett. 1967, 18, 510–514. [Google Scholar] [CrossRef]
- Ray, J.R.; Reid, J.L. More exact invariants for the time-dependent harmonic oscillator. Phys. Lett. 1979, A71, 317–320. [Google Scholar] [CrossRef]
- Reid, J.L.; Ray, J.R. Ermakov systems, Noether’s theorem and the Sarlet-Bahar method. Lett. Math. Phys. 1980, 4, 235–240. [Google Scholar]
- Lewis, H.R.; Riesenfeld, W.B. An Exact Quantum Theory of the Time-Dependent Harmonic Oscillator and of a Charged Particle in a Time-Dependent Electromagnetic Field. J. Math. Phys. 1969, 10, 1458–1473. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Goncharenko, A.M.; Logvin, Y.A.; Samson, A.M.; Shapovalov, P.S.; Turovets, S.I. Ermakov Hamiltonian systems in nonlinear optics of elliptic Gaussian beams. Phys. Lett. A 1991, 160, 138–142. [Google Scholar] [CrossRef]
- Cariñena, J.F. Sistemas de Ermakov y Aplicaciones en Física Clásica y Cuántica; Atencia, J., Ed.; Homenaje a Manuel Quintanilla; Prensas de la Universidad de Zaragoza: Zaragoza, Spain, 2007; p. 555. ISBN 978-84-7733-921-2. [Google Scholar]
- Cerveró, J.M.; Lejarreta, J.D. SO(2, 1) invariant systems: Squeezing and topological phases. Quantum Opt. 1990, 2, 333–349. [Google Scholar] [CrossRef]
- Cerveró, J.M.; Lejarreta, J.D. Generalized two-mode harmonic oscillator: Dynamical group and squeezed states. J. Phys. A Math. Gen. 1996, 29, 7545. [Google Scholar] [CrossRef]
- Cerveró, J.M. Squeezing and dynamical symmetries. Int. J. Theor. Phys. 1999, 38, 2095–2109. [Google Scholar] [CrossRef]
- Euler, M.; Euler, N.; Leach, P. The Riccati and Ermakov-Pinney hierarchies. J. Nonlinear Math. Phys. 2007, 14, 290–310. [Google Scholar] [CrossRef]
- Donchev, V.; Mladenova, C.D.; Mladenov, I. Vector-Parameter Forms of SU(1,1), SL(2,R) and their Connection to SO(2,1). In Geometry, Integrability and Quantization; Bulgarian Academy of Sciences: Sofia, Bulgaria, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).