Theoretical Study of closo-Borate Anions [BnHn]2− (n = 5–12): Bonding, Atomic Charges, and Reactivity Analysis
Abstract
1. Introduction
2. Materials and Methods
Computational Details
3. Results and Discussion
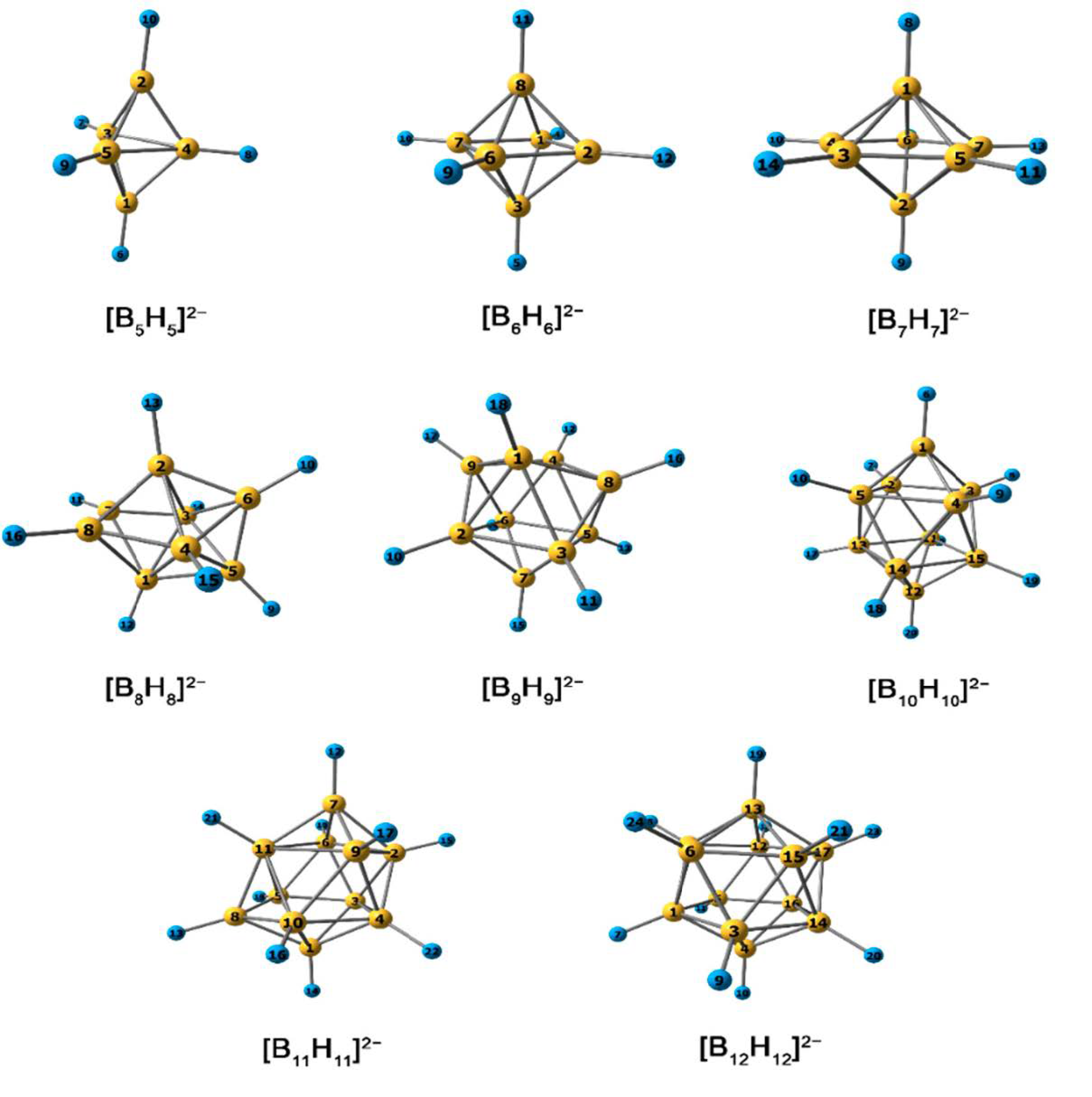
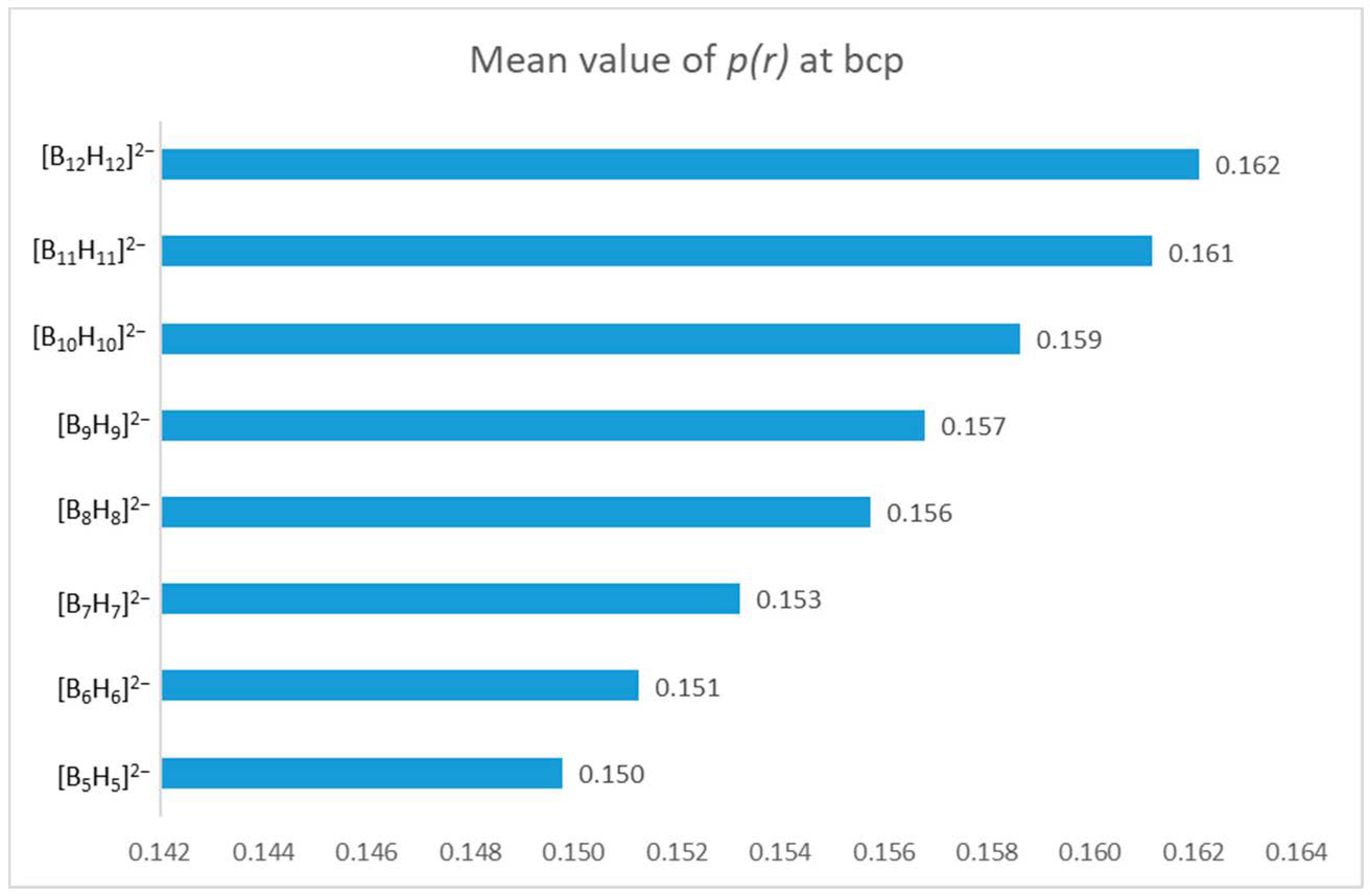
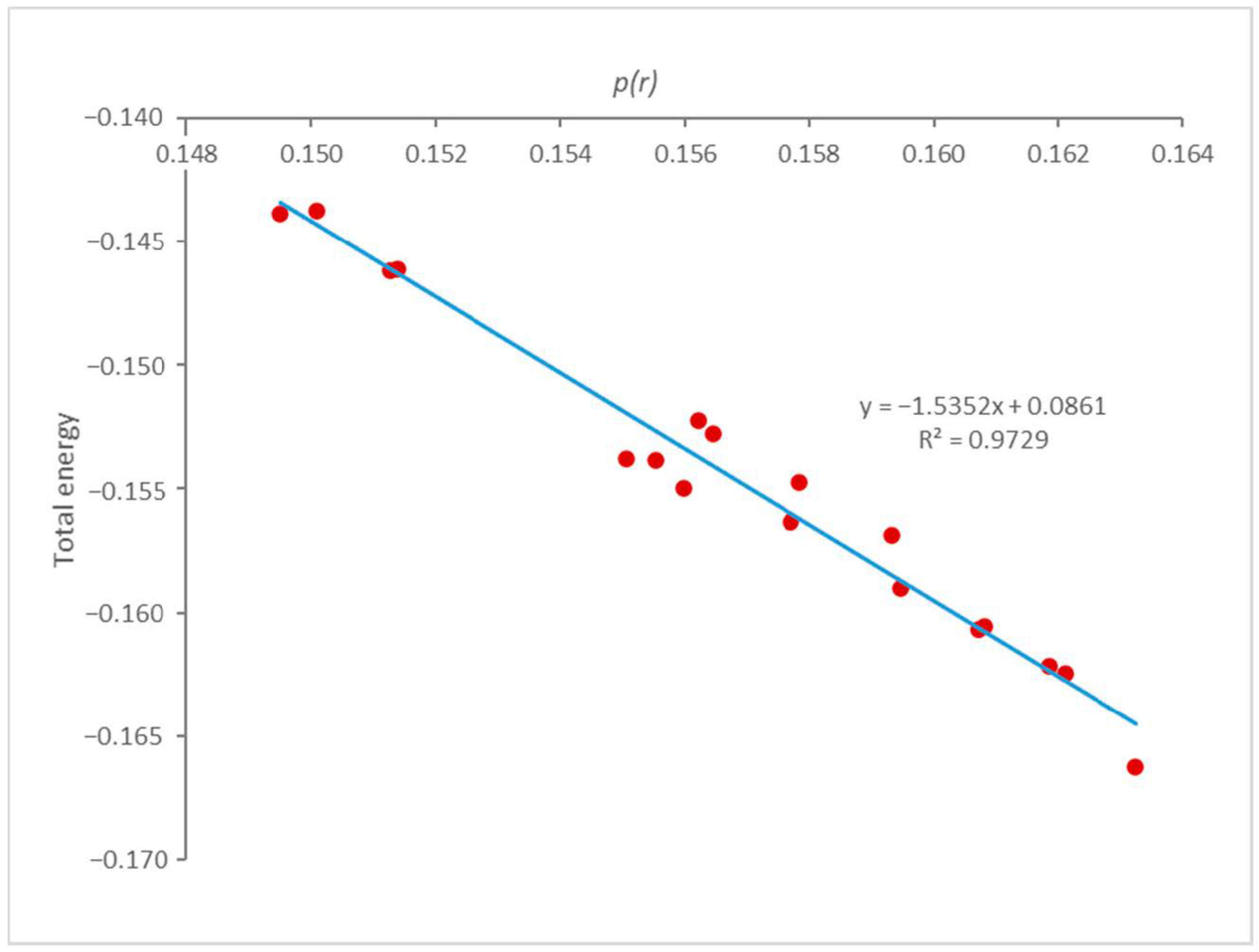
3.1. B–H Bond
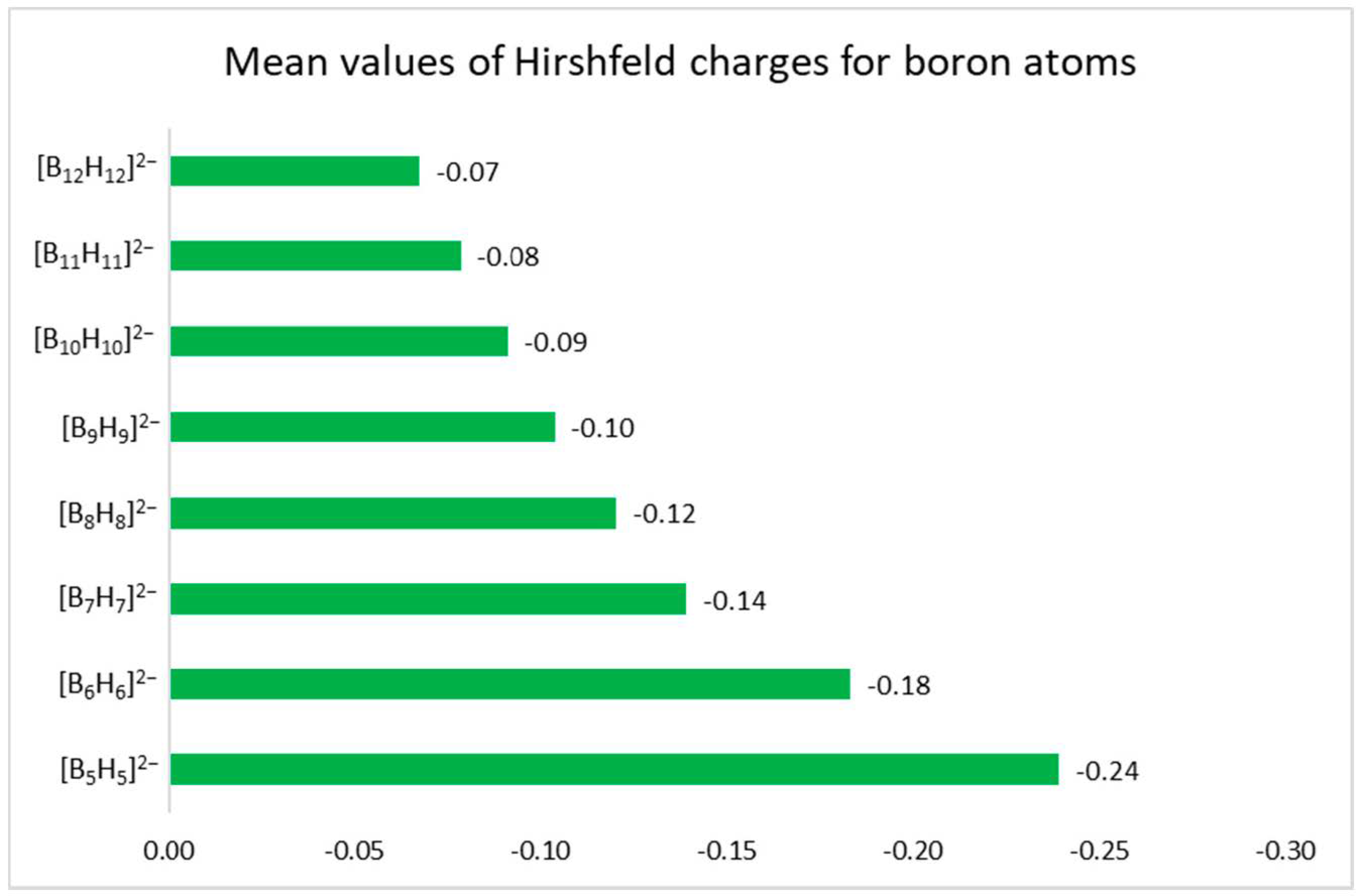
3.2. Atomic Charges
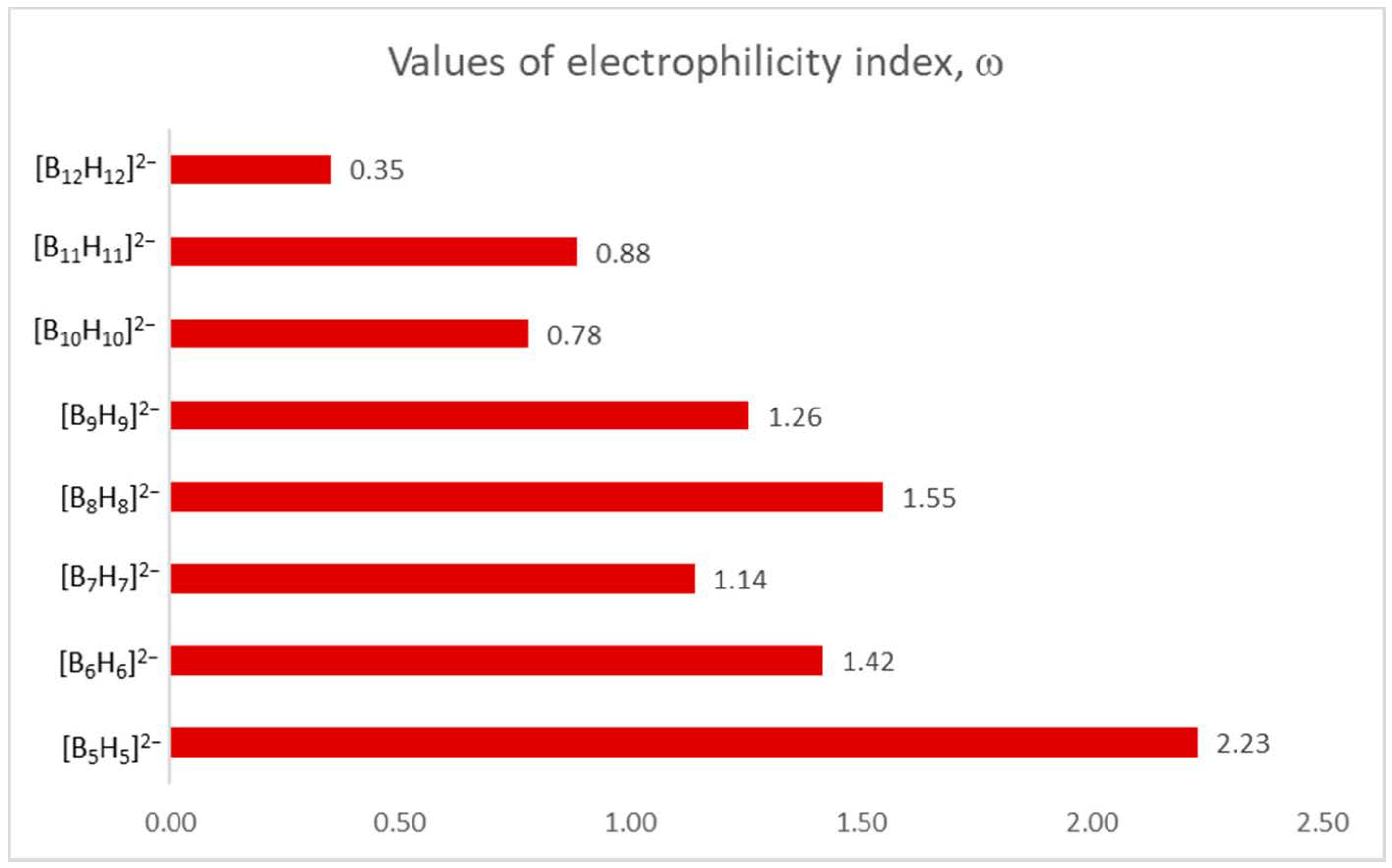
3.3. Reactivity Analysis
3.4. Fukui Functions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIM | atoms in molecules |
| Bcp | bond critical points |
| DFT | density functional theory |
| EINS | electrophile-induced nucleophilic substitution |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest unoccupied molecular orbital |
| NBO | natural bond orbitals |
| NPA | natural population analysis |
| QTAIM | quantum theory of atoms in molecules |
References
- Golub, I.E.; Filippov, O.A.; Kulikova, V.A.; Belkova, N.V.; Epstein, L.M.; Shubina, E.S. Thermodynamic Hydricity of Small Borane Clusters and Polyhedral closo-Boranes. Molecules 2020, 25, 2920. [Google Scholar] [CrossRef] [PubMed]
- Muetterties, E.L. Chemistry of Boranes. XVIII. Inorg. Chem. 1964, 231, 1450–1456. [Google Scholar]
- Hawthorne, M.F.; Mavunkal, I.J.; Knobler, C.B. Electrophilic Reactions of Protonated closo -Bl0Hl02− with Arenes, Alkane C-H Bonds, and Triflate Ion Forming Aryl, Alkyl, and Triflate nido -6-X-Bl0H13 Derivatives. J. Am. Chem. Soc. 1992, 9, 4427–4429. [Google Scholar] [CrossRef]
- Bondarev, O.; Sevryugina, Y.V.; Jalisatgi, S.S.; Hawthorne, M.F. Acid-Induced Opening of [closo-B10H10]2− as a New Route to 6-Substituted nido-B10H13 Decaboranes and Related Carboranes. Inorg. Chem. 2012, 51, 9935–9942. [Google Scholar] [CrossRef]
- Hoffmann, R.; Lipscomb, W.N. Theory of polyhedral molecules. I. Physical factorizations of the secular equation. J. Chem. Phys. 1962, 36, 2179–2189. [Google Scholar] [CrossRef]
- Lipscomb, W.N. Framework Rearrangement in Boranes and Carboranes. Science 1966, 153, 373–378. [Google Scholar] [CrossRef] [PubMed]
- Lipscomb, W.N. The Boranes and Their Relatives. Science 1977, 196, 1047–1055. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Axtell, J.C.; Bernier, N.A.; Kirlikovali, K.O.; Jung, D.; Umanzor, A.; Qian, K.; Chen, X.; Bay, K.L.; Kirollos, M.; et al. Sterically Unprotected Nucleophilic Boron Cluster Reagents. Chem 2019, 5, 2461–2469. [Google Scholar] [CrossRef]
- Keener, M.; Hunt, C.; Carroll, T.G.; Kampel, V.; Dobrovetsky, R.; Hayton, T.W.; Ménard, G. Redox-switchable carboranes for uranium capture and release. Nature 2020, 577, 652–655. [Google Scholar] [CrossRef]
- Černý, R.; Brighi, M.; Murgia, F. The Crystal Chemistry of Inorganic Hydroborates. Chemistry 2020, 2, 805–826. [Google Scholar] [CrossRef]
- Didelot, E.; Łodziana, Z.; Murgia, F.; Černý, R. Ethanol- and Methanol-Coordinated and Solvent-Free Dodecahydro closo-Dodecaborates of 3d Transition Metals and of Magnesium. Crystals 2019, 9, 372. [Google Scholar] [CrossRef]
- Hu, K.; Yang, Z.; Zhang, L.; Xie, L.; Wang, L.; Xu, H.; Josephson, L.; Liang, S.H.; Zhang, M.R. Boron agents for neutron capture therapy. Coord. Chem. Rev. 2020, 405, 213139. [Google Scholar] [CrossRef]
- Nakagawa, F.; Kawashima, H.; Morita, T.; Nakamura, H. Water-Soluble closo-Docecaborate-Containing Pteroyl Derivatives Targeting Folate Receptor-Positive Tumors for Boron Neutron Capture Therapy. Cells 2020, 9, 1615. [Google Scholar] [CrossRef]
- Goswami, L.N.; Ma, L.; Chakravarty, S.; Cai, Q.; Jalisatgi, S.S.; Hawthorne, M.F. Discrete Nanomolecular Polyhedral Borane Scaffold Supporting Multiple Gadolinium(III) Complexes as a High Performance MRI Contrast Agent. Inorg. Chem. 2013, 52, 1694–1700. [Google Scholar] [CrossRef]
- Ali, F.; Hosmane, N.S.; Zhu, Y. Boron Chemistry for Medical Applications. Molecules 2020, 25, 828. [Google Scholar] [CrossRef]
- Axtell, J.C.; Messina, M.S.; Liu, J.Y.; Galaktionova, D.; Schwan, J.; Porter, T.M.; Savage, M.D.; Wixtrom, A.I.; Rheingold, A.L.; Kubiak, C.P.; et al. Photooxidative generation of dodecaborate-based weakly coordinating anions. Inorg. Chem. 2019, 58, 10516–10526. [Google Scholar] [CrossRef] [PubMed]
- Duchêne, L.; Kühnel, R.S.; Rentsch, D.; Remhof, A.; Hagemann, H.; Battaglia, C. A highly stable sodium solid-state electrolyte based on a dodeca/deca-borate equimolar mixture. Chem. Commun. 2017, 53, 4195–4198. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, C.-Y.; Xu, T.-T.; Wu, J.; Wen, X.-Y.; Jiang, W.-J.; Chen, M.; Yang, J. Synthesis of Polyhedral Borane Cluster Fused Heterocycles via Transition Metal Catalyzed B-H Activation. Molecules 2020, 25, 391. [Google Scholar] [CrossRef]
- Stogniy, M.Y.; Erokhina, S.A.; Sivaev, I.B.; Bregadze, V.I. Nitrilium derivatives of polyhedral boron compounds (boranes, carboranes, metallocarboranes): Synthesis and reactivity. Phosphorus Sulfur Silicon Relat. Elem. 2019, 194, 983–988. [Google Scholar] [CrossRef]
- Shmal’ko, A.V.; Sivaev, I.B. Chemistry of Carba-closo-decaborate Anions [CB9H10]− (Review). Russ. J. Inorg. Chem. 2019, 64, 1726–1749. [Google Scholar] [CrossRef]
- Bregadze, V.I.; Sivaev, I.B.; Dubey, R.D.; Semioshkin, A.; Shmal’ko, A.V.; Kosenko, I.D.; Lebedeva, K.V.; Mandal, S.; Sreejyothi, P.; Sarkar, A.; et al. Boron-Containing Lipids and Liposomes: New Conjugates of Cholesterol with Polyhedral Boron Hydrides. Chem. Eur. J. 2020, 26, 13832–13841. [Google Scholar] [CrossRef]
- Semioshkin, A.A.; Sivaev, I.B.; Bregadze, V.I. Cyclic oxonium derivatives of polyhedral boron hydrides and their synthetic applications. J. Chem. Soc. Dalt. Trans. 2008. [Google Scholar] [CrossRef]
- Avdeeva, V.V.; Malinina, E.A.; Zhizhin, K.Y.; Kuznetsov, N.T. Structural Diversity of Cationic Copper(II) Complexes with Neutral Nitrogen-Containing Organic Ligands in Compounds with Boron Cluster Anions and Their Derivatives (Review). Russ. J. Inorg. Chem. 2020, 65, 514–534. [Google Scholar] [CrossRef]
- Leyden, R.N.; Hawthorne, M.F. Synthesis of diazonium derivatives of decahydrodecaborate(2-) from arylazo intermediates. Inorg. Chem. 1975, 14, 2444–2446. [Google Scholar] [CrossRef]
- Hertler, W.R.; Knoth, W.H.; Muetterties, E.L. Chemistry of Boranes. XXIV. Carbonylation of Derivatives of B10H102− and B12H 122− with Oxalyl Chloride. Inorg. Chem. 1965, 4, 288–293. [Google Scholar] [CrossRef]
- Jelinek, T.; Štibr, B.; Mareš, F.; Plešek, J.; Heřmánek, S. Halogenation of 4,5-dicarba-arachno-nonaborane(13),4,5-C2B7H13. Polyhedron 1987, 6, 1737–1740. [Google Scholar] [CrossRef]
- Frank, R.; Adhikari, A.K.; Auer, H.; Hey-Hawkins, E. Electrophile-Induced Nucleophilic Substitution of the nido-Dicarbaundecaborate Anion nido-7,8-C2B9H12—By Conjugated Heterodienes. Chem. Eur. J. 2014, 20, 1440–1446. [Google Scholar] [CrossRef] [PubMed]
- Vatsadze, S.Z.; Medved’ko, A.V.; Bodunov, A.A.; Lyssenko, K.A. Bispidine-based bis-azoles as a new family of supramolecular receptors: The theoretical approach. Mendeleev Commun. 2020, 30, 344–346. [Google Scholar] [CrossRef]
- Giba, I.S.; Tolstoy, P.M. Self-assembly of hydrogen-bonded cage tetramers of phosphonic acid. Symmetry 2021, 13, 258. [Google Scholar] [CrossRef]
- Jiang, P.; Record, M.C.; Boulet, P. Electron density and its relation with electronic and optical properties in 2D Mo/W dichalcogenides. Nanomaterials 2020, 10, 2221. [Google Scholar] [CrossRef] [PubMed]
- Sethio, D.; Daku, L.M.L.; Hagemann, H.; Kraka, E. Quantitative Assessment of B–B–B, B–Hb–B, and B–Ht Bonds: From BH3 to B12H122−. ChemPhysChem 2019, 20, 1967–1977. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.; Legare, D. Properties of atoms in molecules: Structures and reactivities of boranes and carboranes. Can. J. Chem. 1992, 70, 657–677. [Google Scholar] [CrossRef]
- Voinova, V.V.; Selivanov, N.A.; Plyushchenko, I.V.; Vokuev, M.F.; Bykov, A.Y.; Klyukin, I.N.; Novikov, A.S.; Zhdanov, A.P.; Grigoriev, M.S.; Rodin, I.A.; et al. Fused 1,2-Diboraoxazoles Based on closo-Decaborate Anion-Novel Members of Diboroheterocycle Class. Molecules 2021, 26, 248. [Google Scholar] [CrossRef] [PubMed]
- Klyukin, I.N.; Novikov, A.S.; Zhdanov, A.P.; Zhizhin, K.Y.; Kuznetsov, N.T. Theoretical study of closo-borate derivatives of general type [BnHn−1COR]2− (n = 6, 10, 12; R = H, CH3, NH2, OH, OCH3)—Borylated analogue of organic carbonyl compounds. Polyhedron 2020, 187, 114682. [Google Scholar] [CrossRef]
- Klyukin, I.N.; Novikov, A.S.; Zhdanov, A.P.; Zhizhin, K.Y.; Kuznetsov, N.T. Theoretical study of monocarbonyl derivatives of closo-borate anions [BnHn–1CO]− (n = 6, 10, 12): Bonding and reactivity analysis. Mendeleev Commun. 2020, 30, 88–90. [Google Scholar] [CrossRef]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139, 36. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos Gutiérrez, M.; Castellanos Soriano, J. Understanding the Origin of the Regioselectivity in Non-Polar [3+2] Cycloaddition Reactions through the Molecular Electron Density Theory. Organics 2020, 1, 19–35. [Google Scholar] [CrossRef]
- Allgäuer, D.S.; Jangra, H.; Asahara, H.; Li, Z.; Chen, Q.; Zipse, H.; Ofial, A.R.; Mayr, H. Quantification and Theoretical Analysis of the Electrophilicities of Michael Acceptors. J. Am. Chem. Soc. 2017, 139, 13318–13329. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Zhao, Y.L.; Zhao, R.; Houk, K.N. Understand the specific regio-and enantioselectivity of fluostatin conjugation in the post-biosynthesis. Biomolecules 2020, 10, 815. [Google Scholar] [CrossRef]
- Fuentealba, P.; Florez, E.; Tiznado, W. Topological Analysis of the Fukui Function. J. Chem. Theory Comput. 2010, 6, 1470–1478. [Google Scholar] [CrossRef]
- Rodríguez-Zavala, J.G. Local reactivity through fukui function on endohedral mono-metallofullerenes. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 105, 186–195. [Google Scholar] [CrossRef]
- Kochnev, V.K.; Avdeeva, V.V.; Malinina, E.A.; Kuznetsov, N.T. Theoretical study of H2 Elimination from [BnHn+1] monoanions (n = 6–9, 11). Russ. J. Inorg. Chem. 2014, 59, 1268–1275. [Google Scholar] [CrossRef]
- Sivaev, I.B.; Semioshkin, A.A.; Brellochs, B.; Sjoberg, S.; Bregadze, V.I. Synthesis of oxonium derivatives of the dodecahydro--closo-dodecaborate anion [B12H12]2−. Tetramethylene oxonium derivative of [B12H12]2− as a convenient precursor for the synthesis of functional compounds for boron neutron capture therapy. Polyhedron 2000, 19, 627–632. [Google Scholar] [CrossRef]
- Sivaev, I.B.; Prikaznov, A.V.; Naoufal, D. Fifty years of the closo-decaborate anion chemistry. Collect. Czechoslov. Chem. Commun. 2010, 75, 1149–1199. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, K.; Pople, J.A. Self-consistent molecular orbital methods. XII. Further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Da Chai, J.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Nikolova, V.; Cheshmedzhieva, D.; Ilieva, S.; Galabov, B. Atomic Charges in Describing Properties of Aromatic Molecules. J. Org. Chem. 2019, 84, 1908–1915. [Google Scholar] [CrossRef]
- Oller, J.; Pérez, P.; Ayers, P.W.; Vöhringer-Martinez, E. Global and local reactivity descriptors based on quadratic and linear energy models for α, β -unsaturated organic compounds. Int. J. Quantum Chem. 2018, 118, e25706. [Google Scholar] [CrossRef]
- Makhyoun, M.A.; Massoud, R.A. Theoretical calculation of the exchange coupling constant in some polymeric nickel(II) complexes using range-separated functionals. Eur. J. Chem. 2018, 9, 382–385. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Glendening, J.K.E.D.; Badenhoop, A.E.R.; Carpenter, J.E.; Bohmann, J.A.; Morales, P.K.C.M.; Landis, C.R.; Weinhold, T.C.I.F. NBO 7.0; University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comp. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Kononova, E.G.; Leites, L.A.; Bukalov, S.S.; Pisareva, I.V.; Chizhevsky, I.T. Experimental and theoretical study of the vibrational spectrum, structure and electron density distribution of neutral 11-vertex dicarbaborane 2,3-C2B9H11. J. Mol. Struct. 2006, 794, 148–153. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Korlyukov, A.A.; Avdeeva, V.V.; Polyakova, I.N.; Malinina, E.A.; Kuznetsov, N.T. Theoretical QTAIM, ELI-D, and Hirshfeld Surface Analysis of the Cu−(H)B Interaction in [Cu2(bipy)2B10H10]. J. Phys. Chem. A 2013, 2, 13138. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels-Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klyukin, I.N.; Vlasova, Y.S.; Novikov, A.S.; Zhdanov, A.P.; Zhizhin, K.Y.; Kuznetsov, N.T. Theoretical Study of closo-Borate Anions [BnHn]2− (n = 5–12): Bonding, Atomic Charges, and Reactivity Analysis. Symmetry 2021, 13, 464. https://doi.org/10.3390/sym13030464
Klyukin IN, Vlasova YS, Novikov AS, Zhdanov AP, Zhizhin KY, Kuznetsov NT. Theoretical Study of closo-Borate Anions [BnHn]2− (n = 5–12): Bonding, Atomic Charges, and Reactivity Analysis. Symmetry. 2021; 13(3):464. https://doi.org/10.3390/sym13030464
Chicago/Turabian StyleKlyukin, Ilya N., Yulia S. Vlasova, Alexander S. Novikov, Andrey P. Zhdanov, Konstantin Y. Zhizhin, and Nikolay T. Kuznetsov. 2021. "Theoretical Study of closo-Borate Anions [BnHn]2− (n = 5–12): Bonding, Atomic Charges, and Reactivity Analysis" Symmetry 13, no. 3: 464. https://doi.org/10.3390/sym13030464
APA StyleKlyukin, I. N., Vlasova, Y. S., Novikov, A. S., Zhdanov, A. P., Zhizhin, K. Y., & Kuznetsov, N. T. (2021). Theoretical Study of closo-Borate Anions [BnHn]2− (n = 5–12): Bonding, Atomic Charges, and Reactivity Analysis. Symmetry, 13(3), 464. https://doi.org/10.3390/sym13030464