Abstract
In this article, for the first time, a new mathematical model of the schemes for organizing a session of person–system interactions between the registration center server of the information system for critical use (ISCU) and the terminal of the person-user in a wireless communication environment are presented. In contrast to the existing literature, this article uses the mathematical apparatus of queuing systems to describe the schemes of organizing the stochastic process of a session of person–system interaction in discrete or continuous time, namely, models of the type Geo/Geo/1 with group arrival and ordinary service for the case of discrete representation of time and models of the type M/G/1 for the case of continuous time representation. The use of the mathematical apparatus of queuing systems in the studies made it possible to obtain analytical expressions for comparing formalized schemes for organizing the person–system interaction according to such functional characteristics as the average time of downloading a finite number of data blocks into the terminal of the target person-user (average time that the request spent the server of the information system).
1. Introduction
Modeling is an effective means of studying complex systems and involves describing the process of their design, determining their functional parameters, and finding ways to rationalize their structure and quality of work. Of course, the analysis of the results of a correctly staged full-scale experiment on an existing complex system can potentially ensure the achievement of such results, but setting up such an experiment is a long, expensive, and sometimes dangerous process.
The creation of an information system is a directed process of sequential solution of design problems, analysis, and synthesis of its functional units or subsystems. Information systems belong to the class of complex systems with significant uncertainty in the processes of their functioning. The source of this uncertainty is the information which the system operates directly, as well as the methods of its processing and the participation of the human factor in these processes. Such systems can be studied using either a natural experiment or simulation. The first approach involves the collection of operational information on the system under study during a representative time interval, followed by statistical processing of the collected data. Such information is the basis for assessing the quality of the functioning of an existing system. If the goal is to search for approaches to improve the existing system or design a new system, then only the second approach, modeling, remains rational. The use of modern computer technology makes just such types of modeling as mathematical modeling the most reliable and economically justified.
The meaning of mathematical modeling is the definition of structured mathematical apparatus—a mathematical model, the study of which makes it possible to obtain characteristics of the functioning of the original information system. To create a mathematical model, two main types of methods are used: analytical and simulation. Analytical methods, depending on the degree of uncertainty of the characteristic parameters of the system under study, are divided into deterministic and stochastic. Simulation models represent a structural diagram of an information system or its subsystems in dynamics in the form of algorithm-like structures.
All that has been said is directly related to the problem of researching information systems for critical use (ISCU) [1,2,3], the area of application which in the conditions of modern society is rapidly expanding. Considering the critical nature of objects where information systems of this type are used, it is simply impossible to carry out research of the latter by a natural experiment. At the same time, the complexity of the structure of ISCU still does not allow to adequately generalize the description of all its information processes in one complex mathematical model. For example, in study [1], the authors thoroughly describe the control of internal resources of the registration center server of ISCU in order to maximize the availability of the latter, but the impact of the channel in which this interaction occurs on the availability of ISCU is not investigated. Studies [2,3] further reveal the nature of the dependability of such systems, but the channel of information dissemination is again ignored. This circumstance forces the resort to the separate research of external information processes of systems such as ISCU.
Structurally, this article is organized into six main sections, including this one. The second section of the article critically analyzes the results of current research on the selected topic, and based on the obtained results of the analysis, sets the aim and objectives of research. The third section is devoted to the mathematical formalization of the schemes of organization of the session of the person–system wireless communication interaction with the information system for critical use. The chapter presents the formulation of the research task, and the corresponding mathematical models and methods. The fourth section presents the results of experiments conducted to test the models and methods proposed in the third chapter. In the fifth section, a critical analysis of the obtained empirical results is performed focusing on the aspect of applied efficiency of the mathematical apparatus presented in the third section. Concluding the main text of the article are the conclusions, which, in particular, noted the advances in further research.
2. State of the Art
The “bottleneck” of information systems in general and information systems of critical use in particular is their accessibility to person-users. The situation is further complicated by the ever-increasing use of wireless communication technologies in organizing sessions of the person–system interaction, because the wireless communication channel is slower and less noise-resistant than cable. However, it is impossible to ignore the challenges of the time; therefore, a large number of scientific teams around the world are engaged in the study of the availability of information systems. The task of increasing the throughput of wireless communication channels is being worked out most intensively, because both the number of person-users and the amount of information messages that they wish to download using information systems are growing rapidly. There has been a tendency to move from an extensive technology for solving this problem, which consists of increasing the number of servers in the information system with the simultaneous deployment of an appropriate communication infrastructure, to a technology for increasing the throughput of communication channels both on the side of person-user and on the side of a single powerful coordination server as part of the information system [4,5,6,7,8]. What makes this technology even more popular is that it enables an increase in the throughput of the person–system information interaction not only by hardware, increasing the set of communication channels, but also programmatically, at the protocol and software level, by adjusting the rules of QoS technology [9,10,11,12]. Moreover, the best results are shown by well-thought-out strategies for generating such rules [13,14], formalized taking into account the intended purpose and the type of information system as an information donor.
In the studies [15,16], a reverse approach to the synthesis of effective schemes for organizing a session of person–system interaction was proposed. This interaction was considered from the standpoint of modeling interference that can affect the studied selected information communication processes. The influence of interference was analytically taken into account in the information security metric through the formalization of vulnerabilities in the scheme of organizing a session of the person–system interactions. After identifying a set of vulnerabilities, the task of resisting the corresponding threat to information security of the external communication process for the simulated information system was formulated. As a result of solving such a task, sequential and parallel schemes for the reservation of the computing resources of the simulated information system were obtained. The advantage of the described research is its formalization using the rigorous mathematical apparatus of the theory of probability and mathematical statistics. This does not involve experts to optimize the process of external communication of the modeled information system, but carries out the optimization automatically. At the same time, the disadvantage of the described approach is the lack of flexibility and adaptability of the mathematical apparatus presented by the authors.
In particular, the article [17] proposed several options for strategies for the distribution of communication resources when organizing both the person–system and multi-person–system information interaction. The authors of [18] proposed models of such processes using the mathematical apparatus of the theory of queuing systems in continuous time. At the same time, no mathematical justifying of a discrete time study of these strategies has been carried out. We also note that the authors carried out the estimation of the effectiveness of the proposed strategies solely by the value of the throughput [15,16,17,18] or by the value of the probability of servicing the request of the person-user by the system under study [14,15,17].
Therefore, the development of mathematical apparatus for studying strategies for organizing sessions of person–system interaction in the context of the specificity of ISCU with obtaining mathematically correct and complete expressions for calculating such qualitative parameters of queuing systems operating in discrete and continuous time as the average downloading time of an information package by a person-user is of scientific and applied interest.
3. Materials and Methods
3.1. Statement of Research
As noted in articles [19,20,21], at the communication level, the information system for critical use is represented by a sets of data servers and terminals of person-users that interact with each other through the registration center server. At the physical level, the person–system interaction sessions are supported by a set of receiving–transmitting devices on the side of the registration center server and a unified set of receiving–transmitting devices on the side of the terminals of each person-user. To receive an information package of a finite size, the person-user initiates a session of the person–system interaction through the personal terminal, during which they address their request to the registration center server, which, having received the requested data from the corresponding data server, sends them to the target terminal, thus ending the active session, which is marked by the release of the involved receiving–transmitting devices. Assuming that the communication channel between the registration center server of ISCU and the terminals of person-users is wireless, we summarize the above by presenting a structural model of the person–system interaction session in Figure 1.
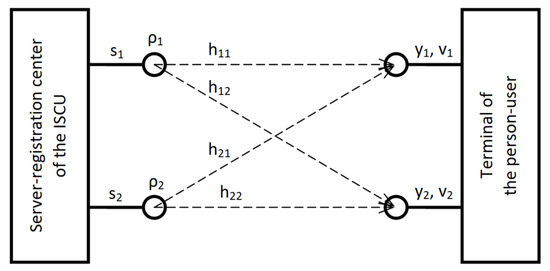
Figure 1.
Basic scheme of organization of the session of person–system interaction at (ISCU is an information system for critical use).
Naturally, the central parameter that characterizes such a session on the terminal of person-user side is the power, which is analytically formalized by the expression , where is a column vector of dimension , formed by data blocks of the information message received by the th terminal; is a vector column of dimension , formed by data blocks of the information message, which is transmitted by the registration center server to the th terminal; is a route matrix of dimension , which contains the distributions of the conditional probabilities of direct transitions of the transmitted data blocks in to the accepted ones for the active session of person–system interaction; and is a vector column of dimension , formed by random values that characterize the noise affecting each receiving–transmitting device of the th terminal. Stochastic values are normally distributed with respect to peak power with zero mathematical expectation and variance , where is the spectral density of noise power. Accordingly, the covariance matrix of noise is defined as , where is a unit matrix of dimension . We also describe the peak power of the information signal for the receiving–transmitting devices of the registration center server with the parameter . The metric of parameters characterizing the session of person–system interaction defined in this way enables the calculation of an important qualitative parameter—the signal-to-noise ratio . To evaluate the effectiveness of the session of person–system interaction, we will use a characteristic known from information theory [22,23]—the peak rate of error-free data transmission or bandwidth. With the route matrix defined on the side of the th terminal, the bandwidth of the person–system interaction session is described by Equation (1):
where , are the eigen values of the matrix , is the power of signal transmission via the th route, operation over the value of is revealed as , and is a constant, the value of which is chosen so that the equality is satisfied. To determine the constant , we will use the known water filling principle [24,25], a graphical interpretation of which for the case of a session of person–system interaction with two routes is shown in Figure 2.
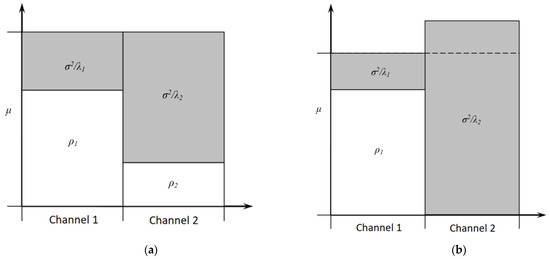
Figure 2.
Example of application of the water filling principle to the basic scheme of organization of the session of person–system interaction at: (a) variant; (b) variant.
The semantics of the principle involves the uneven distribution of power between receiving–transmitting devices in order to maximize the bandwidth of the information exchange process. The registration center server can support more than one active session of the person–system interaction at the same time. For this situation, the total bandwidth (Figure 3) will be determined based on the covariance matrix of the person–system interaction sessions by the following expression:
where condition is satisfied if the covariance matrices are positively defined.
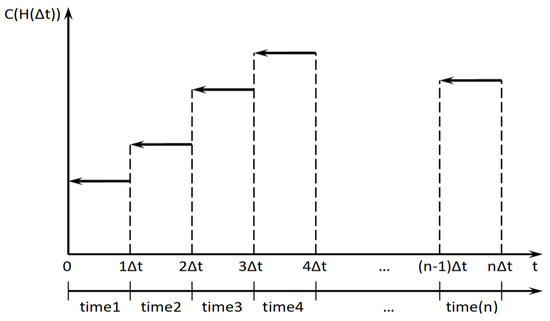
Figure 3.
Schematic interpretation of bandwidth of a person–system interaction session in discrete time.
In addition to bandwidth, we also include a value such as —the average time that it takes a person-user to download a finite amount of data—in the metrics used to evaluate the effectiveness of a session of person–system interaction. Thus, the aim of the study is to formalize effective schemes for organizing a session of person–system interaction with the information system for critical use with a wireless communication component. The objectives of the study are: formalization in the metrics of efficiency parameters in discrete and continuous time the mathematical model of the session of the person–system interaction with the information system for critical use with the wireless communication component; formalization of effective schemes for the organization of sessions of person–system and multi-person–system interactions on the basis of the proposed profile model; empirical proof of the adequacy of the created model and evaluation of the effectiveness of the schemes of organization of sessions of person–system and multi-person–system interactions.
3.2. Mathematical Model of a Person–System Interaction Session in Discrete Time
When studying the process of person–system interactions, we will consider time to be a discrete value with the quantization period . We will also assume that all session activation requests from person-users initiated during the current quantum of time will be considered by the registration center server at the beginning of the new quantum of time simultaneously. We will also assume that after activating the person–system interaction session, the terminals of the person-users do not change their spatial location relative to the registration center server, i.e., the route matrix defined for the th person-user does not change until the end of the quantum of time. Finally, we assume that the active session of the person–system interaction can end only after the end of the quantum of time. Thus, for time , the values of the set of controlled parameters are determined immediately after the beginning of the th quantum of time:
For example, , (). Figure 4 shows a structural model of multi-person–system interaction with , , . In the figure, the queues of data blocks of different lengths for each person-user are schematically shown.
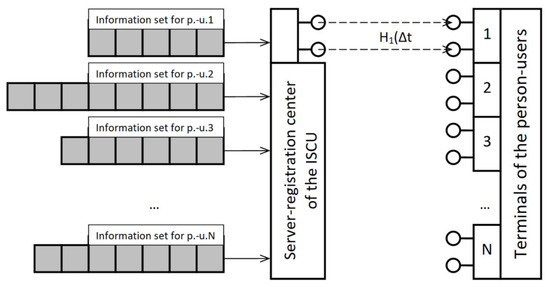
Figure 4.
Structural model of a multi-person–system interaction session at , .
The choice of the scheme of organization of sessions of person–system or multi-person–system interaction will affect the content of the information vector , which will form the registration center server. We formalize three basic schemes, in which the th quantum of time, :
Scheme 1: only the terminal of the person-user that waits the longest for the activation of the session is serviced;
Scheme 2: only the terminal of the person-user with the highest bandwidth is serviced;
Scheme 3: a set of terminals of person-users is served, the superposition of communication capabilities of which provides the best bandwidth.
We describe a session of multi-person–system interaction in discrete time by a stochastic process , where the stochastic value characterizes the number of registered requests for session activation; is a vector formed by the values of the final queue lengths from data blocks for active sessions; is a vector formed by the values of the waiting times for the registered requests for activation of the session at the beginning of the th quantum of time, . Note that the session activation request contains information about the number of data blocks requested by the respective person-user, as well as information about the bandwidth of its communication equipment. Figure 5 clearly shows the active processes on the registration center server of ISCU at the time interval that corresponds to the th quantum of time.
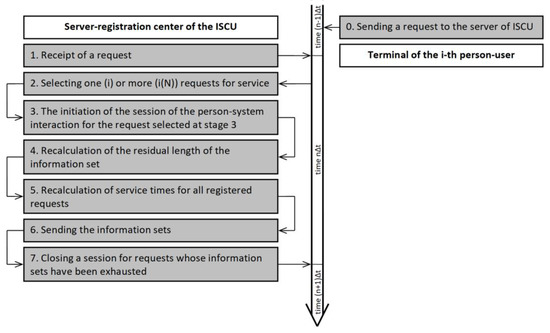
Figure 5.
The sequence UML-diagram of the person–system/multiperson–system interaction session.
In the context described in Figure 5, on registration center server of ISCU at the beginning of the th quantum of time:
- According to Scheme 1, the session is activated to satisfy the request that is waiting for the longest: . The bandwidth is determined on the basis of Equation (1): ;
- According to Scheme 2, the session is activated to satisfy a request from the person-user , which corresponds to the largest declared bandwidth among the requests waiting in line: , where the bandwidth is determined by Equation (1);
- According to Scheme 3, the sessions are activated to satisfy requests from person-users from subset , while providing the best bandwidth: , . Accordingly, the subset is identified by the expression , .
In the formalism of a certain stochastic process , the sequence of operations on registration center server of ISCU on the th quantum of time is defined as follows:
- The registration center server receives a request to activate a person–system interaction session. The probability of such an event is characterized by the stochastic parameter , . Accordingly, the length of the queue of registered requests increases: . Additionally for the registered request: the final number of blocks of requested data is declared in the form of value of stochastic parameter ; countdown of time of stay of request in the queue is considered by the value of parameter begins (at the th quantum of time ); route matrix is initiated by random values;
- Random values redefine route matrices for active sessions of person–system interaction;
- According to the active scheme of organization of sessions of person–system or multi-person–system interactions, the values of the function or are calculated for all registered requests;
- According to the used scheme of organization of sessions of person–system or multi-person–system interactions, the session of person–system interaction is activated for or request;
- For a newly activated person–system interaction session, the final number of blocks of requested data is recalculated: , ;
- The time of each request in the queue is incremented: ;
- The bandwidth for the newly activated person–system interaction session is specified: the speed of loading the data block by the person-user terminal is fixed, provided that the equality is not fulfilled;
- The person–system interaction sessions for which the equality holds are deactivated.
A functional study of the stochastic process in discrete time revealed its semantic similarity with the mathematical apparatus of Markov chains [26,27,28]. Having developed this statement, we can obtain stationary characteristics of the studied process. Note that the dynamics of the studied process, taking into account the available schemes of organization of person–system interaction, can be described using the mathematical apparatus of queuing systems [29,30], namely, models of type with group receipt and ordinary service for the case of discrete representation of time and models of type —for the case of continuous representations of time. The use of the mathematical apparatus of queuing systems for further research will allow obtaining of analytical expressions for the comparison of formalized schemes of organization of person–system interactions according to functional characteristics such as the average downloading time of a finite number of data blocks by the terminal of the target person-user.
3.3. Formalization in the Mathematical Apparatus of Queuing Systems of the Process of Person–System Interaction, Organized According to Schemes 1–3, in Discrete Time
Suppose that with each quantum of time, the registration center server of ISCU with probability , receives a request to activate the session of the person–system interaction in order to download the information package to the terminal of the person-user, which with probability includes , blocks of data. The information package is transmitted in blocks, respectively, and the service life of the transmission process of the entire information package is described by a geometric distribution with the characteristic parameter , . The process is studied in discrete time; therefore, the non-negative parameters and , which characterize the intensity of receipt and service of requests, respectively, will be considered equal to one. Therefore, the registration center server receives a request to receive an information package in the form of a sequence of data blocks (group request). If the person–system interaction session is activated, the request will be serviced by the registration center server on a block-by-block basis. The described process will be presented as a queuing system of type in the form of a Markov chain, which simulates the process of servicing of the incoming request (group request) by the registration center server of ISCU during a finite number of quanta of time .
For such a chain, the stationary probabilities , , are expressed recurrently, and some probability-time characteristics, in particular, the probabilities are expressed by generating functions. We introduce the following notation for the generating functions of the distribution of the number of requests in the group and the stationary probability distribution :
where . The average number of requests in the group is denoted as . Considering the notation for the generating functions (4)–(6), we present the solution of the system of equilibrium equations:
Based on the analytical representation of Equation (7), considering that , we obtain:
The value of characterizes the workload of the registration center server of ISCU, and the condition is a sufficient condition for the stationary nature of the initiated process of subject–system interaction. The stationary distribution of the waiting time for the start of service of the first request in the group (start time of service of request) will be characterized by the generating function of the form:
Accordingly, based on Equation (9), the average waiting time for servicing a group request will be determined by the expression of the form:
Additionally, the average number of requests served by the registration center server of ISCU will be determined by the expression:
The value of in Equation (11) is determined taking into account that the number of requests in the group is described by a geometric distribution with the characteristic parameter (, ). Therefore, we have .
Accordingly, we analytically describe the average time that the group request spends on the registration center server of ISCU (duration of downloading the information package) via the expression:
With a known non-negative value of the bandwidth of the communication equipment of the terminal of the person-user, based on Equation (12) we obtain:
Therefore, a description of the organization of the person–system interaction session according to Scheme 1 as a queuing system of the type with a group receipt and ordinary service is proposed:
This allowed us to analytically formalize the dependence of such functional characteristics as the average time that the group request spent on the registration center server of ISCU (12) and the average duration of the queue (11) from the contents of the group request (the length of the information package, expressed in the number of requested data blocks). Further research in this direction may relate to estimations of the sensitivity of the values of these functional parameters, from which the distribution function describes the value of the length of the information package.
However, another formalization of the process of organization of person–system interaction according to Scheme 1 is admissible. Suppose that the flow of incoming requests to the registration center server has a stochastic nature. Accordingly, the probability of receipt of the input request on the th quantum of time is characterized by a quantity described by the geometric distribution law with the characteristic parameter , . The average duration of query service will be considered a stochastic value with a discrete distribution function and an average value of . Provided that the requests are serviced in the order of their receipt, such an organized session of person–system interaction can be represented by a discrete queuing system of type . In this case, the average time of service of the request by the registration center server of ISCU is described by the expression:
where is the load characteristic of the registration center server of ISCU, and is the second moment of the time of service of request.
Evaluating these characteristics, taking into account that the time of service of each request, depends on the length of the information package and the bandwidth of the communication equipment of the terminal of person-user. As a result, we obtain:
where is a stochastic quantity that characterizes the length of the information package.
We can also estimate the average number of active requests on the registration center server of ISCU by the moments of completion service of requests in a form of the expression:
Note that the parameters and are semantically identical, because both characterize the amount of information transmitted by the registration center server. However, these parameters are not interchangeable, because the parameter , which characterizes the length of the group request, can only be positive and an integer, which determines its presence only in queuing systems that operate in discrete time. At the same time, the value of the stochastic quantity does not apply to the integer condition. Thus, in addition to Equation (14), the person–system interaction session organized according to Scheme 1 is formalized as a model of a queuing system of the form:
Analytical expressions are obtained for Equation (18), in particular, for the average time of service of request by the registration center server of ISCU.
In the case of organizing the process of person–system interaction according to Scheme 2 on each cycle, the registration center server selects for service a request from the person-user with the highest bandwidth of communication equipment. According to the authors, the model of the queuing system of the type which is also identified as random order of service (ROS) [29] or service in random order (SIRO) [30], is best for describing the course of such a process:
In such a model, the registered request can be selected for service with probability , the value of which is determined only by the number of registered requests in the queue. It should be noted that the active session of the person–system interaction, initiated by the registration center server of ISCU to satisfy the request, cannot be interrupted at each quantum of time, and must end correctly after the transmission of the entire information package (this condition is easier to meet the more quanta of time duration and average time for servicing one request, i.e., transmission of one block of data).
The stationary distribution of the number of active requests on the registration center server of ISCU when using Scheme 2 will not differ from the stationary distribution of the same parameter determined for the case of using Scheme 1, but the stationary distribution of times for servicing requests for these schemes will be different. According to Little’s formula [31], the expressions for determining the average waiting time for the start of service of the request and the average time of receipt of a new request will be the same for both schemes. Therefore, the expression for determining the average time for servicing one request by the registration center server of ISCU will not change and will retain the form of Equation (12), except that the need to meet the condition to maximize bandwidth leads to a description of the process of calculating the average time for servicing one request by the expression of the form:
Accordingly, the average speed of service of the group of requests (group request) will increase, because first the requests that correspond to the highest bandwidth of communication equipment will be served.
It should be noted that the above mathematical apparatus to describe the process of organizing the person–system interaction using the model of queuing system of Equation (18) remains correct to describe the situation when the organization of such a process occurs with the involvement of Scheme 2, but the model of queuing system in the form of Equation (19) we pass to model:
It can be argued that Equation (15) for calculating the average time for servicing requests by the registration center server of ISCU will remain relevant for the model of Equation (21). Only the expressions for calculating the values of the parameters and will change, which will take the forms, respectively:
The organization of the session of person–system interaction according to Scheme 3 assumes that the registration center server simultaneously serves more than one request from different person-users. A model of such a process can be a queuing system of type with a random choice for service. Forming such a system, it is first necessary to determine the number of conveyors for service and the intensity of servicing requests on their basis. In the first approximation, the lower limit of the number of conveyors can be the value 2, and the upper the value . The basic assessment of the intensity of the service on each conveyor can be a value which is equal to the value of to the number of conveyors. However, it will be much more efficient to use the model of queuing system with one conveyor of type:
The average time of servicing of the request for which will be equal to:
In this approach, Equation (12) can be used to describe the average servicing time of the request by the registration center server of ISCU. Because Scheme 3 provides for the fulfillment of the condition , from the standpoint of estimating the average time servicing of the request by the registration center server, this scheme is potentially the most effective among those proposed, provided that the content of the generalized route matrix is adequate.
To provide the possibility of random selection of the request from the queue, it is advisable to move from that oriented in Scheme 3 of the model of the queuing system (Equation (23)) to the queuing system of the type:
Equation (15) determines the average time of servicing of the request by the registration center server of ISCU, the processes of person–system interaction for which are described by the model of Equation (25), and will remain correct provided that the parameters , :
3.4. Formalization in the Mathematical Apparatus of Queuing Systems of the Process of Person–System Interaction, Organized According to Schemes 1–3, in a Continuous Time
Assuming that the information system for critical use interacts with the terminals of the person-users in a continuous time, then all the above (Equation (3)) can change their value at any time .
Continuously operating analogues of queuing systems (Equations (14) and (18)), which are oriented to Scheme 1 and operate in discrete time, will be systems of the form and .
For the first of them:
We formalize the average time that the request spent on the registration center server of ISCU, i.e., the sum of the waiting time for servicing the first request from the group and the time of servicing of the entire group of requests (transmission of the entire information package to the person-user according to their request; Equation (28)), by the expression:
where is the intensity of the input stream of the group of requests (request from the person-user to download the information package formed by the sequence of data blocks); is the intensity of servicing of one request; is the load of the registration center server of ISCU; is the average number of requests in the group; is the second moment of the number of requests in the group (if the stochastic value of the number of requests in the group corresponds to the geometric distribution, then ).
For a queuing system of type:
Here, the average time of servicing of the request by the registration center server of ISCU will be characterized by the expression:
where the already mentioned parameters and are redefined as:
The second moment of the stochastic value of time of servicing is defined as:
In the presented expressions, the parameter is a stochastic value with probability density , which characterizes the number of requests in the group for the target person-user.
Continuously operating analogues of queuing systems (Equations (19) and (33)), which are oriented to Scheme 2 and operate in discrete time, will be systems of type and with a random selection of the request from the queue. For a system of type:
With random selection of a request from the queue, the average time that the request spent on the registration center server of ISCU will be determined by Equation (28), provided that the average time of servicing of one request is redefined as:
According to Little’s formula, for a queuing system of the form:
With a random selection of a request from the queue, the average time that the request spent on the registration center server of ISCU will be determined by Equation (30), provided that the parameters and are overridden as follows:
Obviously, the average time that the request spends in the ISCU oriented according to Scheme 2 will be less than the same characteristic for the system oriented according to Scheme 1, provided that the content of the matrix is determined adequately. As mentioned in the previous section, a special case of Scheme 2 is a discrete-time model of a queuing system with a choice to service at each quantum of time of the request from the person-user with the highest bandwidth of the communication equipment. A continuous analogue of such a system will be a queuing system of the form of Equation (36), the average time that the group request of length spent in which we describe by the expression:
When determining the parameter of load of the registration center server of ISCU , the value of the intensity of service of one request will be calculated by Equation (37).
Continuously operating analogues of queuing systems (Equations (23) and (25)), which are oriented to Scheme 3 and operate in discrete time, can be created on the basis of the described systems (Equations (34) and (36)). In this case, Equations (28), (30) and (39) determine the average time that the request spent in the newly created queuing systems and remain relevant provided that the parameters , are determined taking into account the function instead of or . Considering that , such queuing systems will be potentially more productive than the generally considered systems of Equations (27), (29), (34) and (36). However, as the load on the communication component of the person–system interaction session increases, i.e., , the adequacy of this approach will decrease. Therefore, provided that , continuously operating analogues of queuing systems Equations (23) and (25), which are oriented to Scheme 3 and operate in discrete time, will be a system of type .
4. Results
The scientific results presented in the previous chapter of the article are focused on the description of the specifics of the organization of the person–system interaction session between the terminal of the person-user and the registration center server of the information system for critical use which operates in wireless communication space. This circumstance orients experiments on communication equipment certified according to IEEE 802.11 standards, namely, the most common of them being IEEE 802.11n HT and IEEE 802.11ac VHT; this wireless communication equipment operates in the frequency ranges of 2.5 GHz and 5 GHz, respectively, which peak bandwidth up to 7 Gbps. In addition to prevalence, the choice of those from the IEEE 802.11 family of standards is due to the fact that IEEE 802.11n HT and IEEE 802.11ac VHT at the hardware level support the technology of integrating different addressers and QoS settings of the MPDU (MAC protocol data unit, MDPU) packets into a single A-MPDU packet for the target addressee. It is exactly by varying the parameters of QoS settings during the formation of the A-MPDU package that it is possible to practically implement the schemes of organization of the person–system interaction session proposed in Section 3 of the article.
Initially, at a given throughput Mbps for a frequency band of 20 MHz, based on Equations (1) and (2), the values of the dependence of the throughputs and on the numbers of terminals of person-users that accessed the registration center server of ISCU with requests to download information packages with an average volume of kB were calculated. To simulate the change in the conditions of the communication environment in which the sessions of person–system interactions were implemented, determined according to the complex normal distribution the values of the elements of route matrices for each target person-user were incremented randomly at each quantum of time. The obtained analytical results are shown in Figure 6.
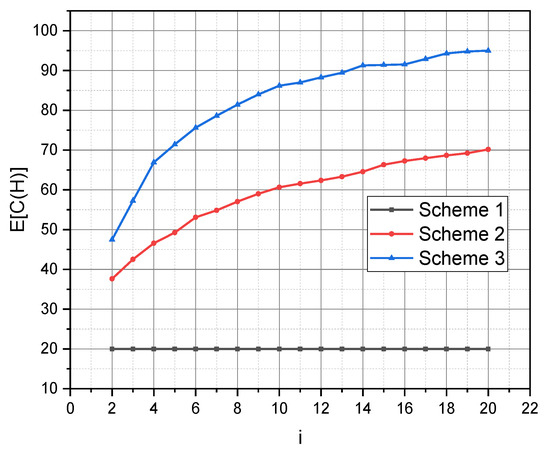
Figure 6.
Dependence of average throughput on the number of requests and the scheme of organization of sessions of person–system interaction.
Next, using Equations (13), (20) and (24), we calculated the parameters of the geometric distribution , , for Schemes 1, 2, 3, respectively. The values of , , obtained at the duration of the quantum of time and determined according to Figure 6 for values of Mbps, Mbps, Mbps for Schemes 1, 2, 3, respectively. According to the condition of stationarity, for the calculated parameters of the geometric distribution at the values of the probabilities are defined as . The defined and calculated parameters allowed when substituting in Equation (12) to calculate the dependences of the average time that the request spent on the server registration center of ISCU on the load level of the latter. The sessions of person–system interactions were organized according to Schemes 1–3 and using protocol with un-guaranteed activation of service . In graphical form, these dependencies are presented in Figure 7.
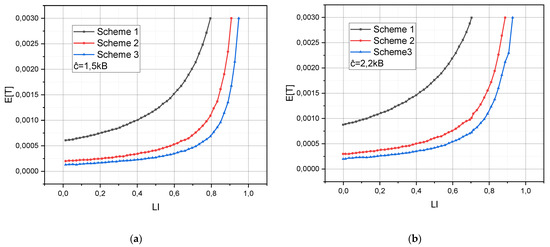
Figure 7.
The dependence of the average duration of the person–system interaction session on the scheme involved for its organization and the intensity of the load on the registration center server, provided that: (a) the volume of the information package is 1.5 kB; (b) The volume of the information package is 2.2 kB.
5. Discussion
As already mentioned, the analysis of the created models of queuing systems to describe the sessions of person–system interaction between the terminals of person-users and the registration center server of ISCU in a wireless communication environment according to the Schemes 1–3 showed that potentially the best criterion of minimizing the average time that a request spends in the ISCU is Scheme 3. The empirical results shown in Figure 7 confirm this hypothesis.
However, the hypothesis, formulated based on the results of the same considerations, regarding the superiority of Scheme 2 over Scheme 1 by the same criterion, turned out to be true with exceptions. Analysis of the reasons for this discrepancy showed that the closeness of the values of the functions and (Scheme 1 and Scheme 2, respectively), and sometimes and (Scheme 1 and Scheme 3, respectively) is observed when the communication capabilities of the registration center server of ISCU are limited (low value of ). Under such conditions, if the probability of receipt of new requests is consistently high and the session of person–system interaction is organized according to Scheme 2 or 3, the probability of gratifying an accepted request becomes smaller the longer the request is in the ISCU. This conclusion is confirmed by the results of the analysis of the values of the second moments for those requests, for which the values of the time spent on the registration center server significantly exceeded the average value of this stochastic indicator.
The revealed circumstance shows that if the task is to minimize the average time that the request spends on the registration center server of ISCU, provided that the communication capabilities of the latter significantly exceed the communication capabilities of the terminals of person-users: , then the scientific and applied results presented in the article are adequate and functional without exception. If the task is to minimize the average time that the requests from a target terminal or from a set of terminals spend on the registration center server of ISCU, then the scientific and applied results presented in the article are adequate but need clarification. The latter, potentially, is the need for an in-depth estimation of the impact of the values of the second moments of the average time that the requests spend on the registration center server of ISCU on the schemes of organizing the sessions of person–system interaction. However, a final conclusion on such a statement can be reached only after further research.
Thus, the analytical analysis of the created models of queuing systems for describing the sessions of the subject–system interaction between the terminals of the person-users and the registration center server of ISCU in a wireless communication environment, organized according to the Schemes 1–3, has shown that potentially the best, according to the criterion of minimizing the average time that the request spends on the registration center server of ISCU, is Scheme 3. The experimental results generally confirmed this hypothesis.
If the task is to minimize the average time that the request spends on the registration center server of ISCU, provided that the communication capabilities of the latter significantly exceed the communication capabilities of the terminals of person-users, then the scientific and applied results presented in this article are adequate and functional without exception. If the task is to minimize the average time that the requests from a target terminal or from a set of terminals spend on the registration center server of ISCU, then the scientific and applied results presented in the article are adequate but need clarification. The latter, potentially, is the need for an in-depth estimation of the impact of the values of the second moments of the average time that the requests spend on the registration center server of ISCU on the schemes of organizing the sessions of person–system interaction. However, a final conclusion on such a statement can be reached only after further research.
6. Conclusions
The relevance of introducing the information systems for critical use into modern social and technological infrastructures is beyond doubt and is constantly growing. At the same time, the only way to avoid significant material and human losses during the actual operation of such information systems is preliminary mathematical modeling of the development of their information processes in potential operating conditions.
In this article, for the first time, new mathematical models of schemes for organizing a session of the person–system interactions between the registration center server of the information system for critical use and the terminal of the person-user, implemented in the wireless communication space, are presented. In contrast to the existing models, this study used the mathematical apparatus of queuing systems to describe the schemes of organizing the stochastic process of a session of person–system interaction in discrete and continuous time, namely, models of the type with group arrival and ordinary service for the case of discrete representation of time and models of the type , for the case of continuous representation of time. The use of the mathematical apparatus of queuing systems in the study made it possible to obtain analytical expressions for comparing formalized schemes for organizing the person–system interaction by the values of such a functional characteristic as the average time of downloading a finite number of data blocks to the terminal of the target person-user (average time that the request spends on the registration center server of ISCU).
Author Contributions
Conceptualization, M.A.-M.; methodology, M.A.-M. and A.S.; software, M.A.-M. and A.A.; validation, M.A.-M. and A.A.; formal analysis, M.A.-M. and A.S.; investigation, M.A.-M.; writing—original draft preparation, M.A.-M. and A.A.; writing—review and editing, M.A.-M. and A.S.; supervision, M.A.-M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no. RG-1441-354.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Most data is contained within the article. All the data available on request due to restrictions eg privacy or ethical.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no. RG-1441-354.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| is a set of receiving–transmitting devices on the side of the registration center server; | |
| is a set of receiving–transmitting devices on side of the terminals of each person-user; | |
| is an index of the person-user terminal; | |
| is a power that characterizes such a session on the terminal of person-user on the side; | |
| is a route matrix; | |
| is a vector formed by data blocks of the information message, which is transmitted by the registration center server to the th terminal; | |
| is a vector formed by random values that characterize the noise affecting each receiving–transmitting device of the th terminal; | |
| is a peak power with zero mathematical expectation and variance ; | |
| is the spectral density of noise power; | |
| is a covariance matrix of noise; | |
| is a unit matrix; | |
| is a peak power of the information signal for the receiving–transmitting devices of the registration center server; | |
| is a signal-to-noise ratio; | |
| are the eigen values of the matrix ; | |
| is the power of signal transmission via the th route; | |
| is a constant, the value of which is chosen so that the equality is satisfied; | |
| is the total bandwidth (Equation (2)); | |
| is a covariance matrix of the person–system interaction sessions; | |
| is an average time it takes a person-user to download a finite amount of data; | |
| is a quantization period; | |
| is a stochastic process that describe a session of multi-person–system interaction in discrete time; | |
| is a stochastic value that characterizes the number of registered requests for session activation; | |
| is a vector formed by the values of the final queue lengths from data blocks for active sessions; | |
| is a vector formed by the values of the waiting times for the registered requests for activation of the session at the beginning of the th quantum of time, ; | |
| is a stochastic parameter that characterizes such an event: a registration center server receives a request to activate a person–system interaction session; | |
| is a speed of loading the data block by the person-user terminal; | |
| are stationary probabilities; | |
| is a workload of the registration center server of ISCU; | |
| is a generating function that characterizes a stationary distribution of the waiting time for the start of service of the first request in the group (start time of service of request); | |
| is an average number of requests served by the registration center server of ISCU; | |
| is the average time that the group request spends on the registration center server of ISCU (duration of downloading the information package); | |
| is a value of the bandwidth of the communication equipment of the terminal of the person-user. |
References
- Bisikalo, O.V.; Kovtun, V.V.; Sholota, V.V. The Information System for Critical Use Access Process Dependability Modeling. In Proceedings of the 9th International Conference on Advanced Computer Information Technologies (ACIT), Ceske Budejovice, Czech Republic, 5–7 July 2019; pp. 5–8. [Google Scholar] [CrossRef]
- Bisikalo, O.V.; Kovtun, V.V.; Yukhimchuk, M.S. Modeling the security policy of the information system for critical use. In Radio Electronics, Computer Science, Control; National University “Zaporizhzhia Polytechnic”: Zaporizhia, Ukraine, 2019; pp. 132–149. [Google Scholar] [CrossRef]
- Bisikalo, O.V.; Kovtun, V.V.; Kovtun, O.V.; Romanenko, V.B. Research of safety and survivability models of the information system for critical use. In Proceedings of the 11th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, 14–18 May 2020; pp. 7–12. [Google Scholar] [CrossRef]
- Maglogiannis, I.; Zafiropoulos, E. Modeling Risk in Distributed Healthcare Information Systems. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 5447–5450. [Google Scholar] [CrossRef]
- Guo, Q.; Xie, P.; Li, F.; Guo, X.; Li, Y.; Ma, L. Research on Linkage Model of Network Resource Survey and Vulnerability Detection in Power Information System. In Proceedings of the 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 May 2019; pp. 1068–1071. [Google Scholar] [CrossRef]
- Maslyanko, P.; Riabushenko, A. Modeling information-communication system of financial investment management. In Proceedings of the International Conference on Modern Problems of Radio Engineering, Telecommunications and Computer Science (TCSET), Lviv-Slavske, Ukraine, 23–27 February 2010; p. 243. [Google Scholar]
- Rogozov, Y.; Sviridov, A.; Degtyarev, A. The information environment for the integrated life cycle model of configurable information system. In Proceedings of the 8th International Conference on Application of Information and Communication Technologies (AICT), Astana, Kazakhstan, 15–17 October 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Lugović, S.; Dunđer, I.; Horvat, M. Primary and secondary experience in developing adaptive information systems supporting knowledge transfer. In Proceedings of the 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 22–26 May 2017; pp. 1207–1210. [Google Scholar] [CrossRef]
- Ongkasae, K.; Nakazato, H.; Koga, T.; Lu, X. QoS Implementation in System Wide Information Management (SWIM) Network Model. In Proceedings of the Twelfth International Symposium on Autonomous Decentralized Systems, Taichung, Taiwan, 25–27 March 2015; pp. 181–184. [Google Scholar] [CrossRef]
- Lopes RR, F.; Balaraju, P.H.; Sevenich, P. Creating Ever-changing QoS-constrained Dataflows in Tactical Networks: An Exploratory Study. In Proceedings of the International Conference on Military Communications and Information Systems (ICMCIS), Budva, Montenegro, 14–15 May 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Mendes, P.; Andres-Colas, J.; Pinho, C. Information model for the specification of QoS agreements among ambient networks. In Proceedings of the 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; Volume 3, pp. 1830–1834. [Google Scholar] [CrossRef]
- Juniang, Y.; Xiaoyuan, J.; Zhanwei, L.; Jia, D. Design and Implementation of Information Supporting System Model. In Proceedings of the WASE International Conference on Information Engineering, Taiyuan, Chanxi, 10–11 July 2009; pp. 427–430. [Google Scholar] [CrossRef]
- Sollfrank, M.; Trunzer, E.; Vogel-Heuser, B. Graphical Modeling of Communication Architectures in Network Control Systems with Traceability to Requirements. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 6267–6273. [Google Scholar] [CrossRef]
- Heo, J.; Shin, J.W.; Kim, H.S.; Shin, D.H.; Lee, G.S.; Lee, J.I. A Study for a New IT Service Information Protection Framework. In Proceedings of the Second International Conference on Systems and Networks Communications (ICSNC 2007), Cap Esterel, France, 25–31 August 2007; p. 70. [Google Scholar] [CrossRef]
- Zhang, M.; Ranjan, R.; Menzel, M.; Nepal, S.; Strazdins, P.; Jie, W.; Wang, L. An Infrastructure Service Recommendation System for Cloud Applications with Real-time QoS Requirement Constraints. IEEE Syst. J. 2017, 11, 2960–2970. [Google Scholar] [CrossRef]
- Gossett, J.; Noll, D.; Corman, D. Experiences in a distributed, real-time avionics domain-Weapons System Open Architecture. In Proceedings of the Fifth IEEE International Symposium on Object-Oriented Real-Time Distributed Computing. ISIRC-2002, Washington, DC, USA, 7 August 2002; pp. 307–314. [Google Scholar] [CrossRef]
- Airy, M.; Bhadra, S.; Heath, R.W.; Shakkottai, S. Transmit Precoding for the Multiple Antenna Broadcast Channel. In Proceedings of the IEEE 63rd Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006; pp. 1396–1400. [Google Scholar] [CrossRef]
- Bhadra, S.; Gupta P: Shakkottai, S. On Network Coding for Interference Networks. In Proceedings of the International Symposium on In Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 207–211. [Google Scholar] [CrossRef]
- Bisikalo, O.V.; Kovtun, V.V.; Kovtun, O.V. Modeling of the Estimation of the Time to Failure of the Information System for Critical Use. In Proceedings of the 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 13–15 May 2020; pp. 140–143. [Google Scholar] [CrossRef]
- Bisikalo, O.; Kovtun, O.; Kovtun, V.; Vysotska, V. Research of pareto-optimal schemes of control of availability of the information system for critical use. CEUR Workshop Proc. 2020, 2623, 174–193. [Google Scholar]
- Bisikalo, O.V.; Kovtun, V.V.; Kovtun, O.V.; Danylchuk, O.M. Mathematical modeling of the availability of the information system for critical use to optimize control of its communication capabilities. Int. J. Sens. 2020, 10. [Google Scholar] [CrossRef]
- Gibson, J. Information Theory and Rate Distortion Theory for Communications and Compression. Morgan Claypool 2013. [Google Scholar] [CrossRef]
- Rong, L.; Baiping, L.; Xinrong, M. The application of modern information technology in communication theory teaching. In Proceedings of the 2nd International Conference on Consumer Electronics, Communications and Networks (CECNet), Yichang, China, 21–23 April 2012; pp. 3566–3569. [Google Scholar] [CrossRef]
- Razavi, S.M.; Zamiri-Jafarian, H. Joint subspace beamforming and space-time coding in wireless MIMO systems. In Proceedings of the International Conference on Advanced Technologies for Communications, Hai Phong, Vietnam, 12–14 October 2009; pp. 99–103. [Google Scholar] [CrossRef]
- Fasano, A.; Barbarossa, S. Information Lossless Space-Time Coding for Multiple Access Systems. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; pp. III-45–III-48. [Google Scholar] [CrossRef]
- Tang, L.; Jing, X.; Zhang, Z. Adaptive switching based on Markov model for multiuser MIMO-OFDM systems. In Proceedings of the 22nd Wireless and Optical Communication Conference, Chongqing, China, 16–18 May 2013; pp. 101–104. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Liu, W.; Zeng, X. Wireless channel modeling and performance analysis based on Markov chain. In Proceedings of the 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 2256–2260. [Google Scholar] [CrossRef]
- Mo, J. Performance Modeling of Communication Networks with Markov Chains. Morgan Claypool 2010. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Z.; Li, X.; Han, Z.; He, Z.; Fu, Y. Performance analysis for multimedia communication systems with a multilayer queuing network model. China Commun. 2018, 15, 67–76. [Google Scholar] [CrossRef]
- Basukala, R.K.; Han, K.; Choi, D.; Kim, Y.; Han, S. QoS Assurance of Multimedia Traffic in Residential Network with Hybrid Co-ordination Function and Queuing Disciplines. In Proceedings of the Pacific-Asia Conference on Circuits, Communications and Systems, Chengdu, China, 16–17 May 2009; pp. 767–770. [Google Scholar] [CrossRef]
- Ciampa, M.; Franciosi, M.; Poletti, M. A note on impulse response for continuous, linear, time-invariant, continuous-time systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 106–113. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).