Abstract
This paper presents a large eddy simulation of a centrifugal pump impeller during a transient condition. The flow rate is sinusoidal and oscillates between 0.25Qd (Qd indicates design load) and 0.75Qd when the rotating speed is maintained. Research shows that in one period, the inlet flow rate will twice reach 0.5Qd, and among the impeller of one moment is a stall state, but the other is a non-stall state. In the process of flow development, the evolution of low-frequency pressure fluctuation shows an obviously sinusoidal form, whose frequency is insensitive to the monitoring position and equals to that of the flow rate. However, inside the impeller, the phase and amplitude in the stall passages lag behind more and are stronger than that in the non-stall passages. Meanwhile, the strongest region of the high-frequency pressure fluctuation appears in the stall passages at the transient rising stage. The second dominant frequency in stall passages is 2.5 times to that in non-stall passages. In addition, similar to the pressure fluctuation, the evolution of the low-frequency head shows a sinusoidal form, whose phase is lagging behind that by one-third of a period in the inlet flow rate.
1. Introduction
The centrifugal pump impeller is one of the key parts of a centrifugal pump, which is widely used in petrochemical, hydraulic engineering, and the coal chemical and aerospace industries. The biggest characteristic of a centrifugal pump during normal operation is that the flow rate and rotating speed do not change with time. This operating condition is called a quasi-steady condition. At present, the main achievements of centrifugal pump research are mainly concentrated in this field. With the deepening of research, some transient operations (such as start-up, shutdown, quick adjustment of the valve) can lead to transient load, where the impeller internal flow is more complex. In this case, the inlet flow rate of the centrifugal pump or the impeller rotary speed will change with time. The flow caused by these operations is called transient flow. The stall phenomenon of a centrifugal pump may appear under the condition of a quasi-steady low flow rate, which will not only increase the complexity of internal flow, but also will cause irregular changes of pressure and velocity field, and even causes strong pressure fluctuation. These phenomena will be further intensified during the transient condition. The quasi-steady study of centrifugal pumps has difficultly in explaining these transient flow phenomena. Therefore, the research on the transient flow of centrifugal pumps is of great significance for understanding the transient operation phenomena of centrifugal pumps.
Through experimental measurements and numerical simulations, there have been many studies focusing on the pressure fluctuation with the stall [1,2,3,4] in the centrifugal pump impeller. The stall is a common flow phenomenon in centrifugal pump impellers. Among them, the alternative stall has significant symmetry, while the rotating stall does not. In addition, most previous studies have been considered under a quasi-steady condition, which means that no operating process changes with the time. For example, Pedersen et al. [5] and Byskov et al. [6] studied the flow characteristics in a centrifugal pump impeller at design and off-design conditions. They found that significant differences are revealed between the two adjacent impeller passages at quarter load. One passage is dominated by rotational effects causing high velocities along the blade pressure side. The other passage exhibits a highly separated flow field in the entry section and a significant stall is observed. Zhao et al. [7] analyzed the mechanism of pressure fluctuation and stall propagation caused by rotating stalls and found that flow separation occurred near the leading edge of the pressure surface and transformed into vortices along the channel. Jia [8] studied the transient fluid excitation force caused by the unsteady flow in a centrifugal pump and obtained that the internal flow loss and low-frequency vibration energy of the impeller varies with the flow conditions, showing similar changes. Ni [9] found that the coupling between the rotor–stator interaction and the collision of the fluid discharged from the diffuser with the circulating flow to the casing bottom is the main cause of the strong pressure pulsation. Zheng et al. [10] found that the dominant frequency amplitude of the pressure fluctuation at the impeller inlet increased with the flow rate increase, whereas an inverse trend was observed at the wear ring clearance region. Gao et al. [11] found that a reasonable blade trailing edge of a centrifugal pump impeller can effectively reduce pressure pulsation. Wang et al. [12] found that the pressure pulsation of a centrifugal pump impeller is greatly affected by the flow rate and speed, and the pressure pulsation at partial speed is greater than that at higher speed. Huang [13] studied the pressure fluctuation characteristics in the water pump mode and obtained that the amplitude of the rotor–stator interaction frequency is continuously attenuated from the bladeless area to the exit of the tie rod blades, and the amplitude attenuation of each frequency is mainly concentrated in the guide vane area.
Although many studies have been carried out for centrifugal pump impellers and have provided a good understanding of the pressure fluctuation characteristics during a quasi-steady condition, these conclusions are difficult to be directly extended to a transient condition. Compared with the quasi-steady condition, the reports of transient flow characteristics in the centrifugal pump are relatively few, and are concentrated at the pump start-up process [14,15,16,17,18,19,20] or shutdown process [21,22,23,24]. For example, Zhang et al. [14] found that the flow characteristics at the pump start-up process cannot be accurately represented by the results during the quasi-steady condition. Li [15,16] and Liu [21] investigated the influence of the pump start-up and shutdown process on the external characteristics. Tanaka and Tsukamoto [22] studied the evolution of pressure and velocity at the shutdown process. They found that the pressure fluctuation was caused by the separation of the water column. Tanaka and Tsukamoto [25] explained that the transient flow would lead to pressure fluctuation, which was related to cavitation or column separation. In addition, the rotating speed of the centrifugal pump is transient. Tsukamoto and Ohashi [26,27] found that the shock pressure difference caused the initial stage of the centrifugal pump start-up, and the phenomenon can be explained by the total pressure coefficient being greater than that for the quasi-steady condition.
The research on the pressure fluctuation of the centrifugal pump impeller under a transient condition is still few, especially when the flow rate includes both transient rising and transient dropping stages within one working condition. However, such a working condition is a common industrial problem due to the inlet of a centrifugal pump impeller being blocked temporarily or the valve being adjusted quickly. In order to explain the pressure fluctuation process under such a working condition, accurate data of the centrifugal pump impeller are required. Compared with the data obtained by experimental measurements [28] and Reynolds-averaged Navier–Stokes (RANS) [29,30,31,32], large eddy simulation (LES) can solve the model with more accurate data of internal flow and has been applied to the centrifugal pump impeller [33,34,35].
In the present study, a LES of a centrifugal pump impeller, whose flow rate is periodically varied, is performed to investigate the evolution of pressure fluctuation during a transient condition. The flow rate change of the centrifugal pump impeller in one period is symmetrical. For comparison, three LES for the quasi-steady condition are also carried out to study the influence of transient flow on the pressure fluctuation. The paper structure is as follows. The model descriptions and numerical considerations are given in Section 2 and Section 3, respectively. Simulation verification is given in Section 4. Section 5 presents LES results and discussions. Finally, we summarize our findings in Section 6.
2. Model Descriptions
2.1. Geometric Model
The geometric model of the centrifugal pump impeller is a single stage in the low specific speed multi-stage centrifugal pump commonly used in industry, as shown in Figure 1. The impeller has six vertical blades. The impeller parameters are as follows: the head H = 1.75 m, rotating speed n = 725 rev/min, and flow rate at design load Qd = 3.06 L/s. The outer radius of the impeller is 95 mm, and the inlet height and outlet height are 13.8 and 5.8 mm, respectively. Several other parameters of the centrifugal pump impeller are listed in Table 1.
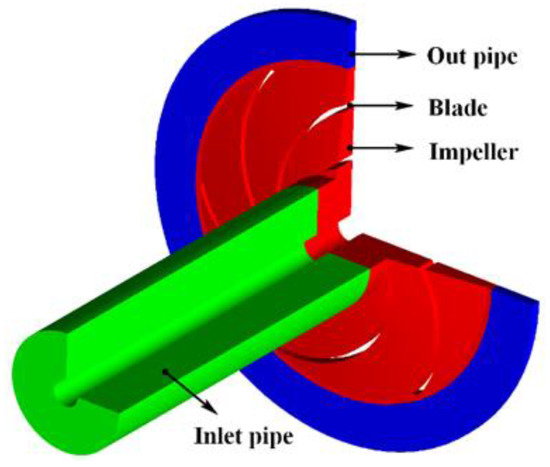
Figure 1.
Three dimensional model of the centrifugal pump impeller.

Table 1.
Geometric parameters of centrifugal pump impeller.
It should be justified to set the flow rate as a sinusoidal function which oscillates between 0.25Qd and 0.75Qd when the rotating speed is maintained, as shown in Figure 2, which can be expressed as follows:
where 0.5Qd and 0.25Qd are the equilibrium and amplitude flow rates, respectively; n/6 is the frequency. The initial phase of the function is zero. Five instantaneous points, including two maximum (1 and 5), one minimum (3), and two equilibrium (2 and 4) flow rates, are selected to investigate the behavior of pressure fluctuation. At this time, the evolution of flow rate includes a dropping stage (instantaneous points from 1 to 3) and a rising stage (instantaneous points from 3 to 5). For comparison, three flow rates (0.25Qd, 0.5Qd, 0.75Qd) during the quasi-steady conditions are also performed.
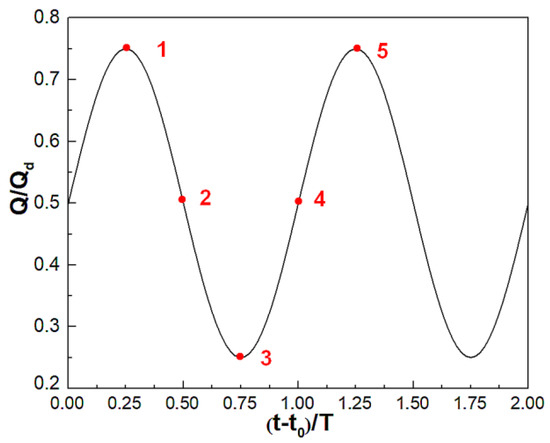
Figure 2.
Centrifugal pump impeller inlet flow rate.
2.2. Mesh Generation
The centrifugal pump impeller is divided into three computational domains: inlet pipe, impeller, and outlet pipe. ICEM is used to divide the three computational domains into structural grids. In order to accurately simulate the complex flow in the impeller, the near-wall area with a large pressure gradient and velocity gradient is encrypted. The grid used for calculation is shown in Figure 3. The height of the first layer of the blade wall is about 0.01 mm, and it grows to the center area at a growth rate of 1.2. The total grid number of the centrifugal pump impeller is 11 million, of which the impeller domain is 7.67 million, the single flow passage is 1.26 million, the inlet pipe is 2.55 million, and the outlet pipe is 0.78 million.
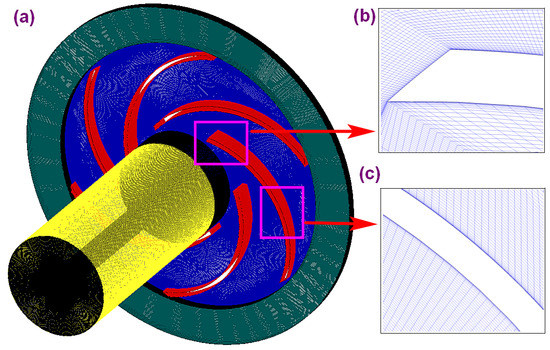
Figure 3.
Grids of centrifugal pump impeller: (a) view of centrifugal pump impeller, (b) blade front view, (c) blade middle view.
In this paper, the change of the external characteristics of the centrifugal pump with the number of grids at 0.25Qd was studied. As shown in Figure 4, with the increase of the number of grids, the head of the centrifugal pump impeller gradually increases. After 10 million grids, the head of the centrifugal pump impeller becomes stable. Compared with 14 million grids, the relative error of the head calculated with 12 million grids was less than 0.1%. Considering the efficiency of the calculation process and the minimum requirements of the LES computing grid, the 12 million grids number model was finally selected for follow-up research.
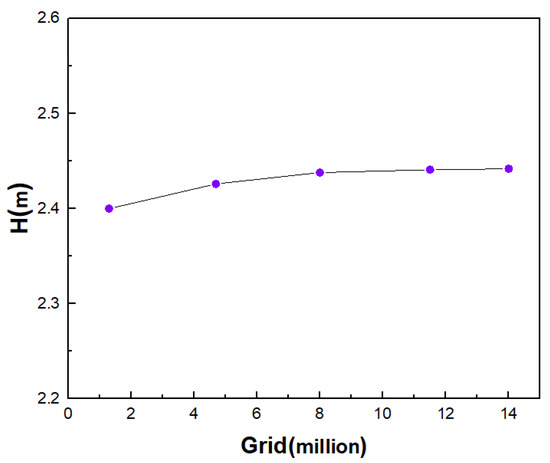
Figure 4.
Grid refinement research.
3. Numerical Considerations
The simulation was carried out by ANSYS CFX 16.0. The finite volume method and the LES were used to calculate the single-phase flow of the centrifugal pump impeller. The basic principle of LES is to separate the large vortex from the small vortex by introducing a filter length. Additionally, the influence of the unresolved (or sub-grid) scale is taken into account through an appropriate sub-grid scale (SGS) model. The paper chooses the dynamic SGS (sub-grid scale) LES model to calculate the internal flow in the pump, which has high precision for predicting the rotating stall phenomenon.
The advection scheme for the overall solution accuracy was set to high resolution, and the solution accuracy for the non-stationary part used the second order backward Euler transient scheme. The interface of the impeller adopts the transient rotor–stator method. The velocity was provided at the suction inlet of the computational domain. The pressure was used as the boundary condition of the impeller’s outlet, and the outlet pressure was 0 pa. All walls had specified boundary conditions of no-slip and no penetration velocity. The schematic diagram of the boundary conditions is shown in Figure 5. The numerical solution settings are shown in Table 2.
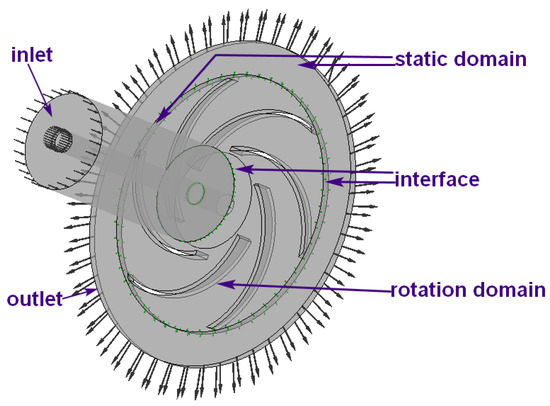
Figure 5.
Calculation domain and boundary conditions of centrifugal pump impeller.

Table 2.
Boundary conditions and numerical setup of the simulations.
The time step, Δt = 0.00023 s, was equivalent to the time it takes for the impeller to rotate one degree. The sampling frequency was 4.35 kHz, which can meet the accuracy requirements of subsequent data processing. At the same time, considering the influence of the matching degree between the grid size and the time step on the accuracy of the calculation results, the different treatment was adopted when the Courant number was too large in the calculation process. The maximum number of iterations per time-step was set to 10. The flow fields during the transient condition, whose flow rate was periodically changed, have developed for 8640 time-steps, which is equivalent to 24 revolutions of the impeller.
LES of the centrifugal pump impeller during a quasi-steady condition was also performed, whose method was consistent with that for a transient condition. Figure 6 shows the distributions of y+ at quasi-steady conditions. It is shown that the value of y+ is less than 9.0 at the overall impeller and 1.0 near the blade. Thus, the grid can meet the requirements of LES.
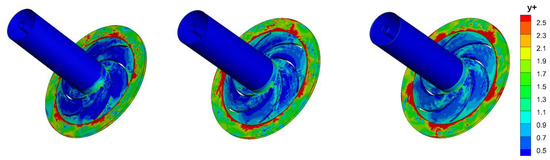
Figure 6.
y+ distribution on the centrifugal pump impeller during a quasi-steady condition. 0.25Qd (left); 0.50Qd (middle); 0.75Qd (right).
4. Simulation Verification
Due to several experimental measurements and numerical simulations having been reported during the quasi-steady condition, the data verifications are based on these conditions.
The head obtained by the LES is in good agreement with the experimental data performed by Pedersen et al. [5]. Although the former averaged head is larger than that for the latter, the relative errors of the two methods are less than 5%, as shown in Figure 7. Compared with 0.25 Qd and 0.5 Qd conditions, the head of the impeller under a 0.75 Qd condition is quite different from the fitted head curve. There are two reasons for this phenomenon. First, Pedersen [5] only conducted experiments on this centrifugal pump impeller under 0.25 Qd and 1.0 Qd conditions. The head curve in Figure 7 is the result depicted by Pedersen [5], which is not absolutely accurate. Second, according to the previous numerical calculation results, this impeller has a hump near the 0.7 Qd condition, so the head of the impeller will be raised in the 0.75 Qd condition. The distributions of the relative velocity for both the two methods are similar, and present obviously “two-channel” (one of the two adjacent channels is in a stall state and the other is in a non-stall state) phenomenon under a quarter load, as shown in Figure 8left,right. The relationship between stall passage and non-stall passage is central symmetry about the impeller rotating shaft.
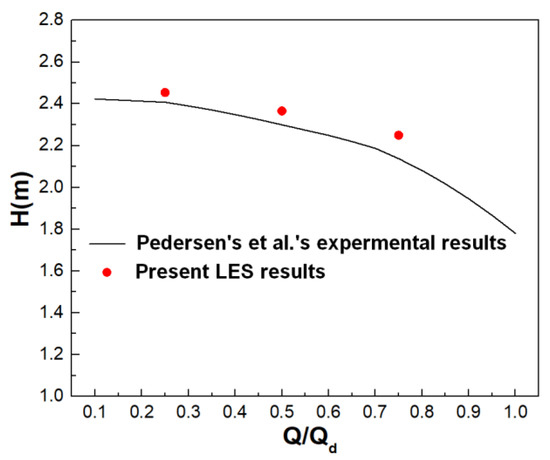
Figure 7.
Performance curve [5] of the centrifugal pump impeller under different quasi-steady conditions with low flow.
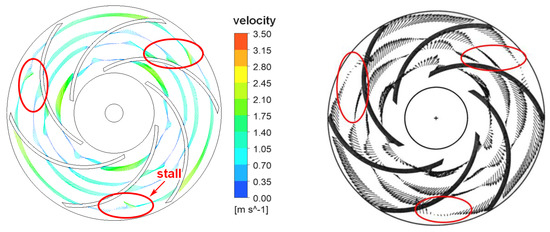
Figure 8.
Relative velocity vectors during a quasi-steady condition at 0.25 Qd in the impeller mid-height, z/b2 = 0.5, given at radial position of r/R2 = {0.5,0.65,0.75,0.9}. Compared using large eddy simulation (LES) (left) and measured using laser doppler velocimetry (LDV) (right) [5].
Pedersen [5,36] measured the mean radial velocity between blade-to-blade at 0.25 Qd by LDV (laser doppler velocimetry) and PIV (particle image velocimetry) experiments. As shown in Figure 9, at r/R2 = 0.5, in the passages A, the experiment results show that the value of mean radial velocity from the pressure surface to the suction surface gradually increases. Compared with the experiment, while the LES results of this paper are similar to the experimental results, the amplitude of the pressure surface is higher. This remarkable difference is mainly attributed to the influence of pre-rotation. This problem is explained in detail in Byskov’s research results [5]. In passages B, the stall phenomenon is obvious in the experimental velocity curve, which shows that mean radial velocity changes sharply in the passage span at r/R2 = 0.5. The mean radial velocity indicates the reverse flow along the suction side, and the position and size of LES and PIV peaks are similar. Because the peak value of mean radial velocity predicted by LES deviates slightly to the suction side, there is a small reverse vortex on the pressure side.
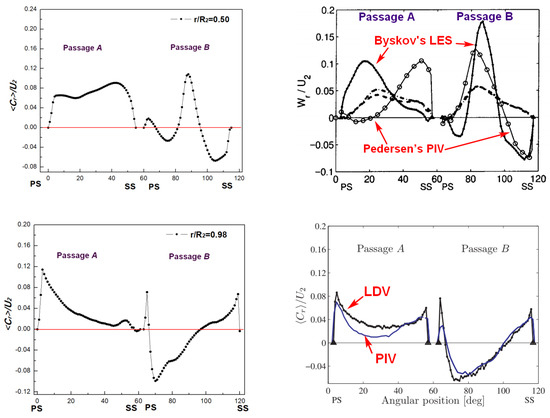
Figure 9.
Blade-to-blade distributions of the mean radial velocity <Cr>/U2 measured with an experiment (right) [36] and LES simulation (left) at 0.25 Qd. r/R2 = 0.50 (up); r/R2 = 0.98 (down).
The mean radial velocity distribution with r/R2 = 0.98 is shown in Figure 9. The LES simulation results are consistent with the experimental results. In passages A, LES results show that the radial velocity amplitude of the impeller suction surface is smaller than that observed by Pedersen’s experiment [36]. This may be due to the stronger jet structure on the pressure surface in LES, which limits the exit velocity of the suction surface. Meanwhile, due to the leakage in the experiment, the jet flow of the impeller is reduced. In passages B, the experimental results are consistent with those of LES in this paper, but LES captures stronger impeller outlet reflow. By comparing the results of the experiment and the LES, it can be found that the LES can effectively capture the internal flow of the impeller, but there are differences in the details.
Therefore, it can be concluded that the present simulation method is feasible, and the results are reliable.
5. Results and Discussion
5.1. Pressure Distribution
The internal pressure of the centrifugal pump impeller was analyzed. The pressure coefficient (Cp) is defined as [37]
Figure 10 shows the distributions of the pressure coefficient during a transient condition in the impeller mid-height plane (z/b2 = 0.5). It is indicated that, at all instantaneous flow rates, the pressure coefficient increases gradually with the axial position increase, and there are several low pressure regions at the impeller inlet. However, the difference of the low-pressure regions is significant at different instantaneous flow rates. A low-pressure region is observed at the suction front edge at instantaneous 0.75Qd, whose phenomena are similar in the six passages. The “two-channel” pattern characteristics appear in the low-pressure region at instantaneous 0.25Qd. It means that the pressure of one passage is obviously lower than that of another passage, which is one of the stall characteristics. Unlike instantaneous 0.75Qd and 0.25Qd, the other instantaneous flow rate includes rising and dropping stages, and those low-pressure characteristics are different. For example, considering the instantaneous 0.5Qd, the low-pressure region in rising and dropping stages is similar to that at 0.25Qd and 0.75Qd, respectively.
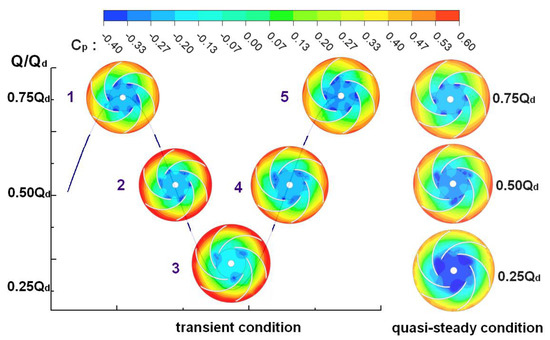
Figure 10.
Distributions of the pressure coefficient under a transient condition at the impeller mid-height, z/b2 = 0.5.
Figure 11 shows the distributions of relative velocity during a transient condition in the impeller mid-height plane (z/b2 = 0.5). The results show that the maximum value of the relative velocity is mainly concentrated in the impeller inlet and outlet regions. The area of those regions decreases with the instantaneous flow rate decreases. Although the value of the relative velocity is opposite of that for static pressure, similar channel pattern characteristics can be obtained in the region of the impeller inlet. Moreover, these channel pattern characteristics will be developed and evolved in the impeller passage. According to the above analysis, it can be concluded that non-stall is observed on instantaneous 0.75Qd, whereas the stall will appear at instantaneous 0.5Qd and 0.25Qd.
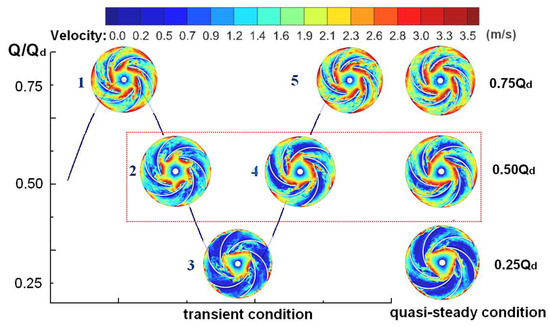
Figure 11.
Distributions of relative velocity in the impeller mid-height, z/b2 = 0.5.
In order to investigate the influence of transient flow rate on the internal flow on the impeller mid-height plane (z/b2 = 0.5), the distributions of pressure and relative velocity during a quasi-steady condition, including three constant flow rates (0.75Qd, 0.5Qd, and 0.25Qd), are also shown in Figure 10 and Figure 11, respectively. Note that non-stall is observed on 0.75Qd, whereas the stall will appear at 0.5Qd and 0.25Qd. It is indicated that the stall characteristics are not varied by a periodic transient condition under the three flow rates. However, there are still several differences between the transient and quasi-steady conditions, especially at 0.5Qd. For example, due to the internal flow field being expanded during a transient condition at the dropping stage, the two-channel phenomenon is weaker than that for the quasi-steady condition. An opposite effect is at the rising stage. Therefore, the transient flow has a significant effect on the internal flow in the centrifugal pump impeller, even the stall.
5.2. Pressure Fluctuation in the Impeller Mid-Height
Figure 12left shows the pressure fluctuation in the impeller mid-height at the passage inlet during a transient condition. Note that the information of pressure fluctuation is abundant, including its low-frequency component. The evolution of low-frequency pressure fluctuation shows obvious periodicity, whose frequency is the same as that for the flow rate. Several differences are observed between the stall passage (B) and non-stall passage (A). Firstly, compared with Passage A, the phase of Passage B is one-tenth of a period behind. Secondly, the maximum and minimum values of pressure of Passage A are approximated as −21,000 Pa and −25,000 Pa, whereas the maximum and minimum values of pressure for Passage B are approximately −22,000 Pa and −29,000 Pa, respectively. It is indicated that the amplitude of the pressure fluctuation for Passage B is twice as large as Passage A.
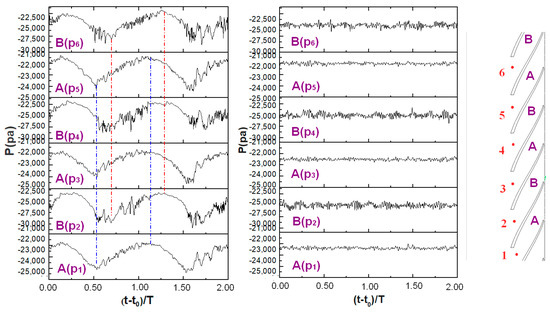
Figure 12.
Distributions of pressure fluctuation at the impeller inlet in the impeller mid-height, z/b2 = 0.5: (left) transient condition; (right) quasi-steady condition at two-quarter load.
The development of the low-frequency pressure fluctuation is accompanied by the high-frequency component. The amplitude of high-frequency components at the transient rising stage is much larger than that at the transient dropping stage, which indicates that the internal flow is more unstable at this stage. Moreover, the high-frequency signal in Passage B is more complicated than that in Passage A, especially at the transient rising stage.
In order to investigate the influence of transient flow rate on the pressure fluctuation, the results of the quasi-steady condition at 0.5Qd are shown in Figure 12right. It is shown that, similar to the transient condition under a corresponding instantaneous flow rate, the high-frequency pressure fluctuation at Passage B is larger than that at Passage A. However, there are no obvious periodic characteristics during the quasi-steady condition, especially in the low-frequency pressure fluctuation.
Figure 13 shows the evolution of static pressure fluctuation on the blade surface, including suction and pressure surfaces, at the impeller mid-height during the transient condition. Note that, with the development of impeller passages, the average pressure increases, which is consistent with the distribution of the static pressure coefficient, as shown in Figure 10. Each evolution of pressure fluctuation with time, including its low and high-frequency components, is similar to that at the impeller inlet. The period amplitude of low-frequency pressure fluctuation decreases with the development of the impeller passage. Moreover, the period amplitude of low-pressure fluctuation on the suction surface is weaker than that on the pressure surface. For the high-frequency pressure fluctuation, with the development of impeller passages, the amplitude on the suction surface decreases, whereas the amplitude on the pressure surface first decreases and then increases to its maximum value. In addition, regardless of the suction and pressure surfaces, the pressure fluctuation in Passage B is stronger than that in Passage A.
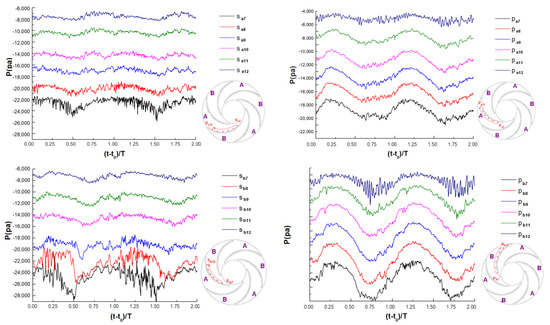
Figure 13.
Distributions of pressure fluctuation during the transient condition in the impeller mid-height, z/b2 = 0.5, given at radial positions of r/R2 = {0.50, 0.58, 0.66, 0.74, 0.82, 0.90}: (left) suction surface, (right) pressure surface; (top) non-stall passages; and (bottom) stall passages.
The difference of pressure fluctuation characteristics has an important relationship with the velocity field, especially in the vortex structures. The stall vortex structure will strengthen the pressure fluctuation. For example, Figure 11 shows that, compared with the pressure surface, the stall vortex is closer to the suction surface, so that the pressure fluctuation on the suction surface is stronger than that on the pressure surface.
In order to further investigate the characteristics of pressure fluctuation in the impeller mid-height, the frequency spectra, performed by the fast Fourier transform (FFT), is shown in Figure 14left. It is shown that the first dominant frequency of both stall and non-stall passages are approximately 2.00 HZ, which is the same as the frequency of the flow rate. The second dominant frequency of stall and non-stall passages are 0.084fBPF (blade passing frequency) and 0.070fBPF, respectively. However, the amplitude of the frequency of pressure fluctuations for stall passages is significantly larger than that for non-stall passages. For example, the relationship between the amplitude of the second dominant frequency of stall and non-stall passages is 2.5 times. However, there is no frequency with an amplitude greater than 140 during the quasi-steady condition at 0.5Qd, as shown in Figure 14right. In addition, the amplitude of the first dominant frequency during the transient condition is obviously greater than that during the quasi-steady condition. Moreover, the second dominant frequency and its higher frequencies will be enlarged because of the coupling of the different frequencies. By analyzing the frequency spectrum of the quasi-steady state and transient flow, it can be obtained that the disturbance at the inlet of the centrifugal pump impeller enhances the complexity and intensity of the pressure pulsation in the impeller.
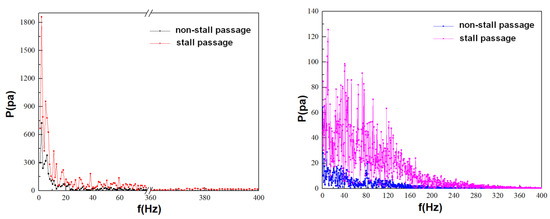
Figure 14.
Distributions of pressure frequency spectra at the impeller inlet in the impeller mid-height, z/b2 = 0.5: (left) transient condition; (right) quasi-steady condition at two-quarter load.
5.3. Pressure Fluctuation in the Impeller Axial Plane
In order to investigate the evolution of pressure fluctuation in the impeller axial plane, four monitoring points, including one point in the impeller inlet and three points in the impeller passages, are selected, as shown in Figure 15.
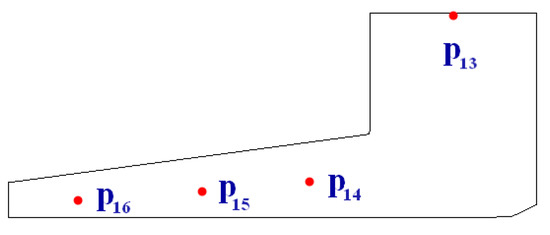
Figure 15.
Monitoring points in the impeller axial plane, x = 0.0, given at radial positions of r/R = {0.25, 0.50, 0.7, 0.9}.
Figure 16left,right shows the evolution of pressure fluctuation in the impeller axial plane during transient and quasi-steady conditions, respectively. Similar to the results in the impeller mid-height, an obvious periodicity of low-frequency pressure fluctuation can be observed during the transient condition, whereas this phenomenon has not appeared during the quasi-steady condition. It is indicated that the lag effects of the phase of low-frequency pressure fluctuation become more significant as the development of impeller passages.
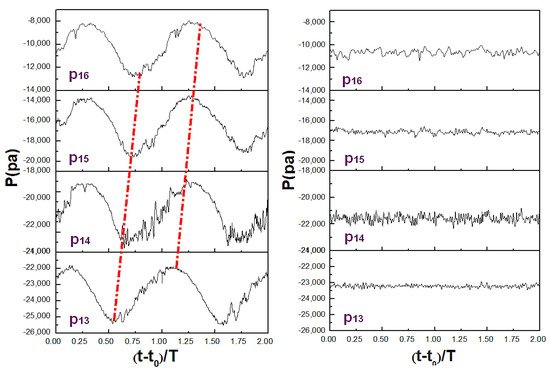
Figure 16.
Distributions of pressure fluctuation in the impeller axial plane, x = 0.0, given at radial positions of r/R2 = {0.25, 0.50, 0.7, 0.9}: (left) transient condition; (right) quasi-steady condition for two quarter-load.
In addition, the difference of the pressure between the inlet and outlet planes of the computational domain can be respected by the head. Figure 17 shows the relationship between the head and time and flow rate. Note that the head for the transient condition cannot be represented by a value but varies within a range of 2.23 and 2.58 m, which is different from the quasi-steady condition. The frequency of the head has no relationship with that for the flow rate. However, compared with the flow rate, the phase of the head lags one-third of period. Moreover, the maximum and minimum values of the head are larger and smaller than that for quasi-steady conditions at three quarter-load and quarter-load, respectively. For the instantaneous two quarter-load, the head under transient rising and dropping stages are always larger and smaller than that for quasi-steady conditions.
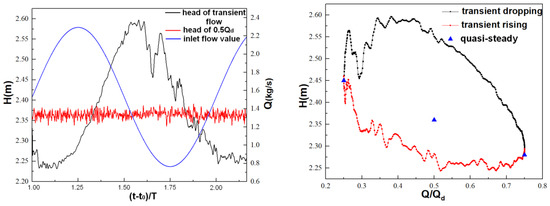
Figure 17.
Relationship between performance curve and (left) time and (right) flow rate.
6. Discussion
Large eddy simulation (LES) of a centrifugal pump impeller during a transient condition was performed to study the characteristics of pressure fluctuation. The flow rate changes in the form of a sinusoidal function with a zero initial phase, whose frequency was one-sixth of the rotating speed, and equilibrium and amplitude values were 0.5Qd and 0.25Qd. The reliability of the LES data was verified by comparing with existing experimental data.
The distributions of the pressure coefficient and relative velocity of adjacent passages show that the non-stall and stall phenomenon will appear alternately, which obviously corresponds to instantaneous 0.75Qd and 0.25Qd, respectively. Moreover, the stall phenomenon at instantaneous 0.5Qd in the rising stage was more significant than that in the dropping stage. The stall passages will not shift with the time development. That is, the symmetry of the stall passage and non-stall passage remains unchanged.
The distribution of low-frequency pressure fluctuation showed a significant periodicity during transient flow, but it was not observed during the quasi-steady condition. Although the frequency of low-frequency pressure fluctuation always equals that of flow rate, its phase and amplitude have a relationship with the monitoring position. The phase in the stall passages on the impeller mid-height plane lags one-tenth of a period than that in non-stall passages of the impeller inlet. As the flow deepens on the impeller axial plane, the lag of the phase becomes more obvious. In addition, the amplitude of the pressure fluctuation of the pressure surface was obviously larger than that of the suction surface.
The high-frequency pressure fluctuation was observed under both transient and quasi-steady conditions. The high-frequency pressure fluctuation at the transient rising stage was stronger than that at the transient dropping stage. Comparing stall passages with non-stall passages, the first and second dominant frequencies presented little change in stall passages, whereas the corresponding amplitude of the first dominant was enlarged by 2.5 times than the one of the second dominant. Moreover, the amplitude of the high-frequency pressure fluctuation of the transient condition was significantly higher than that of the quasi-steady condition because of the coupling of different frequencies.
Similar to the pressure fluctuation, the head not only had high-frequency fluctuation caused by the unsteady flow, but also had low-frequency periodic characteristics, whose phase lagged behind one-third of a period than the phase of the inlet flow rate. Meanwhile, on this account the lag of impeller head, the head of the transient dropping stage was higher than that of the rising stage at the same flow rate.
Author Contributions
Conceptualization, R.K. and X.C.; formal analysis X.C. and R.K.; supervision, X.C., Z.Z. (Zuchao Zhu); Validation, R.K., Z.Z. (Zhiming Zhang), and Y.L.; writing—original draft, R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported under the auspices of the National Natural Science Foundation of China (Grant No. 51976198) and Key Research and Development Program of Zhejiang Province (Grant No. 2020C01163 and 2019C01143).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | channel |
| B | channel |
| Cp | pressure coefficient |
| Cr | radial velocity |
| d | blade thickness |
| h | height |
| H | head |
| n | rotational speed |
| p | monitor point |
| P | static pressure |
| Pi | monitor point static pressure |
| average static pressure | |
| Q | flow rate |
| Qd | design flow rate |
| R1 | inlet radius |
| R2 | outlet radius |
| Rb | blade curvature radius |
| t | time |
| T | the time of one cycle of inlet flow change |
| U2 | circumferential velocity at impeller outlet |
| V | relative velocity |
| x | coordinate components |
| y+ | dimensionless wall distances |
| z | section height |
| Z | number of blades |
| λ1 | inlet blade angle |
| λ2 | outlet blade angle |
Acronyms
| FFT | Fast Fourier Transform |
| LES | Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier-Stokes |
| SST | Shear Stress Transfer |
References
- Zhou, P.-J.; Dai, J.-C.; Li, Y.-F.; Chen, T.; Mou, J.-G. Unsteady flow structures in centrifugal pump under two types of stall conditions. J. Hydrodyn. 2018, 30, 1038–1044. [Google Scholar] [CrossRef]
- Braun, O. Part Load Flow in Radial Centrifugal Pumps. Ph.D. Thesis, Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, Switzerland, 2009. [Google Scholar]
- Braun, O.; Avellan, F.; Dupont, P. Unsteady numerical simulations of the flow related to the unstable energy-discharge characteristic of a medium specific speed double suction pump. In Proceedings of the 5th Joint ASME/JSME Fluids Engineering Conference, San Diego, CA, USA, 30 July–2 August 2007. [Google Scholar]
- Tao, R.; Wang, Z. Comparative modeling and analysis of the flow asymmetricity in a centrifugal pump impeller at partial load. Proc. Inst. Mech. Eng. 2019, 234, 237–247. [Google Scholar] [CrossRef]
- Pedersen, N.; Larsen, P.S.; Jacobsen, C.B. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions—Part I: Particle Image Velocimetry (PIV) and Laser Doppler Velocimetry (LDV) Measurements. J. Fluids Eng. 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Byskov, R.K.; Jacobsen, C.B.; Pedersen, N. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions—Part II: Large Eddy Simulations. J. Fluids Eng. 2003, 125, 73–83. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, Y.; Cao, L. Unsteady Flow and Pressure Pulsation Characteristics Analysis of Rotating Stall in Centrifugal Pumps Under Off-Design Conditions. J. Fluids Eng. 2017, 140, 021105. [Google Scholar] [CrossRef]
- Jia, X.-Q.; Zhu, Z.-C.; Yu, X.-L.; Zhang, Y.-L. Internal unsteady flow characteristics of centrifugal pump based on entropy generation rate and vibration energy. Proc. Inst. Mech. Eng. 2018, 233, 456–473. [Google Scholar] [CrossRef]
- Ni, D.; Zhang, N.; Gao, B.; Li, Z.; Yang, M. Dynamic measurements on unsteady pressure pulsations and flow distributions in a nuclear reactor coolant pump. Energy 2020, 198, 117305. [Google Scholar] [CrossRef]
- Zheng, L.L.; Chen, X.P.; Zhang, W.; Zhu, Z.C.; Cheng, C. Investigation on characteristics of pressure fluctuation in a cen-trifugal pump with clearance flow. J. Mech. Sci. Technol. 2020, 34, 3657–3666. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, N.; Li, Z.; Ni, D.; Yang, M. Influence of the Blade Trailing Edge Profile on the Performance and Unsteady Pressure Pulsations in a Low Specific Speed Centrifugal Pump. J. Fluids Eng. 2016, 138, 051106. [Google Scholar] [CrossRef]
- Wang, Z.; Qian, Z.; Lu, J.; Wu, P. Effects of flow rate and rotational speed on pressure fluctuations in a double-suction cen-trifugal pump. Energy 2018, 170, 212–227. [Google Scholar] [CrossRef]
- Huang, P.; Xiao, Y.; Zhang, J.; Cai, H.; Song, H. The Influence of Flow Rates on Pressure Fluctuation in the Pump Mode of Pump-Turbine with Splitter Blades. Appl. Sci. 2020, 10, 6752. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Zhu, Z.-C.; Dou, H.-S.; Cui, B.-L.; Li, Y.; Zhou, Z.-Z. Numerical Investigation of Transient Flow in a Prototype Centrifugal Pump during Startup Period. Int. J. Turbo JET Engines 2017, 34. [Google Scholar] [CrossRef]
- Li, Z.; Wu, D.; Wang, L.; Huang, B. Numerical Simulation of the Transient Flow in a Centrifugal Pump During Starting Period. J. Fluids Eng. 2010, 132, 081102. [Google Scholar] [CrossRef]
- Li, Z.; Wu, P.; Wu, D.; Wang, L. Experimental and numerical study of transient flow in a centrifugal pump during startup. J. Mech. Sci. Technol. 2011, 25, 749–757. [Google Scholar] [CrossRef]
- Wang, L.Q.; Wu, D.Z.; Zheng, S.Y.; Hu, Z.Y. Study on transient hydrodynamic performance of mixed-flow-pump during starting period. Fluid Mach. 2004, 35, 685–702. [Google Scholar]
- Hu, F.F.; Ma, X.D.; Wu, D.Z.; Wang, L.Q. Transient internal characteristic study of a centrifugal pump during startup process. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 042016. [Google Scholar] [CrossRef]
- Farhadi, K.; Bousbia-Salah, A.; D’Auria, F. A model for the analysis of pump start-up transients in Tehran Research Reactor. Prog. Nucl. Energy 2007, 49, 499–510. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S.; Akrout, M.; Taieb, E.H. Transient behavior of a centrifugal pump during starting period. Appl. Acoust. 2016, 109, 82–89. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Wang, L.; Jiao, L. Numerical Simulation of the Transient Flow in a Radial Flow Pump during Stopping Period. J. Fluids Eng. 2011, 133, 111101. [Google Scholar] [CrossRef]
- Tanaka, T.; Tsukamoto, H. Transient behaviour of a cavitating centrifugal pump at rapid change in operating condi-tions—Part 2: Transient phenomena at pump start-up/shutdown. J. Fluids Eng. 1999, 121, 850–856. [Google Scholar] [CrossRef]
- Thanapandi, P.; Prasad, R. Centrifugal pump transient characteristics and analysis using the method of characteristics. Int. J. Mech. Sci. 1995, 37, 77–89. [Google Scholar] [CrossRef]
- Wu, D.; Wu, P.; Yang, S.; Wang, L. Transient Characteristics of a Closed-Loop Pipe System during Pump Stopping Periods. J. Press. Vessel. Technol. 2014, 136, 021301. [Google Scholar] [CrossRef]
- Tanaka, T.; Tsukamoto, H. Transient behaviour of a cavitating centrifugal pump at rapid change in operating condi-tions—Part 1: Transient phenomena at opening/closure of discharge valve. J. Fluids Eng. 1999, 121, 841–849. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Ohashi, H. Transient characteristics of a centrifugal pump during starting period. J. Fluids Eng. 1982, 104, 6–13. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Yoneda, H.; Sagara, K. The Response of a Centrifugal Pump to Fluctuating Rotational Speed. J. Fluids Eng. 1995, 117, 479–484. [Google Scholar] [CrossRef]
- Westra, R.W.; Broersma, L.; Van Andel, K.; Kruyt, N.P. PIV Measurements and CFD Computations of Secondary Flow in a Centrifugal Pump Impeller. J. Fluids Eng. 2010, 132, 061104. [Google Scholar] [CrossRef]
- Zhang, F.; Appiah, D.; Hong, F.; Zhang, J.; Wei, X. Energy loss evaluation in a side channel pump under different wrap-ping angles using entropy production method. Int. Commun. Heat Mass Transf. 2020, 113, 104526. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Yuan, S.; Chen, K.; Appiah, D. Effect of unrans and hybrid rans-les turbulence models on unsteady turbulent flows inside a side channel pump. J. Fluids Eng. 2020, 142. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Yang, W.; Wang, F. A Comparative Assessment of Spalart-Shur Rotation/Curvature Correction in RANS Simulations in a Centrifugal Pump Impeller. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.-J.; Feng, Z.-P. Two-dimensional analysis of cavitating flows in a centrifugal pump using a single-phase Reynolds averaged Navier—Stokes solver and cavitation model. Proc. Inst. Mech. Eng. 2006, 220, 783–791. [Google Scholar] [CrossRef]
- Liu, H. Numerical Simulation of Hydrodynamic Noise in Centrifugal Pump Based on LES. Chin. J. Mech. Eng. 2013, 49. [Google Scholar] [CrossRef]
- Kye, B.; Park, K.; Choi, H.; Lee, M.; Kim, J.-H. Flow characteristics in a volute-type centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2018, 72, 52–60. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Z.; Dou, H.-S.; Li, Y. Large eddy simulation of energy gradient field in a centrifugal pump impeller. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 4047–4057. [Google Scholar] [CrossRef]
- Pedersen, N. Experimental Investigation of Flow Structures in a Centrifugal Pump Impeller Using Particle Image Velocimetry; ET-PHD, No. 2000-05; Technical University of Denmark: Lynby, Denmark, 2001. [Google Scholar]
- Zhou, P.J. Study on Stall Characteristics of Centrifugal Pump; China Agricultural University: Beijing, China, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).