Recommendation Model Based on a Heterogeneous Personalized Spacey Embedding Method

Abstract

The traditional heterogeneous embedding method based on a random walk strategy does not focus on the random walk fundamentally because of higher-order Markov chains. One of the important properties of Markov chains is stationary distributions (SDs). However, in large-scale network computation, SDs are not feasible and consume a lot of memory. So, we use a non-Markovian space strategy, i.e., a heterogeneous personalized spacey random walk strategy, to efficiently get SDs between nodes and skip some unimportant intermediate nodes, which allows for more accurate vector representation and memory savings. This heterogeneous personalized spacey random walk strategy was extended to heterogeneous space embedding methods in combination with vector learning, which is better than the traditional heterogeneous embedding methods for node classification tasks. As an excellent embedding method can obtain more accurate vector representations, it is important for the improvement of the recommendation model. In this article, recommendation algorithm research was carried out based on the heterogeneous personalized spacey embedding method. For the problem that the standard random walk strategy used to compute the stationary distribution consumes a large amount of memory, which may lead to inefficient node vector representation, we propose a meta-path-based heterogenous personalized spacey random walk for recommendation (MPHSRec). The meta-path-based heterogeneous personalized spacey random walk strategy is used to generate a meaningful sequence of nodes for network representation learning, and the learned embedded vectors of different meta-paths are transformed by a nonlinear fusion function and integrated into a matrix decomposition model for rating prediction. The experimental results demonstrate that MPHSRec not only improves the accuracy, but also reduces the memory cost compared with other excellent algorithms.

1. Introduction

With the rapid development of the Internet, people can choose from more and more products, which leads to the problem of information overload, and recommendations provide a powerful way to address this issue. Recommendation systems help users to select items from a large number of resources. There are three key components of a recommendation system: modeling of user preferences, modeling of product characteristics, and interaction. In a recommendation system, there are a variety of specific problems, and this paper focuses primarily on the problem of rating prediction, which is a prediction on whether a user will click/purchase the current item based on a list of historical clicks/purchasesduct characteristics, and interaction. In a recommendation system, there are a variety of specific problems, and this paper focuses primarily on the problem of rating prediction, which is a prediction on whether a user will click/purchase the current item based on a list of historical clicks/purchases.

With the deepening study of information networks, homogeneous information networks can no longer meet the requirements, so heterogeneous information networks have been proposed, which contain many types of nodes and edges, and can distinguish different semantics in information networks by analyzing multiple types of nodes in the network and multiple links between different types of nodes to uncover more meaningful heterogeneous information. Relevant modeling methods have been proposed in the industry, such as Pathsim [1]. Due to the flexibility of the heterogeneity of modeling data, heterogeneous information networks have been used as a method for characterizing data for recommendation systems. With the ability to characterize heterogeneous information networks, heterogeneous embedding methods can be used to learn the node vectors, and this recommendation model is called the ‘heterogeneous information network-based recommendation algorithm’, which has been applied in many fields [2,3].

The authors in [4] proposed a heterogeneous personalized spacey random walk strategy based on meta-paths and meta-structures. However, in the industry, heterogeneous embedding methods directly use random walk sampling without paying attention to the nature of higher-order Markov chains for the meta-path-guided random walk. The heterogeneous personalized spacey random walk provides an efficient approximation and is mathematically guaranteed to converge to the same stationary distribution (SD). This spacey random walk strategy can generate effective heterogeneous neighborhoods, and the method of extending the spacey random walk strategy to a heterogeneous space embedding can generate effective node-embedding vectors.

In this paper, the heterogeneous personalized spacey embedding method is introduced into the recommendation model to extract and exploit the semantic information in the network by learning in the heterogeneous information network in order to improve the recommendation system’s performance.

2. Related Work

In this section, the current state of research is reviewed in two parts: recommendation algorithms based on heterogeneous information networks; and network-embedded representation learning methods.

There are two traditional approaches to Collaborative Filtering. One is the user-based [5] and product-based [6] Collaborative Filtering algorithm, and the other is the Matrix Factorization [7] algorithm. Since the current recommendation system needs to deal not only with scoring information but also side information, it is difficult to adapt the Collaborative Filtering algorithm to the current recommendation system. Heterogeneous information networks contain more node types and edge types than homogeneous information networks, so more semantics can be obtained as auxiliary information to improve the recommendation system’s performance.

In 2011, Yizhou Sun first proposed the concept of a meta-path [1], which is a sequence of nodes connected by different types of edges. The author proposes a meta-path-based similarity method (PathSim) to measure the similarity between the same types of nodes in a heterogeneous information network based on a symmetric meta-path. The advantage of a meta-path is that it can be used to design various recommendation strategies, which not only improve the recommendation accuracy but also provide an explication. However, the problem of how to choose and weight different meta-paths was not systematic solved.

In 2014 and 2015, Ishikawa proposed HeteSim [8] to measure the similarity between the same or different types of nodes in heterogeneous information networks based on an arbitrary meta-path, introduced heterogeneous information networks into the recommendation domain, and proposed the HeteRec model. This model uses Matrix Factorization to get the implicit vector representation of users and items based on different meta-paths, and then assigns different weights to the inner product to fit the real score to get the weights. In 2015, Ishikawa proposed SemRec, a semantics-based personalized recommendation algorithm [9]. SemRec first uses HeteSim to obtain similarities between users and items based on different meta-paths in a weighted heterogeneous information network, and then merges these similarities with different weights. The method also considers the score on the rating relationship between users and movies, proposing some concepts of heterogeneous information networks and meta-paths with weights and the corresponding similarity calculation methods. The studies of Ishikawa not only have the transparency and credibility of recommendation results, which are lacking in many recommendation models, but also obtain the prioritized and personalized weights representing user preferences on paths. However, the weight setting is not scientific enough. If the weight is not set properly, the efficiency of the algorithm will be low.

In 2017, Huan Zhao [10] proposed a recommendation system based on the fusion of a heterogeneous information network and meta-structures. The algorithm uses different meta-structures designed to obtain similarity matrices between multiple products and users, decomposes the similarity matrices to obtain the implicit features of users and products, and finally uses a factorization mechanism for training and rating prediction. The heterogeneous network algorithm based on meta-structures proposed by the author can better express the complex relationship between two targets, but the processing of this type of algorithm is very complex and inefficient.

In 2019, Li [11] proposed a literature-based recommendation algorithm that uses multiple categories of semantic information and implicit feedback information. This algorithm performs better than other recommendation algorithms that do not use such information. Heterogeneous information network recommendations with different architectures have the following applications: for meta-structures, they are used for citation recommendations [12]; for meta-paths, they are used for e-commerce recommendations [13] and Top-N recommendations [14]. The embedding algorithms based on meta-structures and meta-paths have been applied in different fields; however, there remain some shortcomings, such as the accuracy of the recommendation results not being high and the ability of knowledge expression between nodes.

In recent years, the Graph Neural Network [15,16] has received more and more attention, and there are many applications and methods for recommendation systems, but this article aims to compare it with other recommendation algorithms at the level of heterogeneous embedding methods and also considers applying this technique. The network embedding method aims to learn the low-dimensional node vector representations in the network. The learned node vector representations can be used to handle different tasks, such as classification [17], clustering [18,19,20], link prediction [21,22,23], and similarity search. The development of network embedding methods dates back to the beginning of this century and has traditionally been viewed as a dimension-reduced process that mainly consists of principal component analysis (PCA) [24] and multidimensional scaling (MDS) [25]. These methods work well when the network is not large. However, since information networks may contain billions of nodes and edges, the temporal complexity of these methods is at least quadratic, which makes them impossible to run on large-scale networks in a limited amount of time.

As deep learning methods are becoming increasingly mature, network embedding methods are being added to the deep learning methods. DeepWalk [26] is the first method to use deep learning techniques to do network embedding. DeepWalk takes inspiration from Word2vec and bridges the gap between network embedding and word embedding by treating nodes as words and generates short random walk sequences as sentences. A neural language model such as Skip-Gram [27] can then be applied to the random walk to obtain network embedding. LINE (Line with First-order Proximity or Second-order Proximity) [28] focuses on the representation of network nodes in large-scale networks. LINE can be used for directed and undirected graphs as well as for networks with weighted graphs. In contrast to DeepWalk’s sequence generation method with a random walk, LINE models the first-order and second-order similarity of nodes and samples the edges according to their weights. This method is highly efficient and has been widely used in industry. Metapath2vec [29] is an extension of DeepWalk for heterogeneous information networks. Metapath2vec uses a random walk based on a meta-path to construct heterogeneous neighborhoods for each node, and proposes a heterogeneous Skip-Gram algorithm for the sequence of nodes obtained by the random walk to complete the node embedding and to learn the embedding vector representation of nodes. Based on Metapath2vec, researchers have also proposed Metapath2vec++ to model the structure and semantics of heterogeneous networks. Metagraph2vec [30] is a heterogeneous network embedding method that can capture semantic relationships between distant nodes and learn more information about the embedded vector. The core of the method is the use of a meta-structure to guide the generation of random walk node sequences, which have the ability to describe complex relationships between nodes and provide more flexible matching when generating random walk node sequences.

To sum up, the current recommendation algorithm based on a heterogeneous information network does not fully consider the fact that a random walk is a higher-order Markov chain, which has many shortcomings, such as excessive memory consumption and a slow computing speed. In this article, the heterogeneous personalized spacey embedding method is combined with the recommendation algorithm, which can extract different types of entities and their links in the heterogeneous information network to obtain heterogeneous information for the recommendation system, which can capture more semantic and meaningful information than the homogeneous information network.

3. Proposed Model and Baseline Algorithms

The meta-path-based heterogenous personalized spacey random walk for recommendation (MPHSRec) combines the heterogeneous personalized spacey embedding method with a recommendation algorithm to improve the accuracy of rating prediction. The model has three main components:

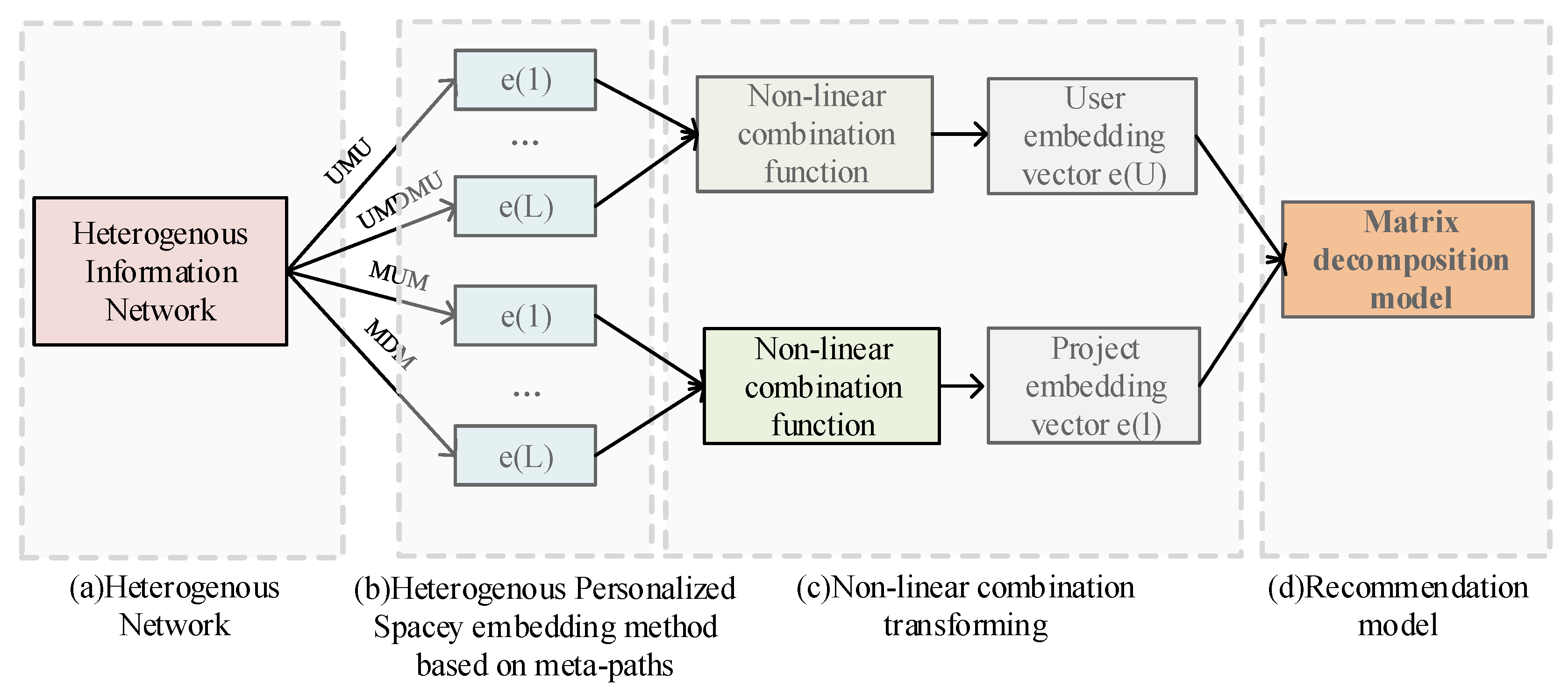
• A meta-path-based heterogeneous personalized spacey random walk (MPHPSRW) strategy and a heterogeneous Skip-Gram algorithm are applied to network representation learning in order to learn the embedding vectors of users and items according to different meta-paths.
• The learned embedding vectors of the different meta-path nodes conduct a nonlinear fusion transformation to generate the final user and item vectors.
• The final user and item vectors are used to construct the objective function. The objective function generates a loss function in the Matrix Factorization framework and updates the parameters by optimizing the loss function. Finally, the specific form of the objective function is obtained, and the rating score is predicted based on the obtained objective function.

The framework of the model is shown in Figure 1. Figure 1a denotes the architecture of a heterogeneous information network, Figure 1b denotes the method of the meta-path-based heterogeneous personalized spacey embedding. Figure 1c is the process of transforming user and item vectors with two kinds of nodes by a nonlinear fusion function. Figure 1d is the process of inputting the final user and item embedding vectors into the Matrix Factorization model. The two main parts of the model, namely heterogeneous information network representation learning and the recommendation model, are highlighted later.

3.1. Meta-Path-Based Heterogeneous Personalized Spacey Random Walk

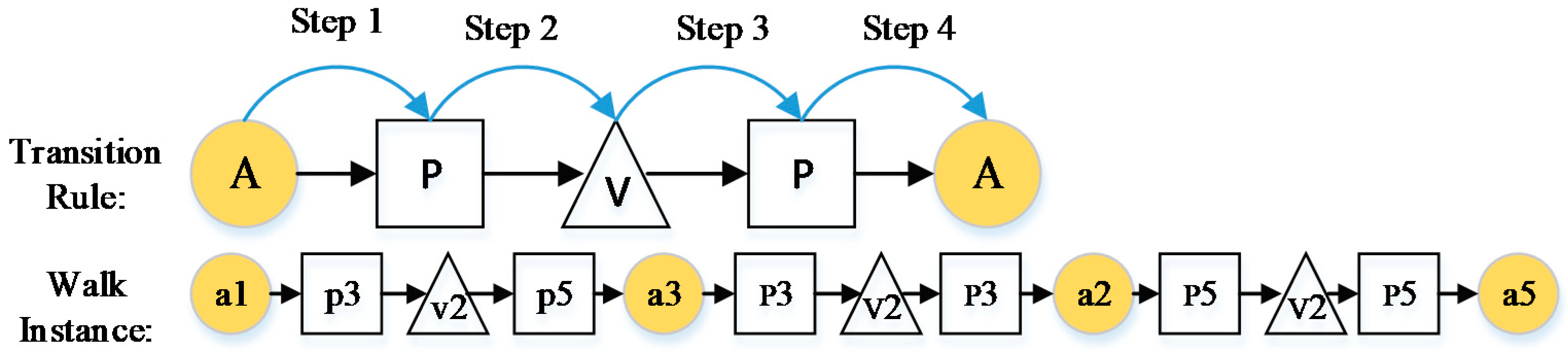
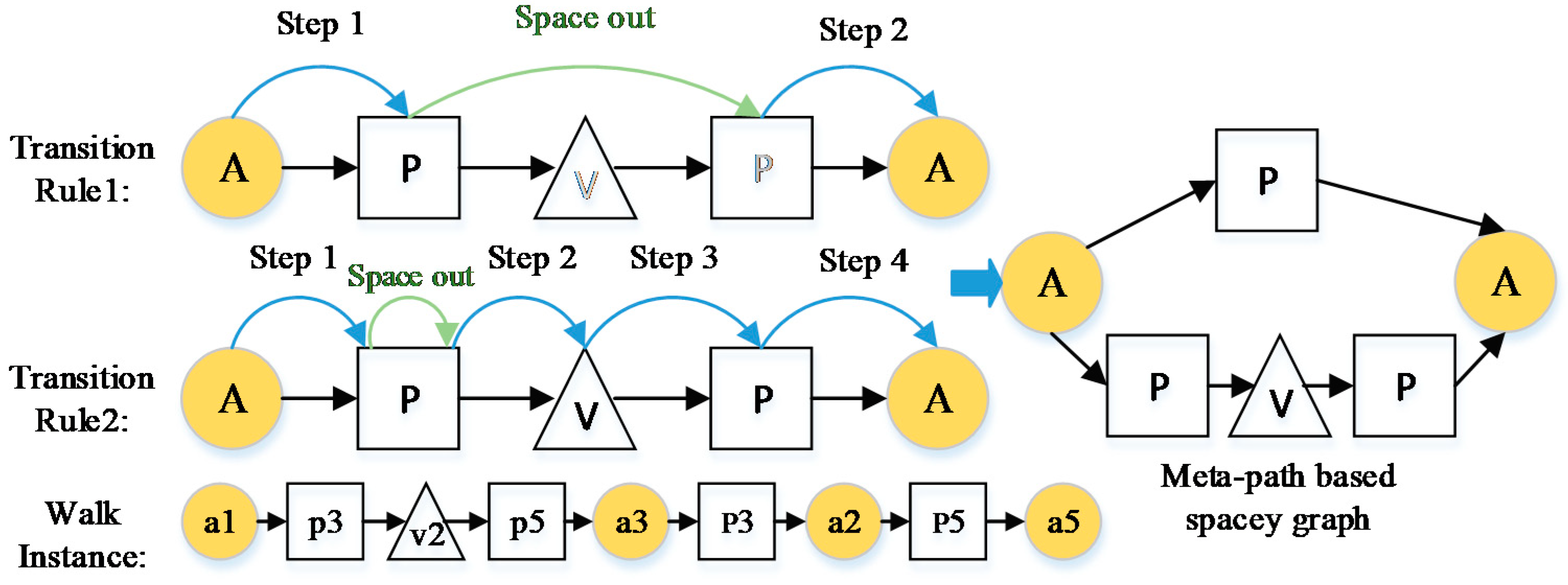
• Algorithm idea: The standard meta-path based random walk is essentially a higher-order Markov chain. Node transfers in a random walk are equivalent to the transfer probabilities of higher-order Markov chains, whose SDs take up a lot of memory, and for large datasets consume a lot of memory for storage. The memory is optimized in the spacey random walk, providing a spatially efficient alternative approximation and mathematically guaranteeing the SD with convergence to the same limit, saving memory usage to some extent. In addition, the spacey random walk also ignores unimportant intermediate states to get a more efficient node sequence. For personalization, α acts as a hyperparameter to control the user’s personalization behavior, and once the spacey random walk visits X(n) at step n it skips and forgets the penultimate state X(n − 1) by probability α.
• Spacey random walk strategy: In heterogeneous networks, the random walk strategy guided by meta-paths was first proposed in the Path Ranking Algorithm [31], which computes the similarity between nodes. Equation (1) is the key transfer probability formula in the Path Ranking Algorithm. It is applied in part (b) of Figure 1 to compute the importance of all meta-paths.

$${ \mathrm{P}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}={\mathrm{D}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}^{-1}{\mathrm{W}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}$$

(1)

${\mathrm{W}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}$ in Equation (1) is the adjacency matrix between a node of type ${\mathrm{A}}_{\mathrm{l}}$ and a node of type ${\mathrm{A}}_{\mathrm{l}+1}$. ${\mathrm{D}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}$ is a degree matrix and also a diagonal matrix, as shown in Equation (2).

$${ \mathrm{D}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}\left({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}}{\mathrm{W}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}\left({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{j}}\right)$$

(2)

When a random walk is performed from node ${\mathrm{v}}_{\mathrm{i}}$of type ${\mathrm{A}}_{\mathrm{l}}$to node ${\mathrm{v}}_{\mathrm{j}}$ of type ${\mathrm{A}}_{\mathrm{l}+1}$, the transfer probability ${\mathrm{P}}_{{\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1}}\left({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{j}}\right)$ can be computed.

The transfer probability for a second-order Markov random walk is represented as Equation (3). It is defined as follows:

$${ \mathrm{H}}_{\mathrm{i},\mathrm{j},\mathrm{k}}\triangleq \{\begin{array}{ll}& \mathsf{\phi }\left({\mathrm{v}}_{\mathrm{i}}\right)={ \mathrm{A}}_{\mathrm{l}}\\ {\mathrm{P}}_{{\mathrm{A}}_{\mathrm{l}+1}, {\mathrm{A}}_{\mathrm{l}+2}}\left({\mathrm{v}}_{\mathrm{j}}, {\mathrm{v}}_{\mathrm{k}}\right),& \mathsf{\phi }\left({\mathrm{v}}_{\mathrm{j}}\right)={ \mathrm{A}}_{\mathrm{l}+1}\\ & \mathsf{\phi }\left({\mathrm{v}}_{\mathrm{k}}\right)={ \mathrm{A}}_{\mathrm{l}+2}\\ 0,& \mathrm{otherwise}\end{array}$$

(3)

${\mathrm{H}}_{\mathrm{i},\mathrm{j},\mathrm{k}}$ in the above equation represents the transfer probability of node ${\mathrm{v}}_{\mathrm{k}}$ for the given previous node ${\mathrm{v}}_{\mathrm{j}}$and penultimate node ${\mathrm{v}}_{\mathrm{i}}$. ${\mathrm{A}}_{\mathrm{l}},{\mathrm{A}}_{\mathrm{l}+1,}{\mathrm{A}}_{\mathrm{l}+2}$ are respectively described as meta-paths “APV“, “PVP”, and “VPA”, which are derived from dividing “APVPA” (all meta-paths are shown in and Figure 2 and Figure 3). The function φ is a node-type mapping function, and ${\mathrm{P}}_{{\mathrm{A}}_{\mathrm{l}+1},{\mathrm{A}}_{\mathrm{l}+2}}$ is defined in Equation (1).

In the following, we describe the heterogeneous personalized spacey random walk of the meta-path-based second-order Markov chain. Given a second-order Markov chain, the transfer hypermatrix probabilities ${\mathrm{H}}_{\mathrm{i},\mathrm{j},\mathrm{k}}$ are linked by the transfer probabilities based on a series of decomposed meta-paths, as defined in Equation (3). These transfer probabilities can be used to personalize a spacey random walk. The random processes consist of a series of states X(0), X(1), ..., X(n), and the penultimate node Y(n) is selected by the rule of transfer probability from [4]. It is described by Equation (4).

$$\mathrm{Pr}\left\{\mathrm{Y}\left(\mathrm{n}\right)={\mathrm{v}}_{\mathrm{i}}|{ℱ}_{\mathrm{n}}\right\}\triangleq \{\begin{array}{c}\left(1-\mathsf{\alpha }\right)+\alpha {\mathrm{w}}_{\mathrm{i}}\left(\mathrm{n}\right), {\mathrm{v}}_{\mathrm{i}}=\mathrm{X}\left(\mathrm{n}-1\right)\\ \alpha {\mathrm{w}}_{\mathrm{i}}\left(\mathrm{n}\right), {\mathrm{v}}_{\mathrm{i}}\ne \mathrm{X}\left(\mathrm{n}-1\right)\end{array}$$

(4)

Then, the next node is selected by the following Equation (5).

$$\mathrm{Pr}\left\{\mathrm{X}\left(\mathrm{n}+1\right)={\mathrm{v}}_{\mathrm{k}}|\mathrm{X}\left(\mathrm{n}\right)={\mathrm{v}}_{\mathrm{j}}, \mathrm{Y}\left(\mathrm{n}\right)={\mathrm{v}}_{\mathrm{i}}\right\}\triangleq {\mathrm{H}}_{\mathrm{i},\mathrm{j},\mathrm{k}}$$

(5)

${ℱ}_{\mathrm{n}}$ in Equation (4) above can generate a $\mathsf{\sigma }$distribution by a random variable $\mathrm{X}\left(\mathrm{i}\right)$, i$\in \left(1,\mathrm{n}\right)$, X(0) is the initial node, $\mathsf{\alpha }$ is the hyper-parameter used to control the user’s personalized behavior, and $\mathsf{\alpha }\in \left(0,1\right)$.

w(n) is behavior vector at step n, defined as in Equation (6):

$${\mathrm{w}}_{\mathrm{i}}\left(\mathrm{n}\right)\triangleq \frac{1}{\mathrm{n}+\mathrm{N}}\left(1+{\displaystyle \sum }_{\mathrm{s}=1}^{\mathrm{n}}\mathrm{Ind}\left\{\mathrm{X}\left(\mathrm{s}\right)={ \mathrm{v}}_{\mathrm{i}}\right\}\right)$$

(6)

where N is the total number of nodes.

Once the spacey random walk has visited X(n) at step n, it skips and forgets its penultimate node with probability α, i.e., state X(n − 1). It then invents a new historical state Y(n) by randomly depicting a series of past states X(1), ..., X(n); if the penultimate two states are X (n) and Y(n), it will convert to X(n + 1).

Now, we present an example of heterogeneous information networks. Figure 3 and Figure 4 show the meta-path-based Markov random walk and the meta-path-based spacey random walk, respectively. The meta-paths comply with “APVPA”. Figure 3 shows that the Markov random walk strictly follows the constraints of the meta-path, and there is no middle skip. While the spacey random walk allows us to jump over intermediate nodes to improve the efficiency and quality of the random walk, it is actually a shortened random walk along a folded sub-path of the original meta-path of a given user. The spacey random walk strategy generates a special meta-structure or multiple meta-paths, which can be called a ‘meta-path-based spatial graph’, and this graph combines the original meta-path and the skipped meta-path in the middle. “APVPA” in Figure 3 obtains the A→P→A meta-path after the application of transfer rule 1, and then through transfer rule 2 obtains the A→P→V→P→A meta-path. The combination of the two is shown in the spatial diagram in the right part of Figure 3.

In Figure 3 and Figure 4, there are two examples of random walk strategies based on the meta-path “APVPA” that were used to obtain two random walk paths for the random walk: the meta-path based on the Markov random walk yields a path length of 13; and the meta-path-based spacey random walk yields a path length of 9. That is, the spacey random walk can capture richer relationships with shorter random walk counts. The spacey random walk was also designed to have personalized probabilities that adaptively adjust the probability of the original meta-path or any folding sub-path spontaneously.

Unlike random walks guided directly by a meta-structure or multiple meta-paths, spacey random walks balance multiple meta-paths with the right ratio, adjust the original meta-path, and skip the gained meta-path according to the personalized probability$\mathsf{\alpha }$.

3.2. Heterogeneous Skip-Gram Algorithm

The set of node sequences can be obtained by a random walk in the previous step. Assuming that the sequence set is ${\mathrm{V}}_{\mathrm{p}}$, for a heterogeneous information network the heterogeneous Skip-Gram model [27] is used to learn the effective node representation by maximizing the heterogeneous neighborhood ${\mathcal{N}}_{\mathrm{A}}\left({\mathrm{v}}_{\mathrm{i}}\right)$ of node ${\mathrm{v}}_{\mathrm{i}}$, as shown in Equation (7).

$${\mathrm{argmax}}_{\mathsf{\theta }}{\displaystyle \sum }_{{\mathrm{v}}_{\mathrm{i}}ϵ{\mathrm{V}}_{𝒫}}{\displaystyle \sum }_{\mathrm{A}ϵ\mathcal{A}}{\displaystyle \sum }_{{\mathrm{v}}_{\mathrm{j}}ϵ{\mathcal{N}}_{\mathrm{A}}\left({\mathrm{v}}_{\mathrm{i}}\right)}\mathrm{logPr}\left({\mathrm{v}}_{\mathrm{j}}{|\mathrm{v}}_{\mathrm{i}},\mathsf{\theta }\right)$$

(7)

In order to simplify the solution of the model parameters, the formula is changed to a minimal objective function, as shown in Equation (8):

$${\mathrm{argmin}}_{\mathsf{\theta }}-{\displaystyle \sum }_{{\mathrm{v}}_{\mathrm{i}}ϵ{\mathrm{V}}_{𝒫}}{\displaystyle \sum }_{\mathrm{A}ϵ\mathcal{A}}{\displaystyle \sum }_{{\mathrm{v}}_{\mathrm{j}}ϵ{\mathcal{N}}_{\mathrm{A}}\left({\mathrm{v}}_{\mathrm{i}}\right)}\mathrm{logPr}\left({\mathrm{v}}_{\mathrm{j}}{|\mathrm{v}}_{\mathrm{i}},\mathsf{\theta }\right)$$

(8)

${\mathcal{N}}_{\mathrm{A}}\left({\mathrm{v}}_{\mathrm{i}}\right)$ denotes the neighborhood of node ${\mathrm{v}}_{\mathrm{i}}$ of category A. For each entity pair, such as $({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{j}})$, their joint probability $\mathrm{Pr}\left({\mathrm{v}}_{\mathrm{j}}{|\mathrm{v}}_{\mathrm{i}},\mathsf{\theta }\right)$ is defined as a softmax-like function [32], as shown in Equation (9).

$$\mathrm{Pr}\left({\mathrm{v}}_{\mathrm{j}}{|\mathrm{v}}_{\mathrm{i}},\mathsf{\theta }\right)= \frac{\exp \left\{{\mathrm{u}}_{\mathrm{j}}^{\mathsf{{\rm T}}}\right\}}{{\sum }_{\mathrm{j}}\exp \left\{{\mathrm{u}}_{\mathrm{j}}^{\mathsf{{\rm T}}},{\mathrm{v}}_{\mathrm{i}}\right\}}$$

(9)

where ${\mathrm{u}}_{\mathrm{j}}$ is the context vector of ${\mathrm{v}}_{\mathrm{j}}$ and ${\mathrm{v}}_{\mathrm{j}}$ is the embedded vector of ${\mathrm{v}}_{\mathrm{i}}$. For the optimization algorithm, the objective function is optimized using negative sampling, which is reduced to the objective function of Equation (10).

$$\log \mathsf{\sigma }\left({\mathrm{u}}_{\mathrm{j}}^{\mathsf{{\rm T}}}{\mathrm{v}}_{\mathrm{i}}\right)+{\displaystyle \sum }_{\mathrm{l}}^{\mathrm{m}}{\mathbb{E}}_{{\mathrm{v}}_{\mathrm{c}}~{\mathrm{P}}_{\mathrm{n}}\left({\mathrm{v}}_{\mathrm{i}}\right)}\left[\log \mathsf{\sigma }\left(-{\mathrm{u}}_{\mathrm{c}}^{\mathrm{T}}{\mathrm{v}}_{\mathrm{i}}\right)\right]$$

(10)

where $\mathsf{\sigma } (·)$ is the sigmoid function and ${\mathrm{P}}_{\mathrm{n}}\left({\mathrm{v}}_{\mathrm{i}}\right)$ is the sampling distribution.

3.3. Personalized Nonlinear Fusion Function

A node can have multiple vector space representations due to its containing multiple meta-paths, and these vectors are processed using the fusion function to allow for subsequent integration with the Matrix Factorization model.

Linear functions have a poor ability to model complex data relationships, so nonlinear functions are used to enhance the effect of the function. σ is a nonlinear function that generally uses a sigmoid function [33]. The fusion function developed in [34] is shown in Equation (11).

$$\mathrm{g}\left(\left\{{\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{l}\right)}\right\}\right)= \mathsf{\sigma }({\displaystyle \sum }_{\mathrm{n}=1}^{\left|\mathrm{P}\right|}{\mathrm{w}}_{\mathrm{u}}^{\left(\mathrm{l}\right)}\mathsf{\sigma }\left({\mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{l}\right)}+{\mathrm{b}}^{\left(\mathrm{l}\right)}\right))$$

(11)

$$\mathrm{g}\left(\left\{{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\right\}\right)= \mathsf{\sigma }({\displaystyle \sum }_{\mathrm{n}=1}^{\left|\mathrm{P}\right|}{\mathrm{w}}_{\mathrm{u}}^{\left(\mathrm{l}\right)}\mathsf{\sigma }\left({\mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}+{\mathrm{b}}^{\left(\mathrm{l}\right)}\right))$$

(12)

where $\left|\mathrm{P}\right|$ is the total number of meta-paths. ${\mathrm{M}}^{\left(\mathrm{l}\right)}\in {\mathrm{R}}^{\mathrm{D}\times \mathrm{d}}$ and ${\mathrm{b}}^{\left(\mathrm{l}\right)}\in {\mathrm{R}}^{\mathrm{D}}$ are the transformation matrix and bias vector of the $\mathrm{l}$th meta-path, respectively.

Since the rating prediction task is only concerned with the user and the item, it only needs to learn the embedding vectors of the user and the item. Therefore, after mapping the fusion functions, the vectors of users and items of different meta-paths can be integrated to get the final embedded vectors of users and items, which can be expressed by the following two equations, where ${\mathrm{e}}_{\mathrm{u}}\left(\mathrm{U}\right)$and ${\mathrm{e}}_{\mathrm{i}}\left(\mathrm{I}\right)$ are the final vectors of user u and item i, respectively, as shown in Equations (13) and (14).

$${\mathrm{e}}_{\mathrm{u}}\left(\mathrm{U}\right) \leftarrow \mathrm{g}\left(\left\{{\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{l}\right)}\right\}\right)$$

(13)

$${\mathrm{e}}_{\mathrm{i}}\left(\mathrm{I}\right) \leftarrow \mathrm{g}\left(\left\{{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\right\}\right)$$

(14)

3.4. Recommendation Model

• Modeling rating prediction: First of all, we need to establish the rating prediction expression, input the user and item embedding vectors obtained in the previous step into the recommendation model based on the Matrix Factorization model [35], and put the fusion function into the Matrix Factorization framework to learn the parameters of the model. The final rating prediction expression is shown in Equation (15).

$${\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }={\mathrm{x}}_{\mathrm{u}}^{\mathsf{{\rm T}}}·{\mathrm{y}}_{\mathrm{i}}+\mathsf{\alpha }·{\mathrm{e}}_{\mathrm{u}}^{{\left(\mathrm{U}\right)}^{\mathsf{{\rm T}}}}·{\mathsf{\gamma }}_{\mathrm{i}}{}^{\left(\mathrm{I}\right)}+\mathsf{\beta }·{\mathsf{\gamma }}_{\mathrm{u}}^{{\left(\mathrm{U}\right)}^{\mathsf{{\rm T}}}}·{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{I}\right)}$$

(15)

where ${\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{U}\right)}$ and ${\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{I}\right)}$ are the vector outputs of the user and item from Equations (13) and (14), respectively, ${\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}$ and ${\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}$ are the implicit variables corresponding to the user and item embedded vectors ${\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{U}\right)}$ and${ \mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{I}\right)}$, respectively, and α and β are the hyperparameters regulating the three expressions. Their values lie between (0,1).

2.

Establishing the loss function: After building the model, the parameters in the model need to be learned and solved. The loss function is shown in Equation (16).

$$ℒ={\displaystyle \sum }_{\langle \mathrm{u},\mathrm{i},{\mathrm{r}}_{\mathrm{u},\mathrm{i}}\rangle \in \mathrm{R}}{\left({\mathrm{r}}_{\mathrm{u},\mathrm{i}}-{\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }\right)}^2+\mathsf{\lambda }{\displaystyle \sum }_{\mathrm{u}}\left(\parallel {\mathrm{x}}_{\mathrm{u}}{\parallel }_2+\parallel {\mathrm{y}}_{\mathrm{i}}{\parallel }_2+\parallel {\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}{\parallel }_2+\parallel {\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}{\parallel }_2+\parallel {\mathsf{\theta }}^{\left(\mathrm{U}\right)}{\parallel }_2+\parallel {\mathsf{\theta }}^{\left(\mathrm{I}\right)}{\parallel }_2\right)$$

(16)

where ${\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }$ is the prediction rating computed from the recommendation model. λ is the regularization coefficient, and ${\mathsf{\theta }}^{\left(\mathrm{U}\right)}$ and ${\mathsf{\theta }}^{\left(\mathrm{I}\right)}$ denote the set of parameters of the fusion function g in Equations (11) and (12), respectively.

3.

Parameter learning: The stochastic gradient descent algorithm is used to optimize the loss function. The original implicit layer factors ${\mathrm{x}}_{\mathrm{u}}$ and ${\mathrm{y}}_{\mathrm{i}}$ are updated in the same way as the original Matrix Factorization. The other parameters in the model can be updated by the following Equations (17)–(20):

$${\mathsf{\theta }}_{\mathrm{u},\mathrm{l}}^{\left(\mathrm{u}\right)}-\mathsf{\eta }·\left(-\mathsf{\alpha }·\left({\mathrm{r}}_{\mathrm{u},\mathrm{i}}-{\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }\right)·{\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}\frac{\partial {\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{U}\right)}}{\partial {\mathsf{\theta }}_{\mathrm{u},\mathrm{l}}^{\left(\mathrm{U}\right)}}+{\mathsf{\lambda }}_{\mathsf{\theta }}{\mathsf{\theta }}_{\mathrm{u},\mathrm{l}}^{\left(\mathrm{U}\right)}\right)$$

(17)

$${\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}\leftarrow {\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}-\mathsf{\eta }·\left(-\mathsf{\beta }·\left({\mathrm{r}}_{\mathrm{u} \mathrm{i}}-{\mathrm{r}}_{\mathrm{u} \mathrm{i}}^{\prime }\right)·{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{I}\right)}+{\mathsf{\lambda }}_{\mathsf{\gamma }}{\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}\right)$$

(18)

$${\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}^{\left(\mathrm{I}\right)}\leftarrow {\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}^{\left(\mathrm{I}\right)}-\mathsf{\eta }·\left(-\mathsf{\beta }·\left({\mathrm{r}}_{\mathrm{u},\mathrm{i}}-{\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }\right)·{\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}\frac{\partial {\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{I}\right)}}{\partial {\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}^{\left(\mathrm{I}\right)}}+{\mathsf{\lambda }}_{\mathsf{\theta }}{\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}^{\left(\mathrm{I}\right)}\right)$$

(19)

$${\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}\leftarrow {\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}-\mathsf{\eta }·\left(-\mathsf{\alpha }·\left({\mathrm{r}}_{\mathrm{u},\mathrm{i}}-{\mathrm{r}}_{\mathrm{u},\mathrm{i}}^{\prime }\right)·{\mathrm{e}}_{\mathrm{u}}^{\left(\mathrm{U}\right)}+{\mathsf{\lambda }}_{\mathsf{\gamma }}{\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}\right)$$

(20)

where η is the learning rate, ${\mathsf{\lambda }}_{\mathsf{\theta }}$ is the regularization term of the parameters ${\mathsf{\theta }}^{\left(\mathrm{U}\right)}$ and ${\mathsf{\theta }}^{\left(\mathrm{I}\right)}$, and ${\mathsf{\lambda }}_{\mathsf{\gamma }}$ is the regularization term of ${\mathsf{\gamma }}_{\mathrm{u}}^{\left(\mathrm{U}\right)}$ and ${\mathsf{\gamma }}_{\mathrm{i}}^{\left(\mathrm{I}\right)}$. The sigmoid function is used as a nonlinear transformation function. θ represents all parameters of the fusion function. $e_u^{\left(U\right)},e_u^{\left(U\right)}$ are described in Equations (13) and (14). The equation for $\frac{\partial {\mathrm{e}}_{\mathrm{i}}}{\partial {\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}}$ is given below:

$$\frac{\partial {\mathrm{e}}_{\mathrm{i}}}{\partial {\mathsf{\theta }}_{\mathrm{i}, \mathrm{l}}}=\{\begin{array}{c}{\mathrm{w}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\sigma \left({\mathrm{Z}}_{\mathrm{s}}\right)\sigma \left({\mathrm{Z}}_{\mathrm{f}}\right)\left(1-\mathsf{\sigma }\left({\mathrm{Z}}_{\mathrm{s}}\right)\right)\left(1-\mathsf{\sigma }\left({\mathrm{Z}}_{\mathrm{f}}\right)\right){\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)} , \theta =M\\ {\mathrm{w}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\sigma \left({\mathrm{Z}}_{\mathrm{s}}\right)\sigma \left({\mathrm{Z}}_{\mathrm{f}}\right)\left(1-\mathsf{\sigma }\left({\mathrm{Z}}_{\mathrm{s}}\right)\right)\left(1-\mathsf{\sigma }\left({\mathrm{Z}}_{\mathrm{f}}\right)\right), \theta =b \\ \sigma \left({\mathrm{Z}}_{\mathrm{s}}\right)\sigma \left({\mathrm{Z}}_{\mathrm{f}}\right)\left(1-\mathsf{\sigma }\left({\mathrm{Z}}_{\mathrm{s}}\right)\right), \theta =\omega \end{array}$$

(21)

${\mathrm{Z}}_{\mathrm{s}}= {\displaystyle \sum }_{\mathrm{l}=1}^{\left|\mathrm{P}\right|}{\mathrm{w}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\mathsf{\sigma }\left({\mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}+{\mathrm{b}}^{\left(\mathrm{l}\right)}\right){\mathrm{and} \mathrm{Z}}_{\mathrm{f}}={ \mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}+{\mathrm{b}}^{\left(\mathrm{l}\right)}$, where ${\mathrm{Z}}_{\mathrm{s}}= {\displaystyle \sum }_{\mathrm{l}=1}^{\left|\mathrm{P}\right|}{\mathrm{w}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}\mathsf{\sigma }({\mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}$$+{\mathrm{b}}^{\left(\mathrm{l}\right)})$and ${\mathrm{Z}}_{\mathrm{f}}={ \mathrm{M}}^{\left(\mathrm{l}\right)}{\mathrm{e}}_{\mathrm{i}}^{\left(\mathrm{l}\right)}+{\mathrm{b}}^{\left(\mathrm{l}\right)}$. After calculating $\frac{\partial {\mathrm{e}}_{\mathrm{i}}}{\partial {\mathsf{\theta }}_{\mathrm{i},\mathrm{l}}}$, it will be substituted into Equations (17) and (19) to get the value of the objective function, which is the prediction rating score.

On the basis of the algorithms mentioned above, the pseudo code of the MPHSRec model is presented as Algorithm 1.

Algorithm 1 Recommendation Model Based on a Heterogeneous Personalized Spacey Embedding Method

Input: Rating Matrix R, Dataset S, walk node time w, walk length l, embedding vector dimension d, neighbor domain k. Output: Model of rating prediction (named by MPHSRec) 1. Create heterogeneous information network HN from S with Networkx tool. 2. Compute Path(U), Path(I) for user meta sets and item meta sets. 3. For each path of Path(U), Path(I): 4.  Ulist = GainNodeSequence(Path(U)), Ilist = GainNodeSequence(Path(I)) 5.  by Equation (1) to Equation (6). 6. ${\left\{e_u^{\left(l\right)}\right\}}_{L=1}^{Path\left(U\right)}=\mathrm{GetEmbeddingVector}\left(Ulist\right),{\left\{e_u^{\left(l\right)}\right\}}_{L=1}^{Path\left(I\right)}=$GetEmbeddi_ 7. $\mathrm{ngVector}\left(Ilist\right) \mathrm{by} \mathrm{Equation}\left(7\right) \mathrm{to} \mathrm{Equation}\left(14\right)$. 8. For each vector of ${\left\{e_u^{\left(l\right)}\right\}}_{L=1}^{Path\left(U\right)}$,${\left\{e_i^{\left(l\right)}\right\}}_{L=1}^{Path\left(I\right)}$: 9.$e_u$=Fusion (${\left\{e_u^{\left(l\right)}\right\}}_{L=1}^{Path\left(U\right)}$), $e_i$=Fusion (${\left\{e_i^{\left(l\right)}\right\}}_{L=1}^{Path\left(I\right)}$) by Equation (11) 10.   to Equation (13). 11. UIMX=Fusion ($e_u,e_{i,}$) into Matrix Factorization model from [35]. 12. Model=CreateMPHSRec(UIMX) by Equation (15). 13. Create loss function $ℒ$ for Model by Equation (16). 14. For each of iterations N: 15.  Optimize loss function $ℒ$ by Equation (17) to Equation (21). 16. Save Model.

3.5. Statement of Baseline Algorithm

This section introduces the embedding algorithm and the recommended algorithm for comparison, which are used to verify the effectiveness of the embedding method in Section 4.4 and the MPHPSRec algorithm in Section 4.5. The embedding method and the recommended algorithm are listed in the following sections.

First, the following is a brief description of four embedding methods.

• DeepWalk is a homogeneous network embedding model that uses the traditional random walk algorithm to obtain contextual information to learn low-dimensional node vectors.
• LINE is a method based on the neighborhood similarity assumption. It uses different definitions of similarity between vertices in the graph, including first-order and second-order similarity.
• Metapath2vec is a heterogeneous information network-based embedding method that generates heterogeneous neighborhoods by an ordinary random walk based on meta-paths and learns node embedding vectors by the heterogeneous Skip-Gram algorithm.

Second, the selected comparative recommendation methods include the classical Matrix-Factorization-based rating prediction model PMF (Probabilistic Matrix Factorization, PMF) [35] as well as the heterogeneous information network-based recommendation models SemRec and HERec.

• PMF is a classical probabilistic Matrix Factorization model, where the score of Matrix Factorization is reduced to a low-dimensional user matrix and a product matrix.
• SemRec is a collaborative filtering method based on a weighted heterogeneous information network constructed by connecting users and items with the same rank. It flexibly integrates heterogeneous information for recommendation using weighted meta-path and weight fusion methods.
• Variation of HERec: HERec is a recommendation algorithm based on a heterogeneous information network that uses the heterogeneous embedding method to learn the low-dimensional vectors of users and items in the heterogeneous network, and then incorporates the representation of users and items into the recommendation algorithm. The DeepWalk, LINE, and Metapath2vec algorithms were used to replace the heterogeneous embedding method module.

3.6. Heterogeneous Information Network Generation

For heterogeneous information network generation, that is, to build a network, we used the Networkx tool. The flow chart of the generation process is shown in Figure 5.

The steps (1)–(3) in Figure 5 correspond to the following steps:

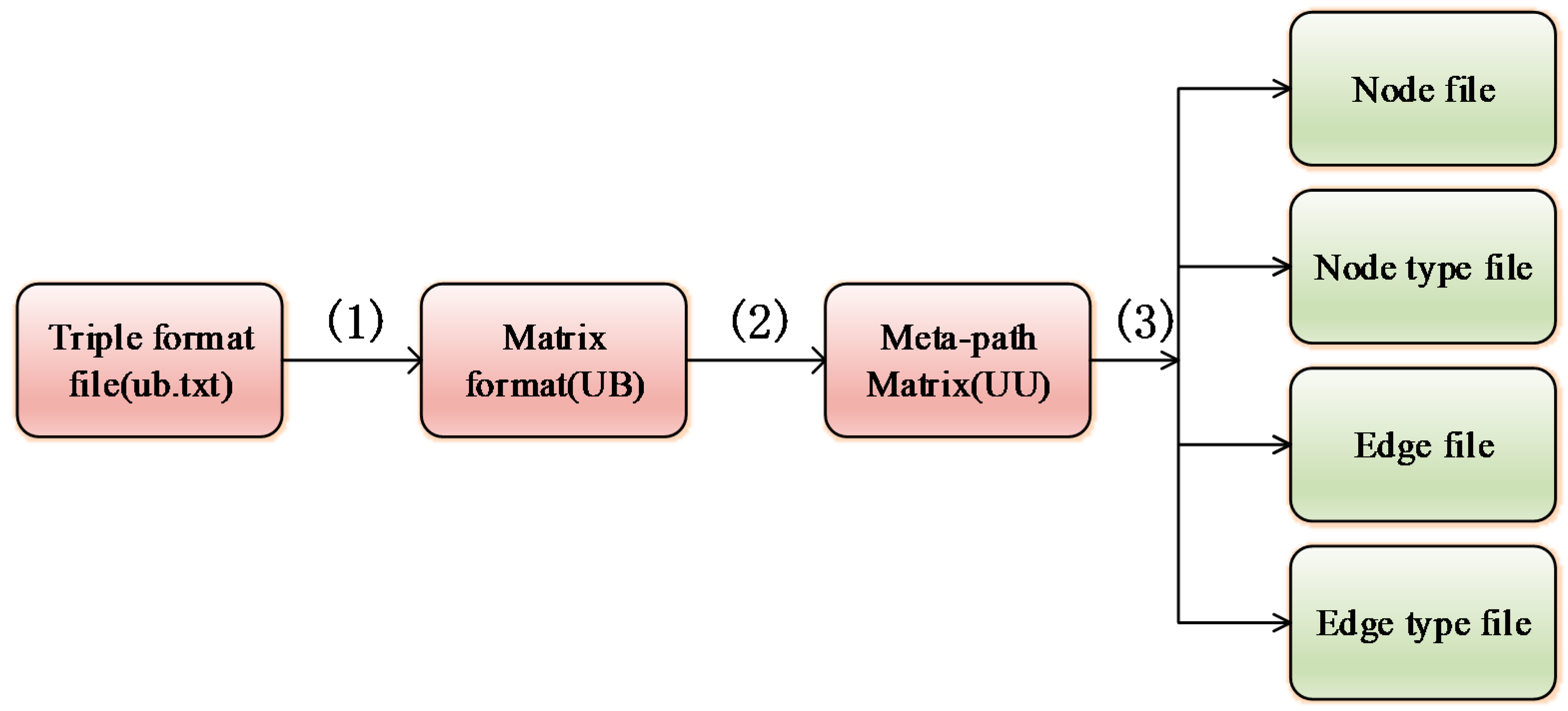
• According to different meta-paths, the dataset file will be processed accordingly. If the meta-path is UBU (User-Business-User, UBU), process the dataset file ub.txt. First, use the information in ub.txt to generate the interaction matrix UB (User-Business, UB). This matrix dimension is the number of users × the number of items.
• Use the following matrix multiplication equation to obtain the matrix UU (User-User, UU) of UBU.
• The meta-path matrix UU is obtained in the previous step. The first sets of different typeIDs of nodes, nodes, and their type settings for the Yelp and Douban Movie datasets are shown in

  Table 1. Nodes and their types for the Yelp dataset.

  Node Name	Type ID
  user	0
  business	1
  Compliment	2
  category	3
  city	4

  and

  Table 2. Nodes and their types for the Douban Movie dataset.

  Node Name	Type ID
  user	0
  Movie	1
  Group	2
  Actor	3
  Director	4
  Type	5

  . Then, according to this mapping relationship, extract node files, edge files, node type files, and edge type files from UU in turn, including UBU.nodes, UBU.nodes_types, UBU.edges, and UBU.edges_types. The following describes the file format in detail. The format of the node file is nodeID node_type. Each line represents the node and its node type. The format of the node type file is node_typeID. Each line has only one value, which represents the typeID of the node, where all the different node types are listed. The format of the edge file is start_nodeID and target_nodeID, which means that there are edges from node start_node to node target_node. The format of the edge type file is start_node_typeID and target_node_typeID, where the node correspondence is changed to the typeID of the node compared to the edge file.

4. Experiment

The experiments of this study are described in several sections. They include verifying the memory effectiveness of the spacey random walk, verifying the effectiveness of the embedding method, verifying the effectiveness of the MPHSRec algorithm, and analyzing the impacts of different parameters in the spacey random walk algorithm.

4.1. Datasets

This study evaluated the proposed model using two different datasets from different neighborhoods: the Douban Movie dataset and the Yelp dataset. These two datasets are described below in detail:

• The Douban Movie dataset [36] (Douban Movie) includes 13,367 users, 12,677 movies, and 1,068,278 ratings, ranging from 1 to 5. The data also include user and movie attribute information, such as Group, Actor, Director, and Type.
• The Yelp dataset [37] includes 16,239 users, 14,284 merchants, 47 cities, and 511 categories. The city information is the city where the merchant is located, and the category information is the category of the merchant.

Table 3. Details of the two datasets.

Data Set	Entity Name	Number of Entities	Relationship Name	Number of Relationships	Meta-Path
Douban Movie	User	13,367	User–Movie	1,068,278	UMU UMAMU UMDMU UMTMU MUM MAM MDM MTM
	Movie	12,677	User–Group	570,047
	Group	2753	User–User	4085
	Actor	6311	Movie–Actor	33,587
	Director	2449	Movie–Director	11,276
	Type	38	Movie–Type	27,668
Yelp	User	16,239	User–Business	198,397	UBU UBCiBU UBCaBU BUB BCiB BCaB
	Business	14,284	User–User	158,590
	Compliment	11	User–Compliment	76,875
	Category	511	Business–City	14,267
	City	47	Business–Category	40,009

lists the details of the two datasets, including entities, relationships, and meta-paths. The meta-path design scheme of [38] was used here.

Since the focus of this article is on improving the effectiveness of recommendations, the focus is on how to learn effective vector representations of users and items, and not much on other types of nodes, so only meta-paths that begin and end with a user type or an item type were chosen as the source of the experiment.

4.2. Memory Effectiveness Verification of Spacey Random Walk Based on Meta-Paths

This section tests the MPHPSRW algorithm and the standard random walk algorithm DeepWalk using the psutil tool to calculate memory usage to verify the effectiveness of the MPHPSRW algorithm on memory. The experiment uses six meta-paths of the Yelp dataset, namely UBU, UBCiBU, UBCaBU, BUB, BCiB, and BCaB, and four meta-paths of the Douban Movie dataset, namely MUM, MAM, MDM, and MTM.

In order to avoid interference from other parameters, the parameter values of several main parameters used in the random walk were fixed. The time of the random walk was set to 10, the random walk’s path length was set to 10, and the spacey random walk’s special parameter, personalized probability, was set to 0.8.

Table 4. Comparison of memory cost for the two algorithms under different meta-paths.

Meta-Path	DeepWalk	MPHPSRW
UBU	237.85 MB	39.45 MB
UBCiBU	53.67 MB	32.23 MB
UBCaBU	70.53 MB	41.97 MB
BUB	104.99 MB	73.42 MB
BCiB	25.34 MB	12.24 MB
BCaB	34.43 MB	23.05 MB
MUM	523.32 MB	159.16 MB
MAM	32.25 MB	21.03 MB
MDM	21.97 MB	9.31 MB
MTM	28.85 MB	15.36 MB

shows the comparison of consumed memory between the DeepWalk and MPHPSRW algorithms for performing random walks in different meta-paths.

From Table 4, it is obvious that MPHPSRW consumes much less memory in different meta-paths than DeepWalk. Some even have a difference of more than 5 times, which shows that compared with the standard random walk DeepWalk algorithm, the spacey random walk algorithm based on meta-paths has obvious advantages in memory cost.

4.3. Effect of Different Parameters on the Random Walk Algorithm

This section analyzes the effect of different parameters of the random walk algorithm on the model. The parameters are the times of a random walk, the length of random walk paths, and the spatial probability. For random walk times and random walk path lengths, classification problems can be used to evaluate the random walk with different parameters. As this section analyzes different parameters of the random walk, it is not necessary to evaluate it for a particular node, as done in Section 2.

In this section, the personalized space embedding method (SpaceyMetapath) based on meta-paths is used, and the algorithms used for comparison are the DeepWalk algorithm and the Metapath2vec algorithm. Different embedding methods can be used to obtain different results for different parameters, and the best results can be obtained by selecting the best parameter embedding method. The use of a good embedding method can obtain more accurate and effective embedding vectors for the recommendation model, which helps to improve the recommendation system’s performance.

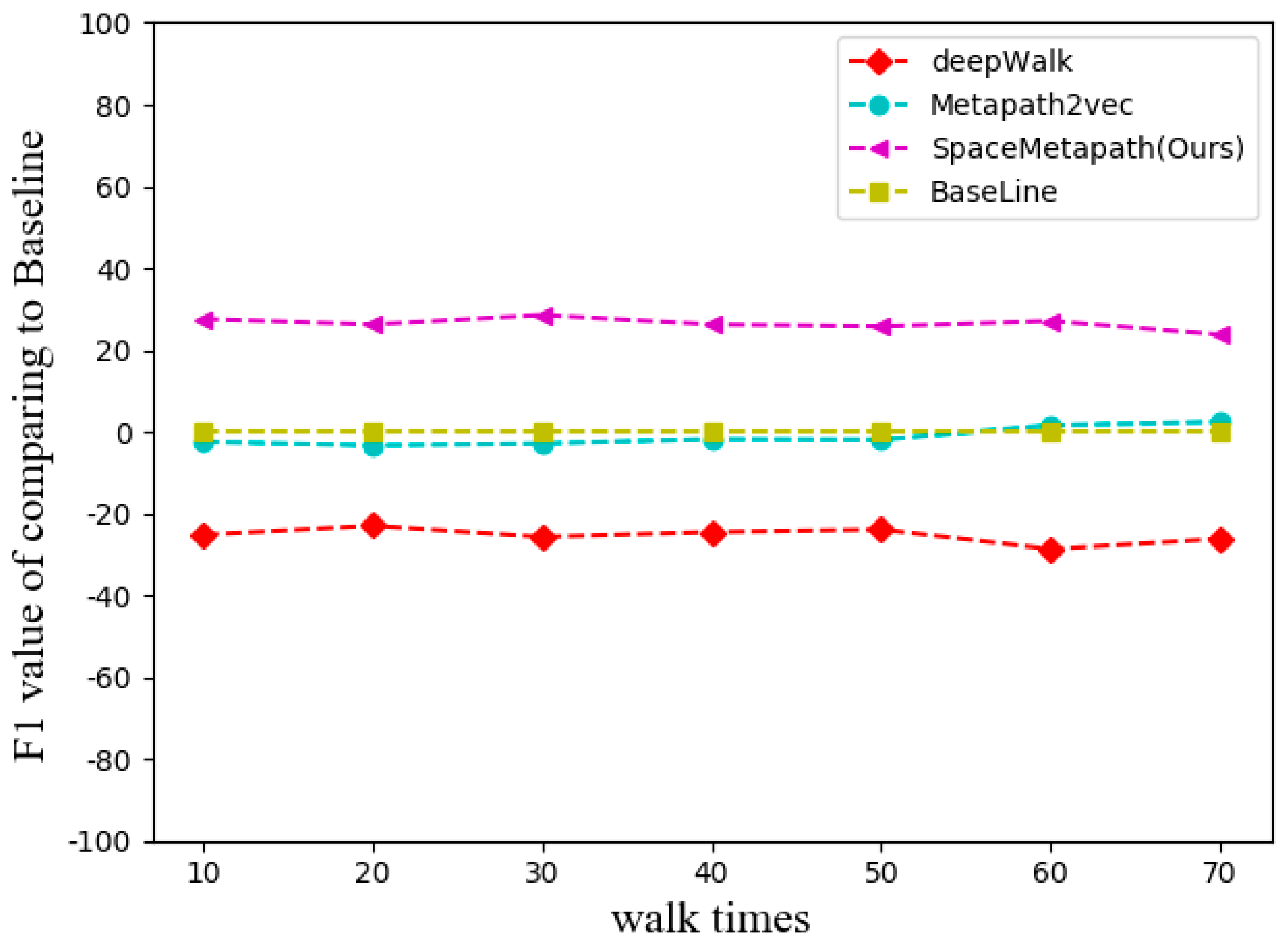
• The times of a random walk. For the times of a random walk, the default value is 10, using values of 10 to 70 for each experiment with an interval of 10. In order to better show the contrast effect, we set up a baseline. The baseline in the figure is the average value of F1 of each algorithm, and the comparison effect of the F1 value of the three algorithms with the baseline is shown in Figure 6.

The times of a random walk are the numbers of iterations of a random walk on the nodes in the network, and the more times of a random walk, the more meaningful it is to the mining of nodes in the network. Figure 6 shows that the overall trend is that when the times of random walk gradually increase, the effect of different algorithms will gradually improve; that is, the F1 value will increase. It shows that an increase in the times of a random walk has an improvement on the effect of different algorithms.

SpaceyMetapath was compared with Deepwalk and Metapath2vec, which can use fewer random walks to get better results and save on the running time of the algorithm. This illustrates the advantage of the spatial random walk over the standard random walk algorithm.

2.

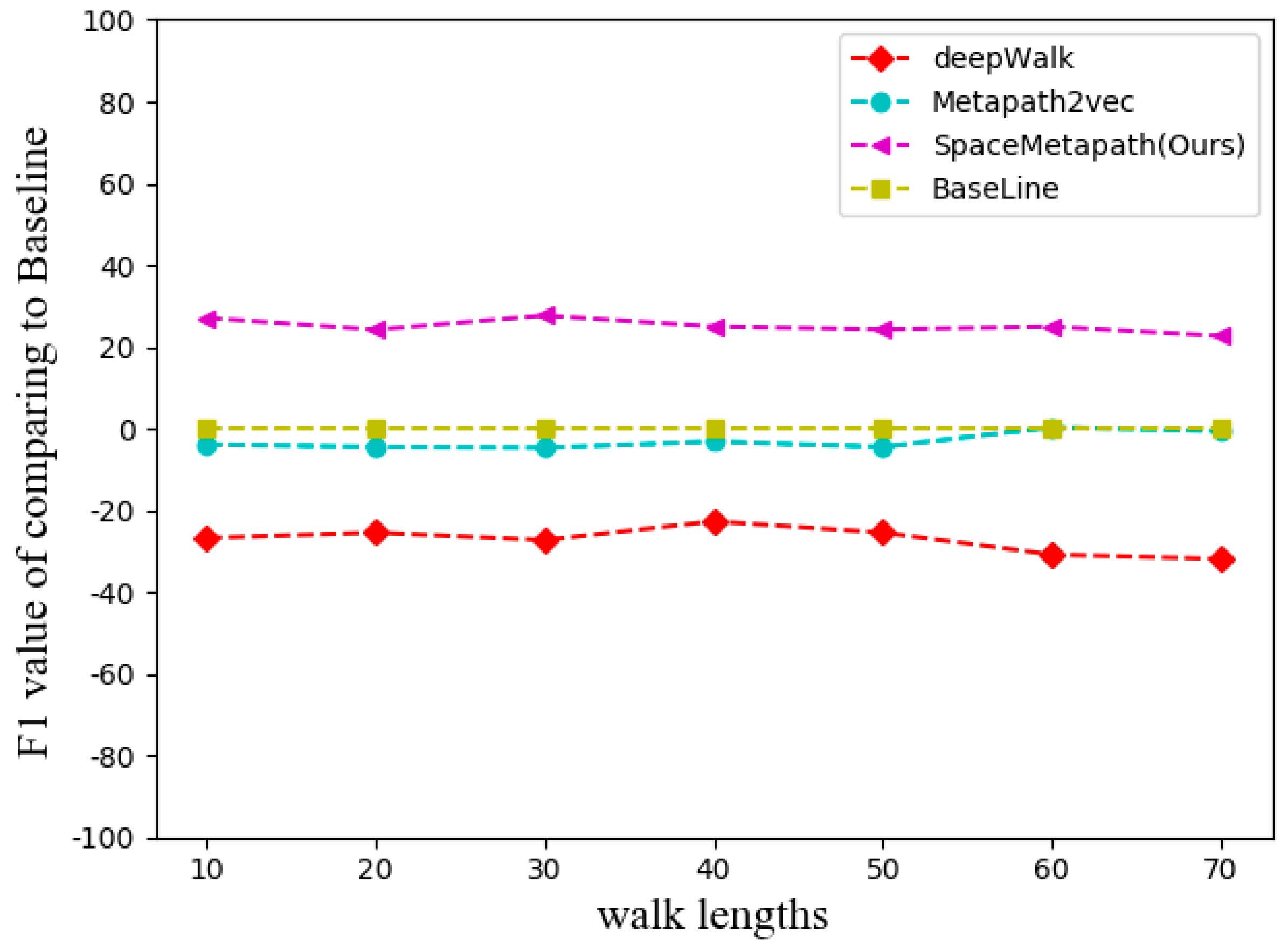
Random walk path length. For a random walk path length, the default value is 10, and the experiments were conducted from 10 to 70 times with an interval of 10 times.

The random walk path length is the length of the sequence of nodes generated by the random walk on the network nodes. An increase in the path length can fully exploit the node information, which is meaningful to the random walk algorithm. Figure 7 shows that the F1 value of different algorithms will gradually increase when the random walk path length increases, which also shows that the greater the random walk length, the better the effect of the algorithm. Similarly, SpaceyMetapath was compared with Deepwalk and Metapath2vec, and it was found that SpaceyMetapath uses a shorter length to obtain the same effect as the standard random walk algorithm using a longer length. For example, when Deepwalk uses a random walk of path length 70, the resulting F1 value is similar to that of SpaceyMetapath using a random walk of path length 10. This is because the spatially random walk will skip some unimportant nodes, so it is good to use a smaller path length.

If the probability of personalization is too high or too low, it will have a restraining effect on the control of the user’s personalization behavior. From Figure 8, the best result is obtained when the probability of personalization is increased to 0.8, and the algorithm’s ability decreases when the probability of personalization is increased. This is because when the probability of personalization is low, the algorithm does not pay much attention to the history state information, and as the probability of personalization increases, the proportion of history state information increases.

The Yelp dataset provided the same results as the Douban Movie dataset in the experiment on the parameters in the random walk strategy, with a small number of random walks and short random walk path lengths yielding better recommendations. SpaceyMetapath obtained the best result with 0.7 on the Yelp dataset.

3.

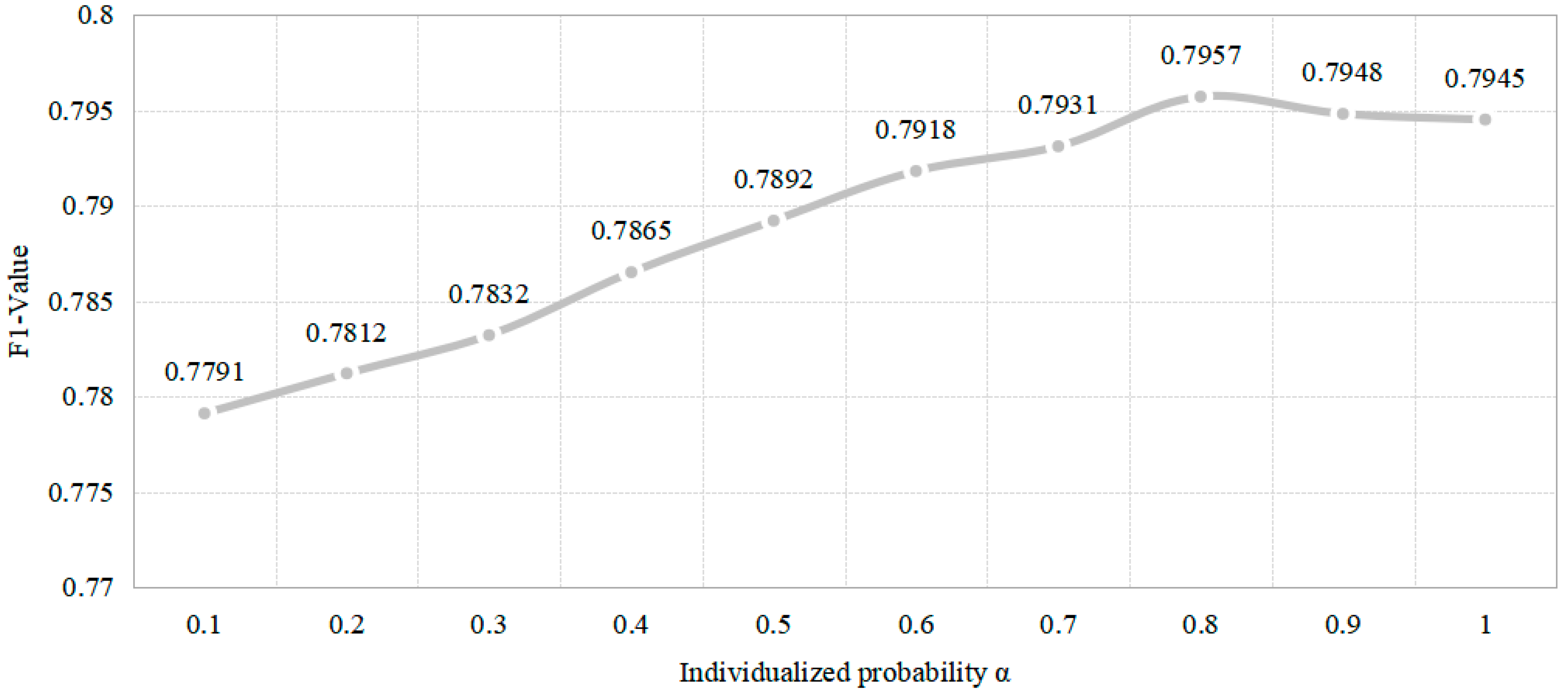
Personalized probability. Here, we used SpaceyMetapath with a parameter range of 0.1–1.0 and an interval of 0.1. Figure 8 shows the F1 result with different personalization probabilities from the Douban Movie dataset. The horizontal coordinate is the probability of different personalized probabilities, and the vertical coordinate is the result of SpaceyMetapath’s classification for different personalized probabilities.

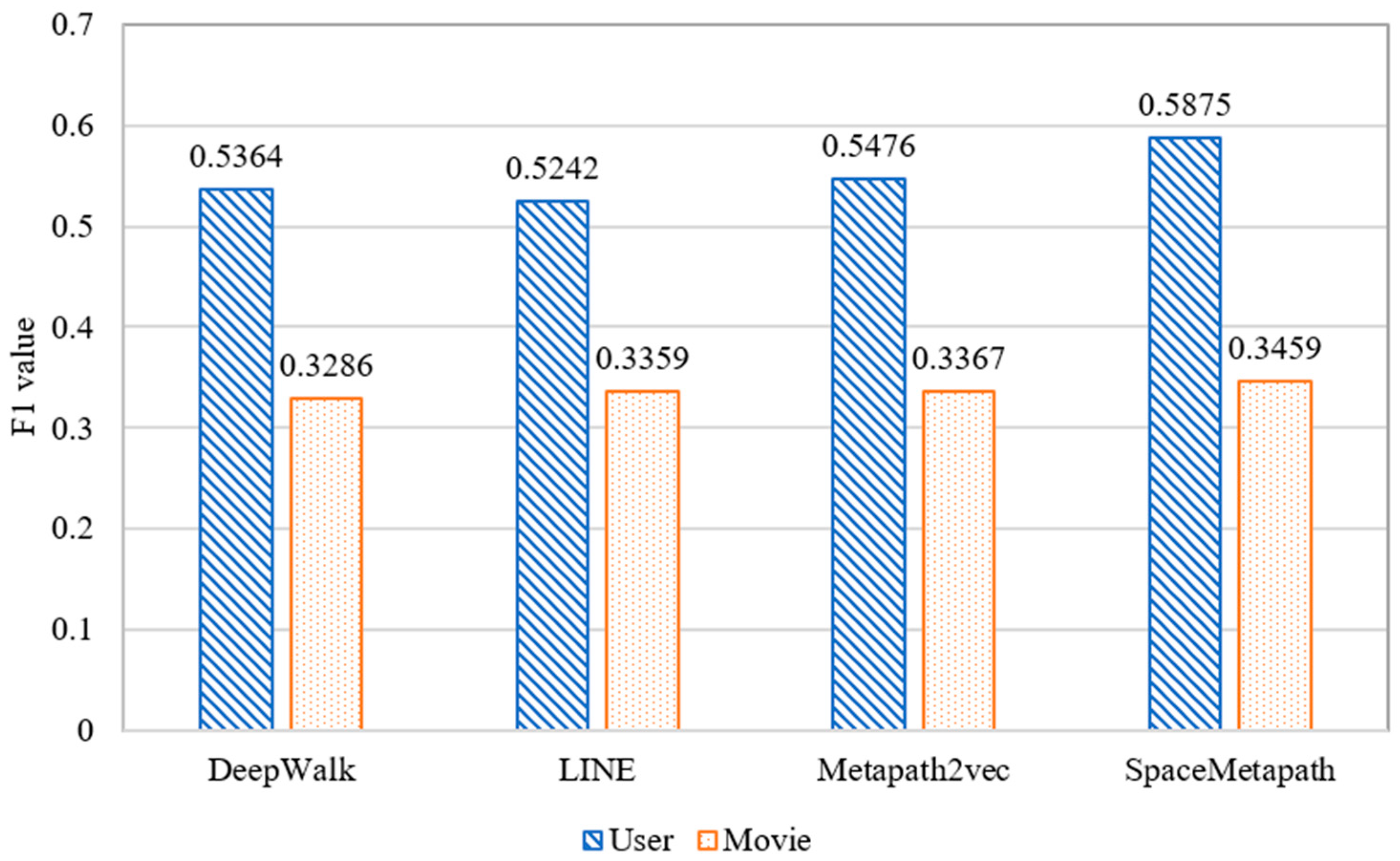
4.4. Validation of the Effectiveness of the Meta-Path-Based Heterogeneous Personalized Spacey Embedding Method

In this section, the effectiveness of the meta-path-based heterogeneous personalized spacey embedding method (SpaceyMetapath) is validated by experiment. There are two typical tasks in the industry for embedding methods: node classification and link prediction. We used node classification to evaluate the quality of embedding vectors obtained from learning different embedding methods. The quality of the embedding vector is represented by the F1 value in the classification problem.

For Metapath2vec and SpaceyMetapath, the meta-paths used in the experiments for the Douban Movie dataset and the Yelp dataset were UMAMU and UBCBU, respectively. Due to hardware limitations, smaller values were used for the selection of parameters, such as the times of the random walk and the path length, in the random walk algorithm to help speed up the experiment.

We used the following parameter indices. The low-dimensional vector dimension after transformation by the embedding method was set to 128; the times of the random walk in an individual node of the random walk was set to 10; the random walk path length was 10; the neighborhood size was 5; and the heterogeneous personalized spacey embedding method’s special parameter, personalization probability α, was set to 0.8. In order to avoid errors, ten experiments were conducted and the results are averaged as the final result. Figure 9 and Figure 10 show the F1 values with different embedding methods in the Douban Movie dataset and the Yelp dataset.

Figure 9 and Figure 10 show that the meta-path-based heterogeneous spacey embedding method performs better than both the homogeneous and the heterogeneous embedding methods. For the Douban Movie dataset, two nodes (user and movie) were classified, and it was found that SpaceyMetapath was 5%~7% and 1%~2% higher than DeepWalk and LINE, respectively. The enhancement effect was very obvious. For a given meta-path in Metapath2vec, the improvement was 2%~5% and 1%~2%, respectively. For the Yelp dataset, in the classification of users and merchants for both nodes, it can also be seen that SpaceyMetapath performed better than DeepWalk, LINE, and Metapath2vec.

Overall, heterogeneous embedding methods based on meta-paths perform better than DeepWalk and LINE because of the physical meaning of the meta-paths themselves, which can provide more semantic information; for SpaceyMetapath, the high F1 value compared with Metapath2vec is due to the random walk, which jumps over unimportant nodes in the middle. More accurate node sequences are obtained, and more efficient node vectors can be obtained using the Skip-Gram algorithm. The experimental results show the advantages of the heterogeneous personalized spacey embedding method over other heterogeneous embedding methods and lay the foundation for the subsequent combination with the recommended model.

Personalized probability helps the random walk algorithm select the previous state and then select the next state based on the previous and current states. The spacey meta-path uses a higher personalized probability than other embedding methods to control the user’s personalized behavior. This is the advantage of the heterogeneous personalized spacey embedding method over traditional heterogeneous embedding methods.

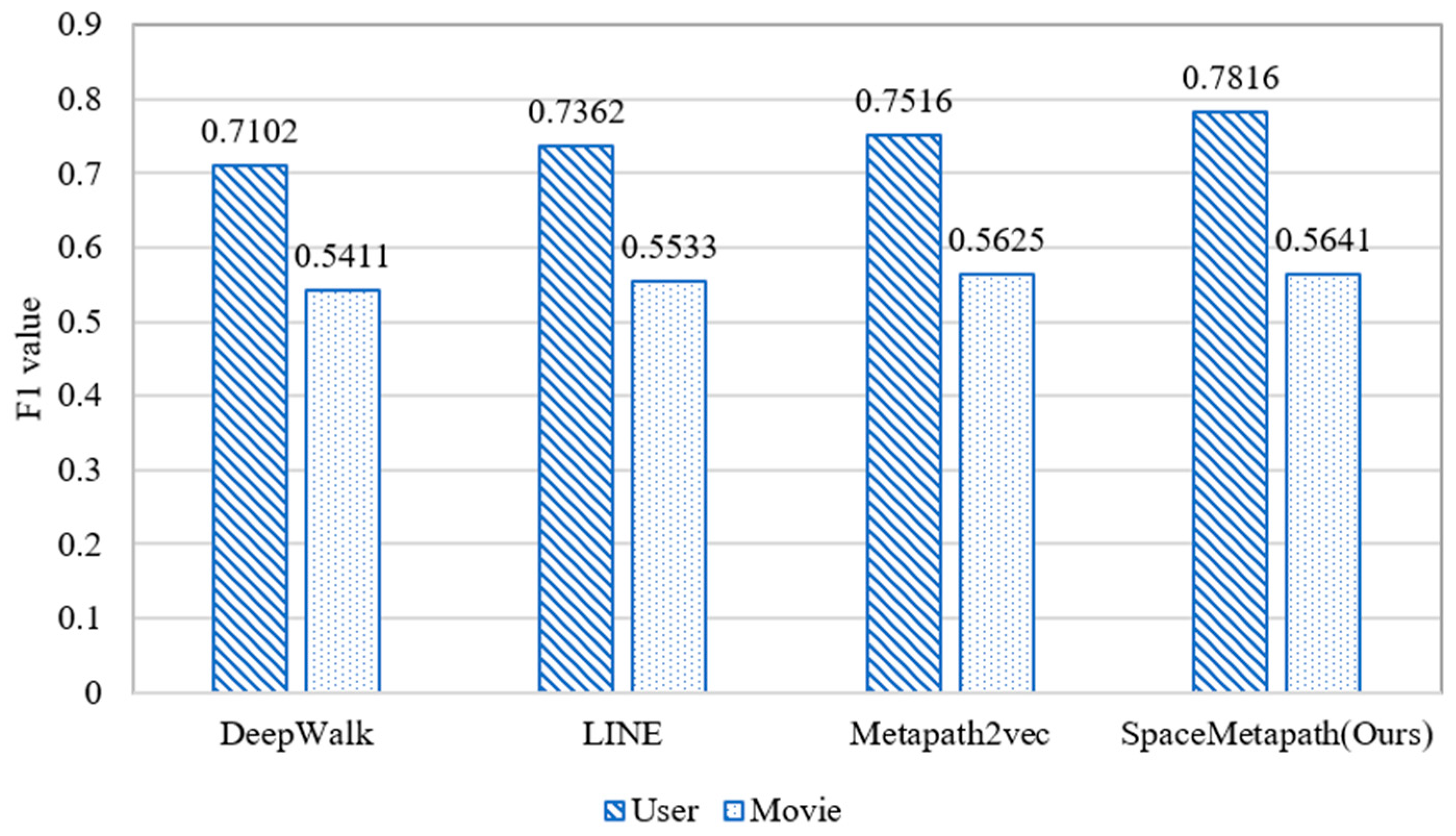
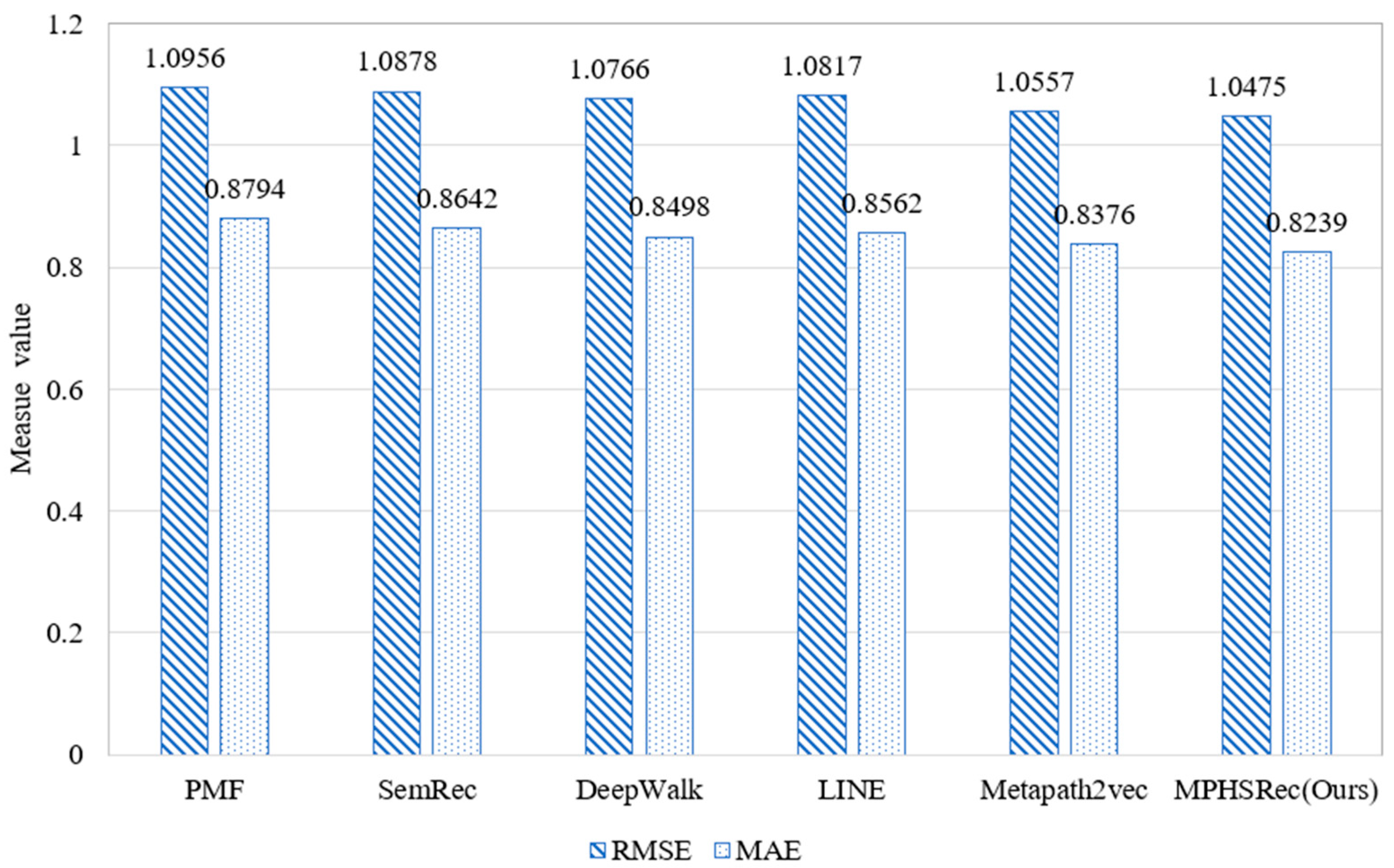
4.5. Validation of MPHSRec

In this section, the effectiveness of MPHSRec is validated, and MPHSRec is compared with the traditional Matrix Factorization model and the recommendation algorithm based on a heterogeneous information network.

According to [1], only short meta-paths were selected in our experiments because a long meta-path may bring about noise semantics. In order to avoid the influence of parameters on the model, the parameters were initialized first. There are three main parameters in the random walk part of the heterogeneous personalized spacey embedding method, namely random walk times (walk_times), random walk path length (walk_length), and spatial probability α, which were set to 20, 5, and 0.8, respectively.

For the two datasets, the Douban Movie dataset used (20%, 40%, 60%, 80%) as the training ratio and the remaining (80%, 60%, 40%, 20%) was used as the testing ratio. Since the Yelp dataset is sparse, the sparsity is 0.08%, so (60%, 70%, 80%, 90%) of the dataset was used as the training ratio set, with the remaining (40%, 30%, 20%, 10%) of the data used as a test set.

Table 5. RMSE and MAE comparison of algorithms on the Douban Movie dataset.

Model	Evaluation Indicators	Training Ratio (20%)	Training Ratio (40%)	Training Ratio (60%)	Training Ratio (80%)
PMF	MAE	1.5472	1.0215	0.9128	0.8794
	RMSE	1.7215	1.2256	1.1782	1.0956
SemRec	MAE	1.4664	0.9863	0.8821	0.8642
	RMSE	1.6742	1.2176	1.1423	1.0878
DeepWalk	MAE	1.4268	0.9664	0.8506	0.8498
	RMSE	1.6641	1.2106	1.1021	1.0766
LINE	MAE	1.4329	0.9782	0.8612	0.8562
	RMSE	1.6721	1.2272	1.0845	1.0817
Metapath2vec	MAE	1.4054	0.9547	0.8424	0.8376
	RMSE	1.6598	1.2012	1.0618	1.0557
MPHSRec (Ours)	MAE	1.3921↓	0.9421↓	0.8319↓	0.8239↓
	RMSE	1.6476↓	1.1982↓	1.0539↓	1.0475↓

shows the MAE(Mean Absolute Error, MAE)and RMSE(Root Mean Square Error, RMSE) results with different training ratios among different models. It can be seen that as the training ratio increases, the MAE and RMSE of different models gradually decrease, indicating that the increase in the training sample had a positive effect on the model fit data.

Figure 11 shows the trend of MAE and RMSE among different models. In the figure, HERec (Deepwalk) indicates the HERec algorithm using DeepWalk, HERec(LINE) indicates the HERec algorithm using LINE, and HERec(Metapath2vec) indicates the HERec algorithm using Metapath2vec.

• From the perspective of heterogeneous information networks, PMF is a traditional recommendation algorithm based on Matrix Factorization, while SemRec, HERec and its variants, and MPHSRec are recommendation algorithms that introduce heterogeneous information networks. Because heterogeneous networks contain a large number of semantic relations, the MAE and RMSE of the latter algorithms have all declined significantly in Figure 7. The recommendation performance can be improved by the heterogeneous embedding method. The dataset contains a lot of attribute information, such as the director of the movie, the actor, the subject matter, and the city and category of the merchant, which is useful for the recommendation model and can improve the recommendation performance of the model. Compared with the heterogeneous information network embedding method, PMF does not introduce this additional attribute information, which is why the heterogeneous network embedding method is advantageous.
• From the perspective of heterogeneous embedding methods, since the algorithms with traditional heterogeneous embedding, namely DeepWalk, LINE, Metapath2vec, and the algorithm proposed in this paper adopt the personalized spatial embedding method, their MAE and RMSE will be decreased, that is, they will have a better recommendation performance. This embedding method can obtain a more efficient node vector representation than the traditional heterogeneous embedding method, which results in a better recommendation performance. Table 5 shows the MAE and RMSE results with different training ratios between the different models on the Yelp dataset. Similar to the Douban Movie dataset, an increase in the number of training samples leads to a gradual decrease in the MAE and RMSE from

  Table 6. RMSE and MAE comparison results for different training ratios on the Yelp dataset.

  Model	Evaluation Indicators	Training Ratio (60%)	Training Ratio (70%)	Training Ratio (80%)	Training Ratio (90%)
  PMF	MAE	1.3412	1.2413	1.1923	1.0738
  	RMSE	1.8215	1.6574	1.4763	1.4384
  SemRec	MAE	1.2664	1.1874	1.1545	1.0423
  	RMSE	1.7742	1.3106	1.2542	1.2438
  DeepWalk	MAE	1.2068↓	1.1624	1.0932	1.0872
  	RMSE	1.6641	1.2106	1.1221	1.1066
  LINE	MAE	1.4329	0.9782	0.8612	0.8562
  	RMSE	1.6721	1.2272	1.1845	1.1817
  Metapath2vec	MAE	1.4054	0.9547	0.9124	0.9076
  	RMSE	1.3598	1.2012	1.1618	1.1457
  MPHSRec (Ours)	MAE	1.3821	0.9415↓	0.8465↓	0.8429↓
  	RMSE	1.3356↓	1.1954↓	1.1056↓	1.0438↓

  . Since the heterogeneous information network contains a large amount of semantic information, and the semantic information can be mined through meta-paths and used for recommendations, the MAE and RMSE of the recommendation algorithm with the heterogeneous embedding method are smaller than those of the PMF of the traditional Matrix Factorization method. In Table 5 and Table 6, ↓ represents the minimum in comparison values.

Figure 12 shows a graph of the results on the Yelp dataset. Similar to the Douban Movie dataset analysis, MPHSRec uses a heterogeneous information network to improve the recommendation effect compared with PMF from the point of view of the heterogeneous information network; and from the point of view of the heterogeneous embedding method, because the heterogeneous personalized spacey embedding method is more effective than the traditional heterogeneous embedding method, the RMSE and MAE of MPHSRec are lower than those of HERec and its variants, which indicates the effectiveness and practicality of the heterogeneous space embedding method applied to the recommendation neighborhood.

For the Yelp dataset, its sparsity is only 0.08%, while MPHSRec performs well on both the Douban Movie and Yelp datasets with low MAE and RMSE values, which show that the algorithm is effective for sparse data and verify the applicability of the algorithm for data sparsity.

The experimental results on the Douban Movie and Yelp datasets show that the accuracy of the proposed algorithm is higher than that of the other five benchmark algorithms. So, it also proves the fact that we used the heterogeneous personalized space random walk strategy to learn the relationship between nodes in a large-scale network, which is conducive to improving the accuracy of the MPHSRec model. The comparison of experimental results for the six algorithms is shown

Table 7. Accuracy comparison of algorithms under different training ratios on two public datasets.

Model	Douban Movie	Yelp
PMF	0.7502	0.7238
SemRec	0.7946	0.7663
DeepWalk	0.9034	0.8824
LINE	0.8465	0.8272
Metapath2vec	0.9162	0.8892
MPHSRec (Ours)	0.9301	0.9038

.

5. Conclusions

In this article, we proposed a recommendation algorithm model named MPHSRec based on the meta-path of the heterogeneous random walk. We used a spacey random walk algorithm based on meta-paths to generate a sequence of nodes and combined it with a heterogeneous Skip-Gram algorithm to learn vector representations of all entities. The resulting vector representations were input into the Matrix Factorization model. Compared with the recommendation model based on the heterogeneous embedding method, MPHSRec provides a more accurate vector representation and improves the recommendation performance. MPHSRec solves the industry standard random walk smoothness problem, has reduced the memory cost, and also solves the problem of the conventional fixed meta-path limitation. The relationships in the Douban Movie dataset are more complex than those in the Yelp dataset. Through experiments on two datasets, the results also show that the spacey random walk method used in this study can save some memory space of the algorithm for datasets with complex relationships and skip some unimportant relationships between nodes, which is conducive to the efficiency and accuracy of the recommendation algorithm.

For the selection of meta-paths, we chose the same meta-path with the same starting point and end point. So, in future work, we will try to choose different meta-paths for heterogeneous embedding learning.