Abstract
Seawater level changes are affected by natural and anthropogenic impacts. While climate changes are considered to be a cause for all significant recent variations in meteorological and hydrological parameters, there is still a need for the analysis at the smaller regional scale, especially of the seawater level changes. A regional analysis is essential for early warning of upcoming changes that could, firstly, affect islands and coastal areas and, subsequently, expand on larger areas. The determined regional changes could affect the salinity of drinking water sources, increase the presence of natural flooding, and impact land degradation. In this paper, an analysis of local seawater level fluctuations is provided for three available locations in Croatia distributed along the Adriatic Sea’s coast. The rescaled adjusted partial sums (RAPS) method was used and applied on time series of the average daily seawater levels for each location. Visual interpretation of the RAPS method indicated the appearance of common regularities of the observed quantities, in this case, averaged daily seawater level changes. Also, it was shown that the regional shape and indentation of the coast did not have a strong effect on the seawater level’s rise. Seasonal changes in the sea level are mostly periodic and, therefore, have symmetry visible in its behavior. Fluctuations in the dynamics of sea level studied in this paper were not regular and predictable with simple linear equations, but the symmetry was also found to be present in the irregularities identified with the RAPS method.
1. Introduction
Generally, relative sea-level changes are caused by transfers of water mass between oceans and continents due to the enlargement and deflation of immense ice layers. These changes are mainly caused by global climate changes. However, significant vertical movements in the Earth’s crust appear over long periods of time that should also be taken into the account. These movements cannot be exactly determined and their value stated, but they can be identified and eliminated to some extent from Earth observations. This includes co-seismic uplift and subsidence during hazardous earthquakes (Mw > 8), Earth’s surface displacements caused by a long-term process of glacial isostatic adjustment, and global ocean volume changes as a result of plate–tectonic movements [1]. Not only are vertical changes affected by the mentioned Earth processes, but sea-level changes also reshape coastal surroundings by their horizontal shift. The main impacts of sea-level rise are increased coastal erosion and loss of the land, increased risk of flooding, and saltwater intrusion into freshwater resources [2].
The abovementioned processes occur at different locations on Earth. There is no single location at which all of these processes are happening at the same time. Therefore, it is impossible to record them collectively at once. However, we can record and monitor the behavior of one of the processes, observing its behavior, and analyze any possible regular trends that can be identified as a systematic and periodic Earth behavior resulting in a clearer set of original measurements.
The rate of sea-level rise has increased. Between the years 1900 and 1990, studies show that the sea level rose between 1.2 mm and 1.7 mm per year on average at a global level as measured by satellite altimetry [3]. By the year 2000, that rate had increased to approximately 3.2 mm per year, and the rate in 2016 was estimated to be 3.4 mm per year. In 2019, the sea level rose 3.3 mm. Figure 1 shows the rise in sea level over the last three decades at a global level. As mentioned in Reference [4], during the period 1993–2018, the sea level varied from −1.41 + −0.47 mm per year for six locations in the Adriatic Sea
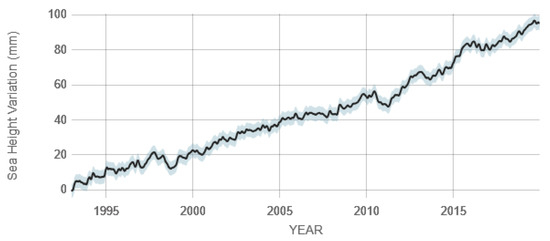
Figure 1.
Rise in the sea level at a global level from 1993 to 2019 [3].
Numerous studies have dealt with the estimation of how much and how fast the global average sea level is rising. The main difference among the studies is the analytical approach. The first approach quantitatively describes the physical processes contributing to the global sea rise [2], such as thermal change influence on ocean water volume, land ice melting, and changing the depth of global ocean basins [5], while the second approach tries to predict the future rise in sea levels based on observed temperature changes. The first approach was used in Intergovernmental Panel on Climate Change (IPCC) climate assessments. Within this approach, physical models are used to estimate contributions from the sea level components, such as thermal expansion and melting from glaciers and the dynamics of ice sheets, with their summation in the last stage of estimation [6,7,8]. The second approach is based on a hypothesis that the sea level rises faster as it gets warmer [2]. This approach uses semiempirical models in order to form statistical relationships between sea-level change and global temperature [9,10,11] or radiative forcing [12,13], respectively.
Sea-level fluctuations, which occur over wide ranging timescales, may have periodic or aperiodic characteristics visible. Symmetry can be detected in irregularities in rescaled adjusted partial sums (RAPS) graphs, since the dynamics of sea level studied in this paper are not predictable with linear trendlines. The most recognizable periodic oscillations are the ones that occur due to the fact of seasonal changes in density or meteorological parameters [14]. Aperiodic sea-level changes cannot be assigned to an exact cause, since their behavior does not reoccur in the same shape at the same time intervals. They are the result of several meteorological dynamic processes that cannot be determined separately and eliminated from observations. In addition, anthropogenic influences [14] were recently acknowledged and recognized as significant factors regarding sea-level changes, comprising greenhouse gases and increases in the temperature of Earth’s atmosphere, which consequently also induce a rise in sea levels.
Figure 2 shows a schematic illustration of the climate and non-climate driven processes that can influence global, regional (green colors), relative, and extreme sea-level events (red colors) along coasts. Major ice processes are shown in purple, while general terms are shown in black. Sea level equivalent (SLE) reflects an increase in the global mean sea level if the mentioned ice mass is completely melted into the ocean [15]. Figure 2 gives insight into the complexity and impacts of the different causes of rises in levels of sea water. Due to the processes’ complexity, which occur due to the rise and fall of the sea, in Croatia, there is the danger of coastal and island settlements becoming flooded.
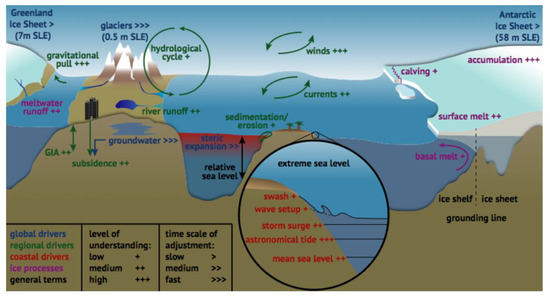
Figure 2.
Natural and anthropogenic impacts on the sea level rising.
The main aim of this study was to identify possible connections between three available seawater level measuring stations, i.e., between their average daily seawater level changes. The RAPS method was used for this purpose, and the effects of the coast’s relief on seawater level changes were analyzed.
2. Methodology
The application of linear trend determination for sea-level observations is a well-established and familiar approach. However, linear trends as a method only point out predictable and obvious disturbances over a large set of data that occur in some repetitive periodical aspect. To detect and identify possible disturbances outside of the scope of seasonal changes, some scientific areas use the RAPS method. It is statistical method which can deal with a large set of data in order to detect and describe periodic and/or aperiodic behavior. This method was chosen due to the fact of its applicability in detecting variational trends apart from the main trend in a time series of a monitored occurrence; it can be used for hydrological analysis of river flows [16] (as well as in most hydrological research [16]), precipitation [17], water temperatures [18], meteorological parameters for the purpose of the clay excavation [19], waste water quality analysis [20], etc.
We used it in this paper on a large time series of available 18 years of averaged daily seawater levels to examine whether it would highlight the subsets of default (original) time series if they existed.
The RAPS method is a time series analysis method based on visual determination of a subseries from the original (given) series of continued data. By using the values of an average value and standard deviations of the observed time series, sums of the RAPS values provide insight into the new subseries parts, where occurrences of the data grouping, fluctuations, and similar appearances during the time is based on:
where Yt is the value of the analyzed member (parameter) of the considered time series, is an average value of the considered time series, Sy is standard deviation of the considered time series, n is a number of members of the considered time series, and k = 1, 2,..., n is a counter during summation procedure [16].
The plot of the RAPS offers a reasonable visualization of the readily apparent mode of the underlying trend, which cannot be seen in the standard time series plots [21]. The RAPS method could be applied to the data time series.
The first step in the analysis is defining the linear trend, which is a common procedure in the determination of the rise or fall of average daily seawater levels time series. In cases where such a determination cannot be realized due to the low values of the determination coefficient, the RAPS method has been found to be suitable. Apart from the main analysis of the resulting subseries, consequently, a comparison of the RAPS single and summed values for all measuring stations was done.
3. Case Study
To apply the RAPS method on time series data of sea levels, the Croatian Meteorological and Hydrological Service (CMHS) provided average daily seawater level data for three locations on the Croatian part of the Adriatic coast. These were Martinščica, on the island of Cres, and Prosika and Golubinka, which are on the coast. Seawater levels were measured using a mareograph on an hourly basis and averaged to daily values. Figure 3 presents the locations of observed measurements, all situated along the eastern side of the Adriatic Sea. Figure 4, Figure 5 and Figure 6 show the available time series of averaged seawater levels (H) for the measuring stations of Martinščica, Prosika, and Golubinka [22].
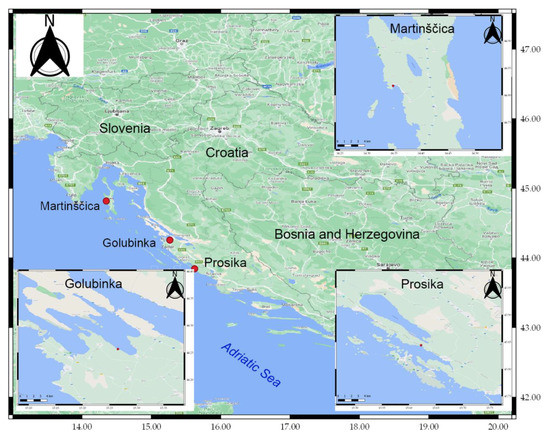
Figure 3.
Locations of the measuring stations for sea water levels [23].
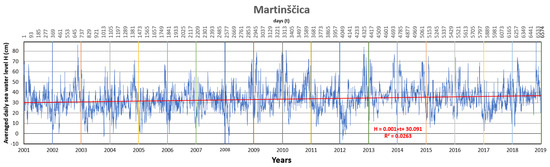
Figure 4.
Linear trend of the averaged daily sea water levels from the Martinščica measuring station [24].
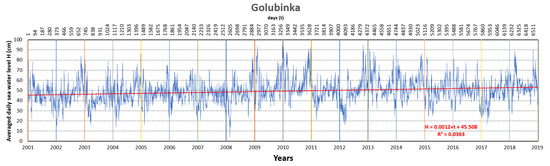
Figure 5.
Linear trend of the averaged daily sea water levels for the Golubinka measuring station [24].
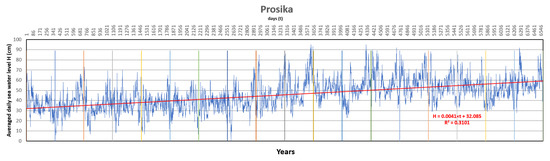
Figure 6.
Linear trend of the averaged daily sea water levels for the Prosika measuring station [24].
The northeastern coast of the Adriatic is the western part of the Balkan Peninsula. It is mostly a hill. Consistent with the relationship between tectonic structures, it refers to a well-defined longitudinal type. As a result of the combined effect of Holocene transverse and tectonic coastal precipitation, the sea in domes with positive structures attacked geosynclinal depressions and exposure wastes, creating numerous long and narrow bays that stretch along the abrupt coast. This is the busiest coast in the world with a large number of ports, coves, peninsulas, 1185 islands and islets, and differently shaped rocky outcrops that make-up the most interesting configurations and have small rocky and pebble beaches. It is intersected by several bays and coves, the largest of which are the Kvarner and Trieste bays, separated by an elevated Istrian peninsula. They align longitudinally near the shore, repeating the corresponding series of positive tectonic folds. The “inner” coast is well protected from the undulating movement of the island fence. It was practically not exposed to the action of the sea and retained vivid traces of initial dissection (tectonic and denudation). [22] Therefore, Martinščica and Golubinka are located in semi-closed bays and are not directly exposed to the waves, which does not affect short-term sea level changes. Prosika, however, is located in a channel between the Adriatic Sea and Lake Vransko jezero and, therefore, water level changes are affected not only by the Adriatic Sea but by lake water as well.
Linear regressions between average daily sea water level H (cm) and time t (days) were also calculated and are shown in Figure 4, Figure 5 and Figure 6. The obtained values of the coefficient of determination, R2 (0.0263 for Martinščica, 0.0363 for Golubinka, and 0.3101 for Prosika), were in favor of that. Although the value of R for Prosika (0.5569) showed salient regression, there was no justification for defining a linear trend. Especially for Martinščica (R = 0.1622) and Golubinka (R = 0.1905), which point out weak regression. It was obvious that defining a linear trend, as a most common procedure for such analysis, was not justified.
Characteristic statistical parameters for the measuring stations Martinščica, Prosika, and Golubinka are shown in Table 1 [24].

Table 1.
Average values, standard deviations, minimum and maximum values, and a range of the averaged daily sea water levels (cm) for the 18 year time series for the measuring stations Martinščica, Prosika, and Golubinka.
Values of standard deviation indicate that changes of the average daily sea water levels are similar. The correctness of this statement needs to be examined using the RAPS method.
4. Results and Discussion
Based on linear trend problem explained in Section 3, the RAPS method was applied to the observed time series for each measuring station. Figure 7, Figure 8 and Figure 9 present the RAPS method applied to each measuring station. The RAPS analysis was based on identifying the next “higher hill” or “lowest bottom”. Such points divide the original time series of the average daily sea water level rising on new subseries.
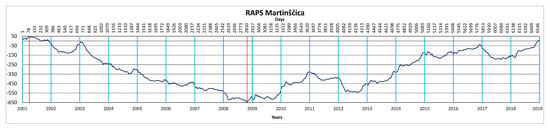
Figure 7.
Rescaled adjusted partial sums (RAPS) values of the averaged daily sea water levels for the Martinščica measuring station.
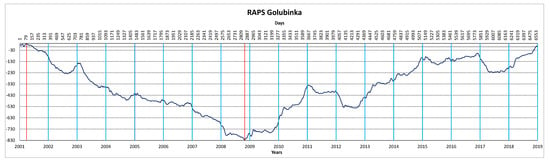
Figure 8.
RAPS values of the averaged daily sea water levels for the Golubinka measuring station.
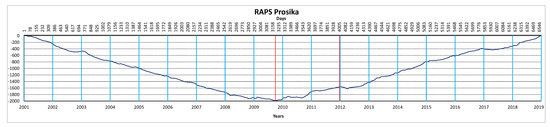
Figure 9.
RAPS values of the averaged daily sea water levels for the Prosika measuring station.
As can be concluded from Figure 7 and Figure 8, the Martinščica and Golubinka measuring stations have almost the same overlapping pattern of the RAPS values. Hence, subseries of the original sea level changes series can have possibly similar causes. RAPS values for Prosika also overlap with RAPS values of the mentioned two stations but not in the same shape of the pattern. It could be seen that RAPS values for the Martinščica and Golubinka stations separated at the end of the 2008, while separation of the Prosika station had a ‘’delay’’ of one year, at the end of 2009. Regarding geographical position and indentation along the coast (Figure 3), it can be concluded that those two factors did not have an impact on the RAPS values due to the topography in the station’s vicinity.
The Prosika measuring station has different RAPS values from Martinščica and Golubinka, which can be seen from Figure 7, Figure 8 and Figure 9. The Martinščica and Golubinka measuring stations are open to the sea, while the Prosika measuring station is located in the channel and between the Adriatic Sea and Lake Vransko jezero.
Possible connections among changes in seawater levels were tested by the analysis of the mutual correlations between RAPS single values (Figure 10, Figure 11 and Figure 12) as well as between RAPS summation values (Figure 13, Figure 14 and Figure 15).
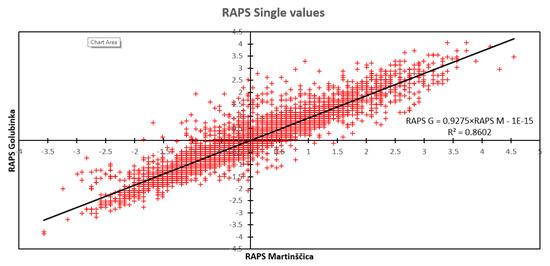
Figure 10.
Correlation among single values of the RAPS for Golubinka and Martinščica.
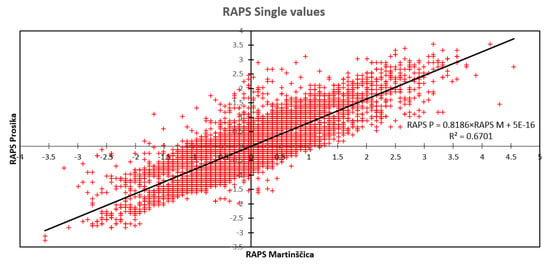
Figure 11.
Correlation among single values of the RAPS for Prosika and Martinščica.
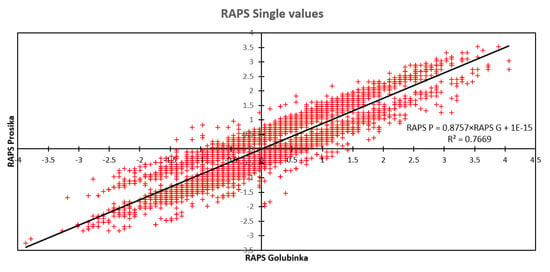
Figure 12.
Correlation among single values of the RAPS for Prosika and Golubinka.
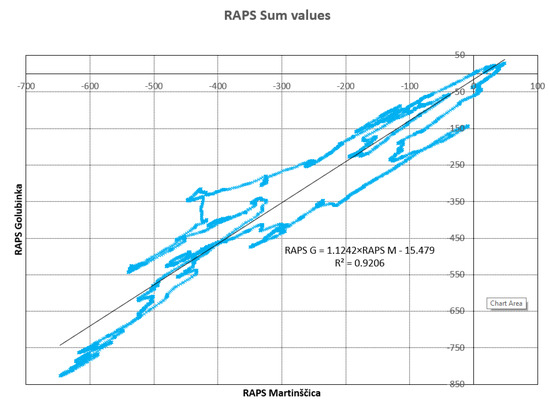
Figure 13.
Correlation between summed values of the RAPS for Golubinka and Martinščica stations.
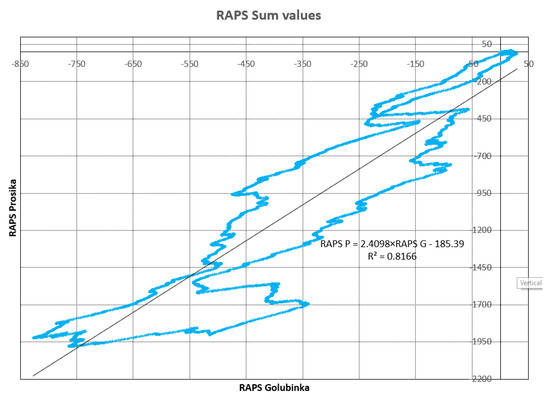
Figure 14.
Correlation between summed values of the RAPS for Prosika and Martinščica stations.
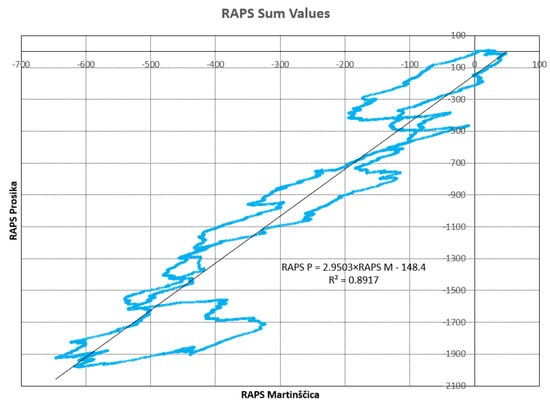
Figure 15.
Correlation between summed values of the RAPS for Prosika and Golubinka stations.
The Martinščica and Golubinka measuring stations had the biggest correlation (R = 0.9275), which means a strong significance. This is due to the observed overlapping of the subseries from Figure 5 and Figure 6.
Other observed correlations between other measuring stations also had significance. Prosika and Martinšćica, with R = 0.8186, as well as Prosika and Golubinka, with R = 0.8757, also had a close significance but smaller compared with the connections between Martinščica and Prosika.
It can be seen that same conclusion regarding the connection between the Martinščica and Golubinka stations, obtained from Figure 10, was derived from Figure 13. In this case, the significance was functional (R = 0.9595). The same conclusion was established for the Prosika and Martinšćica stations (R = 0.9443) as well as between the Prosika and Golubinka stations (R = 0.9037).
The results revealed that a relationship between all three measuring stations, i.e., daily seawater level changes is remarkably high. As mentioned earlier, high average daily seawater levels could result in flooding of settlements that are at lower altitudes. The main correlations between these stations will be thoroughly discussed in further research/papers, where additional parameters will be analyzed. Seawater level changes can especially affect the quality of drinking water in coastal areas, which could pose a huge threat to this area.
5. Conclusions
The presented research was conducted over a sea-level time series to determine the unseasonal non-linear trend of data behavior if present. The preliminary analysis of the RAPS method applied over the sea-level measurements resulted in a possible correlation detected between average daily seawater level rises at the regional scale level in Croatia, regarding the three different locations of observed measurements. Periodic overlapping was observed between all measuring stations. The analysis showed that the regional shape and indentation of the coast did not have an effect on the rise in seawater levels, although land movement could have impact on long-term seawater level changes. Furthermore, the results showed the joint presence throughout the aperiodic visible subset of the observed sea-level time series of different kinds of Earth movements, mentioned in the Introduction, that do have an impact on sea-level rise.
Since the RAPS method is a statistical and not a deterministic method, it is not possible to extract the further impact of such influences on sea-level in deterministic, millimeter values. However, the analysis showed that it can be used as a useful tool for a supplementary insight in data’s behavior and detection of possible sea-level fluctuations apart from seasonal periodic trend.
Further analysis should be more complex with regards to the analysis of the impact of climate factors as well as the measurement of raising and lowering the terrain. The RAPS analyses, as well as mutual connections of RAPS values between particular stations, indicated particular periods that need to be paid attention to during subsequent analysis. This refers primarily to a mutual comparison of the time series of climate factors. The next recommendation is a comparison with values and trends of the coastal terrain. This will complete the overall picture of the problem, while the first step is the analysis presented in this paper. Despite the limitations of using a partly visual analysis comprising RAPS solutions, determined conclusions indicate reliability in identifying nonlinear trends obtained from such an approach.
Author Contributions
Conceptualization, D.M. and N.K.; methodology, B.Đ.; software, B.Đ. and N.K.; validation, D.M. and O.B.O.; formal analysis, B.Đ.; investigation, D.M.; resources, D.M. and N.K.; data curation, B.Đ.; writing—original draft preparation, B.Đ.; writing—review and editing, N.K. and O.B.O.; visualization, N.K.; supervision, D.M. and B.Đ.; funding acquisition, D.M. and N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on www.dhmz.hr the official web site of Croatian Meteorological and Hydrological Service. Data is available on request.
Acknowledgments
The authors want to express their acknowledgment to the Croatian Meteorological and Hydrological Service for providing the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shennan, I. Sea Level Studies—Overview. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 978-0-12-409548-9. [Google Scholar]
- Rahmstorf, S. Modeling Sea Level Rise. Available online: https://www.nature.com/scitable/knowledge/library/modeling-sea-level-rise-25857988 (accessed on 27 December 2020).
- NASA Goddard Space Flight Center Sea Level. Available online: https://climate.nasa.gov/vital-signs/sea-level/ (accessed on 27 December 2020).
- De Biasio, F.; Baldin, G.; Vignudelli, S. Revisiting Vertical Land Motion and Sea Level Trends in the Northeastern Adriatic Sea Using Satellite Altimetry and Tide Gauge Data. J. Mar. Sci. Eng. 2020, 8, 949. [Google Scholar] [CrossRef]
- Rahmstorf, S. A Semi-Empirical Approach to Projecting Future Sea-Level Rise. Science 2013, 368, 10–13. [Google Scholar] [CrossRef] [PubMed]
- Pardaens, A.K.; Lowe, J.A.; Brown, S.; Nicholls, R.J.; Gusmão, D. De Sea—Level rise and impacts projections under a future scenario with large greenhouse gas emission reductions. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Solomon, S.; Plattner, G.; Knutti, R.; Friedlingstein, P. Irreversible climate change due to carbon dioxide emissions. Proc. Natl. Acad. Sci. USA 2009, 106, 1704–1709. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.C.; Grinsted, A.; Zwinger, T.; Jevrejeva, S. Semiempirical and process-based global sea level projections. Rev. Geophys. 2013, 51, 484–522. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef] [PubMed]
- Grinsted, A.; Jevrejeva, S.; Moore, J.C. Reconstructing sea level from paleo and projected temperatures. Clim. Dyn. 2010, 34, 461–472. [Google Scholar] [CrossRef]
- Kemp, A.C.; Horton, B.P.; Donnelly, J.P.; Mann, M.E. Climate related sea-level variations over the past two millennia. Proc. Natl. Acad. Sci. USA 2011, 108, 11017–11022. [Google Scholar] [CrossRef] [PubMed]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C. Anthropogenic forcing dominates sea level rise since 1850. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. How will sea level respond to changes in natural and anthropogenic forcings by 2100? Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Institut, H.H. Web Presentation of Tides and Sea Levels along the Croatian Coast of the Adriatic Sea and Construction of the Corresponding Database. Available online: http://www.hhi.hr/en/projects/viewproject/11 (accessed on 27 December 2020).
- Pörtner, H.-O.; Roberts, D.C.; Masson-Delmotte, V.; Zhai, P.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Nicolai, M.; Okem, A.; Petzold, J.; et al. Special Report on the Ocean and Cryosphere in a Changing Climate; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2019. [Google Scholar]
- Bonacci, O.; Andrić, I. Sinking karst rivers hydrology: Case of the Lika and Gacka (Croatia). Acta Carsologica 2008, 37, 185–196. [Google Scholar] [CrossRef]
- Garbrecht, J.; Fernandez, G.P. Visualization of trends and fluctuations in climatic records. Water Resour. Bull. 1994, 30, 297–306. [Google Scholar] [CrossRef]
- Basarin, B.; Lukic, T.; Pavic, D.; Wilby, R.L. Trends and multi-annual variability of water temperatures in the river Danube, Serbia. Hydrol. Process. 2016. [Google Scholar] [CrossRef]
- Težak, D.; Soldo, B.; Đurin, B.; Kranjčić, N. Impact of Seasonal Changes of Precipitation and Air Temperature on Clay Excavation. Sustainability 2019, 11, 6368. [Google Scholar] [CrossRef]
- Đurin, B.; Ptiček Siročić, A.; Muhar, A. Analiza povezanosti pokazatelja kakvoće otpadne vode s temperaturom i oborinama pomoću RAPS metode. Hrvat. Vode 2017, 25, 247–252. [Google Scholar]
- Machiwal, D.; Jha, M.K. Hydrologic Time Series Analysis: Theory and Practice; Springer: Dordrecht, The Netherlands, 2012; ISBN 978-94-007-1861-6. [Google Scholar]
- Zonn, I.S.; Kostianoy, A.G. The Adriatic Sea. In The Boka Kotorska Bay Environment; Joksimović, A., Djurović, M., Semenov, A.V., Zonn, I.S., Kostianoy, A.G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 19–41. ISBN 978-3-319-51614-1. [Google Scholar]
- Google Maps. Available online: https://www.google.hr/maps/@46.2867434,16.3797178,12.75z?hl=en (accessed on 31 May 2019).
- Croatian Meteorological and Hydrological Service (CMHS), in Croatian. Available online: www.dhmz.hr (accessed on 15 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).