Abstract
A fully analytical treatment of the base-pair and codon dynamics in double-stranded DNA molecules is introduced, by means of a realistic treatment that considers different mass values for G, A, T, and C nucleotides and takes into account the intrinsic three-dimensional, helicoidal geometry of DNA in terms of a Hamitonian in cylindrical coordinates. Within the framework of the Peyrard–Dauxois–Bishop model, we consider the coupling between stretching and stacking radial oscillations as well as the twisting motion of each base pair around the helix axis. By comparing the linearized dynamical equations for the angular and radial variables corresponding to the bp local scale with those of the longer triplet codon scale, we report an underlying hierarchical symmetry. The existence of synchronized collective oscillations of the base-pairs and their related codon triplet units are disclosed from the study of their coupled dynamical equations. The possible biological role of these correlated, long-range oscillation effects in double standed DNA molecules containing mirror-symmetric codons of the form XXX, XX’X, X’XX’, YXY, and XYX is discussed in terms of the dynamical equations solutions and their related dispersion relations.
1. Introduction
The specific role of certain physical properties on the possible biological function of macromolecules of biological interest still remains as a fundamental open question spurring ongoing research in theoretical biophysics. For instance, the study of charge migration through DNA strands of different length has opened new avenues to understand damage recognition processes or protein binding mechanisms at work in nucleic acids, naturally leading to the design of nanoscale devices aimed at sensing genomic mutations within the emerging field of nanobiotechnology [1,2,3]. In physiological conditions, DNA double helix exhibits a full-fledged three-dimensional (3D) geometry, so that the consecutive Watson–Crick base pairs (bps) appear nearly parallel and twisted by a certain angle around the helix axis ( in equilibrium conditions). Now, full-atomistic modular dynamics simulations indicate that double-stranded DNA (dsDNA) undergoes large-scale global oscillatory motions dominated by rise and twist oscillations of the bps planes as a whole, which dominate the range of molecular conformations generated by thermal agitation. Since, by all indications, charge transfer between consecutive bps proceeds through the – aromatic orbital overlap among the stacked bps, one reasonably expects that structural fluctuations modifying their mutual overlapping as a function of time will strongly affect charge carriers’ transport through dsDNA molecules at physiological temperatures [4,5,6,7,8]. In this scenario, the relative orientation of neighboring bases is ever changing, and the motion of consecutive bps can either occur in a synchronized manner or incoherently.
In this work, we will focus on coherent dynamics arising from the coupling between the radial oscillations of complementary bases within Watson–Crick bps and the twisting motion of each bp as a whole around the helical axis. In this way, attending to the local symmetry of the structural unit cell formed by three consecutive bps (the so-called codon in genomics), we disclose a number of remarkable symmetries of the dynamical motion equations, naturally leading to the emergence of synchronized helical waves and orchestrated collective, long-range oscillation modes propagating through the dsDNA molecule. This correlated motion is very important in certain biological processes, such as denaturation and transcription [9], and it is most relevant to any biological process which relies on shape recognition. To this end, we will exploit the Peyrard–Dauxois–Bishop (PDB) model [10,11], which explicitly takes into account the stacking interaction, mediated by the orbital overlapping between adjacent bps and hydrogen bond distortions along the helix [12,13].
The paper is organized as follows: in Section 2, we introduce the model Hamiltonian describing the lattice dynamics, which is expressed in cylindrical coordinates in order to explicitly take into account the 3D geometry of the double helix DNA molecule. Then, in Section 3, we derive the dynamical equations of motion corresponding to the angular and radial variables for both single bps and triplets containing three consecutive bps each (codon units) in polyX-polyX’, polyXX’-polyX’X, and polyXYX-polyX’Y’X’ dsDNA polymers, where X’ stands for the complementary Watson–Crick base of the base X. By comparing the mathematical structure of bp and codon motion equations, we realize that they become identical to each other upon a suitable variable change in certain particular cases, involving dsDNA chains composed of mirror-symmetric codons of the form XXX, XX’X, X’XX’, YXY, and XYX. In doing so, we disclose a number of characteristic frequencies, related to the presence of collective oscillations corresponding to both synchronized helical waves, for which the intertwined angular and radial variables share the same frequency value, and orchestrated long-range waves given by a superposition of two harmonic oscillations with different frequencies for twist and radial motions. The helical waves’ dispersion relations for the acoustic and optical branches are analytically derived in Section 4, and the obtained results are compared to some available experimental results. In Section 5, we solve the codon dynamical equations, reporting on the presence of certain resonance conditions closely related to the nucleotides’ mass values distribution. In the light of these results, the role of possible epigenetic changes in the resulting dynamical behavior of dsDNA molecules is discussed. Finally, the main conclusions of this work are summarized in Section 6.
2. Dynamical DNA Model Hamiltonian
When describing the phonon dynamics DNA, the inner degrees of freedom of the nucleotides can be disregarded, since the fast vibrational atomic motions about their equilibrium positions can be separated from the slower molecular groups ones. Thus, in the lattice model shown in Figure 1, each nucleotide (base + sugar + phosphate) is regarded as a point mass, helically distributed and mutually connected by elastic springs representing both the sugar-phosphate backbone along each strand and the interstrand H-bonding between complementary bases [14,15,16]. We explicitly take into consideration the mass difference among the four nucleotides, namely, , , , amu, where the subscripts stand for guanine (G), adenine (A), thymine (T), and cytosine (C). By inspecting these values, we realize that the mass of each bp as a whole is essentially the same, i.e., amu. Analogously, the bps’ reduced mass, , take on very similar values as well (see Table 1). Adopting the reference frame indicated in Figure 1, the position of the nth nucleobase on the right strand can be expressed as , , and , where n labels the considered bp along the dsDNA, and are usual cylindrical coordinates, and is the rise parameter, where nm (B-DNA form) is the equilibrium distance between two successive bp planes along the z-axis, and is the equilibrium relative angular separation between neighboring bps. Thus, we can express the Euclidean distance between adjacent bases along the right strand as:
( for the left strand is obtained by simply replacing in Equation (1)), where we have defined as the relative angle between two neighboring bps, and as the radial displacements about the equilibrium position ( nm). In equilibrium, both distances reduce to the value nm, where we have adopted °. We note that the distance between successive bps along the z-direction is proportional to the twist angle, thereby preserving the helical structure during the dynamical evolution [17]. It is further assumed that the dsDNA molecule does not move as a whole, so that the center of mass is constant for each bp, and the radial displacements about the equilibrium position satisfy , where .
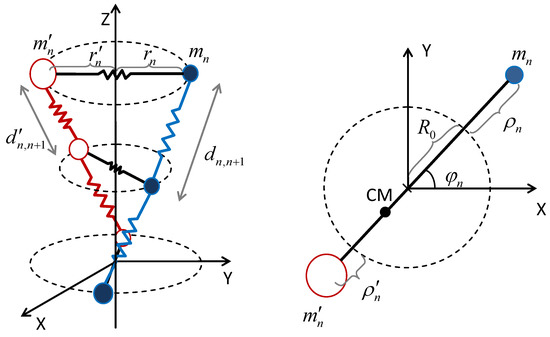
Figure 1.
On the left, sketch of the dsDNA 3D lattice model showing the harmonic bonds between adjacent base pairs through the sugar-phosphate backbone and between complementary bases due to H-bonds. The right strand runs in the 5’ → 3’ direction, whereas the left strand runs in the antiparallel 3’ → 5’ direction. On the right are details of one of the bp planes, showing the effect the mass difference has on radial displacements, shifting the center of mass outside the axis of the helix. Reprinted from Physics Letters A, 376, Torrellas, G.; Maciá, E., Twist–radial normal mode analysis in double-stranded DNA chains, 3407–3410, Copyright (2012), with permission from Elsevier.

Table 1.
Geometrical, dynamical, and potential model parameters adopted in the dsDNA model studied in this work. The same effective Morse potential is used to describe H-bonding in both GC and AT bps. The spring constant is difficult to estimate, and different possible values, ranging from to eV Å, have been reported in the literature [24,25,26,27,28,29].
Therefore, the dsDNA molecule lattice Hamiltonian can be written as [8,18]:
where n runs over the number N of bps, and denote the conjugate momenta of the nth bp radial and twist variables, respectively, and nm is related to the helical geometry of the system, so that measures the helix arc length providing the shortest path between two points along a helical coil. In the limit of small radial and twist oscillations (, , Equation (1) reads , so that the Euclidean distance coincides with the helix arc length in this case [19].
The potential term:
describes the harmonic interaction between neighboring bases along the backbone’s strands, and the term:
describes the elastic energy related to radial displacements. The fist term in Equation (4) represents the radial stretching of the hydrogen bonds between complementary bases sited on opposite strands of the double helix via Morse potentials of depth and width [20]. The second term, with , describes the stacking interaction between adjacent bps, which prevents configurations with large relative radial displacements between neighboring pairs. This interaction gives rise to local constraints in nucleotide motions, and it is characterized by the exponential factor that effectively modulates an otherwise harmonic radial oscillation. This contribution is measured by the stacking stiffness and the interaction range b parameters. The description of the radial degree of freedom via the nonlinear potential given by Equation (4) accounts for long-range cooperative elastic effects caused by hydrogen bonds distortion and -type orbitals overlapping [20], hence being more realistic than a purely harmonic approach. Indeed, this potential has proved successful in capturing denaturation as well as transcription initiation processes in several DNA model chains [21,22,23]. The model parameter values used in this work are listed in Table 1.
3. Dynamical Equations of Motion
3.1. General Expressions
From the lattice Hamiltonian given by Equation (2), we can obtain the linearized canonical equations of motion [8]:
and:
which has introduced the characteristic lengths , with nm, and nm, so that nm (i.e., about 25 bps) and nm, along with the twist frequency:
and the coupled frequencies:
where is a dimensionless ratio, is the radial stretch H-bonding frequency, is the lateral stacking oscillation frequency of bps, and is a dimensionless factor. We note that is invariant upon the transformation , describing the permutation of nucleotides in the Watson–Crick bp (i.e., ). Making use of the M and values listed in Table 1, we get and , so that we can safely make the approximation , , and Equation (8) can be reasonably approximated as , which no longer depends on the site label n.
The time scale of the bp twist Equation (5) is completely determined by the characteristic frequency , whereas the radial Equation (6) involves three different characteristic frequencies, namely, , (related to twist-stacking coupling), and (fully coupling twist, stacking, and stretching interactions). The set of coupled Equations (5) and (6) describes the dynamics of general dsDNA molecules, with two kinds of bps arranged either periodically or aperiodically [32,33,34,35,36], and their mathematical structure clearly shows the correlated nature of next-neighboring bps dynamics. Thus, it is most convenient to zoom our perspective and consider the dynamics of consecutive triplets of bps, known as codon units in genomics. Therefore, we properly add up the dynamical equations of consecutive bps corresponding to sites , n, and , grouping the resulting expression in terms of the collective variables and , to obtain:
with:
and:
with:
where:
where .
By comparing Equations (10) and (12), which describe the codon dynamics as a whole, with Equations (5) and (6), respectively describing the motion of their constituent bps, we can appreciate that they exhibit a closely related algebraic structure, which is further highlighted when the auxiliary functions , , and simultaneously vanish, so that Equations (10) and (12) become formally identical to Equations (5) and (6) upon the variable exchange and , respectively. In order to get , the bps mass ratios must take on correlated values of the form and . Such a relationship is naturally satisfied by bps sequences of the form 5’...XXYXX...3’, which display mirror symmetry with respect to the Y bp, located at the central nth site. On the other hand, the and conditions involve the central bp Y mass ratio value, leading to long-range correlations of the form (hence, ), and , thereby requiring the presence of homogeneous bps sequences of the form 5...XXXXX...3.
3.2. Dynamics of Homopolymer dsDNA Chains
There exist four kinds of homopolymer dsDNA molecules, namely, polyG-polyC, polyA-polyT, polyT-polyA, and polyC-polyG chains, all of them satisfying , , so that and Equations (5), (6), (10) and (12) respectively adopt the form:
and:
where and are constants, and we have introduced the frequency , since is about an order of magnitude smaller than (see Table 2). We note that this characteristic frequency remains exactly the same upon the exchange , describing a bp nucleotides’ permutation. By inspecting Equations (17)–(20), we realize that the bps and codon dynamical equations of motion are exactly identical to each other upon the variable exchange and , respectively. This property can be regarded as expressing a triplet renormalization operation of the dynamical equations when going from the bp local scale to the longer triplet codon scale, hence disclosing an underlying scale-invariant hierarchical symmetry. In fact, by iterating the renormalization process grouping codons in successive triplets of nested codon units recurrently, we will obtain isostructural dynamical equations all the way long up to the entire DNA molecule itself, so that, by solving this fundamental dynamical equations set, we are actually capturing the main features of the dsDNA homopolymer dynamics as a whole.

Table 2.
Characteristic frequencies and their related scale times in the lattice dynamics of polyX-polyX’, poly(XX’)-poly(X’X) and poly(XYX)-poly(X’Y’X’) dsDNA molecules with and . The values for the alternative choice and slightly differ by just a few GHz. The frequencies , , , and are related to the orchestrated codon oscillations described in Section 5.
3.3. Dynamics of Poly(XX’)-Poly(X’X) dsDNA Molecules
Double-stranded DNA chains of the form poly(XX’)-poly(X’X) consist of a periodic repetition of a dinucleotide unit cell, and they provide the next step in an increasing chemical complexity route, going from the single-nucleotide based homopolymers considered in Section 3.2, to the fully informative aperiodically ordered DNA chains. Attending to the possible local ordering of the nucleotide sequence along the poly(XX’)-poly(X’X) chain, two kinds of codons can be identified, namely, X’XX’ and XX’X, both exhibiting a mirror symmetry leading to long-range correlations of the form and , , depending on whether the central nth site is occupied by a X or a X’ base, respectively. Therefore, and , for X’XX’ codons, where . Accordingly, if we choose the reading frame so that the dsDNA sequence can be expressed as a periodic concatenation of codons of the form X’XX’, we have , , and , and Equations (5), (6), (10) and (12) are respectively written:
and
where .
Completely analogous expressions are obtained if we choose the reading frame so that the dsDNA sequence can be expressed as a periodic concatenation of codons of the the form XX’X, by simply replacing in the above expressions. As we see, Equations (21)–(24) do not exactly coincide with each other upon the renormalization transformation and , except in the case (i.e., m = m’), which describes mismatched repeats of the form poly(XX’)-poly(XX’) or poly(X’X)-poly(X’X) that no longer contain complementary Watson–Crick bps. Therefore, at variance with the remarkable self-similar symmetry displayed by homopolymers, such as 5-...GGGGG...3 or 5...CCCCC...3, dsDNA chains based on an alternating sequence of both bases, such as 5-...GCGCGCGCGC...3, completely lack that symmetry property.
3.4. Dynamics of Poly(XYX)-Poly(X’Y’X’) dsDNA Molecules
Another instance of a dsDNA system exhibiting a suitable local mirror symmetry is provided by periodic DNA chains whose unit cell includes codons of the form XYX, so that the local bps arrangement around Y type bases reads 5...XXYXX...3. If we label the bps in such a way that the Y base occupies the n reference site, then we have the relationships , and , , so that we get . Therefore, the bps and codon dynamical equations corresponding to the twist variables just coincide with Equations (17) and (18) previously obtained for the homopolymer case. On the other hand, we have:
where . Thus, the radial motion equations read:
where , with , and:
Completely analogous expressions are obtained for poly(YXY)-poly(Y’X’Y’) polymers by simply permuting in Equations (25)–(27). By comparing Equations (26) and (27), two main differences can be drawn. Firstly, the frequencies and are different in general, and only coincide in the homopolymer case. Secondly, in the codon motion equations, the bps variables explicitly appear in the factor terms, hence they do not coincide with each other upon the transformation .
Making use of the model parameters shown in Table 1, we obtain the values listed in Table 2 for the characteristic frequencies we have introduced through Section 3.2, Section 3.3 and Section 3.4, along with their related time scales. The data in Table 2 indicate that the time scale of pure angular motions, determined by the twist frequency, amounts to ∼6 ps, so that they are an order of magnitude slower than those corresponding to the fully coupled twist-stacking-stretching frequency . The time scale related to twist-stacking oscillations is close to 1 ps, while that related to twist-stretching motions range in within the 0.5–0.6 ps interval. For the sake of comparison, the transition times reported for intrastrand hole transfer in ds-GTGGG oligonucleotides, range from ps for to ps for [37]. Remarkably, recent studies on the electrical response of biological dsDNA chains to light irradiation, performed to engineer a DNA-based molecular switch, have unveiled that electrical current turns on for incident light frequencies above the 2 THz threshold [38], a figure very close to that listed for in Table 2, a frequency involving energy enough to activate all the fundamental interactions present in the system Hamiltonian in a coupled way.
4. Helical Waves Related Dispersion Relations
Motivated by previous results [19,39], we look for solutions of the form and , describing a helical wave propagating throughout the dsDNA with frequency and wave vector q, where rad, and nm, are the twist and radial oscillation amplitudes at ambient temperature, respectively [40]. In so doing, Equations (17) and (19) for dsDNA homopolymers can be expressed in the matrix form [8]:
where and . The solution to Equation (28) requires the matrix determinant to identically vanish, thereby leading to a biquadratic equation whose solutions yield the dispersion relations for the acoustic and optical phonon branches given by:
Since is much smaller than both and terms, the exact dispersion relations given by Equation (29) can be very well approximated by the simpler expressions:
in agreement with previously reported results [15,21].
By comparing Equations (17) and (21), along with Equations (19) and (23), we realize that Equation (28) also holds for poly(XX’)-poly(X’X) chains by simply replacing and , respectively. Thus, we obtain the following dispersion relations for poly(XX’)-poly(X’X) and poly(X’X)-poly(XX’), respectively:
Analogously, by comparing Equations (19) and (26), we realize that Equation (28) holds for poly(XYX)-poly(X’Y’X’) chains as well by simply replacing and , respectively, so that we get the following dispersion relations:
where
satisfies the relationship , and it takes on two possible values: and .
By comparing Equations (30)–(32), we see that the acoustic branch of polyX-polyX’, poly(XX’)-poly(X’X) and poly(XYX)-poly(X’Y’X’) chains is exactly the same, and it is completely determined by twist oscillations, so that it is insensitive to the particular nucleotide sequence order along the dsDNA chain. On the contrary, the optical branches depend on both stretch and stacking oscillations and they reflect the role of the underlying bps ordering throughout the chain, which is expressed by the presence of and factors in Equations (31) and (32) for poly(XX’)-poly(X’X) and poly(XYX)-poly(X’Y’X’) chains, respectively. For homopolymer chains, the bandgap, THz (≃7 meV), is fixed by the H-bond stretching frequency value, whereas it depends on both stacking and stretching frequencies for more complex dsDNA chains, according to the expressions and for poly(XX’)-poly(X’X) and poly(XYX)-poly(X’Y’X’) molecules, respectively. Therefore, the bandgap of poly(XX’)-poly(X’X) molecules is always somewhat wider than that of homopolymers, whereas, in the case of poly(XYX)-poly(X’Y’X’) polymers, it can be wider or narrower depending on the nature of the Y bp. Indeed, by inspecting Figure 2, we observe that poly(GAG)-poly(CTC) chains exhibit the smaller bandgap value ( THz), while the wider bandgap ( THz) corresponds to poly(GC)-poly(CG) chains. The maximum bandgap width occurs for nm, as can be seen in the top inset of Figure 2, with THz for homopolymers. A close look at the bottom inset reveals that the wider the bandgap, the narrower the maximum bandgap at for the considered dsDNA chains.
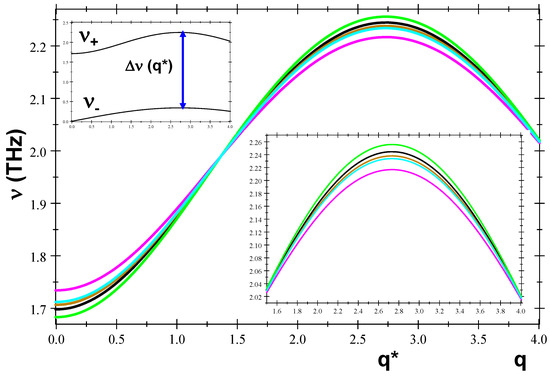
Figure 2.
(Main frame) Optical phonon branches for polyG-polyC (black), poly(GC)-poly(CG) (magenta), poly(AT)-poly(TA) (siena), poly(GAG)-poly(CTC) (green), and poly(AGA)-poly(TCT) (light blue) dsDNA polymers, where q is measured in nm, and we have used the values of the the model parameters and characteristic frequencies listed in Table 1 and Table 2, respectively. (Low inset) Close up view of the optical branch curves shown in the main frame in the interval . (Top inset) Acoustic and optical phonon branches for polyG-polyC dsDNA homopolymers. (Reprinted from Maciá, E. Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules. Materials 2020, 13, 5119).
5. Orchestrated Codon Oscillations
In addition to the synchronized helical waves, for which the intertwined angular and radial variables share the same value, we can also disclose long-range correlated motions of the angular and radial variables in time, orchestrated in such a way that they simultaneously satisfy the conditions and . In that case, the collective variables read and , where the collective motion variable plays for radial oscillations a role completely analogous to that played by the variable for twist ones. In terms of the revamped collective variables, the codon dynamical Equations (10) and (12) can be respectively rewritten in the form:
and:
The condition guarantees that for polyXX’-polyX’X dsDNA molecules (see Section 3.2). In addition, polyX-polyX’ and poly XYX-poly X’Y’X’ polymers satisfy the relationships and in a natural way. Accordingly, codon Equations (34) and (35) can be properly simplified to read:
where (u labels the DNA unit cell type), so that its precise value depends on the nature of the codons present in the considered dsDNA molecule. Thus, for polyX-polyX’ polymers, . This frequency accounts for the collective radial oscillations of XXX (alternatively, X’X’X’) codons, describing a long-range oscillation where stacking interactions become ineffective, giving rise to a coupled twist-stretching mode which cannot be observed at the bp scale. Since homopolymers satisfy the condition, the resulting dynamical equations of motion (36) become effectively decoupled in terms of simple harmonic motions with two different natural frequencies, namely, for twist, and for radial motions, respectively. Solving the twist harmonic expression for the time variable, and plugging it into the radial harmonic expression , where the phases and are determined from the initial conditions, we get the relationship:
describing the spatial pattern of the long-range correlated motion in terms of the collective variables and .
Making use of Equations (13)–(16) into Equation (36), we obtain the following expressions for the radial codon equations corresponding to polyXX’-polyXX’, and polyXYX-polyX’Y’X’ chains, respectively:
where , hence , and:
where
Completely analogous expressions are obtained for poly(YXY)-poly(Y’X’Y’) polymers by simply permuting in Equations (38)–(40). The obtained dynamical equations indicate that for the resonance conditions , for polyXX’-polyXX’ chains, and for polyXYX-polyX’Y’X’ chains, the twist and radial equations decouple from each other leading to two harmonic motions in a way completely analogous to that previously described for the homopolymers case. In the polyXX’-polyX’X case, the relationship given by Equation (37) holds by simply replacing . It is important to note that this resonance can only take place for dsDNA molecules satisfying the mismatch condition , so that it may be regarded as signaling the presence of local alterations in the due bp sequencing. Alternatively, within the framework of epigenetic processes, one may consider the attachment of a small molecule with the required mass value (i.e., ) to the lighter pyrimidine nucleotide in order to get the required resonance condition . In the polyXYX-polyX’Y’X’ case, the resonance condition leads to the expression:
which depends on the mass ratio values and , along with the twist and stacking characteristic frequencies, which, in turn, can be expressed in terms of model parameters.
The general solution to the dynamical equations for polyXX’-polyX’X polymers can be obtained from the knowledge of the general solution to the homogeneous version of Equation (38) given by , plus the particular solution ansatz , leading to the differential equation , whose solution reads . For the sake of simplicity, we adopt the initial conditions , and , so that we get:
describing a modulated oscillation where GHz and THz. Since , we see that all the bps in the codon move in phase. A similar solution describing a modulated oscillation in opposite phase is obtained by choosing as the particular solution to the inhomogeneous differential Equation (38). In this case, we get a larger high frequency value THz. By following a completely analogous procedure, Equation (39) for polyXYX-polyX’Y’X’ polymers can be solved in a similar way.
6. Environmental Effects in the DNA Dynamics
At physiological conditions, nucleotides are fully hydrated in B-DNA, so that the effective mass of nucleotides is increased as compared to that corresponding to the dry model introduced in Section 2. Reasonably assuming that six water molecules are associated with each nucleotide on average, we get a mass increase of amu, which represents more than a 30% of the original nucleotide mass. This figure is further increased if one includes the presence of counterions interspersed along the sugar-phosphate backbone. Generally speaking, any effective bp mass increase leads to a slow down of frequencies , , and , along with their related coupled frequencies. For the sake of illustration, by replacing amu, we obtain THz, THz, and THz, so that the characteristic twist oscillations time scale slows down by about 1 ps (see Table 2). A smaller twist frequency value has two main effects: (1) the acoustic dispersion relation slope declines, so that the sound speed is reduced as well, and (2) the gap between the acoustic and optical branches (see Figure 2) widens. On the other hand, the twist-stacking-stretching coupled frequency, which provides the lower time scale reference value, significantly decreases from THz to THz. In a similar vein, epigenetic processes such as methylation (i.e., the addition of a methyl group -CH to a base), or the presence of ligands attached onto the sugar-phosphate backbone, will modify the nucleobases effective mass, thereby changing their mass ratio parameter value. Albeit the nucleotide’s mass change is in this case significantly smaller than that corresponding to the hydration effect, we must keep in mind that even small changes in the values would break the mirror symmetry relationships discussed in Section 3.3 and Section 3.4, hence affecting the resulting codon dynamics.
Along with the mass increase related dynamical effects, the water–layer shell also leads to dissipative effects that can be described in terms of two main forces, namely, the Stokes viscous forces, caused by the interactions among DNA nucleotides and particles of solvent, and the hydrodynamical viscous forces caused by the hydrodynamic interactions between inner DNA nucleotides. The Stokes viscous force is given by , and the hydrodynamic dissipation is given by , where and are the Stokes and hydrodynamic damping constants, respectively [41,42]. According to Raman spectroscopy measurements, the viscous effects can be confidently neglected in the study of H-bond related stretching oscillations, since the very small amplitude of the motion within the hydrogen bond well (0.12–0.2 Å) should not induce significant rearrangements of surrounding water molecules responsible for viscosity [21]. Notwithstanding this, it is instructive to ascertain the possible effect of both dissipation terms in the mathematical structure of the dynamical equations obtained in previous sections. In doing so, Equations (5), (6), (10) and (12) adopt the form
and:
respectively. Therefore, the dynamical equations corresponding to homopolymer DNA chains can be written as:
and:
Accordingly, the scale invariant hierarchical symmetry of these dynamical equations still holds when dissipative effects are explicitly taken into account, so that the inclusion of damping forces still preserves the general structure of the linear dynamical equations, hence not disturbing the symmetrical properties underlying the very existence of the synchronized reported oscillations. Nevertheless, the amplitudes of both the synchronized helical waves and orchestrated oscillations are now decaying functions with time, leading to a spiral trajectory approaching zero in the space phase portrait. In order to keep the oscillatory motion external forces field arising from inhomogeneities, and additional molecules or external agents acting as gain energy sources must also be added to the motion equations. This external driving force is generally treated as a white noise signal (that is, uncorrelated in time), with an amplitude defined to add just as much energy to the system as is taken out by the friction terms on average [43]. The inclusion of this force into Equations (47)–(50) above does alter their characteristic hierarchical symmetry either. In this scenario, we can regard the synchronized oscillations reported in the previous sections as providing a suitable limit cycle attractor in the phase space.
7. Conclusions
We have performed a systematic analytical study of the nucleotides’ dynamics in dsDNA chains characterized by the presence of mirror-symmetric codons. By considering the mathematical structure of the dynamical equations at the local, single bp scale, and the triplet codon longer scale, two kinds of long-range, collective motions of nucleotides have been identified on the basis of the symmetry properties of these equations upon the variable exchange and describing a renormalization transformation involving suitable collective variables. For one thing, we have helical waves, characterized by intertwined angular and radial oscillations sharing the same frequency value. On the other hand, we have orchestrated motions of codon triplets where twist and radial variables harmonically vibrate with different values of their natural frequencies, giving rise to the presence of a modulated oscillation extending over the whole dsDNA molecule. We have also identified the possible existence of certain resonance conditions related to the presence of mismatch mutations involving a relatively small number of neighboring nucleotides. Indeed, a remarkable feature of our treatment is that, as far as we are concerned on the DNA dynamical behavior, the chemical nature of bps plays no role at all, since the nucleotide sequence along the dsDNA molecule is fully described in terms of the bps mass ratio parameters . As a consequence, the behavior of the reported correlated oscillations can be significantly perturbed when the DNA molecule is bonded with other small molecules, or it is subjected to epigenetic processes.
To conclude, some words are in order regarding possible experimental measurements aimed at exploring some of the results reported in this work. To this end, Raman spectroscopy is a very useful tool for studying the collective modes of DNA molecules in solution, since the Raman scattering intensity is directly related to the density of normal modes, which in turn can be readily derived from the knowledge of the acoustic and optical dispersion relations given by Equations (30)–(32) [21]. The use of terahertz time-domain spectroscopy for recording the far-infrared (– THz) dielectric function of the four nucleobases and nucleosides has also been demonstrated as an efficient method to analyze the collective motions associated with intermolecular hydrogen bond vibrations [44]. In particular, this technique may be employed to check for the expected redshift of the twist-stacking codon frequencies listed in Table 2 due to hydration effects.
Funding
This research received no external funding.
Acknowledgments
I sincerely thank Constantinos Simserides for his continued interest in my research works and Evgeni B. Starikov for illuminating conversations on physico-chemical aspects of DNA molecules. I gratefully thank Victoria Hernández for a critical reading of the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| dsDNA | double-stranded DNA |
| bp | base pair |
| A | adenine |
| C | cytosine |
| G | guanine |
| T | thymine |
| PDB | Peyrard–Dauxois–Bishop |
References
- Chakarborty, T. (Ed.) Charge Migration in DNA: Perspectives from Physics, Chemistry and Biology; Springer: Berlin, Germany, 2007. [Google Scholar]
- Treadway, C.; Hill, M.G.; Barton, J.K. Charge transport through a molecular pi-stack: Double helical DNA. Chem. Phys. 2002, 281, 409–428. [Google Scholar] [CrossRef]
- Zwang, T.J.; Tse, E.C.M.; Barton, J.K. Sensing DNA through DNA Charge Transport. ACS Chem. Biol. 2018, 13, 1799–1809. [Google Scholar] [CrossRef] [PubMed]
- Starikov, E.B.; Fujita, T.; Wanatabe, H.; Sengoku, Y.; Tanaka, S.; Wenzel, W. Effects of molecular motion on charge transfer/transport through DNA duplexes with and without base pair mismatch. Mol. Simul. 2006, 32, 759–764. [Google Scholar] [CrossRef]
- Berlin, Y.A.; Grozema, F.C.; Siebbeles, L.D.A.; Ratner, M.A. Charge transfer in donor-bridge-acceptor systems: Static disorder, dynamic fluctuations, and complex kinetics. J. Phys. Chem. C 2008, 112, 10988–11000. [Google Scholar] [CrossRef]
- Starikov, E.B.; Quintilla, A.; Nganou, C.; Lee, K.H.; Cuniberti, G.; Wenzel, W. Single-molecule DNA conductance in water solutions: Role of DNA low-frequency dynamics. Chem. Phys. Lett. 2009, 467, 369–374. [Google Scholar] [CrossRef]
- Bruinsma, R.; Grüner, G.; D’Orsogna, M.R.; Rudnick, J. Fluctuation-facilitated charge migration along DNA. Phys. Rev. Lett. 2000, 85, 4393–4396. [Google Scholar] [CrossRef]
- Maciá, E. Base-Pairs’ correlated oscillation effects on the charge transfer in double-helix B-DNA molecules. Materials 2020, 13, 5119. [Google Scholar] [CrossRef]
- Peyrard, M. Nonlinear dynamics and statistical physics of DNA. Nonlinearity 2004, 17, R1–R40. [Google Scholar] [CrossRef]
- Peyrard, M.; Bishop, A.R. Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 1989, 62, 2755–2758. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M. Entropy-driven transition in a one-dimensional system. Phys. Rev. E 1995, 51, 4027–4040. [Google Scholar] [CrossRef]
- Peyrard, M.; Cuesta-López, S.; Angelov, D. Experimental and theoretical studies of sequence effects on the fluctuation and melting of short DNA molecule. J. Phys. Condens. Matter 2009, 21, 034103. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Shinwari, W.; Deen, M.J.; Starikov, E.B.; Cuniberti, G. Electrical Conductance in Biological Molecules. Adv. Funct. Mater. 2010, 20, 1865–1883. [Google Scholar] [CrossRef]
- Barbi, M.; Cocco, S.; Peyrard, M. Helicoidal model for DNA opening. Phys. Lett. A 1999, 253, 358–369. [Google Scholar] [CrossRef]
- Cocco, S.; Monasson, R. Statistical mechanics of torque induced denaturation of DNA. Phys Rev. Lett. 1999, 83, 5178–5181. [Google Scholar] [CrossRef]
- Agarwal, J.D.; Hennig, D. Breather solutions of a nonlinear DNA model including a longitudinal degree of freedom. Physica A 2003, 323, 519–533. [Google Scholar] [CrossRef]
- Krisch, M.; Mermet, A.; Grimm, H.; Forsyth, V.T.; Rupprecht, A. Phonon dispersion of oriented DNA by inelastic X-ray scattering. Phys. Rev. E 2006, 73, 061909. [Google Scholar] [CrossRef] [PubMed]
- Torrellas, G.; Maciá, E. Twist–radial normal mode analysis in double-stranded DNA chains. Phys. Lett. A 2012, 376, 3407–3410. [Google Scholar] [CrossRef]
- Maciá, E. Electrical conductance in duplex DNA: Helical effects and low-frequency vibrational coupling. Phys. Rev. B 2007, 76, 245123. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M.; Bishop, A.R. Entropy-driven DNA denaturation. Phys. Rev. E 1993, 47, R44–R47. [Google Scholar] [CrossRef]
- Cocco, S.; Monasson, R. Theoretical study of collective modes in DNA at ambient temperature. J. Chem. Phys. 2000, 112, 10017–10033. [Google Scholar] [CrossRef]
- Campa, A.; Giansanti, A. Experimental tests of the Peyrard-Bishop model applied to the melting of very short DNA chains. Phys. Rev. E 1998, 58, 3585–3588. [Google Scholar] [CrossRef]
- Cule, D.; Hwa, T. Denaturation of Heterogeneous DNA. Phys. Rev. Lett. 1997, 79, 2375–2378. [Google Scholar] [CrossRef]
- Lee, O.; Jeon, J.H.; Sung, W. How double-stranded DNA breathing enhances its flexibility and instability on short length scales. Phys. Rev. E 2010, 81, 021906. [Google Scholar] [CrossRef] [PubMed]
- Michoel, T.; Van de Peer, Y. Helicoidal transfer matrix model for inhomogeneous DNA melting. Phys. Rev. E 2006, 73, 011908. [Google Scholar] [CrossRef]
- Okonogi, T.M.; Alley, S.C.; Harwood, E.A.; Hopkins, P.B.; Robinson, B.H. Phosphate backbone neutralization increases duplex DNA flexibility. Proc. Natl. Acad. Sci. USA 2002, 99, 4156–4160. [Google Scholar] [CrossRef]
- Duduială, C.I.; Wattis, J.A.D.; Dryden, I.L.; Laughton, C.A. Nonlinear breathing modes at a defect site in DNA. Phys. Rev. E 2009, 80, 061906. [Google Scholar] [CrossRef]
- Zdravković, S.; Satarić, M.V. Single-molecule unzippering experiments on DNA and Peyrard-Bishop-Dauxois model. Phys. Rev. E 2006, 73, 021905. [Google Scholar] [CrossRef]
- Ghorbani, M.; Rafiee, F.M. Geometrical correlations in the nucleosomal DNA conformation and the role of the covalent bonds rigidity. Nucleic Acids Res. 2011, 39, 1220–1230. [Google Scholar] [CrossRef]
- Barbi, M.; Lepri, S.; Peyrard, M.; Theodorakopoulos, N. Thermal denaturation of a helicoidal DNA model. Phys. Rev. E 2003, 68, 061909. [Google Scholar] [CrossRef]
- Leal, M.R.; Weber, G. Sharp DNA denaturation in a helicoidal mesoscopic model. Chem. Phys. Lett. 2020, 755, 137781. [Google Scholar] [CrossRef]
- Maciá-Barber, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; Taylor and Francis, CRC Press: Boca Raton, FL, USA, 2009; pp. 209–297. [Google Scholar]
- Maciá, E. Charge transfer in DNA: Effective Hamiltonian approaches. Z. Kristallogr. 2009, 224, 91–95. [Google Scholar] [CrossRef]
- Mantela, M.; Lambropoulos, K.; Theodorakou, M.; Simserides, C. Quasi-Periodic and Fractal Polymers: Energy Structure and Carrier Transfer. Materials 2019, 12, 2177. [Google Scholar] [CrossRef] [PubMed]
- Lambropoulos, K.; Simserides, C. Periodic, quasiperiodic, fractal, Kolakoski, and random binary polymers: Energy structure and carrier transport. Phys. Rev. E 2019, 99, 032415. [Google Scholar] [CrossRef] [PubMed]
- Lambropoulos, K.; Simserides, C. Tight-binding modeling of nucleic acid sequences: Interplay between various types of order or disorder and charge transport. Symmetry 2019, 11, 968. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Peluso, A. Transient and enduring electronic resonances drive coherent long distance charge transport in molecular wires. J. Phys. Chem. Lett. 2019, 10, 1845–1851. [Google Scholar] [CrossRef]
- Behnia, S.; Fathizadeh, S.; Javanshour, E.; Nemati, F. Light-driven modulation of electrical current through DNA sequences: Engineering of a molecular optical switch. J. Phys. Chem. B 2020, 124, 3261–3270. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. π-π orbital resonance in twisting duplex DNA: Dynamical phyllotaxis and electronic structure effects. Phys. Rev. B 2009, 80, 125102. [Google Scholar] [CrossRef]
- Young, M.A.; Ravishanker, G.; Beveridge, D.L. A 5-nanosecond molecular dynamics trajectory for B-DNA: Analysis of structure, motions, and solvation. Biophys. J. 1997, 73, 2313–2336. [Google Scholar] [CrossRef]
- Okaly, J.B.; Mvogo, A.; Woulaché, R.L.; Kofané, T.C. Nonlinear dynamics of damped DNA systems with long-range interactions. Commun. Nonlinear Sci. Numer. Simulat. 2018, 55, 183–193. [Google Scholar] [CrossRef]
- Okaly, J.B.; Mvogo, A.; Tabi, C.B.; Ekobena Fouda, H.P.; Kofané, T.C. Base pair opening in a damped helicoidal Joyeux-Buyukdagli model of DNA in an external force field. Phys. Rev. E 2020, 102, 062402. [Google Scholar] [CrossRef]
- Harris, S.A.; Laughton, C.A. A simple physical description of DNA dynamics: Quasi-harmonic analysis as a route to the configurational entropy. J. Phys. Condens. Matter 2007, 19, 076103. [Google Scholar] [CrossRef] [PubMed]
- Fischer, B.M.; Walther, M.; Uhd Jepsen, P. Far-infrared vibrational modes of DNA components studied by terahertz time-domain spectroscopy. Phys. Med. Biol. 2002, 47, 3807. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).