1. Introduction
The well known Korteweg–de Vries (KdV)–Burgers equation for flat waves is of the form
Its cylindrical and spherical analogues are
and
respectively, see [
1,
2].
The behavior of solutions of the Korteweg–de Vries (KdV) and KdV–Burgers equations was intensively studied for about fifty years. However, these equations remain subjects of various recent studies, mostly in the case of flat waves in one spatial dimension [
3,
4,
5,
6,
7]. However, cylindrical and spherical waves have a variety of applications (e.g., waves generated by a downhole vibrator), and are studied much less.
We consider the initial value boundary problem (IVBP) for the KdV–Burgers equation on a finite interval:
In the case
(that is, for the Burgers equation), it becomes
The case of the boundary conditions and the related asymptotics are of a special interest here. For numerical modeling we use instead of for appropriately large b.
For the flat wave Burgers equation (
) the resulting asymptotic profile looks like a periodical chain of shock fronts with a decreasing amplitude (weak breaks or sawtooth waves). If dispersion is non-zero, each wavefront ends with high-frequency micro-oscillations. Further from the oscillator, shock fronts become decaying smooth quasi-periodic oscillations. After the oscillations cease, the wave develops as a constant height and velocity shock. It almost coincides with a traveling wave solution (TWS) of the Burgers equation [
8,
9].
A traveling wave solution is the solution of the form . Such a solution travels with a constant velocity V along the axis, unchanged in its form. The well-known examples are solitons for KdV, shock waves for the Burgers equation. For the existence of TWS for all values of the parameter V it is necessary that an equation has Galillean symmetry.
In the case
, the Burgers equation has traveling wave solutions, vanishing at
. They are given by the formula [
10]
it is used below.
Our aim is to obtain a similar description of a long-time asymptote for cylindrical and spherical waves with periodic boundary conditions. We demonstrate that, in the case of the above IVBP, the perturbation of the equilibrium state for Equations (
2) and (
3) ultimately takes a form similar to this shock.
This paper is organized as follows. In
Section 2, we demonstrate graphs of our numerical experiments for cylindrical/spherical Burgers/KdV–Burgers equations for different combinations to show their the common patterns. In particular we demonstrate that, after the oscillation cease, a solution becomes a monotonic convex line terminated by a head shock.
In
Section 3, we find symmetries to Equations (
2) and (
3). No Galilean symmetry is found, so no real TWS exists. Then equations are brought to a conservation law form, which is later used to obtain rough estimates for the median parameters of the solution. This rough estimate becomes exact for constant boundary conditions, and in
Section 4, a very close asymptote for said solution is found in self-similar or homothetic form
.
Yet, at the head shock this asymptotic is unsatisfactory. This head shock moves in unchanged form and with numerically equal velocity and amplitude—exactly as the Burgers traveling wave solution does. In
Section 5, using a simple combination of a self-similar approximation and the Burgers traveling wave solution, we obtain the compact closed form approximation. It coincides with a solution in its monotonic part; and this approximation correctly represents the median of the solution in its oscillating part. The quality of the approximation is verified numerically. Connection between the velocity of the solution’s head shock and the median value at the start is obtained.
In the section “Conclusions” we formulate main result and discuss the remaining open questions.
2. Typical Examples
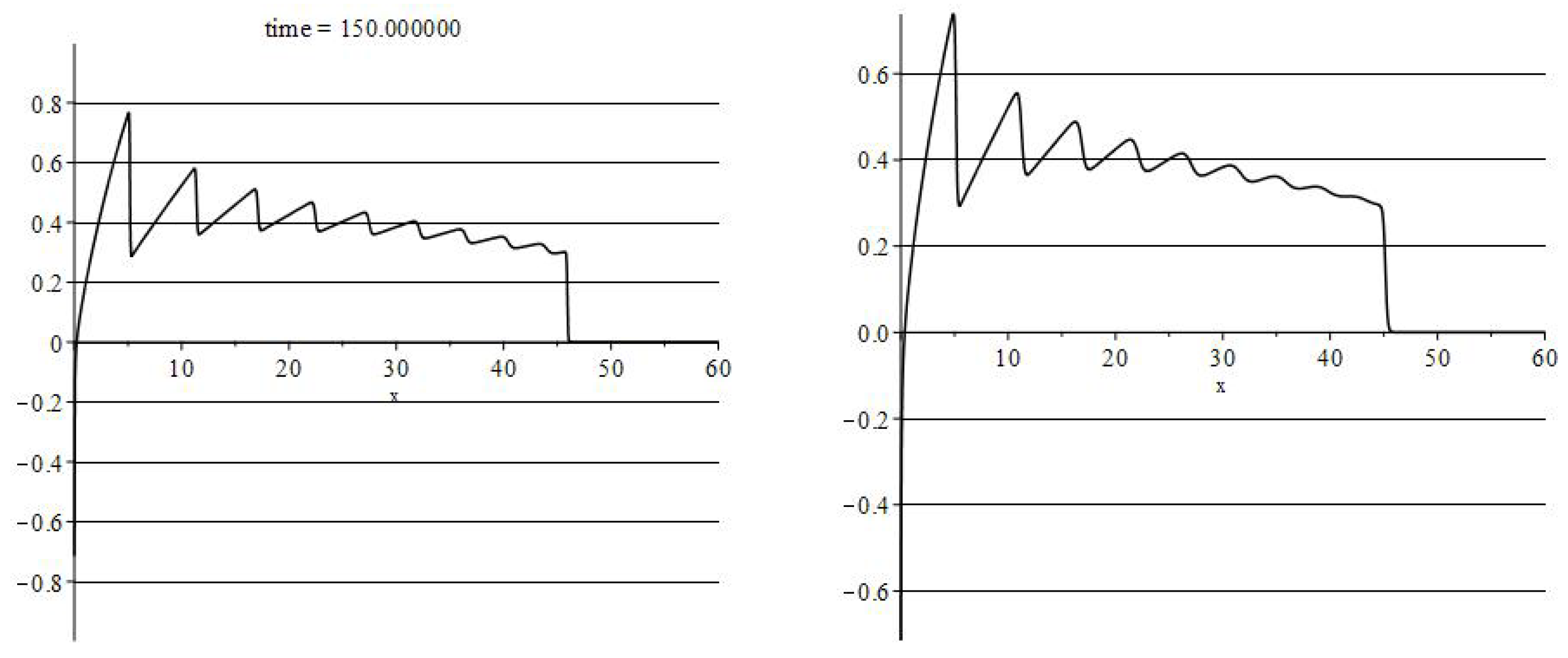
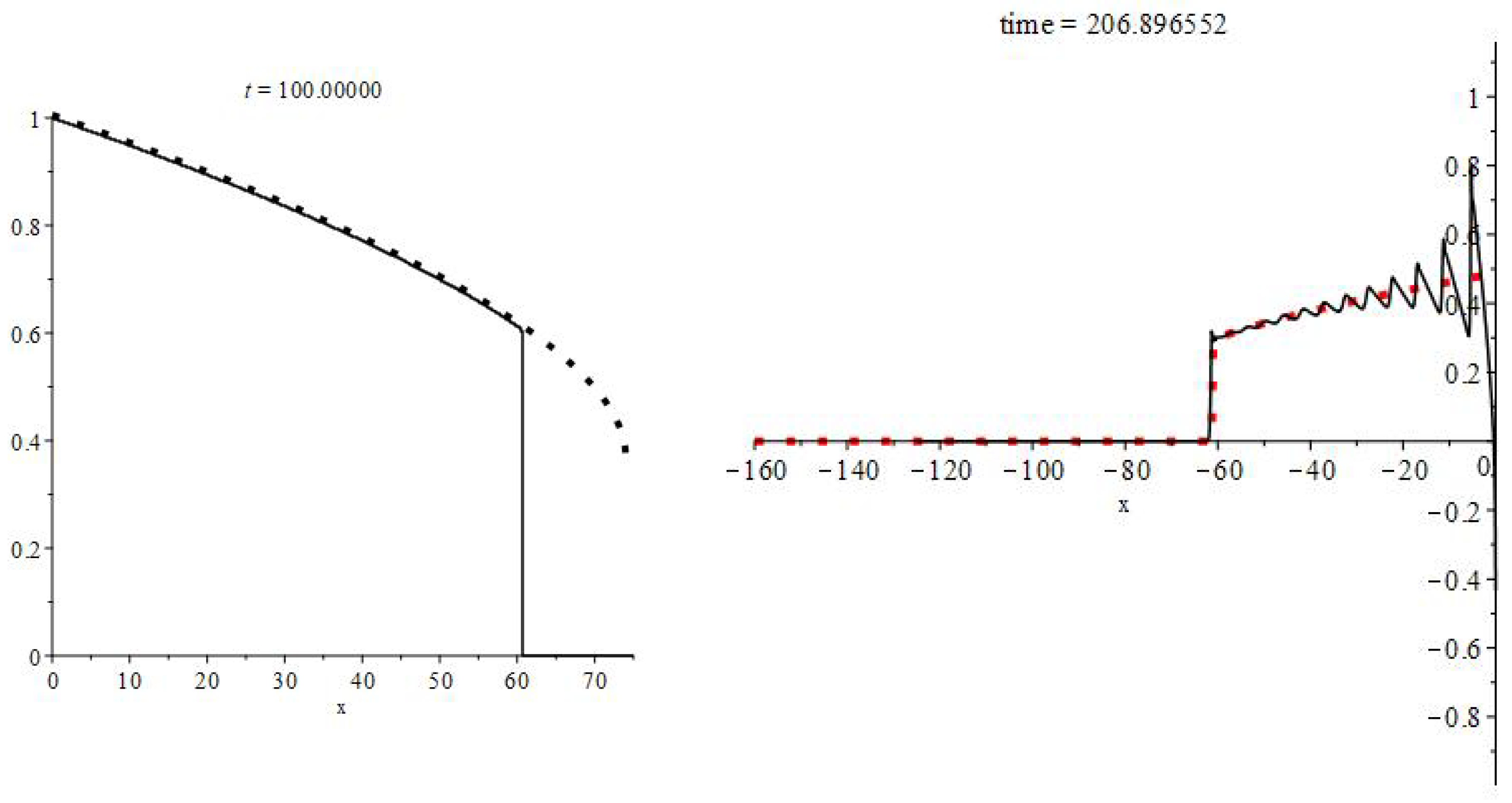
Here we demonstrate typical graphs for cylindrical and spherical Burgers waves (see
Figure 1 and
Figure 2) and for cylindrical and spherical KdV–Burgers (
Figure 3 and
Figure 4). We obtained these graphs using the
Maple PDETools package. The mode of operation used was the default Euler method, which is a centered implicit scheme.
The solution usually starts with a periodical chain of shock fronts with decreasing amplitudes (sawtooth waves). This weak breaks/sawtooth profile is inherent to periodic waves in dissipative media. Sawtooth waves, their decay, amplitudes, width, etc., were intensively studied in 1970 (see [
1,
2]) and later. One can also see a common pattern, previously not described, emerging on these figures. After the decay of initial oscillations, graphs become monotonic declining convex lines, terminated by a shock. Recall that for flat waves this monotonic part almost coincides with a constant height traveling wave solution of Burgers equation [
7]. The new feature of convex declining lines is caused by the space divergence. We obtain an analytical description of this pattern below.
3. Symmetries and Conservation Laws
3.1. Symmetries
Since cylindrical and spherical equations explicitly depend on time, their stock of symmetries is scarce. For the algorithm of symmetry calculations, see [
11]. We found that the algebras of classical symmetries are generated by the following vector fields:
This list does not contain the Galilean symmetry, so no real traveling wave solution exists.
In particular, symmetry algebra for:
Cylindrical Burgers is generated by ;
Cylindrical KdV–Burgers is generated by ;
Spherical Burgers is generated by ;
Spherical KdV–Burgers is generated by .
3.2. Conservation Laws
First rewrite Equations (
1)–(
3) into an appropriate conservation law form
where
for flat, cylindrical and spherical cases, respectively.
Hence, for solutions of the above equations we have
where
is a rectangle
While bearing in mind the initial value/boundary conditions
, for
the integrals read
The right-hand side of Equation (
10) can be computed in some simple cases or estimated. For instance, assume that
is negligible compared to
. Then
It follows that
Another example of exact estimation of right-hand side of Equation (
10) is the case of constant boundary conditions.
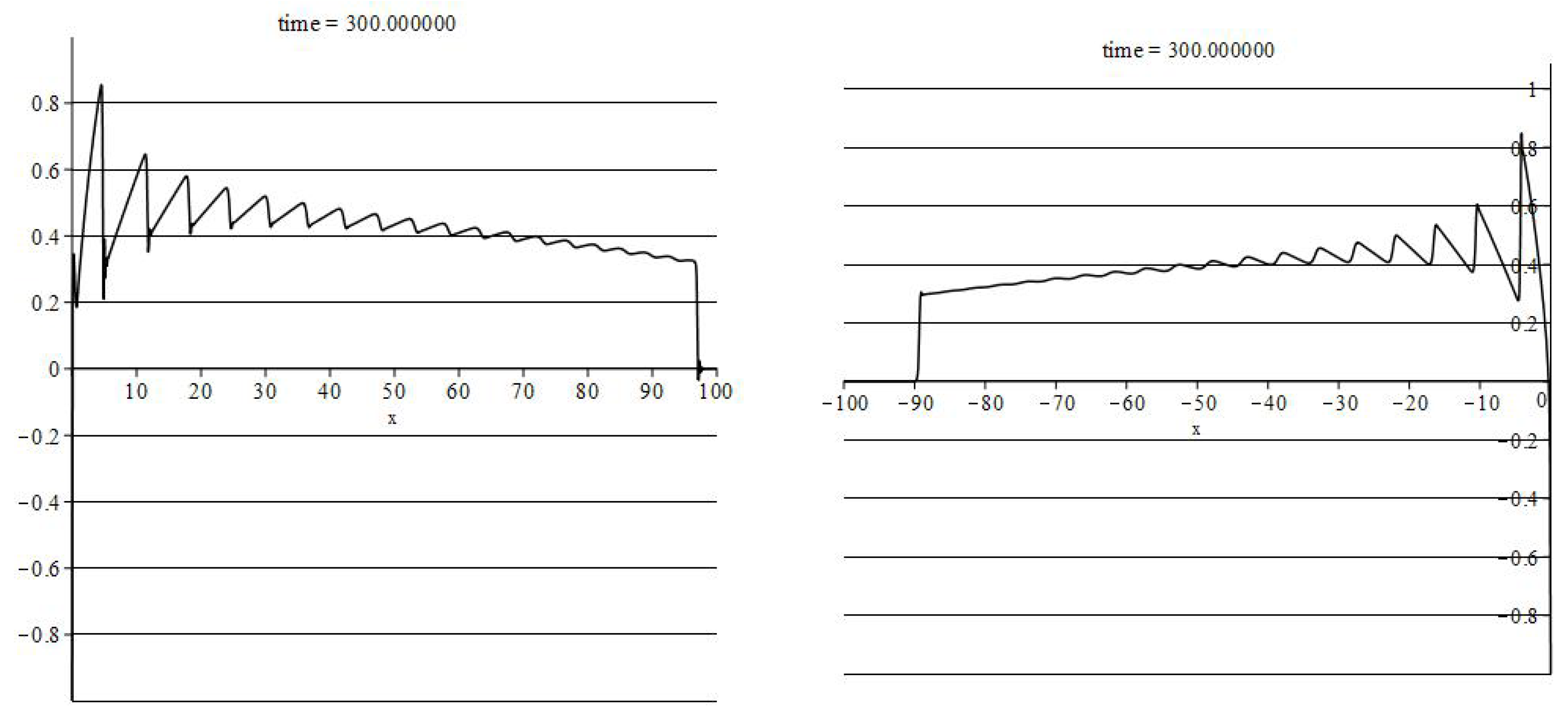
Consider boundary condition
. The graphs of solution are shown in
Figure 5, left (compare their rates of decay caused solely by the spacial dimensions.)
For the resulting compression wave
, the right-hand side of Equation (
10) equals
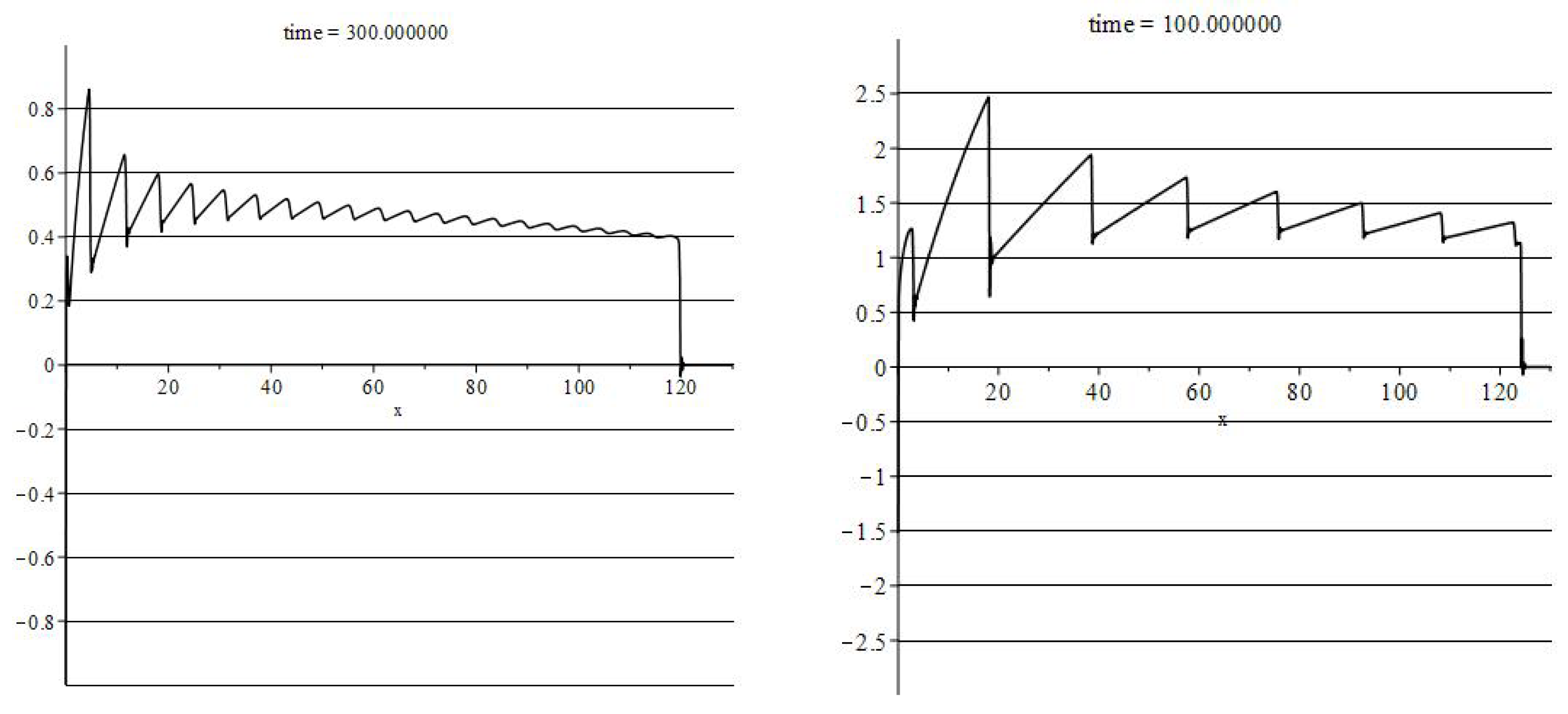
As the
Figure 1,
Figure 2,
Figure 3 and
Figure 4 show, for a periodic boundary condition, after the decay of initial oscillations, graphs become monotonic convex lines. These convex lines break at
and at the height
V. These monotonic lines are similar to the graphs of constant-boundary solutions; see
Figure 5.
4. Self-Similar Approximations To Solutions
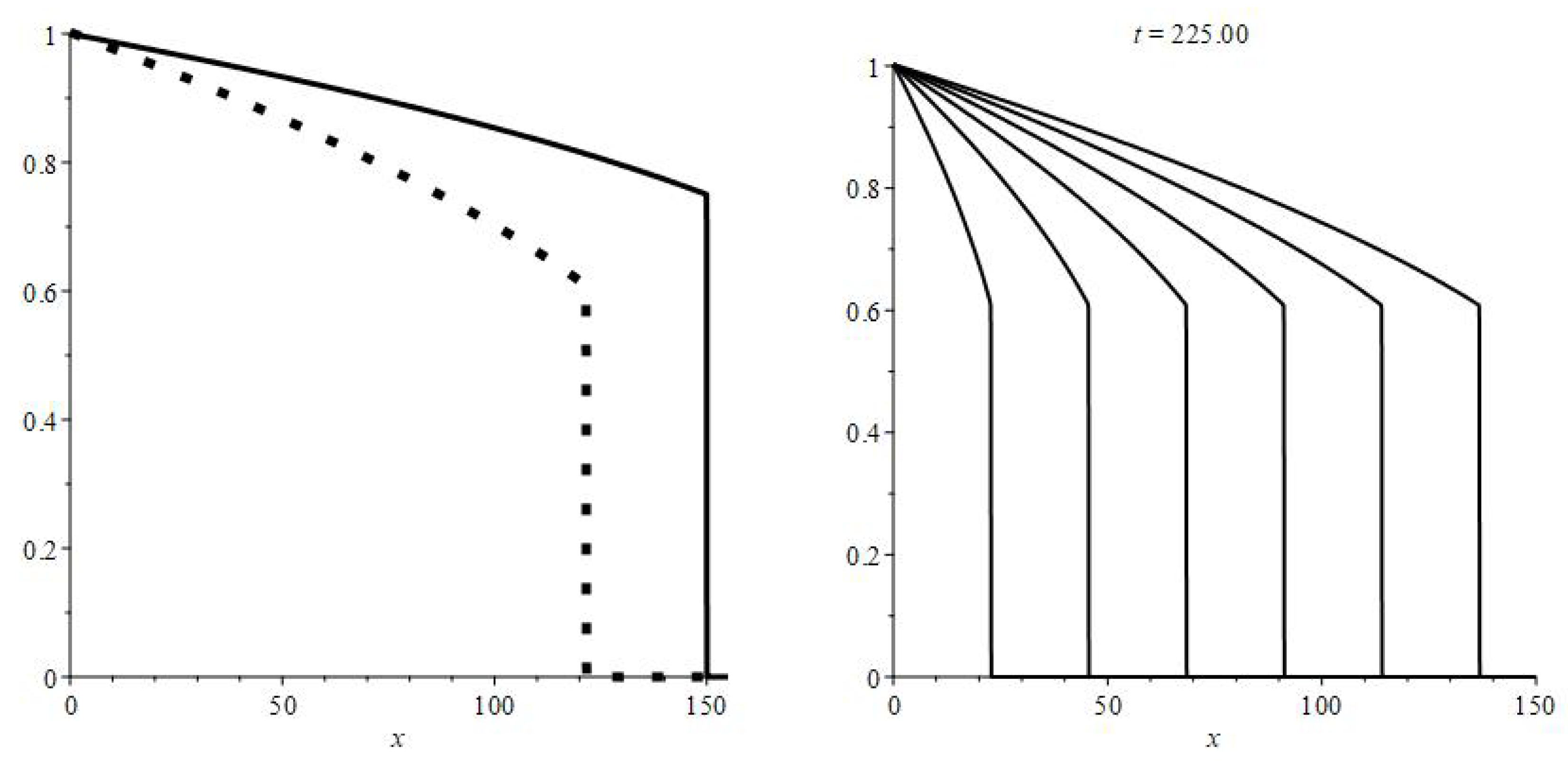
By observing the solution’s graphs, one can clearly see (e.g., on
Figure 5, right) that the monotonic part and its head shock develops as a homothetic transformation of the initial configuration (by
t as a homothety parameter). Hence, we seek solutions in the self-similar form,
. By substituting it into Equations (
1)–(
3), we get the equation:
or
for
and
. For sufficiently large
t we may omit last two terms. It follows that appropriate solutions of these truncated ordinary differential equations are given by
(The function, also called the omega function or product logarithm, is a multivalued function, namely, the branches of the inverse relation of the function , where w is any complex number.
For each integer
k there is one branch, denoted by
, which is a complex-valued function of one complex argument.
is known as the principal branch. When dealing with real numbers the
function satisfies
The
function, introduced in 1758, has numerous applications in solving equations, mathematical physics, statistics, etc.; for more detail, see [
12].)
Let
V be the velocity of the signal propagation in the medium. Since at the head shock we have
and
, we obtain the condition for finding
. It is
. It follows then that
For flat waves, it corresponds to a traveling wave solution of the classical Burgers equation.
For the cylindrical waves, the monotonic part is given by
and for spherical waves
These formulas show that the velocity is proportional to the value of a constant boundary solution at .
The corresponding graphs visually coincide with the graphs obtained by numerical modeling; for instance, see a comparison to the solution (at
) for the problem
in
Figure 6, left.
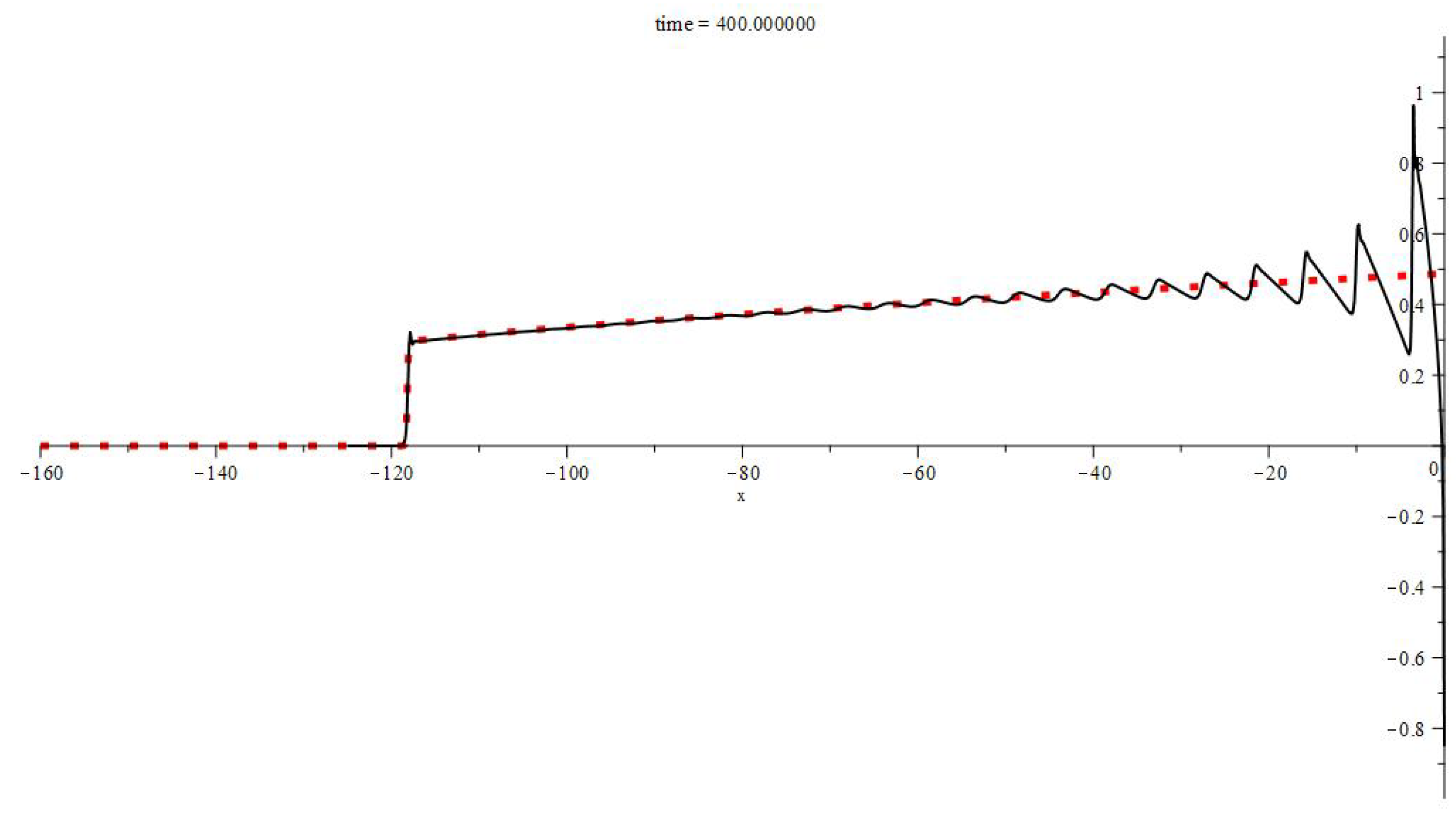
5. Median Approximation
Yet, the monotonic part of the periodic boundary solution ends with a breaking, which travels with a constant velocity and amplitude, very much like the head of the Burgers’ traveling wave solution (Equation (
6)). A rather natural idea is to truncate a self-similar solution, multiplying it by a (normalized) formula for the Burgers TWS. Namely, put
For the cylindrical waves take
This construction produces an approximation of astonishing accuracy (see
Figure 6, right and
Figure 7); these graphs correspond to the spherical KdV–Burgers problem (it comes from Equation) (
3) after the change
.
Moreover, it is evident that the graphs of
neatly represent the median lines of the approximated solutions over their whole ranges. By median we mean
Let us assess the quality of approximations numerically.
Evaluate the trapezoid area under graphs:
For the cylindrical equation
For the spherical equation
Hence, the mean value of the left-hand side of (
10) can be estimated as follows.
This mean value can be also evaluated numerically. In the case illustrated by
Figure 1 the direct numerical evaluation of the integral differs from the estimation (
20) by
. It confirms the quality of the approximation.
For constant-boundary waves, it follows from Equation (
12) that
see Equation (
12); of course this result coincides with Equation (
15). Hence, the mean value
M of an arbitrary solution at the start of oscillations (or in a vicinity of the oscillator) is linearly linked to the velocity of the head shock.
However, to find this mean value for an arbitrary border condition is a tricky task, because the integrands
and
of the right-hand side of Equation (
10) have numerous breaks. Still, one may get an (admittedly rough) estimation for
M using Equations (
11) and (
21). It follows that
for flat, cylindrical and spherical cases. In all these cases it results in
.
Numerical experiments also show (e.g., see
Figure 3) that for the
boundary condition such a value is
, where
is the mean value for
condition. That is,
M depends on
A almost linearly.
Note that this value may be obtained via the velocity V of the head shock, which, in turn, can be measured with great accuracy by the distance passed by the head shock after a sufficiently long time.
6. Conclusions
In this paper, we studied the pattern formation in periodic boundary solutions of spherical and cylindrical KdV–Burgers equations. Such a solution usually starts with a periodical chain of shock fronts with a decreasing amplitude. When oscillations decay and cease, a solution proceeds as a monotonic convex line that ends with a head shock. This last pattern was not described previously and it is the main subject of the paper.
We obtained simple explicit formulas describing the monotonic part of the solution and its head break. These approximate formulas have great accuracy. Moreover, their graphs neatly represent the median lines of the approximated solutions on their entire ranges. (By median line we mean the level around which the periodical oscillations occur).
To obtain these approximations we used self-similar solutions of the dissipationless and dispersionless KdV–Burgers equation and a traveling wave solution of the flat Burgers equation. Formulas depend on only one parameter: either on the velocity of the signal propagation or on the median value of the solution in the vicinity of the periodic boundary.
Some open questions remain. Our approximations are very good for the one-parameter class of constant boundary solutions. The existence of a one-parameter family of solutions points to the existence of a suitable symmetry, but the classical symmetry analysis was, so far, unhelpful. Conservation laws allows us to assess the value of the approximation’s parameter using the boundary condition, but the resulting estimation is rough.