Abstract
The Lie symmetry group transformation method was used to investigate the partial differential equations that model the motion of a natural convective unsteady flow past to a non-isothermal vertical flat surface. The one-parameter Lie group transformation was applied twice consecutively to convert the motion governing equations into a system of ordinary differential equations. The obtained system of ordinary differential equations was solved numerically using the Lobatto IIIA formula (implicit Runge–Kutta method). The effect of the Prandtl number on the temperature and velocity profiles is illustrated graphically.
1. Introduction
Ludwig Prandtl (1875–1953) presented the boundary-layer theory for the first time in 1904 [1]. He obtained the boundary layer for 2D flow equations neglecting the viscosity effect up to the outer edge of the boundary layer to simplify the Navier–Stokes equations [2]. A boundary layer is the thin region of flow relative to the body surface, where the viscosity effect is dominant and the velocity of the flow changes with vertical distance. The fluid relative to a vertical heated surface gradually increases because of the difference in density distribution resulting from a temperature difference or non-uniform distribution of concentration difference without using any external forces. This process is known as the natural convective flow. Properties of free-convective laminar boundary-layer flow are widely involved in several studies due to their ever-increasing engineering and industrial applications such as metal coating, cooling processes, waste disposal, crystal industry, heat removal in nuclear recovery, oil recovery, building construction, and so on. The difficulty in boundary-layer problems is the rapid change in the fluid properties over the thin boundary-layer regions, aside from a host of different parameters that control the basic governing boundary-layer equations.
Recently, several methods have been developed to find the most efficient strategy for solving the complicated non-linear partial differential governing equations system. Lie symmetry transform is an effective technique to deal with non-linear partial differential equations by applying simple assumptions and steps [3,4,5,6,7,8]. It is used widely in the non-linear problems that appear in fluid mechanics studies. For instance, Boutros et al. [9] obtained similarity reductions of the boundary-layer equations governing the incompressible viscous fluid flow on a heated stretching sheet placed in a porous medium. Salem and Fathy [10] used the previous work to study the effect of the mass transfer on a boundary-layer magneto-hydro-dynamic (MHD) flow considering the temperature-dependent viscosity, the thermal conductivity, and the radiation effect. Abd-el-Malek and Amin [11] applied the Lie group method to the non-linear inviscid fluid flow considering a free surface under gravity. Sivasankaran et al. [12] applied the Lie group method to the heat and mass transfer equations of the flow over an inclined surface and investigated changes in temperature, velocity, and concentration of the fluid with Prandtl number. Nanofluids have been the topic of numerous investigations because of their greatly enhanced thermal properties. Lie group analysis was used to study the free-convective flow of the nanofluids over a porous stretching vertical sheet by Rosmila et al. [13] and Hamad and Ferdows [14], past a vertical flat plate by Hamad et al. [15], and on a horizontal plate by Rashidi et al. [16].
This paper aims to analyze the unsteady free convective boundary-layer flow over a vertical surface using the one-parameter Lie group transformation. Abd-el-Malek [17] analyzed the governing equations of boundary-layer flow over a vertical surface by applying the two-parameter group transformation and they used some suitable assumptions in their study. In this analysis, the one-parameter Lie group transformation was professionally applied to the governing equations of conservation of mass, momentum, and energy and introduced advanced generators that could be useful for future research under appropriate initial and boundary conditions. In the boundary conditions of this study, the relation between the wall temperature with the vertical distance and the time was considered, unlike in Hamad et al. [15], who dealt with wall temperature as a constant value. The accepted generators in light of the boundary conditions were re-analyzed using the Lie group transformation to obtain the final system of ordinary differential equations, which is solved numerically with the Runge–Kutta scheme. The accepted generators lead to defining a specific formula of the horizontal and vertical velocities, the temperature, and the wall temperature in terms of the vertical distance “x” and the time “t”. The present work illustrated the effect of the Prandtl number on both temperature and velocity distributions and explained how its value controls the behavior of the thermal boundary layer, which is the main problem in high-performance designs such as “gliders” and airplane airfoils to avoid the increased drag.
2. Mathematical Formulation
Consider the laminar natural-convection fluid flow adjacent to a vertical heated surface. According to the Boussinesq approximation introduced by Abd-el-Malek [18], the basic governing equations of the conservation of mass, momentum, and energy in non-dimensional form are represented by the following system of equations:
where and are velocity components in the and directions, respectively, and represents the temperature.
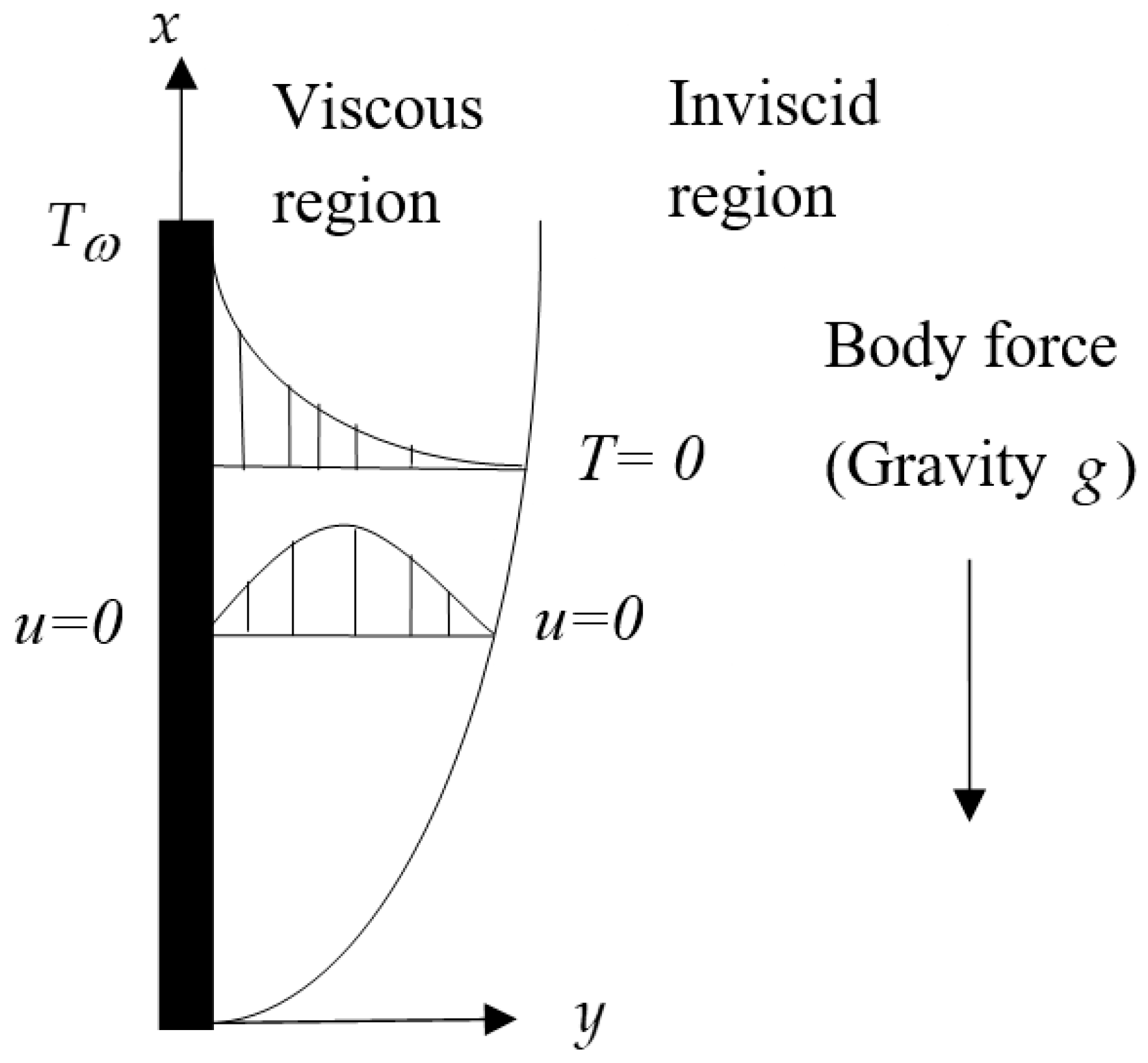
For the vertical surface in Figure 1, the temperature of the fluid starts with the wall temperature , and then gradually decreases. This difference in temperature, aside from the external body force such as gravitational force, leads to density changes. The flow velocity starts from zero at the wall and varies due to buoyancy force generated from density difference inside the boundary layer until reaching zero at its outer edge. Then, the appropriate boundary conditions are given by:
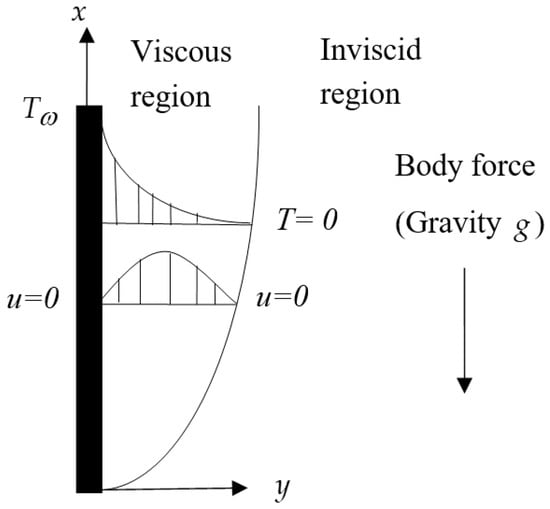
Figure 1.
Physical model of the boundary layer flow over a vertical surface.
Equations (1)–(3) are invariant under the scaling transformation generated by , where is the infinitesimal parameter and is the infinitesimal generator defined as
The one-parameter Lie group infinitesimal transformations of under the invariant condition after applying Taylor series in (neighborhood of ) are given by:
Equations (1)–(3) can be written as follows:
The infinitesimal generator is said to be a Lie point symmetry generator for the system of Equations (1)–(3) if
and represents the prolongation order for each equation according to the highest derivative. Since the system of Equations (1)–(3) has at most second-order derivatives, then the prolonged generator takes the form,
According to Equation (10), applying Equation (11) to Equations (7)–(9) gives the following system of differential equations:
where
and stands for . In addition,
The total derivatives with respect to and should be defined as:
Substitution from (13) and (14) into (12) gives three large expressions, which leads to the following system of determining equations:
Solving the system of determining Equation (15) gives,
In light of the boundary conditions (4), we have . Therefore, a symmetry generator represented by (5) is a linear combination of
3. Invariant Solution Generated by
Under the invariant condition of the Lie group method, the characteristic equations are
Hence, the general solutions are
where . Substitution of (19) into (1)–(3) gives the following system
with boundary conditions:
The one-parameter Lie group infinitesimal transformations of under the invariant condition can be given by:
The given system of equations has the following infinitesimal generator:
According to the system of Equations (20)–(22), the generator (25) prolonged the second-order generator in the form,
where,
and stands for and . In addition,
The total derivatives with respect to and should be defined as:
Following the same technique from the previous section leads to the following system of determining the equation:
Solving the system of determining Equation (29) gives
According to boundary conditions (23), , a symmetry generator represented by (25) is a linear combination of
The generated solution from contradicts the boundary conditions but for , the characteristic equations are
Hence, the general solutions are
This gives the following solutions for the original governing system:
Substitution with (34) into (20)–(22) gives the following ordinary differential equations:
The initial and boundary conditions take the form
4. Invariant Solution Generated by
According to , the auxiliary equations take the form
Hence, the general solutions are
Substitution of (40) into (1)–(3) gives the following system:
The one-parameter Lie group infinitesimal transformations of under the invariant condition can be given by:
Following the same process introduced in Section 3 yields
The auxiliary equation can be expressed as
According to the initial and boundary conditions, both and becomes zero. Then,
Hence, , and take the form
From (48), the forms of and from (40) are similar to (34), thus the invariant solution generated by will lead to the same reduced system of ordinary differential equations from .
5. Invariant Solution Generated by
It is found that and contradict the initial and boundary conditions of the system (4). Here, we try to combine with to find out if it generates a new possible solution. Under the invariant condition of the Lie group method, the characteristic equations are:
Hence, the general solutions are:
where and . Substitution of (50) into (1)–(3) gives the following system:
The one-parameter Lie group infinitesimal transformations of , under the invariant condition, are given by:
The given system of equations has the following infinitesimal generator:
The second prolongation takes the form:
The steps of the one-parameter Lie group leads to the following system of determining equations:
Solving the system of determining Equation (57) yields
In light of the original system, the boundary condition is . Therefore, a symmetry generator represented by (55) is a linear combination of
It was found that all the previous generators contradict the boundary conditions. Therefore, no ordinary differential equations could be obtained for the system of Equations (51)–(53) except considering that , which contradicts the assumption from the beginning.
6. Graphical Results and Discussion
The reduced ordinary differential system of equations from the generator is equivalent to the system obtained from thus analyzing both systems leads to the same results. Ordinary differential Equations (35)–(37) with the boundary conditions (38) were solved numerically using the Lobatto IIIA formula (implicit Runge–Kutta). The impact of Prandtl number on temperature and velocity has been highlighted through graphs.
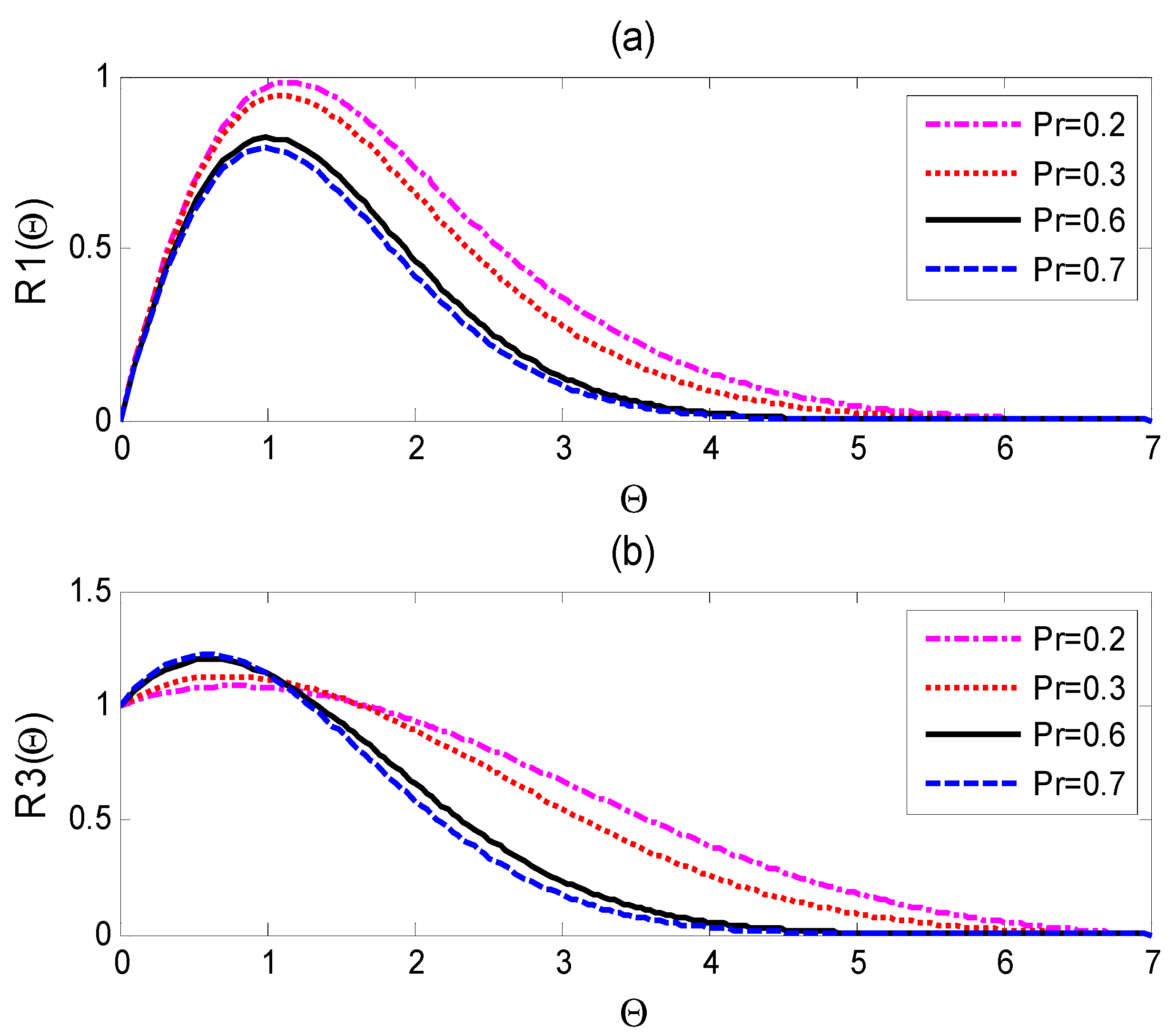
Figure 2a and Figure 3a present the relation between the velocity and Prandtl number. The velocity magnitude decreases with rising values of Prandtl number due to the higher viscosity and small thermal conductivity, which increases the thickness of the fluid and hence decreases its velocity. Both figures show that the velocity is the maximum near the surface, then it approaches the zero far away from the surface.
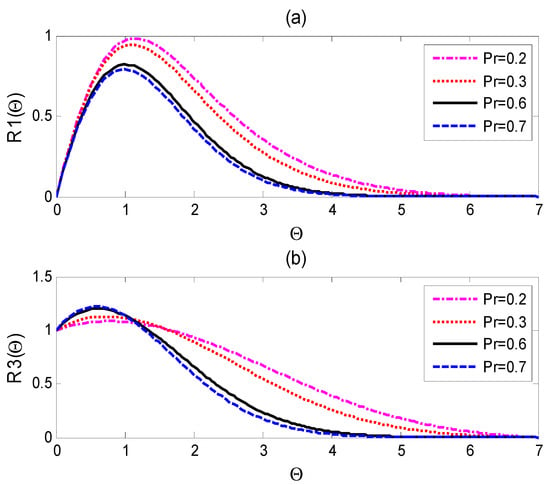
Figure 2.
(a) Dimensionless velocity as a function of and (b) dimensionless temperature as a function of for values of the Prandtl number <1.
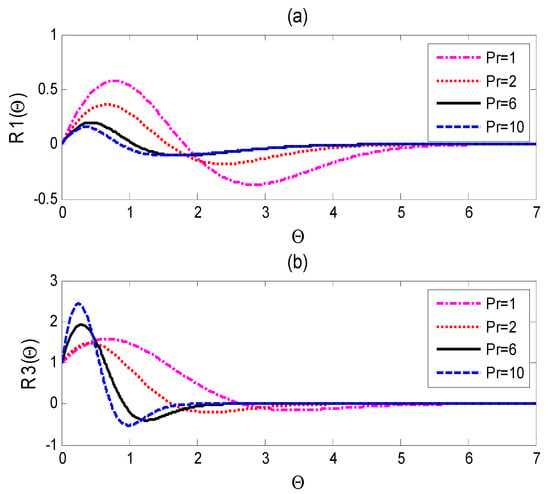
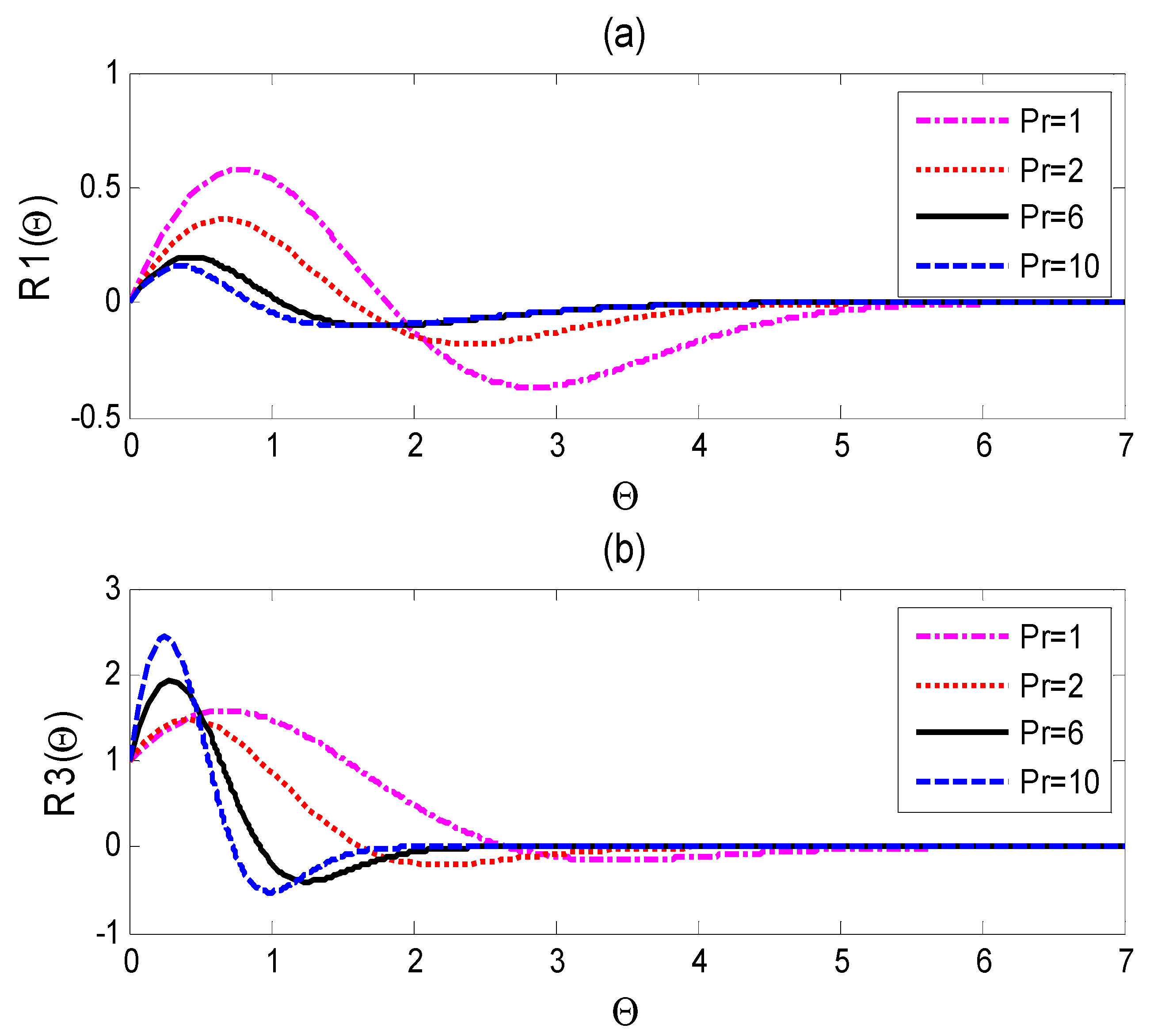
Figure 3.
(a) Dimensionless velocity as a function of and (b) dimensionless temperature as a function of for values of the Prandtl number >1.
The temperature distribution for different Prandtl numbers is plotted in Figure 2b and Figure 3b. It is noticeable that the fluid temperature decreases faster with higher values of Prandtl number because of the low heat transfer of the high viscous fluids with a large Prandtl number. The plots represent the relation between the Prandtl number and the thickness of the thermal boundary layer. Pr < 1 yields a thick thermal boundary layer due to the higher thermal diffusion, but this situation reverses for Pr >1. The presented velocity and temperature graphs found good agreement with the related physical fact in addition to the mathematical results obtained by applying the two-parameter group transformation to the governing equations introduced in [17].
Figure 3a,b documents the phenomenon of flow reverse and temperature defect. Figure 3a indicates the relationship between the flow reversal and the higher Prandtl number. Due to the smaller values of buoyancy, a reverse flow takes place away from the surface. Figure 2b depicts the overshoot in the temperature distribution near the surface with a noticeable drop for higher Pr number (Pr > 1) due to the smaller thermal conductivity and diffusivity. Physically, the temperature reversal occurs when the cool flow that comes from below hits the high ambient temperature, and thus the temperature undershoots. The increment of Prandtl number leads to significant temperature undershoots and a weak flow reversal. The presented attitude of velocity and temperature agrees with the physical results that emerged in [19].
7. Conclusions
In this paper, the unsteady free convective boundary-layer flow over a vertical surface was analyzed using the one-parameter Lie group transformation. Applying the Lie group transformation to the main governing motion equations introduces accurate infinitesimal generators that could be useful in future studies under different study conditions. In light of the appropriate initial and boundary conditions, the Lie group symmetry solutions for the introduced system developed suitable formulas of the velocity components, the temperature, and the wall temperature in terms of the vertical distance “x” and the time “t”. The introduced symmetry solutions can be investigated with different physical parameters for characterizing the velocity and the thermal boundary layer. The present work concentrated on studying the Prandtl number effect on the temperature and velocity profiles, in addition to the thickness of the thermal boundary layer, which were analyzed. Based on the graphical results, the velocity and the temperature distributions decreased by increasing the Prandtl number, and hence the thickness of the thermal boundary layer also decreased. The present work showed the effect of the Prandtl number on the reversal of flow and temperature due to the difference in temperature between the high ambient temperature and the lower temperature flow.
Author Contributions
M.B.A.-e.-M. was responsible for suggesting the problem, reviewing the results and editing the writing; N.A.B. was responsible for writing reviewing and editing; A.M.A. validate the calculations and check the accuracy of plotted results. A.M.H. was responsible for the calculations and writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oleinik, O.A.; Samokhin, V.N. Mathematical Models in Boundary Layer Theory, 1st ed.; Chapman& Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 1999. [Google Scholar]
- Anderson, J.D. Ludwig Prandtl’s boundary layer. Phys. Today 2005, 58, 42–48. [Google Scholar] [CrossRef]
- Steeb, W.H. Invertible Point Transformations and Nonlinear Differential Equations, 1st ed.; World Scientific: London, UK, 1993. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Hundley, J. Introduction to Lie Groups; Miscellaneous; Massachusetts Institute of Technology: Cambridge, MA, USA, 2009. [Google Scholar]
- Hall, B.C. Lie groups, Lie algebras, and representations. In Quantum Theory for Mathematics; Springer: New York, NY, USA, 2013; pp. 333–366. [Google Scholar]
- Chevalley, C. Theory of Lie Groups; Dover Books on Mathematics; Dover Publications Inc.: Garden City, NY, USA, 2018. [Google Scholar]
- Abd-el-Malek, M.B.; Amin, A.M. Lie group method for solving viscous barotropic vorticity equation in ocean climate models. Comput. Math. Appl. 2018, 75, 1443–1461. [Google Scholar] [CrossRef]
- Boutros, Y.Z.; Abd-el-Malek, M.B.; Badran, N.A.; Hassan, H.S. Lie-group method of solution for steady two-dimensional boundary-layer stagnation-point flow towards a heated stretching sheet placed in a porous medium. Meccanica 2006, 41, 681–691. [Google Scholar] [CrossRef]
- Salem, A.M.; Fathy, R. Effects of variable properties on MHD heat and mass transfer flow near a stagnation point towards a stretching sheet in a porous medium with thermal radiation. J Chin. Phys. B. 2012, 21, 054701. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B.; Amin, A.M. Lie group analysis of nonlinear inviscid flows with a free surface under gravity. J Comput. Appl. Math. 2014, 258, 17–29. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Bhuvaneswari, M.; Kandaswamy, P.; Ramasami, E.K. Lie group analysis of natural convection heat and mass transfer in an inclined surface. Nonlinear Anal. Model. Control 2006, 11, 201–212. [Google Scholar] [CrossRef]
- Rosmila, A.B.; Kandasamy, R.; Muhaimin, I. Lie symmetry group transformation for MHD natural convection flow of nanofluid over a linearly stretching sheet in the presence of thermal stratification. Appl. Math. Mech. Engl. Ed. 2012, 33, 593–604. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Ferdows, M. Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing: A lie group analysis. Commun. Nonlinear Sci. Numer Simulat. 2011, 7, 132–140. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Pop, I.; Ismail, A.I. Magnetic field effects on free convection flow of a nanofluid past a vertical semi-infinite flat plate. Nonlinear Anal. Real World Appl. 2011, 12, 1338–1346. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Momoniat, E.; Ferdows, M.; Basiriparsa, A. Lie group solution for free convective flow of a nanofluid past a chemically reacting horizontal plate in porous media. Math. Probl. Eng. 2014, 2014, 239082. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B.; Boutros, Y.Z.; Badran, N.A. Group method analysis of unsteady free-convective boundary-layer flow on a nonisothermal vertical flat plate. J. Eng. Math. 1990, 24, 343–368. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B. Application of the group-theoretical method to physical problems. J. Nonlinear Math. Phys. 1998, 5, 314–330. [Google Scholar] [CrossRef]
- Sarojamma, G.; Lakshmi, R.; Sreelakshmi, K.; Vajravelu, K. Dual Stratification Effects on Double-Diffusive Convective Heat and Mass Transfer of a Sheet-Driven Micropolar Fluid Flow. J. King Saud Univ. Sci. 2018, 32, 366–376. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).