A Compression Resistant Steganography Based on Differential Manchester Code
Abstract
1. Introduction
- 1.
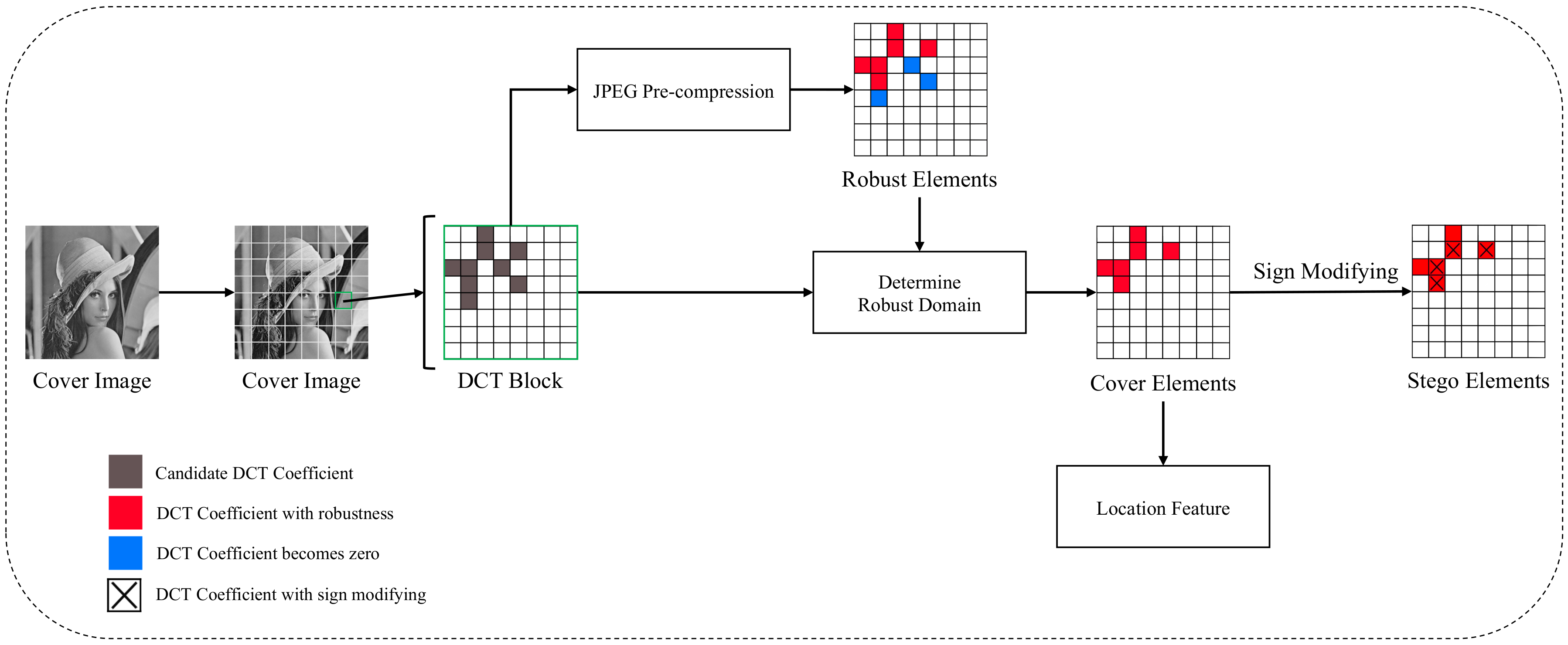
- We design a robust steganography framework which embeds secret message by locating the robust domain of the image. This framework generates the location features by combining the position of the non-zero DCT coefficients and differential Manchester code. These procedures improve the robustness performance, which contributes to the complete extraction of the secret message after JPEG compression attacks.
- 2.
- We analyze and improve the sign steganography algorithm, propose a weighted cost adjustment method, and further optimize the cost selection of cover elements. Numerical experiments empirically demonstrate that our proposed embedding algorithm largely improves the robustness performance of stego image when facing the challenge of JPEG compression attack.
- 3.
- Our algorithm can be applied to a variety of social media platforms and can resist channel processing operations that only include JPEG compression attacks. At the same time, the secret message can still be completely extracted after repeated compression or force compression.
2. Related Works
- Capacity: the stego image carries the maximum number of the secret bits.
- Imperceptibility: the stego image is indistinguishable from the cover image in human visual perception.
- Undetectability: the stego image can bypass the detection from modern advanced steganalysis.
- Robustness: the stego image is capable of preserving the embedded message when suffering different post-processing attacks.
2.1. Symmetry Methods
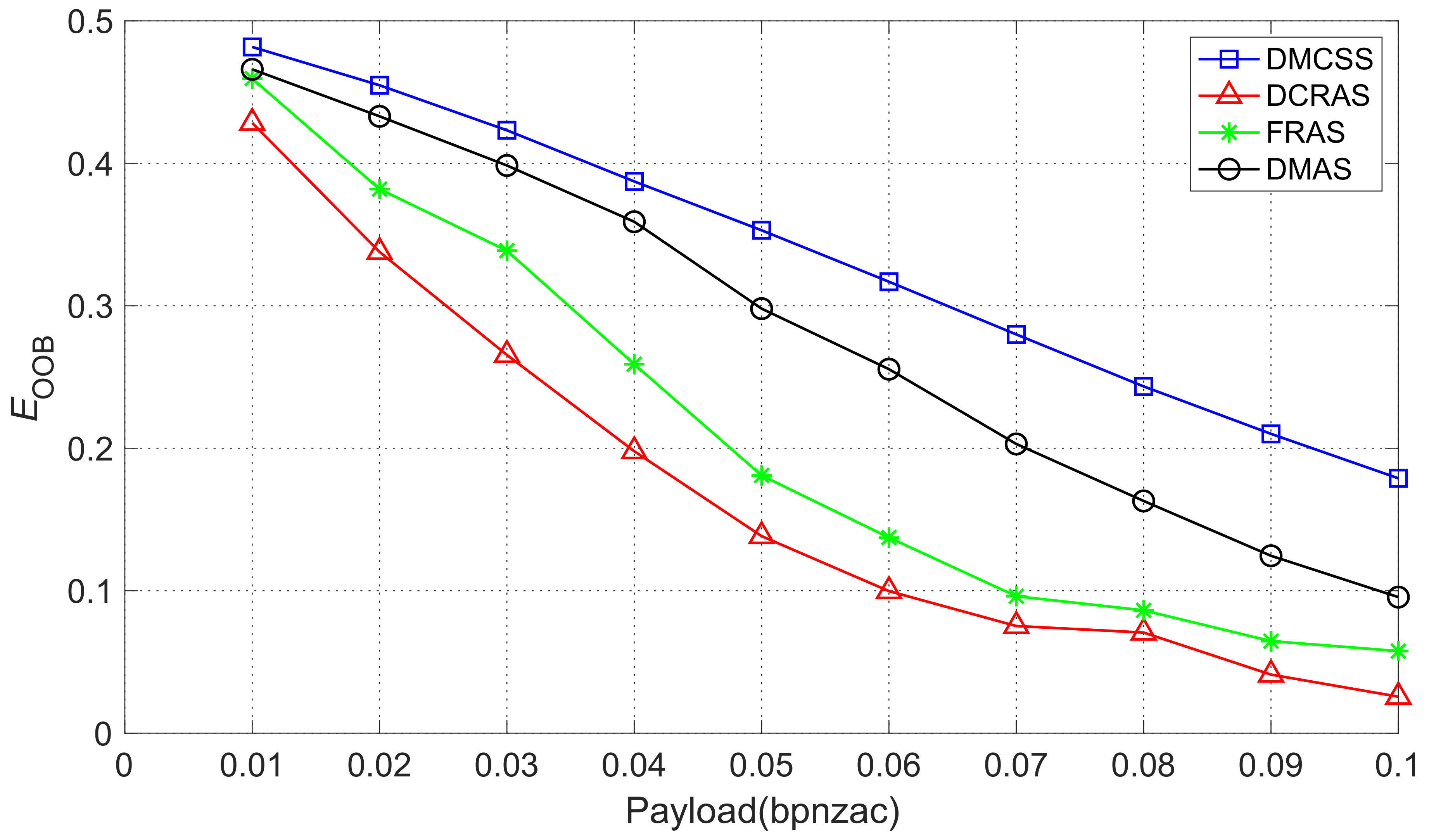
- DCRAS method [15]: In this method, the embedding domain is constructed through the connection between DCT coefficients. DCRAS divides the DCT coefficients into several DCT blocks for the mean value relationship between the DCT coefficients at a certain position. The corresponding position in the three adjacent DCT blocks is basically stable before and after JPEG compression. The authors construct the embedding domain based on this characteristic to extract the cover element from it. At the same time, the secret message is encoded with the RS error correction code and embedded in the cover element to obtain the stego element.
- FRAS method [16]: In this method, the authors first use Harris–Laplacian features [23] to extract the robust domain, then use channel simulation to attack each domain to find the domains suitable for embedding, and finally use the DCRAS algorithm to construct the embedding domain in these domains and extract the cover elements to strike the balance between undetectability and robustness. FRAS combines feature domain selection, and the DCRAS algorithm is better than DCRAS in terms of safety and robustness.
- DMAS method [24]: In this method, according to the JPEG compression quantization table, the authors use Dither modulation to construct the embedding domain. This algorithm uses the principle of compression to construct a more stable embedding domain, which reduces the modification range of the DCT coefficients when embedding the message. Thus, its robustness and undetectability are further improved compared with the two algorithms above.
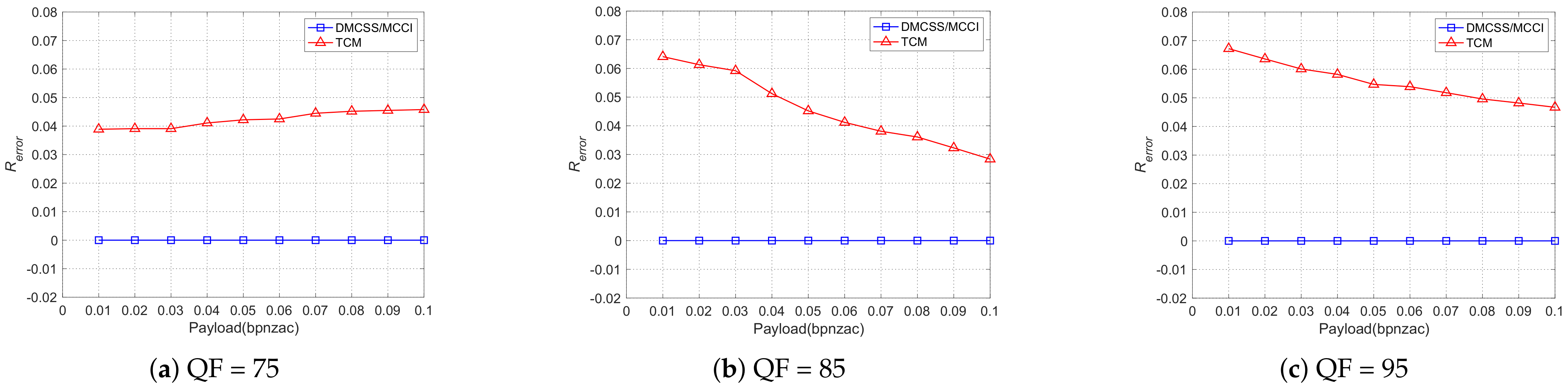
- TCM method [19]: In this method, the authors devised a steganographic method based on matching channels. TCM (Transport Channel Matching), as the main idea of this method, depends on repeated compression of the stego images to reduce errors caused by quantization and rounding. The original image processed by TCM is embedded as the cover image. The algorithm adopts error correction code and cost function to generate the temporary stego image, and uses the transmission channel to repeatedly compress the stego image. In this process, the error correction code will be operated iteratively when the message is incorrectly extracted, until the correctly extracted stego image is generated or the threshold value of the error correcting is met.
- Zernike moment method [25]: Pixels between the original neighboring pixels after scaling attack will be lost or increased. In this method, Zhang et al. proposed a countermeasure based on Zernike moments which can map the characteristic pixels of an image, and has rotation invariance as a set of orthogonal matrices. In other words, scaling the image will not change Zernike moments. The sender extracts the Zernike moments of the image, uses the method of Dither modulation to embed the secret message into the normalized Zernike moments, and then reconstructs the stego image.
- MCCI method [18]: In this method, Tao et al. proposed a new robust steganography framework. The main idea behind the method is to modify and adjust the differences between the DCT coefficients of the original image and the stego image. First, we compress the image and use any frequency domain steganography method to generate the stego image. The intermediate image is obtained by adjusting the DCT coefficients of the original image depending on the stego image; then, the intermediate image is compressed again through the previous channel to obtain a new stego image. The method ensures that the image generated by the intermediate image compression is the same as the stego image, so the secret message can be completely extracted.
2.2. Prior Work
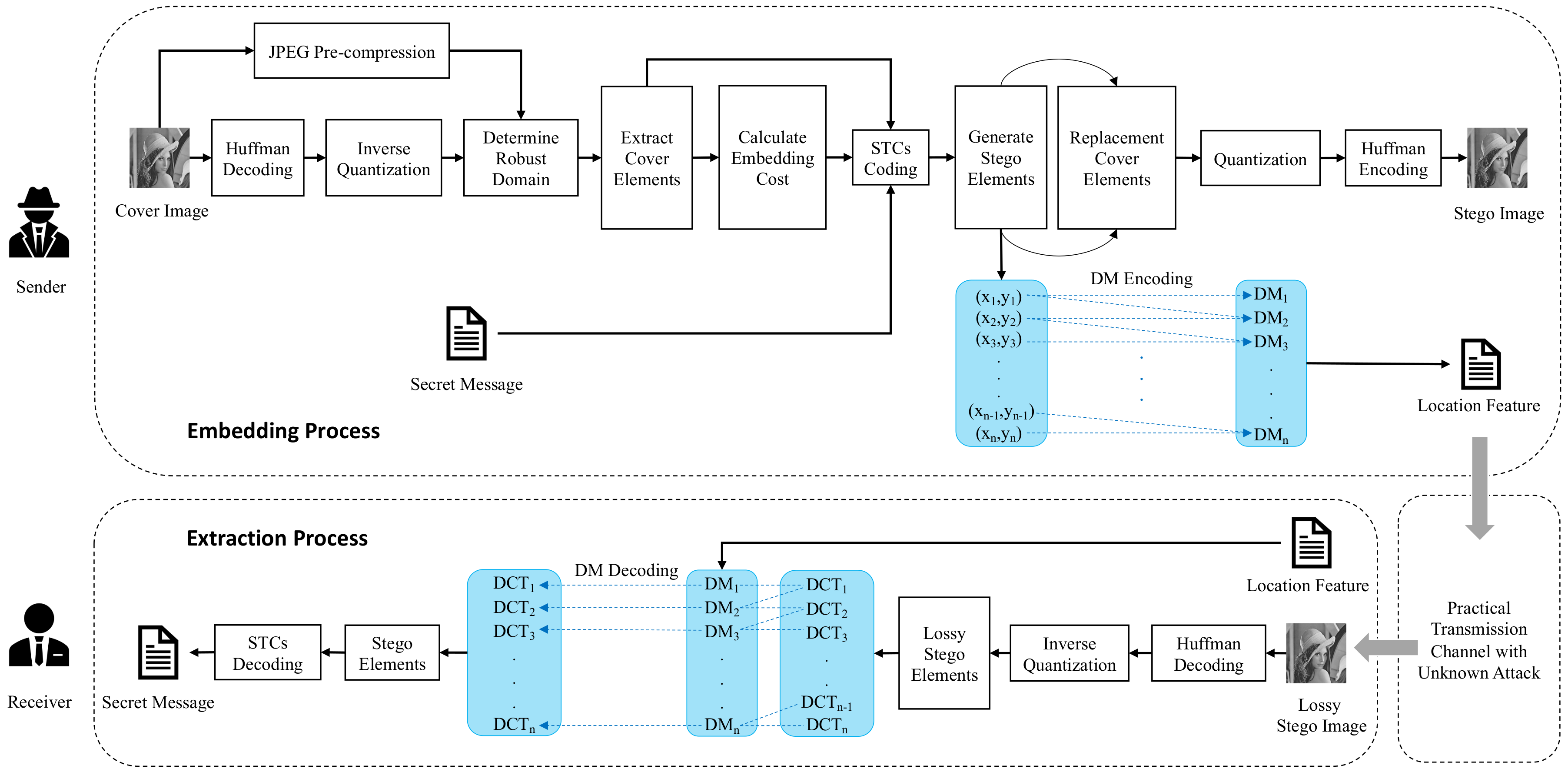
3. Proposed Method
3.1. Motivation
3.2. Weighted Cost Adjustment
3.3. Differential Manchester Code
3.3.1. Differential Manchester Encoding
3.3.2. Differential Manchester Decoding
3.3.3. Correcting Incorrect Elements
4. Numerical Experiments
4.1. Experiment Setup
4.2. Determination of Parameters
4.3. Capacity Analysis
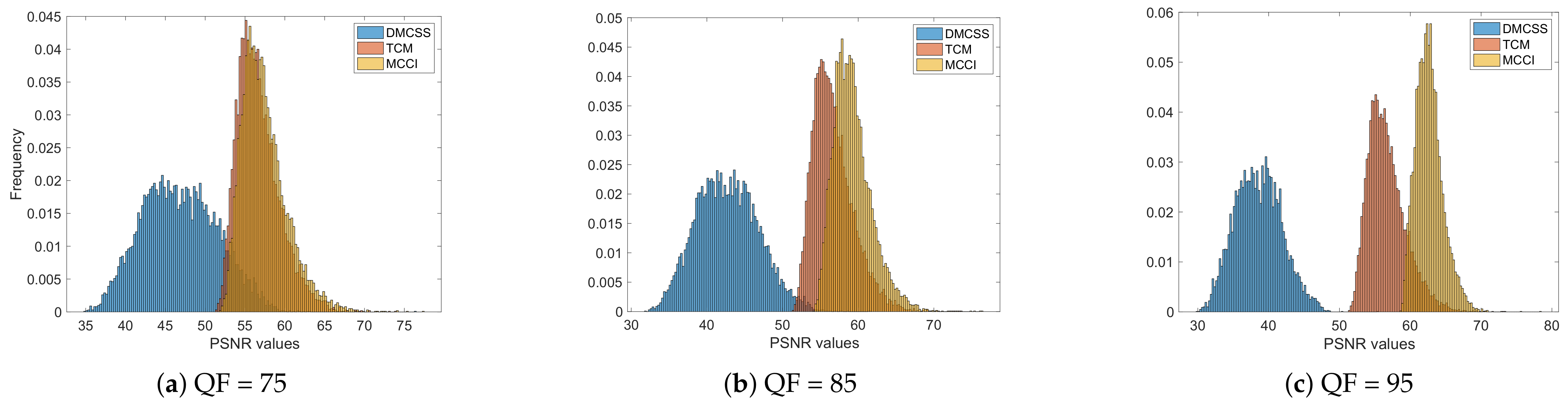
4.4. Imperceptibility Performance
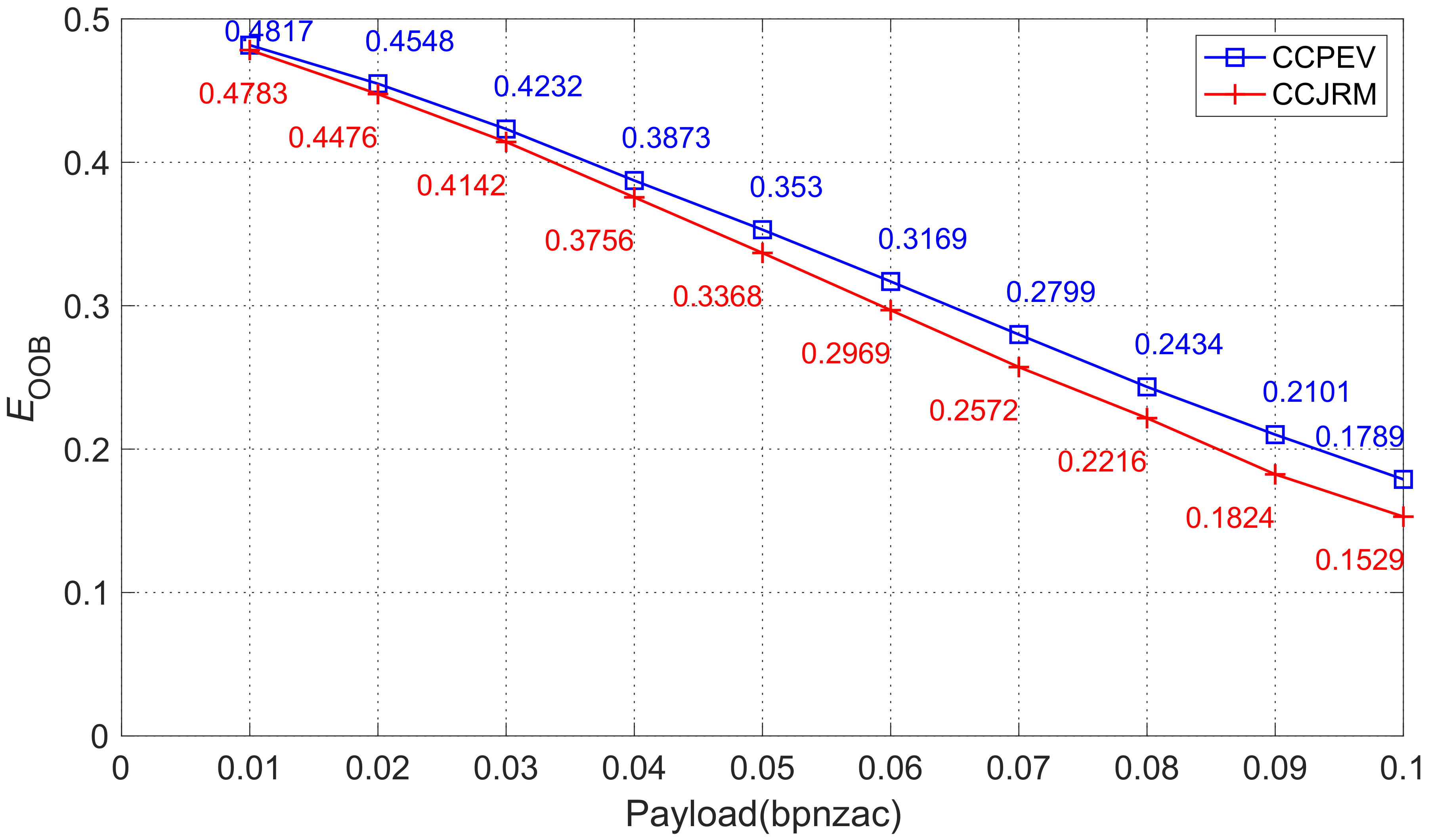
4.5. Undetectability Performance
4.6. Robustness Performance
4.7. Practical Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LSBr | Least Significant Bit replacement |
| LSBm | Least Significant Bit matching |
| HUGO | Highly Undetectable steGo |
| WOW | Wavelet Obtained Weights |
| S-UNIWARD | Side Information UNIversal WAvelet Relative Distortion |
| FRAS | Feature Regions based Adaptive Steganography |
| DMAS | Dither modulation based Adaptive Steganography |
| DCRAS | Coefficients Relationship based Adaptive Steganography |
| JPEG | Joint Photographic Experts Group |
| QF | quality factor |
| TCM | Transmission Channel Matching |
| MCCI | Modifying Coefficients of Cover Image |
| DMCSS | Differential Manchester Code with Sign Steganography |
| CCPEV | PEV features enhanced by Cartesian Calibration |
| CCJRM | Cartesian Calibrated JPEG domain Rich Model |
| FSDC | Flipping the Sign of DCT Coefficients |
| STC | syndrome–trellis codes |
| PSNR | Peak Signal-to-Noise Ratio |
| OOB | out-of-bag |
References
- Asikuzzaman, M.; Pickering, M.R. An overview of digital video watermarking. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2131–2153. [Google Scholar] [CrossRef]
- Liu, T.Y.; Tsai, W.H. A new steganographic method for data hiding in microsoft word documents by a change tracking technique. IEEE Trans. Inf. Forensics Secur. 2007, 2, 24–30. [Google Scholar] [CrossRef]
- Li, B.; Tan, S.; Wang, M.; Huang, J. Investigation on cost assignment in spatial image steganography. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1264–1277. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, C.; Tang, S.; Bai, S. Steganography integration into a low-bit rate speech codec. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1865–1875. [Google Scholar] [CrossRef]
- Xu, D.; Wang, R.; Shi, Y.Q. Data hiding in encrypted H. 264/AVC video streams by codeword substitution. IEEE Trans. Inf. Forensics Secur. 2014, 9, 596–606. [Google Scholar] [CrossRef]
- Pevnỳ, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–177. [Google Scholar]
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, 2–5 December 2012; pp. 234–239. [Google Scholar]
- Li, B.; Wang, M.; Huang, J.; Li, X. A new cost function for spatial image steganography. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 4206–4210. [Google Scholar]
- Holub, V.; Fridrich, J. Digital image steganography using universal distortion. In Proceedings of the First, ACM Workshop on Information Hiding and Multimedia Security, Montpellier, France, 17–19 June 2013; pp. 59–68. [Google Scholar]
- Guo, L.; Ni, J.; Shi, Y.Q. Uniform embedding for efficient JPEG steganography. IEEE Trans. Inf. Forensics Secur. 2014, 9, 814–825. [Google Scholar]
- Guo, L.; Ni, J.; Su, W.; Tang, C.; Shi, Y.Q. Using statistical image model for JPEG steganography: Uniform embedding revisited. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2669–2680. [Google Scholar] [CrossRef]
- Denemark, T.; Fridrich, J. Improving steganographic security by synchronizing the selection channel. In Proceedings of the 3rd ACM Workshop on Information Hiding and Multimedia Security, Portland, OR, USA, 17–19 June 2015; pp. 5–14. [Google Scholar]
- Li, B.; Wang, M.; Li, X.; Tan, S.; Huang, J. A strategy of clustering modification directions in spatial image steganography. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1905–1917. [Google Scholar]
- Zhang, W.; Zhang, Z.; Zhang, L.; Li, H.; Yu, N. Decomposing joint distortion for adaptive steganography. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 2274–2280. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, X.; Yang, C.; Ye, D.; Liu, F. A JPEG-compression resistant adaptive steganography based on relative relationship between DCT coefficients. In Proceedings of the 2015 10th International Conference on Availability, Reliability and Security, Toulouse, France, 24–27 August 2015; pp. 461–466. [Google Scholar]
- Zhang, Y.; Luo, X.; Yang, C.; Liu, F. Joint JPEG compression and detection resistant performance enhancement for adaptive steganography using feature regions selection. Multimed. Tools Appl. 2017, 76, 3649–3668. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, C.; Zhang, W.; Liu, F.; Luo, X. On the fault-tolerant performance for a class of robust image steganography. Signal Process. 2018, 146, 99–111. [Google Scholar] [CrossRef]
- Tao, J.; Li, S.; Zhang, X.; Wang, Z. Towards robust image steganography. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 594–600. [Google Scholar] [CrossRef]
- Zhao, Z.; Guan, Q.; Zhang, H.; Zhao, X. Improving the robustness of adaptive steganographic algorithms based on transport channel matching. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1843–1856. [Google Scholar] [CrossRef]
- Zhu, Z.; Zheng, N.; Qiao, T.; Xu, M. Robust Steganography by Modifying Sign of DCT Coefficients. IEEE Access 2019, 7, 168613–168628. [Google Scholar] [CrossRef]
- Yu, X.; Chen, K.; Wang, Y.; Li, W.; Zhang, W.; Yu, N. Robust adaptive steganography based on generalized dither modulation and expanded embedding domain. Signal Process. 2020, 168, 107343. [Google Scholar] [CrossRef]
- Li, F.; Wu, K.; Qin, C.; Lei, J. Anti-compression JPEG steganography over repetitive compression networks. Signal Process. 2020, 170, 107454. [Google Scholar] [CrossRef]
- Tsai, J.S.; Huang, W.B.; Kuo, Y.H.; Horng, M.F. Joint robustness and security enhancement for feature-based image watermarking using invariant feature regions. Signal Process. 2012, 92, 1431–1445. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, X.; Qin, C.; Yang, C.; Luo, X. Dither modulation based adaptive steganography resisting jpeg compression and statistic detection. Multimed. Tools Appl. 2018, 77, 17913–17935. [Google Scholar] [CrossRef]
- Tahmasbi, A.; Saki, F.; Shokouhi, S.B. An effective breast mass diagnosis system using zernike moments. In Proceedings of the 2010 17th Iranian Conference of Biomedical Engineering (ICBME), Isfahan, Iran, 3–4 November 2010; pp. 1–4. [Google Scholar]
- Bas, P.; Filler, T.; Pevnỳ, T. “Break our steganographic system” The ins and outs of organizing BOSS. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 2011; pp. 59–70. [Google Scholar]
- Filler, T.; Judas, J.; Fridrich, J. Minimizing additive distortion in steganography using syndrome-trellis codes. IEEE Trans. Inf. Forensics Secur. 2011, 6, 920–935. [Google Scholar] [CrossRef]
- Pevny, T.; Fridrich, J. Merging Markov and DCT features for multi-class JPEG steganalysis. In Proceedings of the Electronic Imaging 2007, San Jose, CA, USA, 28 January–1 February 2007; p. 650503. [Google Scholar]
- Kodovskỳ, J.; Fridrich, J. Steganalysis of JPEG images using rich models. In Proceedings of the IS&T/SPIE Electronic Imaging, Burlingame, CA, USA, 22–26 January 2012; p. 83030A. [Google Scholar]
- Kodovsky, J.; Fridrich, J.; Holub, V. Ensemble classifiers for steganalysis of digital media. IEEE Trans. Inf. Forensics Secur. 2011, 7, 432–444. [Google Scholar] [CrossRef]





| Cover Image | Steganography Algorithm | Attack Process | ||
|---|---|---|---|---|
| JPEG Compression | Steganalysis | |||
| Image source | BOSSbase 1.01 | DMCSS | 75 85 95 | PSNR CCPEV CCJRM |
| Image size | 512 × 512 | DCRAS | ||
| Number of images | 10,000 | FRAS | ||
| Image format | JPEG | DMAS | ||
| Quality factor | 75, 85, 95 | TCM | ||
| Payload | 0.01 to 0.1 | MCCI | ||
| Quality Factor | 75 | 85 | 95 | |
|---|---|---|---|---|
| Method | ||||
| DMCSS | 41,529 | 28,748 | 31,525 | |
| TCM | 33,387 | 33,362 | 33,440 | |
| MCCI | 41,592 | 56,206 | 98,065 | |
| Method | DMCSS | TCM | MCCI | |
|---|---|---|---|---|
| Quality Factor | ||||
| 75 | 46.8188 | 56.6977 | 57.4343 | |
| 85 | 42.7146 | 56.6986 | 59.2747 | |
| 95 | 38.5466 | 56.6959 | 62.6871 | |
| Quality Factor | Methods | Payloads | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.08 | 0.1 | ||
| QF = 75 | DMCSS | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| TCM | 9.983 | 9.986 | 9.984 | 9.983 | 9.980 | 9.981 | 9.982 | 9.983 | 9.981 | 9.980 | |
| MCCI | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| QF = 85 | DMCSS | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| TCM | 9.973 | 9.971 | 9.973 | 9.970 | 9.965 | 9.963 | 9.962 | 9.960 | 9.959 | 9.958 | |
| MCCI | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| QF = 95 | DMCSS | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| TCM | 9.923 | 9.920 | 9.914 | 9.917 | 9.913 | 9.906 | 9.905 | 9.903 | 9.897 | 9.895 | |
| MCCI | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| Methods | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.1 |
|---|---|---|---|---|---|---|---|---|---|---|
| MCCI | 0.5001 | 0.4997 | 0.4998 | 0.5002 | 0.4997 | 0.5001 | 0.4999 | 0.5001 | 0.5001 | 0.4999 |
| DMCSS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Method | DMCSS | MCCI | TCM | J-UNIWRD | UERD | |
|---|---|---|---|---|---|---|
| Results | ||||||
| 50/50 | 0/50 | 0/50 | 0/50 | 0/50 | ||
| 0 | 0.3537 | 0.5013 | 0.4593 | 0.4600 | ||
| Method | DMCSS | MCCI | TCM | J-UNIWRD | UERD | |
|---|---|---|---|---|---|---|
| Results | ||||||
| 50/50 | 0/50 | fail | 0/50 | 0/50 | ||
| 0 | 0.4226 | fail | 0.4991 | 0.4993 | ||
| Method | DMCSS | MCCI | TCM | J-UNIWRD | UERD | |
|---|---|---|---|---|---|---|
| Results | ||||||
| 50/50 | 50/50 | 50/50 | 50/50 | 50/50 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| Method | DMCSS | MCCI | TCM | J-UNIWRD | UERD | |
|---|---|---|---|---|---|---|
| Results | ||||||
| 50/50 | 0/50 | 0/50 | 0/50 | 0/50 | ||
| 0 | 0.4807 | 0.5008 | 0.4977 | 0.4979 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zheng, N.; Xu, M. A Compression Resistant Steganography Based on Differential Manchester Code. Symmetry 2021, 13, 165. https://doi.org/10.3390/sym13020165
Wang S, Zheng N, Xu M. A Compression Resistant Steganography Based on Differential Manchester Code. Symmetry. 2021; 13(2):165. https://doi.org/10.3390/sym13020165
Chicago/Turabian StyleWang, Shuai, Ning Zheng, and Ming Xu. 2021. "A Compression Resistant Steganography Based on Differential Manchester Code" Symmetry 13, no. 2: 165. https://doi.org/10.3390/sym13020165
APA StyleWang, S., Zheng, N., & Xu, M. (2021). A Compression Resistant Steganography Based on Differential Manchester Code. Symmetry, 13(2), 165. https://doi.org/10.3390/sym13020165






