Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity
Abstract
:1. Introduction
2. An Overview of Vieta–Lucas Functions
The Shifted VL Polynomials
3. The VL-Collocation Approach
4. -Error Bound and Error Analysis
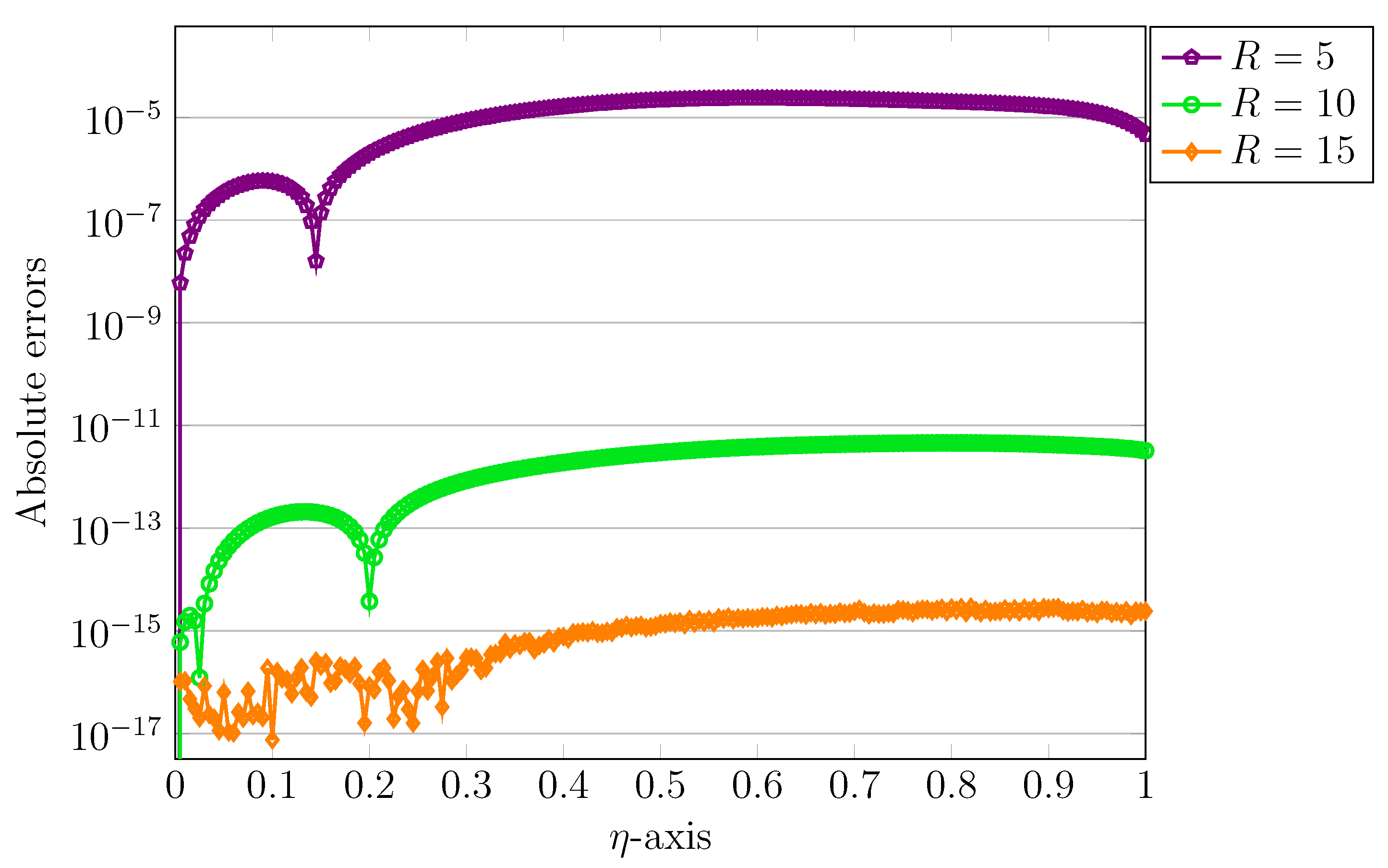
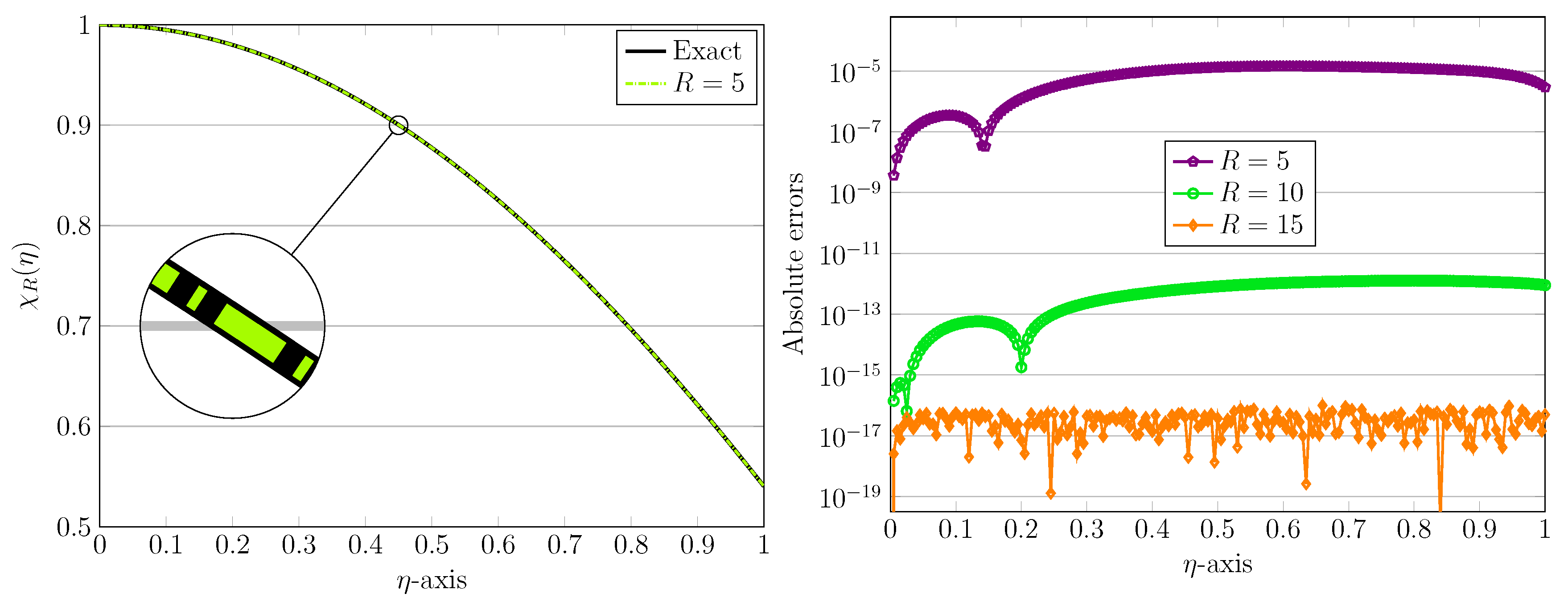
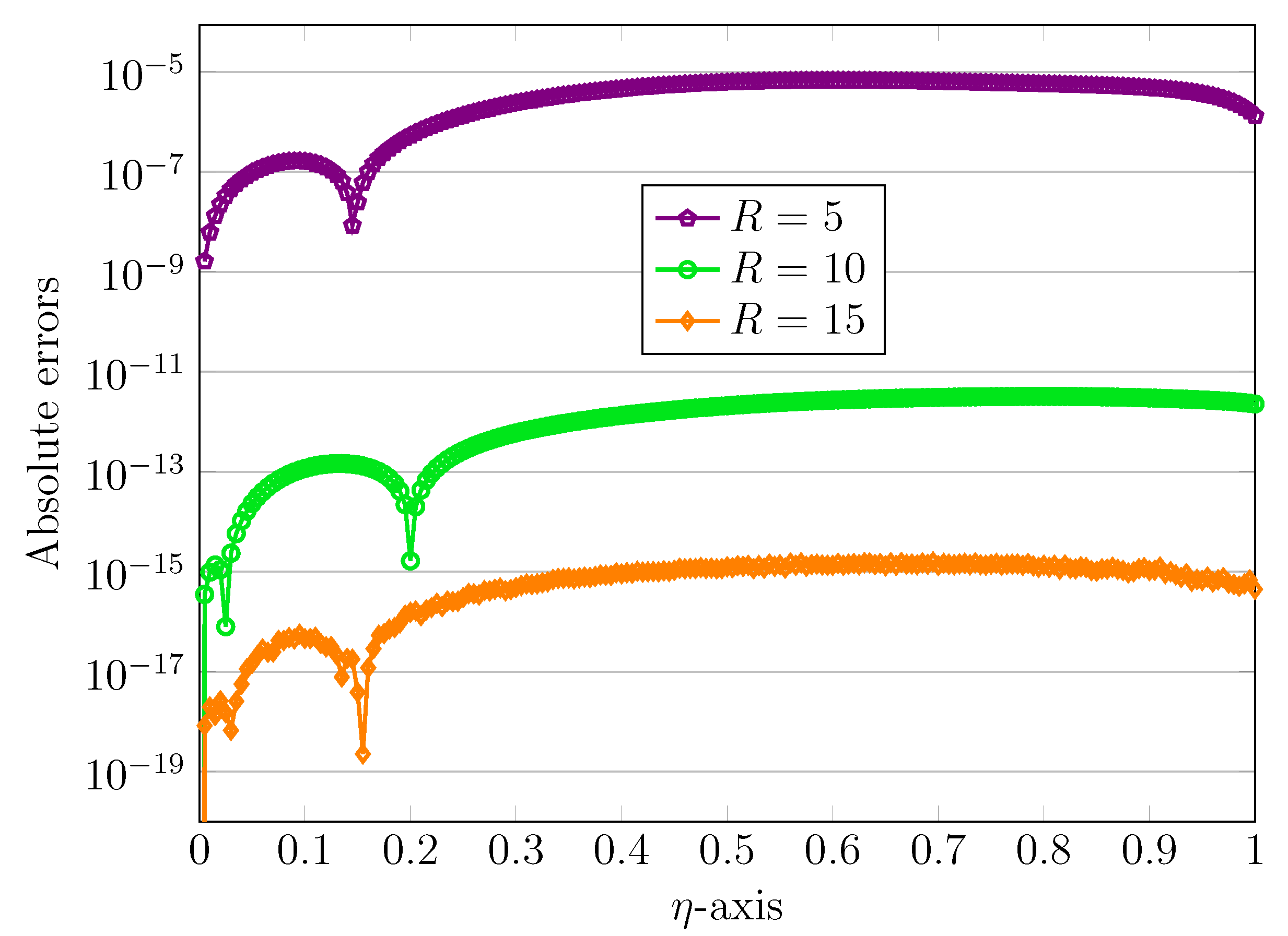
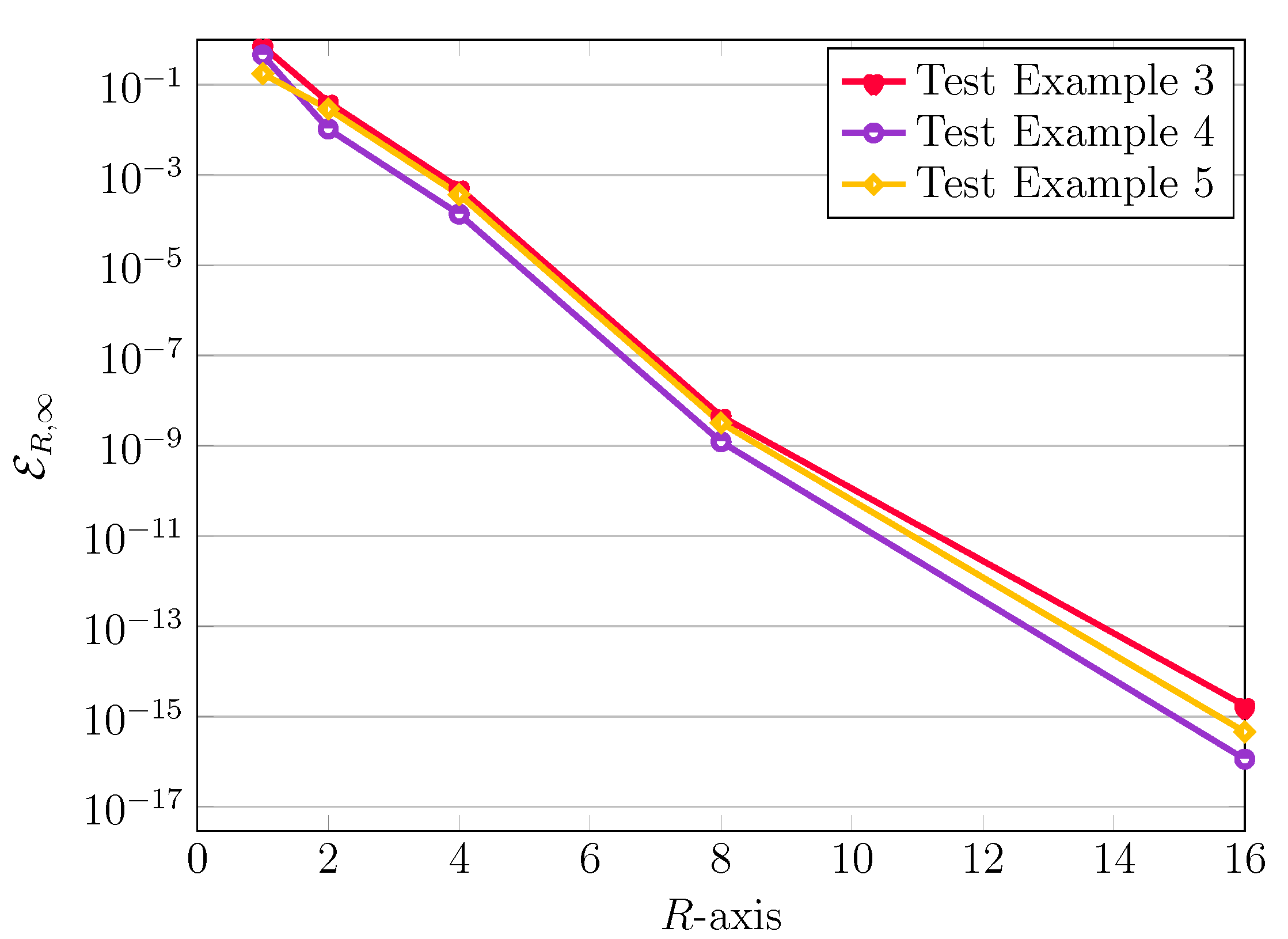
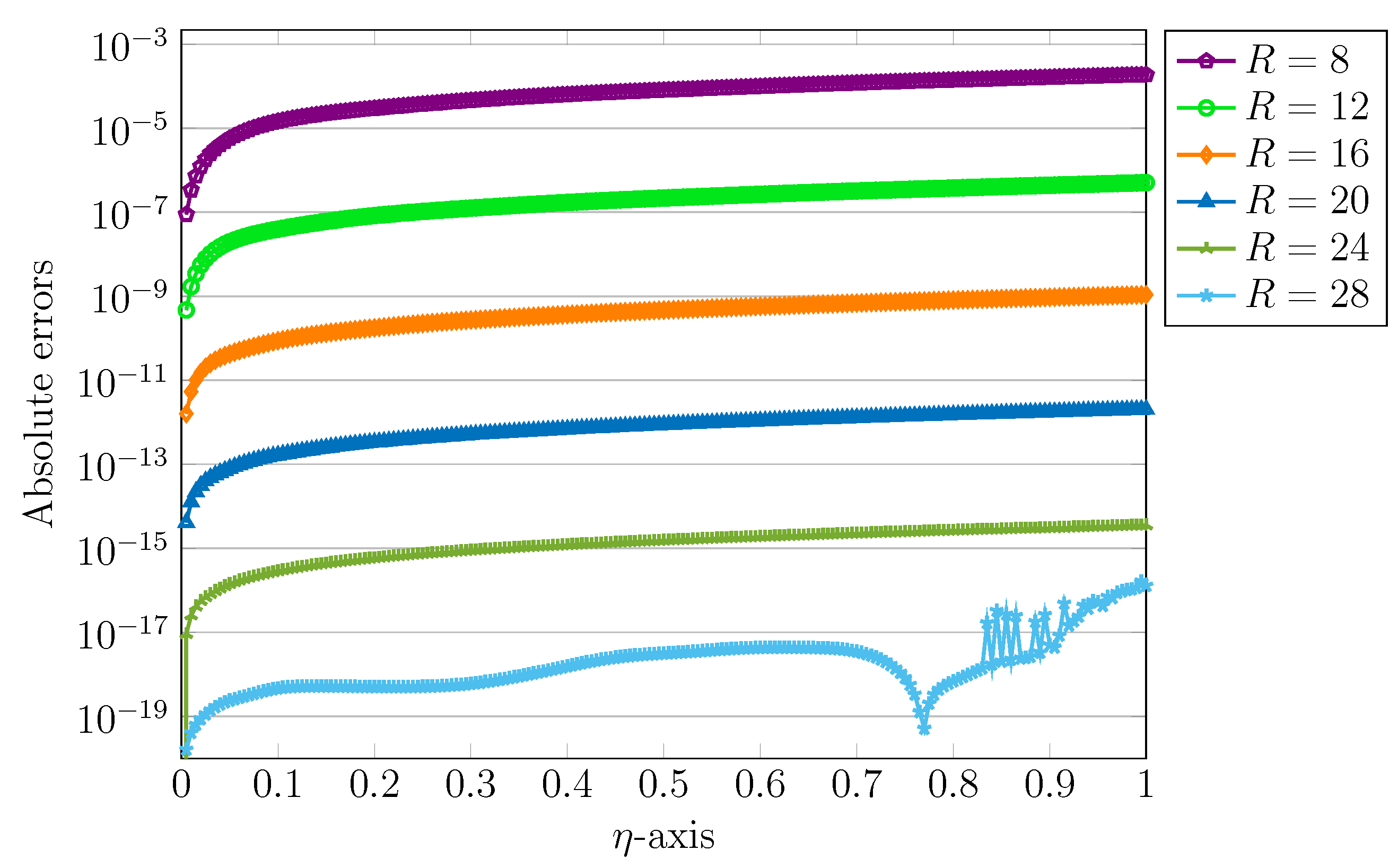
5. Numerical Test Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yüzbaşı, Ş.; Karaçyır, M. A Galerkin-like approach to solve multi-pantograph type delay differential equations. Filomat 2018, 32, 409–422. [Google Scholar] [CrossRef]
- Adel, W.; Zulqurnain, S. Solving a new design of nonlinear second-order Lane-Emden pantograph delay differential model via Bernoulli collocation method. Eur. Phys. J. Plus 2020, 135, 427. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. An efficient approximation technique applied to a non-linear Lane-Emden pantograph delay differential model. Appl. Math. Comput. 2021, 401, 126123. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Shampine, L.F.; Gahinet, P. Delay-differential-algebraic equations in control theory. Appl. Numer. Math. 2006, 56, 574–578. [Google Scholar] [CrossRef]
- Campbell, S.A. Time delays in neural systems. In Handbook of Brain Connectivity; Springer: Berlin/Heidelberg, Germany, 2007; pp. 65–90. [Google Scholar]
- Culshaw, R.V.; Ruan, S. A delay-differential model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Just, W.; Bernard, T.; Ostheimer, M.; Reibold, E.; Benner, H. Mechanism of time-delayed feedback control. Phys. Rev. Lett. 1997, 78, 203–206. [Google Scholar] [CrossRef] [Green Version]
- Rossetti, M.; Bardella, P.; Montrosset, I. Modeling passive mode-locking in quantum dot lasers: A comparison between a finite-difference traveling-wave model and a delayed differential equation approach. IEEE J. Quant. Electron. 2011, 47, 569–576. [Google Scholar] [CrossRef]
- Battisti, D.S. On the role of off-equatorial oceanic Rossby waves during ENSO. J. Phys. Oceanogr. 1989, 19, 551–559. [Google Scholar] [CrossRef]
- Forde, J.E. Delay Differential Equation Models in Mathematical Biology. Ph.D. Dissertation, University of Michigan, Ann Arbor, Michigan, 2005. [Google Scholar]
- Shampine, L.F.; Thompson, L. Numerical Solution of Delay Differential Equations. In Delay Differential Equations; Springer: Boston, MA, USA, 2009; pp. 1–27. [Google Scholar]
- Aiello, W.G.; Freedman, H.; Wu, J. Analysis of a model representing stage-structured population growth with state-dependent time delay. SIAM J. Appl. Math. 1992, 52, 855–869. [Google Scholar] [CrossRef]
- Ockendon, J.R.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A 1971, 322, 447–468. [Google Scholar]
- Spiridonov, V. Universal superpositions of coherent states and self-similar potentials. Phys. Rev. A 1995, 52, 1909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunt, B.V.; Wake, G.C. A Mellin transform solution to a second-order pantograph equation with linear dispersion arising in a cell growth model. Eur. J. Appl. Math. 2011, 22, 151–168. [Google Scholar] [CrossRef]
- Wake, G.; Cooper, S.; Kim, H.; Van-Brunt, B. Functional differential equations for cell-growth models with dispersion. Commun. Appl. Anal. 2000, 4, 561–574. [Google Scholar]
- Du, P.; Geng, F. A new method of solving singular multi-pantograph delay differential equation in reproducing kernel space. Appl. Math. Sci. 2008, 2, 1299–1305. [Google Scholar]
- Sabir, Z.; Baleanu, D.; Raja, M.A.Z.; Guirao, J.L. Design of neuro-swarming heuristic solver for multi-pantograph singular delay differential equation. Fractals 2021, 29, 2140022-49. [Google Scholar] [CrossRef]
- Mosavi, A.; Shokri, M.; Mansor, Z.; Qasem, S.N.; Band, S.S.; Mohammadzadeh, A. Machine learning for modeling the singular multi-pantograph equations. Entropy 2020, 22, 1041. [Google Scholar] [CrossRef]
- Yüzbaşı, Ş.; Sezer, M. Shifted Legendre approximation with the residual correction to solve pantograph-delay type differential equations. Appl. Math. Model. 2015, 39, 6529–6542. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A novel matrix technique for multi-order pantograph differential equations of fractional order. Proc. Roy. Soc. Lond. Ser. A Math. Phys. Engrg. Sci. 2021, 477, 2021031. [Google Scholar] [CrossRef]
- Yüzbaşı, Ş.; Ismailov, N. A Taylor operation method for solutions of generalized pantograph type delay differential equations. Turk. J. Math. 2018, 42, 395–406. [Google Scholar] [CrossRef]
- Bahgat, M.S. Approximate analytical solution of the linear and nonlinear multi-pantograph delay differential equations. Phys. Script. 2020, 95, 055219. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Baleanu, D.; Hafez, R.M. A new Jacobi rational-Gauss collocation method for numerical solution of generalized pantograph equations. Appl. Numer. Math. 2014, 77, 43–54. [Google Scholar] [CrossRef]
- Li, D.; Liu, M.Z. Runge-Kutta methods for the multi-pantograph delay equation. Appl. Math. Comput. 2005, 163, 383–395. [Google Scholar] [CrossRef]
- Javadi, S.; Babolian, E.; Taheri, Z. Solving generalized pantograph equations by shifted orthonormal Bernstein polynomials. J. Comput. Appl. Math. 2016, 303, 1–14. [Google Scholar] [CrossRef]
- Yousefi, S.A.; Noei-Khorshidi, M.; Lotfi, A. Convergence analysis of least squares-Epsilon-Ritz algorithm for solving a general class of pantograph equations. Kragujevac J. Math. 2018, 42, 431–439. [Google Scholar] [CrossRef]
- Izadi, M.; Afshar, M. Solving the Basset equation via Chebyshev collocation and LDG methods. J. Math. Model. 2021, 9, 61–79. [Google Scholar]
- Babaei, A.; Jafari, H.; Banihashemi, S. A collocation approach for solving time-fractional stochastic heat equation driven by an additive noise. Symmetry 2020, 12, 904. [Google Scholar] [CrossRef]
- Izadi, M. Fractional polynomial approximations to the solution of fractional Riccati equation. Punjab Univ. J. Math. 2019, 51, 123–141. [Google Scholar]
- Izadi, M.; Srivastava, H.M. Generalized Bessel quasilinearlization technique applied to Bratu and Lane-Emden type equations of arbitrary order. Fractal Fract. 2021, 5, 179. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbası, Ş.; Cattani, C. Approximating solutions to fractional-order Bagley-Torvik equation via generalized Bessel polynomial on large domains. Ric. Mat. 2021. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Youssri, Y.H. Two spectral Legendre’s derivative algorithms for Lane-Emden, Bratu equations, and singular perturbed problems. Appl. Numer. Math. 2021, 169, 243–255. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbası, Ş.; Noeiaghdam, S. Approximating solutions of non-linear Troesch’s problem via an efficient quasi-linearization Bessel approach. Mathematics 2021, 9, 1841. [Google Scholar] [CrossRef]
- Horadam, A.F. Vieta polynomials. Fibonacci Quart. 2002, 40, 223–232. [Google Scholar]
- Agarwal, P.; El-Sayed, A.A. Vieta-Lucas polynomials for solving a fractional-order mathematical physics model. Adv. Differ. Equ. 2020, 2020, 626. [Google Scholar] [CrossRef]
- Yüzbaşı, Ş.; Gok, E.; Sezer, M. Residual correction of the Hermite polynomial solutions of the generalized pantograph equations. New Trends Math. Sci. 2015, 3, 118–125. [Google Scholar]
| ANN-PSO-AS [19] | ||||||||
|---|---|---|---|---|---|---|---|---|
| MED | Min | Mean | SI-R | |||||
| ANN-PSO-AS [19] | ||||||||
|---|---|---|---|---|---|---|---|---|
| MED | Min | Mean | SI-R | |||||
| ANN-PSO-AS [19] | ||||||||
|---|---|---|---|---|---|---|---|---|
| MED | Min | Mean | SI-R | |||||
| Example 3 | Example 4 | Example 5 | ||||
|---|---|---|---|---|---|---|
| R | NOC | NOC | NOC | |||
| 1 | − | − | − | |||
| 2 | ||||||
| 4 | ||||||
| 8 | ||||||
| 16 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izadi, M.; Yüzbaşı, Ş.; Ansari, K.J. Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry 2021, 13, 2370. https://doi.org/10.3390/sym13122370
Izadi M, Yüzbaşı Ş, Ansari KJ. Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry. 2021; 13(12):2370. https://doi.org/10.3390/sym13122370
Chicago/Turabian StyleIzadi, Mohammad, Şuayip Yüzbaşı, and Khursheed J. Ansari. 2021. "Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity" Symmetry 13, no. 12: 2370. https://doi.org/10.3390/sym13122370
APA StyleIzadi, M., Yüzbaşı, Ş., & Ansari, K. J. (2021). Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry, 13(12), 2370. https://doi.org/10.3390/sym13122370







