Abstract
A new population of correlative and switchable 4D hyperchaotic systems and their switch-synchronization are investigated. First, the switched system with the self-contained subsystems which show some symmetry are constructed. The Lyapunov exponent spectrums and Lyapunov dimensions are displayed to indicate the existence of hyperchaos, and the complex dynamical properties are discussed. Second, its real circuit implement is exhibited for application, and the switching with the flexible and diverse operation assembled can be accomplished randomly by using system selector. Third, nonlinear control strategies are presented to ensure the synchronization stability of the switched system. Simulations are displayed to verify the effectiveness of the control.
1. Introduction
Switched systems consisting of a population of continuous or discrete-time subsystems with certain switching rules are important. They are special classes of hybrid systems. As they exhibit many complicated phenomena and are ubiquitous in different fields such as chemical processes [1], transportation systems [2], biology systems [3], control systems [4], communication networks [5] and so on, especially in secure communication, they have been interesting subjects on the wide applications of modeling many practical problems. The studies on construction, implement and synchronization of the switched system have wide application prospect and attract more and more attention in recent years.
The dynamical characteristics of the subsystems and the switching between these multiple systems are two important factors that influence the performance of switched system. From one point of view, because chaotic systems have complex dynamical behaviors such as initial value sensitivity, chaos attractors, internal randomness, they are unpredictable, noise-like and are always applied to generate chaos signals in the process of secure communication in the past decades. With the development of chaos theory and technology, it is found that hyperchaotic system has at least two positive Lyapunov exponents in general, that is to say, the hyperchaotic system dynamics expand in more than one direction so that it usually possesses more complex and richer dynamical behaviors than chaotic system has, which means the security of the messages to be transmitted in secure communication can be enhanced. In addition, the circuit implement of hyperchaotic system is feasible in practice [6,7,8,9]. So hyperchaotic system can be used as subsystem components of the switched system to enhance complexity. From another point of view, switched system is changed by a switching rule in which the discrete dynamics of the switching function is neglected [10]. The rule dictates the sequence in which the subsystems are switched according to the corresponding active time. It can select drive-response systems freely, transmit diverse signals flexibly and improve the security of communication [11]. In comparison with synchronization between general chaotic slave (response) system and master (drive) system which was first introduced and verified in the electric current experiment by Pecora and Carroll [12], chaos synchronization of switched systems is challengeable if switching laws are unknown. As far as we know, the established switched systems in existing literatures mainly involve two parts, on the one hand, subsystems can be set as normal systems, chaotic systems with integer or fractional order, hyperchaotic systems with integer or fractional order, on the other hand, switching rule can be set as a law independent of the system or in the expressions of the system. Unfortunately, there exist few switched systems with complex dynamics and good switching rules, which can also be realized easily.
In addition, based on existing chaos synchronization methods such as linear and nonlinear feedback control [13,14], control [15], time delayed feedback control [16], backstepping control [17,18], adaptive sliding mode control, [7,19], etc., giving suitable synchronization strategy and finding sufficient conditions on synchronization stability under arbitrary switching are usually concerned as stability analysis problems of switched systems. In [5], synchronization of switched system is considered by output feedback control, together with security analysis. In [11], synchronization of identical switched chaotic systems is explored according to Lyapunov method and bilinear matrix inequalities (BMIs). In [20], the stability of autonomous dynamical switched systems is investigated by using multiple Lyapunov functions. In [21], multi-switching synchronization involving nonidentical chaotic systems is discussed, however, the switching law was not given. However, there are few relative jobs on chaos synchronization of switched system as far as we know.
Motivated by the two aspects, we first propose a switched system consisting of a new population of switchable 4D hyperchaotic systems, which are obtained by adding a new state to the following 3D chaotic system in [22]
with real parameters. These subsystems have common parameters and different nonlinear cross-product or quadratic terms, which show some symmetry, and the switching between two of them can be realized by a certain suitable switching rule. Second, the dynamical characteristics are demonstrated, such as the types of equilibrium points, the phase diagrams of chaotic attractors and Lyapunov exponents, and the circuit for practical application is designed to integrate the function of these multiple systems. Third, the switchable nonlinear feedback controllers with simple structures are given, and sufficient stability criteria to chaos synchronization of the corresponding controlled switched system are obtained. Finally, numerical simulations are provided to show the effectiveness and feasibility. In comparison with existing literatures, the model has the following advantages:
- (1)
- The subsystems are hyperchaotic in a wide parameter range, and they are correlative so that the circuit implement is easier to established. Moreover, the hyperchaotic characteristics enhance the safety of information transmission.
- (2)
- The switching rule adopted can be fast accomplished, which makes the actual application of the switched system possible.
- (3)
- The nonlinear controllers are lower-dimensional and they have variable structures and common style, which can be switched in the response system according to the identical switching rule with drive system and are more convenient to implement.
The organizational structure of the article is as follows. In Section 2, the new population of switchable hyperchaotic subsystems are constructed and their dynamical properties are analyzed, together with the circuit implement. In Section 3, sufficient conditions are derived and control strategies are proposed to ensure the synchronization of switched systems based on Lyapunov method, and simulations are also shown. The conclusions are drawn in Section 4 at last.
2. A New Switched System and Its Circuit Implement
A system composed of a new population of correlative and switchable 4D hyperchaotic subsystems and switching rule is proposed. Every subsystem is obtained mainly by modifying the nonlinear terms of 3D chaotic system (1) in [22] and adding a new state feedback variable to it. The expression is described unitedly as follows:
where are constants to be tuned, are state variables, is a linear function and are nonlinear functions which can be set to describe different hyperchaotic subsystems. Aiming at easy circuit implement and convenient switching, we set as nonlinear cross-product or quadratic functions and Q as or , then six different subsystems are listed in Table 1. They show symmetry in system (b), (d), (e), (f) and partial symmetry in system (a) and (c). In additon, systems (b), (d), (e) and (f) are dissipative when , since the divergence of vector field F has the form:

Table 1.
Subsystems with different terms.
The bifurcation versus parameter can illustrate their chaotic characteristics such as the initial value sensitivity. Let , and d vary from 5 to 15, the bifurcation graphs on the evolution of the variable of six subsystems according to parameter d are exhibited in Figure 1. It can be seen that every subsystem appears its bifurcation, ergodicity and pseudo-randomness in the range of parameter d, and they are all chaotic when . Furthermore, because Lyapunov exponents can exhibit initial value sensitivity from another point, which indicate the degree of trajectories separation in distinct directions according to time iteration, Lyapunov exponent spectrums is given in Figure 2. Let and b vary from 0 to 50, the corresponding Lyapunov exponent spectrums for and of the six subsystems versus parameter b are exhibited. It appears the conditions of , and , then two positive Lyapunov exponents with the increase of b, which suggest that the subsystems go through periodic state, chaotic state, and are all hyperchaotic after the value of b which is less than and close to 20. It is noted that the absolute values of two positive Lyapunov exponents are far less than that of the fourth one which is negative, here we only show the first three Lyapunov exponents.
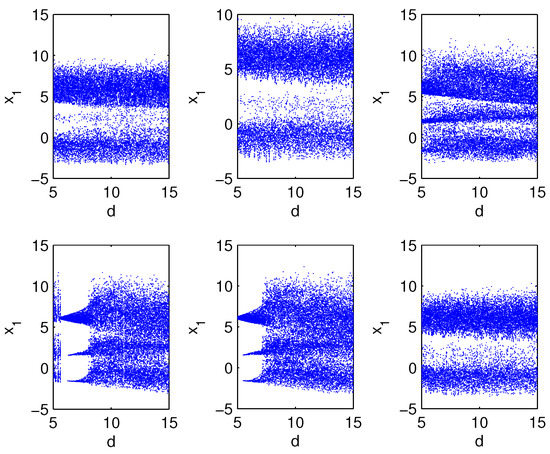
Figure 1.
The bifurcation diagrams on the evolution of the variable y of six subsystems according to parameter d.
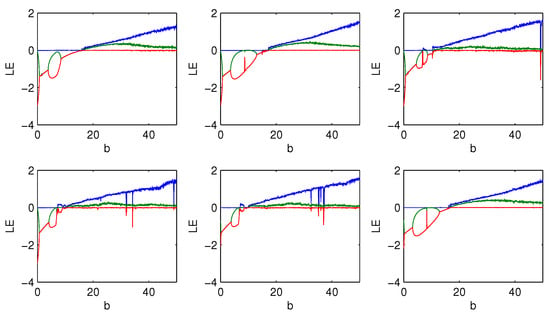
Figure 2.
The Lyapunov exponent spectrums of six subsystems with versus parameter b.
Take subsystem (a) with for example, which is expressed as
When setting and , it has five equilibrium points , . The class of equilibrium points can be determined by calculating the eigenvalues of the corresponding Jacobian matrix J and be listed in Table 2. Furthermore, the system (3) is hyperchaotic by getting calculated Lyapunov Exponents (LE) , respectively, and Lyapunov Dimension (LD) . Figure 3 shows its beautiful hyperchaotic attractor when the parameters are set as above. It exhibit the projections of two-scroll hyperchaotic attractor to 3D space and 2D planes , , and the classical “butterfly wings” appears in phase diagram of .

Table 2.
The eigenvalues of Jacobian matrix and corresponding class of equilibrium points.
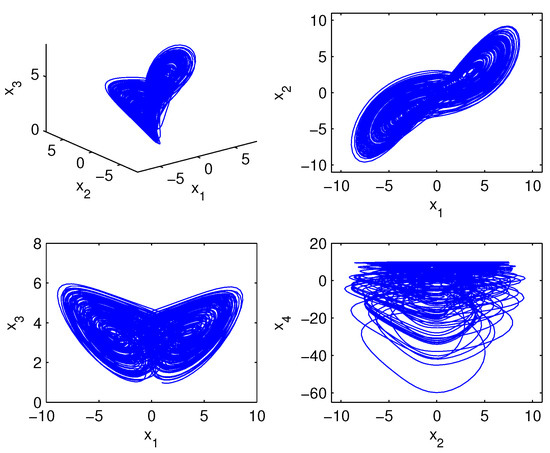
Figure 3.
Hyperchaotic attractor of subsystem (a) marked as system (3) with .
Meanwhile, subsystem (b) has three equilibrium points , and . is also an USNP just like the class in subsystem (a). The eigenvalues of matrix J on and are , so and are both unstable saddle-focus points. Moreover, calculated Lyapunov Exponents (LEs) are and Lyapunov dimension (LD) is . Similarly, the properties of the other four subsystems are exhibited in Table 3.

Table 3.
Properties of the other four subsystems.
It is concluded from the analysis above that the zero equilibria of six subsystems are all USNP and the nonzero equilibria are all USFP. Moreover, all subsystems are hyperchaotic systems, although they have evolution differences led by the nonlinearity, they are so closely linked that they can be realized in a circuit by switching. In the following, a real circuit which can function as a switched system made up of six hyperchaotic subsystems is designed as is shown in Figure 4 according to (2) for the application. The transformation between nonlinear functions of the subsystems can be accomplished by switching, which can be operated easily according to certain rules to realize the functions of six hyperchaotic systems. By choosing proper component parameters and switching rules, the switched system can be implemented conformably. In Figure 4, the operational amplifiers are all LF353, the values of all components dependent on the system parameters are marked, respectively, the unit of every resistance is and the analog multipliers are selected as AD633JN to generate quadratic functions. If the k1 and k2 keys are toggled simultaneously, the nonlinear terms and are switched, also is changed to , so that the switching between subsystem (a) and (d) is accomplished. Other switchings can be implemented in this way too.
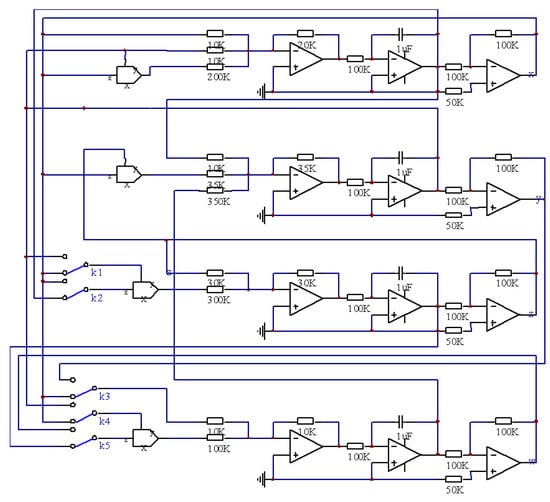
Figure 4.
The circuit graph of the switchable hyperchaotic systems.
3. Chaos Synchronization of the Switched System
Generally, autonomous chaotic systems described by a set of nonlinear continuous-time differential equations can be naturally separated into linear and nonlinear parts as:
where is the state vector, is a coefficient matrix, and is a continuous nonlinear function. So a drive switched system can be expressed as:
where is a signal switched in a finite set , that is to say, can be selected at particular time as for . Similarly, the response switched system can be described as:
where is the state vector of the response system, is the controller, is also a signal switched in K. Hereinafter, the switching rule is assumed to be instantaneously available in real time and priori known to the receiver, and an indicator function is defined as:
with . It follows that for any time t and under any switching rule. Hence, the drive switched system can be rewritten as:
Furthermore, assume the response system is switched according to the same switching rule as the drive switched system (8) and define state error vector as , then we have
where the variable structure of changes according to nonlinear functions of drive system, and the error system has the form:
Theorem 1.
Assume nonlinear functions satisfy Lipschitz condition, namely, there exists constants such that
for any . If there exists a positive definite matrix , a constant matrix , a feedback gain matrix , and a positive constant γ such that
for each , then systems (8) and (9) achieve synchronization under the control
which has variable structure depending on the switching rules.
Proof of Theorem 1.
Construct Lyapunov candidate function , then the derivative of V along the trajectories of (10) is calculated as:
where . Based on (12), . Furthermore, by using Barbalat’s Lemma, that is to say the error system (10) is asymptotically stabilized to zero. Then the switched systems (8) and (9) achieve synchronization under the control strategy (13). □
Theorem 1 ensures that the synchronization of switched systems is achievable. It is noting that in the actual application of secure communication, the driving switched system needs to switch between multiple subsystems to ensure the safety of information transfer, while the response system can be fixed without changing. In this way, the process of information reply and the controller design for specific system can be simplified. Therefore, chaos synchronization between presented driving switched system and a response hyperchaotic system is discussed in the following. If the switched system is in the same mode as the response system, it means one-to-one chaos synchronization, otherwise it means many-to-one chaos synchronization.
Let the driving switched system constitute from the new switchable 4D hyperchaotic system (2) and choose the indicator function as (7), then we have:
thereafter without loss of generality, set a common 4D hyperchaotic system such as subsystem (b) to be response system. The response system is injected by nonlinear feedback control switched according to (7) with the driving switched system every other interval at the same time, and is expressed as:
where , and is a nonlinear feedback control with variable structure and changes according to nonlinear functions of driving switched system, then the error system led by (14) and (15) is obtained as:
where can be changed by toggling switch in Figure 3.
Theorem 2.
Suppose that is the upper bound of for all , and the system parameters are positive constants. For any initial conditions, the driving switched system (14) and the response system (15) are completely synchronized by the nonlinear state feedback controller with the variable structure:
where is an undetermined feedback gain constant and .
Proof of Theorem 2.
Construct a candidate Lyapunov function
It is a positive definite function. By applying the controller (17) to (16), the error dynamics can be expressed as:
Then the time derivative of along the solution of error dynamical system (18) is obtained as:
where
and
When , the symmetric matrix P is positive definite on account of:
and . Then, is negative semi-definite, further based on Barbalat’s Lemma, the error system (18) is asymptotically stable to zero. Consequently, the switched system (14) and hyperchaotic system (15) are in complete synchronization by controlled (17). □
Remark 1.
It can be seen that the controllers (17) with variable structure and common style are lower-dimensional and easy-switched according to identical switching rule to the driving switched system, so it is convenient to the actual application.
Remark 2.
Once the drive switched system is fixed according to switching rule, of the controller (17) are also determined and one-to-one chaos synchronization is realized. It is the special case of the model and usually appears in real applications.
4. Numerical Simulation
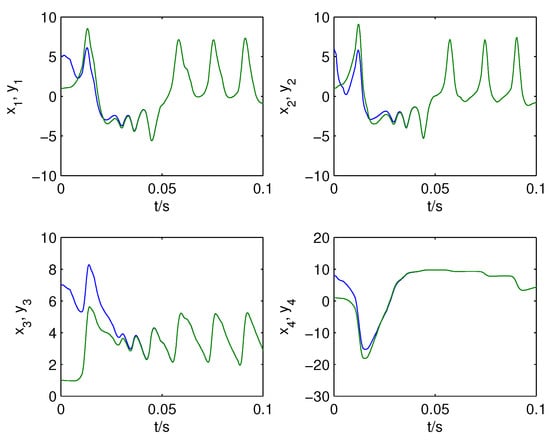
Simulations are illustrated to demonstrate the theory analysis of synchronization between switched system (14) and (15) under nonlinear control (17) with variable structure in this part. First, the system (15) is chosen as response system and the driving switched system is fixed according to the switching rule which means , then the nonlinear functions are as the same as those in system (15). It means synchronization between two identical hyperchaotic subsystems is considered. Let parameters be and , the initial states of the drive-response systems be and , respectively, and feedback control gain constant is selected as . Then the error curves and the state trajectories of drive-response systems are shown in Figure 5 and Figure 6, respectively. It can be seen that the synchronization errors converge to zero asymptotically in a short time and the state trajectories achieve synchronization under the control, which illustrate one-to-one chaos synchronization stability.
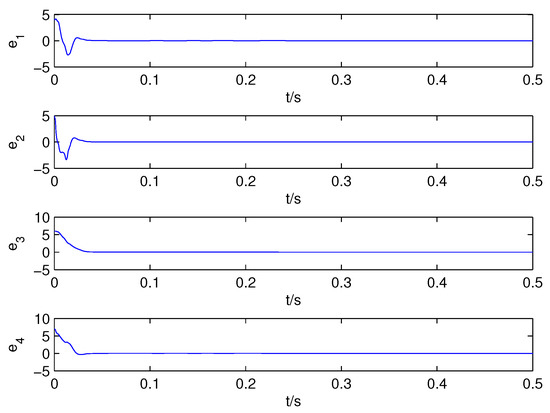
Second, change the driving switched system among hyperchaotic systems (a), (c), (d), (e), (f) by shifting switches every 5 second, and change the initial condition of response system to , then the error curves of response system (15) and the switched system can been observed in Figure 7. The first figure in it shows the synchronization error of subsystem (a) and response system fast converge to zero and there are only small amplitude fluctuations every 5 second. Simultaneously, the synchronization error states are fast stabilized to zero too when subsystem is switched to (c), (d), (e), (f), respectively, which are shown in Figure 7 from left to right. The result of simulations means that many-to-one chaos synchronization is stabilized.
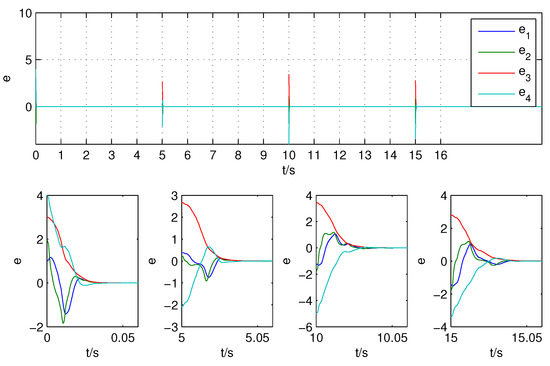
The numerical simulations suggest that both one-to-one and many-to-one chaos synchronization can be achieved by nonlinear feedback control (17) with variable structure. The variety of switching shows the combination flexibility and randomness of the switchable drive subsystem and response system, and also leads to the variety of synchronization signals changing in the transmission channel. So many-to-one synchronization of switched systems can probably enhance the security performance of chaotic secure communication. In addition, there are some elements to be pointed out and listed below to successfully realize the synchronization:
- (1)
- The switching of the driving switched system and control strategies needs to be determined by certain protocols which provide switch time to guarantee the operational coherence. Meanwhile, the construction of intervals totally depends on the protocols.
- (2)
- It requires some time to achieve synchronization after every switching.
5. Conclusions
Chaos synchronization of a switched system consisting of a new population of correlative and switchable hyperchaotic systems is investigated in this paper. First, a family of correlative and switchable 4D hyperchaotic subsystems with some symmetry are derived from an original chaotic system, which are self-contained and independent, closely linked and have rich dynamical characteristics. After that, the circuit implement is shown and the switching can be accomplished randomly by using system selector and the operation is flexible and diversely assembled. Furthermore, sufficient conditions to achieve one-to-one and many-to-one synchronization stability of the presented switched system under newly presented nonlinear control strategies are given based on Lyapunov method and Barbalat’s Lemma. Finally, simulation results demonstrate the theory analysis.
The model has potential application prospect in real life because of the feasibility of its circuit implementation. For example, in actual application of secure communication, the switched system is set as drive system to switch between multiple subsystems which can ensure and enhance the safety of information transmission, while the response system can be fixed without changing so that the process of information reply and the controller design for specific system can be simplified. The information to be transmitted is modulated with the signal of the drive system, and the switch is toggled randomly, so that the transmitted information can be hidden in the signals of different hyperchaotic subsystems. In this way, the safety of information transmission is enhanced.
The future studies will involve in two main aspects:
- (1)
- As the dynamics of the proposed model are not presented completely, more detailed theoretical simulation and investigations are expected in the forthcoming study, such as further bifurcation and stability analysis and so on.
- (2)
- More synchronization problems of the switched system will be considered, such as the adaptive synchronization and so forth.
Author Contributions
Conceptualization, T.W.; methodology, T.W.; software, T.W.; validation, T.W.; formal analysis, N.J.; writing—original draft preparation, N.J.; writing—review and editing, N.J.; supervision, T.W.; funding acquisition, N.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Doctoral Program of Harbin Normal University, China (Grant No. XKB201805).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Putyrski, M.; Schultz, C. Switching heterotrimeric G protein subunits with a chemical dimerizer. Chem. Biol. 2011, 18, 1126–1133. [Google Scholar] [CrossRef] [Green Version]
- Hamdouch, Y.; Florian, M.; Hearn, D.W.; Lawphongpanich, S. Congestion pricing for multi-modal transportation systems. Transport. Res. B-Meth. 2007, 41, 275–291. [Google Scholar] [CrossRef]
- Singh, A.; Hespanha, J.P. Moment closure techniques for stochastic models in population biology. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 4730–4735. [Google Scholar]
- Antsaklis, P.J.; Stiver, J.A.; Lemmon, M. Hybrid system modeling and autonomous control systems. In Hybrid Systems; Volume 736 of Lecture Notes in Computer Science; Springer: New York, NY, USA, 1993; pp. 366–392. [Google Scholar]
- Yu, W.; Cao, J.; Yuan, K. Synchronization of switched system and application in communication. Phys. Lett. A 2008, 372, 4438–4445. [Google Scholar] [CrossRef]
- Qi, G.; Wyk, M.A.V.; Wyk, B.J.V.; Chen, G. A new hyperchaotic system and its circuit implementation. Chaos Solitons Fractals 2009, 40, 2544–2549. [Google Scholar] [CrossRef]
- Singh, S.; Han, S.; Lee, S.M. Adaptive single input sliding mode control for hybrid-synchronization of uncertain hyperchaotic Lu systems. J. Franklin Inst. 2021, 358, 7468–7484. [Google Scholar] [CrossRef]
- Yang, L.B.; Yang, Q.G.; Chen, G.R. Hidden attractors, singularly degenerate heteroclinic orbits, multistability and physical realization of a new 6D hyperchaotic system. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105362. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.B.; Lei, T.F.; Liu, Z.H.; Tao, C.Y. A symmetric controllable hyperchaotic hidden attractor. Symmetry 2020, 12, 550. [Google Scholar] [CrossRef] [Green Version]
- Liberzon, D. Switching in Systems and Control. In Systems & Control: Foundations & Applications; Springer, Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Pan, I.; Das, S.; Routh, A. Towards a global controller design for guaranteed synchronization of switched chaotic systems. Appl. Math. Model. 2015, 39, 2311–2331. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Yassen, M. Controlling chaos and synchronization for new chaotic system using linear feedback control. Chaos Solitons Fractals 2005, 26, 913–920. [Google Scholar] [CrossRef]
- Emad, E.M.; Higazy, M.; Ohood, A.A. A novel strategy for complete and phase robust synchronizations of chaotic nonlinear systems. Symmetry 2021, 12, 1765. [Google Scholar]
- Zhao, Y.; Pang, M.C.; Yu, S.H.; Li, L.L. H∞ finite-time composite anti-disturbance switching control for switched systems. ISA Trans. 2021, 115, 71–78. [Google Scholar] [CrossRef]
- Liao, X.X.; Chen, G.R. Chaos synchronization of general Lur’e systems via time-delay feedback control. Internat. J. Bifur. Chaos 2003, 13, 207–213. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H. Adaptive hybrid projective synchronization of uncertain chaotic systems based on backstepping design. Nonlinear Anal. Real World Appl. 2011, 12, 388–393. [Google Scholar] [CrossRef]
- Shikha, S.; Sandhya, M.; Ahmad, T.A.; Sundarapandian, V.; Nashwa, A.K. Backstepping Control of Nonlinear Dynamical Systems. In Advances in Nonlinear Dynamics and Chaos (ANDC); Academic Press: New York, NY, USA, 2020; pp. 425–447. [Google Scholar]
- Jawaada, W.; Noorani, M.S.M.; Al-sawalha, M.M. Robust active sliding mode anti-synchronization of hyperchaotic systems with uncertainties and external disturbances. Nonlinear Anal. Real World Appl. 2012, 13, 2403–2413. [Google Scholar] [CrossRef]
- Nosov, V.; Meda-Campa, J.A.; Gomez-Mancilla, J.C.; Escobedo-Alva, J.O.; Hernández-García, R.G. Stability analysis for autonomous dynamical switched systems through nonconventional Lyapunov functions. Math. Probl. Eng. 2015, 2015, 12. [Google Scholar] [CrossRef] [Green Version]
- Nitish, P.; Ayub, K.; Dinesh, K. On multi switching compound synchronization of non identical chaotic systems. Chin. J. Phys. 2018, 56, 1656–1666. [Google Scholar]
- Tigan, G.; Opris, D. Analysis of a 3D chaotic system. Chaos Solitons Fractals 2008, 36, 1315–1319. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).