Racetrack Microtron—Pushing the Limits
Abstract
1. Introduction
2. Comparison of Classical and Racetrack Microtrons
2.1. RTM Advantages
2.2. Common Problems of CM and RTM
2.3. RTM Problems
2.3.1. Beam Defocusing and Distortion by the Magnet Fringe Field
2.3.2. Phase Slip
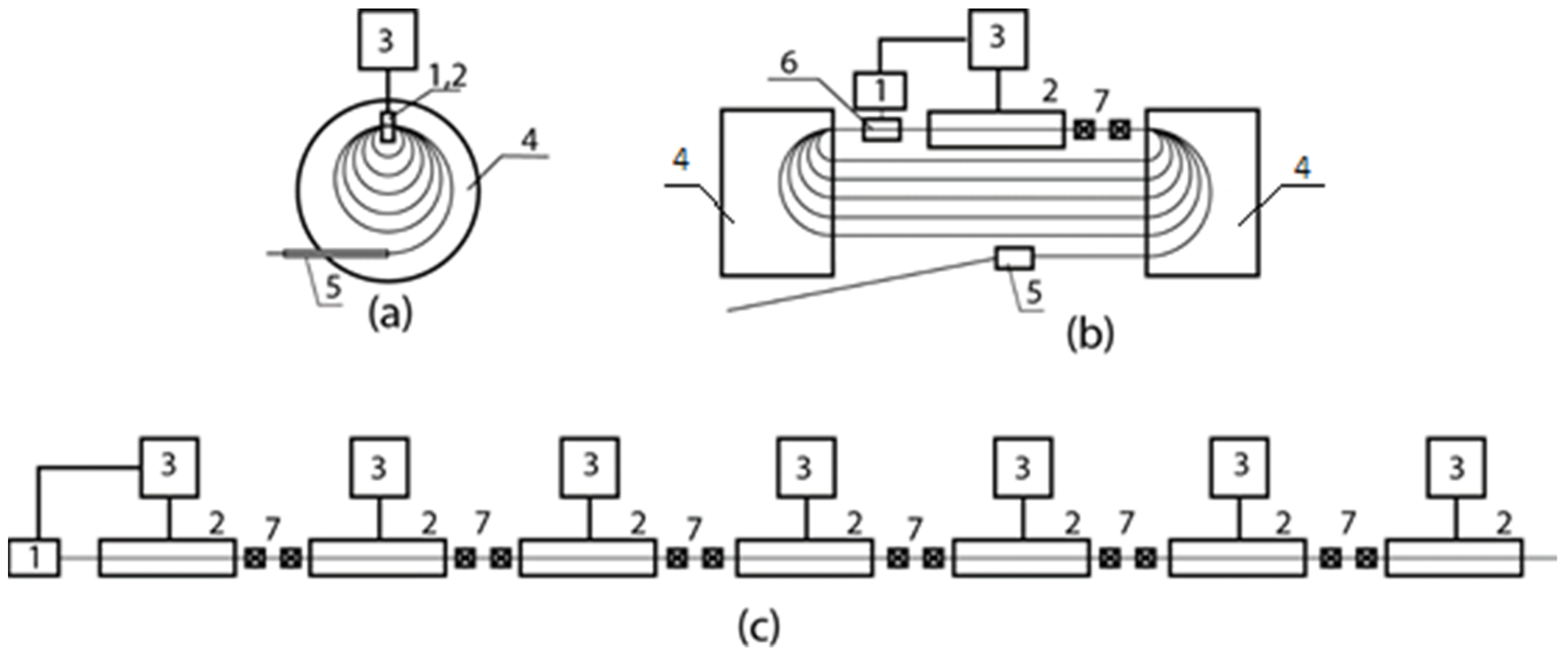
2.3.3. Errors in Magnets Manufacturing and Magnet Poles Positioning
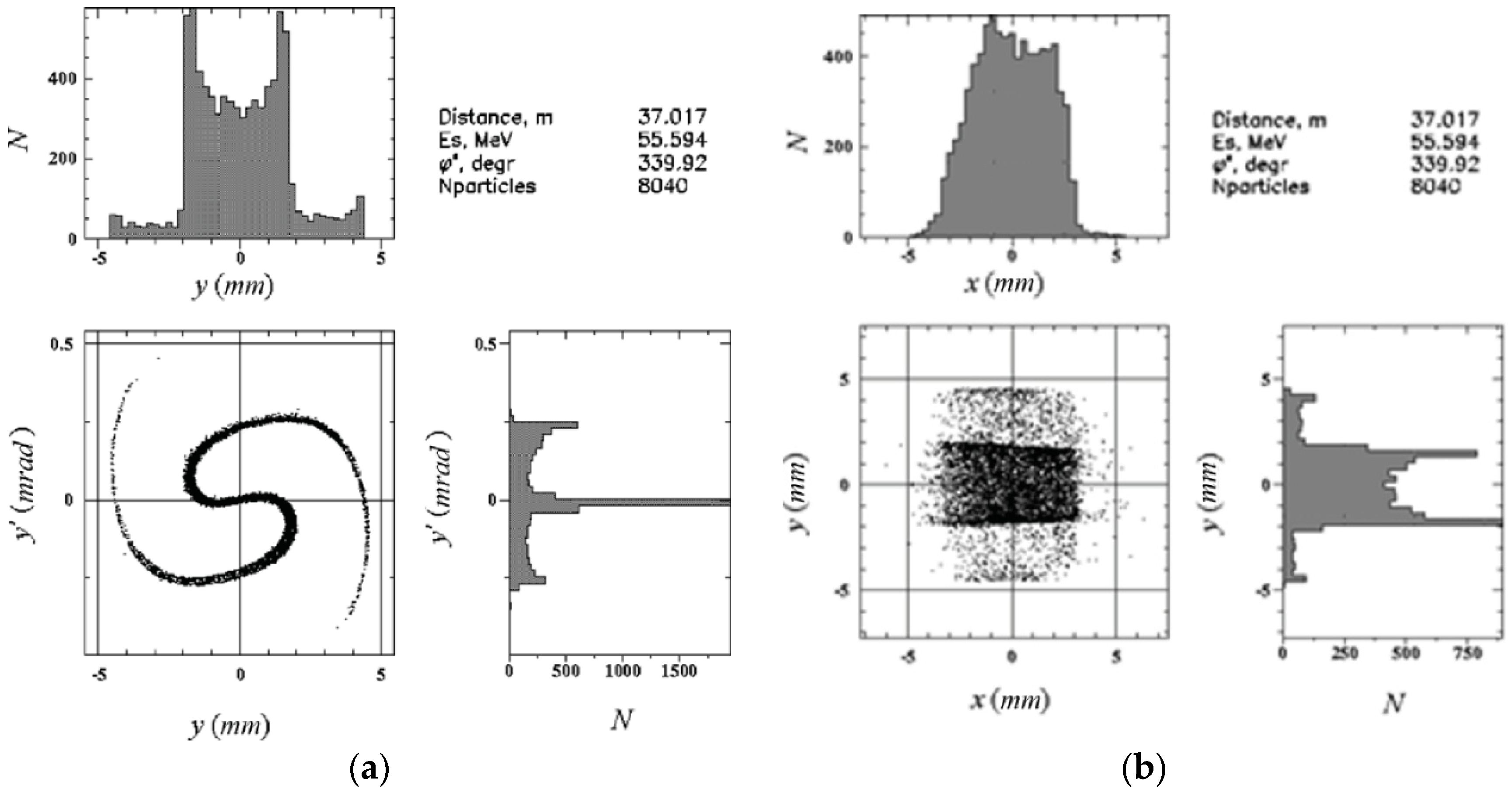
2.3.4. Beam Blow-Up
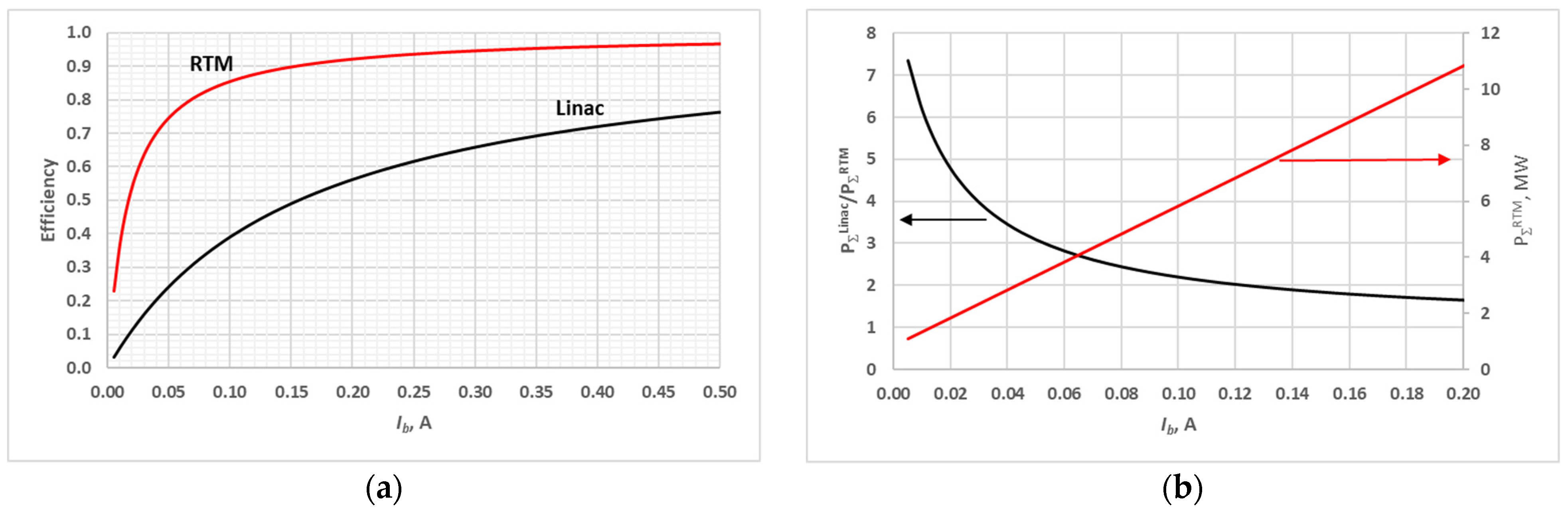
3. Comparison of RTM and LINAC
4. Approaches for Minimizing Beam Current Losses in RTM
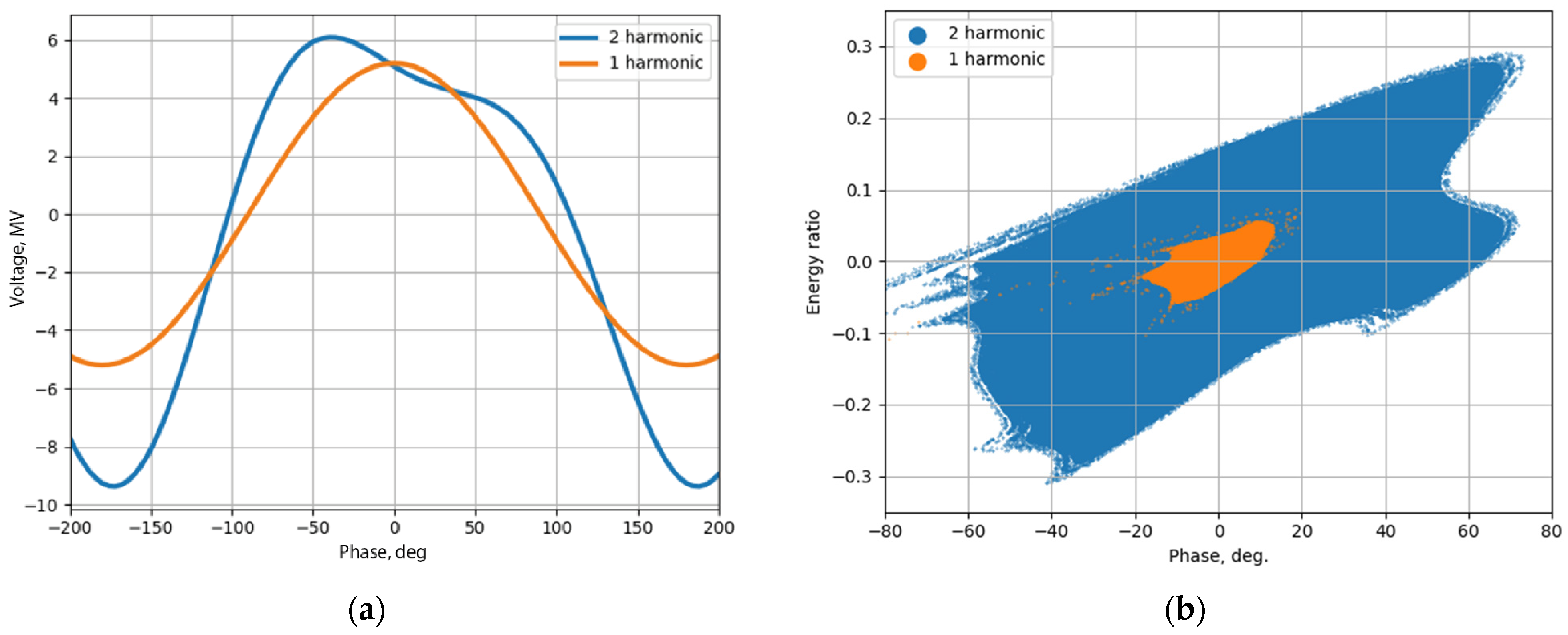
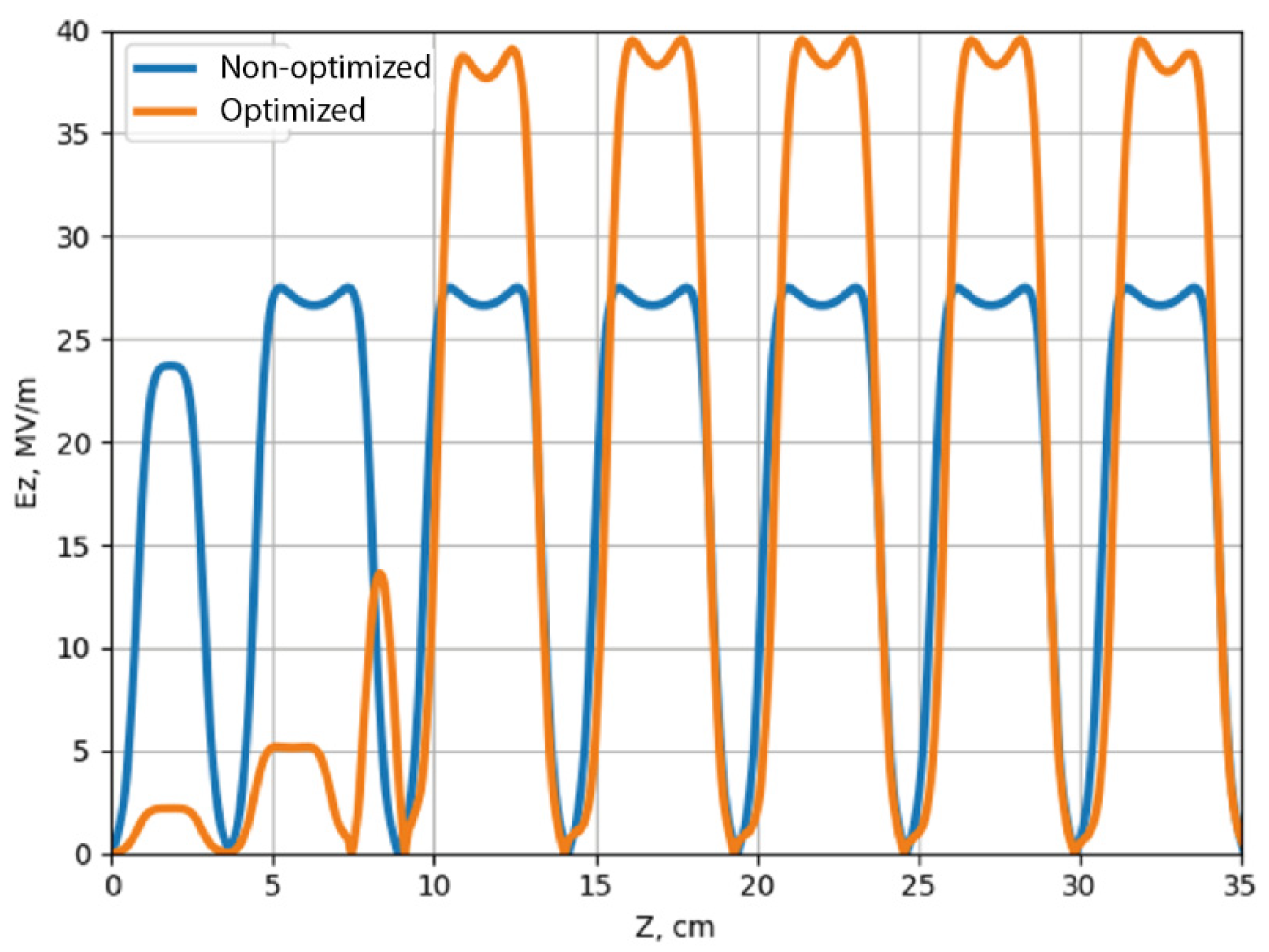
4.1. Increasing the Longitudinal Acceptance of the RTM by Linearizing the Accelerating Field
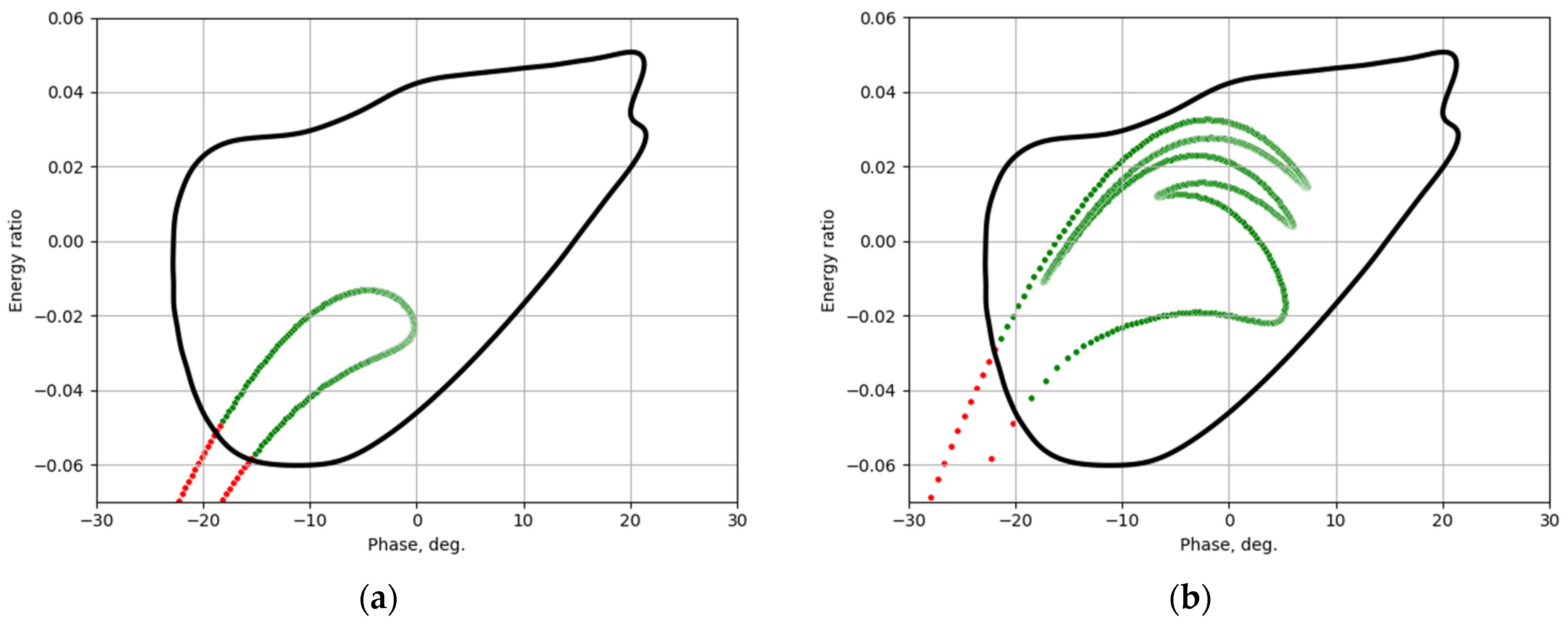
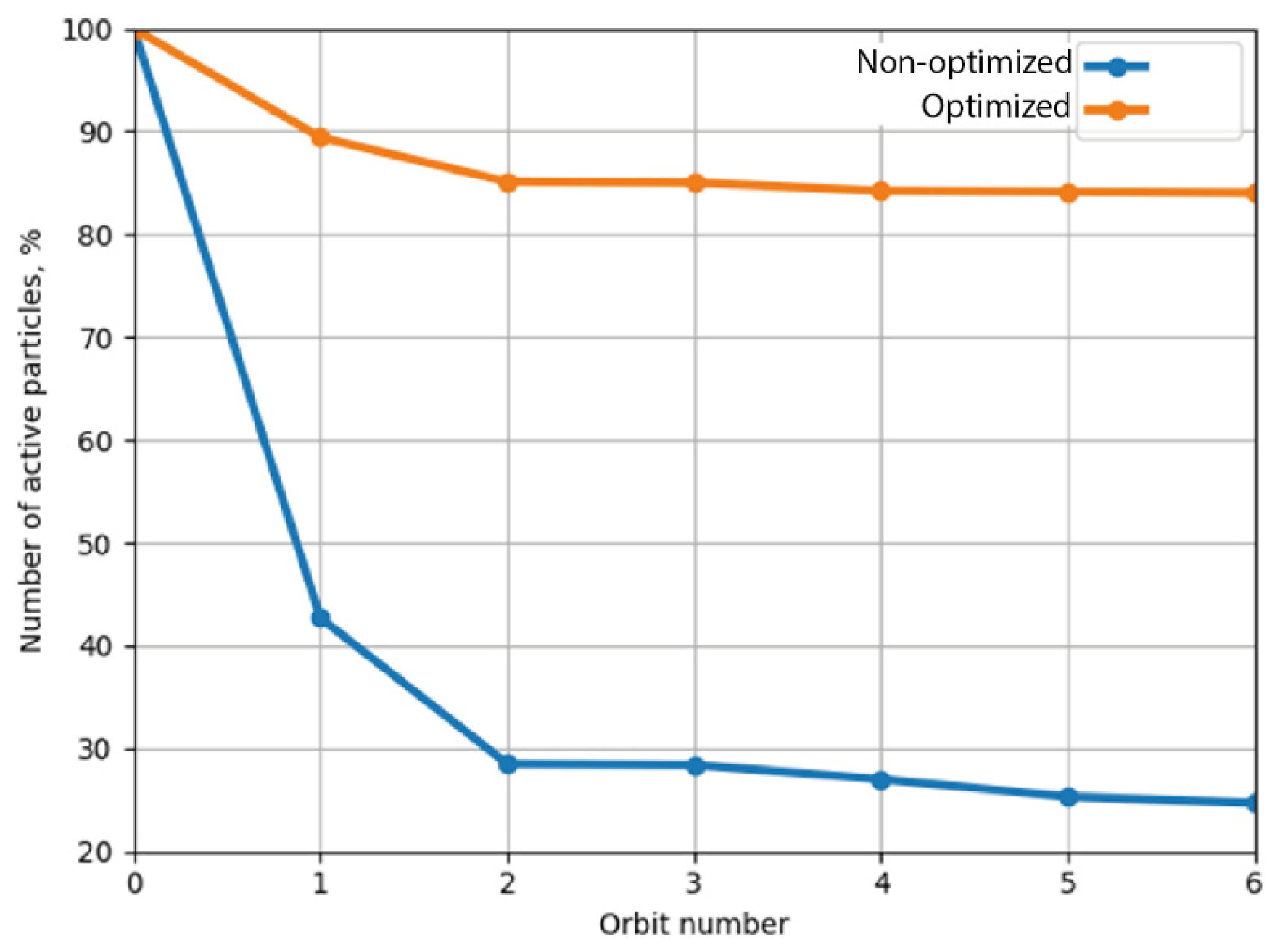
4.2. Matching the Longitudinal Emittance of the Injected Beam with the RTM Acceptance by Optimizing the Initial Part of the Accelerating Structure
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veksler, V.I. A new method of accelerating of relativistic particles. J. Phys. USSR 1945, 9, 153–168. [Google Scholar]
- Schiff, L.I. Production of particle energies beyond 200 MeV. Rev. Sci. Instrum. 1946, 17, 6–14. [Google Scholar] [CrossRef]
- Kapitza, S.; Melekhin, V. The Microtron; Rowe, E.M., Ed.; Harwood Academic Publishers: London, UK, 1978. [Google Scholar]
- Rand, R.E. Recirculating Electron Accelerators; Harwood Academic Publishers: New York, NY, USA, 1984. [Google Scholar]
- Lidbjôrk, P. Microtrons. In Proceedings of the CAS—CERN Accelerator School: 5th General Accelerator Physics Course, Jyväskylä, Finland, 7–18 September 1994. [Google Scholar]
- Jankowiak, A. Microtrons and Recirculators. In Proceedings of the CERN Accelerator School Programme, Zeegse, The Netherlands, 24 May–2 June 2005. [Google Scholar]
- Tsipenyuk, Y.M. Microtron: Development and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2019; 368p. [Google Scholar]
- Herminghaus, H.; Feder, A.; Kaiser, K.; Manz, W.; Schmitt, H. The design of a cascaded 800 MeV normal conducting C.W. race track microtron. Nucl. Instrum. Methods 1976, 138, 1–12. [Google Scholar] [CrossRef]
- Herminghaus, H.; Dreher, B.; Futeneuer, B.; Kaiser, K.H.; Kelliher, M.; Klein, R.; Kreidel, H.J.; Loch, M.; Ludwig-Mertin, U.; Merle, K.; et al. Status Report on the Normal Conducting CW Racetrack Microtron Cascade “MAMI”. IEEE Trans. Nucl. Sci. 1983, 30, 3274–3278. [Google Scholar] [CrossRef]
- Jankowiak, A.; Aulenbacher, K.; Euteneuer, H.; Herr, R.; Jennewein, P.; Kaiser, K.; Kreidel, H.; Ludwig-Mertin, U.; Negrazus, M.; Ratschow, S. Design and Status of the 1.5 GeVHarmonic Double Sided Microtron for MAMI. In Proceedings of the 8th European Particle Accelerator Conference, Paris, France, 3–7 June 2002. [Google Scholar]
- Dehn, M.; Aulenbacher, K.; Heine, R.; Kreidel, H.-J.; Ludwig-Mertin, U.; Jankowiak, A. The mami c accelerator. Eur. Phys. J. Spec. Top. 2011, 198, 19–47. [Google Scholar] [CrossRef]
- Khryachkov, V.A. Current status and prospects of 225Ac production by the photonuclear method at JSC “SSC RF-IPPE”. In Proceedings of the Production of Alpha Emitters and Prospects for Creating RPD on Their Basis, Obninsk, Russia, 22 November 2019; JSC”SSC RF-IPPE”. p. 18. [Google Scholar]
- Takeda, T.; Fujiwara, M.; Kurosawa, M.; Takahashi, N.; Tamura, M.; Kawabata, T.; Fujikawa, Y.; Suzuki, K.; Abe, N.; Kubota, T. 99m Tc production via the (γ, n) reaction on natural Mo. J. Radioanal. Nucl. Chem. 2018, 318, 811–821. [Google Scholar] [CrossRef]
- Fujiwara, M.; Kurosawa, M.; Tamura, M.; Kudomi, N.; Nishimura, M. Medical 15O production via the 16O (γ, n) 15O reaction for blood flow examination. J. Radioanal. Nucl. Chem. 2021, 330, 141–148. [Google Scholar] [CrossRef]
- Shvedunov, V.; Alimov, A.; Chepurnov, A.; Chubarov, O.; Gribov, I.; Ishkhanov, B.; Surma, I.; Tiunov, A. Moscow State University CW race-track microtron status. In Proceedings of the International Conference on Particle Accelerators, Washington, DC, USA, 17–20 May 1993; pp. 2059–2061. [Google Scholar]
- Shvedunov, V.; Barday, R.; Frolov, D.; Gorbachev, V.; Gribov, I.; Knapp, E.; Novikov, G.; Pakhomov, N.; Shvedunov, I.; Skachkov, V. A racetrack microtron with high brightness beams. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 2004, 531, 346–366. [Google Scholar] [CrossRef]
- Shvedunov, V.; Ermakov, A.; Gribov, I.; Knapp, E.; Novikov, G.; Pakhomov, N.; Shvedunov, I.; Skachkov, V.; Sobenin, N.; Trower, W. A 70 Mev racetrack microtron. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 2005, 550, 39–53. [Google Scholar] [CrossRef]
- Ermakov, A.N.; Ishkhanov, B.S.; Kamanin, A.N.; Pakhomov, N.I.; Khankin, V.V.; Shvedunov, V.I.; Shvedunov, N.V.; Zhuravlev, E.E.; Karev, A.I.; Sobenin, N.P. A Multipurpose Pulse Race-Track Microtron with an Energy of 55 MeV. Instrum. Exp. Tech. 2018, 61, 173–191. [Google Scholar] [CrossRef]
- Tiunov, A.; Shvedunov, V.; Surma, I.; Hizanidis, K.; Kalfas, C.; Trikalinos, C.; Tigelis, J. Variants of optics schemes and ac-celerator configurations for the Athens microtron: Preliminary considerations. In Proceedings of the 16th Biennial Particle Accelerator Conference and International Conference on High-Energy Accelerators, Dallas, TX, USA, 1–5 May 1995; pp. 3285–3287. [Google Scholar]
- Kubyshin, Y.A.; Berenguer, J.; Crisol, A.; Gonzalez, X.; Montoro, G.; Rigla, J.P.; Roure, F.; Carrillo, D.; Garcia-Tabares, L.; Toral, F.; et al. Current status of the 12 MeV UPC race-track microtron. In Proceedings of the 23rd Particle Accelerator Conference, Vancouver, BC, Canada, 4–8 May 2009; pp. 2775–2777. [Google Scholar]
- Kolomensky, A.A.; Lebedev, A.N. Theory of Cyclic Accelerators; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Melekhin, V.N. Vertical focusing in a microtron. J. Exp. Theor. Phys. 1962, 42, 821. (In Russian) [Google Scholar]
- Melekhin, V. New considerations concerning the high-frequency focusing of relativistic particles and Panofsky-Wenzel theo-rem. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 1997, 400, 170–172. [Google Scholar] [CrossRef]
- Kapitsa, S.P.; Bykov, V.P.; Melekhin, V.N. Effective high-current microtron. J. Exp. Theor. Phys. 1961, 41, 368. (In Russian) [Google Scholar]
- Melekhin, V.N.; Luganskii, L.B. High-current microtron instability. Sov. Phys.–Tech. Phys. 1971, 15, 1930. [Google Scholar]
- Grishin, V.K.; Sotnikov, M.A.; Shvedunov, V.I. Phase motion in a classical microtron near nonlinear resonances. Moscow Univ. Bull. 1986, 41, 28. [Google Scholar]
- Kubyshin, Y.; Larreal, O.; Ramirez-Ros, R.; Seara, T. Stability of the phase motion in race-track microtrons. Phys. D Nonlinear Phenom. 2017, 349, 12–26. [Google Scholar] [CrossRef][Green Version]
- Kosarev, E.L. Establishment processes and limiting current in the microtron. J. Tech. Phys. 1972, 42, 2239. (In Russian) [Google Scholar]
- Karev, A.I.; Kurakin, V.G. Self-oscillatory mechanism of destruction of an electron beam in a racetrack microtron. Preprint FIAN 1978, 174, 18. [Google Scholar]
- Ermakov, A.; Shvedunov, V. RF-systems and pulsed racetrack microtron current instabilites. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 2005, 550, 82–89. [Google Scholar] [CrossRef]
- Robinson, K.W. Stability of Beam in Radiofrequency System. Available online: https://www.osti.gov/servlets/purl/4075988/ (accessed on 25 September 2021).
- Shvedunov, V.; Euteneuer, H.; Kaiser, K.-H. Bunch space charge limits in an RTM. In Proceedings of the 1997 Particle Accelerator Conference (Cat. No. 97CH36167), Vancouver, BC, Canada, 16 May 1997; pp. 1902–1904. [Google Scholar]
- Nodvick, J.S.; Saxon, D.S. Suppression of Coherent Radiation by Electrons in a Synchrotron. Phys. Rev. 1954, 96, 180–184. [Google Scholar] [CrossRef]
- Babic, H.; Sedlaček, M. A method for stabilizing particle orbits in the race-track microtron. Nucl. Instrum. Methods 1967, 56, 170–172. [Google Scholar] [CrossRef]
- Grishin, V.; Sotnikov, M.; Ishkanov, B.; Shvedunov, V. Computer simulation of phase motion in the CW racetrack microtron. Part. Accel. 1988, 23, 227–237. [Google Scholar]
- Kubyshin, Y.A.; Poseryaev, A.; Shvedunov, V. Longitudinal beam dynamics with phase slip in race-track microtrons. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 2008, 596, 147–156. [Google Scholar] [CrossRef]
- Novikov, G.; Ermakov, A.; Pakhomov, N.; Semyachkin, V.; Shvedunov, V.; Skachkov, V.; Tyurin, S. A permanent magnet electron beam phase-shifter. Nuclear Instruments and Methods in Physics Research Section A. Accel. Spectrometers Detect. Assoc. Equip. 2004, 524, 60–67. [Google Scholar] [CrossRef]
- Vladimirov, I.Y.; Pakhomov, N.I.; Shvedunov, V.I.; Kubyshin, Y.A.; Rigla, J.P.; Zakharov, V.V. End magnets with rare earth permanent magnet material for a compact race-track microtron. Eur. Phys. J. Plus 2014, 129, 1–21. [Google Scholar] [CrossRef]
- Volodin, V.; Hanson, A. On beam blowup in a racetrack microtron. IEEE Trans. Nucl. Sci. 1975, 22, 1194–1196. [Google Scholar] [CrossRef]
- Herminghaus, H.; Euteneuer, H. Beam blowup in race track microtrons. Nucl. Instrum. Methods 1979, 163, 299–308. [Google Scholar] [CrossRef]
- Kraft, G.A.; Bisognano, J.J. Two-Dimensional Simulation of Multipass Beam Breakup. In Proceedings of the 12th Particle Accelerator Conference (PAC’87), Washington, DC, USA, 16–19 March 1987; pp. 1356–1358. [Google Scholar]
- Loew, G. Electron Linac Instabilities. IEEE Trans. Nucl. Sci. 1967, 14, 529–540. [Google Scholar] [CrossRef]
- Blach, N.M. Internal Memorandum of Brookhaven National Laboratory; Brookhaven National Laboratory: Upton, NY, USA, 1949.
- Foldy, L.L. A method for expanding the phase-stable regime in synchronous accelerators. Nuovo Cim. 1961, 19, 1116–1120. [Google Scholar] [CrossRef]
- Rosander, S. Accelerating Particles in the Microtron by Non-Sinusoidal Field; Kungliga Tekniska Hoegskolan: Stockholm, Sweden, 1974. [Google Scholar]
- Rosander, S. Two frequency microtron. Nucl. Instrum. Methods 1967, 56, 154–156. [Google Scholar] [CrossRef]
- Wilson, P.B.; Griffin, J.E. High energy electron linacs; application to storage ring RF systems and linear colliders. AIP Conf. Proc. 1982, 87, 450–555. [Google Scholar] [CrossRef]
- Kubyshin, Y.A.; Gonzalez, X.; Montoro, G.; Carrillo, D.; Garcia-Tabares, L.; Toral, F.; Mathot, S.; Shvedunov, V. RF and ac-celerating structure of 12 MeV UPC race-track microtron. In Proceedings of the 2nd International Conference IPAC 2011, San Sebastian, Spain, 4–9 September 2011; pp. 169–171. [Google Scholar]
- Ovchinnikova, L.; Shvedunov, V. Design of C-band electron linear accelerator for a complex of radiation therapy. In Proceedings of the 29th Linear Accelerator Conference (LINAC2018), Beijing, China, 16–21 September 2018. [Google Scholar]
- Chetverikov, I.; Kalinichenko, M.; Ryabtsov, A.; Zuev, Y.V. Design study of the UELV-10/5-15S accelerating structure. Vopr. At. Nayki I Tekhniki 2001, 5, 106–108. [Google Scholar]
- Alimov, A.; Alimov, E.; Kamanin, A.; Khankin, V.; Pakhomov, N.; Shvedunov, V.; Gryzlov, A.; Lamonov, S.; Musatov, A.; Sigalaev, V. Beam parameters measurement of technological 10 MEV Linac. In Proceedings of the XXI Russian Particle Accelerators Conference (RuPac), Zvenigorod, Russia, 28 September–3 October 2008. [Google Scholar]
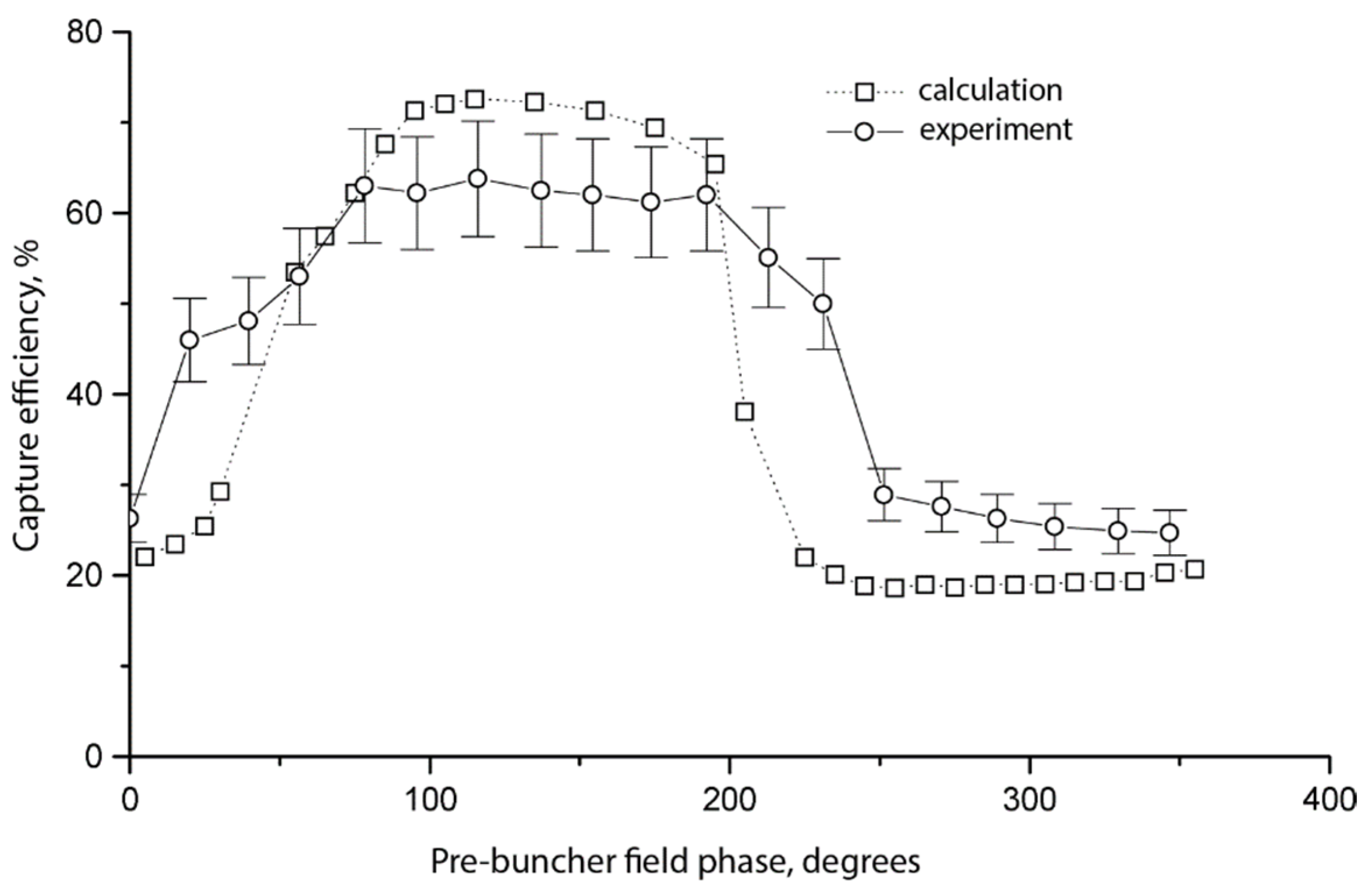
- Setiniyaz, S.; Castilla, A.; McKenzie, J.; Apsimon, R.; Militsyn, B.; Angal-Kalinin, D.; Burt, G. Pushing the capture limit of thermionic gun linacs. Phys. Rev. Accel. Beams 2021, 24, 080401. [Google Scholar] [CrossRef]
- Ermakov, A.N.; Ermakov, D.I.; Ishkhanov, B.S.; Novikov, G.A.; Chepurnov, A.S.; Shvedunov, V.I.; Yailiyan, V.R.; Trower, W.P.; Milovanov, O.S.; Sobenin, N.P.; et al. An Injection and Acceleration System of a Pulsed Race-Track Microtron. Instrum. Exp. Tech. 2002, 45, 482–489. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borisov, M.; Ermakov, A.; Khankin, V.; Kubyshin, Y.; Shvedunov, V. Racetrack Microtron—Pushing the Limits. Symmetry 2021, 13, 2244. https://doi.org/10.3390/sym13122244
Borisov M, Ermakov A, Khankin V, Kubyshin Y, Shvedunov V. Racetrack Microtron—Pushing the Limits. Symmetry. 2021; 13(12):2244. https://doi.org/10.3390/sym13122244
Chicago/Turabian StyleBorisov, Maxim, Andrey Ermakov, Vadim Khankin, Yuri Kubyshin, and Vasiliy Shvedunov. 2021. "Racetrack Microtron—Pushing the Limits" Symmetry 13, no. 12: 2244. https://doi.org/10.3390/sym13122244
APA StyleBorisov, M., Ermakov, A., Khankin, V., Kubyshin, Y., & Shvedunov, V. (2021). Racetrack Microtron—Pushing the Limits. Symmetry, 13(12), 2244. https://doi.org/10.3390/sym13122244






