Abstract
The present research paper considers a three-level atom (3LA) that interacts with a field mode primarily in a photon-added coherent state of Morse potential (PACSMP). The dynamics of entanglement, the photon statistics, and the quantum Fisher information are investigated. The statistics of field photons are discussed by evaluating the Mandel parameter. We check the influence of the energy dissipation and intensity-dependent function. Finally, we detect the relationship between the entanglement, the field’s nonclassical characteristics, and atomic quantum Fisher information throughout the evolution of time. The findings illustrate the important role of the number of added photons and CSMP in affecting the entanglement’s time evolution, the quantum Fisher information, and the Mandel parameter. Based on the obtained results, we reached significant physical phenomena, including the sudden birth and death of the nonlocal correlation between atom-Morse potential field structures.
1. Introduction
The Morse Potential (MP) [1] is considered to be a realistic and simple three-parameter anharmonic potential model. Authors can utilize the MP for certain calculations in many fields, such as spectroscopy [2], as well as diatomic molecule scattering and vibration [3,4,5]. In addition, MP is important in other fields related to quantum optics and in describing the vibrations of polyatomic molecules through the representation of each bond in the molecule [6]). Coherent states of Morse oscillators (CSMP) have been constructed using several techniques. One of these techniques depends on the momentum and position operators selected to make the resultant Hamiltonian system resemble a harmonic oscillator [7]. Furthermore, the CSMP has also been studied in the broad domain of building analytic CSs for comprehensive potentials [8,9].
As known, the CSMP has many important applications in quantum optics and Quantum Information Processing (QIT). The CS is used to build the SO(2, 1) for the Morse oscillator and is written using Green’s function as a path integral over the SO(2, 1) [10]. The CSMP was presented using a novel analytical technique within the operators of annihilation and creation [11,12]. Therefore, the MP method is used to solve many problems in different physical and chemical fields. The CSs associated with the SU(2) realization for the MP was introduced by [13]. In addition, the Klauder coherent state for Morse potential was constructed, and the identity resolution with a positive measure is satisfied [14]. As an extension of this work, the CSMP was constructed based on an SU(2)-like approach [15]. The generalization and Gaussian formula of CSMP was investigated [16]. The dynamics of a quantum system that initially had a four-level atom and a field in the CSMP were introduced, where the nonclassical properties of the field were discussed based on an evaluation of the Mandel parameter [17]. The results showed a strong effect in the nonclassical properties of the field under the form of time-dependent coupling between the CSMP domain and the four-level atom. Moreover, the number of photons added to the CSMP strongly influenced the dynamical performance of the Mandel parameter, geometric phase, and quantum entropy [18].
The use of appropriate measures to estimate some physical quantities leads to an understanding of the behavior of different physical systems [19,20]. Moreover, QIT provides further improvement in the quality of critical information and increases awareness of non-local correlation phenomena. These phenomena perform an important task in relation to QIT and quantum metrology [21,22,23,24,25,26]. The entanglement or the nonlocal correlation can be relied upon at the heart of different implementations of quantum technologies [27,28,29]. Other results for bodies with microstructures can be found in [30,31,32,33]. Additionally, entanglement performs optimal tasks in quantum algorithms and quantum image processing. The present paper considers a generalized model according to the interaction between a three-level atomic system and the field initially prepared for exited state of CSMP. The following is a breakdown of the paper’s structure. The proposed model and its dynamics are introduced in Section 2. Several measures of quantumness are introduced and their dynamical behaviors are investigated, such as the atomic population, the degree of entanglement, the quantum Fisher information, and the Mandel parameter, in Section 3, Section 4, Section 5, and Section 6, respectively. The final part contains the conclusions.
2. 3LA System and Its Dynamics
We consider an extension of the -type of 3LA system combined with a mode field with an intensity-dependent coupling and energy dissipation effects. The extended Hamiltonian system is represented as
In Equation (1), the 3LA contains a two photon transitions between the upper level and the middle level . The operators and that denote the field’s operators of annihilation and creation, and defines the atomic operators. In addition, and denote the field–atom coupling constants. The transition between the lower atomic level and the middle atomic level is achieved by one photon. Finally, the transition among levels and are dipole forbidden. The intensity-dependent function rely on the photon number [34]. We assume that the coefficients of coupling between the mode field and 3LA are equal, represented as . This also helps in defining the effect of energy dissipation on the considered structure through the nonzero value of the parameter .
Moreover, the 3LA system, which is at in its upper state and in the field, undergoes arrangement in the PACSMP as
where is the Gamma function, is the number of added photons to the coherent state of MP and is the greatest integer, which is less than or equal to N.
The 3LA-field system is evaluated using the time-dependent form Schrödinger equation, presented as
The bipartite system wave function at t = 0 is assumed to take the form
The final 3LA-field state at any time is formulated as
Under the Hamiltonian system (1) and substituting in the Schrödinger Equation (4), we can obtain a three-coupled ODE
The reduced density operator , based on 3LA-field state, is written as
in which the diagonal components of the reduced density matrix describe the probabilities of the atomic occupation at the levels of , and u. As the reduced atomic density (8) was obtained, the other quantities related to the dynamical performance of the degree of entanglement, the quantum Fisher information, and the photon statistics of the field can be investigated [35].
To quantify the entanglement between 3LA and the field in the PACSMP, we examine the entanglement based on the evolution of von Neumann entropy [36]
Hence, the entanglement amount of the 3LA-field state takes the form
where ϖj denotes the density operator’s eigenvalues (8) to satisfy the 3rd-order equation
where
Equation (11) is thought to contain three dissimilar real roots introduced through
where
3. The Atomic Population
In this section, the discovery of periods of revival and collapse is explored. The collapse and revival periods are characterized using their association with the entanglement of field and qubits [37,38,39]. In addition, the impact of the function of deformation and the parameter of decay on the collapse and revival periods are examined.
At first, exclude the deformation and the dissipation parameter , and the periods of revival and collapse are generated clearly and repeatedly. Furthermore, the amplitude of the oscillations decreases with increasing time. The amplitude of the oscillations decreases after taking into account the decay parameter . Moreover, the atomic population gradually collapses over time and reaches a stable state (separable state) following a period of time, see Figure 1a. The concentration of oscillation decreases significantly after the function of deformation is included in the interaction cavity. The revival and collapse periods are markedly achieved, which reflects the effect of the deformation function on the atomic population. The atomic population function decays gradually with increasing time. The population function needs a longer time than the previous case to reach the stable state, see Figure 1b. To study the effect of multiple the addition of photons, set k as 5 and neglect the deformation function and decay term. The oscillations are formed concentrically, and the termination period is slightly increased compared to the case of a single photon. As usual, the oscillations decrease slowly after considering the decay parameter, see Figure 1c. The collapse periods disappear after the deformation function is taken into account, and the amplitudes of the oscillations upsurge within the revival periods. Fluctuations appear chaotically in periods of collapse, which reflects the effect of the strong deformation function on the population. In this case, the dissipation effect on the population decreases, and the population function declines with increasing time and reaches a stable state after long periods, see Figure 1d.
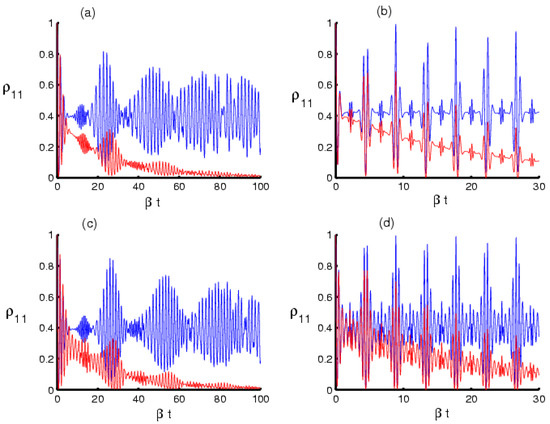
Figure 1.
The time evolution of the atomic population probability of a 3LA interaction with the field of radiation within PACSMP (photon-added coherent state of Morse potential) where the MP parameter . The is plotted, with and without the coupling and depending on the intensity, as for (a,c) and for (b,d) respectively. In addition, in (c,d), the same conditions as (a,b) apply but for the addition of five photons to the CSMP (i.e., k = 5). The blue (red) curves represent the absence (presence ) of the energy dissipation effect .
4. The Degree of Entanglement
Because it is widely applicable in the field of information technology, including teleportation and certain quantum cryptographic protocols [40,41,42], the entanglement between the quantum systems’ parts is of great concern within quantum information. Therefore, we devote this section to studying the effect of the deformation and dissipation function on the entanglement between the field and the atom.
Neglecting the deformation and dissipation function, Figure 2a shows that a strong entanglement was formed in the collapse period, while the entanglement decreased before and after the revival periods’ center. The entanglement gradually decayed after adding the dissipation parameter. The field–atom entanglement reached a state of separation (pure state) after a while. Figure 2b shows the impact of the deformation function on the field–atom entanglement. Strong entanglement was generated periodically. The von Neumann formula achieved the highest value within the middle of the collapse periods, while it reached its lowest ones at the middle of the revival periods. The entanglement improved more noticeably over time. In fact, the Morse potential was a finite state and, therefore, was different from the coherent state (infinitely dimensional), so the deformation function had a clear effect on the field cavity. Moreover, the entanglement improved by increasing the number of levels; thus, the entanglement between a domain and a three-level atom was better than that of a two-level atom [42]. The entanglement decreased after considering the dissipation, and it reached the state of separation quickly compared to the previous case. For the multi-photon addition state, there was never a strong effect on the field–atom entanglement. Therefore, the entanglement never improved after taking k = 5 into account, see Figure 2c, while the effect of deformation on entanglement in the case of multi-photon addition was clearly demonstrated. Moreover, the dissipation effect was weak on the entanglement, so the function needed a long time to reach the separation state, as shown in Figure 2d.
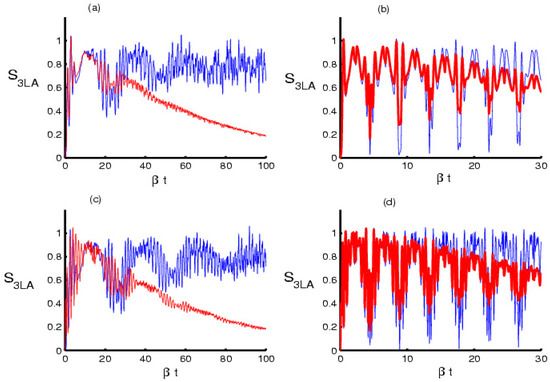
Figure 2.
The time evolution of the entanglement degree measured by the von Neumann entropy with identical values and parameters to Figure 1.
5. Quantum Fisher Information Dynamics
The dynamics of the quantum Fisher information (QFI) for the atomic density matrix was evaluated for phase shift parameter as [43,44,45]. The dynamics of the atomic density matrix within the estimator depended on the initial 3LA-field state .
The quantum Fisher information is the QFI is given by
in which denotes the symmetric logarithmic derivative operator satisfying [46]
and has the spectral decomposition
The classical Fisher information based on Equation (15) is given by
Then, the QFI is related to the classical Fisher information by
where the second one defines its quantum counterpart.
Figure 3a describes the Fisher information without both the dissipation and the deformation function. There is a monotonic relation between von Neumann formula and Fisher information function. The maximum and minimum values are met symmetrically. Therefore, we noticed that the Fisher information function quickly achieved the lowest values after taking the dissipation into account. When the deformation role was activated, the field–atom entanglement was improved, and the minimum and maximum values were regularly achieved. These oscillations were gradually erased following the inclusion of the dissipation term of the interaction cavity. The function reached a stable state after a short period, as shown in Figure 3b. The value of k was set to 5 to activate the role of the multi-photon addition. The Fisher information was slightly affected in the multi-photon case. This result confirms that which was obtained from the von Neumann formula, namely that there was no effect of multi-photons on field-qubit entanglement, as seen in Figure 3c. The entanglement was clearly improved after taking into account the deformation function. This entanglement was erased after taking the dissipation into account. The Fisher information function reached a stable state after a short time, as shown in Figure 3d.
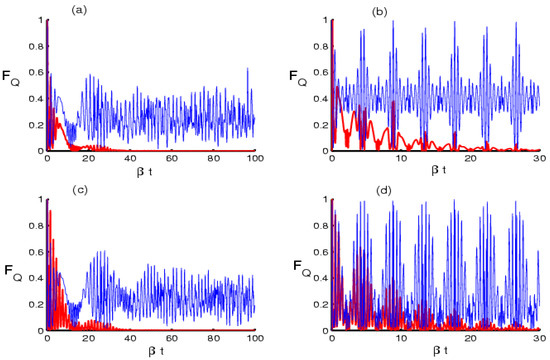
Figure 3.
The time evolution of the quantum Fisher information for with the same values and parameters as Figure 1.
6. Photon Statistics and Mandel Parameter
The photon statistics and nonclassical properties of field photons are detected by the Mandel parameter. This detection depends on the comparison with Glauber’s coherent states during the time evolution. The Mandel’s parameter concerning as [47,48]
The statistical properties of the field can be characterized according to the value of as follows: For , the field is Poissonian photon number distribution, while the field states are sub-Poissonian for . It will be super-Poissonian for .
At this point, we begun to analyze the behavior of photon distribution for some different values of system parameters. After neglecting the effect of deformation and dissipation, a non-classical distribution was formed in most of the interaction periods. With the exception of some points, the case reached the Poisson distribution. The state changed entirely to a classical distribution after taking the dissipation into account, see Figure 4a. In general, when deformation was considered, a non-classical distribution was generated. There were also short periods of classical distribution. In all cases, a clearly classical distribution was generated after taking the dissipation into account. This result confirms that the dissipation generated a strong classical distribution, as shown in Figure 4b. After considering the multi-photon addition, the state began with a non-classical distribution that quickly faded into a classical distribution. The non-classical state increased after adding the dissipation parameter to the reaction, as seen in Figure 4c. The periods of the non-classical state increased dramatically when the deformation function was included, while this state was erased if the deformation was taken into account and turned into a purely classical state, as shown in Figure 4d.
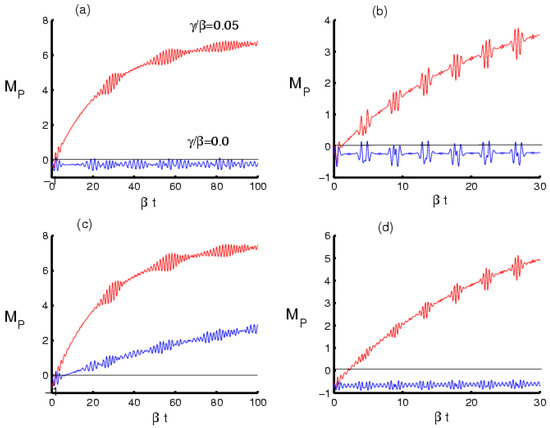
Figure 4.
The time evolution of the Mandel parameter MP with identical values and parameters as Figure 1.
7. Summary
The previous sections explored the interaction of a triple-level atom with a single-mode field prepared in a photon-added coherent state of Morse potential. The effects of the deformation function and dissipation term on the atomic population and entanglement using the von Neumann formula, the Fisher information, and the distribution of photons were studied. The inclusion of the deformation function in the interaction cavity caused a clear increase in periods of collapse and revival. Moreover, the oscillation intensity increased, and the collapse phenomenon disappeared after considering the addition of multi-photons in the atomic population. The oscillations gradually decayed after taking the dissipation into account. The entanglement improved after taking into account the deformation function, while the entanglement was not affected after the addition of multi-photons. The entanglement was erased after dissipation was taken into account. The non-classical distribution improved when the deformation function was added to the interaction, while the distribution changed from non-classical to classical after taking into account the multi-photon addition. The dissipation generated a strong classical distribution, and the non-classical distribution appeared only at the beginning of the interaction period.
Author Contributions
Conceptualization, E.M.K. and S.A.-K.; methodology, H.A.; software, E.M.K.; validation, S.M.A.-D. and E.E.M.; formal analysis, M.H.; investigation, S.A.-K.; resources, M.M.; data curation, E.M.K.; writing—review and editing, E.M.K.; visualization, S.A.-K.; supervision, M.M.; project administration, S.M.A.-D.; funding acquisition, H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research, Taif University, KSA (research group number 1-1441-105).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was funded by the Deanship of Scientific Research, Taif University, KSA (research group number 1-1441-105). The authors thank to the anonymous referees for their useful comments which contributed to the improvement of our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morse, P.M. Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Sage, M.L. Energetics, wave functions, and spectroscopy of coupled anharmonic oscillators. Chem. Phys. 1978, 35, 375. [Google Scholar] [CrossRef]
- Popov, D.; Zaharie, I.; Dong, S.-H. Photon-added coherent states for the Morse oscillator. Czechoslov. J. Phys. 2006, 56, 157–176. [Google Scholar] [CrossRef]
- Vasan, V.S.; Cross, R.J. Matrix elements for Morse oscillators. J. Chem. Phys. 1983, 78, 3869–3871. [Google Scholar] [CrossRef]
- Tipping, R.H.; Ogilvie, J.F. Expectation values for Morse oscillators. J. Chem. Phys. 1983, 79, 2537–2540. [Google Scholar] [CrossRef]
- Iachello, F.; Oss, S. Flux dynamics and the growth of the superconducting phase. Phys. Rev. Lett. 1991, 66, 2946. [Google Scholar]
- Nieto, M.M.; Simmons, L.M. Eigenstates, coherent states, and uncertainty products for the Morse oscillator. Phys. Rev. A 1979, 19, 438–444. [Google Scholar] [CrossRef]
- Nieto, M.M. Coherent states for general potentials. V. Time evolution. Phys. Rev. D 1980, 22, 403. [Google Scholar] [CrossRef]
- Nieto, M.M.; Simmons, L.M. Coherent states for general potentials. I. Formalism. Phys. Rev. D 1979, 20, 1321. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Gerry, C.C. Coherent states and a path integral for the Morse oscillator. Phys. Rev. A 1986, 33, 2207–2211. [Google Scholar] [CrossRef]
- Drag, G.E.; Avram, N.M. Creation and annihilation operators for the Morse oscillator and the coherent states. Can. J. Phys. 1998, 76, 273. [Google Scholar]
- Dong, S.-H. The SU(2) realization for the Morse potential and its coherent states. Can. J. Phys. 2002, 80, 129–139. [Google Scholar] [CrossRef]
- Quesne, C. Deformed Shape Invariant Superpotentials in Quantum Mechanics and Expansions in Powers of ℏ. Symmetry 2020, 12, 1853. [Google Scholar] [CrossRef]
- Belfakir, A.; Hassouni, Y.; Curado, E.M.F. Construction of coherent states for Morse potential: A su(2)-like approach. Phys. Lett. A 2020, 384, 126553. [Google Scholar] [CrossRef]
- Angelova, M.N.; Hussin, V. Squeezed coherent states and the one-dimensional Morse quantum system. J. Phys. A Math. Theor. 2012, 45, 244007. [Google Scholar] [CrossRef] [Green Version]
- Alqannas, H.S.; Abdel-Khalek, S. Physical and nonclassical properties of the interaction between a four-level atom and field in coherent state of Morse potential. Opt. Quantum Electron. 2019, 51, 50. [Google Scholar] [CrossRef]
- Alsahhaf, M.A.; Aldaghfag, S.A.; Abdel-Khalek, S. Physical Properties, Field Purity, and Quantum Phase for a Two-Level Atom in Photon-Added Coherent States for the Morse Potential. J. Russ. Laser Res. 2017, 38, 437–445. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Yoshihisa, Y.; Kouichi, S. Principles and Methods of Quantum Information Technologies: Lecture Notes in Physics; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Alber, G.; Beth, T.; Horodecki, M.; Horodecki, P.; Horodecki, R.; Rtteler, M.; Weinfurter, H.; Zeilinger, A. Quantum Information; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press (CUP): Cambridge, UK, 2004. [Google Scholar]
- Bigelow, N.P.; Eberly, J.H.; Stroud, C.R., Jr.; AWalmsley, I. Introductory Quantum Optics. In Proceedings of the Eighth Rochester Conference on Coherence and Quantum Optics, Rochester, NY, USA, 13–16 June 2001. [Google Scholar]
- de Faria, J.G.P.; Nemes, M.C. Dissipative dynamics of the Jaynes-Cummings model in the dispersive approximation: Analytical results. Phys. Rev. A 1999, 59, 3918–3925. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Ooi, R. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86, 033823. [Google Scholar] [CrossRef] [Green Version]
- Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef] [Green Version]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum Metrology with Entangled Coherent States. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Marin, M. A domain of influence theorem for microstretch elastic materials. Nonlinear Anal. Real World Appl. 2010, 11, 3446–3452. [Google Scholar] [CrossRef]
- Marin, M.; Agarwal, R.P.; Mahmoud, S.R. Modeling a microstretch thermo-elastic body with two temperatures. Abstr. Appl. Anal. 2013, 2013, 583464. [Google Scholar] [CrossRef] [Green Version]
- Abbas, I.A.; Marin, M. Analytical Solutions of a Two-Dimensional Generalized Thermoelastic Diffusions Problem Due to Laser Pulse. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 57–71. [Google Scholar] [CrossRef]
- Marin, M.; Othman, M.I.A.; Seadawy, A.R.; Carstea, C. A domain of influence in the Moore–Gibson–Thompson theory of dipolar bodies. J. Taibah. Univ. Sci. 2020, 14, 653–660. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Establishment of an entangled atom-field state in the Jaynes-Cummings model. Phys. Rev. A 1991, 44, 6023–6029. [Google Scholar] [CrossRef]
- Abdel-Aty, M. Quantum field entropy and entanglement of a three-level atom two-mode system with an arbitrary nonlinear medium. J. Mod. Opt. 2003, 50, 161–177. [Google Scholar] [CrossRef]
- Jamal Anwar, S.; Ramzan, M.M. Usman and M. Khalid Khan Entanglement Dynamics of Three and Four Level Atomic System under Stark Effect and Kerr-Like Medium. Quantum Rep. 2019, 1, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Abdalla, M.S.; Khalil, E.; Obada, A.S.-F.; Peřina, J.; Křepelka, J. Quantum statistical characteristics of the interaction between two two-level atoms and radiation field. Eur. Phys. J. Plus 2015, 130, 1–19. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Khalil, E.M.; Ahmed, M. Generation of a nonlinear two-mode Stark shift through the adiabatic elimination method. J. Mod. Opt. 2006, 53, 1149–1163. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Thermodynamics and the measure of entanglement. Phys. Rev. A 1997, 56, R3319–R3321. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Brassard, G. WITHDRAWN: Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2011, 175, 8. [Google Scholar] [CrossRef]
- Kak, S. A Three-Stage Quantum Cryptography Protocol. Found. Phys. Lett. 2006, 19, 293–296. [Google Scholar] [CrossRef] [Green Version]
- Abdalla, M.S.; Khalil, E.; Obada, A.-F. Quantum effect of the Kerr-like medium in terms of SU(1,1) Lie group in interaction with a two-level atom. Phys. A Stat. Mech. Its Appl. 2017, 466, 44–56. [Google Scholar] [CrossRef] [Green Version]
- Amari, S.-I.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2007; Volume 191. [Google Scholar]
- Abdel-Khalek, S. Quantum Fisher information flow and entanglement in pair coherent states. Opt. Quantum Electron. 2014, 46, 1055–1064. [Google Scholar] [CrossRef]
- Abu-Zinadah, H.H.; Abdel-Khalek, S. Fisher information and quantum state estimation of two-coupled atoms in presence of two external magnetic fields. Results Phys. 2017, 7, 4318–4323. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Gill, R.D.; Jupp, P. On quantum statistical inference. J. R. Stat. Soc. Ser. B Stat. Methodol 2003, 65, 775–804. [Google Scholar] [CrossRef] [Green Version]
- Mandel, L. Sub-Poissonian photon statistics in resonance fluorescence. Opt. Lett. 1979, 4, 205–207. [Google Scholar] [CrossRef] [PubMed]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).